Virtual Inertia Implemented by Quasi-Z-Source Power Converter for Distributed Power System
Abstract
:1. Introduction
- Modeling and analyzing a single-area power system with a synchronous generator, a grid-connected power converter, and different types of loads;
- Developing a virtual synchronous generator control strategy for an inverter to simulate the AC grid and provide grid support;
- Designing a virtual inertia scheme based on the energy stored in the DC-link capacitors of the quasi-Z-source power converter, and deriving the control parameters for the quasi-Z-source side and the AC side;
- Simulating and experimenting with the proposed virtual inertia control strategy using Matlab/Simulink software and a 1 kW prototype.
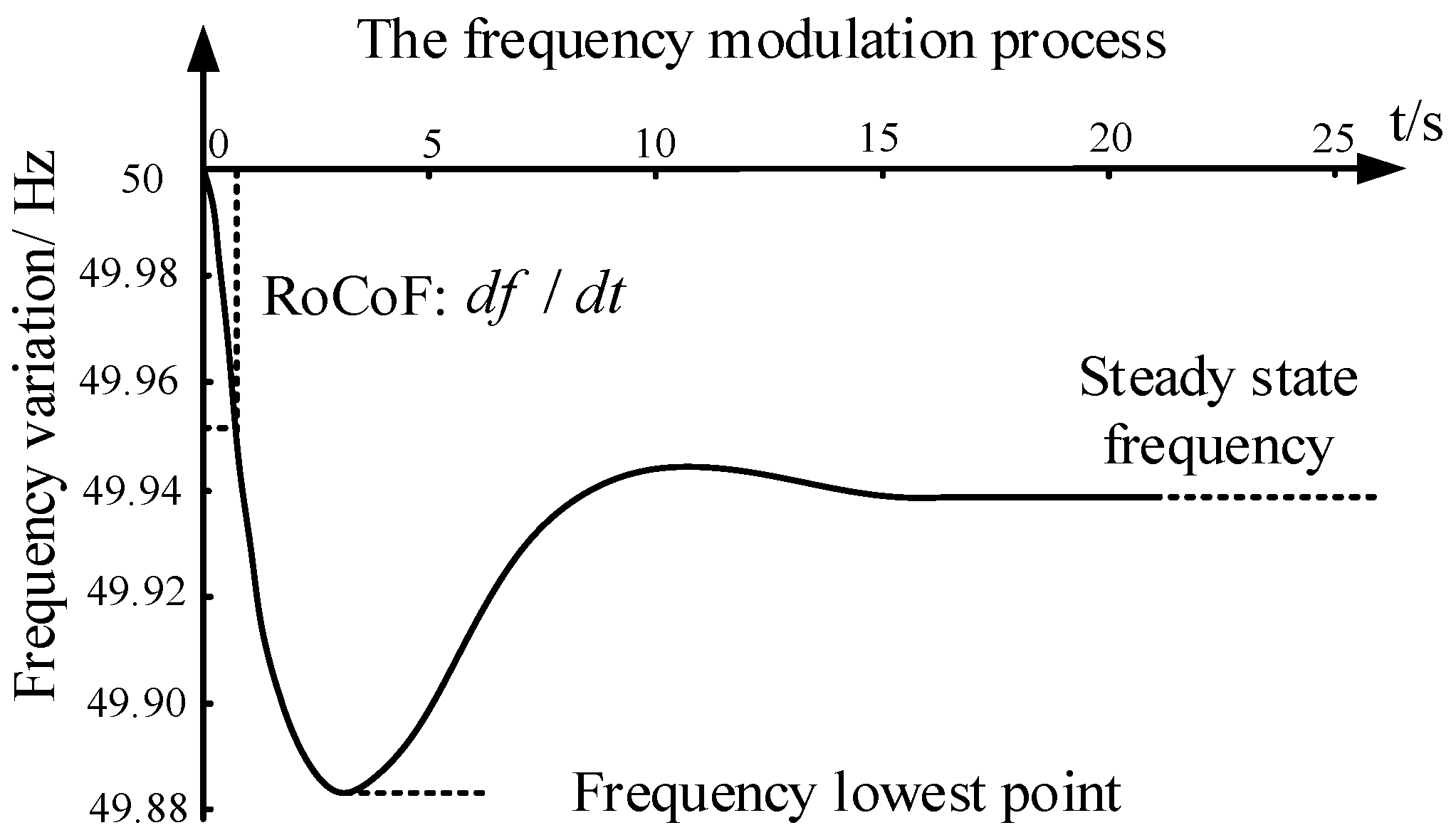
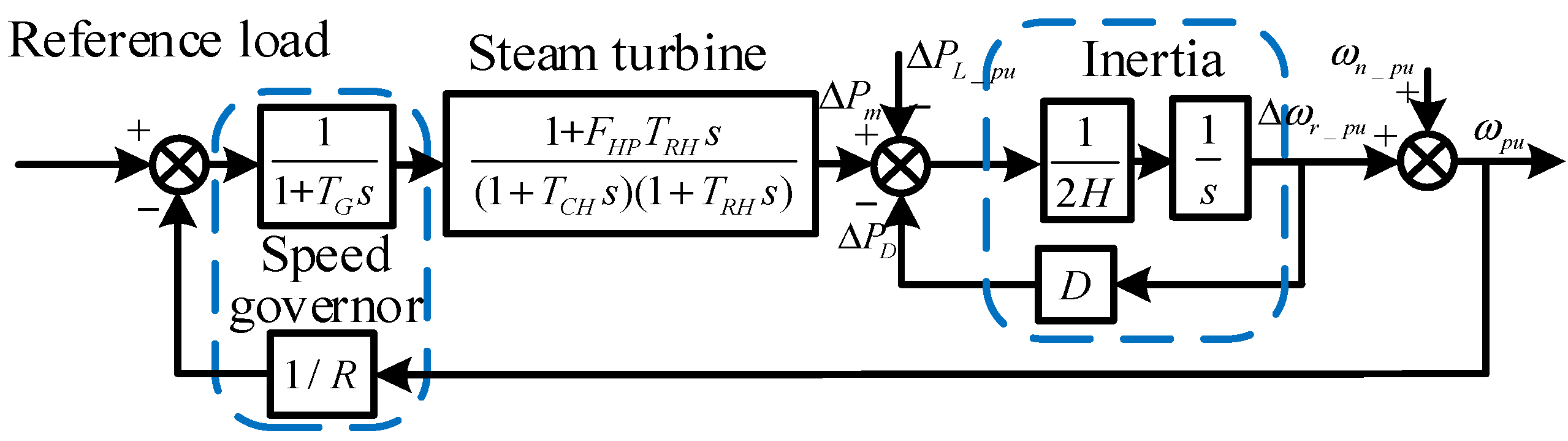
2. Effect of Inertia on Frequency Regulation of Power Systems
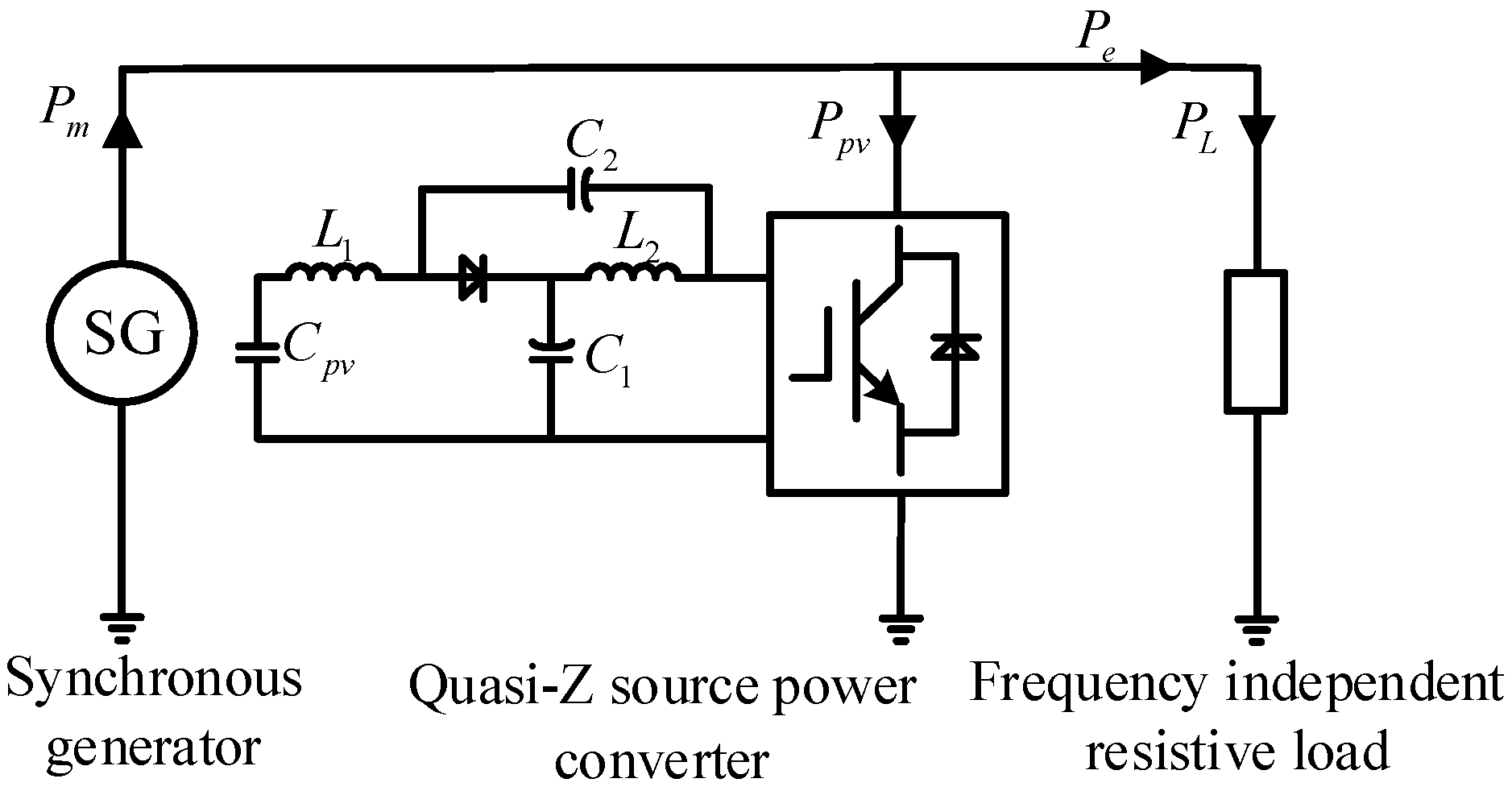
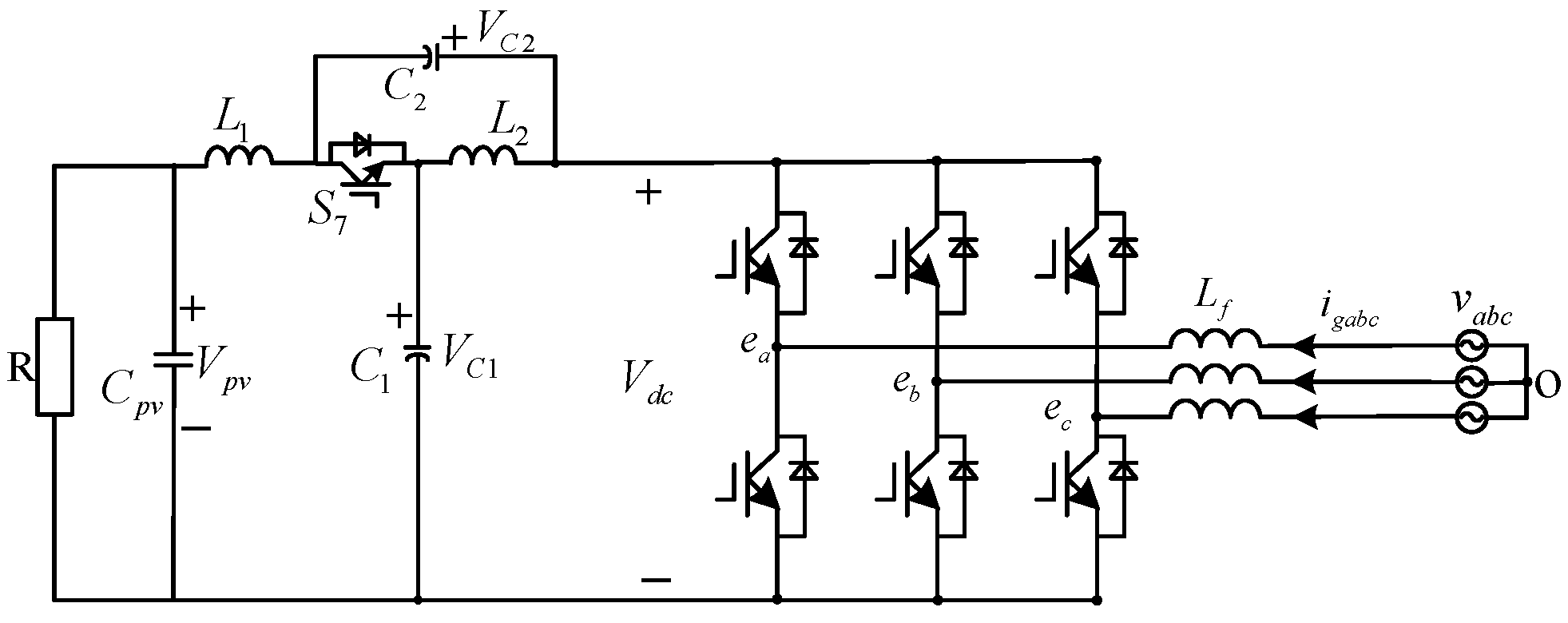
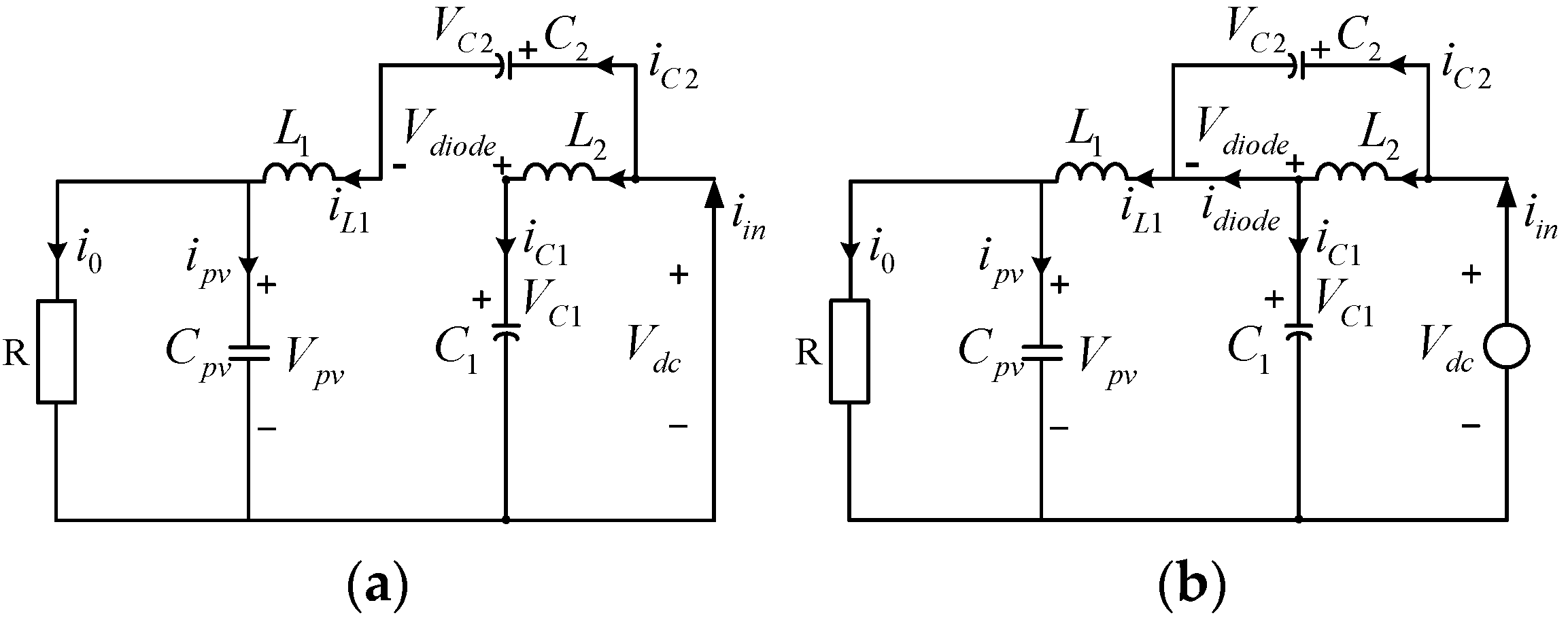
3. Analysis of Quasi-Z-Source Power Converter
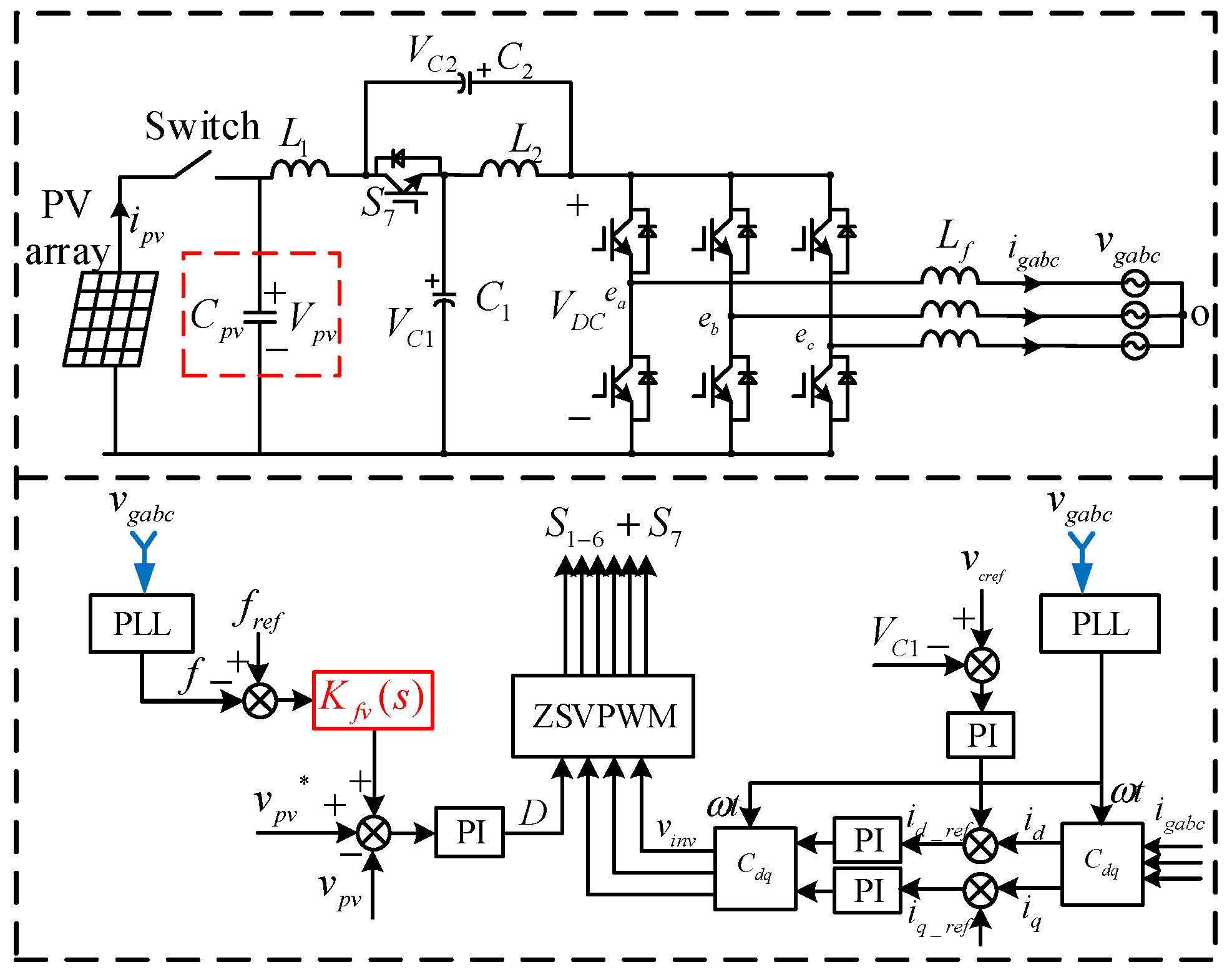
4. Virtual Inertia Control Strategy
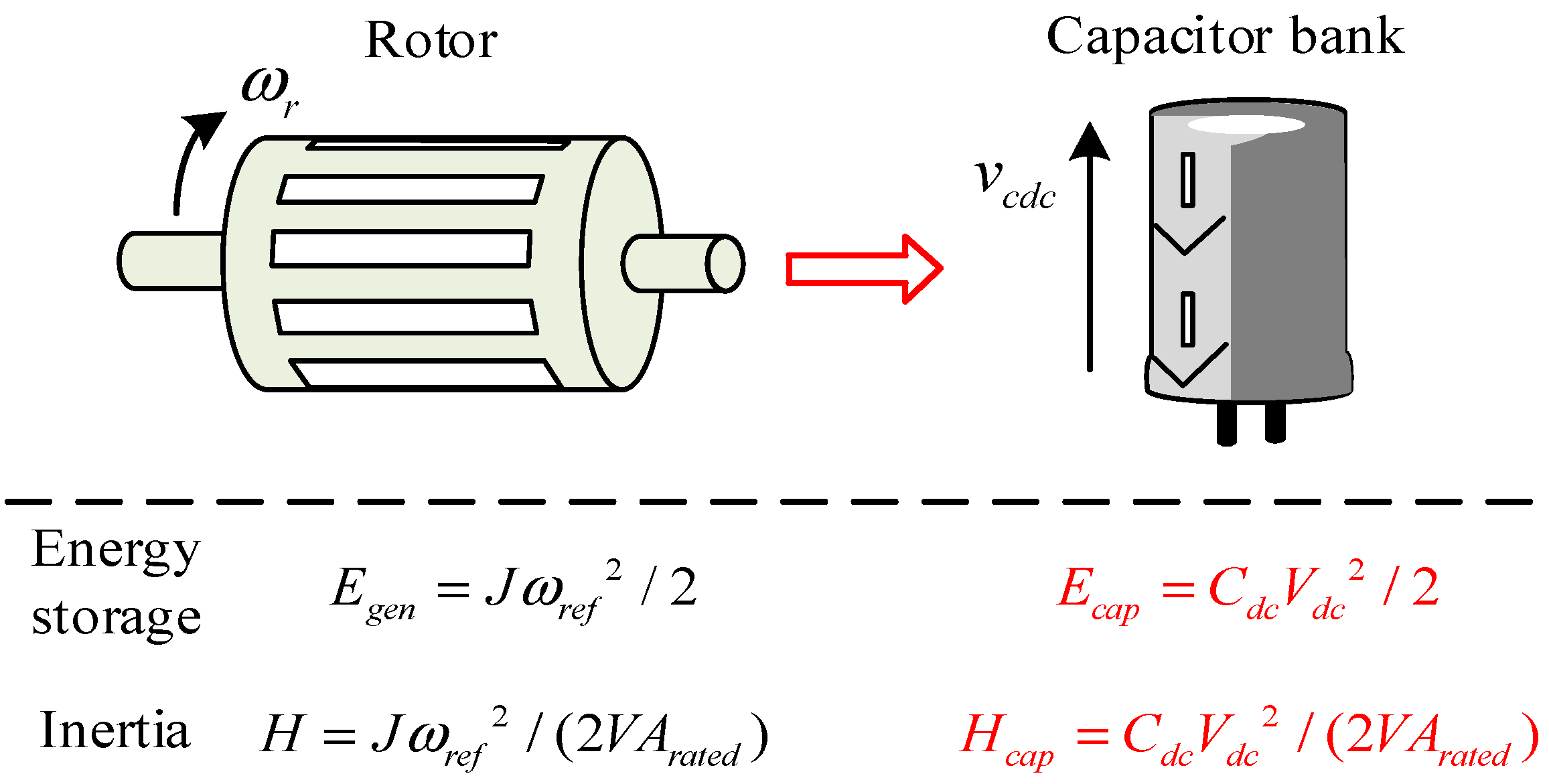
4.1. Mapping of Capacitors to Motor Rotors
4.2. Quasi-Z-Source Power Converter with Virtual Inertia Strategy
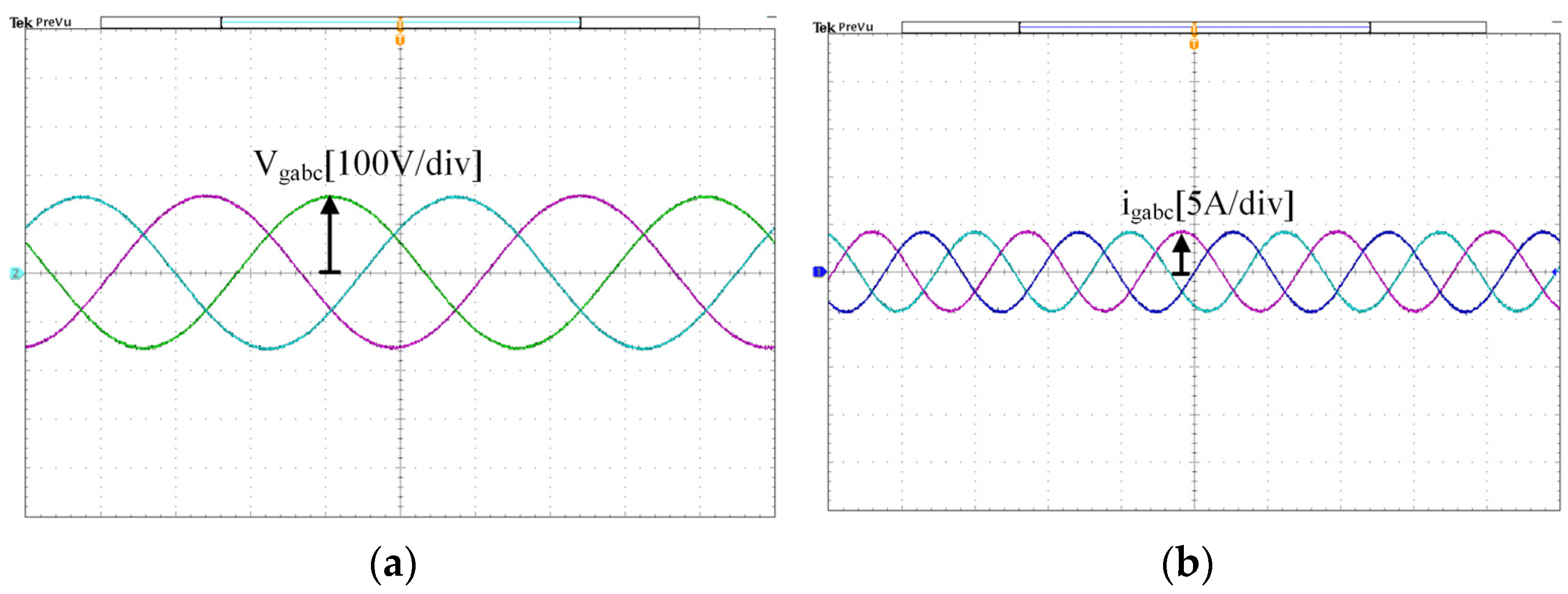
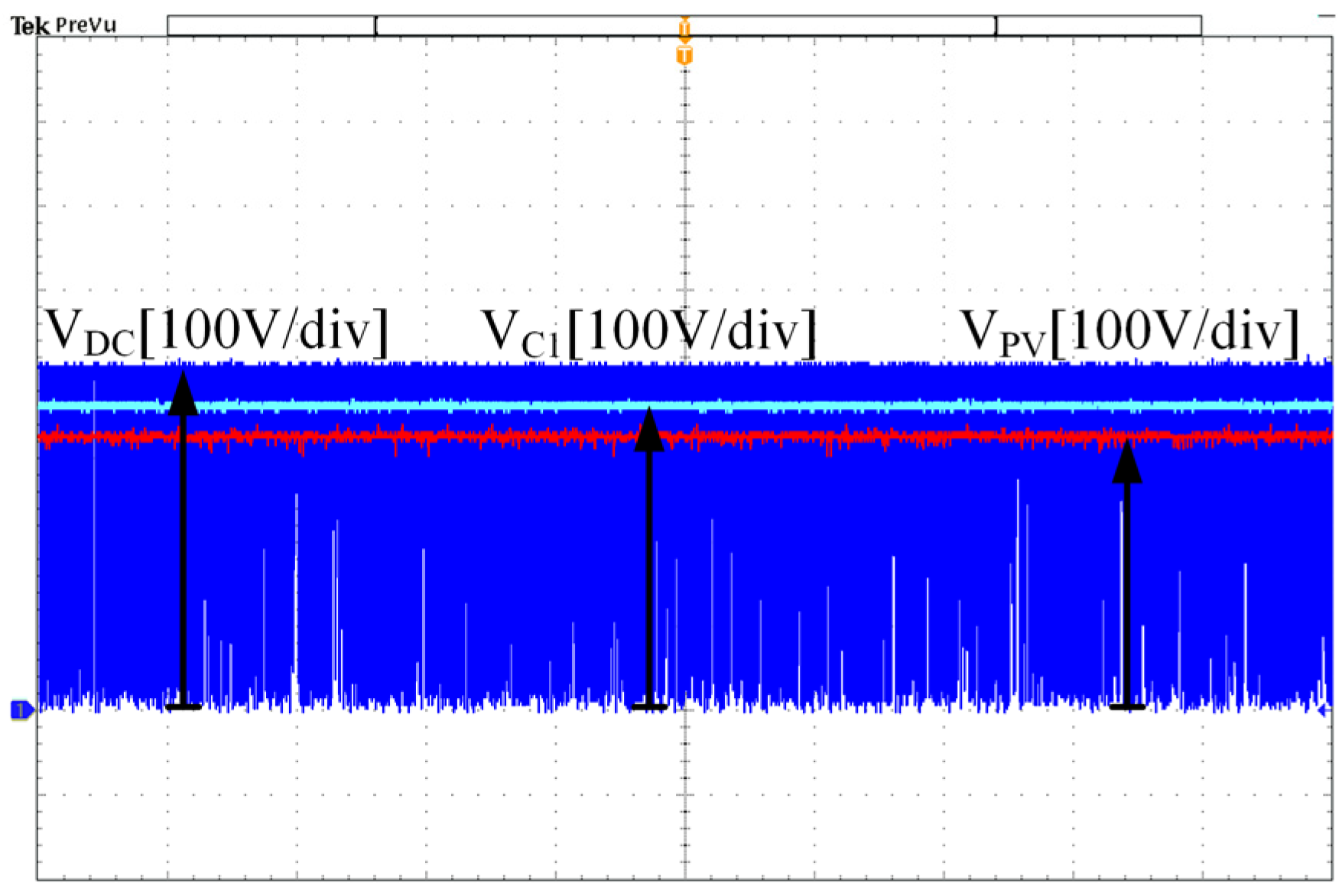
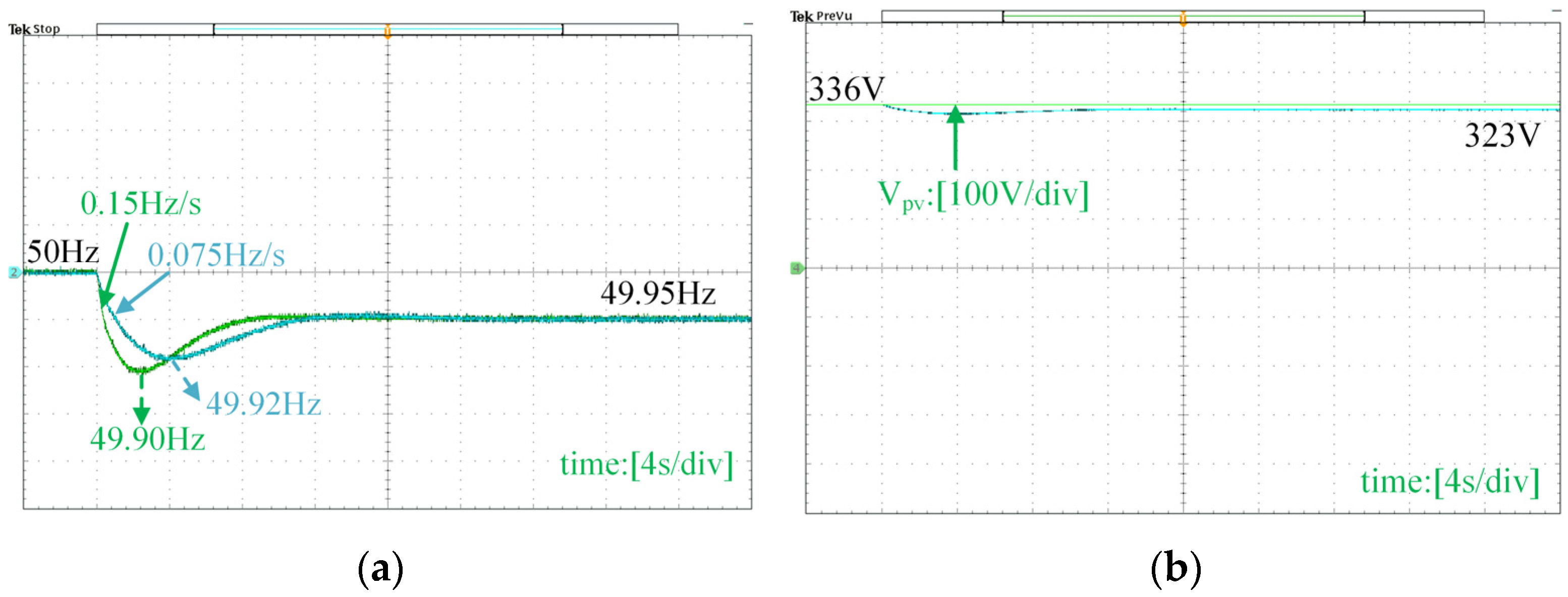
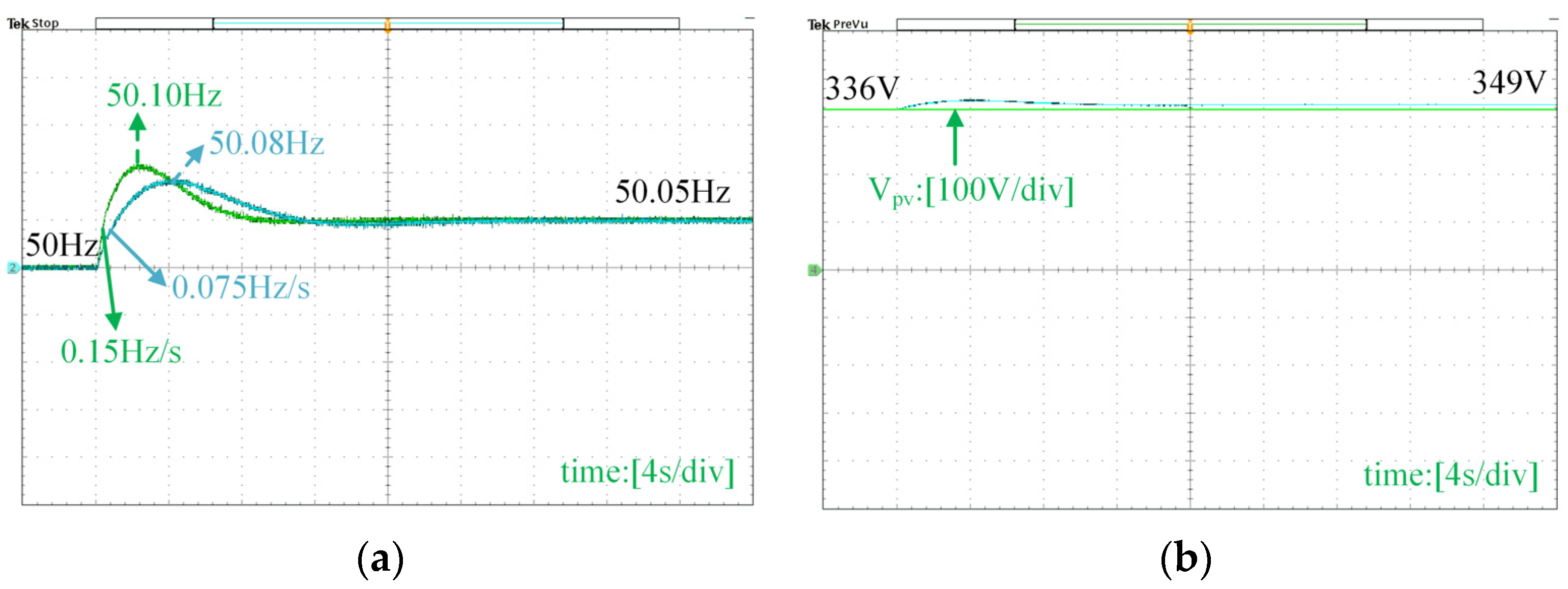
5. Simulation and Experiment Verification
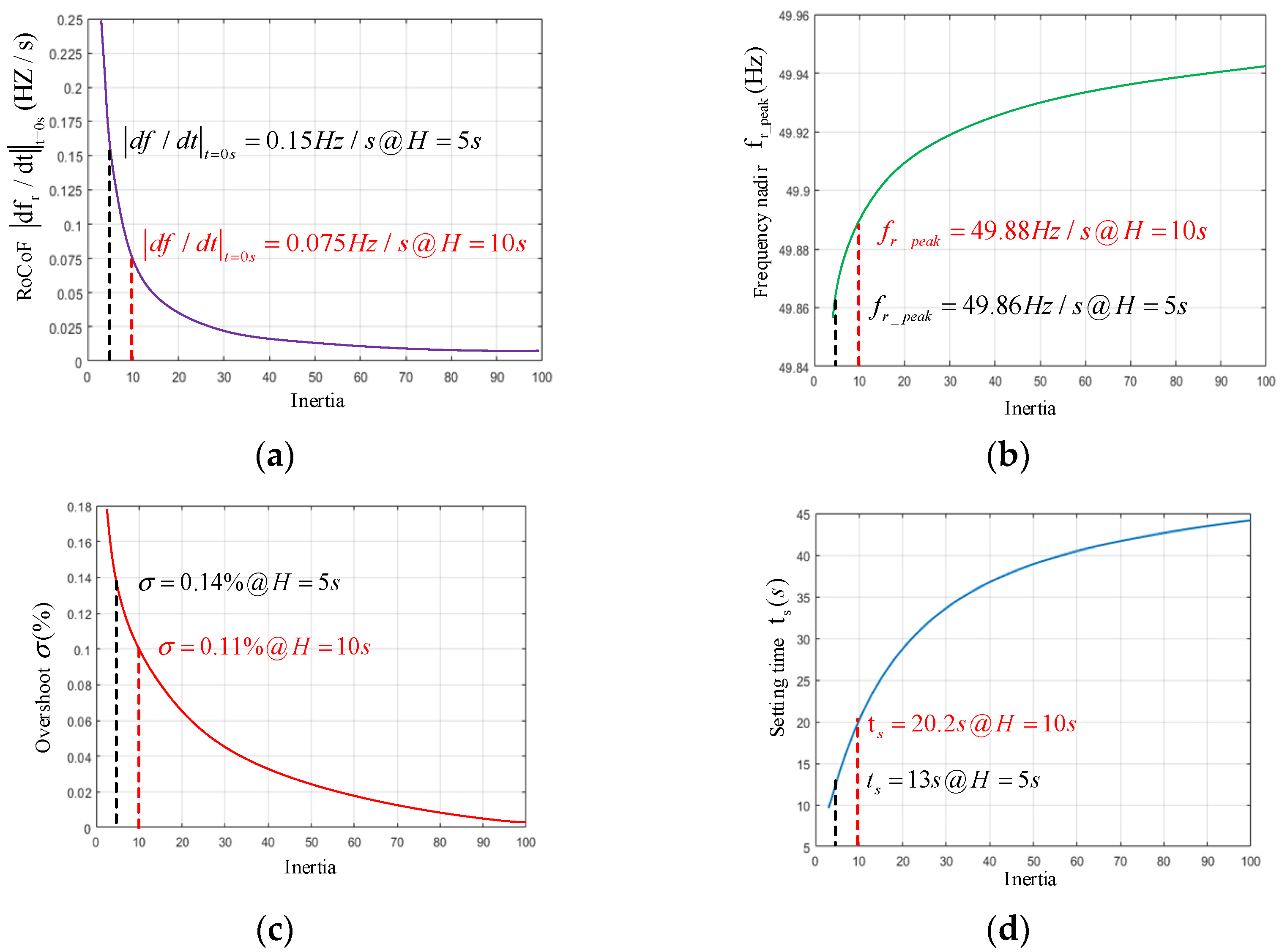
5.1. Simulation Results
5.2. Experiment Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jurasz, J.; Canales, F.; Kies, A.; Guezgouz, M.; Beluco, A. A review on the complementarity of renewable energy sources: Concept, metrics, application and future research directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
- Zongxiang, L.; Haiyan, T.; Ying, Q.; Xinshou, T.; Yongning, C. The impact of power electronics interfaces on power system frequency control: A review. Electr. Power 2018, 51, 51–58. [Google Scholar]
- Bera, A.; Chalamala, B.R.; Byrne, R.H.; Mitra, J. Sizing of energy storage for grid inertial support in presence of renewable energy. IEEE Trans. Power Syst. 2021, 37, 3769–3778. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the inertia of future more-electronics power systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 2130–2146. [Google Scholar] [CrossRef]
- Liu, F.; Liu, Z.; Mei, S.; Wei, W.; Yao, Y. ESO-based inertia emulation and rotor speed recovery control for DFIGs. IEEE Trans. Energy Convers. 2017, 32, 1209–1219. [Google Scholar] [CrossRef]
- Liu, R.; Wang, Z.; Xing, H. Virtual inertia control strategy for battery energy storage system in wind farm. In Proceedings of the 2019 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Macao, China, 1–4 December 2019; pp. 1–5. [Google Scholar]
- Yan, W.; Wang, X.; Gao, W.; Gevorgian, V. Electro-mechanical modeling of wind turbine and energy storage systems with enhanced inertial response. J. Mod. Power Syst. Clean Energy 2020, 8, 820–830. [Google Scholar] [CrossRef]
- Martínez, J.C.; Gómez, S.A.; Amenedo, J.L.R.; Alonso-Martínez, J. Analysis of the frequency response of wind turbines with virtual inertia control. In Proceedings of the 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2020; pp. 1–6. [Google Scholar]
- Zhang, X.; Yang, L.; Zhu, X. Virtual rotational inertia control of PV generation system with energy storage devices. Electr. Power Autom. Equip. 2017, 37, 109–115. [Google Scholar]
- You, F.; Si, X.; Dong, R.; Lin, D.; Xu, Y.; Xu, Y. A State-of-Charge-Based Flexible Synthetic Inertial Control Strategy of Battery Energy Storage Systems. Front. Energy Res. 2022, 10, 908361. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, R.; Li, H.; Tang, Y. Frequency derivative-based inertia enhancement by grid-connected power converters with a frequency-locked-loop. IEEE Trans. Smart Grid 2018, 10, 4918–4927. [Google Scholar] [CrossRef]
- Karrari, S.; Baghaee, H.R.; Carne, G.D.; Noe, M.; Geisbuesch, J. Adaptive inertia emulation control for high-speed flywheel energy storage systems. IET Gener. Transm. Distrib. 2020, 14, 5047–5059. [Google Scholar] [CrossRef]
- Tian, B.; Gu, Y.; Wang, F.; Wang, X.; Yang, X. Virtual inertia dynamic control simulation model for renewable energy generation system. Renew. Energy 2018, 36, 1692–1696. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Tang, Y.; Li, H. Design of virtual synchronous generators with enhanced frequency regulation and reduced voltage distortions. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1412–1419. [Google Scholar]
- Shi, K.; Ye, H.; Song, W.; Zhou, G. Virtual inertia control strategy in microgrid based on virtual synchronous generator technology. IEEE Access 2018, 6, 27949–27957. [Google Scholar] [CrossRef]
- Wu, X.; Wei, Q. Virtual synchronous machine rotor angle droop control using virtual reactance. Electr. Technol. 2020, 21, 31–36. [Google Scholar]
- Chen, D.; Xu, Y.; Huang, A.Q. Integration of DC microgrids as virtual synchronous machines into the AC grid. IEEE Trans. Ind. Electron. 2017, 64, 7455–7466. [Google Scholar] [CrossRef]
- Shadoul, M.; Ahshan, R.; AlAbri, R.S.; Al-Badi, A.; Albadi, M.; Jamil, M. A comprehensive review on a virtual-synchronous generator: Topologies, control orders and techniques, energy storages, and applications. Energies 2022, 15, 8406. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual inertia: Current trends and future directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef]
- Zheng, X.; Liu, Y.; Pang, S.; Liu, Z.; Li, Y.; Wang, C. Sliding mode combined VSG control to microgrid inverters. In Proceedings of the IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; pp. 2453–2456. [Google Scholar]
- Yan, X.; Wang, C.; Wang, Z.; Ma, H.; Liang, B.; Wei, X. A united control strategy of photovoltaic-battery energy storage system based on voltage-frequency controlled VSG. Electronics 2021, 10, 2047. [Google Scholar] [CrossRef]
- Babaei, E.; Abu-Rub, H.; Suryawanshi, H.M. Z-source converters: Topologies, modulation techniques, and application–part I. IEEE Trans. Ind. Electron. 2018, 65, 5092–5095. [Google Scholar] [CrossRef]
- Babae, E.; Suryawanshi, H.M.; Abu-Rub, H. Z-source converters: Topologies, modulation techniques, and applications—Part II. IEEE Trans. Ind. Electron. 2018, 65, 8274–8276. [Google Scholar] [CrossRef]
- Jeyasudha, S.; Geethalakshmi, B.; Saravanan, K.; Kumar, R.; Son, L.H.; Long, H.V. A novel Z-source boost derived hybrid converter for PV applications. Analog Integr. Circuits Signal Process. 2021, 109, 283–299. [Google Scholar] [CrossRef]
- Kundur, P.S.; Malik, O.P. Power System Stability and Control; McGraw-Hill Education: New York, NY, USA, 2022. [Google Scholar]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed power system virtual inertia implemented by grid-connected power converters. IEEE Trans. Power Electron. 2017, 33, 8488–8499. [Google Scholar] [CrossRef]
- Konga, C.K.; Gitau, M. Three-phase quasi-Z-source rectifier modeling. In Proceedings of the 2012 Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 February 2012; pp. 195–199. [Google Scholar]
- Liu, Y.; Ge, B.; Abu-Rub, H.; Peng, F.Z. Overview of space vector modulations for three-phase Z-source/quasi-Z-source inverters. IEEE Trans. Power Electron. 2013, 29, 2098–2108. [Google Scholar] [CrossRef]


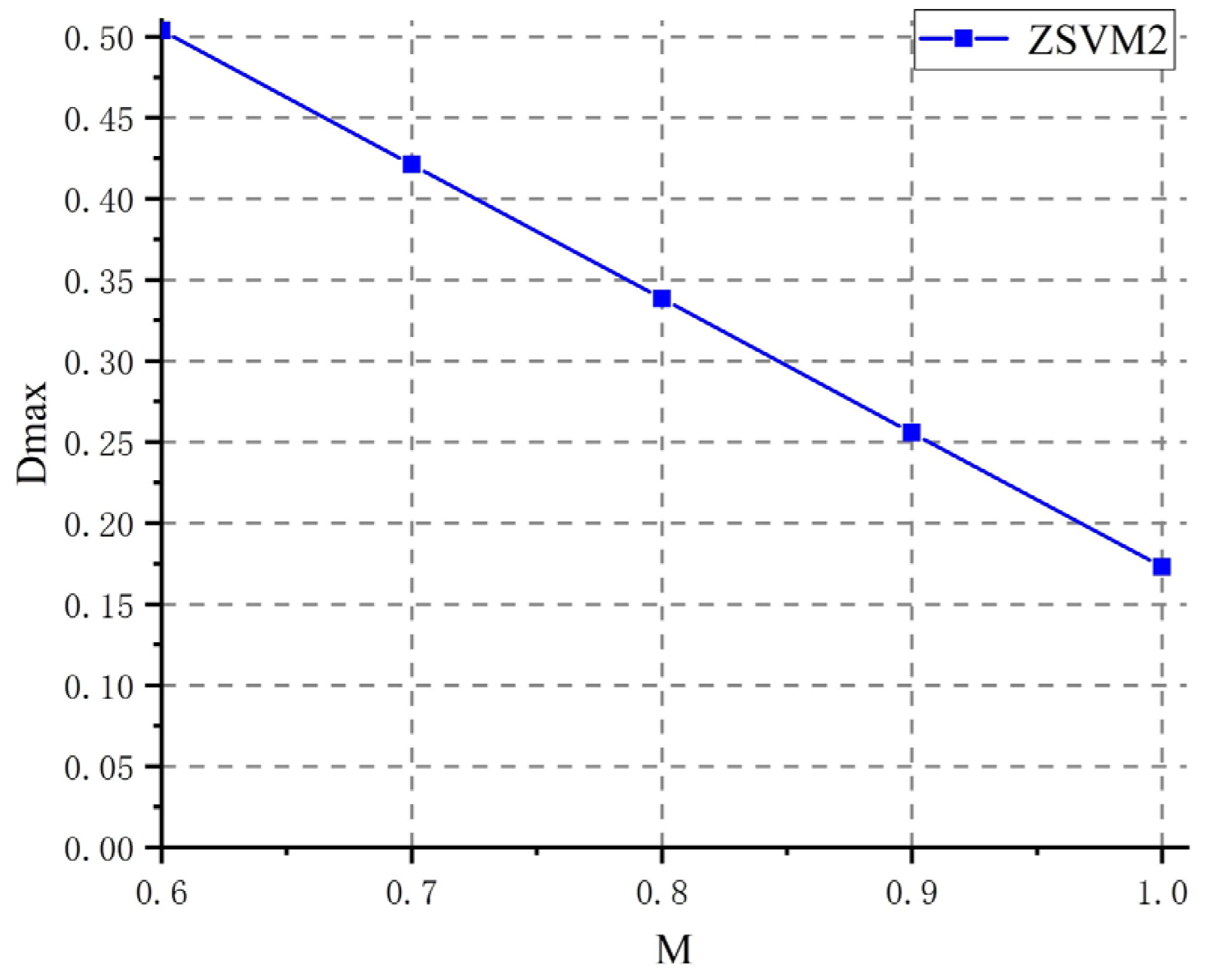

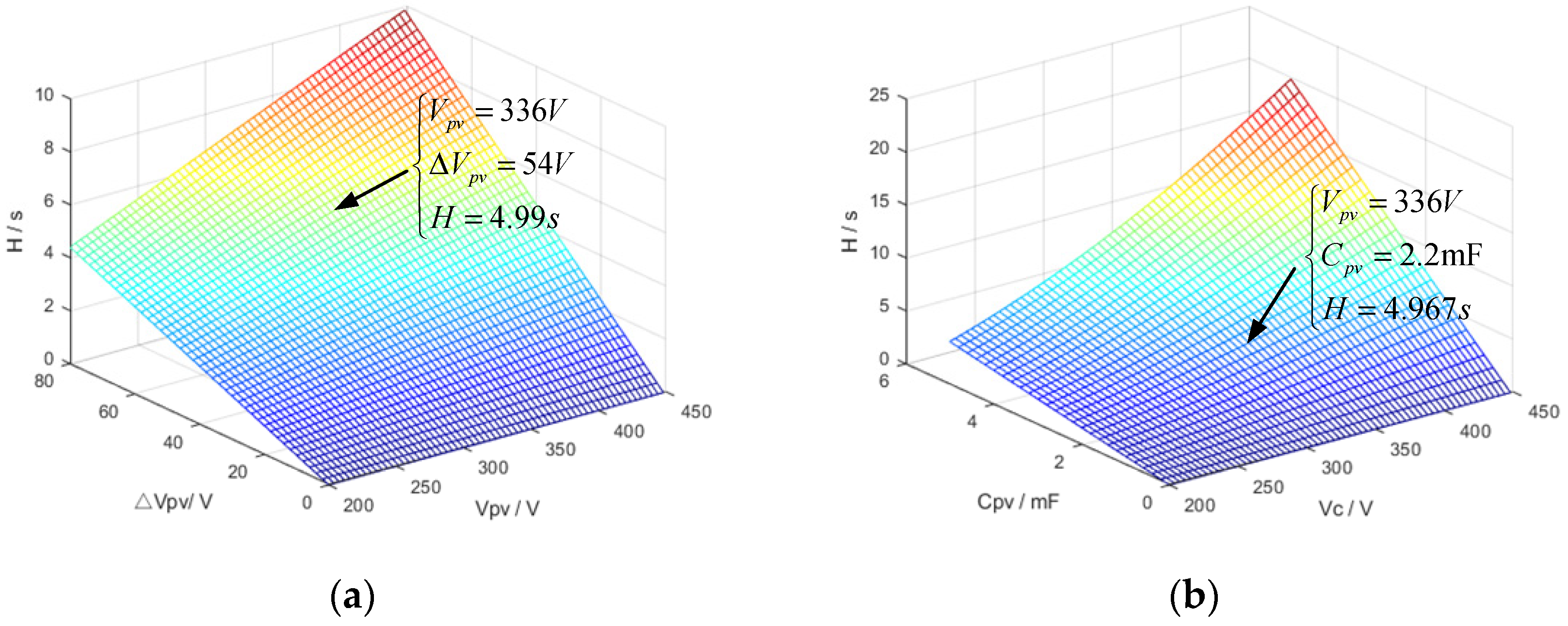
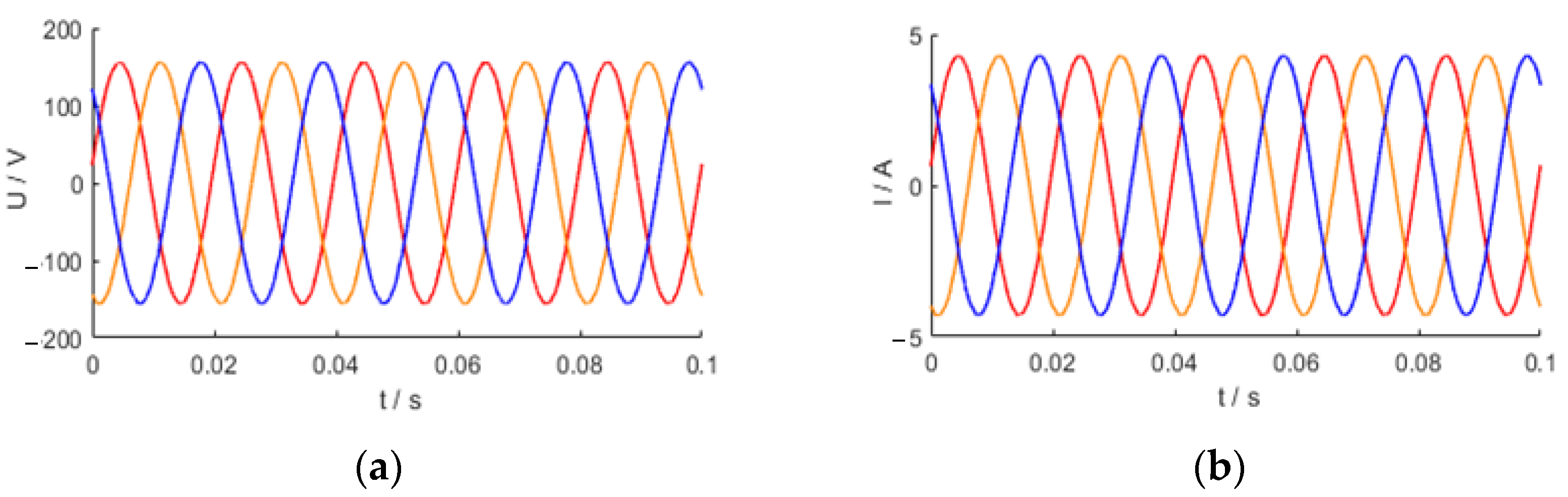


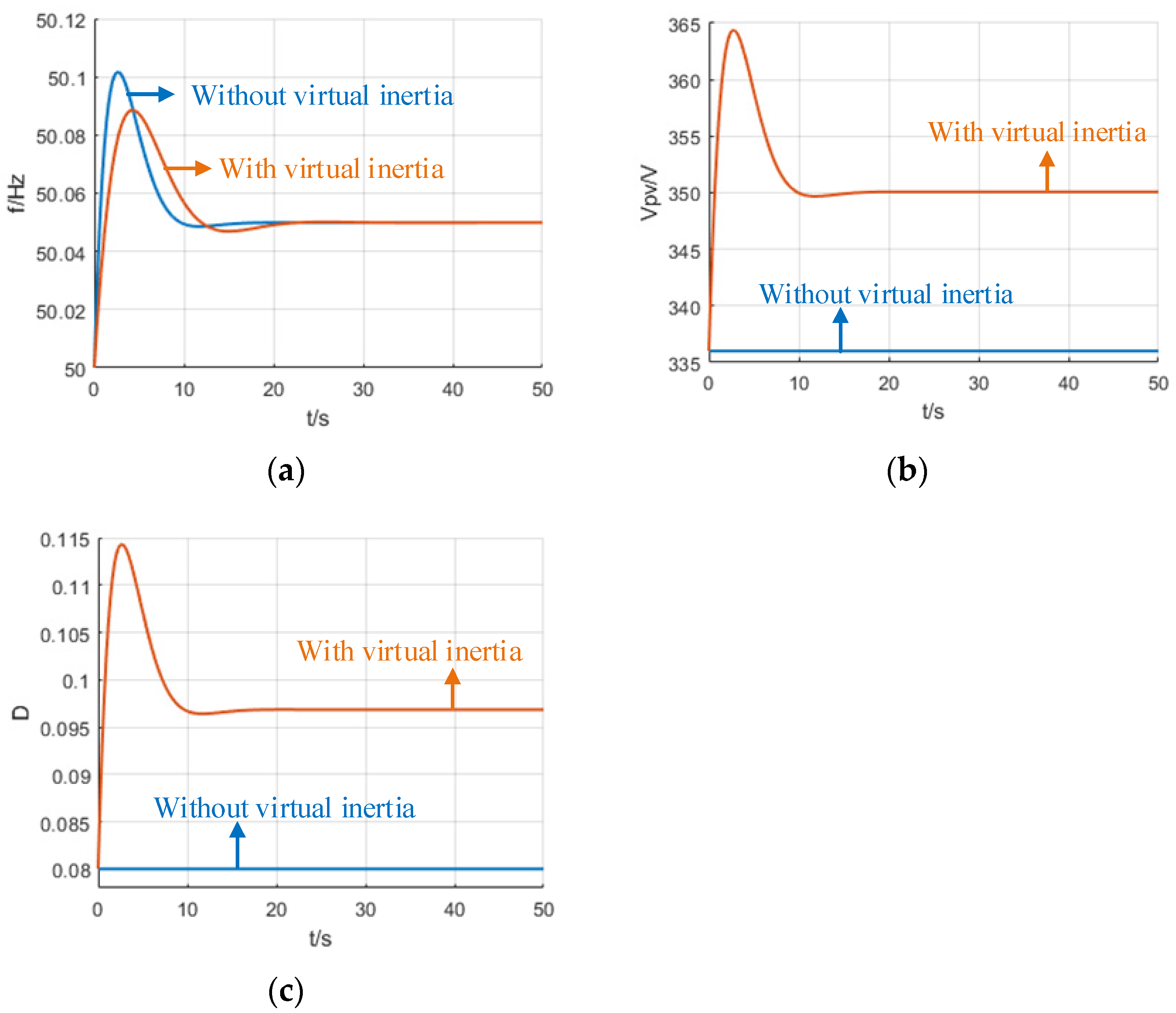

| Description | Parameter | Value |
|---|---|---|
| Droop coefficient | R | 0.02 |
| Rotor speed coefficient | TG | 0.1 s |
| Turbine coefficient | FHP | 0.3 s |
| Reheat engine time constant | TRH | 7.0 s |
| Main inlet time constant | TCH | 0.2 s |
| Inertia time constant | H | 5 s |
| Rated frequency | fref | 50 Hz |
| Damping coefficient | D | 1.0 |
| Rated power | VArated | 1 kVA |
| Description | Parameter | Value |
|---|---|---|
| Rated DC Chain Voltage | Vdc | 336 V |
| Max. DC Chain Voltage | Vpv_max | 390 V |
| Min. DC Chain Voltage | Vpv_min | 282 V |
| DC chain capacitance | Cpv | 2.2 mF |
| Virtual inertia time constant | Hp | 5.0 s |
| Rated frequency | fref | 50 Hz |
| Max. frequency deviation | Δfr_max | 0.2 Hz |
| Voltage-frequency controller | Kfv | 270/40.2 |
| Rated power | VArated | 1 kVA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Chen, H.; Fang, R. Virtual Inertia Implemented by Quasi-Z-Source Power Converter for Distributed Power System. Energies 2023, 16, 6667. https://doi.org/10.3390/en16186667
Liu Y, Chen H, Fang R. Virtual Inertia Implemented by Quasi-Z-Source Power Converter for Distributed Power System. Energies. 2023; 16(18):6667. https://doi.org/10.3390/en16186667
Chicago/Turabian StyleLiu, Yitao, Hongle Chen, and Runqiu Fang. 2023. "Virtual Inertia Implemented by Quasi-Z-Source Power Converter for Distributed Power System" Energies 16, no. 18: 6667. https://doi.org/10.3390/en16186667
APA StyleLiu, Y., Chen, H., & Fang, R. (2023). Virtual Inertia Implemented by Quasi-Z-Source Power Converter for Distributed Power System. Energies, 16(18), 6667. https://doi.org/10.3390/en16186667







