Analysis of Entropy Generation on Magnetohydrodynamic Flow with Mixed Convection through Porous Media

Abstract

Various industrial operations involve frequent heating and cooling of electrical systems. In such circumstances, the development of relevant thermal devices is of extreme importance. During the development of thermal devices, the second law of thermodynamics plays an important role by means of entropy generation. Entropy generation should be reduced significantly for the efficient performance of the devices. The current paper reports an analytical study on micropolar fluid with entropy generation over a stretching surface. The influence of various physical parameters on velocity profile, microrotation profile, and temperature profile is investigated graphically. The impact of thermal radiation, porous medium, magnetic field, and viscous dissipation are also analyzed. Moreover, entropy generation and Bejan number are also illustrated graphically. Furthermore, the governing equations are solved by using HAM and code in MATHEMATICA software. It is concluded from this study that velocity and micro-rotation profile are reduced for higher values of magnetic and vortex viscosity parameter, respectively. For larger values of Eckert number and thermal radiation parameters, Bejan number and entropy generation are increased, respectively. These findings are useful in petroleum industries and engineering designs.

1. Introduction

In recent decades, the study of Newtonian fluids has not been considered adequate to specify the flow properties such as coal slurries, polymeric fluids, and mine tailings, and these properties are expressed in non-Newtonian fluid flow model. The application of non-Newtonian fluid in industrial processes are extensive. Micropolar fluid is also one of the important kinds of non-Newtonian fluid. Eringen [1] was the first scientist to investigate certain microscopic effects arising from the local structure and micro-rotations of fluid elements. Eringen stated that due to the micro-rotation of the fluid particles and their stress tensors in micropolar fluids, there are additional terms. Consequently, they are viewed as the non-Newtonian fluids [2]. The micropolar fluids precisely replicate the flow properties of geomorphic sediments, colloidal suspensions, polymeric additives, liquid crystals, lubricants, hematological suspensions, etc. Several studies have been carried out related to micropolar fluid. For example, Abbas et al. [3] studied the non-orthogonal stagnation point flow towards a stretching sheet. They obtained the solution of coupled ordinary differential equation by using a well-known analytical technique of Homotopy Perturbation Method (HPM) and obtained the results graphically and numerically. Su, Jingrui [4] discussed the weak solution for micropolar fluid with compressible flow. He established the global existence of the weak solution. Ratchagar, Nirmala P., and S. Seyalmurugan [5] examined the horizontal micropolar fluid with Sorat effect. They took Brinkman porous media parameter in this study and calculated the exact solution. A few more references about micropolar fluid can be viewed in the available reference [6,7,8,9,10,11,12,13,14,15].

In 1939, Hartmann [16] solved the exact solution of magneto hydrodynamics (MHD) equations and stated that MHD deals with the stream of fluids having non-negligible electrical conductivity which interact with a magnetic field. MHD has numerous applications, particularly, power generator, MHD accelerator, and fusion research. Some researchers studied the effect of magnetic field on unsteady free convective micropolar fluid flow between vertical walls, etc. M. M. Khader et al. [17] analyzed the effect of non-uniform heat source sink and thermal radiation on MHD unsteady flow of micropolar fluid. They transformed the partial differential equation into an ordinary differential equation and solved it using a predictor-corrector method. They plotted the graphs of velocity, microrotation profile, and skin friction. Ram Prakash Sharma et al. [18] used a numerical technique to solve the radiative heat energy and thermophoretic heat energy on MHD unsteady micropolar fluid. They discussed the behavior on the characterization of parameters on flow phenomena. B. Shankar Goud [19] examined the heat generation and absorption influence on MHD unsteady micropolar fluid flow through porous medium in the presence of variable suction and injection. Some more investigations related to MHD micropolar fluid can be found through studies [20,21,22,23] and many therein.

Moreover, the combination of free convections and forced is called mixed convection. Such flows have huge demands in several industrial processes and engineering in nature, for instance, electronic devices that are being cooled by fans, solar receivers uncovered to wind currents, transmission due to different densities along the vertical path in a lake owing to cyclic changes, flows in the ocean and in the airspace, atmospheric flow at different temperature, and many others. The significance feature of mixed convection is buoyancy force which is caused by differing temperature and density. Mathematically, the highly coupled mixed convections are described by the energy and momentum equations. Patel R. Harshad [24] examined the mixed convection MHD flow of micropolar fluid in porous media towards a nonlinear stretching sheet. They analyzed the properties of heat and mass transfer with thermophoresis, Brownian motion, chemical reaction, and nonlinear thermal radiation. In another investigation, Govardhan, K. et al. [25] presented the effect of MHD and thermal radiation on mixed convection micropolar fluid towards a stretching sheet. In this investigation, they assumed the stretching velocity linearly with the distance along the sheet. Two-dimensional mixed convection stagnation point micropolar fluid flow towards a permeable sheet has been discussed by Bhattacharyya, K. and S. Shafie [26]. They concluded that the boundary layer thickness becomes thicker and thicker with increases in shrinking parameter.

Most of the energy-related applications and production of thermal and engineering devices have great concern of irreversible loss of heat. The devices which are facing this issue are the cooling of modern electronic devices, geothermal energy systems, and solar power collectors. It is a challenging task to minimize the irreversible losses of heat that lead to increase entropy generation. The second law of thermodynamics is used to analyze the entropy generation because it is utilized to measure the importance of irreversibility connected to the friction, heat transfer, and thermal system. Several studies have been done related to entropy generation by various authors [27,28,29,30,31]. Recently, entropy generation with micropolar fluid has become of great interest in the field of petroleum industries, heat transfer, and thermal design. For example, magnetic field effects of entropy generation of micropolar fluid in a rectangular conduit has been analyzed by Yadav, Pramod Kumar, and Ankit Kumar [32]. These authors used momentum equation and energy equation to obtain an entropy generation number and illustrated the impact of hydrodynamics and thermal parameters on entropy generation through graphs. In another article related to entropy generation, Fatunmbi, E. O., and A. Adeniyan [33] developed entropy generation using Joule heating, thermal radiation, and viscous dissipation. In their findings, it is mentioned that the Prandtl number and Eckert number enhance entropy generation while with the increment in these two parameters, there is dominance in viscous and Ohmic heating irreversibility over heat transfer.

Keeping in view the above-mentioned studies, no analysis has been conducted related to entropy generation in a mixed convection micropolar fluid. Although Zaib, A., et al. [34] studied the optimization of entropy generation of micropolar fluid with convective magnetite Ferro particle in a vertical plane, much more attention is needed in this area. Therefore, the current study addresses the entropy generation model of mixed convection MHD micropolar fluid. The main objective of the present study is to investigate the characteristics of magnetized micropolar fluid, heat transfer, and entropy generation. These investigations will be greatly beneficial in industrial applications, thermal design, and many other engineering sectors. The nonlinear coupled partial differential equation was transformed into ordinary differential equations and they were solved using the Homotopy Analysis Method [35,36,37]. The graphical and numerical results were analyzed and the conclusion points also shared in this article.

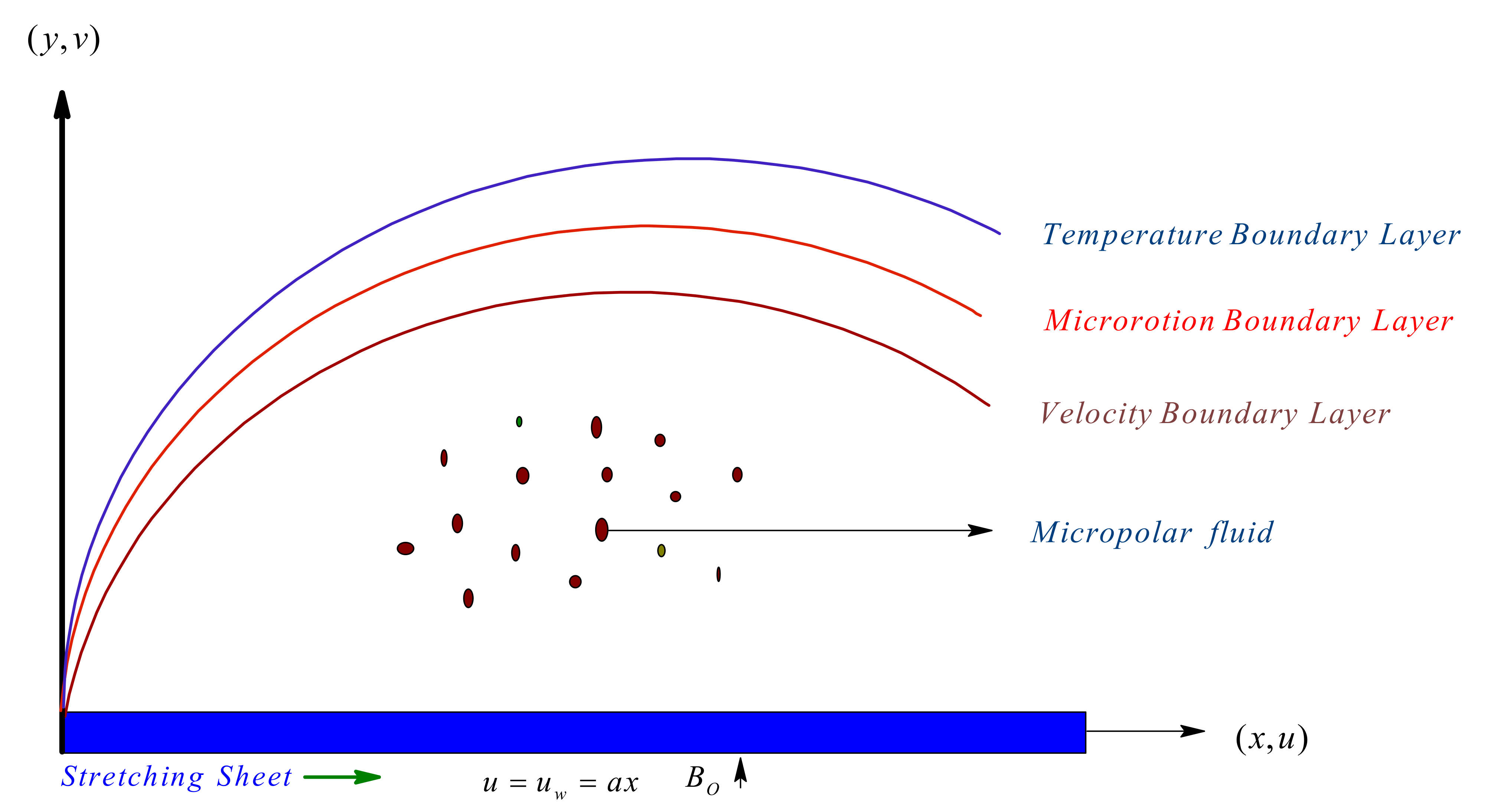
2. Mathematical Modeling

The present research reports an analytical study on micropolar fluid with entropy generation over stretching surface. The strength of uniform magnetic field B₀ is applied perpendicular to the surface. The system of Cartesian coordinated is taken in such a way that $x$-axis is in the direction of stretching sheet with stretching velocity $u_w=ax$ and $y$-axis is normal to the stretching surface. The physical geometry of the modeled problem is shown in Figure 1. Furthermore, the governing equations of micropolar fluid [3,38] with suitable boundary conditions are expressed as:

$$\left.\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,\hspace{1em}\right\}$$

(1)

$$\left.\frac{u\partial u}{\partial x}+v\frac{\partial u}{\partial y}=\left(\nu +\frac{K}{\rho }\right)\frac{{\partial }^{2}u}{\partial y^2}+\frac{K}{\rho }\frac{\partial N}{\partial y}-\frac{\sigma B_o^2}{\rho }u-\frac{\nu }{K_1}u+g_1{\beta }_T(T-T_{\infty }),\right\}$$

(2)

$$\left.u\frac{\partial N}{\partial x}+v\frac{\partial N}{\partial y}=\frac{\gamma }{\rho j}\frac{{\partial }^{2}N}{\partial y^2}-\frac{K}{\rho j}\left(2N+\frac{\partial u}{\partial y}\right),\right\}$$

(3)

$$\left.u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{{\partial }^{2}T}{\partial y^2}+\frac{\nu +\frac{K}{\rho }}{Cp}{\left(\frac{\partial u}{\partial y}\right)}^2+\frac{\sigma B_o^2}{\rho C_P}{u}^2-\frac{1}{\rho C_p}\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k^{\circ }}\frac{{\partial }^{2}T}{\partial y^2},\right\}$$

(4)

with

$$\left.\begin{array}{c}u=u_w=ax,v=0,N=-m\frac{\partial u}{\partial y},T=T_w,at y=0,\\ u=0,N=0,T=T_{\infty } as y\to \infty ,\end{array}\right\}$$

(5)

Considering

$$\left.\begin{array}{c}\eta =\sqrt{\frac{a}{\upsilon }}y,u=ax{f}^{\prime }\left(\eta \right),v=-\sqrt{a\nu }f\left(\eta \right),N=\sqrt{\frac{a}{\upsilon }}axg\left(\eta \right)\\ \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}.\end{array}\right\}$$

(6)

In the above equations, different parameters are represented as $\left(u\right)$ and $\left(v\right)$ are components of velocity in $\left(x\right)$ and $\left(y\right)$ direction, kinematic viscosity $\left(\nu \right)$, vortex viscosity $\left(K\right)$, magnetic field $B_0$ fluid density $\left(\rho \right)$, permeability of porous medium $\left(k_1\right)$, spin gradient viscosity $\left(\gamma =(\mu +\frac{K}{2})j\right)$, microinertia per unit mass $\left(j\right)$, molecular thermal diffusivity $\left(\alpha \right)$, specific heat $\left(Cp\right)$, electrical conductivity $\left(\sigma \right)$, Stefan Boltzmann constant $\left({\sigma }^{\ast }\right)$, mean absorption coefficient $\left(k^{\circ }\right)$, constant characterizing the mainstream flow $\left(a\right)$, temperature of fluid $\left(T\right)$, surface temperature $\left(T_w\right)$, ambient temperature $\left(T_{\infty }\right)$, and angular velocity or microrotation velocity $\left(N\right)$.

The incompressibility condition Equation (1) is automatically satisfied while Equations (2)–(6) have the following dimensionless forms:

$$\left.f{f}^{″}-f^{\prime 2}+\left(1+\Gamma \right)f^{″\prime }+\Gamma g^{\prime }-H{a}^2{f}^{\prime }-K^{\ast }{f}^{\prime }+{\lambda }_1\theta =0,\right\}$$

(7)

$$\left.\lambda g^{\prime \prime }-f^{\prime }g+f{g}^{\prime }-\Gamma {\beta }_1\left(2g+f^{\prime \prime }\right)=0,\right\}$$

(8)

$$\left.\mathrm{Pr}f{\theta }^{\prime }+\mathrm{Pr}Ec\left(1+\Gamma \right)f^{\prime \prime 2}+\mathrm{Pr}H{a}^{2}Ec{f}^{\prime 2}+\left(1+\frac{4}{3}Rd\right){\theta }^{″}=0,\right\}$$

(9)

with

$$\begin{gathered} f\left(0\right)=f_w, f^{\prime \left(0\right)}=1, g\left(0\right)=-mf\left(0\right), \theta \left(0\right)=1 at \eta =0\hspace{1em}f\prime \left(\infty \right)\to 0, \\ f\left(\infty \right)\to 0 , g\left(\infty \right)\to 0, \theta \left(\infty \right)\to 0 at\hspace{1em}\eta =\infty \end{gathered}$$

(10)

Non-dimensional parameters which are used in above equations are denoted and mathematically defined within brackets such as Vortex viscosity constant $\left(\Gamma =\frac{K}{\mu }\right)$, magnetic parameter $\left(H_a^2=\frac{\sigma B_{\sigma }^2}{\rho a}\right)$, porosity parameter $\left(K^{\ast }=\frac{\nu }{a{k}_1}\right)$, dimensionless material property $\left(\lambda =\frac{\gamma }{\rho \nu j}\right)$, dimensionless material property $\left({\beta }_1=\frac{\nu }{aj}\right)$, Prandtl number $\left(\mathrm{Pr}=\frac{\nu }{\alpha }\right)$, Eckert number $\left(Ec=\frac{a^2{x}^2}{\nu C_p\left(T_w-T_{\infty }\right)}\right)$, linear thermal radiation parameter $\left(Rd=\frac{4{\sigma }^{\ast }{T}_{\infty }^3}{3k^{\ast }k}\right)$, local buoyancy parameter $\left({\lambda }_1=\frac{G{r}_x}{{{Re}_x}^2}\right)$, Grashof number $\left(G{r}_x=\frac{g_{1{\beta }_T(T_w-T_{\infty })}}{a^{2}x}\right)$, and local Reynold number $\left({\mathrm{Re}}_x=\frac{a{x}^2}{\nu }\right)$.

3. Investigation of Entropy Generation

In the modern age, most of researchers’ and engineering’s focus is on finding a technique that can control the destruction of fruitful energy. Entropy is one of the novel techniques that can be used to control wastage in actual performance of the system. In this research, entropy can be generated through the friction of fluid, mass, and heat transfer. Thus, result of volumetric entropy generation rate for micropolar fluid is given as:

$$\left.E_{gen}=E_a+E_b+E_c+E_d,\right\}$$

(11)

where

$$\left.E_a=\frac{K}{T_{\infty }^2}{\left(\frac{\partial T}{\partial y}\right)}^2\left(1+\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k^{\ast }k}\right),\right\}$$

(12)

$$\left.E_b=\frac{2k}{T_{\infty }}\left(N^2+N\frac{\partial u}{\partial y}\right),\right\}$$

(13)

$$\left.E_c=\left[\frac{\sigma B_O^2{u}^2}{T_{\infty }}\right],\right\}$$

(14)

$$\left.E_d=\left[\frac{\nu }{T_{\infty }{k}_1}{u}^2\right],\right\}$$

(15)

The dimensionless entropy generation characteristics rate can be defined as

$$\left.E_s=\frac{k{(T_w-T_{\infty })}^2}{T_{\infty }^2{x}^2},\right\}$$

(16)

By using entropy generation characteristics rate ($E_1$), the dimensionless form of entropy generation of Equation (13) can be written as

$$E_G=\frac{E_{gen}}{E_S}=R{e}_x \left(1+\frac{4}{3}Rd\right){\theta }^2 \frac{2BrR{e}_x\mathsf{\Gamma }}{\delta } \left(g^2+gf\right)+\frac{BrR{e}_x}{\delta }H{a}^2{f}^2+\frac{BrR{e}_x}{\delta }{{\rm K}}^{*}{f}^{\prime 2}$$

(17)

and

$$E_1=R{e}_x\left(1+\frac{4}{3}Rd\right){\theta }^{\prime 2}$$

(18)

then Bejan number ($Be$) can be defined as the ratio of entropy generation due to heat transfer ($E_1$) to the total entropy generation ($E_G$). Bejan number can be expressed as.

$$Be=\frac{\mathrm{Entropy} \mathrm{generation} \mathrm{due} \mathrm{to} \mathrm{heat} \mathrm{transfer}}{\mathrm{Total} \mathrm{entropy} \mathrm{generation}}$$

(19)

$$Be=\frac{E_1}{E_G}$$

(20)

Dimensionless parameters which are used in above equation are described as linear thermal radiation parameter $\left(Rd=\frac{4{\sigma }^{\ast }{T}_{\infty }^3}{3k^{\ast }k}\right)$, Reynold number $\left(Re=\frac{a{x}^2}{\nu }\right)$, Brinkman number, temperature difference parameter $\left(\delta =\frac{T_w-T_{\infty }}{T_{\infty }}\right)$, and magnetic parameter $\left(H_a^2=\frac{\sigma B_O^{2}l}{\rho a}\right)$.

4. Solution of Problem

To obtain series solution through Homotopy Analysis Method (HAM), we chose initial guesses and corresponding linear operators. Initial guesses and auxiliary operators are given as:

$$\left.f_0\left(\eta \right)=1-\exp \left(-\eta \right),g_0\left(\eta \right)=m\hspace{0.33em}\exp \left(-\eta \right),\hspace{0.33em}{\theta }_0\left(\eta \right)=\exp \left(-\eta \right)\right\}$$

(21)

$$\left.L_f=\frac{d^{3}f}{d{\eta }^3}+f,\hspace{0.33em}{L}_f=\frac{d^{3}f}{d{\eta }^3}+f,\hspace{0.33em}{L}_g=\frac{d^{2}g}{d{\eta }^2}+g,\hspace{0.33em}{L}_{\theta }=\frac{d^2\theta }{d{\eta }^2}+\theta \right\}$$

(22)

the above linear operators have the following properties

$$\left.L_f[c_1+c_2{e}^{\eta }+c_3{e}^{-\eta }]=0,\hspace{0.33em}{L}_g[c_4{e}^{\eta }+c_5{e}^{-\eta }]=0,\hspace{0.33em}{L}_{\theta }[c_6{e}^{\eta }+c_7{e}^{-\eta }]=0\right\}$$

(23)

where $c_j(j=1,2,\dots ,7)$ show the arbitrary constants.

4.1. Zeroth-Order Problems

$$\left.(1-r)L_f[\stackrel{\sim }{{\displaystyle f}}(\eta ,r)-f_0(\eta )]=r{h}_f{N}_f[\stackrel{\sim }{{\displaystyle f}}(\eta ,r),\stackrel{\sim }{{\displaystyle g}}(\eta ,r),\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)]\right\}$$

(24)

$$\left.(1-r)L_g[\stackrel{\sim }{{\displaystyle g}}(\eta ,r)-g_0(\eta )]=r{h}_g{N}_g[\stackrel{\sim }{{\displaystyle g}}(\eta ,r),\stackrel{\sim }{{\displaystyle f}}(\eta ,r),\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)]\right\}$$

(25)

$$\left.(1-r)L_{\theta }[\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)-{\theta }_0(\eta )]=r{h}_{\theta }{N}_{\theta }[\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r),\stackrel{\sim }{{\displaystyle g}}(\eta ,r),\stackrel{\sim }{{\displaystyle f}}(\eta ,r)]\right\}$$

(26)

$$\left.\begin{array}{l}\stackrel{\sim }{{\displaystyle f}}(0,r)=0,{\stackrel{\sim }{{\displaystyle \hspace{0.33em}f}}}^{\prime }(0,r)=1,\stackrel{\sim }{{\displaystyle \hspace{0.33em}{f}^{\prime }}}(\propto ,r)=0,\hspace{0.33em}\stackrel{\sim }{{\displaystyle g}}(0,r)=m^{~}{\stackrel{\sim }{{\displaystyle f}}}_n^{\prime \prime }(0,r),\\ \stackrel{\sim }{{\displaystyle g}}(\propto ,r)=0,\hspace{0.33em}\stackrel{\sim }{{\displaystyle \theta }}(0,r)=1,\hspace{0.33em}\stackrel{\sim }{{\displaystyle \theta }}(\propto ,r)=0\end{array}\right\}$$

(27)

$$\left.\begin{array}{l}{N}_f[\stackrel{\sim }{{\displaystyle f}}(\eta ,r),\stackrel{\sim }{{\displaystyle g}}(\eta ,r),\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)]=\hspace{0.33em}\left(1+\Gamma \right)\frac{{\partial }^3\stackrel{\sim }{{\displaystyle f}}}{\partial {\eta }^3}+\stackrel{\sim }{{\displaystyle f}}\frac{{\partial }^2\stackrel{\sim }{{\displaystyle f}}}{\partial {\eta }^2}-{\left(\frac{\partial \stackrel{\sim }{{\displaystyle f}}}{\partial \eta }\right)}^2\\ +\Gamma \frac{\partial \stackrel{\sim }{{\displaystyle g}}}{\partial \eta }-H{a}^2\frac{\partial \stackrel{\sim }{{\displaystyle f}}}{\partial \eta }-K^{\ast }\frac{\partial \stackrel{\sim }{{\displaystyle f}}}{\partial \eta }+{\lambda }_1\theta \end{array}\right\}$$

(28)

$$\left.\begin{array}{l}{N}_g[\stackrel{\sim }{{\displaystyle g}}(\eta ,r),\stackrel{\sim }{{\displaystyle f}}(\eta ,r),\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)]=\lambda \frac{{\partial }^2\stackrel{\sim }{{\displaystyle g}}}{\partial {\eta }^2}-\frac{\partial \stackrel{\sim }{{\displaystyle f}}}{\partial \eta }\stackrel{\sim }{{\displaystyle g}}+\stackrel{\sim }{{\displaystyle f}}\frac{\partial \stackrel{\sim }{{\displaystyle g}}}{\partial \eta }-\Gamma {\beta }_1\left(2\stackrel{\sim }{{\displaystyle g}}+\frac{{\partial }^2\stackrel{\sim }{{\displaystyle f}}}{\partial {\eta }^2}\right)\\ +\mathrm{Pr}Ec\left(1+\Gamma \right){\left(\frac{{\partial }^2\stackrel{\sim }{{\displaystyle f}}}{\partial {\eta }^2}\right)}^2+\mathrm{Pr}H{a}^{2}Ec{\left(\frac{\partial \stackrel{\sim }{{\displaystyle f}}}{\partial \eta }\right)}^2=0\end{array}\right\}$$

(29)

where $r$ belongs to [0, 1] and it is represents the inserting parameter, $h_f,\hspace{0.33em}{h}_g,\hspace{0.33em}{h}_{\theta }$ stand for non-zero auxiliary parameters and $N_f,\hspace{0.33em}{N}_g,\hspace{0.33em}{N}_{\theta }$ show the nonlinear operators.

4.2. nth-Order Problems

$$\left.L_f[f_n(\eta )-{\gamma }_n{f}_{n-1}(\eta )]=h_f{R}_n^f(\eta )\right\}$$

(30)

$$\left.L_g[g_n(\eta )-{\gamma }_n{g}_{n-1}(\eta )]=h_f{R}_n^g(\eta )\right\}$$

(31)

$$\left.L_{\theta }[{\theta }_n(\eta )-{\gamma }_n{\theta }_{n-1}(\eta )]=h_f{R}_n^{\theta }(\eta )\right\}$$

(32)

$$\left.\begin{array}{l}{f}_n(0)=0,\hspace{0.33em}{f}_n^{\prime }(0)=1,\hspace{0.33em}{f}_n^{\prime }(\infty )=0,\hspace{0.33em}{g}_n(0)=m^{~}{f}_n^{\prime \prime }(0),\hspace{0.33em}\\ g_n(\infty )=0,\hspace{0.33em}{\theta }_n(0)=1,\hspace{0.33em}{\theta }_n(\infty )=0\end{array}\right\}$$

(33)

$$\left.\begin{array}{c}{R}_n^f(\eta )={\displaystyle \sum _{j=0}^{n-1}(f_{n-1-j}}{f}_j^{″}-f_{n-1-j}^{\prime }{f}_j^{\prime })+\left(1+\Gamma \right)f_{n-1}^{″\prime }+\Gamma g_{n-1}^{\prime }-H{a}^2{f}_{n-1}^{\prime }\hfill \\ -K^{\ast }{f}_{n-1}^{\prime }+{\lambda }_1{\theta }_{n-1}=0\end{array}\right\}$$

(34)

$$\left.R_n^g=\lambda g_{n-1}^{″}-{\displaystyle \sum _{j=0}^{m-1}{f}_{n-1-j}^{\prime }}{g}_j+{\displaystyle \sum _{j=0}^{m-1}{f}_{n-1-j}}{g}_j^{\prime }-\Gamma {\beta }_1\left(2g_{n-1}+f_{n-1}^{\prime \prime }\right)=0\right\}$$

(35)

$$\begin{gathered} \left.\begin{array}{l}{R}_n^{\theta }(\eta )=\left(1+\frac{4}{3}Rd\right){\theta }_{n-1}^{\prime \prime }+{\displaystyle \sum _{j=0}^{n-1}{\theta }_{n-1-j}^{\prime }}{f}_j+\mathrm{Pr}Ec\left(1+\Gamma \right){\displaystyle \sum _{j=0}^{n-1}{f}_{n-1-j}^{″}}{f}_j^{″}\\ +\mathrm{Pr}H{a}^{2}Ec{\displaystyle \sum _{j=0}^{n-1}{f}_{n-1-j}^{\prime }}{f}_j^{\prime }=0\end{array}\right\} \\ {\gamma }_n=\left\{\begin{array}{l}0,\hspace{0.33em}n\le 1\\ 1,\hspace{0.33em}n>1\end{array}\right. \end{gathered}$$

(36)

Here, if $r=0$ and $r=1$, we have the following forms

$$\left.\stackrel{\sim }{{\displaystyle f}}(\eta ,0)=f_0(\eta ),\hspace{1em}\stackrel{\sim }{{\displaystyle f}}(\eta ,1)=f(\eta )\right\}$$

(37)

$$\left.\stackrel{\sim }{{\displaystyle g}}(\eta ,0)={\theta }_0(\eta ),\hspace{1em}\stackrel{\sim }{{\displaystyle g}}(\eta ,1)=\theta (\eta )\right\}$$

(38)

$$\left.\stackrel{\sim }{{\displaystyle \theta }}(\eta ,0)={\theta }_0(\eta ),\hspace{1em}\stackrel{\sim }{{\displaystyle \theta }}(\eta ,1)=\theta (\eta )\right\}$$

(39)

and when p differs 0 to 1, then $\stackrel{\sim }{{\displaystyle f}}(\eta ,r)$,$g(\eta ,r)$, and $\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)$ represent variation from initial solutions $f_0(\eta )$, $g_0(\eta )$, and ${\theta }_0(\eta )$ to the final solutions f(η), g(η) and θ(η), respectively. According to Taylor series expansion, we have the following expressions

$$\left.\stackrel{\sim }{{\displaystyle f}}(\eta ,r)=f_0(\eta )+{\displaystyle {\sum }_n^{\infty }{f}_n(\eta )}{r}^n,\hspace{1em}{f}_n(\eta )={\left.\frac{1}{n!}\frac{{\partial }^n\stackrel{\sim }{{\displaystyle f}}(\eta ,r)}{\partial r^n}\right|}_{r=0}\right\}$$

(40)

$$\left.\stackrel{\sim }{{\displaystyle g}}(\eta ,r)=g_0(\eta )+{\displaystyle {\sum }_n^{\infty }{g}_n(\eta )}{r}^n,\hspace{1em}{g}_n(\eta )={\left.\frac{1}{n!}\frac{{\partial }^n\stackrel{\sim }{{\displaystyle g}}(\eta ,r)}{\partial r^n}\right|}_{r=0}\right\}$$

(41)

$$\left.\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)={\theta }_0(\eta )+{\displaystyle {\sum }_n^{\infty }{\theta }_n(\eta )}{r}^n,\hspace{1em}{\theta }_n(\eta )={\left.\frac{1}{n!}\frac{{\partial }^n\stackrel{\sim }{{\displaystyle \theta }}(\eta ,r)}{\partial r^n}\right|}_{r=0}\right\}$$

(42)

The convergence of Equations (44)–(46) depends on ${\mathrm{ћ}}_f$, ${\mathrm{ћ}}_{\theta }$, and ${\mathrm{ћ}}_{\varphi }$. These equations converge at p = 1, the value of auxiliary variables selected in such method

$$\left.f(\eta ,r)=f_0(\eta )+{\displaystyle {\sum }_n^{\infty }{f}_n(\eta )}\right\}$$

(43)

$$\left.g(\eta ,r)=g_0(\eta )+{\displaystyle {\sum }_n^{\infty }{g}_n(\eta )}\right\}$$

(44)

$$\left.\theta (\eta ,r)={\theta }_0(\eta )+{\displaystyle {\sum }_n^{\infty }{\theta }_n(\eta )}\right\}$$

(45)

The general solutions $(f_n,g_n,{\theta }_n)$ of the Equations (30)–(32) in term of special solutions $(f_n^{*},g_n^{*},{\theta }_n^{*})$ are following form

$$\left.f_n(\eta )=M_1^{*}+M_2^{*}{e}^{\eta }+M_2^{*}{e}^{-\eta }+f_n^{*}\right\}$$

(46)

$$\left.g_n(\eta )=M_4^{*}{e}^{\eta }+M_5^{*}{e}^{-\eta }+g_n^{*}\right\}$$

(47)

$$\left.{\theta }_n(\eta )=M_6^{*}{e}^{\eta }+M_7^{*}{e}^{-\eta }+{\theta }_n^{*}\right\}$$

(48)

where the arbitrary constants $M_j^{*}(j=1,2,\dots ,7)$ through the boundary conditions Equation (27) and are the following forms

$$\left.\begin{array}{l}{M}_2^{*}+M_4^{*}+M_6^{*}=0, M_3^{*}={\left.\frac{\partial f_n^{*}(\eta )}{\partial \eta }\right|}_{\eta =0},\\ M_3^{*}=-M_3^{*}-f_n^{*}(0), M_5^{*}=g_n^{*}(0), M_7^{*}={\theta }_n^{*}(0)\end{array}\right\}$$

(49)

5. Results and Discussion

The main purpose of this section is to investigate the influence of various physical parameters on entropy $(E_G(\eta ))$, Bejan number $(Be(\eta ))$, microrotation $(g(\eta ))$, temperature $(\theta (\eta ))$, and velocity $(f^{\prime }(\eta ))$ distributions over stretching sheet. Moreover, the graphical presentation of analytical results are also shown.

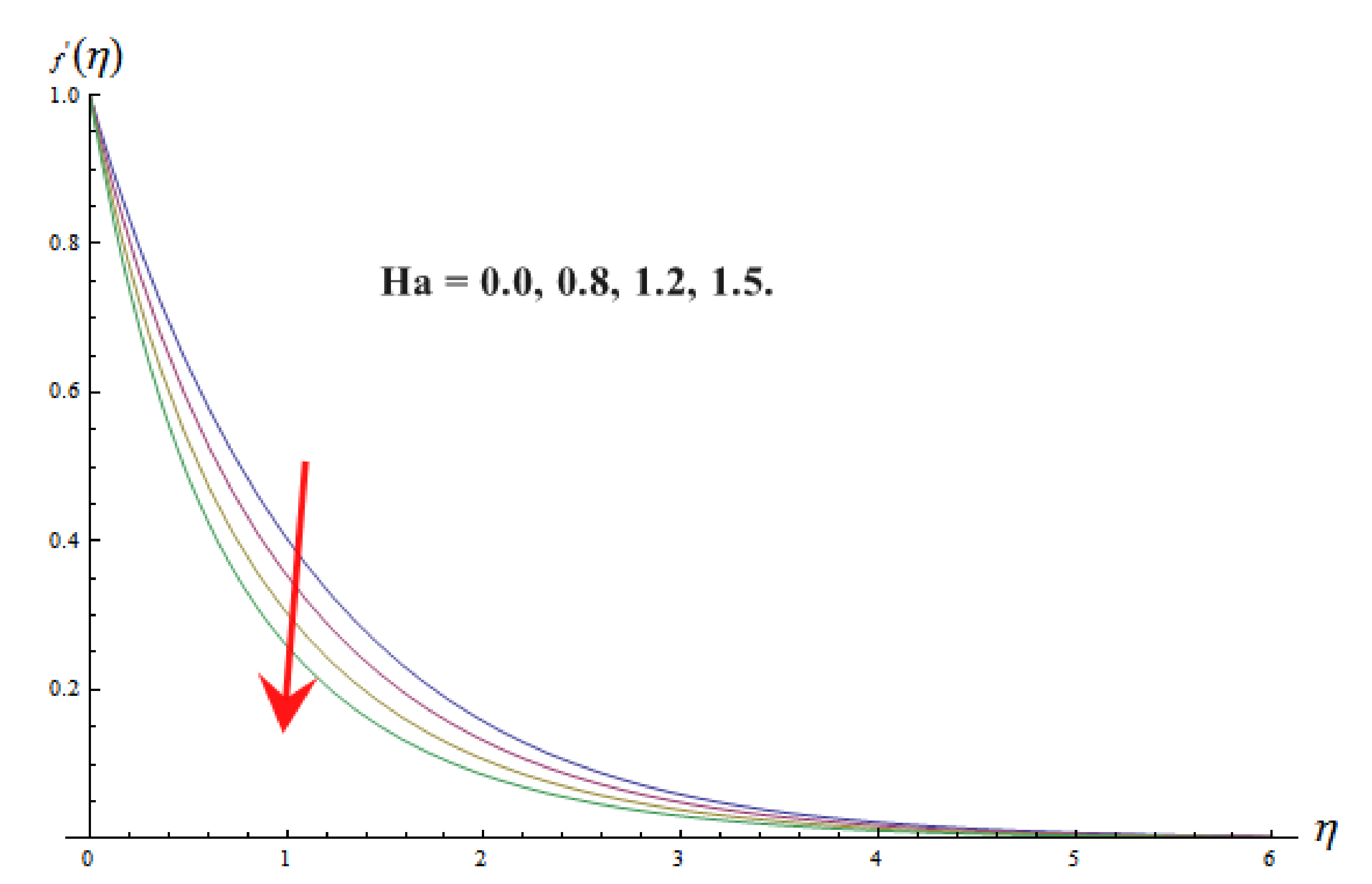
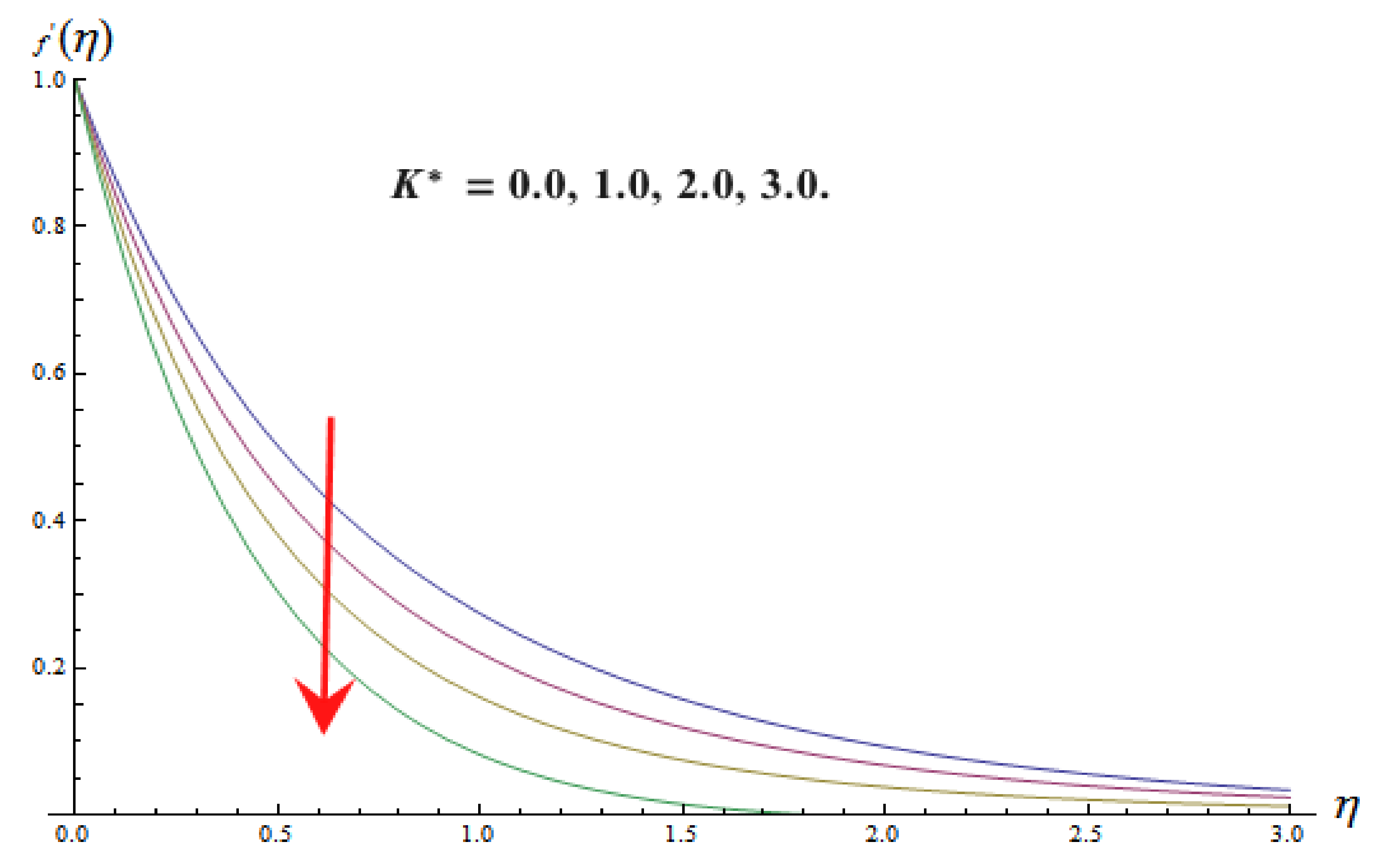
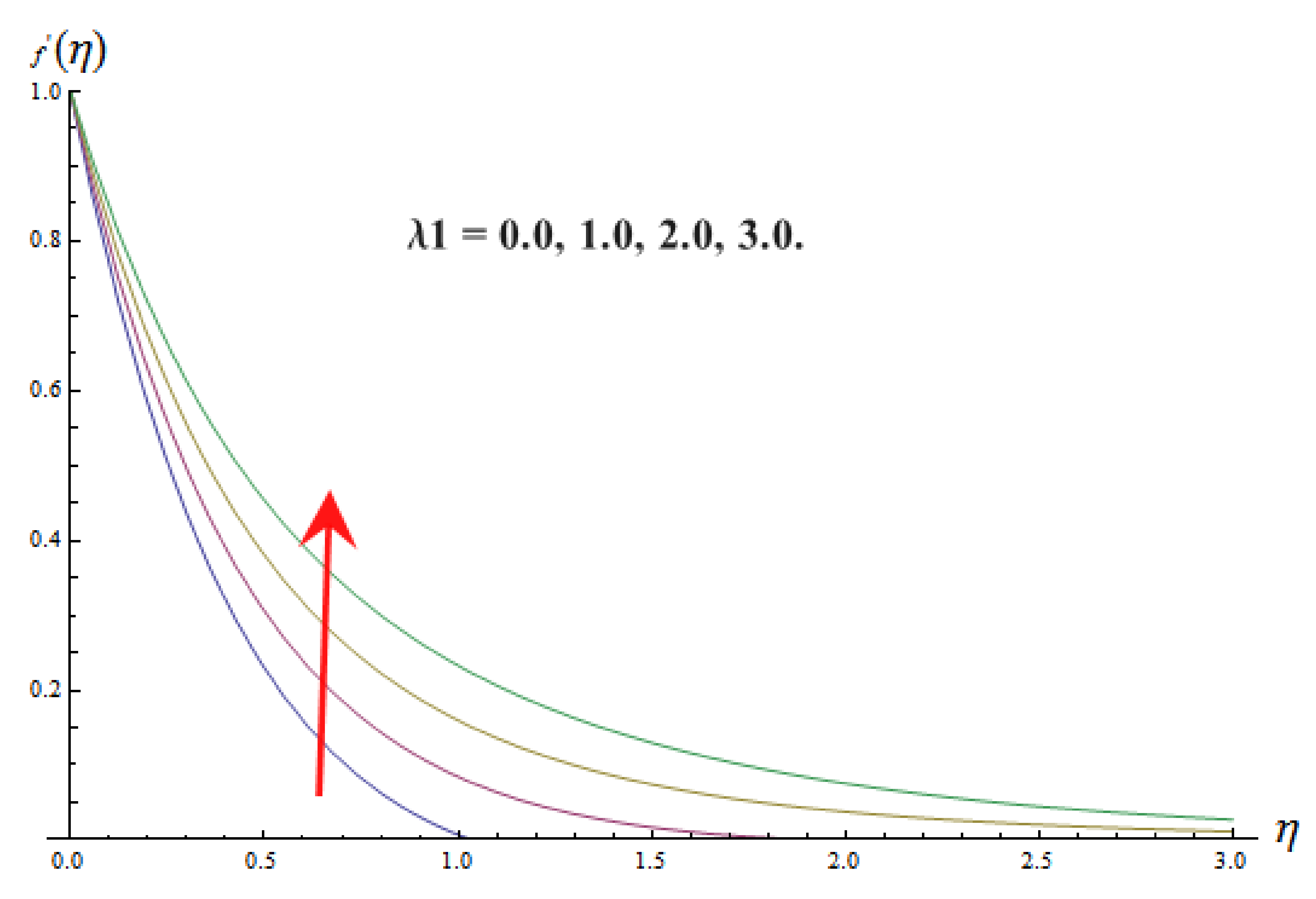
6. Velocity Distribution

Figure 2, Figure 3 and Figure 4 show the impact of pertinent parameter $Ha$, $K^{*}$, and ${\lambda }_1$ on velocity distribution. Figure 2 illustrates the control of magnetic field parameter $(Ha)$ on velocity field, increasing numerical values of magnetic parameter decays the velocity. The outcome of this phenomenon is because of opposing force (Lorentz force) created by magnetic field applied normal to the flow. Figure 3 explains the consequence of the porosity parameter $\left(K^{\ast }\right)$ on fluid velocity, various values of porosity parameter decrease the velocity of micropolar fluid flow. Figure 4 concerns of local buoyancy parameter $({\lambda }_1)$ on velocity field, different numerical values of local buoyancy parameter cause an increase in the velocity.

7. Micro Rotation

Figure 5, Figure 6 and Figure 7 explore the effect of significant parameters dimensionless material properties $(\lambda )$, $({\beta }_1)$ and vortex viscosity constant $(\Gamma )$ on microrotation. Figure 5 reveals the impression of dimensionless material property $({\beta }_1)$ on angular velocity profile; the observation of the graph gives the clear result of decreasing of microrotation profile but the reverse result is shown for dimensionless material property $(\lambda )$ in Figure 6. It should be noted that strong streamline circulations are generated for larger values in the micro rotation parameter and weak circulation occurs near the upper plate in the presence of angular rotation of particles

Figure 7 demonstrates the sway of vortex viscosity constant on the microrotation profile. It is obvious from the figure that enhances the values of vortex viscosity constant decays microrotation profile.

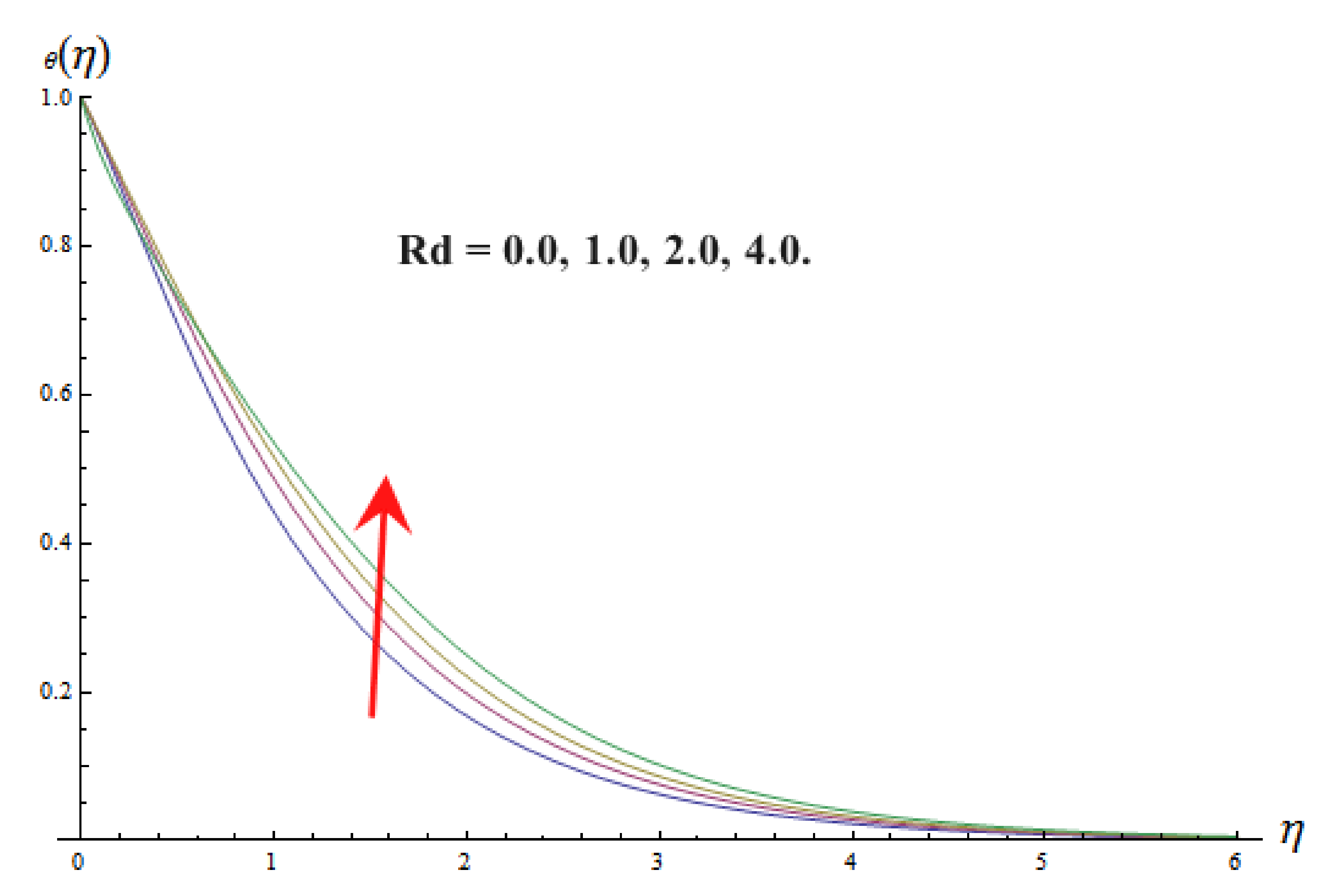
8. Temperature Distribution

Figure 8, Figure 9 and Figure 10 are sketched to elaborate the bearing of reflecting parameters, namely magnetic parameter $\left(Ha\right)$, Eckert number $\left(Ec\right)$, and linear thermal radiation parameter $\left(Rd\right)$, on temperature distribution. The effect of the Eckert number $\left(Ec\right)$ on temperature distribution is visualized in Figure 8. It has been noticed that temperature shoots up due to rising estimations of the Eckert number. It is worth mentioning that increasing in Ec number leads to an increase in the density of microorganisms due to which penetration rate of microorganisms and fluid particles from the sheet to fluid grows. The behavior of the magnetic parameter $\left(Ha\right)$ on temperature distribution is observed in Figure 9. It elucidates that temperature rises with enhancing values in $Ha$. Figure 10 sketches the properties of temperature profile via higher thermal radiation parameter $\left(Rd\right)$. It can clearly be seen from the figure that temperature distribution rises as the numerical value of $Rd$ enhances. The reason behind this phenomenon is that an increase in thermal radiation leads to an increase in the Rosseland radiation absorbability. Consequently, the fluid temperature increases.

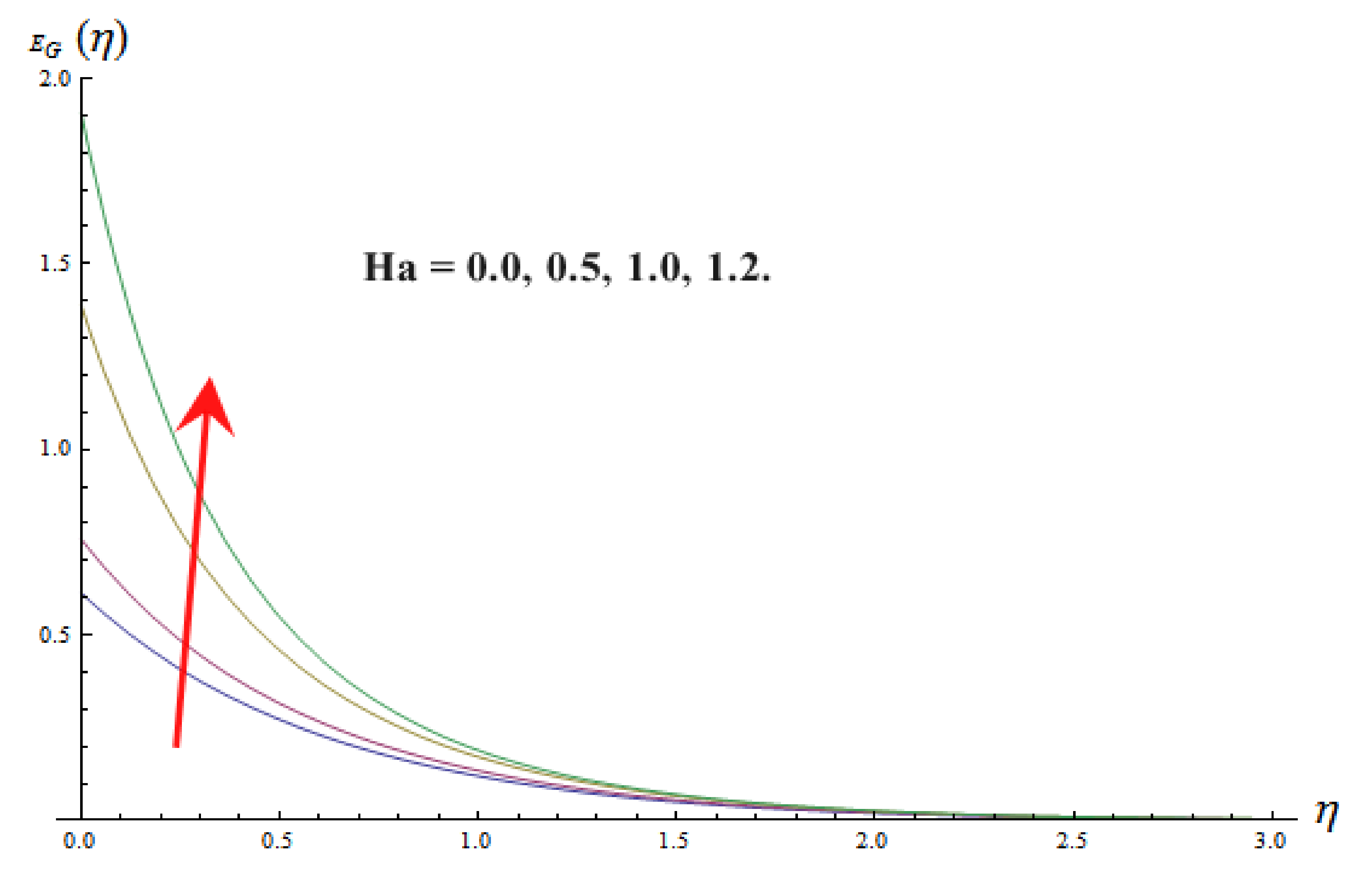
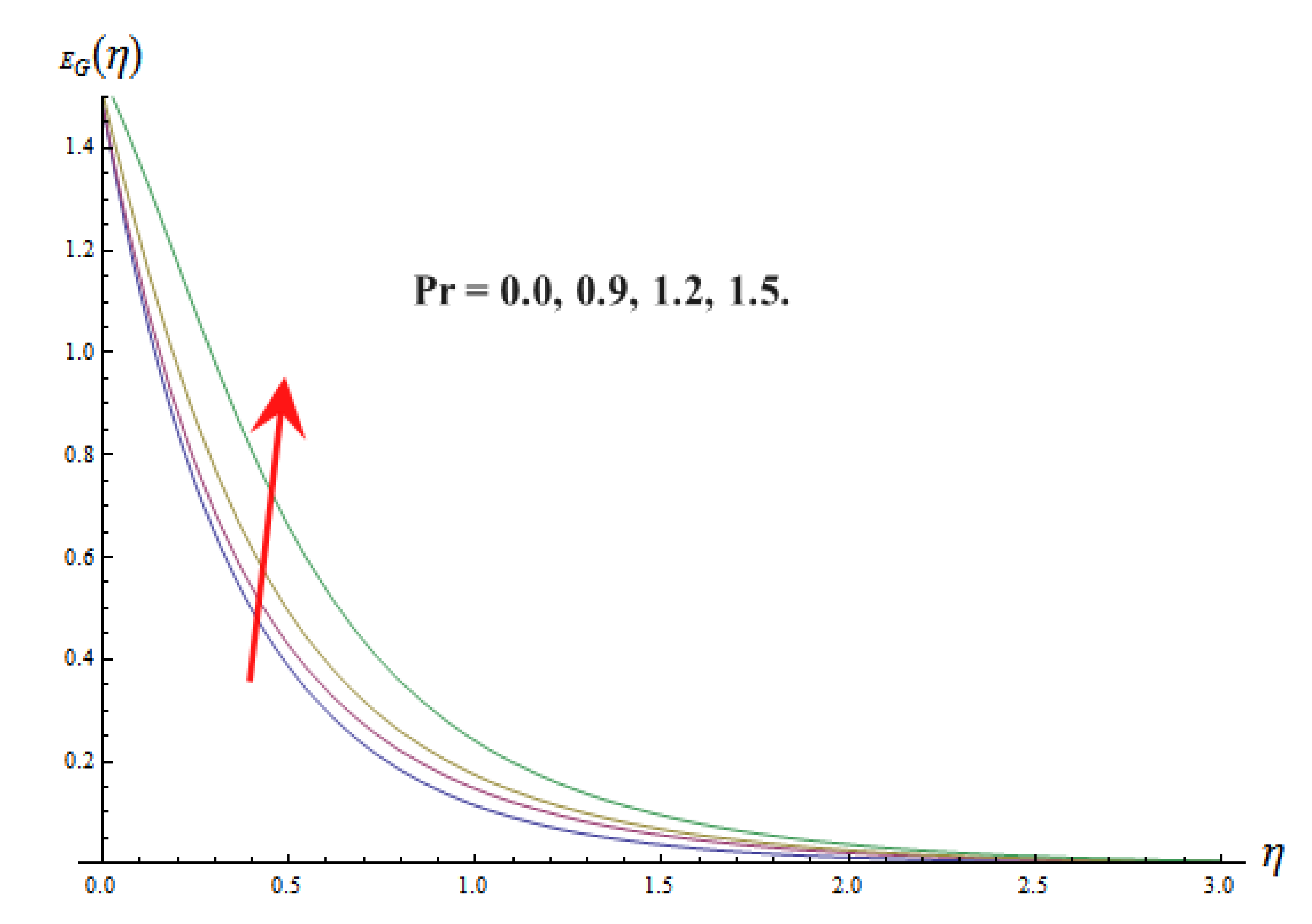
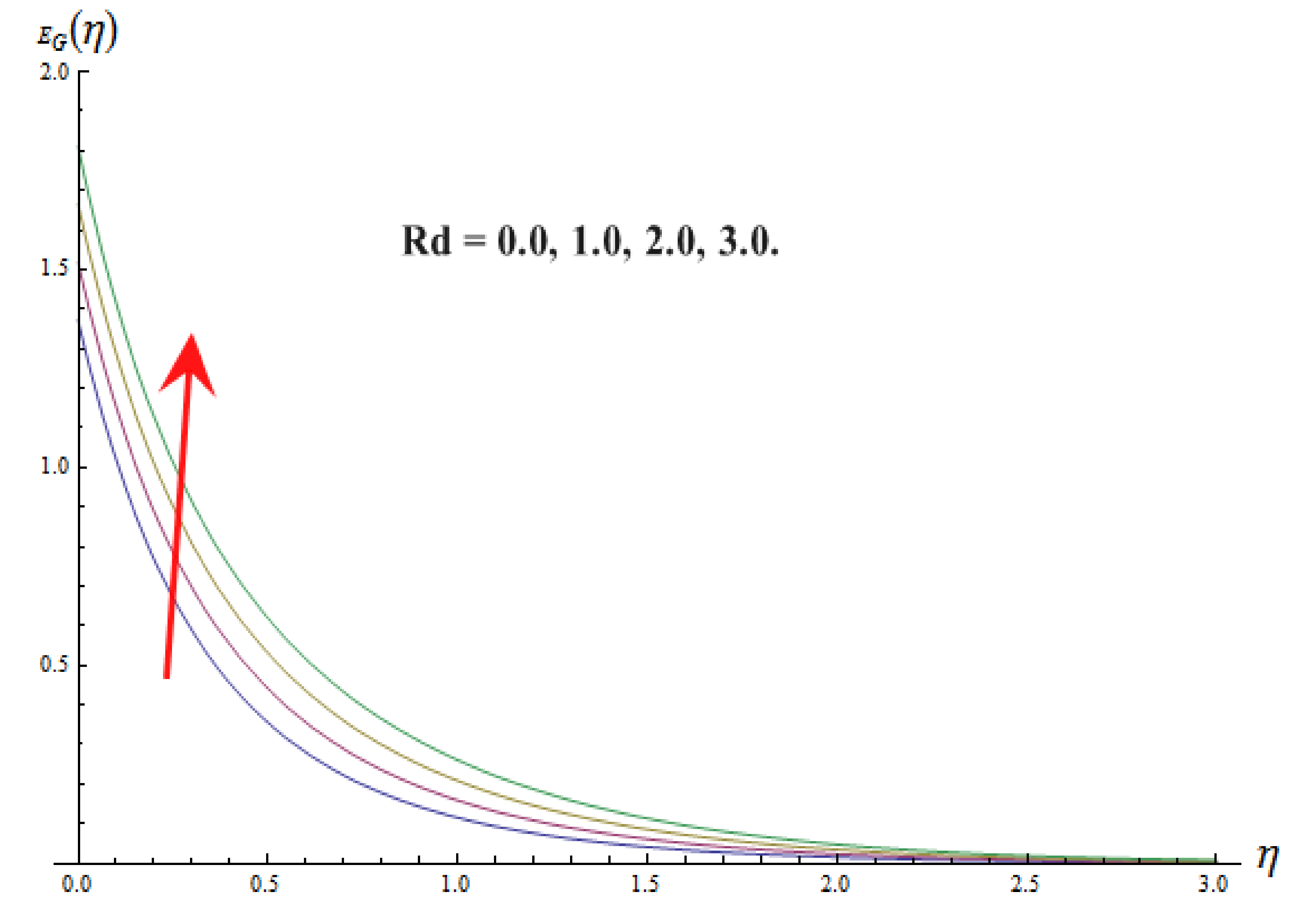
9. Entropy Generation and Bejan Number

The effect of Prandtl number $\left(\mathrm{Pr}\right)$, Brinkman number $\left(Br\right)$, magnetic parameter $\left(Ha\right)$, thermal radiation parameter $\left(Rd\right)$, and Eckert number $\left(Ec\right)$ on entropy generation $(E_G(\eta ))$ and Bejan number $(Be(\eta ))$ are displayed in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15. Figure 11 depicts that augmentation in the Brinkman number causes increase in entropy generation. This fact is because of effecting viscosity by the Brinkman number and the fluid friction produced by the viscous force produced, which resists fluid flow that causes an upshot in entropy generation. Figure 12 shows the bearing of the magnetic parameter on entropy generation. The figure gives us the notice of augmentation of $(E_G(\eta ))$ advancing the numerical values of $\left(Ha\right)$. Figure 13 signifies the enhancing of the Prandtl number causing ascending in $(E_G(\eta ))$. Figure 14 presents the graph of entropy generation corresponding variation of thermal radiation parameter. Figure 14 depicts augmentation of $(E_G(\eta ))$ with advancing $\left(Rd\right)$. Figure 15 indicates the effect of $(Br)$ on the Bejan number. It can be clearly observed that the Bejan number decreases on the different ascending values of the Brinkman number. Figure 16 demonstrates the impact of the Eckert number on $(Be(\eta ))$. It is observed from the figure that the Bejan number has ascending behavior for increasing values of $\left(Ec\right)$. The influence of $(\Gamma )$ on $(Be(\eta ))$ is visualized in Figure 17. It is obvious from the figure that various enhancing values of vortex viscosity constant decay the Bejan number. The impact of the Prandtl number is illustrated in Figure 18. It shows the increasing behavior of the Bejan number corresponding to ascending values of $\left(\mathrm{Pr}\right)$. The effect of the thermal radiation parameter on the Bejan number is demonstrated in Figure 19. It can be observed from the figure that the different increasing numerical values of the thermal radiation parameter causes an increase in the Bejan number.

10. Summarized Conclusions

In this study, analytical investigation of micropolar fluid with entropy generation over stretching surface was analyzed. HAM was implemented to compute the problem and the results are represented through graphs for the impacts of all pertinent parameters. It is worth mentioning here that when putting the parameter values to zero in Equations (7) and (8) ($\lambda \to 0 {\lambda }_1\to 0$), we get same ordinary differential equation for micropolar fluid flow as obtained by [39]. Further, the same graphical behavior was obtained by S.M. Atif et al. [39] for velocity profile against magnetic parameter and micro rotation profile for different values of material parameters. The main points of the current article are summarized as below.

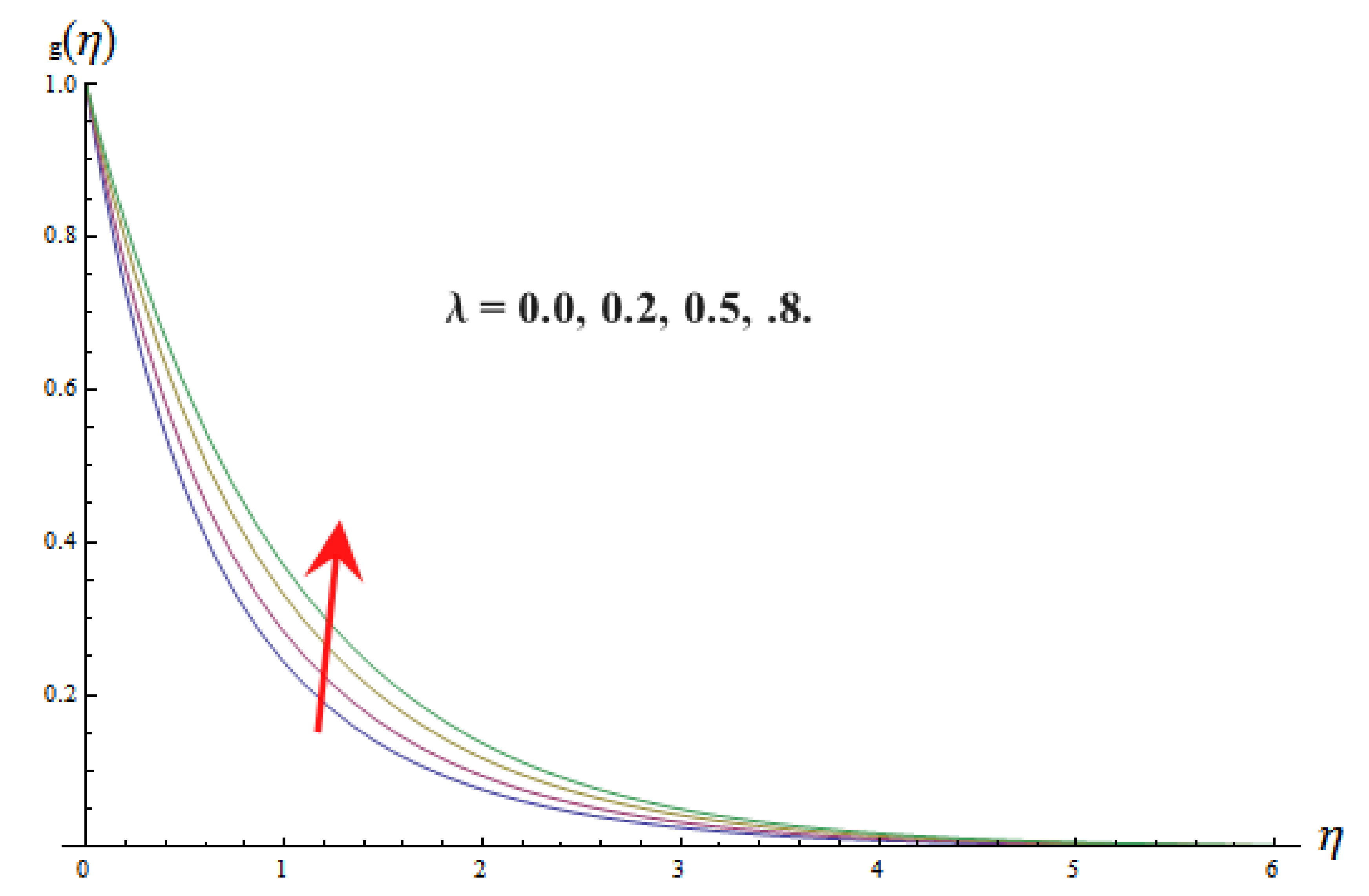
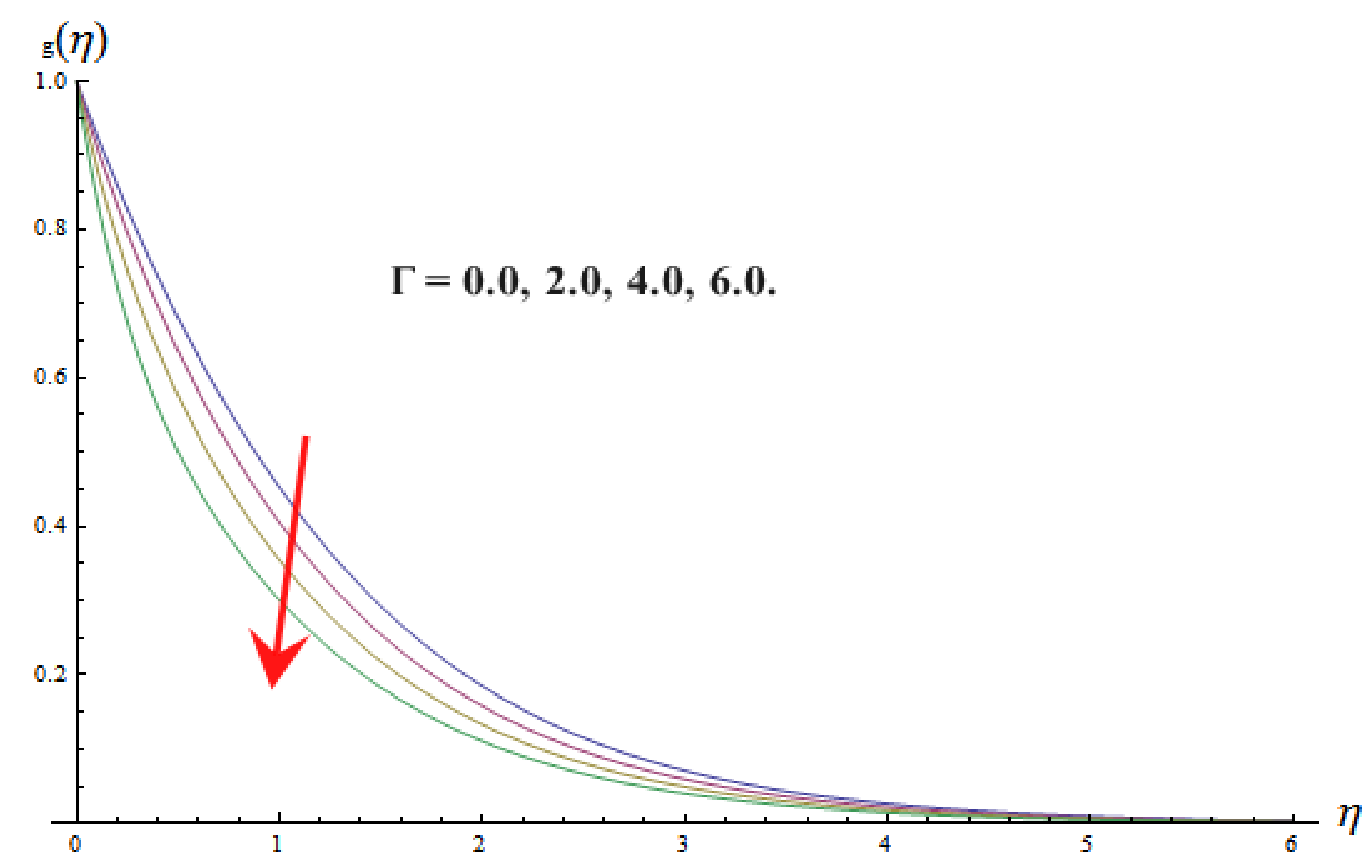
• By raising the values of the magnetic field parameter $(Ha)$, porosity parameter $\left(K^{\ast }\right)$, and vortex viscosity constant $(\Gamma )$, velocity distribution of micropolar fluid is reduced, while the inverse consequence is observed by raising values of local buoyancy parameter $({\lambda }_1)$.
• It is observed that angular velocity enhances with the greater estimations of dimensionless material property $(\lambda )$, while it reduces with increasing values of dimensionless material property $\left({\beta }_1\right)$.
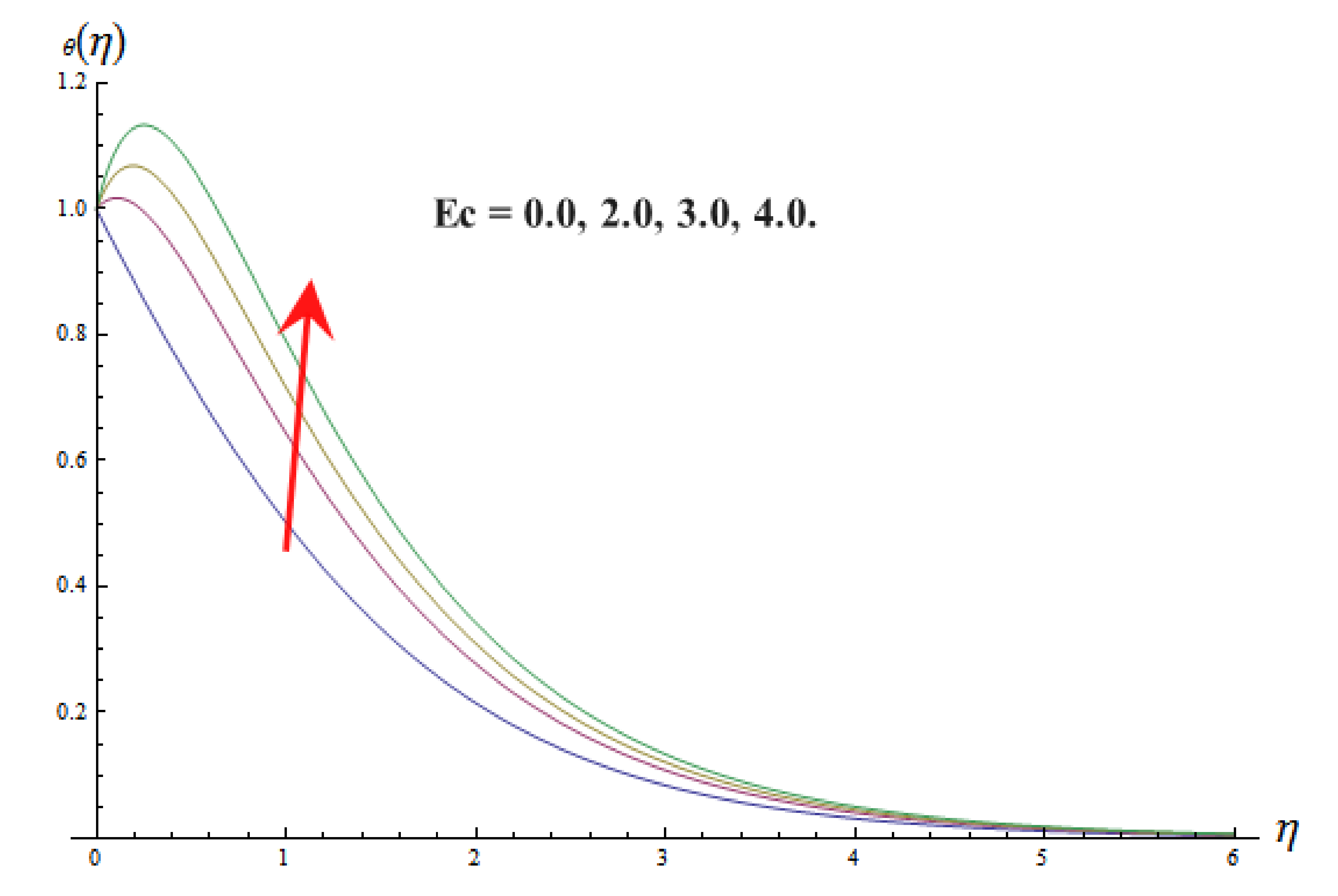
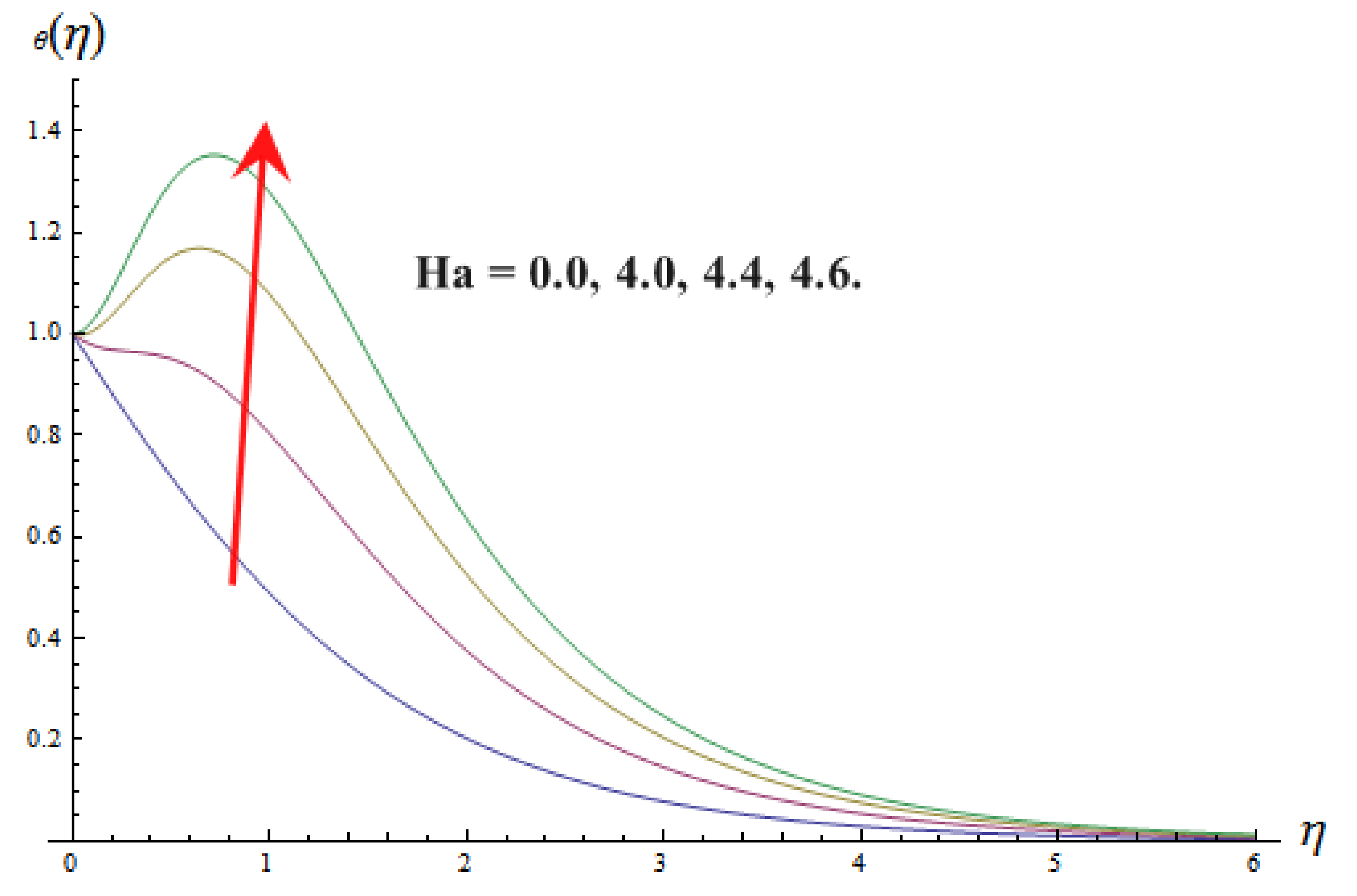
• It is also observed that magnetic parameter $\left(Ha\right)$, Eckert number $\left(Ec\right)$, and linear thermal radiation parameter $\left(Rd\right)$ upsurges the temperature distribution.
• The entropy generation enhances with increasing values of Prandtl number $\left(\mathrm{Pr}\right)$, Brinkman number $\left(Br\right)$, vortex viscosity constant $(\Gamma )$, magnetic parameter $\left(Ha\right)$, and thermal radiation parameter $\left(Rd\right)$.
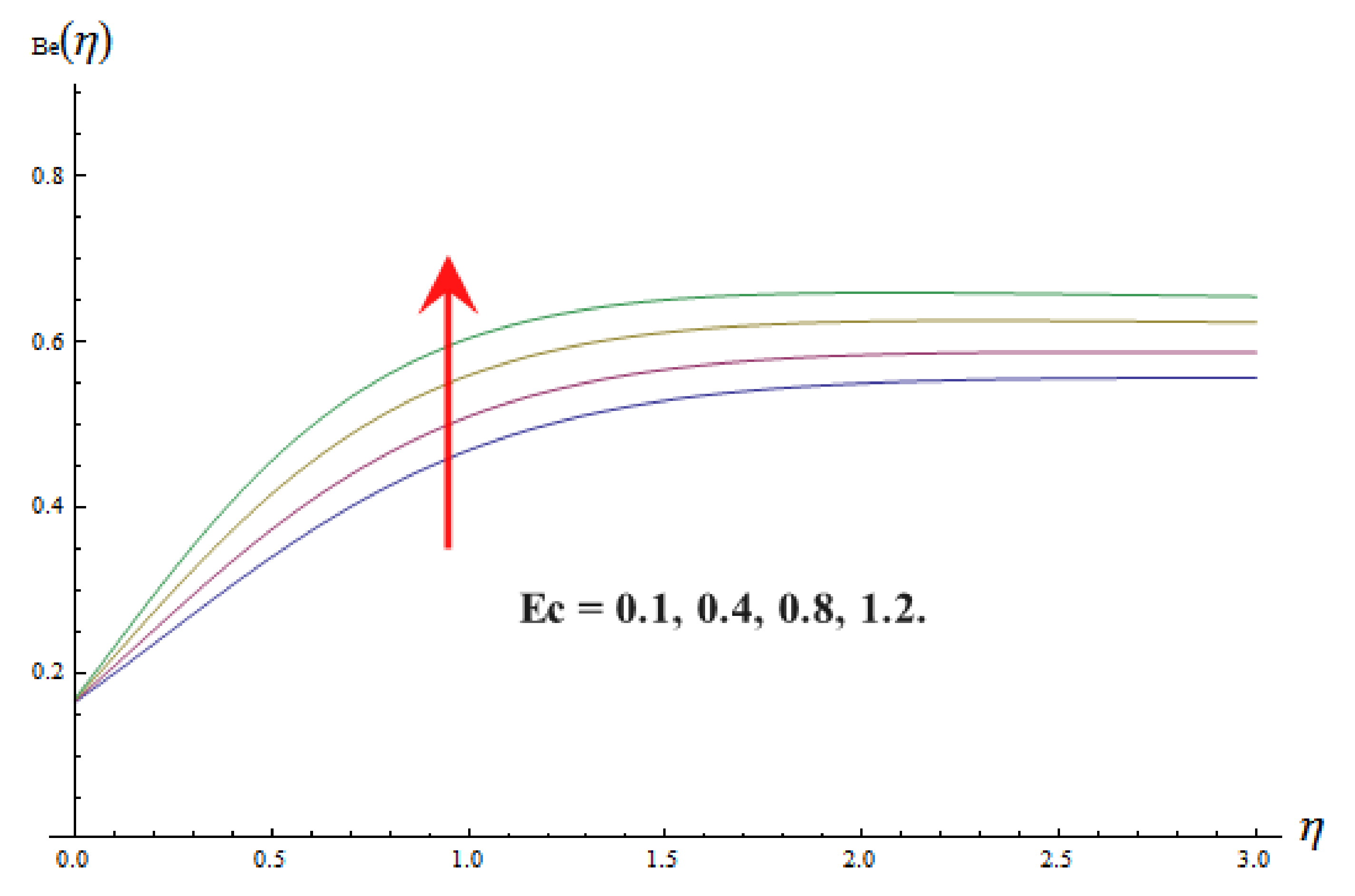
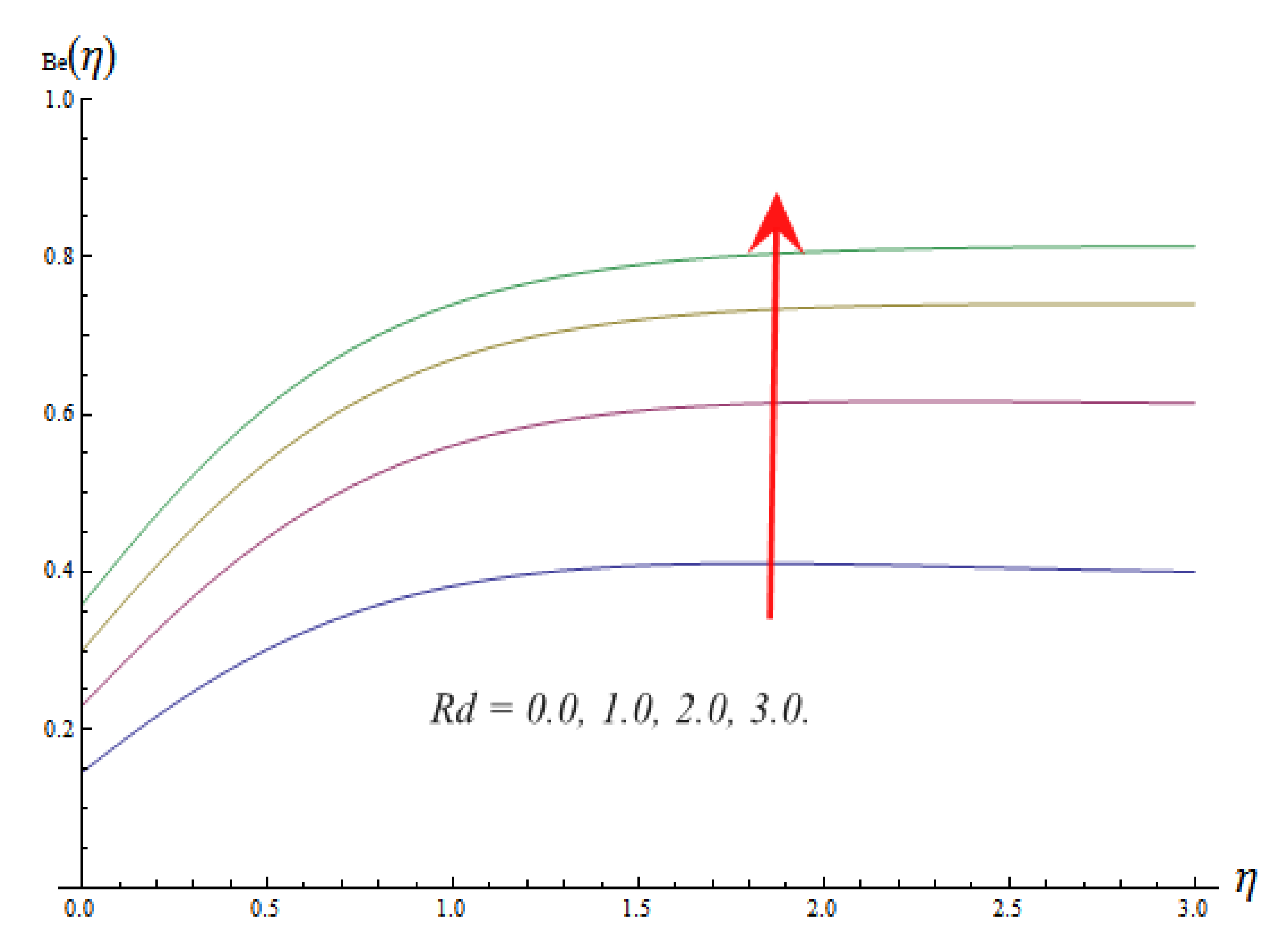
• It is concluded that the Bejan number is increasing in function of the Eckert number $\left(Ec\right)$ and linear thermal radiation parameter $\left(Rd\right)$ and Prandtl number $\left(\mathrm{Pr}\right)$, while decreasing in function of the vortex viscosity constant and Brinkman number.