Abstract
With large penetration of wind power into power grids, the accurate prediction of wind power generation is becoming extremely important. Planning, scheduling, maintenance, trading and smooth operations all depend on the accuracy of the prediction. However due to the highly non-stationary and chaotic behaviour of wind, accurate forecasting of wind power for different intervals of time becomes more challenging. Forecasting of wind power generation over different time spans is essential for different applications of wind energy. Recent development in this research field displays a wide spectrum of wind power prediction methods covering different prediction horizons. A detailed review of recent research achievements, performance, and information about possible future scope is presented in this article. This paper systematically reviews long term, short term and ultra short term wind power prediction methods. Each category of forecasting methods is further classified into four subclasses and a comparative analysis is presented. This study also provides discussions of recent development trends, performance analysis and future recommendations.
1. Introduction
According to the global wind energy council report 2022, wind power capacity added in 2021 was 93.6 GW which was the second best year. However, in the same report it is mentioned that, to meet net zero, a four times increase in installation is required by the end of the decade. This implies that wind power is going to play a key role in future worldwide energy requirements. However, irregularities and randomness in wind power generation severely affect large-scale access of wind power to the grid [1,2]. This impacts dispatch operation, power quality and stable power system operations. Therefore, an accurate wind power prediction method is very important to reduce the burden on grid dispatching operations and to improve wind farm management [3,4]. However, the accurate prediction of wind power generation is a complex task owing to the stochastic nature of wind speed. The accurate prediction of wind power is challenging due to the nonlinear behaviour of wind speed, its random patterns and its dependence on atmospheric pressure and temperature [5,6]. Due to the stochastic nature of wind speed, the accurate prediction of wind power generation is a complex task.
Being a very active field of research, a large number of wind power prediction models have been developed. Few review articles [7,8] on this topic are available. Reference [7] presents a detailed review of past and present methods in WPP along with the future scope in this area. Reference [8] presented a review of hybrid models based on empirical mode decomposition. In this article we present recent developments in WPP and provide quick access to meaningful works. Based on the type of prediction models, existing wind power prediction (WPP) methods are categorised into physical models [9], statistical models [10,11], and hybrid models [12,13]. Detailed physical analyses and descriptions of wind farm layout and wind turbines, and physical descriptions of meteorological and geographical conditions are required to build physical models. Physical attributes of geographical location such as terrain and wind turbulence affect the accuracy of the physical models. The physical models need various environmental parameters such as wind speed, wind direction, and air pressure. These parameters are obtained from the numerical weather prediction data which is updated once every few hours. In areas where the numerical weather prediction (NWP) system is not available the physical models are not useful. Due to the low update frequency of NWP data, physical models are not suitable for a prediction horizon of more than 6hrs, i.e., short-term prediction [14,15].
Several statistical models have been developed in the literature for WPP. In this review we have classified them into time series methods, machine learning methods and deep learning methods. Time series methods consist of linear and nonlinear time series-based models such as auto-regressive (AR), auto-regressive moving average (ARMA) [16], moving average (MA) and auto-regressive integrated moving average (ARIMA) [17]. Various machine learning (ML) methods such as support vector machine (SVM) [18], support vector regression (SVR), Gaussian process regression (GPR) [19], random forest and k-means clustering artificial neural networks are used for WPP.
With the development of high computing power and advanced machine learning and deep learning methods, accurate and effective wind power prediction methods have been developed. Various combinations of physical, statistical and deep learning methods have also evolved to improve prediction accuracy. Furthermore, data cleaning, preprocessing and feature extraction methods combined with advanced learning algorithms lead to improved results.
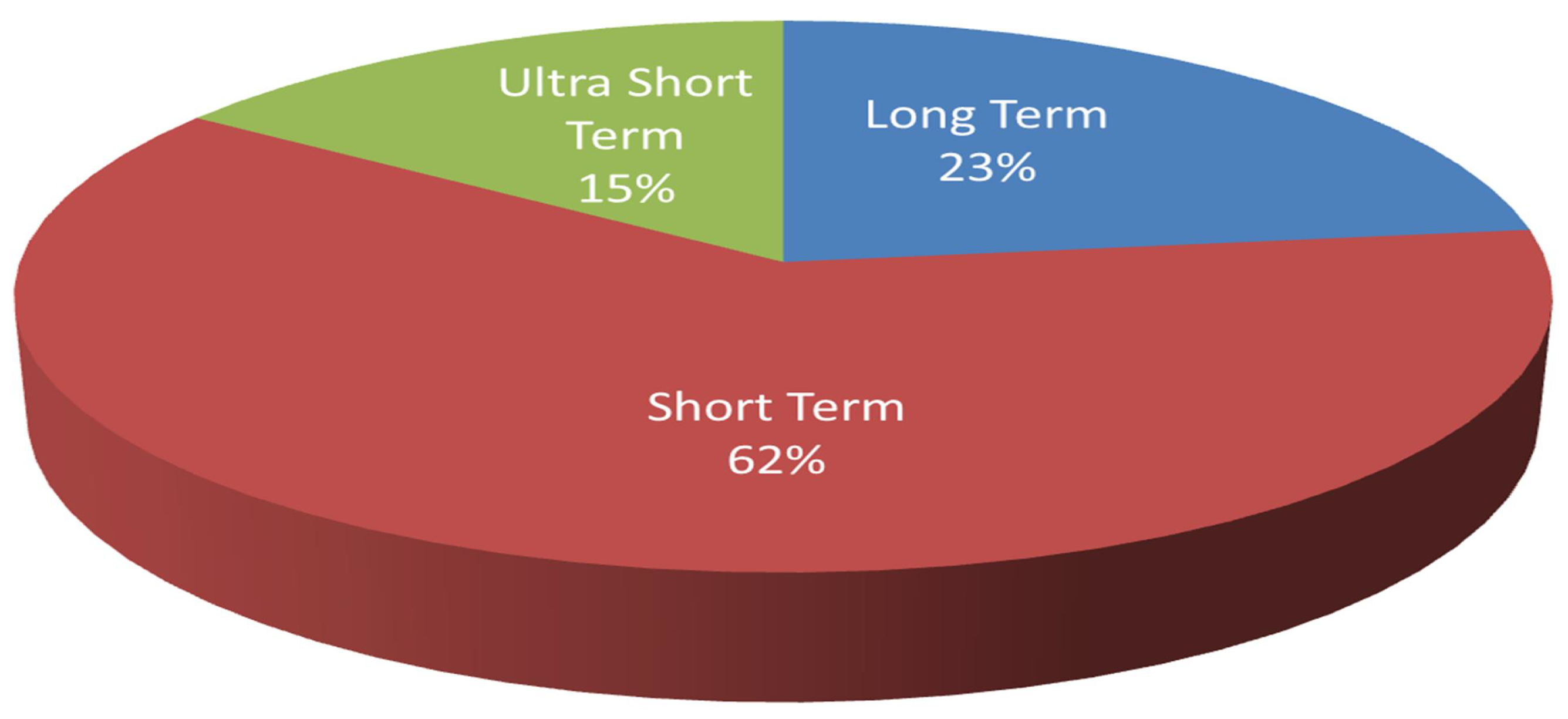
In this paper, we have systematically investigated WPP methods based on different prediction horizons, algorithms and evaluation criteria. In this review, we present detailed documentation of various algorithms, their performance and discussions. Wind power forecasting can be categorised depending on prediction horizon or prediction methodology. In Table 1 prediction horizons and the corresponding time range are listed. According to the prediction horizon, they can be categorised as long-term, short-term or ultra-short-term methods. Prediction methodologies are classified as physical, statistical and hybrid methods. With the recent developments in computing power and ML techniques, the statistical methods are further classified as time series methods, machine learning methods and deep learning (DL) methods. Hybrid methods are a combination of different prediction methodologies; it can be a combination of time series and ML or ML and DL or a combination of all of them. In this article, we have followed the prediction horizon for the categorization of WPP methods and, for each category, related prediction methodologies are discussed. The statistics of the number of articles referred to in this article are shown in Figure 1. In this review, we have considered articles published on WPP after 2015. It is clear from Figure 1 that recent research in this field mainly focuses on short-term wind power prediction.

Table 1.
Prediction horizons in WPP.
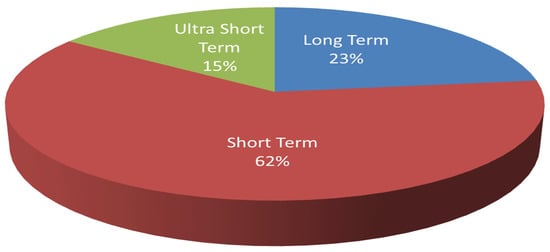
Figure 1.
The distribution of articles reviewed into long-term, short-term and ultra-short-term predictions.
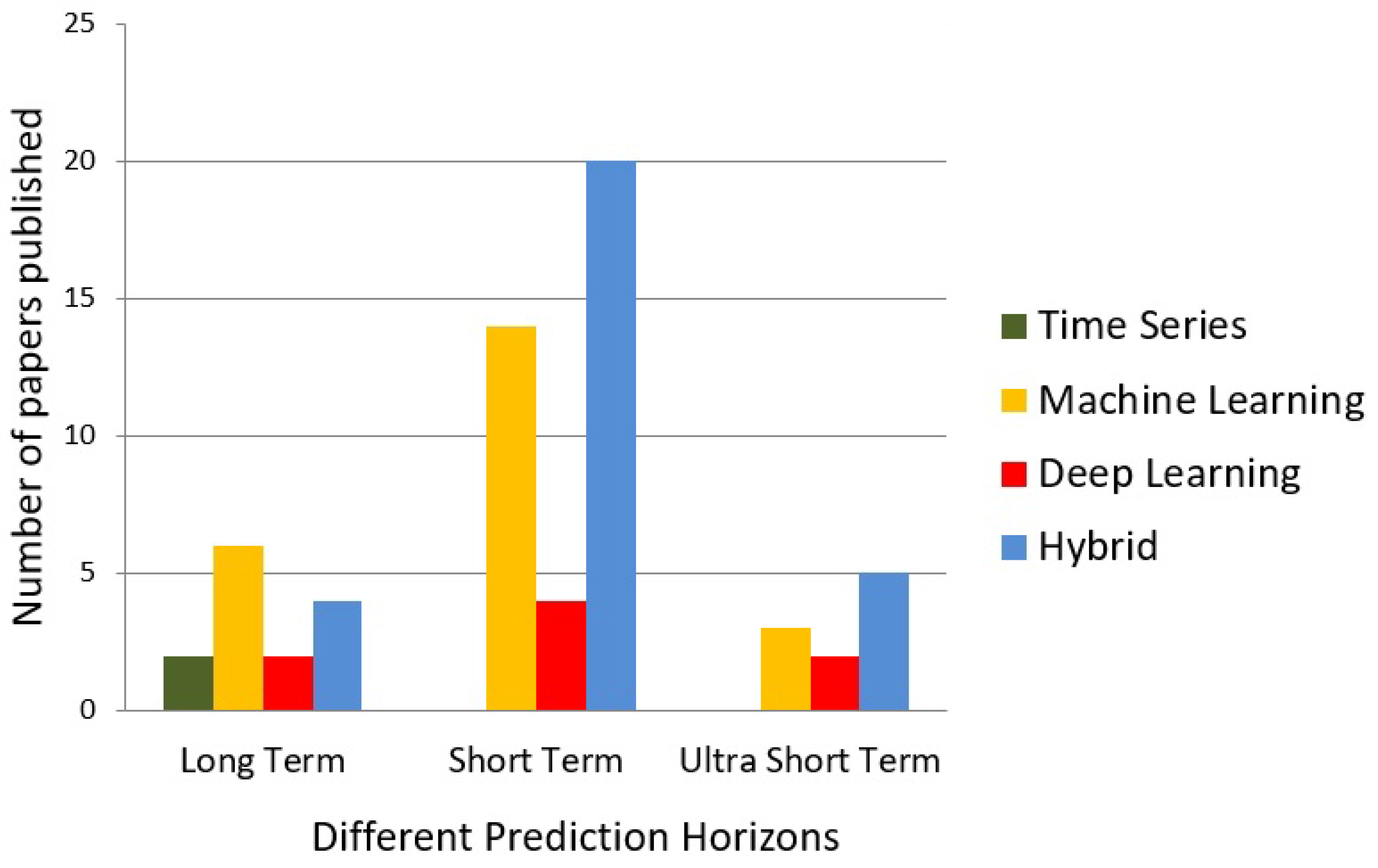
Depending on the amount of power generated in different time scales, the prediction methodologies are classified as long term, short-term and ultra short-term. For example, for turbine maintenance scheduling, optimization of operating cost and other management issues, a day ahead or 2 to 3 days ahead, i.e., long term predictions are required. From a day until several hours ahead, predictions are enough for planning related to load dispatch and for treading issues. Further, a shorter prediction horizon is required for turbine control, and real time grid operations. Several learning algorithms have been developed since the past decade that cover the wide range of forecasting horizons. Figure 2 shows recently published prediction methodologies (referred in this article) for long term, short-term and ultra short-term WPP. Clearly it can be seen that recently, researchers are focusing on short-term WPP. As far as prediction methodologies are concerned, a number of publications on hybrid methods are more for all the three prediction horizons. This implies that the hybrid models are more suitable and widely used for short-term prediction applications.
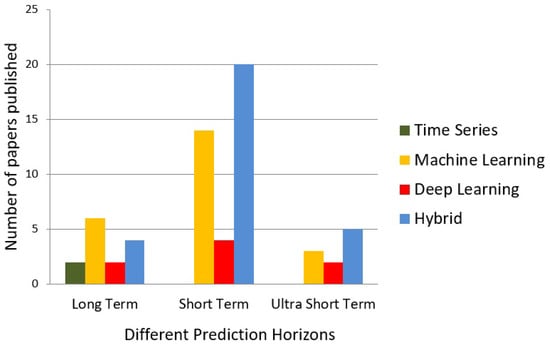
Figure 2.
Distribution of different categories of articles reviewed.
In this paper, recent advancements in wind power forecasting approaches are reviewed. Performance evaluation metrics are presented in Section 2. Classification of WPP methods based on prediction algorithms is presented in Section 3, Section 4 and Section 5. Detailed review of long term forecasting methods is discussed in Section 3. Different prediction algorithms developed for short-term forecasting are presented in Section 4, Furthermore, Section 5 reviews ultra short-term WPP methods in detail. Section 6 is devoted to detailed discussions and future scope in this area. Finally, the conclusions are presented in Section 7.
2. Performance Evaluation Metrics
Performance evaluation metrics are measures to judge or quantify the goodness or usefulness of the prediction algorithm. These metrics generally estimate the distance between original output and the estimated output. Performance of the wind power prediction models is evaluated using several statistical metrics; the following are frequently used performance measures. Let be the ith actual load value, be the ith predicted load value, the mean of the actual load value and N the total number of predicted points. Different evaluation metric used as performance measures are listed below.
- Mean absolute error (MAE):MAE is average value of absolute different between predicted and actual value.
- Root Mean Square Error (RMSE):RMSE computes the standard deviation of the residuals between predicted and actual values. Residuals defined the distance between regression line data points and RMSE measures the spread of these residuals.
- Mean Square Error (MSE):The mean squared error calculates the average of the squares of the error in the prediction.
- Mean Absolute Percentage Error (MAPE):The mean absolute percentage error (MAPE) is average of the absolute percentage error in the forecasts.
- Normalised RMSE (NRMSE):Normalization of the RMSE value is useful for fair comparison of the model on different scales. The normalization can be performed with respect to mean or standard deviation. The following is the Mean NRMSE.
- Normalized Mean Absolute Error (NMAE):NMAE is used to compare the MAE of models with different scales. The NMAE is a two-step process. The normalization can be performed with respect to mean, range or inter quartile range. The following is Range NMAE.
- Root Mean Square Prediction Error (RMSPE):RMSPE calculates the root mean squared percentage error regression loss.
- R-Square ():is the coefficient of determination, it computes the variance of the prediction from the measured data. A negative value of implies worse prediction while it can reach a maximum value of 1.
3. Long Term Prediction
Maintenance of wind turbines and other management issues are planned with the help of long term prediction. These activities do not require highly accurate prediction accuracy.
3.1. Time Series Analysis
Time series prediction models are mathematical models that estimate model parameters from the historic data. Time series prediction models can capture nature of system and generate predictions. Time series models with different orders generate different results.
A polynomial extension of the AR model, i.e., PAR is presented in [20]. A polynomial AR (PAR) model of degree 2 derived from Volterra series expansion (9) is used for wind power prediction. A comparative study of PAR with MLFF, MLP, ANN, AR and ANFIS is also presented in [20]. Compared to these nonlinear models PAR requires less parameters, is computationally efficient, and performs better for longer prediction horizons (more than 12 h). Experimental analysis was performed on the data published for Global Energy Forecasting Competition 2012 [21] and NRMSE, NMAPE and bias were used as error measures. In (9), is the intercept, excitation sequence is n independent and identically distributed with distribution and are coefficients for first, second and order polynomials, respectively, degree of the non-linearity is p and the AR order k.
Large fluctuations in wind power within a relatively short time interval caused by wind is defined as a wind power ramp event. These power ramps lead to a potential disaster and affect the stability and safety of the wind farms and power grids. In order to take preventive action before such disaster happens, the accurate prediction of power ramp events is most important. Wind power prediction and ramp event detection algorithm is presented in [22]. Two models have been proposed for wind power prediction. Long term trends in the data are captured using wind power curve model utilizing NWP. A correction model improves the local prediction accuracy using a multivariate prediction algorithm. For power ramp event detection a well-known swinging door algorithm [23] is used and a higher accuracy of ramp event prediction was reported. Table 2 list the time series methods for long term WPP and their respective performances.

Table 2.
Time series methods for long term WPP.
3.2. Machine Learning
A wide range of machine learning models including extreme learning machine, support vector machine (SVM) [18] and the Gaussian process [19], backpropagation network [24] and radial basis function are applied for WPP. These methods learn a nonlinear regression function that fits the relationship between the input feature space and the output wind power from the data.
Back propagation neural network (BPNN) is a widely used nonlinear method for wind power prediction. In [25], the basic structure of BPNN is used along with the conjugate gradient method for weight optimization and termed the method as conjugate gradient neural network (CGNN). There are various meteorological factors such as air pressure, humidity, temp etc. influence the wind power, in [25] along with wind speed and wind cos above mentioned parameters are also taken as input to the CGNN. For experimental validation the data from wind farms in Mongolia and China is used. Accuracy as well as time taken by the proposed CGNN and existing Racial Basis Function Neural Network (RBFNN), Steepest Gradient Neural Network (SGNN), and Extreme Learning Machine (ELM) is reported. Due to conjugate gradient optimization, the training time as well as MAE of the CGNN are less than those of the other compared methods. Ref. [26] also used the swinging door algorithm for power ramp prediction. In [26], first, the data are divided into two data segments—a ramp window or a non-ramp window. The optimum window size for these two events is decided using a genetic algorithm. Once the optimum window size is decided then the power in the optimized window is predicted using SVM, which receives NWP data as input data. Depending on the predicted power, the swinging door algorithm detects whether it is a power ramp event or not. To validate the results, different window sizes were analysed and the accuracy and false positive rate of ramp detection were reported.
Support vector machine (SVM) [18] is a popular machine learning algorithm due to its generalization ability and high dimensional data handling capability. SVM is widely used for wind speed and wind power prediction. The accuracy of the SVM depends on various hyper-parameters of kernel and cost function. In [15], SVM with hybrid kernel function is proposed for wind power prediction. Two separate kernels polynomial and radial basis function (RBF) were used to build a hybrid kernel that can capture correlation in the local and distant data samples. The parameters of the hybrid kernel are estimated using an improved particle swarm optimization algorithm. Experimental analysis showed better accuracy of SVM with hybrid kernel in terms of RMSE, MAE and MAPE compared to ARMA, SVM with only RBF and the echo state network. Table 3 shows machine learning models developed for long term WPP.
Due to the no-nstationary behaviour of the wind energy, a single algorithm is not able to fit the data accurately. In this situation, ensemble learning methods are used to improve the accuracy. In ensemble learning, multiple base learning methods are combing. Improvement of the accuracy can be achieved by one of the following approaches—to perturb the training data, model parameters, attributes of the data and base models. The selection of appropriate base learners is also important to increase accuracy. Non-probabilistic learning methods provide point prediction outputs but do not provide an estimate of uncertainty. Gaussian process regression is a powerful nonparametric Bayesian method for supervised learning. Along with the probabilistic predictions, it also provides confidence intervals of predictions. Ensemble learning model in [27] utilizes Gaussian process regression as the base learners. In order to improve the accuracy and diversity of the learning methods, first the perturbations on training data and input attributes are combined. Next, the Gaussian mixture model (GMM) clustering is applied to create different clusters of the data. Further, GPR is applied on each cluster separately to fit each cluster individually. This method is termed the selective ensemble of finite mixture Gaussian process regression models (SEFMGPR). Performance of the ensemble learning improves with the pruning method. In [27], a genetic algorithm-based pruning method has been adopted to select significant models. The pruning algorithm enhanced the performance as well as reduced the model complexity.

Table 3.
Machine learning methods for long term WPP.
Table 3.
Machine learning methods for long term WPP.
| Sr. No. | Articles | Models | Evaluation Metric | Evaluation Value |
|---|---|---|---|---|
| 1 | Fang et al., 2016 [28] | Improved GPR | NRMSE | 0.14564 |
| 2 | Tian et al., 2016 [25] | CGNN | MSE | 0.004 |
| 3 | Tinghui et al., 2017 [26] | Swinging door+SVM | Precision, Recall Accuracy, Error | 0.8059, 0.8390 0.8747, 0.1253 1 |
| 4 | Zhongda et al., 2018 [15] | Modified SVM | RMSE MAE MAPE | 59.313 50.344 0.038 |
| 5 | Bogdan et al., 2021 [29] | Comparison of ML | RMSE MAPE | 412 0.267 2 |
| 6 | Huaiping et al., 2021 [27] | ensemble of mixture of GPR | RMSE R² | 1.7771 0.9057 3 |
1 for 2 h time window. 2 indicate hourly prediction, daily prediction values are 13.9% 65.60. 3 indicate 4 step ahead prediction.
Another Gaussian process based approach in [28] proposed a composite covariance function (CF) for the GP. Performance of the GPR varies with the CF. The composite CF proposed in models the relation between wind features and auxiliary features. The composite CF is the multiplication of squared exponential CF that can integrate multiple NWP features into a single composite CF. The GP approach in [28] used the 2012 global energy forecasting competition wind power forecasting data, and outperformed all of the competitors on this data.
A comparative analysis of different machine learning techniques to forecast the production of wind energy not for a single wind farm but for an entire country Poland has been presented in [29]. They have presented the results of two decision tree based algorithms, i.e., random forest (RF) and Extreme Gradient Boosting (XGB) and two neural network based algorithms, i.e., artificial neural network (ANN) and deep neural network (DNN). For the experimental analysis, various interesting inferences were also presented in [29]. Although all four algorithms predicted wind power with high accuracy, XGB was better in terms of MAPE for hourly predictions and ANN for daily sums of produced energy. Performance analysis for different seasons was also presented and it was inferred that MAPE was the highest in June and the lowest in January. This is due to the fact that the windiest day occurs in January and the calmest day appears in August. The lowest variance in prediction was reported in the winter season and was highest in the summer season.
3.3. Deep Learning Models
Wind power data are characterised as highly nonlinear as well as high dimensional. Compared to shallow machine learning models, deep learning models are more suitable for such data. With high computing power and the ability to fit complex and nonlinear function deep learning methods are widely used for WPP.
In [30], instead of statistical features, stacked autoencoder (SAE) features are proposed for wind power prediction. Structural properties of the wind data are effectively extracted using an autoencoder. A two level autoencoder is designed for structural feature extraction. During the training stage, the input data are divided into small data segments and predictions are performed on those segments individually. Features are also extracted for each segment. For wind power, a cluster-based ensemble regression is proposed, where the data segments are first clustered and then a regression model is learned separately for each cluster. Compared to statistical features 12.63% improvement in the prediction accuracy was reported when SAE features are used.
A combinatory approach for feature generation, feature selection and power prediction is presented in [31]. They presented an improved wavelet neural network (WNN) that uses the Morlet wavelet as an activation function of the neural network for feature extraction. Next, relevant features are selected using a maximum dependence, maximum relevancy, and minimum redundancy (MDMRMR) feature selection algorithm. Later they trained a 2D CNN using these selected features as input and PSO based improved optimization algorithm. Shallow 2D CNN is build that consist of input layer, two convolutional layers, two pooling layers and one fully connected layer. Extensive experimentation was performed to validate the proposed method. This combinatory approach is evaluated for three different prediction horizons i.e., an hour ahead, day-ahead, and 48 h and two separate databases for this analysis. Accuracy of both the methods is reported with respect to different measures. Comparative analysis of deep learning methods in long term WPP is shown in Table 4.

Table 4.
Deep learning methods for long term WPP.
3.4. Hybrid Approach
Multiple prediction horizons are proposed in [32] using a hybrid approach for long term prediction and reinforcement learning for short-term prediction. For long term wind power prediction sigma point Kalman filter is modified using complementary ensemble empirical mode decomposition. Initially, sigma points are used to limit the boundary effects; next the historic data are decomposed into various intrinsic mode functions with steady-state features using the complementary ensemble empirical mode decomposition (CEEMD) method. For power prediction, each stable sequence is updated to reconstructed using sigma point based Kalman filter. For short-term prediction, a deep deterministic policy gradient (DDPG) method is proposed in [32]. Prediction results are compared with different state-of-the-art methods on the basis of MAE, MAPE, SDE and RMSE.
A hybrid approach to predicting wind power from the numerical weather prediction data and actual wind power data are presented in [33]. Daily similarities are observed in the wind power and based on these similarities the data can be easily clustered. Using spatial similarities in the NWP data, k-means clustering is used to split the data into different subsets. Next, the samples matching with the predicted day are used to train the generalized regression neural network (GRNN) model. Experimental analysis shows that GRNN can effectively model the nonlinear relationship between the wind data and the predicted output. The results also show the impact of clustering on the long term wind power prediction. In [34], a bagging neural network (BaNN) is also combined with k-means clustering for long term wind power prediction. Prediction accuracy is enhanced by fine tuning the BaNN parameters using an optimization method. They also used improved empirical mode decomposition (IEMD) to reduce the fluctuations during the forecasting process to improve the accuracy. The Experimental analysis was performed on the data collected from three different farms. Since CNN do not provide good prediction results, such hybrid approaches with improved clustering methods and advance neural networks need to be further explored for long term predictions.
An hourly forecast of day-ahead wind power method proposed in [35] combines variational mode decomposition (VMD) and LSTM. Compared to empirical mode decomposition (EMD), VMD provides less fluctuation and retains more adequate data information for forecasting. VMD decomposes the input wind series data into different modes, separate LSTM with three layers is trained for each mode. Experimental analysis of two different VMDs, recursive (R) VMD and direct (D) VMD with LSTM is presented in [35]. Performance of the VMD-LSTM method is compared with the BP, ELM, and SVM and results show that VMD- LSTM achieved significant results. RMSE, MAE and MAPE are reported for one-day, two day and three day-ahead prediction. Hybrid methods and their corresponding performances referred to in this article are listed in Table 5.

Table 5.
Hybrid methods for long term WPP.
4. Short-Term Prediction
Short-term wind power prediction assists with deciding power generation plans, regional dispatching, and maintenance plans.
4.1. Machine Learning
Instead of using a single ML algorithm, the combining of different ML models into an ensemble predictor provides improved results. The heterogeneous ensemble approach in [36] used decision trees (DT), k-NN, or support vector regressors as base algorithms. They also analysed the performance of individual as well as different combinations of the base predictors. Different combinations provide different accuracies and computational complexity. On the basis of these two parameters, the combination of DT and SVR provided improved results. Experiments were conducted using the power output data of the five wind parks. Ensemble of Boosted Trees, Random Forest, and Generalized Random Forest are presented in [37] for short-term wind power prediction. Correlation or time dependencies in the data are considered in ensemble learning, which improved the accuracy. Time lagged values are added as new features and a feature importance analysis is performed to decide the impact of features on the forecast. The proposed method is evaluated using data from five farms and compared with SVR and GPR in terms of , RMSE and MAE.
A variant of Gaussian process regression model is proposed for short-term prediction in [38]. Computational complexity of the GPR increases with dimensionality of the data. In order to reduce computational complexity and to model the non-stationarities in the wind data, a new teaching learning based optimization (TLBO) is proposed. Optimal parameters of the Gaussian process are learned during the training process using the TLBO. It also helped to improve the learning rate and computational complexity. This method effectively forecasted the data from a single farm as well as from an entire Ireland. Performance of the GPR outperforms many other ML methods with proper selection of covariance function and optimization. However, even with the optimally tuned parameters, a drastic reduction in accuracy and confidence interval is observed if the missing data are encountered. In [39], data imputation approach is used to handle missing data and new datasets are generated. Missing data are reconstructed from the distribution of the data and the iterative learning algorithm. Next, the GPR model is built using the reconstructed data for wind power prediction. Performance of the proposed approach is compared with SVM and MLP using data from three different wind farms and GPR reported better results in terms of RMSE and MAE.
Appropriate parameter selection usually helps to improve the accuracy of the learning algorithm. Out of multiple parameters and features available in the meteorological data, the work in [40], used most useful features of the wind data. Using the correlation and the importance measures, spatially averaged wind speed and wind direction are selected for the wind power prediction. Next, random forest is selected as a prediction algorithm due to its low computation complexity compared to other ML methods. Impact of selected features on the prediction accuracy is also analysed.
Short-term wind power prediction in [41] explores correlation between wind speed and wind power data. This method combines NN and PLS to form Nonlinear Partial Least Square (NPLS) method. The historic data are applied as input to the NN and the output of the NN is provided as input to the PLS which provides the final wind power predicted value. For experimental analysis two well known NNs i.e., BPNN and RBFNN are used and combined with PLS. The performance of BPE-PLS and RBFE-PLS and compared with SVM, BPNN, RBFNN and PLS. For experimentation, datasets with three different weather conditions are used. In terms of RMSEP measure, the RBFE-PLS algorithms outperformed all the other method on all the dataset.
Extreme learning machine is a feed forward neuron network with three layers, input layer, hidden layer and output layer. A few wind power prediction method used ELM as a regressor, but the training strategy (leave one out) is not suitable for high dimensional data. Kernel ELM is proposed in [42] adopts k-fold cross validation with its average MSE as error function. High nonlinearity of wind data are effectively captured by kernel ELM. Performance of learning machines depend on the parameter selection, in case of KELM, optimal values of regularization coefficient and kernel width improves the performance. In [42], KELM is trained using the wind power data and optimal parameters are learned using differential evolution (DE) optimizer and average MSE of k-fold cross validation. This approach improves the generalizability as well as stability of the model. Performance of the KLEM with cross validation and DE optimizer (DECVKLEM) is compared with KLEM with cross validation and GA as an optimizer. Compared to GACVKLEM, only 8.34% improvement has been observed in case of DECVKLEM, but the convergence speed of DE base CVKLEM is more. In [43] ELM is trained using PSO and combined with Adaboost for short-term wind power prediction. Performance of the Adaboost-PSO-ELM is compared with PSO-BP, GPR, PSO-SVM, PSO-ELM, GA-ELM, few tree based methods and Adaboost-PSO-BP and better performance of Adaboost-PSO-ELM is reported.
Accurate wind speed prediction is important for NWP based WPP, so to improve the accuracy of WPP, the NWP data from three different organizations is combined in [44] and used for prediction. Three forecasted wind speeds from NWP are fused using weighted naive Bayes (WNB) method and accurate wind speed is estimated. Next, wind power prediction is performed using BPNN. Ref. [45] modified BPNN and proposed a small-world BPNN (SWBP). Small-world networks ties to reduce the gap between artificial and biological neural networks [46] by modifying node type, connections between the nodes, and realization function. Input features for the SWBP are selected using modified mutual information (MI) and applied to the SWBP. The proposed model is compared with BPNN for 15 min-ahead power prediction and found better than BPNN in terms of training time, prediction accuracy and convergence.
Uncertainty and missing values in the wind data incurs difficulties in the accurate prediction. In such cases, grey models are found useful. In [47], grey model GM(1,1) with background value optimization is proposed for wind speed prediction. Two separate grey models are designed and combined to improve the wind speed prediction accuracy. Further, for WPP, SVR is designed. Various parameters of SVR such as cost function, precision and variance of the kernel function are estimated using PSO optimizer. Results of PSO-SVR are compared with ARIMA on the basis of MAE, MAPE and RMSE and nearly 30% improvement in speed prediction and 35% improvement in power prediction are reported.
Multimodality, nonstationarity, and skewness are characteristics of the wind power which make wind power prediction a challenging task. In [48], an infinite Markov switching autoregressive model is used for wind power forecast. Using a nonparametric Bayesian approach, a posterior predictive distribution is computed which is further used to predict wind power and uncertainty of the forecast. Probabilistic methods provide estimate of the value as well as uncertain in prediction. Compared to MSAR, TVQR and BELM model, the proposed nonparametric method performed better.
Pattern Sequence-based forecasting (PSF) [49,50,51] method has shown its potential in short-term wind speed forecasting accurately [52], but for the first time, it offers higher accuracy for wind power time series in [53]. This is a kind of its own approach, where the wind power time series was first smoothened down with the reference of the corresponding wind speed time series dataset and then a smoother wind power time series was forecasted with the PSF algorithm. This smoothening process comprised of generation of label sequences in the PSF method and a matching process with Naive Bayesian. The proposed approach was observed to be less chaotic for wind speed predictions than the existing ones.
An integrated approach is employed in [54] for short-term wind power prediction. Uncertainty, nonlinearity, missing data extended training time and computational complexity these are various factors that affects performance of the prediction system. Uncertainties and missing information in the data are modelled and the controlled fuzzy network, wavelet decomposition models the dynamic behaviour, and nonlinearities are modelled with NN. In [54], an integrated approach of these methods is presented. Similar to ANFIS, a fuzzy NN is proposed where a wavelet function is used as an activation function and the combined model is termed as Fuzzy WNN (FWNN). Optimization of this combined model is carried out using PSO and gradient descent. Performance of the FWNN is compared with 7 ML methods, RBF, SVR, ANN, ANN-GA, ANN-PSO, ANFIS, ANFIS-GA and ANFIS-PSO. Table 6 list the details of the machine learning methods in short-term WPP.

Table 6.
Machine learning methods for short-term WPP.
4.2. Deep Learning Methods
In [56], DNN based ensemble learning is proposed where base-regressors and a meta-regressor both are built using DNN. First several autoencoders act as base methods and are trained using the training data and transfer learning. Transfer learning saves the time to train the system from scratch as well as provides suitable weight initialization for training. Due to abrupt changes in the meteorological conditions, the transients are observed in the predictions. These transients are smoothed with the help of a meta-regressor. In [56], Restricted Boltzmann Machines (RBMs) are stacked to Deep Belief Network (DBN) which acts as a meta learner. Once the base learner is trained, the test data features and predictions from the base learners on test data are applied as input to DBN for final prediction value. Data from five wind farms is uses for evaluation of the algorithm and the results in terms of RMSE, MAE and SDE are reported. Two step approach in [57] uses DBN and k-means clustering for wind power prediction. The noise in the NWP greatly affects the accuracy of the learning method, so the NWP data are divided into different clusters using k-means clustering. Next the clustered data (e.g., NWP wind speed, wind direction, humidity, temp etc.) is applied as input to the DBN. The DBF consists of five layers with three hidden layers. For prediction, the test data are divided into clusters and the clusters belonging to those data are fed to the trained model to obtain the wind power. In comparison to BPNN and WMNN, the performance of the proposed method improved by 44%.
A Gaussian mixture model combined with NN is termed the Gaussian Mixture Density Network (MDN). The conditional density function of the data is predicted using a trained MDN which is further used to predict the required uncertainty information. The parameters of the Gaussian mixture are computed using a feed forward NN. An improved deep MDN proposed in [58] uses beta distribution to solve density leakage associated with MDN and modified ReLU activation function to handle NaN issue associated with activation function. Data from seven wind farms is used and proposed method is compared with 8 existing methods and the improvement in the performance is recorded. Time and memory complexity analysis is also presented and the proposed method requires 10 min training time.
NWP provides various parameters such as wind speed, wind direction, temp, air pressure etc. of which wind speed is an important parameter for power prediction. A gated recurrent unit neural network (GRUNN) presented in [59] makes use of the variance of the NWP wind speed prediction error for wind power prediction. It utilizes both temporal as well as statistical characteristics of the time series data. Bidirectional GRUNN in [59] is a simple version of LSTM [60] with two gates in GRU. In the proposed method, first, local features are extracted from the NWP data and a weight time series is constructed using the NWP wind speed prediction error and extracted features. This weight time series is applied as input to GRUNN which corrects the NWP wind speed. Once correct wind speed is obtained then Power Forecasting is performed using the Wind Power Curve Model. This computationally efficient method is compared with SVN and ANN and the results in terms of RMSE and MAE are presented.
Data cleaning and feature reconfiguration approach using CNN is proposed in [61] for WPP. It has been observed that performance of the prediction system degrades in presence of outliers. In [61], outliers are identified using density based clustering method. After data cleaning the wind data are applied to CNN, since CNN requires images as an input; a feature reconfiguration is an essential step. Each sample of wind data has two features; wind direction and wind speed along with the label, i.e., wind power. Wind direction and wind speed sample along with the corresponding temporal information and label are arranged in a 2D matrix which is applied as an input to the CNN. The CNN architecture consists of one input layer, two convolutional layers, and one fully connected layer, ReLU is used as an activation function, no pooling layers are used and parameter tuning is performed by trial and error. MAE, MAPE and NRMSE are used as performance measures for the evaluation of the proposed scheme. This is the only method that re-configures wind data as a 2D matrix and uses an image based deep learning approach. In our opinion, if parameter tuning is performed by an optimization method then accuracy can further increase. Table 7 shows the deep learning methods for short-term WPP and their performances.

Table 7.
Deep learning methods for short-term WPP.
4.3. Hybrid Methods
LSTM and genetic algorithm (GA) are combined for wind power prediction in [62]. The performance of the LSTM algorithm largely depends on the window size. A smaller window size implies no information is forwarded and carried, whereas a larger window size implies noise in the past samples. A genetic algorithm is used to learn optimum window size. Experiments were performed on the dataset from seven wind farms in the European region. The data consisting of sixteen features measures a duration of 48 h and a 12 h interval is applied as an input to the Genetic LSTM (GLSTM) network. GA is used to train the network to find the optimum window size and number of neurons. Performance of GSTM is compared with the ARIMA, a few deep learning methods and SVR of three different kernel functions. To validate the effectiveness, six variants of GLSTM are applied on the seven datasets and improvement in the performance was reported. Closed to zero MSE, MAE and RMSE were reported with the proposed GLSTM network.
Wind power ramps events are predicted in [63] using different ML algorithms. A comparative analysis of ML methods to predict ramp events has been presented. In this hybrid approach the data from numerical-physical models is applied as input the various ML algorithms. The effectiveness of SVM, GPR, ELM and MLP for ramp event prediction is experimentally verified in [63]. RMSE, MAE and sensitivity are used as performance measures for evaluation of these methods on three wind farm dataset. The performance of GPR outperformed other methods in terms of all the measures.
Decomposition methods for WPP decompose the wind power time series into different components depending on different characteristics such as frequency, scale [64,65]. Next different prediction algorithms can be applied on these components for WPP. These decomposition methods can efficiently model the nonlinearities, however in many cases these components shows chaotic behaviour which degrades the prediction accuracy. To remove the uncertainty and low amplitude variations from these components and to improve the accuracy, singular spectrum analysis (SSA) [66,67] was found to be very useful. In [14], ensemble empirical mode decomposition (EEMD) is used to decomposed the time series data into different components. After determining the chaotic components, SSA is applied to remove the impact of the chaotic components on the accuracy. The proposed method has two stages—a decomposition stage and a prediction stage. The first stage consists of EEMD, chaotic TS analysis, and SSA and is referred to as multi-scale singular spectrum analysis (MSSSA). In the next stage, the authors used LSSVM-based framework as a prediction algorithm and developed an iterative multi-step short-term WPP method. Due to chaotic TS analysis and iterative multi-step algorithm, the accuracy of the prediction for both chaotic as well as non-chaotic components increases. The proposed method is evaluated on historical data from farms located in Spain and Canada.
A short-term wind power prediction method with high accuracy is presented in [68]. The hybrid prediction method combines empirical mode decomposition and kernel ridge regression (KRR). Mutual effects in different components of time series data are isolated using EMD. They further combined RVFL and ELM with EMD and comparative analysis of EMD-KRR, EMD-RVFL and EMD-ELM is also presented. To reduce computation complexity and improve the training time, an improved version of EMD-KRR is also presented in [68]. The proposed algorithm is evaluated on four different prediction horizons, i.e., 10 min, 30 min, 1 h and 3 h ahead and comparable improvement in accuracy and computation time is reported. In order to avoid limitations of EMD (mentioned in an earlier section), Ref. [48] combined VMD with multi-kernel ridge regression (MKRR) instead of EMD. Improvement in the performance is reported over its EMD counterpart.
Wavelet decomposition is widely used to decompose a signal into different frequency bands. Use of the wavelet kernels as an activation function of the CNN is recently trending in wind power prediction algorithms. In [69], wavelet kernel is used in LSTM and achieved 30% improvement in performance compared to existing wind power prediction methods. Gaussian, Morelet, Ricker and Shannon are four different wavelets that are used as activation functions. LSTM composed of four layers is trained using Rmsprop optimizer for wind power prediction. Data from seven farms in the European region are used for the evaluation of the work, results of four different wavenets (wavelet + LSTM network) on the data from seven wind farms are reported in terms of MSE, MAE, MAER, MAPE, and R2. The lowest prediction errors are observed in the case of all four networks.
Depending on the weather conditions, the wind speed varies and hence wind power generated. Based on the wind speed there exists different wind grades such as breeze, cool breeze, strong wind etc. Fuzzy k-means clustering is applied in [70] to classify the historic time series data into these wind classes. Each class corresponds to different speed hence the wind power data corresponding to each class and amount of power generated by each class will be different. Therefore instead of learning single function that can fit all these classes, separate SVR is trained for each class. The optimization of various SVR models is performed using enhanced harmony search (EHS) algorithm. The authors also presented the uncertainty analysis in terms of confidence interval using EHS-based QR approach. The proposed multiple SVR-based method provides 3 h-ahead 15 min wind power forecasts.
Wind power series is characterised by long memory characteristics and strong unpredictability. The forecasting method should be able to capture both the characteristics. Hybrid approach in [71] combines autoregressive fractionally integrated moving average ARFIMA to capture long memory characteristic and LSSVR to capture nonlinearities in the data. Such integration of linear and nonlinear component for wind power forecast improves the performance. Experimental analysis and comparison with ARFIMA, LSSVM and hybrid ARFIMA-BP demonstrates the superiority of the ARFIMA-LSSVM model. Combination of time series and ML method are computationally efficient solution for short-tern wind power prediction.
Two optimization algorithms are employed in [72] to optimize ANFIS [73] for short-term wind power prediction. The initial parameters of ANFIS are randomly initialized and fuzzy c-means (FCM) clustering is used to generate fuzzy inference structure (FIS). Two optimizers GA and the PSO run simultaneously and independently and optimal model parameters are selected based on RMSE. The GA–PSO hybrid algorithm performs better than BPNN, GA-BPNN, and NF-based forecast models. Hybrid approach composed of DWT, seasonal autoregressive integrated moving average (SARIMA), and LSTM is proposed in [74]. First, the input data are cleaned using data pre-processing methods such as isolation forest, re-sampling, and interpolation. Next, the pair of DWT and IDWT is applied on the cleaned data to decompose data into different components and to remove noise. Next the approximation and detail components are analysed by SARIMA model. SARIMA being sensitive to seasonal components is more suitalbe than ARIMA for non-stationary datasets to improve the prediction accuracy. Finally each decomposed band is processed through LSTM for power prediction. Combined effect of DWT, SARIMA and LSTM has shown drastic improvement in the prediction accuracy.
In the case of ML and DL models, it has been observed that accuracy largely depends on hyperparameters and therefore optimization methods play an important role. In [75], training an LSTM novel optimization method is proposed. The hybrid approach in [75], ARIMA and LSTM are combined for short-term WPP. After data preprocessing and assessing stationarity, three different optimization approaches are applied for WPP. Grid search is applied to find optimum hyperparameters of ARIMA, LSTM. Along with grid search Optuna optimizer is proposed to accelerate the process of hyperparameter search. The integration of preprocessing, outlier removal, imputation, resampling and optimizer along with ARIMA and LSTM has resulted into significant improvements in results. Hybrid methods for short-term WPP are listed in Table 8.

Table 8.
Hybrid methods for short-term WPP.
5. Ultra Short-Term Wind Power Prediction
5.1. Machine Learning
A multi-linear regression algorithm is presented in [87] for ultra short-term WPP. Initially, the dimensionality of the data is reduced and only relevant parameters from the NWP data are selected. Next, phase space reconstruction is performed using a covariance matrix and eigen values. Further, state variables of the regressive model are extracted from the proposed phase space. Finally the multivariate regression model provides the predicted wind power. Performance of this approach is compared ARIMA, BPNN, LSSVR and single-variable phase space reconstruction and proposed model found more accurate and fast.
Ultra short-term (10 min) wind power prediction is presented in [88] using ELM wherein the weights are optimized using the Salp Swarm Algorithm. The input dataset consists of wind speed, wind direction, temperature and other climate factors. The ELM has single hidden layer, the weights and bias of this network are first optimized by SSA using historic wind data. SSA helps to avoid overfitting and improves generalization ability of ELM. This method is compared with other variants of ELM and found better in terms of accuracy. However, the performance of this method degrades in the presence of outliers.
An efficient yet low-complexity algorithm based on k-nearest neighbour classifier is proposed in [89] for very short-term wind power prediction. The proposed method utilizes the power of information that lies in different parameters of meteorological data. Instead of using highly complex ML method or an ensemble of them, in [89], a simple but efficient KNN classifier is trained using multidimensional data. The authors selected wind speed, wind power, wind direction, air temperature and barometric pressure time series as input data. The combined and individual influence of each of these parameters and different distance measures on the prediction accuracy is also analysed. Through this analysis, wind speed and barometric pressure are found to be most influential parameters for WPP whereas, wind direction and air pressure are decided as ineffective for WPP. Although this method is simple and effective its performance is not compared with existing methods.
5.2. Deep Learning
The prediction horizon of ultra short-term wind power prediction ranges from a few minutes toa few hours. Therefore, the prediction algorithms need to capture spatial as well as temporal variations in the data. Existing deep learning methods captures nonlinear relation between the input parameters and predicted power using spatial features. For accurate ultra short-term wind power prediction, Ref. [90] proposed combination of spatio-temporal correlation model (STCM) and LSTM. CNN is used for spatial feature extraction and LSTM extracts the temporal relation between input and output. Performance of the combined model is compared with individual CNN and LSTM and better results are reported in terms of MAE, MAPE, RMSE and NRMSE. Ref. [91] also explored the spatio-temporal relationship for ultra short-term WPP. Wherein, attention mechanism that automatically calculates the contribution of input in the output is used for feature selection. In general, the convolutional network carries only spatial information; in [91], a temporal CNN is introduced for spatial as well as temporal feature extraction. The performance of TCN for ultra short-term WPP is improved by incorporating a self-attention mechanism in the TCN. The proposed SATCN extracts temporal features that improve the performance of the LSTM connected to it. Performance evaluation of the combined TCN-LSTM system is carried out using meteorological data and wind power data of full year. Combined feature extraction and prediction scheme shows better results than other methods. For ultra short-term WPP prediction—spatial as well as temporal—both the trends are important. Therefore, for this category of WPP, the combined effect of spatio-temporal features and a learning algorithm seems to be a promising future dimension.
5.3. Hybrid Methods
An improved EMD (IEMD) is proposed in [92] to overcome shortcomings of EMD through analysis and improvement of sifting process of EMD. IEMD decomposes non-stationary data into stationary components. Depending on the fluctuations in the data, a series of intrinsic mode functions (IMFs) is obtained from the IEMD. Large fluctuations degrade the prediction accuracy while a moderate one improves it [13]. That means depending on the available fluctuations in the data one can change the prediction model, i.e., for moderate variations linear prediction can provide required accuracy and for large fluctuations we need complex models. The authors used ANN for high frequency and separate SVM for mid frequency, low frequency and and trend item. Validation is performed using two different datasets and results are compared with only ANN and EMD.
A hybrid method combining k-means clustering and an adaptive neuro-fuzzy inference system (ANFIS) is proposed in [73] for ultra short-term wind power prediction. In this approach, phase space variables are first obtained from PSR; next, optimal input variables are selected using a feature selection method. Selected input variables are categorised into different subsets using k-means clustering and ANFIS is trained using these clusters. Parameters of the ANFIS are optimized using PSO.
In [93], a hybrid approach combining LSTM, wavelet transform and PCA was utilized to forecast ultra-short-term wind power. Initially, for signal decomposition and feature extraction, wavelet transform and PCA are applied on the time series. Further these features are applied as input to the LSTM network. Next the authors used normal condition distribution to find the prediction error of the wind power.
A deep learning based hybrid approach is proposed in [94] for ultra short-term (5 min) wind power prediction. Feature extraction is performed using CNN and the extracted features are used to train gated recurrent units. Long term trends in the data across the time steps are captured using GRU. Next, a fully connected NN is used to forecast wind power generation. Comparison with existing advanced prediction methods such as RNN, LSTM, Bi-LSTM, GRU, ARIMA and SVM is presented to show the effectiveness of the proposed hybrid scheme. The authors presented a fair comparison by separately tuning parameters of all the compared methods to their best setting. The results show that performance of proposed scheme is close to ARIMA and SVM in terms of MAE, RMSE and MAPE. Similar approach using GRU, CNN and LSTM is proposed in [95] for ultra short-term (5 min) wind power prediction. Authors used CNN for feature extraction, GRU to learn long-term variations and LSTM for prediction. However, parameter tuning has been carried out using Harris Hawks Optimization algorithm [96]. This combined approach outperformed all the compared method with large gap in terms of MAPE. Table 9 shows ultra short-term WPP methods reviewed in this article.

Table 9.
Ultra short-term wind power prediction.
6. Discussion
In this paper, we have presented a selective review of state-of-the-art wind power prediction methods. We do not aim to compare different methods and reported results rather, we highlight recent developments and benchmarks in this field. We presented three different classes of WPP based on prediction horizon and for each class, detail discussions on prediction methodology or algorithms are also presented.
From the presented review it has been observed that, in recent times, relatively few publications report on time series methods for WPP. Time series models are not competent enough to capture high degree of nonlinearity and stochastic behaviour of wind. Higher order polynomials can model nonlinear behaviour, but complexity increases with the degree of the polynomial and finding global minima not guaranteed.
Machine learning methods are suitable for all the prediction horizon. Variants of BPNN and ELM are proposed with different optimization methods. It is noted that, same network with different optimizers produce different results, since datasets are not same. Variants of Gaussian process regression and ELM with advanced optimizers shown improved results. Along with the accuracies, GP based approaches provide the confidence interval of the results. Being a nonparametric method, GP-based approaches do not require cross validation. Instead of using a single ML method, ensemble learning methods are widely used for WPP in different horizons. Through ensemble learning different base learner effectively models the non-stationary behaviour of wind. Ensemble of different learning algorithms have shown improvement in the accuracies.
With increased computing power and ability to model complex nonlinear functions, deep learning models can provide accurate predictions than shallow machine learning methods. The deep learning models extract optimal features as well as learn a regression function. Each of these models perform well individually, combination of time series and ML and deep learning models substantially improves the results.
Rightly pointed out in [8], in recent years, a substantial increase in hybrid approaches has been observed. It is effectively applicable to all prediction horizons. Variants of EMD are combined with different ML, LSTM and deep learning models to improve the prediction accuracy. Decomposition power of wavelets are incorporated in deep learning by using wavelet as an activation function and substantial improvement is observed. Combination of LSTM, CNN and decomposition methods drastically improves accuracy of short-term and ultra short-term WPP. However, these methods become computationally very heavy. It is noted that appropriate feature selection, data cleaning and optimizers and network selection are key to improving the accuracy of WPP.
It has been observed that the selection of an optimizer is a very crucial step in the case of ML and DL models. Recently developed hybrid approaches make use of LSTM and CNN along with different decomposition methods; however, the combination of decomposition methods and deep learning models does not perform well unless hyperparameters are properly tuned. In our opinion, with sufficiently large development in the deep learning area, efficient optimization algorithms are needed, and researchers need to focus on this aspect as well.
Data preprocessing is an important step in WPP; it can be seen that, in [74,75], data preprocessing such as outlier removal, anomaly detection and removal, resampling and interpolation substantially improved the performance of the algorithm. Therefore, along with the algorithmic development data, preprocessing is also an important factor. The R package for data cleaning and preprocessing is presented in [97]. Researchers can used such tools for data preprocessing and also to analyze data at various scales and resolutions to find relevant features.
7. Conclusions
This paper presents a selective review of wind power forecasting methods. In this paper, WPP methods are classified based on the prediction horizon and for each category we investigated time series, machine learning, deep learning and hybrid approaches for WPP. Among these four categories, recent developments are skewed towards hybrid methods. This paper focuses on a comparison of existing state-of-the-art methods based on pre-processing, feature extraction, algorithm and performance. Compared to long term approaches, due to the high requirement for stable dispatching of the power grid, short-term forecasting methods are gaining more attention. A combination of feature extraction, time series decomposition and learning algorithms improves the forecasting accuracy. Investigations in this paper favour the hybrid methods, which show high performance for all three prediction horizons. It is noted that there is a large variation in databases, related NWP data and performance measures; therefore common datasets and parameters are needed for bench-marking. The discussions in this paper provide guidelines about current achievements and future requirements.
Author Contributions
Conceptualization, M.S. and R.P.; methodology, M.S., T.S., S.N. (Shreyas Nagle), S.C. and S.N. (Shivang Negi); software, M.S., T.S., S.N. (Shreyas Nagle), S.C. and S.N. (Shivang Negi); validation, M.S., R.P. and N.D.B.; formal analysis, M.S., T.S., S.N. (Shreyas Nagle), S.C. and S.N. (Shivang Negi); investigation, M.S., T.S., S.N. (Shreyas Nagle), S.C. and S.N. (Shivang Negi); resources, M.S., R.P. and N.D.B.; data curation, M.S., T.S., S.N. (Shreyas Nagle), S.C. and S.N. (Shivang Negi); writing—original draft preparation, M.S., R.P., T.S., S.N. (Shreyas Nagle), S.C., S.N. (Shivang Negi) and N.D.B.; writing—review and editing, M.S., R.P., T.S., S.N. (Shreyas Nagle), S.C., S.N. (Shivang Negi) and N.D.B.; visualization, M.S. and N.D.B.; supervision, M.S., R.P. and N.D.B.; project administration, M.S., R.P. and N.D.B.; funding acquisition, N.D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| ANN | Artificial Neural Network |
| AR | Autoregressive |
| ARX | Autoregressive with exogenous variable |
| ARIMA | Autoregressive Integrated Moving Average |
| ARMA | Autoregressive Moving Average |
| AWNN | Adaptive Wavelet Neural Network |
| BP | Back Propagation |
| BPNN | Back-Propagation Neural Network |
| CNN | Convolutional Neural Network |
| DBN | Deep Belief Network |
| ELM | Extreme Learning Machine |
| ENN | Elman Neural Network |
| EVS | Explained Variance Score |
| FFNN | Feed Forward Neural Network |
| GA | Genetic Algorithm |
| GFS | Global Forecasting System |
| GMM | Gaussian Mixture Model |
| GP | Gaussian Process |
| GPR | Gaussian Process Regression |
| IF | Isolation Forest |
| LSSVM | Least Square Support Vector Machine |
| LSTM | Long Short-Term Memory |
| MA | Moving Average |
| MAPE | Mean Absolute Percentage Error |
| MARE | Mean Absolute Relative Error |
| MDN | Mixture Density Neural Network |
| MLP | Multilayer Perceptron |
| MSE | Mean Square Error |
| MSLE | Mean Squared Logarithmic Error |
| NAAE | Normalised Absolute Average Error |
| NMAE | Normalised Mean Absolute Error |
| NMBE | Normalized Mean Bias Error |
| NMSE | Normalized Mean Square Error |
| NN | Neural Network |
| NRMSE | Normalised Root Mean Square Error |
| NWP | Numerical Weather Prediction |
| PSO | Particle Swarm Optimisation |
| R-Square | |
| RBFNN | Radial Basis Function Neural Network |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| RVM | Relative Vector Machine |
| SDE | Standard Deviation Error |
| SNMAE | Square Normalized Mean Bias Error |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| WNN | Wavelet Neural Network |
References
- Zhang, Y.; Liu, K.; Qin, L.; An, X. Deterministic and probabilistic interval prediction for short-term wind power generation based on variational mode decomposition and machine learning methods. Energy Convers. Manag. 2016, 112, 208–219. [Google Scholar] [CrossRef]
- Bokde, N.; Tranberg, B.; Andresen, G.B. A graphical approach to carbon-efficient spot market scheduling for Power-to-X applications. Energy Convers. Manag. 2020, 224, 113461. [Google Scholar] [CrossRef]
- Tao, S.; Xu, Q.; Feijóo, A.; Kuenzel, S.; Bokde, N. Integrated wind farm power curve and power curve distribution function considering the wake effect and terrain gradient. Energies 2019, 12, 2482. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Villanueva, D. Wind turbine power curves based on the weibull cumulative distribution function. Appl. Sci. 2018, 8, 1757. [Google Scholar] [CrossRef]
- Sawant, M.; Thakare, S.; Rao, A.P.; Feijóo-Lorenzo, A.E.; Bokde, N.D. A review on state-of-the-art reviews in wind-turbine-and wind-farm-related topics. Energies 2021, 14, 2041. [Google Scholar] [CrossRef]
- Bokde, N.D.; Yaseen, Z.M.; Andersen, G.B. ForecastTB—An R package as a test-bench for time series forecasting—Application of wind speed and solar radiation modeling. Energies 2020, 13, 2578. [Google Scholar] [CrossRef]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A critical review of wind power forecasting methods—Past, present and future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Villanueva, D.; Kulat, K. A review on hybrid empirical mode decomposition models for wind speed and wind power prediction. Energies 2019, 12, 254. [Google Scholar] [CrossRef]
- Landberg, L. A mathematical look at a physical power prediction model. Wind Energy Int. J. Prog. Appl. Wind Power Convers. Technol. 1998, 1, 23–28. [Google Scholar] [CrossRef]
- Catalao, J.; Pousinho, H.; Mendes, V. Hybrid wavelet-PSO-ANFIS approach for short-term wind power forecasting in Portugal. IEEE Trans. Sustain. Energy 2010, 2, 50–59. [Google Scholar] [CrossRef]
- Bhaskar, K.; Singh, S.N. AWNN-assisted wind power forecasting using feed-forward neural network. IEEE Trans. Sustain. Energy 2012, 3, 306–315. [Google Scholar] [CrossRef]
- Chen, N.; Qian, Z.; Nabney, I.T.; Meng, X. Wind power forecasts using Gaussian processes and numerical weather prediction. IEEE Trans. Power Syst. 2013, 29, 656–665. [Google Scholar] [CrossRef]
- Sideratos, G.; Hatziargyriou, N.D. An advanced statistical method for wind power forecasting. IEEE Trans. Power Syst. 2007, 22, 258–265. [Google Scholar] [CrossRef]
- Safari, N.; Chung, C.; Price, G. Novel multi-step short-term wind power prediction framework based on chaotic time series analysis and singular spectrum analysis. IEEE Trans. Power Syst. 2017, 33, 590–601. [Google Scholar] [CrossRef]
- Tian, Z.; Li, S.; Wang, Y.; Wang, X. Wind power prediction method based on hybrid kernel function support vector machine. Wind Eng. 2018, 42, 252–264. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. ARMA based approaches for forecasting the tuple of wind speed and direction. Appl. Energy 2011, 88, 1405–1414. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction. Appl. Energy 2012, 98, 415–424. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian processes in machine learning. In Summer School on Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Karakuş, O.; Kuruoğlu, E.E.; Altınkaya, M.A. One-day ahead wind speed/power prediction based on polynomial autoregressive model. IET Renew. Power Gener. 2017, 11, 1430–1439. [Google Scholar] [CrossRef]
- Hong, T.; Pinson, P.; Fan, S. Global energy forecasting competition 2012. Int. J. Forecast. 2014, 30, 357–363. [Google Scholar] [CrossRef]
- Ouyang, T.; Huang, H.; He, Y. Ramp events forecasting based on long-term wind power prediction and correction. IET Renew. Power Gener. 2019, 13, 2793–2801. [Google Scholar] [CrossRef]
- Cui, M.; Ke, D.; Sun, Y.; Gan, D.; Zhang, J.; Hodge, B.M. Wind power ramp event forecasting using a stochastic scenario generation method. IEEE Trans. Sustain. Energy 2015, 6, 422–433. [Google Scholar] [CrossRef]
- Lee, D.; Baldick, R. Short-term wind power ensemble prediction based on Gaussian processes and neural networks. IEEE Trans. Smart Grid 2013, 5, 501–510. [Google Scholar] [CrossRef]
- Li, T.; Li, Y.; Liao, M.; Wang, W.; Zeng, C. A new wind power forecasting approach based on conjugated gradient neural network. Math. Probl. Eng. 2016, 2016, 8141790. [Google Scholar] [CrossRef]
- Ouyang, T.; Zha, X.; Qin, L.; Kusiak, A. Optimisation of time window size for wind power ramps prediction. IET Renew. Power Gener. 2017, 11, 1270–1277. [Google Scholar] [CrossRef]
- Jin, H.; Shi, L.; Chen, X.; Qian, B.; Yang, B.; Jin, H. Probabilistic wind power forecasting using selective ensemble of finite mixture Gaussian process regression models. Renew. Energy 2021, 174, 1–18. [Google Scholar] [CrossRef]
- Fang, S.; Chiang, H.D. A high-accuracy wind power forecasting model. IEEE Trans. Power Syst. 2016, 32, 1589–1590. [Google Scholar] [CrossRef]
- Bochenek, B.; Jurasz, J.; Jaczewski, A.; Stachura, G.; Sekuła, P.; Strzyżewski, T.; Wdowikowski, M.; Figurski, M. Day-ahead wind power forecasting in Poland based on numerical weather prediction. Energies 2021, 14, 2164. [Google Scholar] [CrossRef]
- Tasnim, S.; Rahman, A.; Oo, A.M.T.; Haque, E. Autoencoder for wind power prediction. Renew. Wind. Water Sol. 2017, 4, 6. [Google Scholar] [CrossRef]
- Abedinia, O.; Bagheri, M.; Naderi, M.S.; Ghadimi, N. A new combinatory approach for wind power forecasting. IEEE Syst. J. 2020, 14, 4614–4625. [Google Scholar] [CrossRef]
- Zhang, H.; Yue, D.; Dou, C.; Li, K.; Hancke, G.P. Two-step wind power prediction approach with improved complementary ensemble empirical mode decomposition and reinforcement learning. IEEE Syst. J. 2021. [Google Scholar] [CrossRef]
- Dong, L.; Wang, L.; Khahro, S.F.; Gao, S.; Liao, X. Wind power day-ahead prediction with cluster analysis of NWP. Renew. Sustain. Energy Rev. 2016, 60, 1206–1212. [Google Scholar] [CrossRef]
- Abedinia, O.; Lotfi, M.; Bagheri, M.; Sobhani, B.; Shafie-Khah, M.; Catalão, J.P. Improved EMD-based complex prediction model for wind power forecasting. IEEE Trans. Sustain. Energy 2020, 11, 2790–2802. [Google Scholar] [CrossRef]
- Shi, X.; Lei, X.; Huang, Q.; Huang, S.; Ren, K.; Hu, Y. Hourly day-ahead wind power prediction using the hybrid model of variational model decomposition and long short-term memory. Energies 2018, 11, 3227. [Google Scholar] [CrossRef]
- Heinermann, J.; Kramer, O. Machine learning ensembles for wind power prediction. Renew. Energy 2016, 89, 671–679. [Google Scholar] [CrossRef]
- Lee, J.; Wang, W.; Harrou, F.; Sun, Y. Wind power prediction using ensemble learning-based models. IEEE Access 2020, 8, 61517–61527. [Google Scholar] [CrossRef]
- Yan, J.; Li, K.; Bai, E.; Yang, Z.; Foley, A. Time series wind power forecasting based on variant Gaussian Process and TLBO. Neurocomputing 2016, 189, 135–144. [Google Scholar] [CrossRef]
- Liu, T.; Wei, H.; Zhang, K. Wind power prediction with missing data using Gaussian process regression and multiple imputation. Appl. Soft Comput. 2018, 71, 905–916. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Hour-ahead wind power forecast based on random forests. Renew. Energy 2017, 109, 529–541. [Google Scholar] [CrossRef]
- Wang, Q.; Lei, Y.; Cao, H. Wind power prediction based on nonlinear partial least square. Math. Probl. Eng. 2018, 2018, 6829274. [Google Scholar] [CrossRef]
- Li, N.; He, F.; Ma, W.; Wang, R.; Zhang, X. Wind power prediction of kernel extreme learning machine based on differential evolution algorithm and cross validation algorithm. IEEE Access 2020, 8, 68874–68882. [Google Scholar] [CrossRef]
- An, G.; Jiang, Z.; Cao, X.; Liang, Y.; Zhao, Y.; Li, Z.; Dong, W.; Sun, H. Short-term wind power prediction based on particle swarm optimization-extreme learning machine model combined with AdaBoost algorithm. IEEE Access 2021, 9, 94040–94052. [Google Scholar] [CrossRef]
- An, J.; Yin, F.; Wu, M.; She, J.; Chen, X. Multisource wind speed fusion method for short-term wind power prediction. IEEE Trans. Ind. Inf. 2020, 17, 5927–5937. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Jiang, M.; Yuan, Y. Prediction interval of wind power using parameter optimized Beta distribution based LSTM model. Appl. Soft Comput. 2019, 82, 105550. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, H.; Guo, Y. Wind power prediction based on PSO-SVR and grey combination model. IEEE Access 2019, 7, 136254–136267. [Google Scholar] [CrossRef]
- Xie, W.; Zhang, P.; Chen, R.; Zhou, Z. A nonparametric Bayesian framework for short-term wind power probabilistic forecast. IEEE Trans. Power Syst. 2018, 34, 371–379. [Google Scholar] [CrossRef]
- Bokde, N.; Asencio-Cortés, G.; Martínez-Álvarez, F.; Kulat, K. PSF: Introduction to R Package for Pattern Sequence Based Forecasting Algorithm. R J. 2017, 9, 324–333. [Google Scholar] [CrossRef]
- Shende, M.K.; Salih, S.Q.; Bokde, N.D.; Scholz, M.; Oudah, A.Y.; Yaseen, Z.M. Natural Time Series Parameters Forecasting: Validation of the Pattern-Sequence-Based Forecasting (PSF) Algorithm; A New Python Package. Appl. Sci. 2022, 12, 6194. [Google Scholar] [CrossRef]
- Bokde, N.; Asencio-Cortes, G.; Martinez-Alvarez, F. PSF: Forecasting of Univariate Time Series Using the Pattern Sequence-Based Forecasting (PSF) Algorithm. R Package Version 0.4. 2017. Available online: https://cran.r-project.org/web/packages/PSF/PSF.pdf (accessed on 10 June 2022).
- Bokde, N.; Troncoso, A.; Asencio-Cortés, G.; Kulat, K.; Martínez-Álvarez, F. Pattern sequence similarity based techniques for wind speed forecasting. In Proceedings of the International Work-Conference on Time Series, Granada, Spain, 18–20 September 2017; pp. 18–20. [Google Scholar]
- Bokde, N.; Feijóo, A.; Villanueva, D.; Kulat, K. A novel and alternative approach for direct and indirect wind-power prediction methods. Energies 2018, 11, 2923. [Google Scholar] [CrossRef]
- Ghoushchi, S.J.; Manjili, S.; Mardani, A.; Saraji, M.K. An extended new approach for forecasting short-term wind power using modified fuzzy wavelet neural network: A case study in wind power plant. Energy 2021, 223, 120052. [Google Scholar] [CrossRef]
- Wang, S.X.; Li, M.; Zhao, L.; Jin, C. Short-term wind power prediction based on improved small-world neural network. Neural Comput. Appl. 2019, 31, 3173–3185. [Google Scholar] [CrossRef]
- Qureshi, A.S.; Khan, A.; Zameer, A.; Usman, A. Wind power prediction using deep neural network based meta regression and transfer learning. Appl. Soft Comput. 2017, 58, 742–755. [Google Scholar] [CrossRef]
- Wang, K.; Qi, X.; Liu, H.; Song, J. Deep belief network based k-means cluster approach for short-term wind power forecasting. Energy 2018, 165, 840–852. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Yan, J.; Han, S.; Li, L.; Long, Q. Improved deep mixture density network for regional wind power probabilistic forecasting. IEEE Trans. Power Syst. 2020, 35, 2549–2560. [Google Scholar] [CrossRef]
- Ding, M.; Zhou, H.; Xie, H.; Wu, M.; Nakanishi, Y.; Yokoyama, R. A gated recurrent unit neural networks based wind speed error correction model for short-term wind power forecasting. Neurocomputing 2019, 365, 54–61. [Google Scholar] [CrossRef]
- Schmidhuber, J.; Hochreiter, S. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar]
- Wang, S.; Li, B.; Li, G.; Yao, B.; Wu, J. Short-term wind power prediction based on multidimensional data cleaning and feature reconfiguration. Appl. Energy 2021, 292, 116851. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Muneeb, M. A novel genetic LSTM model for wind power forecast. Energy 2021, 223, 120069. [Google Scholar] [CrossRef]
- Cornejo-Bueno, L.; Cuadra, L.; Jiménez-Fernández, S.; Acevedo-Rodríguez, J.; Prieto, L.; Salcedo-Sanz, S. Wind power ramp events prediction with hybrid machine learning regression techniques and reanalysis data. Energies 2017, 10, 1784. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Kulat, K. Analysis of differencing and decomposition preprocessing methods for wind speed prediction. Appl. Soft Comput. 2018, 71, 926–938. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Al-Ansari, N.; Tao, S.; Yaseen, Z.M. The hybridization of ensemble empirical mode decomposition with forecasting models: Application of short-term wind speed and power modeling. Energies 2020, 13, 1666. [Google Scholar] [CrossRef]
- Xie, H.B.; Guo, T.; Sivakumar, B.; Liew, A.W.C.; Dokos, S. Symplectic geometry spectrum analysis of nonlinear time series. Proc. R. Soc. A Math. Phys. Eng. Sci. 2014, 470, 20140409. [Google Scholar] [CrossRef]
- Ghanbarzadeh, M.; Aminghafari, M. A new hybrid-multiscale SSA prediction of non-stationary time series. Fluct. Noise Lett. 2016, 15, 1650005. [Google Scholar] [CrossRef]
- Naik, J.; Satapathy, P.; Dash, P. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 2018, 70, 1167–1188. [Google Scholar] [CrossRef]
- Shahid, F.; Zameer, A.; Mehmood, A.; Raja, M.A.Z. A novel wavenets long short term memory paradigm for wind power prediction. Appl. Energy 2020, 269, 115098. [Google Scholar] [CrossRef]
- Huang, C.M.; Kuo, C.J.; Huang, Y.C. Short-term wind power forecasting and uncertainty analysis using a hybrid intelligent method. IET Renew. Power Gener. 2017, 11, 678–687. [Google Scholar] [CrossRef]
- Yuan, X.; Tan, Q.; Lei, X.; Yuan, Y.; Wu, X. Wind power prediction using hybrid autoregressive fractionally integrated moving average and least square support vector machine. Energy 2017, 129, 122–137. [Google Scholar] [CrossRef]
- Zheng, D.; Semero, Y.K.; Zhang, J.; Wei, D. Short-term wind power prediction in microgrids using a hybrid approach integrating genetic algorithm, particle swarm optimization, and adaptive neuro-fuzzy inference systems. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 1561–1567. [Google Scholar] [CrossRef]
- Dong, W.; Yang, Q.; Fang, X. Multi-step ahead wind power generation prediction based on hybrid machine learning techniques. Energies 2018, 11, 1975. [Google Scholar] [CrossRef]
- Zhang, W.; Lin, Z.; Liu, X. Short-term offshore wind power forecasting-A hybrid model based on Discrete Wavelet Transform (DWT), Seasonal Autoregressive Integrated Moving Average (SARIMA), and deep-learning-based Long Short-Term Memory (LSTM). Renew. Energy 2022, 185, 611–628. [Google Scholar] [CrossRef]
- Hanifi, S.; Lotfian, S.; Zare-Behtash, H.; Cammarano, A. Offshore Wind Power Forecasting—A New Hyperparameter Optimisation Algorithm for Deep Learning Models. Energies 2022, 15, 6919. [Google Scholar] [CrossRef]
- Liang, Z.; Liang, J.; Wang, C.; Dong, X.; Miao, X. Short-term wind power combined forecasting based on error forecast correction. Energy Convers. Manag. 2016, 119, 215–226. [Google Scholar] [CrossRef]
- Liu, Y.; Guan, L.; Hou, C.; Han, H.; Liu, Z.; Sun, Y.; Zheng, M. Wind power short-term prediction based on LSTM and discrete wavelet transform. Appl. Sci. 2019, 9, 1108. [Google Scholar] [CrossRef]
- Son, N.; Yang, S.; Na, J. Hybrid forecasting model for short-term wind power prediction using modified long short-term memory. Energies 2019, 12, 3901. [Google Scholar] [CrossRef]
- Mishra, S.; Dash, P. Short-term prediction of wind power using a hybrid pseudo-inverse Legendre neural network and adaptive firefly algorithm. Neural Comput. Appl. 2019, 31, 2243–2268. [Google Scholar] [CrossRef]
- Zhang, C.; Ding, M.; Wang, W.; Bi, R.; Miao, L.; Yu, H.; Liu, L. An improved ELM model based on CEEMD-LZC and manifold learning for short-term wind power prediction. IEEE Access 2019, 7, 121472–121481. [Google Scholar] [CrossRef]
- Zhao, Y.; Jia, L. A short-term hybrid wind power prediction model based on singular spectrum analysis and temporal convolutional networks. J. Renew. Sustain. Energy 2020, 12, 056101. [Google Scholar] [CrossRef]
- Yan, H.; Wu, Z. A hybrid short-term wind power prediction model combining data processing, multiple parameters optimization and multi-intelligent models apportion strategy. IEEE Access 2020, 8, 227126–227140. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, S.; Yu, X.; Zhang, L.; Wang, Q. A novel deep learning approach for wind power forecasting based on WD-LSTM model. Energies 2020, 13, 4964. [Google Scholar] [CrossRef]
- Han, Y.; Tong, X. Multi-step short-term wind power prediction based on three-level decomposition and improved grey wolf optimization. IEEE Access 2020, 8, 67124–67136. [Google Scholar] [CrossRef]
- Duan, J.; Wang, P.; Ma, W.; Tian, X.; Fang, S.; Cheng, Y.; Chang, Y.; Liu, H. Short-term wind power forecasting using the hybrid model of improved variational mode decomposition and Correntropy Long Short-term memory neural network. Energy 2021, 214, 118980. [Google Scholar] [CrossRef]
- Huang, L.; Li, L.; Wei, X.; Zhang, D. Short-term prediction of wind power based on BiLSTM–CNN–WGAN-GP. Soft Comput. 2022, 26, 10607–10621. [Google Scholar] [CrossRef]
- Liu, R.; Peng, M.; Xiao, X. Ultra-short-term wind power prediction based on multivariate phase space reconstruction and multivariate linear regression. Energies 2018, 11, 2763. [Google Scholar] [CrossRef]
- Tan, L.; Han, J.; Zhang, H. Ultra-short-term wind power prediction by salp swarm algorithm-based optimizing extreme learning machine. IEEE Access 2020, 8, 44470–44484. [Google Scholar] [CrossRef]
- Yesilbudak, M.; Sagiroglu, S.; Colak, I. A novel implementation of kNN classifier based on multi-tupled meteorological input data for wind power prediction. Energy Convers. Manag. 2017, 135, 434–444. [Google Scholar] [CrossRef]
- Wu, Q.; Guan, F.; Lv, C.; Huang, Y. Ultra-short-term multi-step wind power forecasting based on CNN-LSTM. IET Renew. Power Gener. 2021, 15, 1019–1029. [Google Scholar] [CrossRef]
- Xiang, L.; Liu, J.; Yang, X.; Hu, A.; Su, H. Ultra-short term wind power prediction applying a novel model named SATCN-LSTM. Energy Convers. Manag. 2022, 252, 115036. [Google Scholar] [CrossRef]
- Yang, M.; Chen, X.; Du, J.; Cui, Y. Ultra-short-term multistep wind power prediction based on improved EMD and reconstruction method using run-length analysis. IEEE Access 2018, 6, 31908–31917. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, P.; Zhai, S.; Hou, D.; Wang, S.; Zhou, Y. Ultra short-term probability prediction of wind power based on LSTM network and condition normal distribution. Wind Energy 2020, 23, 63–76. [Google Scholar] [CrossRef]
- Hossain, M.A.; Chakrabortty, R.K.; Elsawah, S.; Ryan, M.J. Very short-term forecasting of wind power generation using hybrid deep learning model. J. Clean. Prod. 2021, 296, 126564. [Google Scholar] [CrossRef]
- Hossain, M.A.; Chakrabortty, R.K.; Elsawah, S.; Gray, E.M.; Ryan, M.J. Predicting wind power generation using hybrid deep learning with optimization. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Shende, M.K.; Feijoo-Lorenzo, A.E.; Bokde, N.D. cleanTS: Automated (AutoML) Tool to Clean Univariate Time Series at Microscales. Neurocomputing 2022, 500, 155–176. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).