Robust Output Feedback Control of the Voltage Source Inverter in an AC Microgrid
Abstract
:1. Introduction
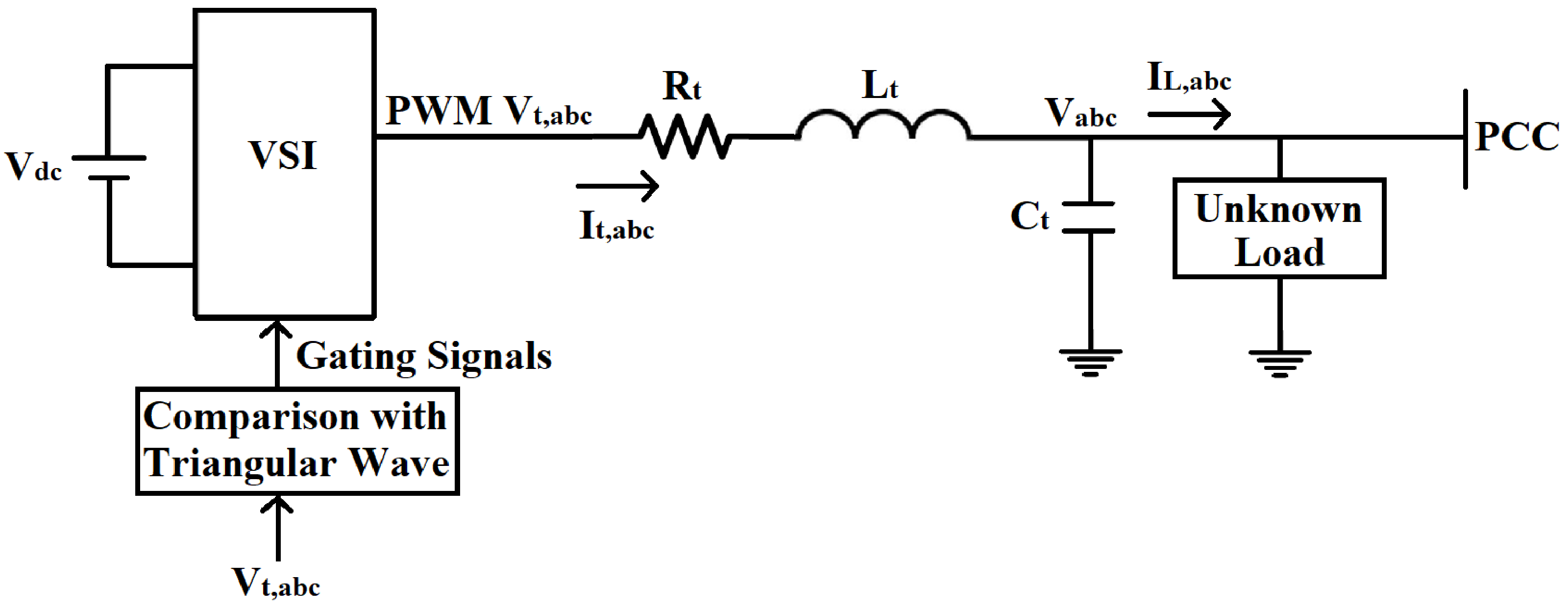
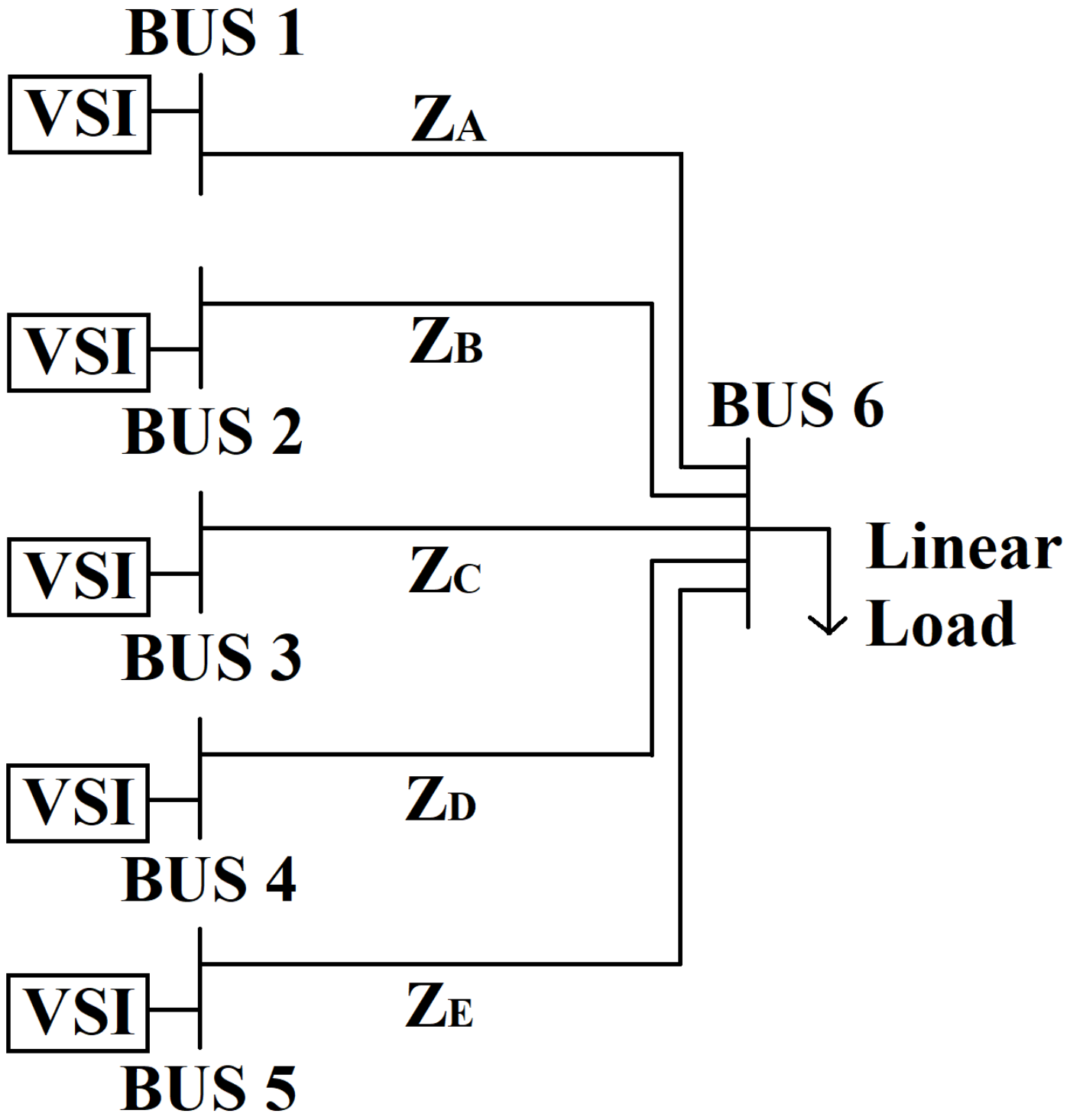
2. Problem Formulation
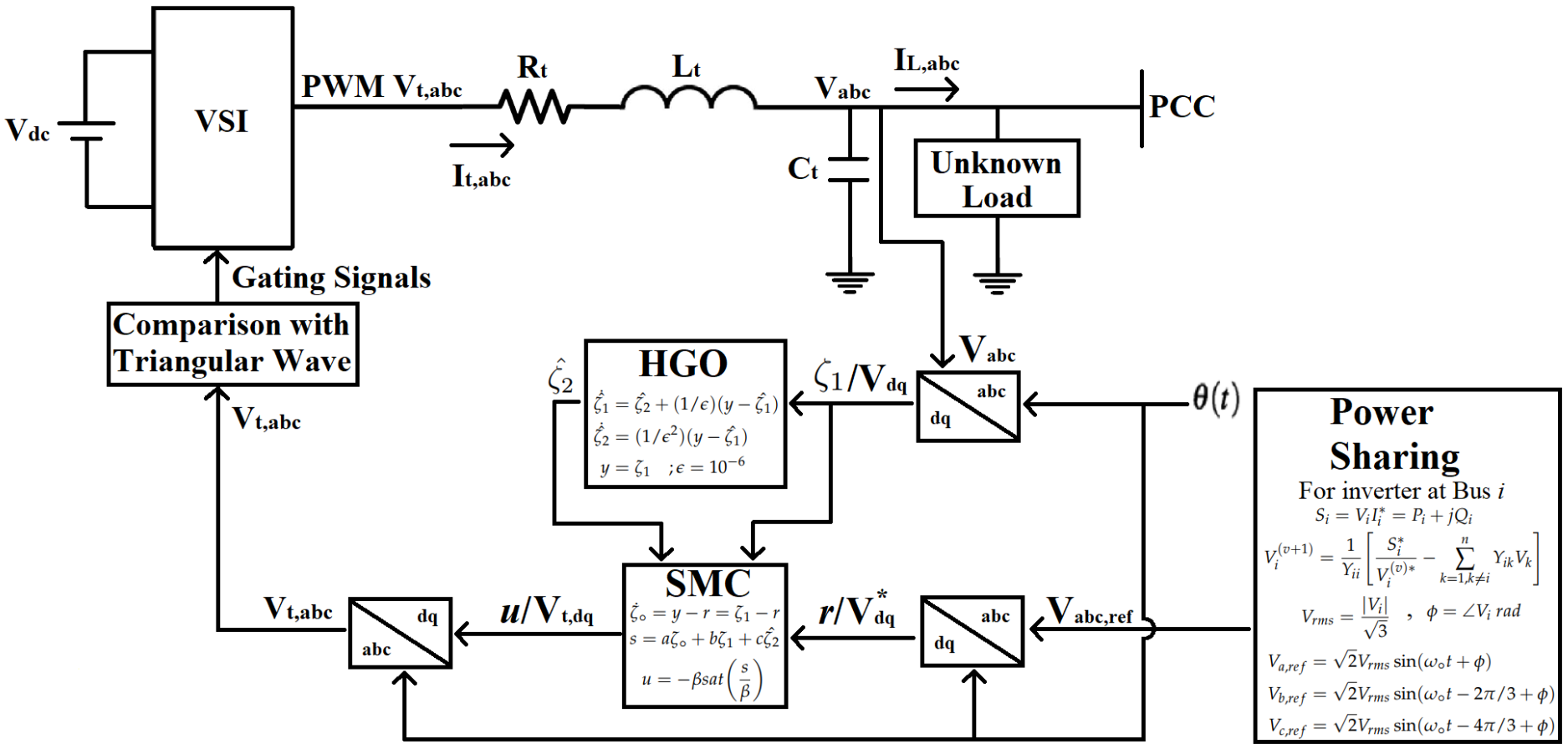
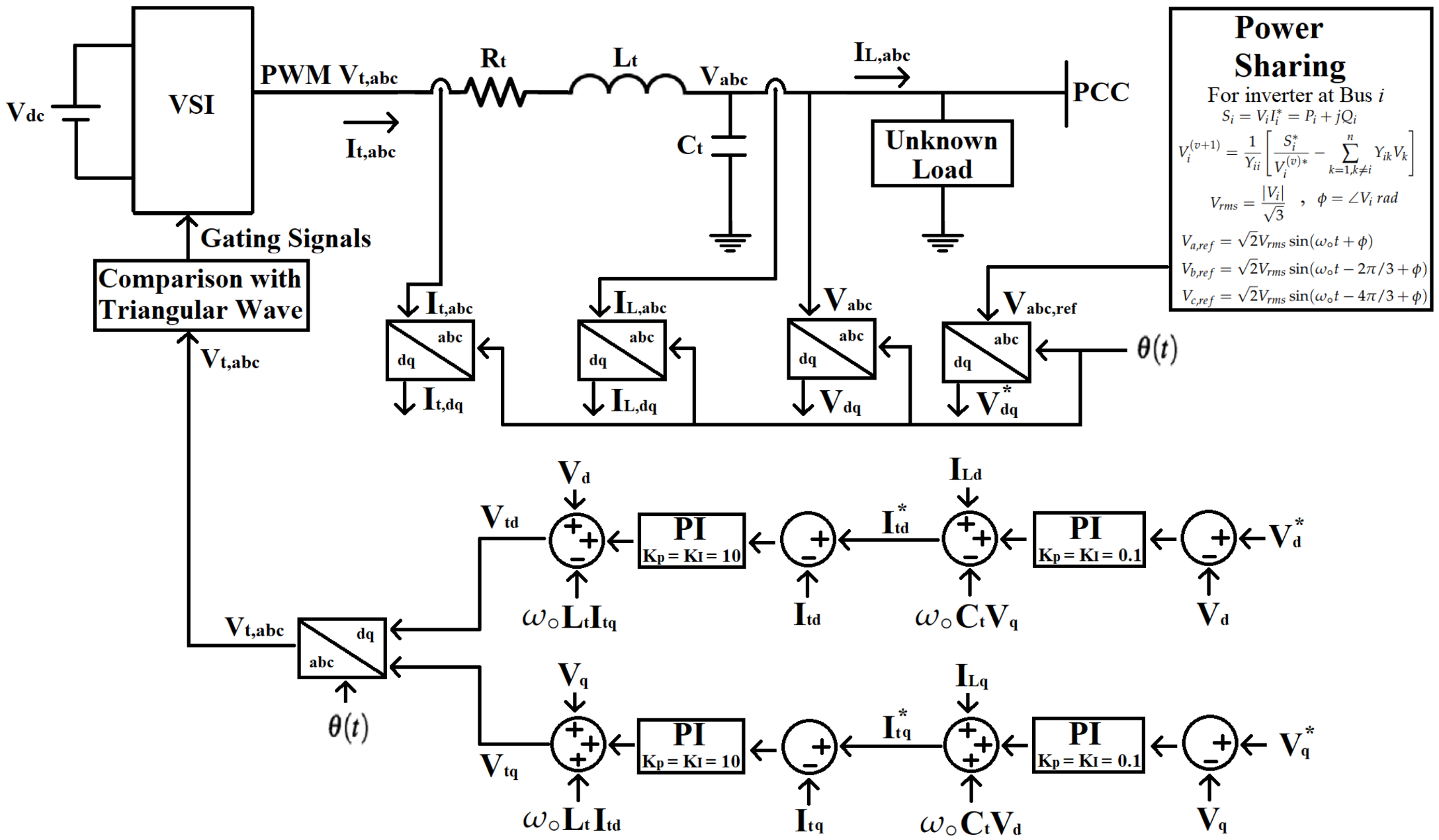
3. Control Scheme
4. Stability Analysis
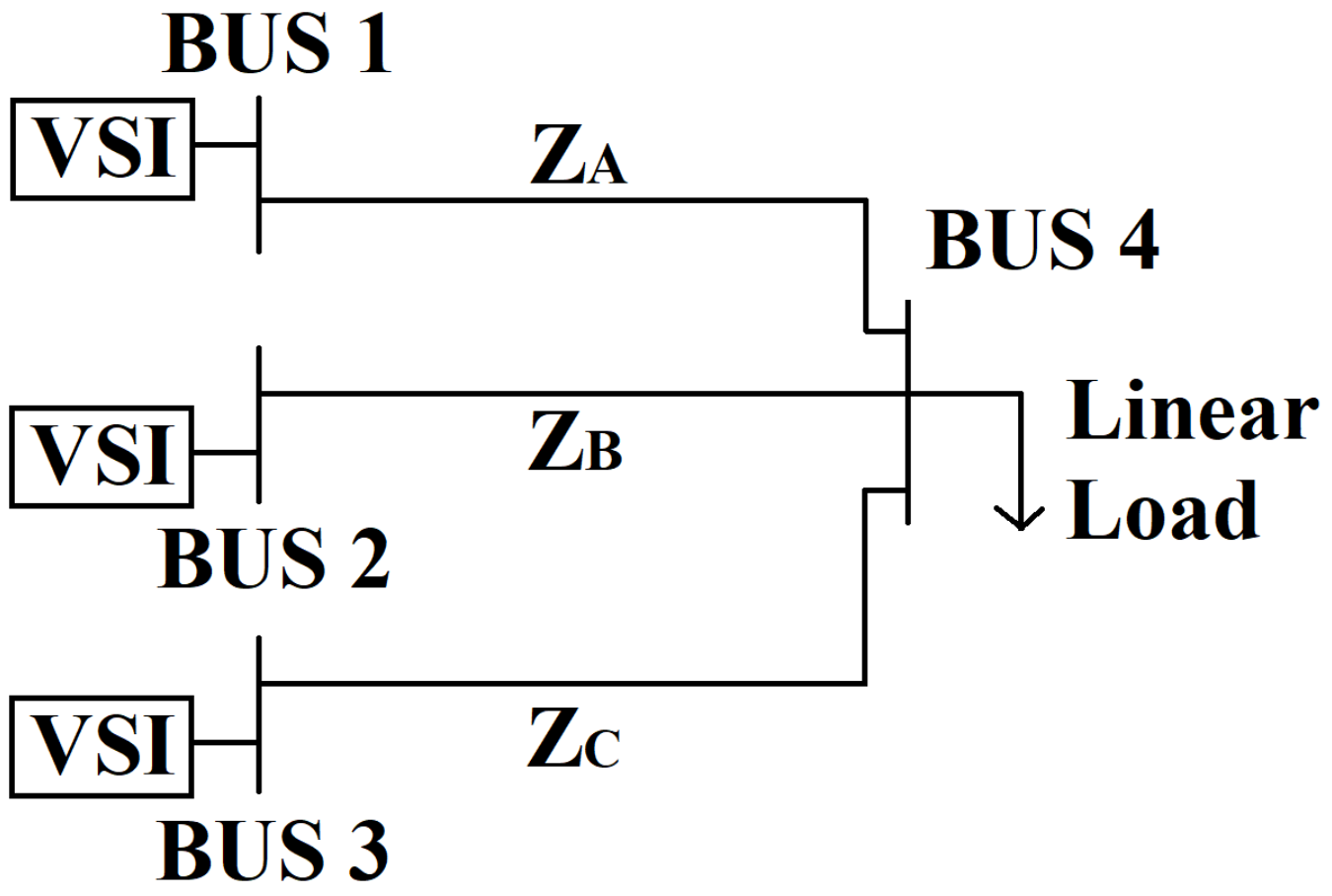
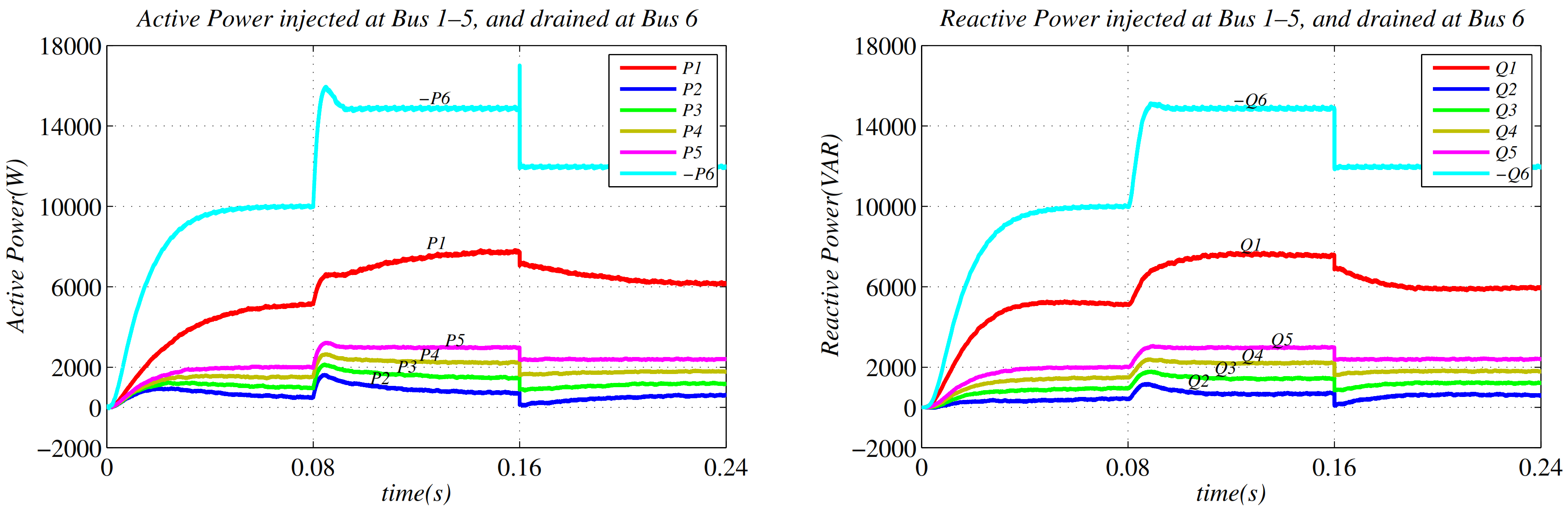
5. Power-Sharing
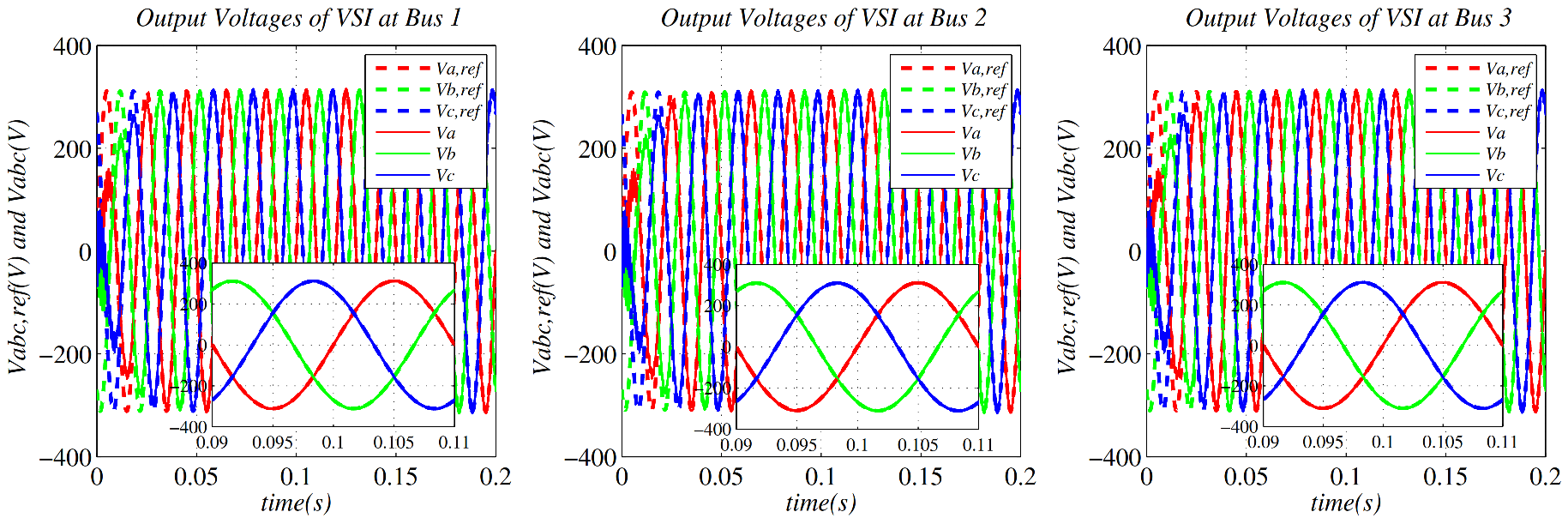
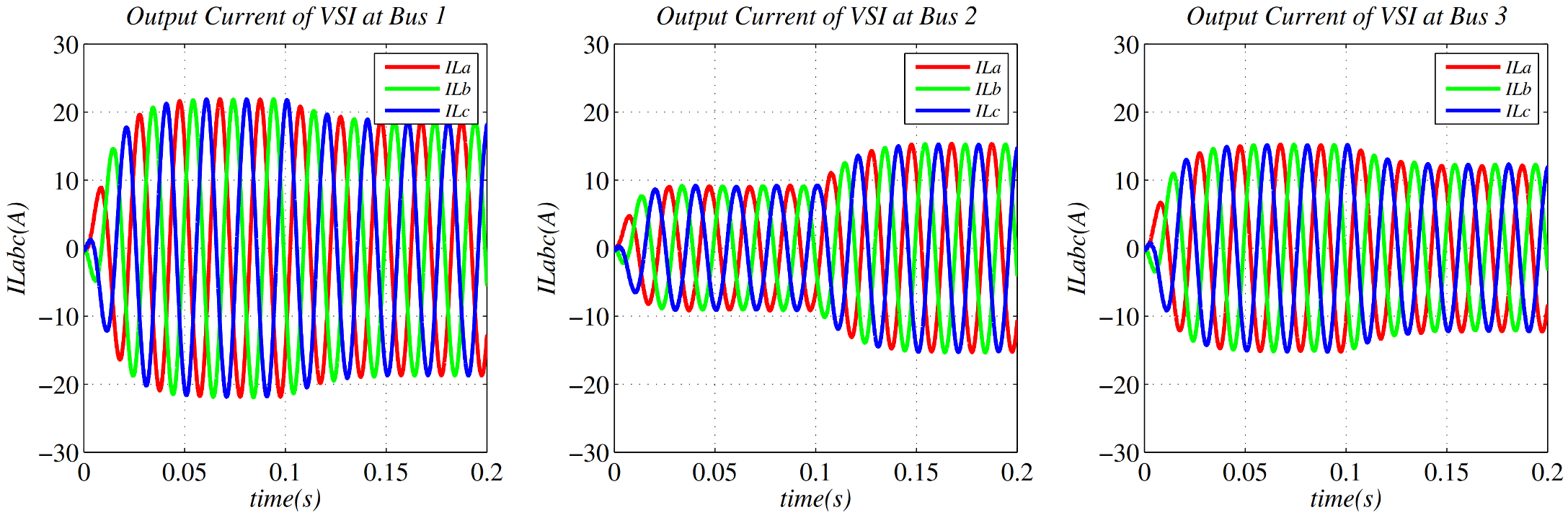
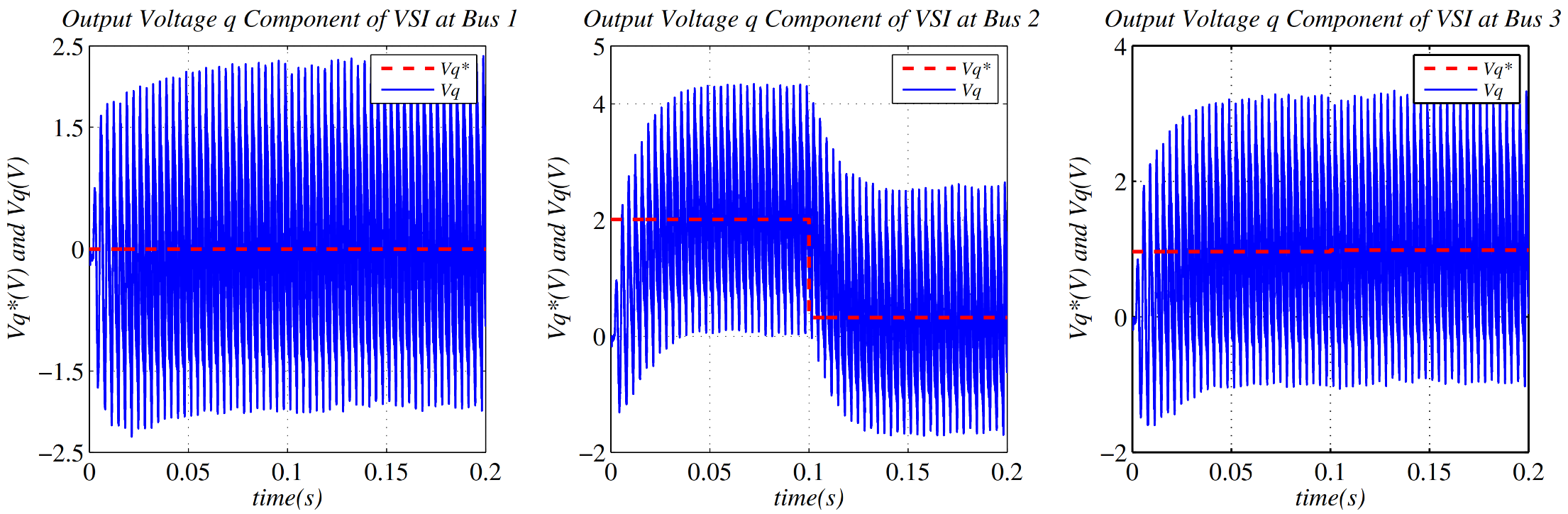
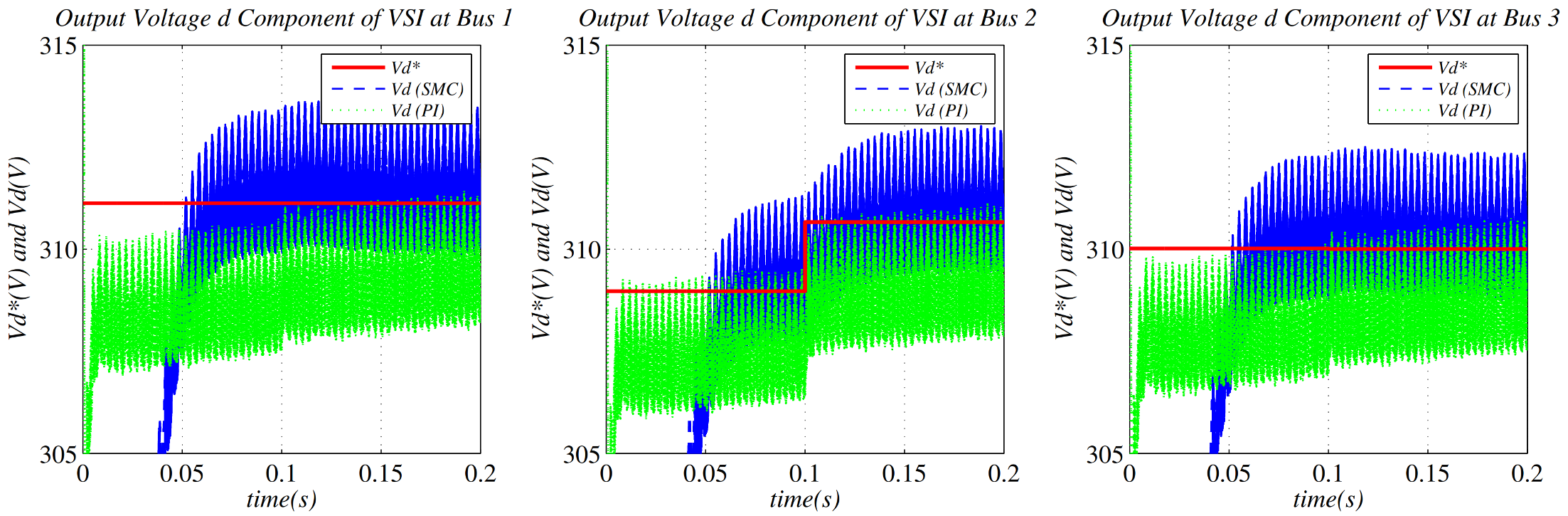
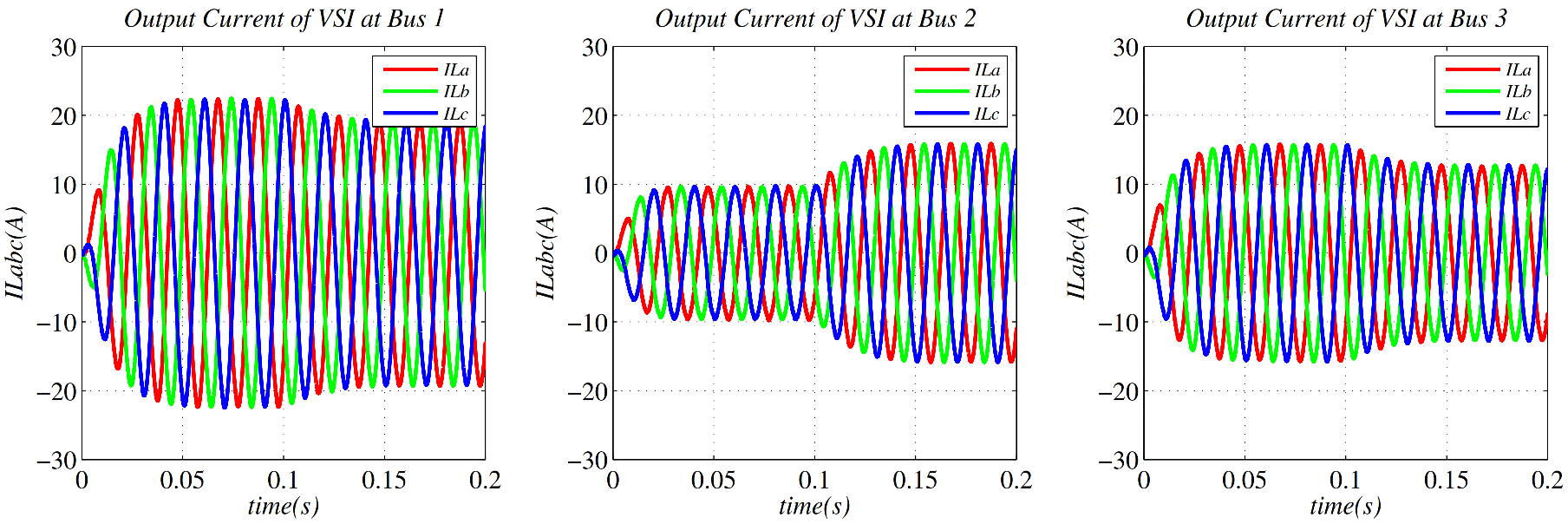
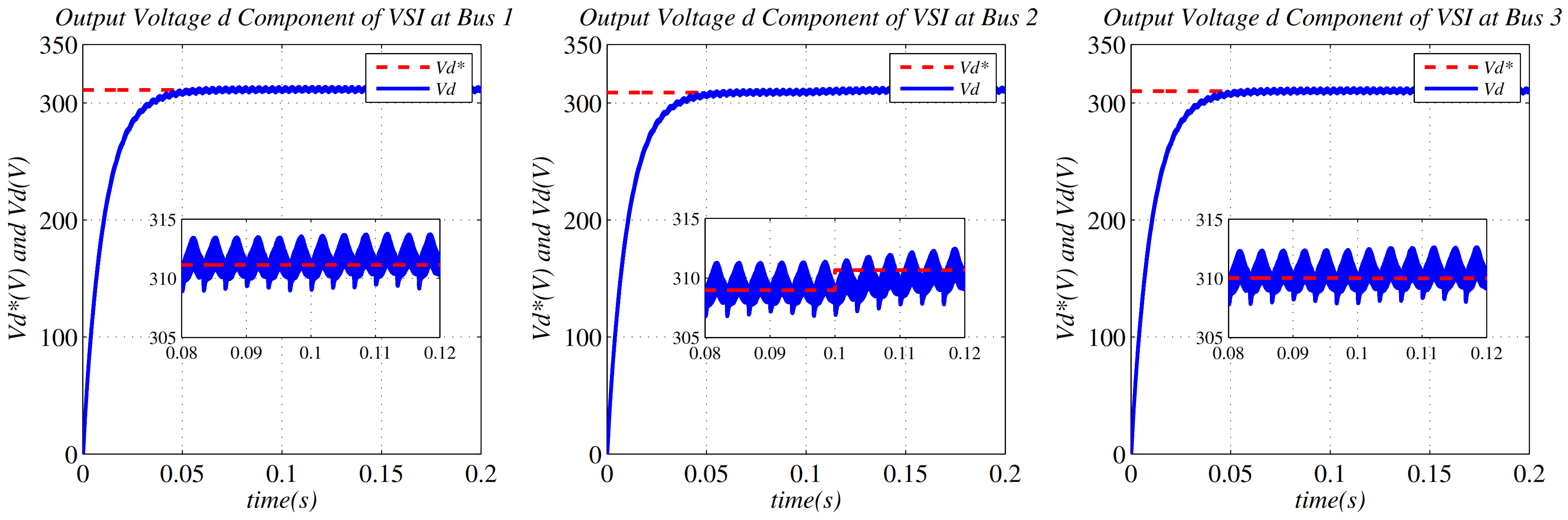
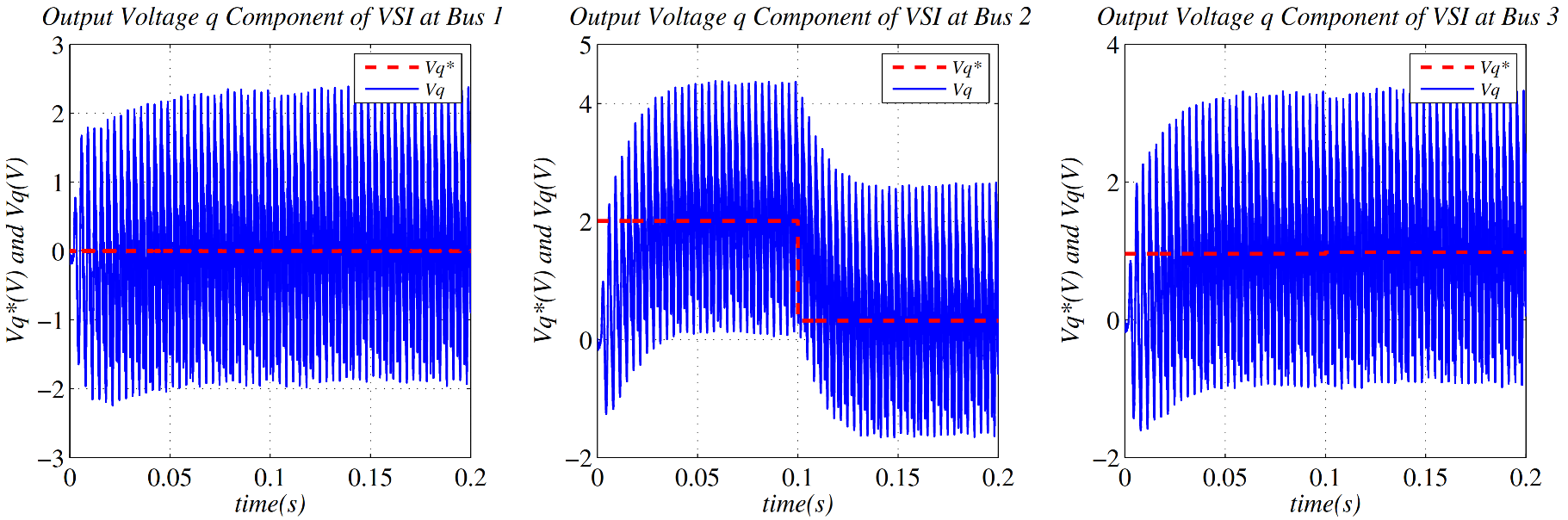
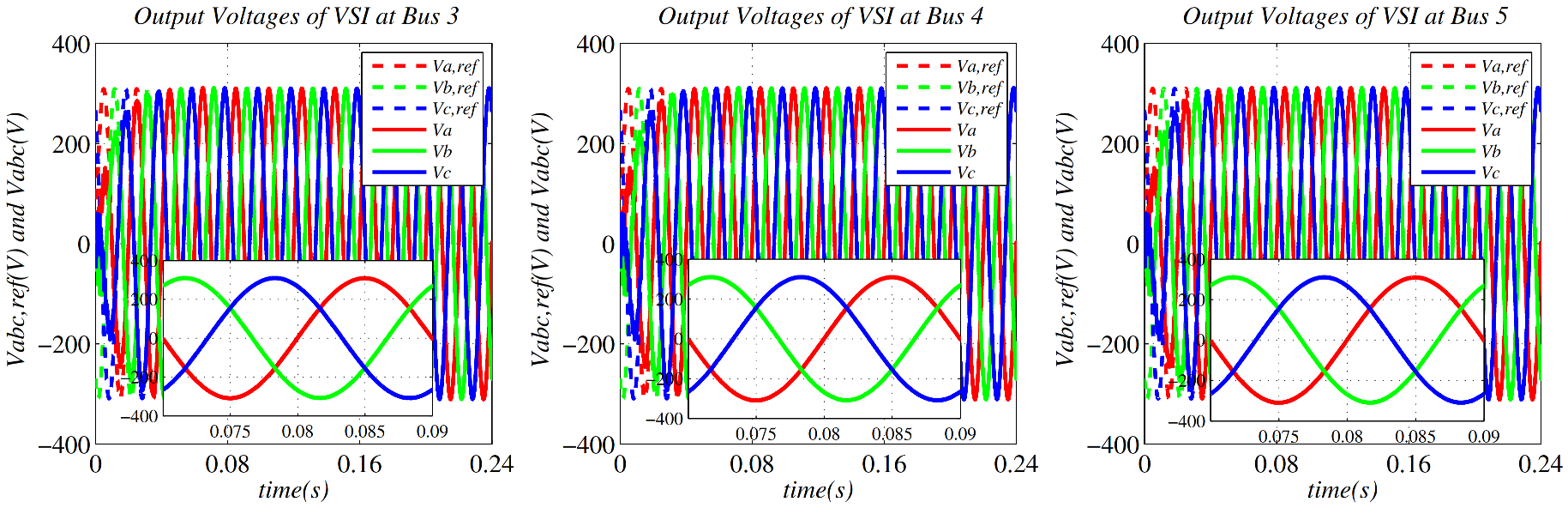
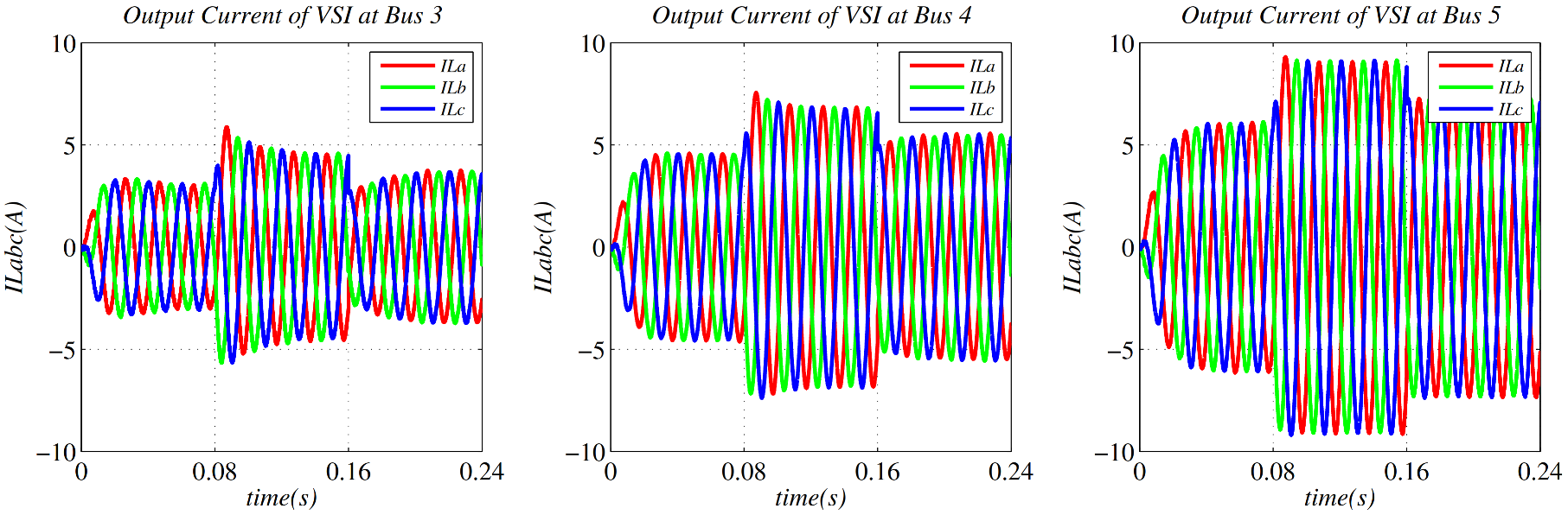
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| VSI | voltage source inverter |
| PWM | pulse width modulation |
| SMC | sliding mode controller |
| HGO | high-gain observer |
| VCM | voltage control mode |
| PCC | point of common coupling |
References
- Farrokhabadi, M.; Cañizares, C.A.; Simpson-Porco, J.W.; Nasr, E.; Fan, L.; Mendoza-Araya, P.A.; Tonkoski, R.; Tamrakar, U.; Hatziargyriou, N.; Lagos, D.; et al. Microgrid stability definitions, analysis, and examples. IEEE Trans. Power Syst. 2019, 35, 13–29. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Canizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in the microgrid Control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Andishgar, M.H.; Gholipour, E.; Hooshm, R.A. An overview of control approaches of the inverter-based microgrids in islanding mode of operation. Renew. Sustain. Energy Rev. 2017, 80, 1043–1060. [Google Scholar] [CrossRef]
- Zhou, Y.; Ho, C.N.M. A review on microgrid architectures and control methods. In Proceedings of the 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3149–3156. [Google Scholar]
- Guo, W.; Mu, L. Control principles of micro-source inverters used in the microgrid. Prot. Control Mod. Power Syst. 2016, 1, 1–7. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.; Loh, P.C. Advanced Control Architectures for Intelligent Microgrids—Part I: Decentralized and Hierarchical Control. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef] [Green Version]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Saad, N.H.; El-Sattar, A.A.; Mansour, A.E.-A.M. A novel control strategy for grid connected hybrid renewable energy systems using improved particle swarm optimization. Ain Shams Eng. J. 2018, 9, 2195–2214. [Google Scholar] [CrossRef]
- Rezaei, N.; Mazidi, M.; Gholami, M.; Mohiti, M. A new stochastic gain adaptive energy management system for smart microgrids considering frequency responsive loads. Energy Rep. 2020, 6, 914–932. [Google Scholar] [CrossRef]
- Parisio, A.; Rikos, E.; Glielmo, L.A. Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Shrivastava, S.; Subudhi, B.; Das, S. Distributed voltage and frequency synchronisation control scheme for islanded inverter-based microgrid. IET Smart Grid 2018, 1, 48–56. [Google Scholar] [CrossRef]
- Sadabadi, M.S.; Shafiee, Q.; Karimi, A. Plug-and-Play Voltage Stabilization in Inverter-Interfaced Microgrids via a Robust Control Strategy. IEEE Trans. Control Syst. Technol. 2016, 25, 781–791. [Google Scholar] [CrossRef] [Green Version]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of Control and Grid Synchronization for Distributed Power Generation the systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef] [Green Version]
- Chattopadhyay, S.; Mitra, M.; Sengupta, S. Clarke and Park Transform. In Electric Power Quality. Power Systems; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar] [CrossRef]
- Liu, R.; Wang, S.; Liu, G.; Wen, S.; Zhang, J.; Ma, Y. An Improved Virtual Inertia Control Strategy for Low Voltage AC Microgrids with Hybrid Energy Storage Systems. Energies 2022, 15, 442. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. Generalized Closed-Loop Control Schemes with Embedded Virtual Impedances for Voltage Source Converters with LC or LCL Filters. IEEE Trans. Power Electron. 2012, 27, 1850–1861. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Fattah, R.M.A.; Saied, E.M.M.; Maksoud, S.M.A.; Khashab, H.E. Real-time implementation of self-adaptive salp swarm optimization based microgrid droop control. IEEE Access 2020, 8, 185738–185751. [Google Scholar] [CrossRef]
- Ebrahim, M.A.; Ayoub, B.A.A.; Nashed, M.N.F.; Osman, F.A.M. A Novel Hybrid-HHOPSO Algorithm Based Optimal Compensators of Four-Layer Cascaded Control for a New Structurally Modified AC Microgrid. IEEE Access 2020, 9, 4008–4037. [Google Scholar] [CrossRef]
- Jiang, X.-Y.; He, C.; Jermsittiparsert, K. Online optimal stationary reference frame controller for inverter interfaced distributed generation in a microgrid system. Energy Rep. 2019, 6, 134–145. [Google Scholar] [CrossRef]
- Gao, T.; Lin, Y.; Chen, D.; Xiao, L. A novel active damping control based on grid-side current feedback for LCL-filter active power filter. Energy Rep. 2020, 6 (Suppl. 9), 1318–1324. [Google Scholar] [CrossRef]
- Agrawal, S.; Tyagi, B.; Kumar, V.; Sharma, P. 3ph qZSI Controller Design using PI for DC side and PR for AC side Controller including Droop Characteristic in standalone mode. In Proceedings of the IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Trivandrum, India, 2–5 January 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Mohiuddin, S.M.; Qi, J. Optimal Distributed Control of AC Microgrids With Coordinated Voltage Regulation and Reactive Power Sharing. IEEE Trans. Smart Grid 2022, 13, 1789–1800. [Google Scholar] [CrossRef]
- Perez-Ibacache, R.; Castro, R.S.; Pimentel, G.A.; Bizzo, B.S. Dynamic Output-Feedback Decentralized Control Synthesis for Integration of Distributed Energy Resources in AC Microgrids. IEEE Trans. Smart Grid 2021, 13, 1225–1237. [Google Scholar] [CrossRef]
- Batmani, Y.; Khayat, Y.; Najafi, S.; Guerrero, J.M. Optimal Integrated Inner Controller Design in AC Microgrids. IEEE Trans. Power Electron. 2022, 37, 10372–10383. [Google Scholar] [CrossRef]
- Hu, C.; Liu, C.; Luo, S.; Yan, H. Joint Control Strategy of the microgrid Inverter Based on Optimal Control and Residual Dynamic Compensation. J. Phys. 2022, 2215, 012003. [Google Scholar] [CrossRef]
- Yaramasu, V.; Rivera, M.; Narimani, M.; Wu, B.; Rodriguez, J. Model Predictive Approach for a Simple and Effective Load Voltage Control of Four-Leg Inverter with an Output LC Filter. IEEE Trans. Ind. Electron. 2014, 61, 5259–5270. [Google Scholar] [CrossRef]
- Ma, D.; Cao, X.; Sun, C.; Wang, R.; Sun, Q.; Xie, X.; Peng, W. Dual-Predictive Control With Adaptive Error Correction Strategy for AC Microgrids. IEEE Trans. Power Deliv. 2021, 37, 1930–1940. [Google Scholar] [CrossRef]
- Shan, Y.; Pan, A.; Liu, H. A Switching Event-Triggered Resilient Control Scheme for Primary and Secondary Levels in AC Microgrids. ISA Trans. 2022, in press. [Google Scholar] [CrossRef]
- Konneh, K.V.; Adewuyi, O.B.; Lotfy, M.E.; Sun, Y.; Senjyu, T. Application Strategies of the model Predictive Control for the Design and Operations of Renewable Energy-Based Microgrid: A Survey. Electronics 2022, 11, 554. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. A Decentralized Robust Mixed H2/H∞ Voltage Control Scheme to Improve Small/Large-Signal Stability and FRT Capability of Islanded Multi-DER Microgrid Considering Load Disturbances. IEEE Syst. J. 2017, 12, 2610–2621. [Google Scholar] [CrossRef]
- Babazadeh, M.; Karimi, H. A Robust Two-Degree-of-Freedom Control Strategy for an Islanded Microgrid. IEEE Trans. Power Deliv. 2013, 28, 1339–1347. [Google Scholar] [CrossRef]
- Fathi, A.; Shafiee, Q.; Bevrani, H. Robust Frequency Control of the microgrids Using an Extended Virtual Synchronous Generator. IEEE Trans. Power Syst. 2018, 33, 6289–6297. [Google Scholar] [CrossRef]
- Derakhshan, S.; Shafiee-Rad, M.; Shafiee, Q.; Jahed-Motlagh, M.R. Decentralized Robust Voltage Control of Islanded AC Microgrids: An LMI-Based H∞ Approach. In Proceedings of the 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Shafiee-Rad, M.; Shafiee, Q.; Motlagh, M.-R.J. Decentralized Scalable Robust Voltage Control for Islanded AC Microgrids with General Topology. In Proceedings of the 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, M.; Chen, X.; Shahidehpour, M.; Zhou, Q.; Wen, J. Observer-Based Resilient Integrated Distributed Control Against Cyberattacks on Sensors and Actuators in Islanded AC Microgrids. IEEE Trans. Smart Grid 2021, 12, 1953–1963. [Google Scholar] [CrossRef]
- Jouda, M.S.; Kahraman, N. Improved Optimal Control of Transient Power Sharing in the microgrid Using H-Infinity Controller with Artificial Bee Colony Algorithm. Energies 2022, 15, 1043. [Google Scholar] [CrossRef]
- Gholami, S.; Saha, S.; Aldeen, M. Robust multiobjective control method for power sharing among distributed energy resources in islanded microgrids with unbalanced and nonlinear loads. Int. J. Electr. Power Energy Syst. 2018, 94, 321–338. [Google Scholar] [CrossRef]
- Raeispour, M.; Atrianfar, H.; Baghaee, H.R.; Gharehpetian, G.B. Robust Sliding Mode and Mixed H2/H∞ Output Feedback Primary Control of AC Microgrids. IEEE Syst. J. 2020, 15, 2420–2431. [Google Scholar] [CrossRef]
- Hu, W.; Shen, Y.; Yang, Z.; Min, H. Mixed H2/H∞ Optimal Voltage Control Design for Smart Transformer Low-Voltage Inverter. Energies 2022, 15, 365. [Google Scholar] [CrossRef]
- Hua, H.; Qin, Y.; He, Z.; Li, L.; Cao, J. Energy sharing and frequency regulation in energy network via mixed H2/H∞ control with Markovian jump. CSEE J. Power Energy Syst. 2020, 7, 1302–1311. [Google Scholar]
- Azizi, S.M. Robust Controller Synthesis and Analysis in Inverter-Dominant Droop-Controlled Islanded Microgrids. IEEE/CAA J. Autom. Sin. 2021, 8, 1401–1415. [Google Scholar] [CrossRef]
- Chen, Z.; Luo, A.; Wang, H.; Chen, Y.; Li, M.; Huang, Y. Adaptive sliding-mode voltage control for inverter operating in islanded mode in the microgrid. Int. J. Electr. Power Energy Syst. 2015, 66, 133–143. [Google Scholar] [CrossRef]
- Kalla, U.K.; Singh, B.; Murthy, S.S.; Jain, C.; Kant, K. Adaptive Sliding Mode Control of Standalone Single-Phase Microgrid Using Hydro, Wind, and Solar PV Array-Based Generation. IEEE Trans. Smart Grid 2017, 9, 6806–6814. [Google Scholar] [CrossRef]
- Xu, D.; Dai, Y.; Yang, C.; Yan, X. Adaptive fuzzy sliding mode command-filtered backstepping control for islanded PV microgrid with energy storage system. J. Frankl. Inst. 2019, 356, 1880–1898. [Google Scholar] [CrossRef]
- Hu, J.; Sun, Q.; Wang, R.; Wang, B.; Zhai, M.; Zhang, H. Privacy-Preserving Sliding Mode Control for Voltage Restoration of AC Microgrids Based on Output Mask Approach. IEEE Trans. Ind. Inf. 2022, 18, 6818–6827. [Google Scholar] [CrossRef]
- Krishnan, U.B.; Mija, S.J.; Cheriyan, E.P. Improved small signal stability of the microgrid—A droop control scheme with SMC. Electr. Eng. 2022, 1–19. [Google Scholar] [CrossRef]
- Yang, C.; Hua, T.; Dai, Y.; Liu, G.; Huang, X.; Zhang, D. Disturbance-Observer-Based Adaptive Fuzzy Control for Islanded Distributed Energy Resource Systems. Math. Probl. Eng. 2022, 2022, 1527705. [Google Scholar] [CrossRef]
- Al Sumarmad, K.A.; Sulaiman, N.; Wahab, N.I.A.; Hizam, H. Energy Management and Voltage Control in the microgrids Using Artificial Neural Networks, PID, and Fuzzy Logic Controllers. Energies 2022, 15, 303. [Google Scholar] [CrossRef]
- Nasir, M.; Bansal, R.; Elnady, A. A Review of Various Neural Network Algorithms for Operation of AC Microgrids. In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Trivedi, R.; Khadem, S. Implementation of artificial intelligence techniques in the microgrid control environment: Current progress and future scopes. Energy 2022, 8, 100147. [Google Scholar] [CrossRef]
- Etemadi, A.H.; Davison, E.J.; Iravani, R. A Generalized Decentralized Robust Control of Islanded Microgrids. IEEE Trans. Power Syst. 2014, 29, 3102–3113. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dorfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavaei, J. A Survey of Distributed Optimization and Control Algorithms for Electric Power Systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Atassi, A.; Khalil, H. A separation principle for the stabilization of a class of the nonlinear systems. IEEE Trans. Autom. Control 1999, 44, 1672–1687. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Khalil, H.K. High-gain observers in nonlinear feedback control. In Proceedings of the International Conference on Control, Automation and Systems, Seoul, Korea, 14–17 October 2008; pp. xlvii–lvii. [Google Scholar] [CrossRef]
- Kothari, D.P.; Nagrath, I.J. Modern Power System Analysis; Tata McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]


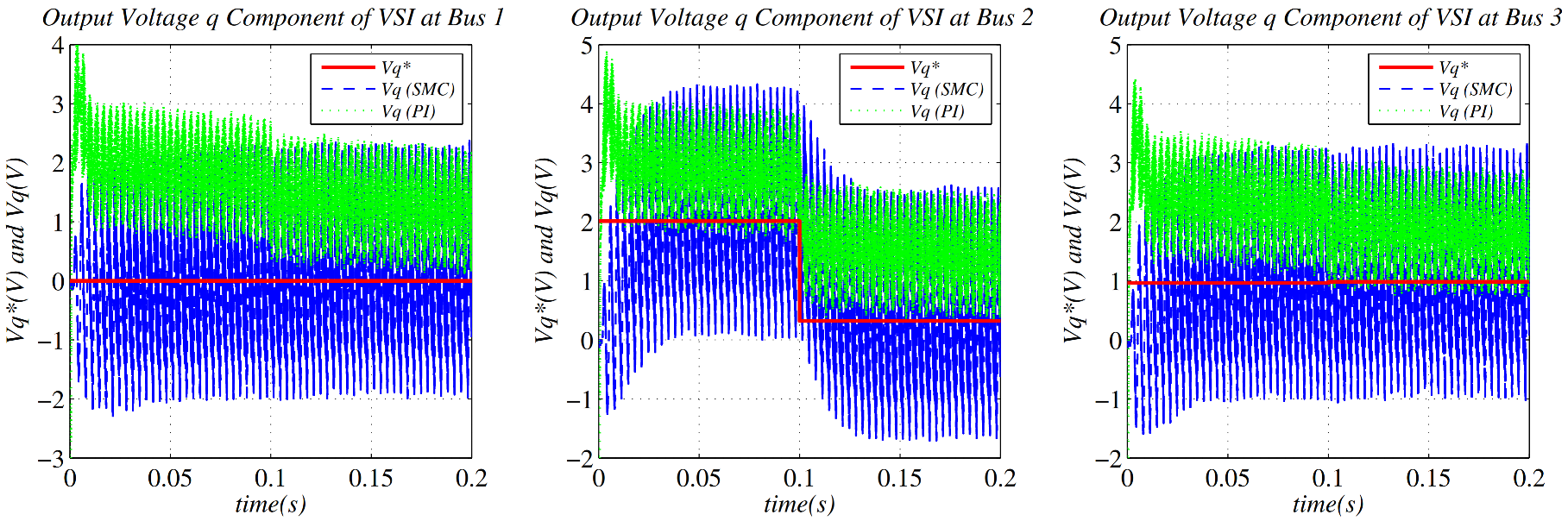
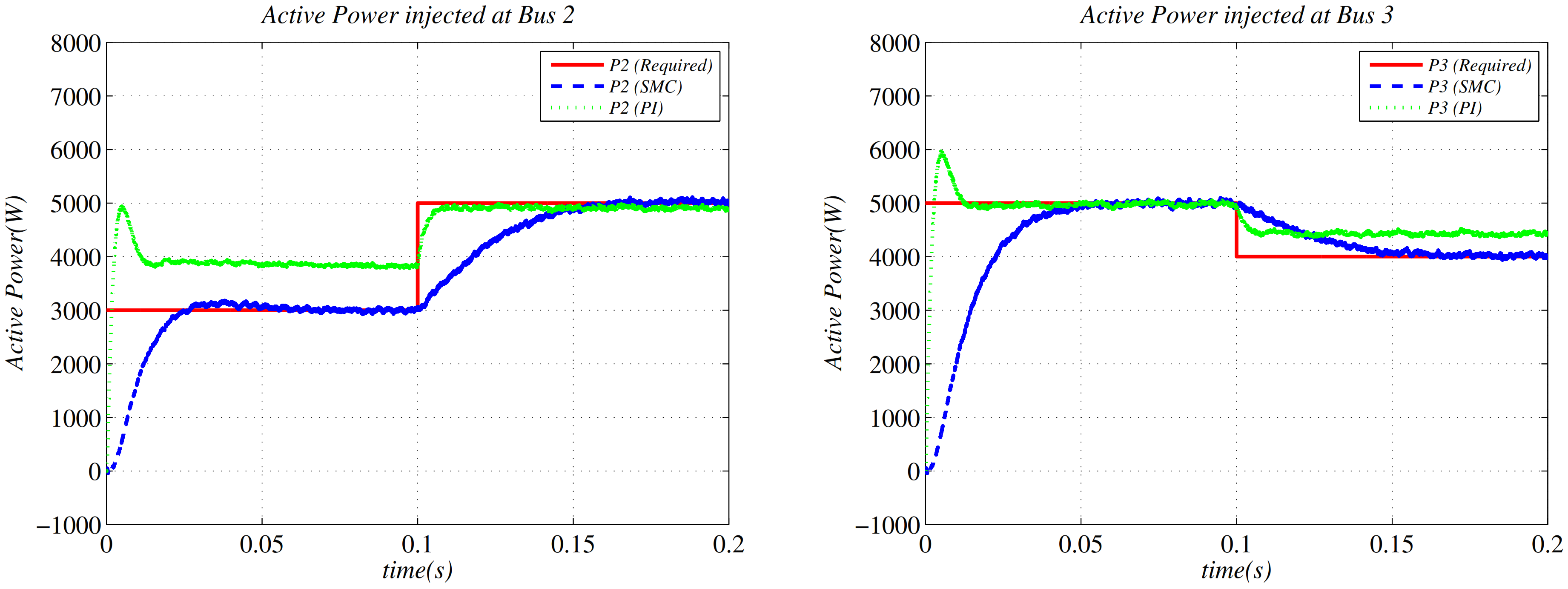
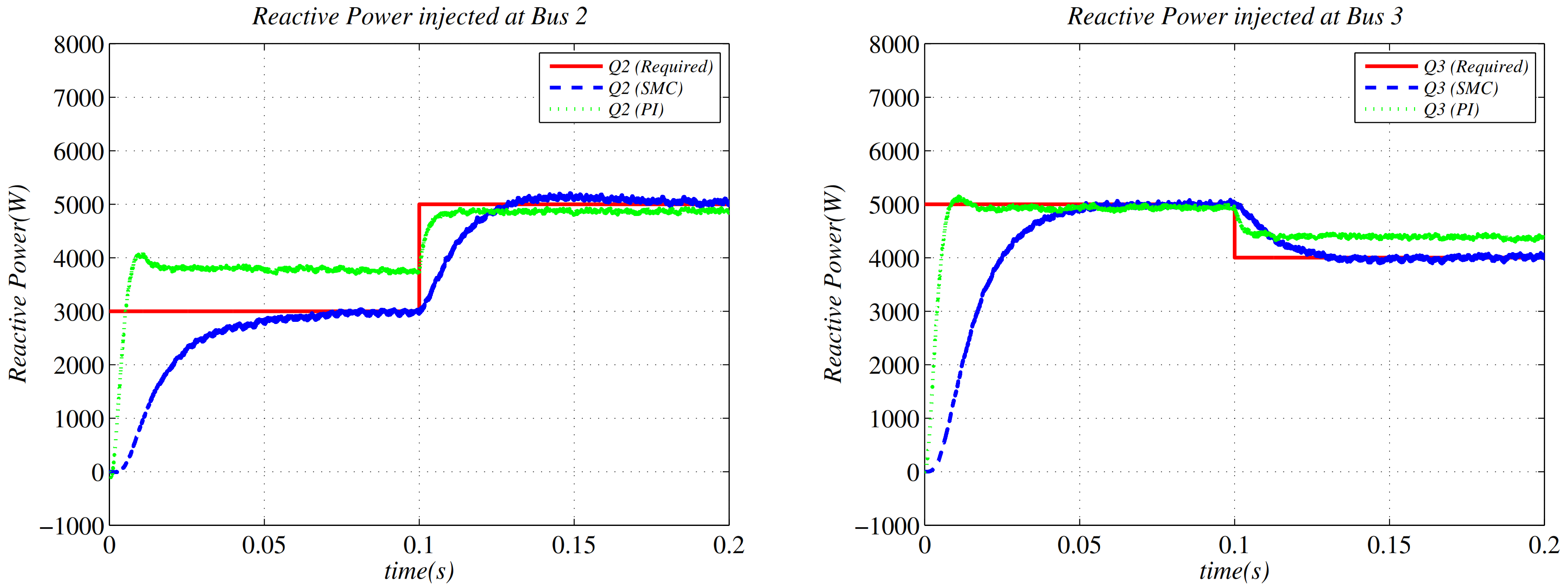

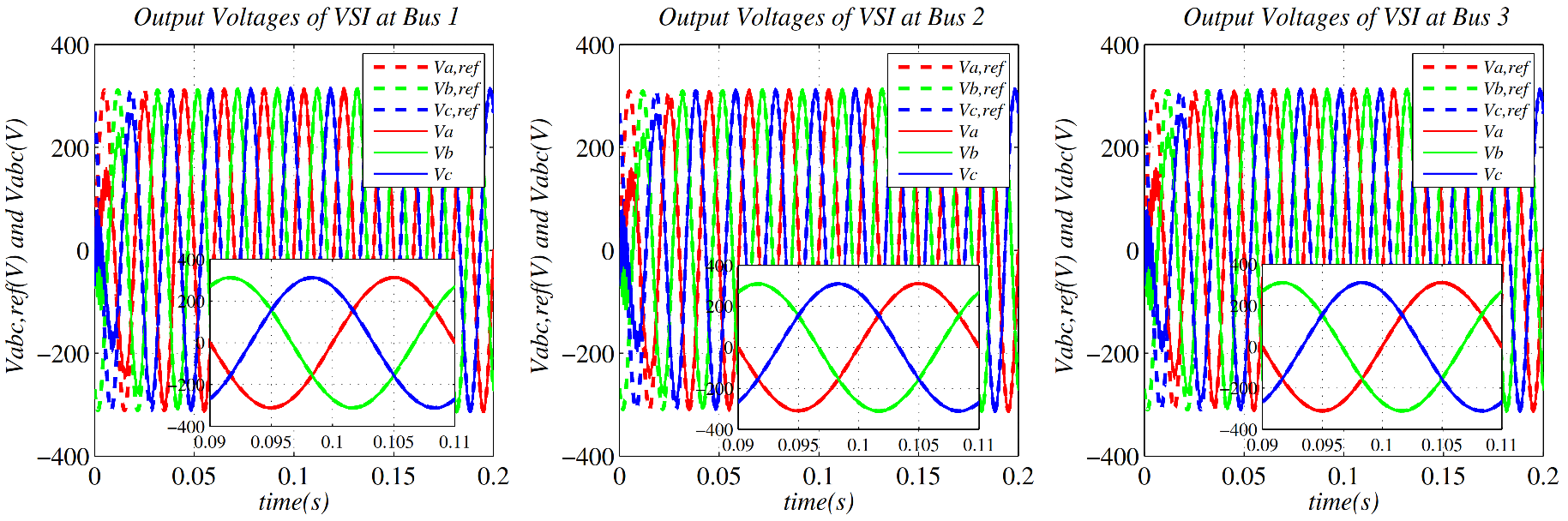

| Electrical Parameters | Values |
|---|---|
| DC voltage source () | 1000 V |
| PWM carrier frequency | 12.8 KHz |
| Nominal voltage of the system (phase-to-neutral) | |
| Nominal frequency of the system | rad/s |
| Resistance of the VSI output filter | 0.2 |
| Inductance of the VSI output filter | 1 mH |
| Capacitance of the VSI output filter | 20 F |
| Line resistance | 0.25 |
| Line inductance | 1.2 H |
| Line resistance | 0.27 |
| Line inductance | 1.3 H |
| Line resistance | 0.26 |
| Line inductance | 1.4 H |
| Bus i | ||||
|---|---|---|---|---|
| Bus 1 | 0 | |||
| Bus 2 | ||||
| Bus 3 | ||||
| Bus 4 |
| Bus i | ||||
|---|---|---|---|---|
| Bus 1 | 0 | |||
| Bus 2 | ||||
| Bus 3 | ||||
| Bus 4 |
| Controller Parameters | Values |
|---|---|
| a | 200 |
| b | |
| c | |
| for d controller | 500 |
| for q controller | 250 |
| Bounds on the System Variables and Parameters | ||
|---|---|---|
| 0 | 350 | |
| 0 | 30 | |
| 0 | ||
| 150 | ||
| 10 | ||
| 10 | ||
| 0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.S.; Memon, A.Y. Robust Output Feedback Control of the Voltage Source Inverter in an AC Microgrid. Energies 2022, 15, 5586. https://doi.org/10.3390/en15155586
Khan HS, Memon AY. Robust Output Feedback Control of the Voltage Source Inverter in an AC Microgrid. Energies. 2022; 15(15):5586. https://doi.org/10.3390/en15155586
Chicago/Turabian StyleKhan, Hamid Saeed, and Attaullah Y. Memon. 2022. "Robust Output Feedback Control of the Voltage Source Inverter in an AC Microgrid" Energies 15, no. 15: 5586. https://doi.org/10.3390/en15155586
APA StyleKhan, H. S., & Memon, A. Y. (2022). Robust Output Feedback Control of the Voltage Source Inverter in an AC Microgrid. Energies, 15(15), 5586. https://doi.org/10.3390/en15155586






