A Data-Driven Reduced-Order Model for Estimating the Stimulated Reservoir Volume (SRV)
Abstract
:1. Introduction
2. Methodologies and Mathematical Formulation
2.1. Data-Based Framework for SRV Prediction
2.1.1. Used Dataset
2.1.2. Model Construction
2.2. Global Sensitivity Analysis and Reduced Order Model
2.2.1. The Mathematical Background of the Sobol Method
- f0 should be constant.
- The integral of each member over its variables = 0
- 3
- All the terms in Equation (3) are orthogonal, meaning that if (i1,..., is) ≠ (j1,…, jt), then
2.2.2. Sobol Method for Complex Functions
3. Results and Discussion
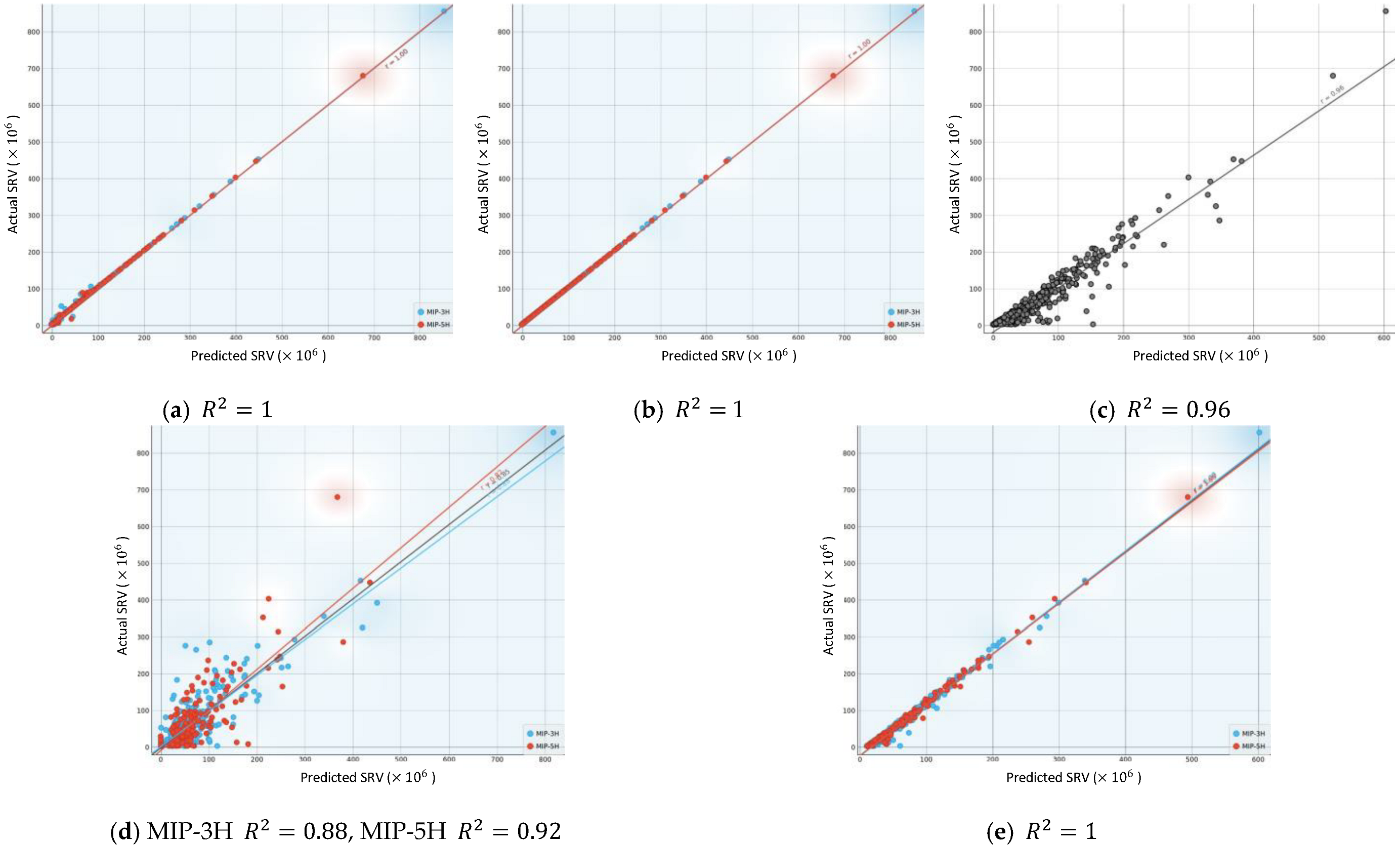
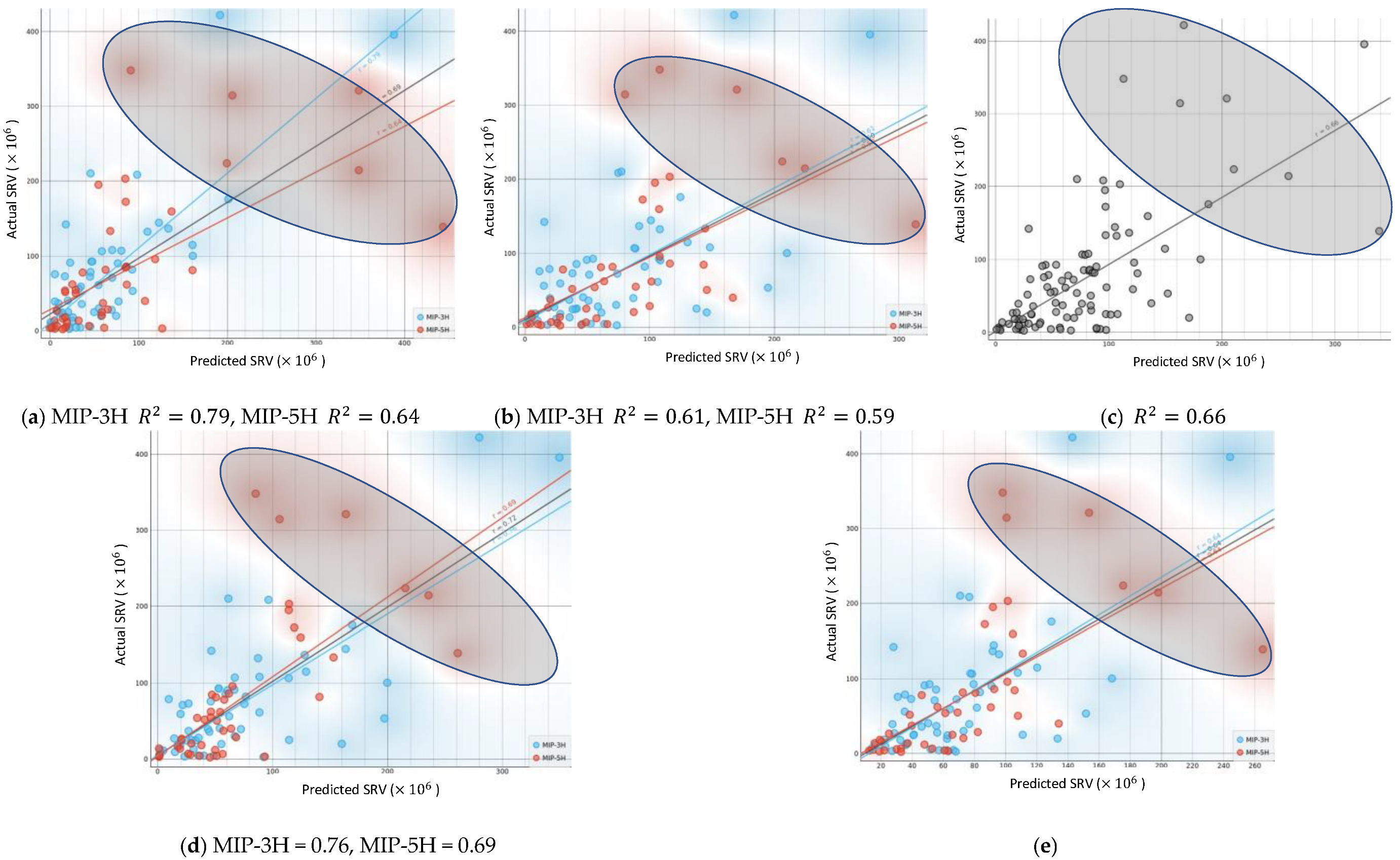
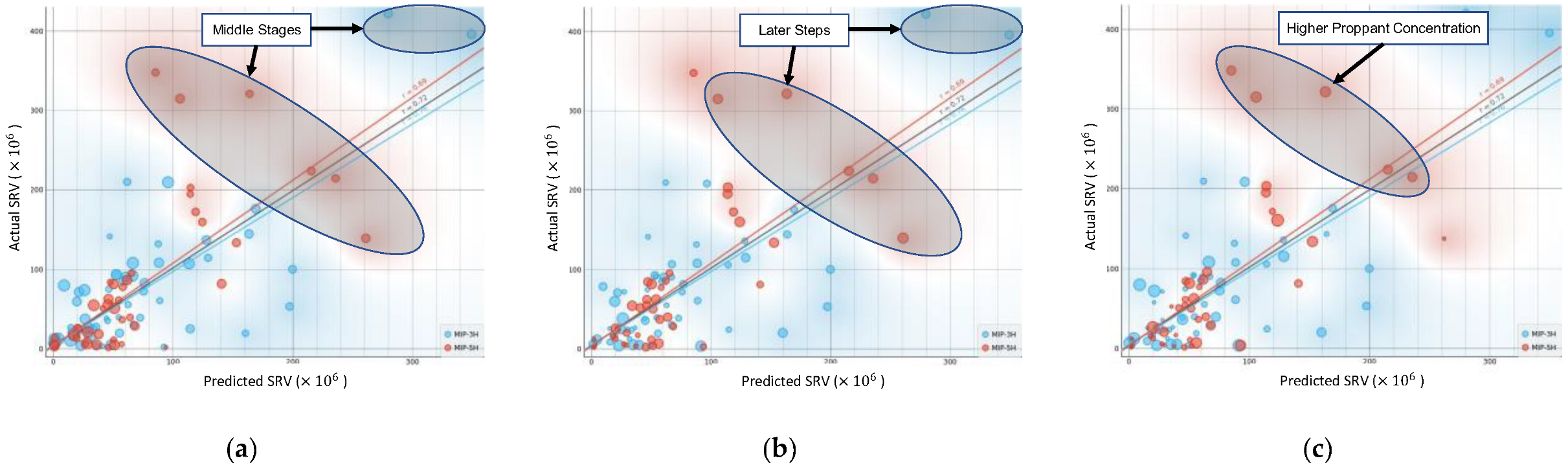
3.1. ML Models Performances
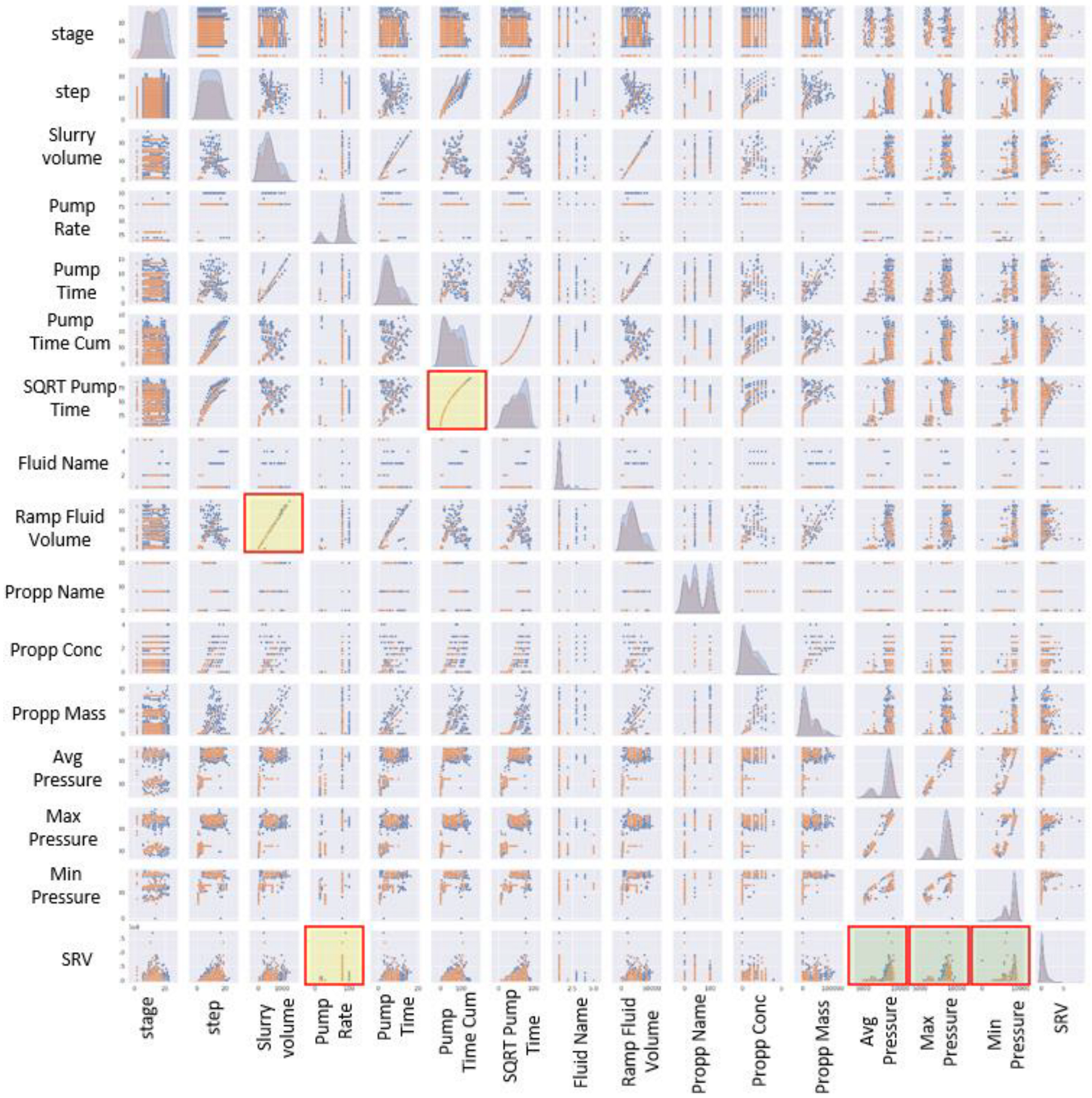
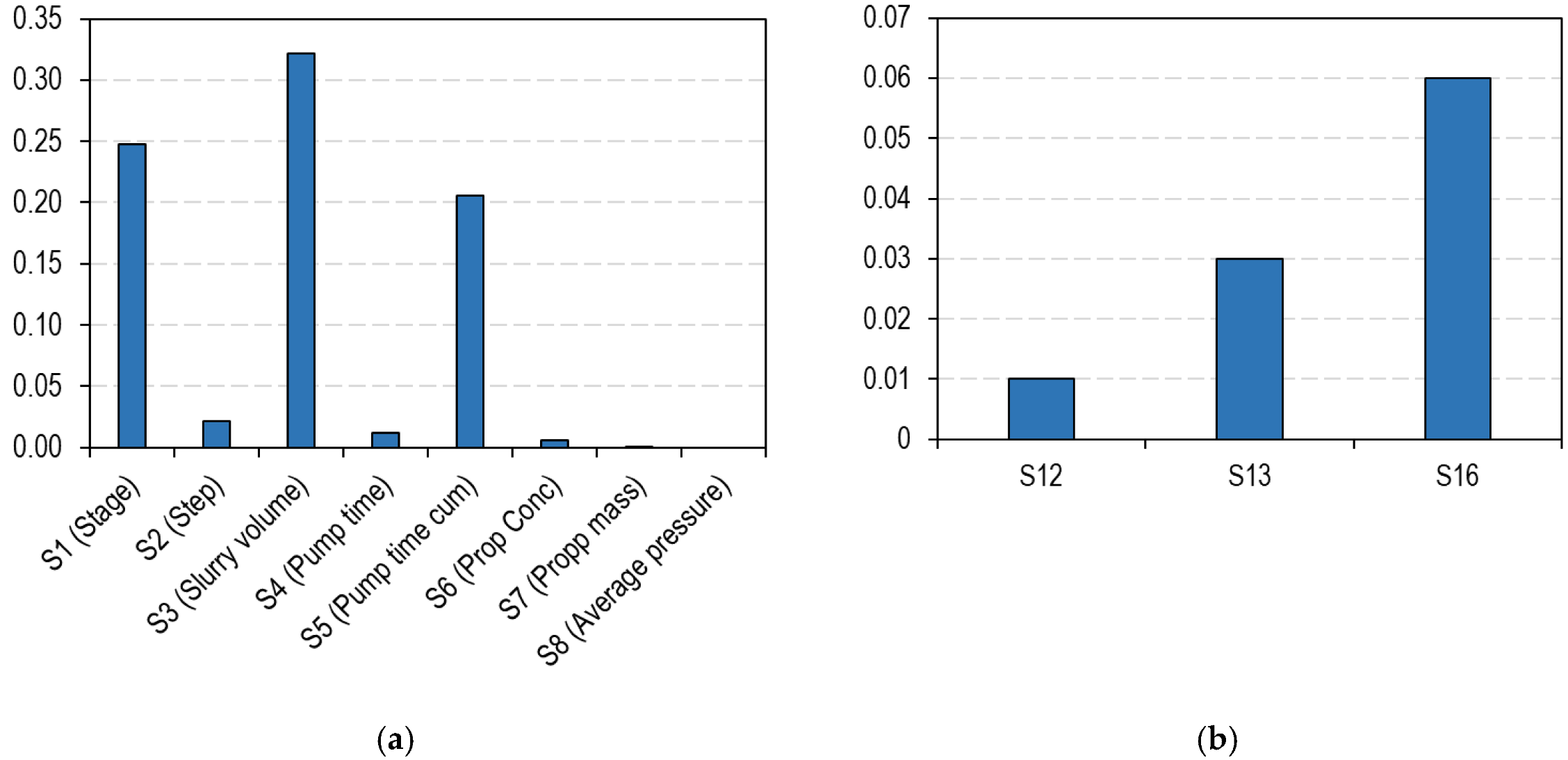
3.2. Global Sensitivity Analysis on Parameters Affecting the SRV
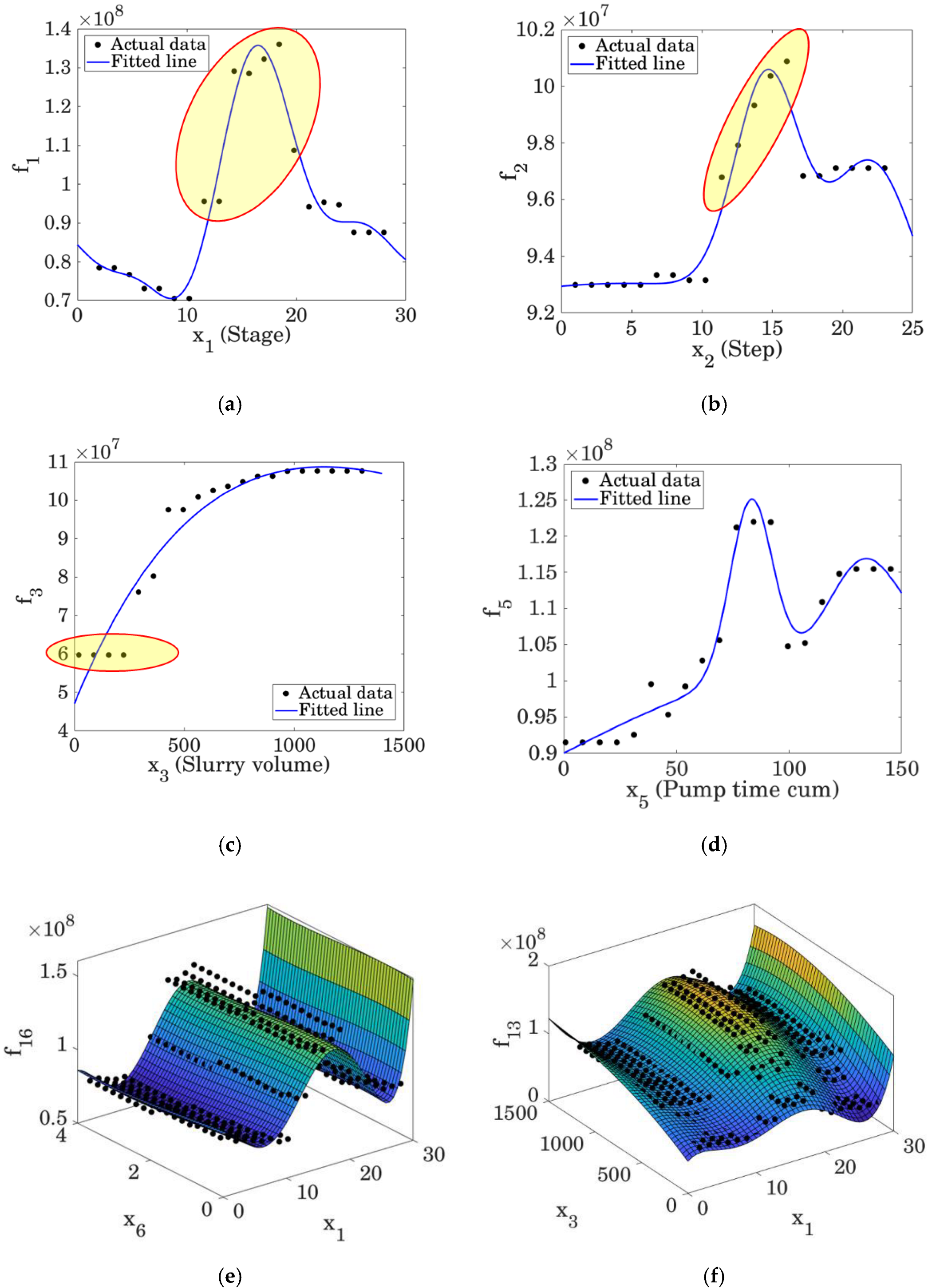
3.3. ROM for Predicting SRV Using Recorded Field Data
3.4. Steps to Improve the Models
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.; Qin, C.; Feng, Q.; Javadpour, F.; Rui, Z. A framework for predicting the production performance of unconventional resources using deep learning. Appl. Energy 2021, 295, 117016. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S. Insights to fracture stimulation design in unconventional reservoirs based on machine learning modeling. J. Pet. Sci. Eng. 2019, 174, 682–695. [Google Scholar] [CrossRef]
- Siddiqui, F.; Rezaei, A.; Dindoruk, B.; Soliman, M.Y. Eagle ford fluid type variation and completion optimization: A case for data analytics. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Luo, G.; Tian, Y.; Bychina, M.; Ehlig-Economides, C. Production optimization using machine learning in Bakken shale. In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 23–25 July 2018; Society of Exploration Geophysicists, American Association of Petroleum Geologists, Society of Petroleum Engineers: Tulsa, OK, USA; pp. 2174–2197. [Google Scholar]
- Chen, X.; Li, J.; Gao, P.; Zhou, J. Prediction of shale gas horizontal wells productivity after volume fracturing using machine learning—An LSTM approach. Pet. Sci. Technol. 2022, 40, 1861–1877. [Google Scholar] [CrossRef]
- Srinivasan, S.; O’Malley, D.; Mudunuru, M.K.; Sweeney, M.R.; Hyman, J.D.; Karra, S.; Frash, L.; Carey, J.W.; Gross, M.R.; Viswanathan, H.S. A machine learning framework for rapid forecasting and history matching in unconventional reservoirs. Sci. Rep. 2021, 11, 21730. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Gray, K.E. Analytical and Machine-Learning Analysis of Hydraulic Fracture-Induced Natural Fracture Slip. SPE J. 2021, 26, 1722–1738. [Google Scholar] [CrossRef]
- Urban-Rascon, E.; Aguilera, R. Machine Learning Applied to SRV Modeling, Fracture Characterization, Well Interference and Production Forecasting in Low Permeability Reservoirs. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, OnePetro, Virtual, 27–31 July 2020. [Google Scholar]
- Sprunger, C.; Muther, T.; Syed, F.I.; Dahaghi, A.K.; Neghabhan, S. State of the art progress in hydraulic fracture modeling using AI/ML techniques. Model. Earth Syst. Environ. 2021, 8, 1–13. [Google Scholar] [CrossRef]
- Tandon, S. Improved Analysis of Stimulated Reservoir Volumes in Unconventional Reservoirs Using Supervised Learning Techniques. In Proceedings of the SPE Eastern Regional Meeting, Charleston, WV, USA, 15–17 October 2019. [Google Scholar]
- Wang, L.K.; Sun, A.Y. Well Spacing Optimization for Permian Basin Based on Integrated Hydraulic Fracturing, Reservoir Simulation and Machine Learning Study. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Virtual, 20–22 July 2020. [Google Scholar]
- Lecampion, B.; Desroches, J.; Weng, X.; Burghardt, J.; Brown, J.E. Can we engineer better multistage horizontal completions? Evidence of the importance of near-wellbore fracture geometry from theory, lab and field experiments. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015. [Google Scholar]
- Morozov, A.D.; Popkov, D.O.; Duplyakov, V.M.; Mutalova, R.F.; Osiptsov, A.A.; Vainshtein, A.L.; Burnaev, E.V.; Shel, E.V.; Paderin, G.V. Data-driven model for hydraulic fracturing design optimization: Focus on building digital database and production forecast. J. Pet. Sci. Eng. 2020, 194, 107504. [Google Scholar] [CrossRef]
- Rafiee, M.; Rezaei, A.; Soliman, M. Investigating hydraulic fracture propagation in multi well pads: A close look at stress shadow from overlapping fractures. Hydraul. Fract. J. 2015, 2, 23–27. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Sobol, I.M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 2001, 55, 271–280. [Google Scholar] [CrossRef]
- Rezaei, A.; Nakshatrala, K.B.; Siddiqui FA, H.D.; Dindoruk, B.; Soliman, M. A global sensitivity analysis and reduced-order models for hydraulically fractured horizontal wells. Comput. Geosci. 2020, 24, 995–1029. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Hu, R.; Walsh, S.D. Development of Reduced Order Hydro-mechanical Models of Fractured Media. Rock Mech. Rock Eng. 2022, 55, 235–248. [Google Scholar] [CrossRef]
- Cheng, C.; Bunger, A.P. Reduced order model for simultaneous growth of multiple closely-spaced radial hydraulic fractures. J. Comput. Phys. 2019, 376, 228–248. [Google Scholar] [CrossRef]
- Siddhamshetty, P.; Wu, K.; Kwon, J.S.I. Optimization of simultaneously propagating multiple fractures in hydraulic fracturing to achieve uniform growth using data-based model reduction. Chem. Eng. Res. Des. 2018, 136, 675–686. [Google Scholar] [CrossRef]
- Sidhu, H.S.; Narasingam, A.; Siddhamshetty, P.; Kwon, J.S.I. Model order reduction of nonlinear parabolic PDE systems with moving boundaries using sparse proper orthogonal decomposition: Application to hydraulic fracturing. Comput. Chem. Eng. 2018, 112, 92–100. [Google Scholar] [CrossRef] [Green Version]
- Rezaei, A.; Aminzadeh, F.; Von Lunen, E. Applications of Machine Learning for Estimating the Stimulated Reservoir Volume (SRV). In Proceedings of the Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021. [Google Scholar]
- Carr, T.; Ghahfarokhi, P.K.; Carney, B.J.; Hewitt, J.; Vargnetti, R. Marcellus Shale Energy and Environmental Laboratory (MSEEL) Results and Plans: Improved Subsurface Reservoir Characterization and Engineered Completions. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019; Society of Exploration Geophysicists: Houston, TX, USA, 2019; pp. 215–224. [Google Scholar]
- Mayerhofer, M.J.; Lolon, E.P.; Warpinski, N.R.; Cipolla, C.L.; Walser, D.; Rightmire, C.M. What is stimulated reservoir volume? SPE Prod. Oper. 2010, 25, 89–98. [Google Scholar] [CrossRef]
- Hastie, T.; Rosset, S.; Zhu, J.; Zou, H. Multi-class adaboost. Stat. Its Interface 2009, 2, 349–360. [Google Scholar] [CrossRef] [Green Version]
- Cipolla, C.L.; Wright, C.A. State-of-the-Art in Hydraulic Fracture Diagnostics. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 16–18 October 2000. [Google Scholar] [CrossRef]
- Johnson, S.; Settgast, R.; Fu, P.; Antoun, T.; Ryerson, F.J. GEOS Code Development Road Map-May 2013 (No. LLNL-TR-636127); Lawrence Livermore National Lab (LLNL): Livermore, CA, USA, 2013. [Google Scholar]
- Sherman, C.S.; Morris, J.P.; Fu, P.; Settgast, R.R. Recovering the microseismic response from a geomechanical simulation. Geophysics 2019, 84, KS133–KS142. [Google Scholar] [CrossRef]
- Levitus, M. Mathematical Methods in Chemistry; Arizona State University: Phoenix, AZ, USA, 2022; Available online: https://libretexts.org/ (accessed on 11 April 2022).






| Well | Stage | Step | Step Name | Slurry Vol. | Pump Rate | Pump Time | Pump Time Cum. | Fluid Name | Ramp Fluid Vol. | Propp. Name | Propp. Conc. | Propp. Mass | Avg. Treating Press. | Max. Treating Press. | Min. Treating Press. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bbl | bbl/min | min | min | gal | ppa | lb | psi | psi | psi | ||||||
| MIP-3H | 8 | 1 | Rate | 20 | 15 | 01.30 | 1.30 | 1 | 840 | 0 | 0 | 0 | 5470 | 5833 | 4303 |
| MIP-3H | 8 | 2 | Acid | 71 | 15 | 04.80 | 6.10 | 2 | 2999 | 0 | 0 | 0 | 6028 | 6101 | 5839 |
| MIP-3H | 8 | 3 | Pad | 595 | 80 | 07.40 | 13.50 | 1 | 25,000 | 0 | 0 | 0 | 7996 | 9143 | 6028 |
| MIP-3H | 8 | 4 | 0.25 PPA | 529 | 80 | 06.60 | 20.10 | 1 | 22,000 | 100 | 0.20 | 5500 | 8991 | 9089 | 8900 |
| MIP-3H | 8 | 5 | 0.5 PPA | 803 | 80 | 10.00 | 30.10 | 1 | 33,000 | 100 | 0.50 | 16,500 | 8877 | 8902 | 8855 |
| MIP-3H | 8 | 6 | 0.75 PPA | 902 | 80 | 11.30 | 41.40 | 1 | 36,667 | 100 | 0.70 | 27,500 | 8913 | 8948 | 8893 |
| MIP-3H | 8 | 7 | 1 PPA | 1149 | 80 | 14.40 | 55.80 | 1 | 46,200 | 100 | 1.00 | 46,200 | 8951 | 8988 | 8915 |
| MIP-3H | 8 | 8 | 1.5 PPA | 1025 | 80 | 12.80 | 58.60 | 1 | 40,333 | 100 | 1.50 | 60,449 | 9058 | 9150 | 8944 |
| MIP-3H | 8 | 9 | 1.75 PPA | 1156 | 80 | 14.50 | 83.10 | 1 | 44,982 | 100 | 1.80 | 78,718 | 9153 | 9197 | 9124 |
| MIP-3H | 8 | 10 | 2 PPA | 748 | 80 | 09.40 | 92.50 | 1 | 28,812 | 100 | 2.00 | 57,624 | 9066 | 9200 | 8361 |
| Well | Stage | Step | Time | Time Difference | Cum. Time | YLoc | XLoc | TVD (Z) |
|---|---|---|---|---|---|---|---|---|
| Ft | Ft | Ft | ||||||
| MIP-5H | 2 | 1 | 10:30:10 | 00:00:00 | 00:00:00 | 407,735.31 | 1,831,598.25 | −5986 |
| MIP-5H | 2 | 1 | 10:30:34 | 00:00:24 | 00:00:24 | 407,753.94 | 1,831,645.44 | −5968 |
| MIP-5H | 2 | 1 | 10:30:41 | 00:00:07 | 00:00:31 | 407,653.12 | 1,831,692.37 | −6271 |
| MIP-5H | 2 | 2 | 10:32:38 | 00:01:57 | 00:02:28 | 407,590.36 | 1,831,319.54 | −5865 |
| MIP-5H | 2 | 3 | 10:37:08 | 00:04:30 | 00:06:58 | 407,606.55 | 1,831,496.50 | −5840 |
| MIP-5H | 2 | 3 | 10:44:45 | 00:07:37 | 00:14:35 | 1,831,301.72 | 407,706.51 | −6135 |
| MIP-5H | 2 | 7 | 11:01:14 | 00:16:29 | 00:31:04 | 1,831,879.96 | 407,641.13 | −5475 |
| MIP-5H | 2 | 9 | 11:11:24 | 00:10:10 | 00:41:14 | 1,831,688.69 | 407,965.96 | −6320 |
| MIP-5H | 2 | 9 | 11:11:53 | 00:00:29 | 00:41:43 | 1,831,600.45 | 408,043.02 | −6503 |
| MIP-5H | 2 | 9 | 11:14:01 | 00:02:08 | 00:43:51 | 1,831,564.41 | 407,803.99 | −6201 |
| Well | Stage | Step | Slurry Volume | Pump Time | Pump Time Cum. | Propp. Conc. | Propp. Mass | Avg. Treating Press. | SRV (Estimated) | |
|---|---|---|---|---|---|---|---|---|---|---|
| bbl | min | min | PPA | lb × 103 | psi | ft3 | ||||
| Min | - | 1 | 1 | - | - | 0 | 0 | - | 5000 | 0 |
| Max | - | 26 | 24 | 1500 | 20 | 160 | 4 | 100 | 9000 | 3 × 108 |
| Function | Mathematical Form |
|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaei, A.; Aminzadeh, F. A Data-Driven Reduced-Order Model for Estimating the Stimulated Reservoir Volume (SRV). Energies 2022, 15, 5582. https://doi.org/10.3390/en15155582
Rezaei A, Aminzadeh F. A Data-Driven Reduced-Order Model for Estimating the Stimulated Reservoir Volume (SRV). Energies. 2022; 15(15):5582. https://doi.org/10.3390/en15155582
Chicago/Turabian StyleRezaei, Ali, and Fred Aminzadeh. 2022. "A Data-Driven Reduced-Order Model for Estimating the Stimulated Reservoir Volume (SRV)" Energies 15, no. 15: 5582. https://doi.org/10.3390/en15155582
APA StyleRezaei, A., & Aminzadeh, F. (2022). A Data-Driven Reduced-Order Model for Estimating the Stimulated Reservoir Volume (SRV). Energies, 15(15), 5582. https://doi.org/10.3390/en15155582







