Abstract
Forecasting energy demand within a distribution network is essential for developing strategies to manage and optimize available energy resources and the associated infrastructure. In this study, we consider remote communities in the Arctic located at the end of the radial distribution network without alternative energy supply. Therefore, it is crucial to develop an accurate forecasting model to manage and optimize the limited energy resources available. We first compare the accuracy of several models that perform short-and medium-term load forecasts in rural areas, where a single industrial customer dominates the electricity consumption. We consider both statistical methods and machine learning models to predict energy demand. Then, we evaluate the transferability of each method to a geographical rural area different from the one considered for training. Our results indicate that statistical models achieve higher accuracy on longer forecast horizons relative to neural networks, while the machine-learning approaches perform better in predicting load at shorter time intervals. The machine learning models also exhibit good transferability, as they manage to predict well the load at new locations that were not accounted for during training. Our work will serve as a guide for selecting the appropriate prediction model and apply it to perform energy load forecasting in rural areas and in locations where historical consumption data may be limited or even not available.
1. Introduction
Accurate load forecasting systems can reduce additional costs related to inaccurate prediction of the energy demand and provide a better understanding of the dynamics of existing power systems [1,2]. If the forecasts overestimate the demand, the result will be excess power supply. Consequently, this will result in increased costs and contract curtailments for the energy market participants. On the other hand, underestimation of the demand could lead to a lack of energy availability at heavy loads, which in turn leads to consequences for end-users, who in the worst-case scenario will not have sufficient energy supply [3,4]. The global energy market is now evolving from centralized systems with large power stations connected to a single electricity grid which support the area of interest, towards the inclusion of more decentralized energy systems where the area of interest may be supplied by multiple energy sources, such as local renewable distributed generation (DG) technologies and battery storage systems [5,6,7,8,9,10,11]. In addition, inhabitants should have the ability to participate actively in the energy market by acting as prosumers where they both generate and consume electricity [12,13,14,15,16,17].
In the transition from centralized to decentralized energy systems, there is a need to develop methodologies for understanding and interpreting the dynamics of existing energy systems, which in turn will be an essential tool in developing emerging energy systems [18,19,20]. The Norwegian Water Resources and Energy Directorate (NVE) states that using the current electricity grid costs the households and industries in Norway approximately 27 billion NOK per year [21,22]. This cost is expected to increase significantly in the future, as the current electricity network must be upgraded to handle the increased electrification in society. Therefore, NVE has proposed new power tariff schemes that penalize the use of electricity during periods of heavy loads [21]. By optimizing the energy flows in the electricity network, the profile of the load demand will become more evenly distributed throughout the day and could allow postponement of upgrades to the current infrastructure. The requirements by NVE show the importance of optimizing the use of resources in an energy grid and developing accurate energy-forecasting systems are fundamental to achieving this goal.
To manage the limited availability of energy at locations that rely on the stable power supply, accurate predictions of energy demand are essential. In this study, we analyze two remote communities on the island of Senja in Northern Norway, which represent extreme examples of the challenges stated by NVE. The two communities experience frequent power outages due to heavy loads in specific periods and, if the current grid is not optimized, upgrading the whole energy system will be inevitable. The energy consumption on the grid is heavily affected by the activities of the islands’ major industries [23].
Besides Northern Norway, the challenges mentioned above also apply to remote communities worldwide, especially developing countries [24,25]. In 2018, there were approximately 860 million inhabitants of remote areas that either do not have reliable sources of electricity or are not connected to power grids at all [26]. In addition, remote areas in Russia, Alaska, and Canada are heavily dependent on diesel generators for electricity supply, which imposes an economic, environmental, and social burden on the local populations as diesel generators create noise pollution, aggravate the local air quality and increase the emissions of greenhouse gases [27]. These examples confirm the importance of transitioning towards new energy systems to improve economic, social, and environmental conditions, in addition to ensuring a reliable power supply [27,28,29].
In the remote communities served by the Senja network analyzed in this paper, there are still no services available for predicting the energy demand [23]. We evaluate approaches to forecasting energy demand based on both statistical and machine learning-based approaches to project future energy demand from historical data. The total energy demand is characterized by a combination of load profiles from two sectors (households and industry) that exhibit very different consumption profiles and require dedicated forecast models. Unlike energy load profiles in cities and residential communities, where the household sector is the main contributor to the total energy consumption, the total load profiles for the remote communities analyzed here are dominated by industry [30]. Industrial activities are therefore essential to consider when developing an accurate forecasting model.
The contribution of our work is twofold. First, we investigate which model achieves the best performance in predicting the energy load in rural areas, as a function of the forecast horizon. Our analysis evaluates several statistical and machine learning approaches.
Secondly, we analyze the transferability of each prediction model, in terms of the capability of predicting time series of energy demand at different locations within the Senja electricity grid. Our study provides important insights about the possibility of applying the models considered in our study to new geographical sites.
2. Background and Related Work
The energy load profiles are typically represented by time series that describe the dynamics of the underlying energy distribution system and are characterized by typical human-based seasonal and cyclic consumption patterns. Indeed, load patterns can vary significantly depending on the observation period, the nature of each system, and external factors such as climate and weather. Achieving accurate load forecasting has been one of the principal foci in several research areas. Different models have been proposed, each one characterized by different properties in terms of complexity and effectiveness in predicting on different forecasting horizons [31,32,33].
In this paper, we examine several approaches to predict energy consumption on both short and longer forecasting horizons. Two different forecasting methodologies are used, one statistical-based method, and one method based on neural networks.
2.1. Statistical Methods
For the statistical method, two different approaches were investigated. First, we consider the statistical Autoregressive Integrated Moving Average (ARIMA) model, which has been a baseline tool in prediction problems for several years [34]. The ARIMA model is well known for its simplicity of implementation and high accuracy in predicting long forecasting horizons [35]. The second approach is a newer statistical model called Prophet. Prophet is a tool that has recently gained popularity due to its simplicity and flexibility when performing predictions [36].
ARIMA models require an elaborated statistical analysis to optimize the model configuration [37]. Moreover, ARIMA models make strong assumptions about the nature of the underlying dynamical system that generates the observed time series. This usually introduces strong biases that, in some cases, might be wrong and will hinder the accuracy of the predictions [38]. In the study by Taylor [35], the ARIMA predictions at longer forecasting horizons were shown to outperform more complex models in terms of accuracy. In Reference [39], short-term load forecasting with window-based ARIMA algorithms was applied to predict electricity consumption to optimize the available energy supply. The study concluded that it is sufficient to consider daily consumption data and aggregated hourly coefficients of daily profiles to obtain accurate short-term predictions by use of the sliding window-based forecasting algorithms proposed by the authors. In the study by Bianchi et al. [40], the authors proposed a comparative study for heat demand forecasting in a real-world case. The authors tested ARIMA models on different load time series and the results showed that the ARIMA models can perform accurate predictions on long-term horizons.
Prophet is implemented as an open-source library designed for making predictions on univariate time series [36]. The library is easy to use and allows the identification of optimum hyperparameter configurations for the model that will make a forecast of the time series. The Prophet library offers a practical prediction tool that can be used by analysts without expertise in time series modeling. In the original paper [36], the authors compare the Prophet method against several automated forecast procedures such as ARIMA, exponential smoothing models, random walk model with weekly seasonality, and a TBATS model with both weekly and yearly seasonality. The result shows that the Prophet forecasts result in lower prediction errors.
2.2. Machine Learning Methods
Five different neural network architectures are considered to predict the energy demand. In particular, we examine both Recurrent Neural Networks (RNNs) and Convolutional Neural Networks (CNNs).
In prediction-related problems, RNNs have gained significant attention due to their ability to capture complex non-linear dynamics in the time series [41], and RNN architectures have been shown to outperform other models in tasks related to forecasting energy demand [42]. The RNNs examined in this paper have been previously applied to solve different types of prediction related tasks [43]. As trainable RNN architectures, we consider Long Short-Term Memory (LSTM), Gated Recurrent Units (GRU), and Elman Recurrent Neural Networks (ERNN). In addition, we consider the Echo State Network (ESN), which is a randomized neural network from the family of Reservoir Computing approaches [42].
The RNNs are capable of modeling any non-linear dynamical systems up to a given precision and have been applied in many contexts where the temporal dependency is an important feature that characterize the data [41]. A popular RNN architecture is the LSTM, which provides the capability of storing information for long periods of time [44,45]. In load forecasting problems characterized by complex and variable temporal dependencies, RNNs have been shown to outperform several forecasting methods like ARIMA, Support Vector Machines (SVM), Multilayer Perceptron, and Adaptive Network-Based Fuzzy Inference System (ANFIS) [40]. The authors in Reference [43] reviewed and evaluated two real-world datasets of electricity load, comparing modern deep learning architectures on short-term load forecasting problems. In particular, the paper focused on feedforward and recurrent neural networks, sequence-to-sequence models, and temporal convolutional neural networks. The authors found that on short-term load forecasting problems, the simpler ERNN performs comparably to more advanced networks such as GRU and LSTM when adopted in aggregated load forecasting cases. Therefore, in such cases, the authors conclude that the ERNN may represent the most effective solution as it offers the benefits of a low-complexity model without compromising the prediction accuracy.
The Echo State Network is an RNN model that has received increased interest among researchers for simplicity of training and high-accuracy performance in predicting real-valued time series [42]. In predictions of real-world energy load time series, the application of the ESN model has achieved state-of-the-art results on 1-h and 24-h forecast horizons [31,40,46,47,48]. The authors in References [31,49] performed predictions by using ESN and ARIMA approaches and combined the models to obtain high-accuracy results. In a study by Jaeger and Haas [50], the ESN model was applied on both real and benchmark datasets, and the authors highlighted the capability of the network to compute accurate predictions even when forecasting chaotic processes. In a comparative study by Bianchi et.al [40], the ESN model was tested against several RNNs on synthetic and real-world time series in different contexts. The result showed that the ESN architecture was competitive in most tasks in terms of prediction accuracy. Moreover, the simplicity of its implementation and training compared to other RNNs makes the ESN architecture especially attractive. For load forecasting problems on real-world time series, the ESN architecture was therefore concluded to be a convenient prediction tool for real-valued time series [40].
So far, CNNs have received less attention compared to RNNs in energy load forecasting tasks [43]. However, recent work indicates that CNNs achieve high performance in several sequence and time series prediction tasks [51]. The authors in Reference [52], developed a deep CNN called DeepEnergy. The experimental results show that DeepEnergy can predict energy loads with high accuracy over three days and outperforms SVM and LSTM. The authors of Reference [53] compared a CNN to recurrent and feed-forward architectures, showing promising results on benchmark time-series. Several works combined CNNs together with RNNs to achieve a hybrid prediction tool that increases the prediction accuracy. For example, the authors in Reference [54] combined a CNN and RNN to integrate different input sources and use the convolutional layer to extract features from the historical data. The RNN was thereafter used to learn the dynamics of the system. In Reference [55], another hybrid model was presented where the historical load was processed by a CNN and LSTM. Then, the features from both networks were used to predict the day-ahead load.
2.3. Transfer Learning
A large amount of scientific work on forecasting time series has resulted in a large number of methodologies that provide accurate results in several prediction-related challenges. However, accurate forecasting of time series is a challenging task when the availability of training data is limited. Recently, the transferability of machine learning models has gained increased attention due to the necessity of generating predictions in systems where training data are not available. In Reference [56], the authors investigated how to transfer CNNs for the time series classification (TSC) task. A hybrid transfer learning model for short-term electric load forecasting was proposed by Reference [57] and shows significant improvement in electric load predictions for a location by using additional data from another location. In Reference [58], the monthly electric load was predicted by collecting data from different districts in Seoul. After collecting all historical data from the different districts, the model was trained to predict the electric load in a target district by using transfer learning. The authors also proposed a novel load-forecasting scheme for a district by using similar data from other cities or districts. To demonstrate the performance, the model was compared to other popular machine learning techniques. The authors in Reference [59] considered the problem of developing predictive models with limited data for energy assets. An energy predictive model based on CNN’s was developed and applied by using a transfer learning strategy. The approach was demonstrated on a case study of daily energy demand time series. In Reference [60], the authors show for the first time that using an LSTM auto-encoder with attention trained on a large-scale dataset with pre-processing can effectively transfer time-series features. The authors in Reference [61] proposed a new training strategy for time-series transfer learning with two source datasets that outperforms existing approaches when predicting a target dataset. The authors tested the performance of the approach on predicting financial time series, and the experiments show that transfer learning based on two datasets (market indexes) is superior to other baseline methods with only one source dataset.
While not comprehensive, this short overview gives an idea of the significant amount of research that has been carried out on developing forecasting methodologies. In addition, the transferability of forecasting models has recently gained increased interest, and several works have addressed the problem of accurate predictions when there are limited data available for training.
3. Methodology
In this study, three trainable RNNs (LSTM, GRU, and Elman), a randomized RNN (ESN), a CNN, and two statistical methods (ARIMA and Prophet) are compared for predicting energy demand for multiple cases. The models are trained to predict energy demand at the next hour and at longer time horizons (2, 6, 12, 24, and 165-h ahead). The predictions are performed on two sectors (Households and Industry) at both communities of the Senja grid.
Section 3 explains the process of training the model and how to transfer them to a new dataset. A brief description of the models used (LSTM, GRU, Elman, ESN, CNN, ARIMA, and Prophet) is deferred to the Supplementary Materials (Chapter S7). In addition, the Supplementary Materials briefly discusses the advantages and disadvantages of the different approaches. All hyperparameter configurations used for predictions with the different models are listed in Section S7.5 in the Supplementary Materials Section.
An overview of the methodology for making predictions with the different approaches are provided in Figure 1. A brief explanation of each step is given in the Supplementary Materials Section.
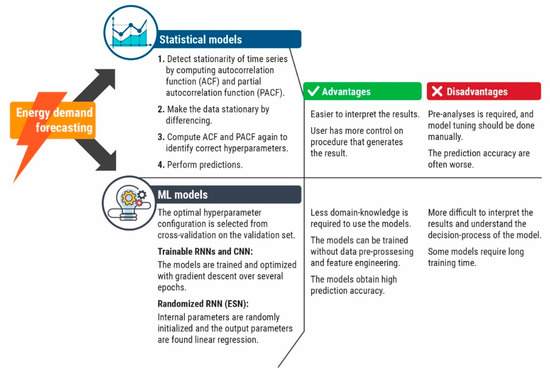
Figure 1.
Overview of methodology for making predictions with statistical-and machine-learning models. The advantages and disadvantages of each approach are given.
3.1. Prediction Strategy
3.1.1. Training, Validation, and Test
To train and evaluate the models, the time series is split into a training set (70%), validation set (15%), and test set (15%). The training set is used to fit the model parameters by minimizing the prediction loss; the validation set is used to find the optimal configuration of the hyperparameters and to compute the stop criterion for the models trained with gradient descent; once the optimal model is found, its performance is evaluated on the test set. We pre-process the data by removing the linear trend and the main seasonality (see Section 4.2 for more details). Additionally, the data are standardized by subtracting the mean and dividing by the standard deviation computed on the training set.
3.1.2. Transferability
The strategy used to transfer the model is similar to the one proposed in Reference [61]. The model is first optimized on the training and validation set of a source dataset (location 1). Then, the trained model is used to predict the test set of the target dataset (location 2). The data of both source and target datasets are pre-processed according to the statistics computed on the target dataset.
3.2. Normalized Root Mean Squared Error
The normalized root mean squared error (NRMSE) is used both as the loss function and as the metric to evaluate the prediction performance. The root mean squared error (RMSE) is defined as:
where and are the predicted and true values, accordingly. The RMSE measures the discrepancy between the predicted values and observed values at time , over number of observations [62]. The NRMSE relates the RMSE to the observed average value in the observation period and is defined as:
where is the average of the time series values.
4. Case Study
At present, the 66 kV cable that supplies Senja is operating close to its maximum capacity. At Northern-Senja, the communities are provided with a 22 kV distribution network. The total energy demand is characterized by a combination of load profiles from two sectors (households and industry) that are very different from each other. The particular feature of the rural communities in Senja is that industry accounts for more than 50% of the total energy consumption [23]. When the industries operate at heavy load, the risk of voltage drop at the end of the radial distribution network increases. Voltage drops increase the risk of interruption in the power supply. These communities have no alternative energy supplies that can provide a backup when the voltage decreases. Therefore, given the limited capacity of the existing grid, it is paramount to predict the periods with high consumption. An accurate prediction tool is necessary for developing efficient strategies to reduce the challenges in the existing grid. One way to deal with the current situation is to build a new electricity grid connection with a higher capacity. However, this is costly and time-consuming, has a huge environmental impact, and contradicts the vision to better utilize the current electricity grid as stated by NVE [22]. Moreover, since the communities are strongly industry-dominated, such an investment will be wasted if the companies will stop their activities in the future, and the power companies will be left with an over-dimensioned distribution network.
4.1. Real-World Time Series
The time series analysis in this paper is based on hourly energy consumption data in the period spanning from 1 March 2019 to 1 February 2020. The time series are from two separate communities located approximately 9 km apart in air distance, located at the end of separate radials of the electricity network in the region. Both communities are small with approximately 100 households at location 1, and 300 households at location 2.
The time series is provided from the power company Ishavskraft AS [63], which collects consumption data for all their customers in the specific locations studied in this paper. The time series is divided into three sectors: cabins, households, and industry. Due to privacy policies, the household and cabin consumption is aggregated. From Figure 2, it is possible to see that the industry sector in both locations is clearly the dominant source for the total energy consumption pattern and the total energy consumption is significantly larger for location 2 than for location 1, with average hourly consumption of 2553 kW/h and 860 kW/h, respectively. Figure 2 illustrates that the consumption pattern decreases significantly during the main holiday periods (Easter at end of April, summer vacation in July, and Christmas in December/beginning of January). The period between September and December is characterized by an increase in the total energy consumption due to the electric heating because of colder temperatures. In addition, during this period the fishing industries are heading towards the main fishing season when they operate frequently at full load.
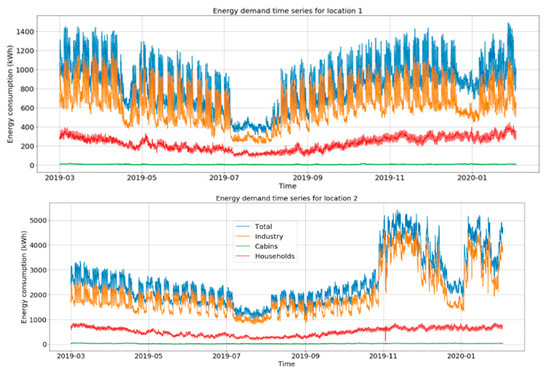
Figure 2.
Real-world time series of consumption for location 1 and 2. The demand for the industry sector is strongly correlated with the fishing season, while the energy demand for households is correlated with temperature changes, where cold temperatures during wintertime give higher energy demand for heating purposes.
To design an accurate predictive model, it is necessary to account for the different consumption patterns, which vary between the holidays and the working periods.
We disregard the holiday periods, as the requirements for stable power supply are not as critical as they are during working days. Consequently, we only consider the workdays that are characterized by higher load consumption that is critical given the limited capacity of the grid, and there is a risk of interruptions in the power supply.
For this reason, we train our prediction models only to predict the consumption during workdays. The workdays also include the weekends, because especially in high-season, the fishing industries have a high level of activity every day, including weekends. Specifically, the periods with low consumption during holidays are removed from the data set and we obtain a time series with 6544 time-steps in total. The resulting time series for both locations with holidays removed are depicted in Figure 3.
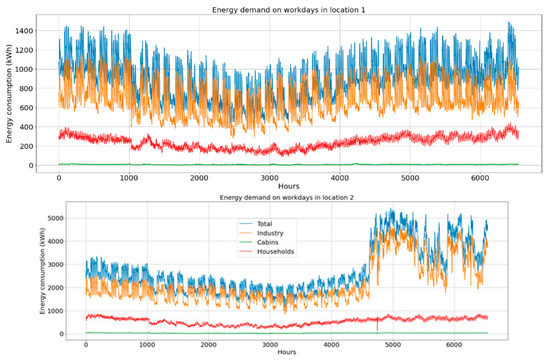
Figure 3.
Real-world time series of consumption for location 1 (upper) and 2 (lower). The periods of holidays are removed, leaving a time series of 6544 samples instead of 8129 samples (1 March 2019 to 1 February 2020).
At each location, we analyze the consumption of households and industry separately. The consumption of cabins is too low in both locations to significantly affect the overall consumption patterns in the communities and the occurrence of power outages. Therefore, the consumption of cabins is disregarded in this study.
4.2. The Industry Time Series in Location 1
Statistical analysis of real-world time series is important to gain a better understanding of the consumption data and to interpret the results. Additionally, statistical models such as ARIMA assume the data to be stationary, which implies that the trend, seasonality, and short-term correlations must be removed before feeding the data into the models. On the other hand, machine-learning models do not require the time series to be stationary [64]. By removing the trend and the seasonality from the data, the neural networks can exploit all their resources to predict the “difficult” component of the time series. Such components are fast and noise-like oscillations.
As an example, in the following, we show how the trend and the main seasonality are computed for the industry sector in location 1. The trend is computed as the running mean with a window size of one week (168 h).
The running mean of the industry consumption during workdays is plotted in Figure 4; it shows a minor decrease from timestamp 0 to 3000 while increasing from 3000 to 6000 where the industry is heading towards the fishing season during the winter period. Figure 4 also shows that the consumption is cyclic with a similar load pattern every week.
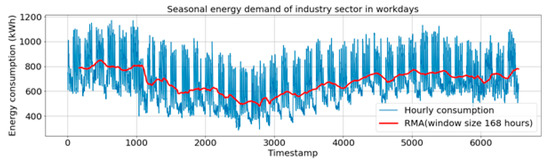
Figure 4.
The industry energy consumption during workdays.
In order to identify the main consumption pattern in the time series, some statistical analyses and pre-processing are required. First, the autocorrelation function (ACF) and partial autocorrelation functions (PACF) are computed to get a better understanding of the data provided. In addition, the ACF and PACF are interpreted to investigate whether the data are stationary or not. When making predictions with statistical models such as ARIMA, the time series are required to be stationary. If the ACF and PACF plots show no correlations, the time series are stationary and ARIMA predictions can be performed [64]. The representation of the main consumption pattern together with the ACF and PACF for the industry consumption is shown in Figure 5.
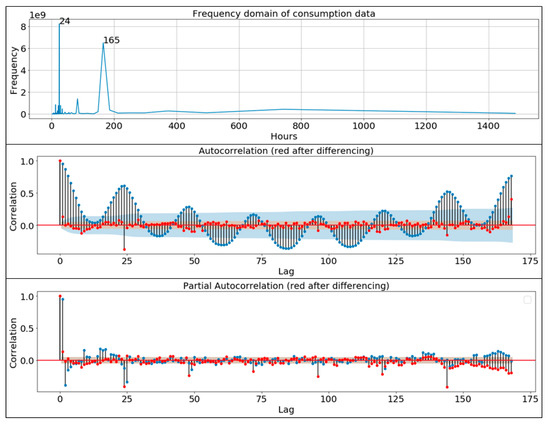
Figure 5.
Frequency domain of consumption data by Fourier transformation with autocorrelation function (ACF) and partial autocorrelation functions (PACF) functions. The correlation outside the standard deviations are correlations and not a statistical fluke. The red color represents the ACF and PACF after differencing the time series.
The ACF and PACF show strong correlations outside the 95% confidence interval (depicted as a blue area in Figure 5) at 24 h and between 150 and 175 h. We note that the values outside of the blue cone are very likely actual correlations.
Another way to identify the seasonality is through the Fourier transform, which allows identifying the main periodicities in the time series [65]. The Fourier transformation shows that the main seasonality is 24 h, which is expected as we have hourly data and the consumption pattern follows a daily cycle. The time series has also a strong seasonality at 165 h, which corresponds to a week. This shows that the industry sector is strongly driven by weekly consumption patterns in addition to the daily-varying consumption.
5. Results and Discussion
5.1. Result of Short-Term Predictions (1-h Forecasting Horizon)
The resulting predictions on 1-h ahead energy demand obtained by statistical approaches and neural networks are reported in Figure 6.
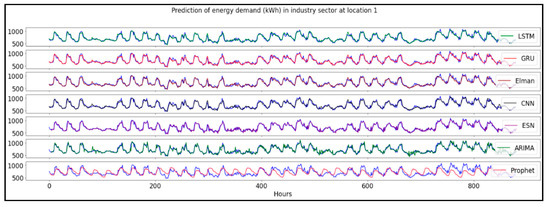
Figure 6.
Short-term prediction for industry sector at location 1.
5.1.1. Industry Energy Prediction for Location 1
Figure 6 indicates that all models achieve good performance in predicting the energy consumption, except for the Prophet model. This model clearly underperforms compared to the rest of the models as it makes larger prediction errors compared to the actual consumption. This indicates that the Prophet model performs poorly in predicting the energy load profiles. For this reason, the Prophet model is not considered further in this study. The other statistical model, ARIMA, predicts the load consumption data with high accuracy (NRMSE = 0.070), but it overestimates consumption patterns. We experience larger errors from ARIMA predictions when the consumption is low.
All the neural networks used in this study achieve accurate results, and the ESN model outperforms the rest with an NRMSE result of 0.012. Among the trainable neural networks, the GRU and Elman underperform compared to the rest with an NRMSE of 0.074. All results are provided in Table 1.

Table 1.
Results from 1-h prediction for all cases with all models.
We also note that all the neural networks seem to capture the peak loads with high accuracy. At peak loads, strategies for demand response by use of accurate forecasts are fundamental. The strategies are developed to plan what measures can be carried out to create an immediate change in the energy load profile. For the particular industry analyzed in this study, reducing the peak load is critical to avoid production stops resulting from power outages. The capability of capturing peak loads indicate that the neural networks are suitable tools when developing demand response strategies. Such strategies could contribute to avoiding production stops in periods where the industry operates at high loads.
5.1.2. Short-Term Transferability Predictions of Industry Consumption at Location 2
To evaluate the transferability of the models in terms of the capability of predicting the load time series associated with different energy grids we perform the following experiments:
- the energy consumption at location 2 is predicted with the models trained on the time series on location 1;
- the energy consumption at location 1 is predicted with the models trained on the time series on location 2.
When examining the transferability by predicting the energy consumption at location 2 with the models trained on the time series on location 1, there is a larger difference in terms of prediction accuracy.
Regarding transferability predictions, the data reported in Figure 7 illustrate how the ARIMA model is no longer able to predict the load profile. In addition, ARIMA does not capture any of the actual consumption patterns. This could be because the statistics between the two-time series are significantly different.
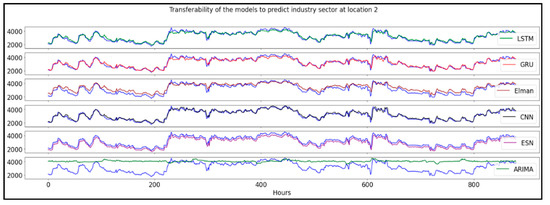
Figure 7.
Short-term transferability predictions. The models are trained on the time series at location 1 to predict the energy consumption at location 2.
On the other hand, all the neural networks we considered in this study seem to capture the dynamics of the load profile with high precision. Figure 7 shows that the ESN model systematically underestimates the energy consumption. This could be due to the property of the dynamical system which changes from one location to the other. When making predictions, the ESN uses a very large reservoir, which implies many parameters in the readout layer. While this helps to achieve a high prediction accuracy at location 1, the ESN can tend to over-fit the data of location 1 used for training. For this reason, the ESN makes more errors when transferred to the second location. On the other hand, the other RNNs have fewer parameters and the resulting model can generalize better to the data of the second location (see Supplementary Materials Section for more details about each model). In fact, the results show that the CNN is the model that achieves the highest prediction accuracy in transferability predictions with an NRMSE of 0.075, slightly better than LSTM with a result of NRMSE = 0.084.
5.1.3. All Periods and Sectors for Both Locations
The NRMSE for both household and industry sectors and both locations are given in Table 1. The highest reported prediction accuracy is in bold. The results show that the ESN model provides the highest accuracy in predicting the energy consumption one hour onward at both locations.
Looking at the average prediction accuracy for the two sectors studied, the error is larger in the industry sector than for the household sector. The reason may be the fact that the industry sector has higher energy consumption in terms of magnitude. In addition, the larger differences between maximum and minimum load thorough the day could make the load profile more difficult to capture with high accuracy. The Fourier transformations show that the seasonality for each sector is different; the main seasonality for the household sectors was 24 and 12 h (see Supplementary Materials Section), while for industry sectors, the main seasonality were 24 and 165 h, which in turn also could affect the accuracy of the models and should be considered when performing predictions.
For transferability predictions, the ESN still outperforms all the other models in the household sector. However, when making transferability predictions in the industry sector, the CNN outperforms all other models at both locations.
Looking at the validation case where the models are trained on location 2 to predict at location 2 and location 1, the results are the same: The ESN model outperforms the other models when predicting energy demand in location 2 for both sectors. For transferability predictions, the ESN outperforms the other models in the household sector, while the CNN outperforms the other models in the industry sector.
The results show that the ESN and CNN models can predict the dynamics of the time series with high accuracy at several locations, even when trained on one source-dataset.
5.2. Predicting at Longer (2, 6, 12, 24, and 165-h) Forecasting Horizons
In some cases, it is necessary to have a prediction tool that can predict longer than one hour ahead [66]. One-hour predictions are useful when examining what demand response measures can be taken to create an immediate change in the energy load profile.
When planning for strategies in the longer term to create a more stable energy system, it is necessary to have a prediction tool that can provide accurate forecasts days and weeks in advance [66]. To investigate whether the models can predict at longer forecasting horizons, the models are tested on the industry time series for location 1, now with longer-term forecasting horizons of 2, 6, 12, 24, and 165 h. Without changing the order of the ARIMA model or any configurations in the neural networks, the results in terms of NRMSE are the following.
Again, the bold values indicate the model with the highest prediction accuracy. Table 2 shows that the ARIMA model outperforms all the other models at the 24-h forecasting horizon. The ESN model provides the highest prediction accuracy at the 1-h forecasting horizon, while the lowest accuracy is for the 12-h forecasting horizon. However, at the 24-and 165-h forecasting horizons, the accuracy increases again, which is in line with the main seasonality of 24 and 165 h observed by means of the Fourier transform discussed in Section 4.2. Since we remove the seasonality, the ARIMA model is not that sensitive to the seasonality in the data and provides significantly better prediction result at 6 h and 12 h relative to the neural networks.

Table 2.
Normalized root mean squared error (NRMSE) at short- and longer-term forecasting horizon.
Looking at the neural networks, there is no clear indication that there is a model that achieves higher accuracy than the others at longer forecast horizons. It is noteworthy that all the trainable RNNs and the CNN outperform the ESN on longer forecasting horizons, which indicates that the ESN model is most suitable for being used on short-term prediction tasks. The Elman model outperforms the other models at both 2- and 165-h forecasting horizons. Again, the CNN shows impressive results, with the highest accuracy of all models at 6 h horizon, and acceptable accuracy for all horizons except for more than 24 h ahead.
The results suggest that the Elman RNN, ARIMA, and the CNN are the preferable models for longer-term energy planning purposes. However, from the results in Section 5.1, we see that the ARIMA model is difficult to transfer. This means that ARIMA must be trained on the same location where the energy consumption must be predicted and, therefore, it is necessary to possess historical energy consumption data. If no such historical data are available for training the ARIMA model, the CNN model is suggested as the optimal one.
6. Conclusions
In this paper, we studied the application of statistical models and neural networks to perform predictions of energy demand. The paper focused on predicting future loads for two communities that experience frequent power outages due to heavy loads on the existing electricity grid. Since the most important task is to predict the consumption when the load is high and there is a risk of interruptions in the power supply, we focused on energy consumption during workdays. Therefore, the periods with low consumption during holidays was removed, and we analyzed a time series of 6544-time steps.
We performed statistical analysis on both aggregated household and industry sectors and investigated the autocorrelation and partial autocorrelation functions before prediction was performed. To determine the seasonality in consumption patterns within each sector, the time series were transformed from the time domain to frequency domain by Fourier transformations. From the Fourier transforms it is clear that the industry sectors have a strong seasonality every 24 h and every 165 h, i.e., the seasonality of the industry consumption is strongly dependent on the weekly pattern, while the households have a strong seasonality every 24 h and 12 h (see Supplementary Materials Section).
The results of the predictive models in terms of NRMSE show that the ESN provides the highest accuracy when making short-term predictions. In addition, the simplicity in implementation and the fast training procedure makes the ESN model an appealing instrument for time series prediction.
To evaluate the transferability of each model, we trained each model on location 1 (or 2) and used the trained models to predict the energy consumption at location 2 (or 1). For transferability predictions, the ESN model does also provide high accuracy results when predicting at location 2 by use of the model trained on location 1. However, when the differences in energy consumption in terms of magnitude are large, the ESN model systematically underestimates the load at location 2, which has significantly larger energy consumption. For the industry sector, the CNN model outperforms all the other models and achieves impressive results in the transferability prediction. In particular, the CNN model captured both the magnitude and consumption pattern with remarkable high accuracy. In the household sector, where differences in energy consumption in terms of magnitude were lower, the ESN model again outperforms the other models.
For longer-term predictions, the ARIMA model outperforms all models at all 24-h forecasting horizons. However, the ARIMA model is limited in that it must be trained on the same time series that are being predicted. Therefore, the ARIMA model cannot be transferred effectively. In contrast, the neural networks, and the CNN model especially, perform well when transferred to a second location. In addition, the CNN model achieves accurate predictions at multiple forecasting horizons.
The study suggests that productive future research can be undertaken to investigate the possibility of combining the ESN and CNN models for long- and short-term prediction purposes. If such a model were able to achieve high prediction results in multiple locations at both long-and short-term, it would be a valuable prediction tool to use for energy planning purposes at several locations and sectors with different time series dynamics.
Supplementary Materials
The following are available online at https://www.mdpi.com/1996-1073/14/4/798/s1, Figure S1: Energy demand for the aggregated household sector. Figure S2: ACF and PACF plots for the energy consumption in households’ sector. The correlation outside the standard deviations are correlations and not a statistical fluke. Figure S3: ACF and PACF plots for the residuals after predictions with the ARIMA(1,0,1) model. Table S1: Each hyperparameter is searched in the interval [min,max]. The parameters in Table S1 are the following: Order of the autoregressive term (p), order of differentiation (d), and order of moving average term (p). The optimum hyperparameter configurations for each sector are selected as the one yielding the highest prediction accuracy on the validation set. The ARIMA(1,0,1) configuration are the model providing highest prediction accuracy for both industry and household sector. Table S2: The hyperparameter configuration for the trainable RNNs are specified as: Number of layers (L), number of units per layer (n). The hyperparameter configuration are trained over 50 epochs. Table S3: The hyperparameter configuration for the CNN are: Number of layers (L), number of units per layer (n), the convolutional kernel size (k). The dilation rate dr, specifies how each convolutional layer L, are dilated with a factor a factor 2i. Here i are the specific layer of the network. The hyperparameter configuration are trained over 50 epochs. Table S4: Each hyperparameter is searched in the interval [min,max]. The parameters in the table are the following: Neurons in the reservoir (Nr), connectivity (Rc), noise in the state uptdate (ξ), spectral radius (ρ), the scaling of input, teaching and feedback weights (ωi, ωo, ωf), and regression parameter C. The optimum hyperparameter configurations for each sector are selected as the one yielding the highest prediction accuracy on the validation set.
Author Contributions
O.F.E. performed all analyzes and had the main responsibility for writing the manuscript. F.M.B. contributed to the inception of the study and supervised in the analysis. H.A. contributed by improving the English and the structure of the manuscript. M.H. contributed with the data collections for the analyzes in the study. Y.-C.C. contributed with analyzing the data. M.C. assisted in the analysis and interpretation of the results and contributed to the inception of the manuscript O.F.E., F.M.B. and M.C. wrote the manuscript with input from all authors. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by UiT-the Arctic University of Norway, grant number 310026. The APC was funded by 310026.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
O.F.E. and M.C. acknowledge the support from the research project “Transformation to a Renewable & Smart Rural Power System Community (RENEW)”, connected to the Arctic Centre for Sustainable Energy (ARC) at UiT-the Arctic University of Norway through Grant No. 310026. We thank Ishavskraft AS for providing the necessary datasets for the studies in this paper. We thank Maritsa Kissamitaki for designing Figure 1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- De Gooijer, J.G.; Hyndman, J.R. 25 years of time series forecasting. Int. J. Forecast. 2006, 22, 443–473. [Google Scholar] [CrossRef]
- Simchi-Levi, D.; Simchi-Levi, E.; Kaminsky, P. Designing and Managing the Supply Chain: Concepts, Strategies and Cases; McGraw-Hill: New York, NY, USA, 1999. [Google Scholar]
- Bunn, D. Forecasting loads and prices in competitive power markets. Proc. IEEE 2000, 88, 163–169. [Google Scholar] [CrossRef]
- Ruiz, P.A.; Gross, G. Short-term resource adequacy in electricity market design. IEEE Trans. Power Syst. 2008, 23, 916–926. [Google Scholar] [CrossRef]
- Child, M.; Kemfert, C.; Bogdanov, D.; Breyer, C. Flexible electricity generation, grid exchange and storage for the transition to a 100% renewable energy system in Europe. Renew. Energy 2019, 139, 80–101. [Google Scholar] [CrossRef]
- International Renewable Energy Agency. Power System Flexibility for the Energy Transition, Part 2: IRENA FlexTool Methodology; IRENA: Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
- Alstone, P.; Gershenson, D.; Kammen, D.M. Decentralized energy systems for clean electricity access. Nat. Clim. Chang. 2015, 5, 305–314. [Google Scholar] [CrossRef]
- Olauson, J.; Ayob, M.N.; Bergkvist, M.; Carpman, N.; Castellucci, V.; Goude, A.; Lingfors, D.; Waters, R.; Widén, J. Net load variability in Nordic countries with a highly or fully renewable power system. Nat. Energy 2016, 1, 16175. [Google Scholar] [CrossRef]
- Bordin, C.; Thomasgard, A. SMACS MODEL, a stochastic multihorizon approach for charging sites management, operations, design, and expansion under limited capacity conditions. J. Energy Storage 2019, 26, 100824. [Google Scholar] [CrossRef]
- Orehounig, K.; Evins, R.; Dorer, V. Integration of decentralized energy systems in neighbourhoods using the energy hub approach. Appl. Energy 2015, 154, 277–289. [Google Scholar] [CrossRef]
- Ringkjøb, H.-K.; Haugan, P.M.; Nybø, A. Transitioning remote Arctic settlements to renewable energy systems—A modelling study of Longyearbyen, Svalbard. Appl. Energy 2020, 258, 114079. [Google Scholar] [CrossRef]
- Olkkonen, L.; Korjonen-Kuusipuro, K.; Grönberg, I. Redefining a stakeholder relation: Finnish energy “prosumers” as co-producers. Environ. Innov. Soc. Transit. 2017, 24, 57–66. [Google Scholar] [CrossRef]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy-sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Morstyn, T.; Farrell, N.; Darby, S.J.; McCulloch, D.M. Using peer-to-peer energy-trading platforms to incentivize prosumers to form federated power plants. Nat. Energy 2018, 3, 94–101. [Google Scholar] [CrossRef]
- An, J.; Lee, M.; Yeom, S.; Hong, T. Determining the peer-to-peer electricity trading price and strategy for energy prosumers and consumers within a microgrid. Appl. Energy 2020, 261, 114335. [Google Scholar] [CrossRef]
- Xiao, X.; Wang, J.; Lin, R.; Hill, D.J.; Kang, C. Large-scale aggregation of prosumers toward strategic bidding in joint energy and regulation markets. Appl. Energy 2020, 271, 115159. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhou, K.; Lu, X.; Yang, S. Electricity trading pricing among prosumers with game theory-based model in energy blockchain environment. Appl. Energy 2020, 271, 115239. [Google Scholar] [CrossRef]
- Hafeez, G.; Alimgeer, K.S.; Khan, I. Electric load forecasting based on deep learning and optimized by heuristic algorithm in smart grid. Appl. Energy 2020, 269, 114915. [Google Scholar] [CrossRef]
- Arcos-Aviles, D.; Pascual, J.; Guinjoan, F.; Marroyo, L.; Sanchis, P.; Marietta, M.P. Low complexity energy management strategy for grid profile smoothing of a residential grid-connected microgrid using generation and demand forecasting. Appl. Energy 2017, 205, 69–84. [Google Scholar] [CrossRef]
- Giaouris, D.; Papadopoulos, A.I.; Patsios, C.; Walker, S.; Ziogou, C.; Taylor, P.; Voutetakis, S.; Papadopoulou, S.; Seferlis, P. A systems approach for management of microgrids considering multiple energy carriers, stochastic loads, forecasting and demand side response. Appl. Energy 2019, 226, 546–559. [Google Scholar] [CrossRef]
- Stokland, J.; Løksa, K. Omlegging til en Framtidsrettet Nettleie, NVE. 2020. Available online: https://www.nve.no/reguleringsmyndigheten/nytt-fra-rme/nyheter-reguleringsmyndigheten-for-energi/omlegging-til-en-framtidsrettet-nettleie/ (accessed on 9 July 2020).
- Norges Vassdrags-Og Energidirektorat; Miljødirektoratet; ENOVA; Statens Vegvesen; Kystverket; Landbruksdirektoratet. Klimakur 2030: Tiltak og Virkemidler mot 2030; Miljødirektoratet: Oslo, Norway, 2020. [Google Scholar]
- ENOVA. Sluttrapport på Konseptutredning; Troms Kraft Nett AS: Tromsø, Norway, 2019. [Google Scholar]
- Herran, D.S.; Nakata, T. Design of decentralized energy systems for rural electrification in developing countries considering regional disparity. Appl. Energy 2012, 91, 130–145. [Google Scholar] [CrossRef]
- Schäfer, M.; Kebir, N.; Neumann, K. Research needs for meeting the challenge of decentralized energy supply in developing countries. Energy Sustain. Dev. 2011, 15, 324–329. [Google Scholar] [CrossRef]
- International Energy Agency. SDG7: Data and Projections–Access to Electricity; IEA: Paris, France, 2020; Available online: https://www.iea.org/reports/sdg7-data-and-projections/access-to-electricity (accessed on 15 June 2020).
- Boute, A. Off-grid renewable energy in remote Arctic areas: An analysis of the Russian Far East. Renew. Sustain. Energy Rev. 2016, 59, 1029–1037. [Google Scholar] [CrossRef]
- Quitoras, R.M.; Campana, P.E.; Rowley, P.; Crawford, C. Remote community integrated energy system optimization including building enclosure improvements and quantitative energy trilemma metrics. Appl. Energy 2020, 267, 115017. [Google Scholar] [CrossRef]
- Aberilla, J.M.; Gallego-Schmid, A.; Stamford, L.; Azapagic, A. Design and environmental sustainability assessment of small-scale off-grid energy systems for remote rural communities. Appl. Energy 2020, 258, 114004. [Google Scholar] [CrossRef]
- Statistics Norway (SSB). Elektrisitet 10314: Nettoforbruk av Elektrisk Kraft, Etter Forbrukergruppe (GWh) (K) 2010–2019; Statistics Norway: Oslo, Norway, 2020; Available online: https://www.ssb.no/statbank/table/10314/ (accessed on 23 October 2020).
- Deihimi, A.; Orang, O.; Showkati, H. Short-term electric load and temperature forecasting using wavelet echo state networks with neural reconstruction. Energy 2013, 57, 382–401. [Google Scholar] [CrossRef]
- Van Oldenborgh, G.J.; Balmaseda, M.A.; Ferranti, L.; Stockdale, T.N.; Anderson, D.L.T. Did the ECMWF seasonal forecast model outperform statistical ENSO forecast models over the last 15 years? J. Clim. 2005, 18, 3240–3249. [Google Scholar] [CrossRef]
- Dang-Ha, T.H.; Bianchi, F.M.; Olssson, R. Local short term electricity load forecasting: Automatic approaches. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; IEEE: Anchorage, AK, USA, 2017. [Google Scholar]
- Hyndman, R.; Koehler, A.; Ord, K.; Snyder, R. Forecasting with Exponential Smoothing: The State Space Approach; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Taylor, J.W. A Comparison of univariate time series methods for forecasting intraday arrivals at a call center. Manag. Sci. 2008, 54, 253–265. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 74. [Google Scholar]
- Box, G.E.P.; Cox, D.R. An analysis of transformations. J. R. Stat. Soc. Ser. B Methodol. 1964, 26, 211–243. [Google Scholar] [CrossRef]
- Alberg, D.; Last, M. Short-term load forecasting in smart meters with sliding window-based ARIMA algorithms. Vietnam J. Comput. Sci. 2018, 5, 241–249. [Google Scholar] [CrossRef]
- Bianchi, F.M.; De Santis, E.; Rizzi, A.; Sadeghian, A. Short-term electric load forecasting using echo state networks and PCA decomposition. IEEE Access 2015, 3, 1931–1943. [Google Scholar] [CrossRef]
- Schäfer, A.M.; Zimmermann, H.-G. Recurrent neural networks are universal approximators. Int. J. Neural Syst. 2007, 17, 253–263. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. An Overview and Comparative Analysis of Recurrent Neural Networks for Short Term Load Forecasting. arXiv 2018, arXiv:1705.04378. [Google Scholar]
- Gasparin, A.; Lukovic, S.; Alippi, C. Deep Learning for Time Series Forecasting: The Electric Load Case; Cornell University,: Ithaca, NY, USA, 2019. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 8, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Sak, H.; Senior, A.W.; Beaufays, F. Long short-term memory based recurrent neural network architectures for large vocabulary speech recognition. arXiv 2014, arXiv:1402.1128. [Google Scholar]
- Deihimi, A.; Showkati, H. Application of echo state networks in short-term electric load forecasting. Energy 2012, 39, 327–340. [Google Scholar] [CrossRef]
- Varshney, S.; Verma, T. Half hourly electricity load prediction using Echo State Network. Int. J. Sci. Res. (IJSR) 2014, 3, 885–888. [Google Scholar]
- Bianchi, F.M.; Scardapane, S.; Uncini, A.; Rizzi, A.; Sadeghian, A. Prediction of telephone calls load using Echo State Network with exogenous variables. Neural Networks 2015, 71, 204–213. [Google Scholar] [CrossRef]
- Peng, Y.; Lei, M.; Li, J.-B.; Peng, X.-Y. A novel hybridization of echo state net-works and multiplicative seasonal ARIMA model for mobile communication traffic series forecasting. Neural Comput. Appl. 2014, 24, 883–890. [Google Scholar] [CrossRef]
- Jaeger, H.; Haas, H. Harnessing nonlinearity: Predicting chaotic systems and saving energy in wireless communication. Science 2004, 304, 78–80. [Google Scholar] [CrossRef]
- Borovykh, A.; Bothe, S.; Oosterlee, C.W. Conditional time series forecasting with convolutional neural networks. arXiv 2018, arXiv:1703.04691. [Google Scholar]
- Kuo, P.-H.; Huang, C.-J. A High precision artificial neural networks model for short-term energy load forecasting. Energies 2018, 11, 213. [Google Scholar] [CrossRef]
- Amarasinghe, K.; Marino, D.L.; Manic, M. Deep neural networks for energy load forecasting. In Proceedings of the 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, 19–21 June 2017; IEEE: Edinburgh, Scotland, UK, 2017; pp. 1483–1488. [Google Scholar]
- He, W. Load forecasting via deep neural networks. Procedia Comput. Sci. 2017, 122, 308–314. [Google Scholar] [CrossRef]
- Tian, C.; Ma, J.; Zhang, C.; Zhan, P. A deep neural network model for short-term load forecast based on long short-term memory network and convolutional neural network. Energies 2018, 11, 3493. [Google Scholar] [CrossRef]
- Fawaz, H.I.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.-A. Transfer learning for time series classification. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; IEEE: Seattle, WA, USA, 2018; pp. 1367–1376. [Google Scholar]
- Xu, X.; Meng, Z. A hybrid transfer learning model for short-term electric load forecasting. Electr. Eng. 2020, 102, 1371–1381. [Google Scholar] [CrossRef]
- Jung, S.-M.; Park, S.; Jung, S.-W.; Hwang, E. Monthly electric load forecasting using transfer learning for smart cities. Sustainability 2020, 12, 6364. [Google Scholar] [CrossRef]
- Hooshmand, A.; Sharma, R. Energy predictive models with limited data using transfer learning. In Proceedings of the e-Energy ’19: The Tenth ACM International Conference on Future Energy Systems, Phoenix, AZ, USA, 25–28 June 2019; pp. 12–16. [Google Scholar] [CrossRef]
- Nikolay, L.; Yu, J.; Rajagopal, R. Applied time-series transfer learning. Stanford, CA, USA. Workshop track; ICLR; Standford university: Standford, CA, USA, 2018; pp. 1–4. [Google Scholar]
- He, Q.-Q.; Pang, P.C.-I.; Si, Y.-W. Transfer learning for financial time series forecasting. In Proceedings of the PRICAI 2019: Trends in Artificial Intellegence, Yanuca Island, Fiji, 26–30 August 2019; Nayak, A., Sharma, A., Eds.; Lectore Notes in Computer Science. Springer: Cham, Switzerland, 2019; Volume 11671. [Google Scholar] [CrossRef]
- Holmes, S. RMS Error, Stanford. 28 November 2000. Available online: https://statweb.stanford.edu/~susan/courses/s60/split/node60.html (accessed on 9 July 2020).
- Ishavskraft AS. Om Oss. Available online: https://www.ishavskraft.no/om/ (accessed on 21 April 2020).
- Hyndman, R.J.; Athanasopoulos, G. Forecasting: Principles and Practice, 2nd ed.; OTexts: Melbourne, Australia, 2018; Available online: https://otexts.com/fpp2/ (accessed on 18 January 2021).
- Omar, K. Deconstructing Time Series Using Fourier Transform, Medium. Available online: https://medium.com/@khairulomar/deconstructing-time-series-using-fourier-transform-e52dd535a44e (accessed on 9 July 2020).
- Hong, T.; Fan, S. Probabilistic electric load forecasting: A tutorial review. Int. J. Forecast. 2016, 32, 914–938. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).