Adaline-Based Control Schemes for Non-Sinusoidal Multiphase Drives–Part I: Torque Optimization for Healthy Mode

Abstract

More degrees of freedom not only enable multiphase drives to be fault-tolerant but also allow non-sinusoidal electromotive forces (NS-EMFs) in high-quality vector control. NS-EMFs lead to lower costs of design and manufacturing of electrical machines. However, the presence of multi-harmonics in NS-EMFs possibly generates pulsating torque in both healthy and faulty conditions of multiphase drives. To facilitate the use of NS-EMFs, this two-part study proposes control schemes to adaptively improve torque quality of multiphase drives in dealing with multi-harmonics of NS-EMFs. The proposed schemes are based on a simple but effective type of artificial intelligence, Adaptive Linear Neuron (Adaline). The knowledge of multiphase drives including the harmonic ranks of NS-EMFs and the rotor position is exploited to design the online-trained optimal Adalines. The first part of this study is to propose a control scheme using an Adaline for healthy mode with high-quality torque regardless of numerous harmonics in NS-EMFs. The second part of this study introduces a control scheme using another Adaline for open-circuit faults. The proposed schemes are numerically and experimentally validated on a seven-phase permanent magnet synchronous machine (PMSM) possessing a high total harmonic distortion (THD = 38%) of NS-EMFs.

1. Introduction

Multiphase PMSMs have been a suitable solution for applications requiring high functional reliability and high torque density. Owing to the high number of phases (more than 3), multiphase machines possess more degrees of freedom for design and control compared to the conventional three-phase machines. Notably, multiphase drives can continue to properly operate under fault conditions without any additional hardware, leading to fault-tolerant property [1,2]. This present paper proposes a new control scheme for better utilization of more degrees of freedom of multiphase drives in healthy mode, obtaining smooth torque with multi-harmonics existing in NS-EMFs and phase currents.

Importantly, constraints on machine design are relaxed due to the high number of phases, possibly leading to lower costs of machine design and manufacturing. Indeed, according to the multi-reference frame theory [3], a n-phase symmetrical machine is characterized by (n − 1)/2 orthogonal planes (if n is odd), or (n − 2)/2 orthogonal planes (if n is even). These orthogonal planes are also known as two-dimensional reference frames or fictitious machines (FMs). Each reference frame (FM) is associated with a given group of harmonic components. If only a single harmonic of back electromotive forces (back-EMFs) presents in each reference frame (FM), constant d-q currents can generate constant torque. For example, in a three-phase machine, there is (3 − 1)/2 = 1 characteristic plane, hence, only one harmonic is allowed to present in its back-EMFs. Therefore, sinusoidal electromotive forces (S-EMFs) and sinusoidal currents have been used to generate smooth torque in high-quality vector control of a three-phase drive.

An increase in the number of phases n leads to more reference frames (FMs), allowing more harmonics in back-EMFs in high-quality vector control. For example, a five-phase machine has (5 − 1)/2 = 2 characteristic orthogonal planes, hence, two harmonics are allowed to present in its back-EMFs. Similarly, in a seven-phase machine, three harmonics are allowed to present in its back-EMFs. Consequently, for a NS-EMF multiphase machine, the constant torque can be generated by non-sinusoidal currents but their values in d-q frames are constant. Therefore, the use of multi-harmonics to generate torque in NS-EMF multiphase machines leads to higher torque density compared to S-EMF counterparts as well as three-phase machines [4]. This is a special characteristic only existing in NS-EMF multiphase machines. In healthy mode, the vector control using the classical rotor field-oriented control (RFOC) technique with proportional integral (PI) controllers is facilitated with constant reference d-q currents.

Nevertheless, NS-EMFs possibly contain more than one harmonic per reference frame due to machine design and manufacturing (concentrated windings, rotor magnet shape and orientation) [5,6], and the mechanical load in real-time operations [7,8]. These additional harmonics are called unwanted harmonics in this study. It conflicts the multi-reference frame theory [3]. If the torque is required to be constant, reference currents in d-q frames are no longer constant. In contrast, when d-q currents are kept constant to facilitate the control with PI controllers, the presence of torque ripples is inevitable [9]. In this case, the electromagnetic torque contains an average torque and harmonic components.

If a constant torque is prioritized, corresponding optimal reference currents can be determined by Maximum Torque Per Ampere (MTPA) strategy. MTPA can be obtained by using Lagrangian multipliers in [10] or the vectorial approach in [11]. Although MTPA has minimum copper losses, varying reference d-q currents for control require higher bandwidth controllers at high speed. Therefore, hysteresis controllers have been chosen to control phase currents in [10,11], leading to inevitable variable switching frequencies, high switching losses, and electromagnetic compatibility problems. Recently, study [12] has applied a multiple resonances structure, with PI resonant (PIR) controllers, to control phase currents. However, accurate estimations of frequencies and tuning procedures of many parameters are required in the design of PIR controllers. Other control techniques, such as model predictive control [13] or pulse width modulation (PWM) carrier phase shift [14], have been applied to reduce torque ripples. However, torque ripples caused by multi-harmonics in NS-EMFs cannot be eliminated. Especially, study [15] proposes I-power approach for NS-EMF five-phase machines in which additional currents are added to phase currents to compensate torque ripples. However, only finite element simulations are considered without the impact of varying reference currents on control quality.

Intelligent control approaches have been applied to improve control quality of electric motor drives. An artificial Gaussian-type radial basis function neural network is applied to control the speed of a five-phase drive without the knowledge of accurate machine model [16]. However, this artificial neural network (ANN) with multi-layers is complicated, dealing with long training time (about 3 s). In addition, hysteresis-type controllers have been used for the control with time-variant reference currents in [16], resulting in unexpected effects as in [10,11] such as variable switching frequencies, high switching losses, and electromagnetic compatibility problems. A neural network-based model reference adaptive system, robust to parameter variations, is used in [17] to estimate the speed of sensorless multiphase induction machines. However, poor performance at zero and low speeds is a limiting factor of the proposed method.

Adaline, the simplest type of ANN, requiring low computational demand with advantages such as fast response, self-learning, and easy-to-implement, can be found in [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. An Adaline in [18] is used to estimate the q-axis current of a three-phase PMSM in real time. This current estimation is to calculate torque, providing the feedback signal for direct torque control. It means that more Adalines are required for NS-EMF multiphase machines on which torque is usually generated by more q-axis currents, leading to the calculation burden. Study [19] proposes a torque ripple reduction method for a three-phase PMSM. For the torque ripple estimation, two Adalines are applied to extract harmonics of two d-q currents from measured phase currents, and one Adaline is used to extract harmonics of the rotating speed. Similar to [18], the number of Adalines with the method in [19] significantly increases when it is applied to NS-EMF multiphase machines. Another Adaline is proposed to determine optimal currents for three-phase and multiphase machines in [20]. As MTPA in [10,11], all reference d-q currents in [20] have high-frequency oscillations, challenging PI controllers at high speed. Other Adalines can be found in [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22] to eliminate harmonic components in d-q currents which are caused by multi-harmonics in NS-EMFs or nonlinearity of power converters. However, although constant d-q currents are obtained, smooth torque cannot be guaranteed because NS-EMFs with multi-harmonics in d-q frames are time-variant.

In the first part of this study, an Adaline-based control scheme for healthy mode of multiphase drives is proposed to obtain smooth torque, regardless of multi-harmonics existing in NS-EMFs. The proposed control scheme is a combination of the classical RFOC technique using PI controllers and only one simple online-trained Adaline. It means that the existing classical RFOC can be inherited with only an addition of an Adaline. Importantly, the Adaline takes advantage of the knowledge of torque harmonic components and of the rotating position to optimize the learning process, avoiding the calculation burden. Especially, only pulsating components of torque are adaptively used for the learning process, resulting in more constant d-q reference currents to facilitate PI controllers. Basically, the torque harmonic orders in healthy mode are multiples of the phase number.

Without loss of generality, the proposed control scheme is tested on a seven-phase PMSM having a high THD (38%) of NS-EMFs. The proposed control scheme can be easily applied to other electric machines with different numbers of phases and NS-EMF waveforms. This part of the study is an extension of [23] with additional explanations and experimental results. A demonstration Video S1 is provided with this part of the study.

This paper is organized as follows. Mathematical model of a multiphase machine is described in Section 2. Conventional vector control for healthy mode of multiphase drives is shown in Section 3. The proposed control scheme for healthy mode of multiphase drives is introduced in Section 4. Numerical and experimental results are presented in Section 5.

2. Mathematical Model of a Seven-Phase PMSM

The following assumptions are considered to model a seven-phase PMSM: Seven-phase windings of the machine are symmetrically shifted and star-connected; NS-EMFs of the machine contain multi-harmonics (more than (n − 1)/2 = 3) in which the 1st, 9th, and 3rd account for the highest proportions; the magnetic circuit saturation is not considered in calculations of NS-EMFs and fluxes.

The phase voltages can be expressed in natural frame as follows:

$$\underset{\_}{v}=R\underset{\_}{i}+\left[\mathit{L}\right]\frac{d\underset{\_}{i}}{dt}+\Omega {\underset{\_}{e}}_{sn}$$

(1)

with

$$\underset{\_}{v}={\left[\begin{array}{ccccccc}{v}_A& v_B& v_C& v_D& v_E& v_F& v_G\end{array}\right]}^{\mathrm{T}}$$

$${\underset{\_}{e}}_{sn}={\left[\begin{array}{ccccccc}{e}_A& e_B& e_C& e_D& e_E& e_F& e_G\end{array}\right]}^{\mathrm{T}}$$

where v, i, and e_sn are the 7-dimensional vectors of phase voltages, phase currents, and speed-normalized NS-EMFs, respectively; R is the stator winding resistance of one phase; [L] is the 7-by-7 stator inductance matrix; Ω is the rotating speed of the rotor.

To facilitate the classical RFOC technique, Clarke transformation is applied to convert parameters of the machine from natural frame into decoupled stator reference frames (α-β). For example, the transformation for currents is given by:

$${\underset{\_}{i}}_{\alpha \beta }=\left[\mathit{T}\right]\underset{\_}{i}$$

(2)

with

$${\underset{\_}{i}}_{\alpha \beta }={\left[\begin{array}{ccccccc}{i}_{\alpha 1}& i_{\beta 1}& i_{\alpha 2}& i_{\beta 2}& i_{\alpha 3}& i_{\beta 3}& i_z\end{array}\right]}^{\mathrm{T}}$$

where i_αβ is the 7-dimensional vector of currents in α-β frames; (i_α1, i_β1), (i_α2, i_β2), and (i_α3, i_β3) are currents in two-dimensional decoupled frames (α₁-β₁), (α₂-β₂), and (α₃-β₃), respectively; i_z is a current in zero-sequence frame z (one-dimensional); [T] is the 7-by-7 Clarke transformation matrix expressed by the spatial angular displacement δ (δ = 2π/7) as follows:

$$\left[\mathit{T}\right]=\sqrt{\frac{2}{7}}\left[\begin{array}{ccccccc}1& \cos \left(\delta \right)& \cos \left(2\delta \right)& \cos \left(3\delta \right)& \cos \left(4\delta \right)& \cos \left(5\delta \right)& \cos \left(6\delta \right)\\ 0& \sin \left(\delta \right)& \sin \left(2\delta \right)& \sin \left(3\delta \right)& \sin \left(4\delta \right)& \sin \left(5\delta \right)& \sin \left(6\delta \right)\\ 1& \cos \left(2\delta \right)& \cos \left(4\delta \right)& \cos \left(6\delta \right)& \cos \left(8\delta \right)& \cos \left(10\delta \right)& \cos \left(12\delta \right)\\ 0& \sin \left(2\delta \right)& \sin \left(4\delta \right)& \sin \left(6\delta \right)& \sin \left(8\delta \right)& \sin \left(10\delta \right)& \sin \left(12\delta \right)\\ 1& \cos \left(3\delta \right)& \cos \left(6\delta \right)& \cos \left(9\delta \right)& \cos \left(12\delta \right)& \cos \left(15\delta \right)& \cos \left(18\delta \right)\\ 0& \sin \left(3\delta \right)& \sin \left(6\delta \right)& \sin \left(9\delta \right)& \sin \left(12\delta \right)& \sin \left(15\delta \right)& \sin \left(18\delta \right)\\ 1/\sqrt{2}& 1/\sqrt{2}& 1/\sqrt{2}& 1/\sqrt{2}& 1/\sqrt{2}& 1/\sqrt{2}& 1/\sqrt{2}\end{array}\right]$$

(3)

In other words, a seven-phase machine can be mathematically decomposed into three two-phase fictitious machines (FM1, FM2, FM3) and one zero-sequence machine (ZM), corresponding to reference frames (α₁-β₁), (α₂-β₂), (α₃-β₃), and z, respectively [3]. A fictitious machine with its corresponding decoupled reference frame is associated with a group of harmonics as presented in

Table 1. Fictitious machines, reference frames, and associated harmonics of a seven-phase machine (Only odd harmonics).

Fictitious Machine	Reference Frame	Associated Harmonic *
1st fictitious machine (FM1)	α1-β1	1, 13, 15, …, 7k ± 1
2nd fictitious machine (FM2)	α2-β2	5, 9, 19, …, 7k ± 2
3rd fictitious machine (FM3)	α3-β3	3, 11, 17, …, 7k ± 3
Zero-sequence machine (ZM)	z	7, 21, …, 7k

* With k ∈ N₀.

.

The sinusoidal parameters of the machine in (α-β) frames in (2) are projected onto the rotor reference frames (also known as rotating or d-q frames) by using Park transformation. An example of Park transformation for currents is given by:

$${\underset{\_}{i}}_{dq}=\left[\mathit{P}\right]{\underset{\_}{i}}_{\alpha \beta }=\left[\mathit{P}\right]\left[\mathit{T}\right]\underset{\_}{i}$$

(4)

with

$${\underset{\_}{i}}_{dq}={\left[\begin{array}{ccccccc}{i}_{dh1}& i_{qh1}& i_{dh2}& i_{qh2}& i_{dh3}& i_{qh3}& i_z\end{array}\right]}^{\mathrm{T}}$$

where i_dq is the 7-dimensional vector of currents in rotor reference frames; (i_dh1, i_qh1), (i_dh2, i_qh2), and (i_dh3, i_qh3) are currents in two-dimensional rotating frames (d_h1-q_h1), (d_h2-q_h2), and (d_h3-q_h3), respectively; h₁, h₂, and h₃ are respectively main NS-EMF harmonics presenting in FM1, FM2, and FM3 (see associated harmonics in Table 1); [P] is the 7-by-7 Park transformation matrix with the electrical position θ as follows:

$$\left[\mathit{P}\right]=\left[\begin{array}{ccccccc}\cos (h_1\theta )& \sin (h_1\theta )& 0& 0& 0& 0& 0\\ -\sin (h_1\theta )& \cos (h_1\theta )& 0& 0& 0& 0& 0\\ 0& 0& \cos (h_2\theta )& \sin (h_2\theta )& 0& 0& 0\\ 0& 0& -\sin (h_2\theta )& \cos (h_2\theta )& 0& 0& 0\\ 0& 0& 0& 0& \cos (h_3\theta )& \sin (h_3\theta )& 0\\ 0& 0& 0& 0& -\sin (h_3\theta )& \cos (h_3\theta )& 0\\ 0& 0& 0& 0& 0& 0& 1\end{array}\right]$$

(5)

The selection of harmonics (h₁, h₂, h₃) in rotating frames depends on main harmonics (with highest amplitudes) presenting in fictitious machines of the considered NS-EMFs. In our case, the considered experimental seven-phase prototype has the 1st, 9th, and 3rd harmonics of NS-EMFs which account for the highest proportions in FM1, FM2, and FM3, respectively. Therefore, the corresponding rotating frames are (d₁-q₁), (d₉-q₉), and (d₃-q₃). If there is only one harmonic of NS-EMFs existing in one fictitious machine (e.g., only 1st in FM1, only 9th in FM2, and only 3rd in FM3), constant d-q currents (i_d1, i_q1, i_d9, i_q9, i_d3, i_q3) can be used to generate constant torque, facilitating PI controllers in the classical RFOC scheme.

However, NS-EMFs may contain more than one harmonic per fictitious machine (reference frame). Without loss of generality, to see impacts of multi-harmonics in NS-EMFs, it is assumed that there are two associated harmonics existing in one fictitious machine. For the considered seven-phase prototype, these harmonics are described as follows:

• The 1st and 13th are associated with FM1;
• The 9th and 19th are associated with FM2;
• The 3rd and 11th are associated with FM3.

The speed-normalized NS-EMF of one phase can be rewritten as

$$e_j=\left\{\begin{array}{l}{E}_{n1}\sin \left[\theta -\left(j-1\right)\frac{2\pi }{7}+{\phi }_1\right]+E_{n3}\sin \left[3\left(\theta -\left(j-1\right)\frac{2\pi }{7}\right)+{\phi }_3\right]+\\ E_{n9}\sin \left[9\left(\theta -\left(j-1\right)\frac{2\pi }{7}\right)+{\phi }_9\right]+E_{n11}\sin \left[11\left(\theta -\left(j-1\right)\frac{2\pi }{7}\right)+{\phi }_{11}\right]+\\ E_{n13}\sin \left[13\left(\theta -\left(j-1\right)\frac{2\pi }{7}\right)+{\phi }_{13}\right]+E_{n19}\sin \left[19\left(\theta -\left(j-1\right)\frac{2\pi }{7}\right)+{\phi }_{19}\right]\end{array}\right\}$$

(6)

where (E_n1, E_n3, E_n9, E_n11, E_n13, E_n19) and (φ₁, φ₃, φ₉, φ₁₁, φ₁₃, φ₁₉) are the speed-normalized amplitudes and initial phase angles of EMF harmonics 1st, 3rd, 9th, 11th, 13th, and 19th, respectively; j is the phase number from 1 to 7 or A to G; θ is the electrical position.

By using Clarke and Park transformation matrices in (3) and (5), back-EMFs in d-q frames are time-variant and expressed by:

$${\underset{\_}{e}}_{dq}=\left[\mathit{P}\right]\left[\mathit{T}\right]{\underset{\_}{e}}_{ns}={\left[\begin{array}{ccccccc}{e}_{d1}& e_{q1}& e_{d9}& e_{q9}& e_{d3}& e_{q3}& e_z\end{array}\right]}^{\mathrm{T}}$$

(7)

with

$$\{\begin{array}{l}{e}_{d1}=\sqrt{7/2}{E}_{n13}\sin \left(14\theta +{\phi }_{13}\right)\\ e_{q1}=\sqrt{7/2}\left\{E_{n1}+E_{n13}\cos \left(14\theta +{\phi }_{13}\right)\right\}\\ e_{d9}=\sqrt{7/2}{E}_{n19}\sin \left(28\theta +{\phi }_{19}\right)\\ e_{q9}=\sqrt{7/2}\left\{E_{n9}+E_{n19}\cos \left(28\theta +{\phi }_{19}\right)\right\}\end{array}$$

and

$$\{\begin{array}{l}{e}_{d3}=\sqrt{7/2}{E}_{n11}\sin \left(14\theta +{\phi }_{11}\right)\\ e_{q3}=\sqrt{7/2}\left\{E_{n3}+E_{n11}\cos \left(14\theta +{\phi }_{11}\right)\right\}\\ e_z=0\end{array}$$

From (7), e_dq can be a constant vector only if E_n11, E_n13, and E_n19 are zero. It means that NS-EMFs contain only 1st, 9th, and 3rd harmonics. In this study, the considered 13th, 19th, and 11th harmonics are called unwanted NS-EMF harmonics. It is noted that, harmonics 7k ($k\in \mathrm{N}$) associated with the zero-sequence machine ZM have no impact on torque generation due to the star connection (current i_z = 0).

The electromagnetic torque T_em can be expressed by:

$$T_{em}={\underset{\_}{e}}_{ns}^{\mathrm{T}}\underset{\_}{i}={\displaystyle \sum _{j=A}^G(e_j{i}_j)}={\underset{\_}{e}}_{dq}^{\mathrm{T}}{\underset{\_}{i}}_{dq}={\displaystyle \sum _{\ell =1}^3(e_{d\ell }{i}_{d\ell }+e_{q\ell }{i}_{q\ell })}={\displaystyle \sum _{\ell =1}^3{T}_{FM\ell }}$$

(8)

where $T_{FM\ell }$ is the torque of fictitious machine $\mathrm{FM}\ell$ ($\ell =\left\{1,2,3\right\}$).

3. Classical Control of Multiphase Drives for Healthy Mode

The classical RFOC scheme for torque control of a seven-phase PMSM is described in Figure 1. For a given reference torque T_{em_ref}, seven reference phase currents i_ref with minimum total copper losses can be calculated by using MTPA strategy [10,11] using the estimated NS-EMFs e_sn. These currents are transformed into d-q frames (i_{d1_ref}, i_{q1_ref}, i_{d9_ref}, i_{q9_ref}, i_{d3_ref}, i_{q3_ref}, i_{z_ref}). Current i_{z_ref} is equal to zero due to the star connection. The electrical position θ obtained from an encoder is provided for the speed-normalized NS-EMF estimation and Park transformations.

If NS-EMFs contain only three main harmonics (1st, 9th, 3rd), the reference d-q currents are constant. However, e_sn contains additional unwanted harmonics (11th, 13th, and 19th as previously assumed). Therefore, to generate a constant torque, six reference d-q currents need to be time-variant and have main frequencies of 14θ, 28θ, and kn in the general case ($k\in \mathrm{N}$ and n is the phase number) [20]. Consequently, the use of six PI controllers with low bandwidth to control six varying reference d-q currents in the classical RFOC scheme may reduce torque quality at high speed.

The outputs of the current controllers are reference voltages used to generate switching signals for a 7-leg Voltage Source Inverter (VSI) using carrier-based PWM strategy.

4. Proposed Adaline-Based Control Scheme for Healthy Mode

4.1. Simplified MTPA (SMTPA)

In this study, SMTPA is used to develop the proposed control scheme. SMTPA considers only one harmonic of NS-EMFs per fictitious machine (1st, 9th, 3rd) to calculate reference currents.

$${\underset{\_}{i}}_{ref}=\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}{\underset{\_}{e}}_{sn}^{sim}$$

(9)

where ${\underset{\_}{e}}_{sn}^{sim}$ is the simplified NS-EMF vector created from e_sn in (1) and (6) by keeping only 1st, 9th, and 3rd harmonics.

From (7), the simplified NS-EMFs in d-q frames become constants as follows:

$${\underset{\_}{e}}_{dq}^{sim}={\left[\begin{array}{ccccccc}{e}_{d1}& e_{q1}& e_{d9}& e_{q9}& e_{d3}& e_{q3}& 0\end{array}\right]}^{\mathrm{T}}$$

(10)

with

$$\{\begin{array}{l}{e}_{d1}=0\\ e_{q1}=\left(\sqrt{7/2}\right)E_{n1}\end{array}\hspace{1em}\{\begin{array}{l}{e}_{d9}=0\\ e_{q9}=\left(\sqrt{7/2}\right)E_{n9}\end{array}\hspace{1em}\{\begin{array}{l}{e}_{d3}=0\\ e_{q3}=\left(\sqrt{7/2}\right)E_{n3}\end{array}$$

Thus, reference d-q currents with SMTPA are calculated from (4), (9), and (10) as

$${\underset{\_}{i}}_{dq\_ref}=\left[\mathit{P}\right]\left[\mathit{T}\right]{\underset{\_}{i}}_{ref}=\left(\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right){\underset{\_}{e}}_{dq}^{sim}={\left[\begin{array}{ccccccc}{i}_{d1\_ref}& i_{q1\_ref}& i_{d9\_ref}& i_{q9\_ref}& i_{d3\_ref}& i_{q3\_ref}& 0\end{array}\right]}^{\mathrm{T}}$$

(11)

with

$$\begin{gathered} \{\begin{array}{l}{i}_{d1\_ref}=0\\ i_{q1\_ref}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n1}\end{array}\hspace{1em}\{\begin{array}{l}{i}_{d9\_ref}=0\\ i_{q9\_ref}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n9}\end{array} \\ \{\begin{array}{l}{i}_{d3\_ref}=0\\ i_{q3\_ref}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n3}\end{array} \end{gathered}$$

In this case, the squared norm ${\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2$ is constant. Therefore, from (11), the reference d-q currents are constant, facilitating current control using conventional PI controllers. However, from (8), the interaction between reference currents in (11) and the full NS-EMFs in (6)–(7) theoretically generates the total electromagnetic torque as follows:

$$T_{em\_139}=T_{ave}+T_{14\theta }+T_{28\theta }$$

(12)

with

$$T_{ave}=\frac{7}{2}\left(\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)\left(E_{n1}^2+E_{n9}^2+E_{n3}^2\right)$$

and

$$\{\begin{array}{l}{T}_{14\theta }=\frac{7}{2}\left(\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)\left\{E_{n1}{E}_{n13}\cos \left(14\theta +{\phi }_{13}\right)+E_{n3}{E}_{n11}\cos \left(14\theta +{\phi }_{11}\right)\right\}\\ T_{28\theta }=\frac{7}{2}\left(\frac{T_{em\_ref}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n9}{E}_{n19}\cos \left(28\theta +{\phi }_{19}\right)\end{array}$$

where T_{em_139} is the total torque generated by SMTPA (with only 1st, 3rd, and 9th harmonics of currents); T_ave is the average torque; T_14θ and T_28θ are harmonics 14θ and 28θ of the torque; E_n1, E_n3, E_n9, E_n11, E_n13, and E_n19 are amplitudes of six NS-EMF harmonics as described in (6).

From (12), the total torque for a seven-phase machine contains a constant component T_ave and two harmonic components 14θ and 28θ. In general, torque harmonics of a n-phase machine under healthy condition are multiples of nθ, specifically 2knθ if n is odd and knθ if n is even ($k\in \mathrm{N}$) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Theoretically, to obtain a constant torque, torque ripples T_14θ and T_28θ in (12) can be used to calculate compensating currents. However, the estimated NS-EMFs are usually obtained from measured NS-EMFs in open-circuited stator windings. The mechanical load in the real-time operation of the drive may significantly affect the NS-EMF waveform, including amplitudes and initial phase angles of harmonic components. In addition, the dead-time voltages of VSI may impose harmonic components in machine phase voltages [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. Therefore, the compensating currents directly calculated from T_14θ and T_28θ cannot guarantee a constant torque.

Consequently, the compensating currents to eliminate torque ripples need to be adaptively determined. In this study, an Adaline for healthy mode (“Adaline_HM”) is proposed to adaptively determine the compensating currents. Indeed, Adaline possesses advantages such as fast convergence, self-learning, and easy-to-implement [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. The specific Adaline will be presented in the next subsections.

4.2. Structure of Proposed Control Scheme for Healthy Mode

The proposed control scheme to eliminate torque ripples for healthy mode is described in Figure 2. This scheme is developed from the classical RFOC scheme in Figure 1 and SMTPA. The transformations and six PI controllers for current control are preserved. Compensating currents are added to the existing reference currents from SMTPA to adaptively eliminate torque ripples. The total torque T_em of the seven-phase machine is calculated from measured phase currents and estimated NS-EMFs according to (8).

Based on torque ripples T_14θ and T_28θ in (12), a compensating torque T_{em_com} will be adaptively determined from a specific Adaline. Thereafter, compensating currents are calculated from T_{em_com} by using SMTPA as follows:

$${\underset{\_}{i}}_{com}=\frac{T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}{\underset{\_}{e}}_{sn}^{sim}$$

(13)

where i_com is the 7-dimensional vector of compensating currents; ${\underset{\_}{e}}_{sn}^{sim}$ is the simplified NS-EMF vector created from e_sn in (1) and (6) by keeping only 1st, 9th, and 3rd harmonics.

Then, i_com is transformed into d-q frames as follows:

$${\underset{\_}{i}}_{dq\_com}={\left[\begin{array}{ccccccc}{i}_{d1\_com}& i_{q1\_com}& i_{d9\_com}& i_{q9\_com}& i_{d3\_com}& i_{q3\_com}& 0\end{array}\right]}^{\mathrm{T}}=\left(\frac{T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right){\underset{\_}{e}}_{dq}^{sim}$$

(14)

with

$$\{\begin{array}{l}{i}_{d1\_com}=0\\ i_{q1\_com}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n1}\end{array}\{\begin{array}{l}{i}_{d9\_com}=0\\ i_{q9\_com}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n9}\end{array}\{\begin{array}{l}{i}_{d3\_com}=0\\ i_{q3\_com}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n3}\end{array}$$

where i_{dq_com} is the 7-dimensional vector of d-q compensating currents; ${\underset{\_}{e}}_{dq}^{sim}$ is the constant vector as described in (10).

Finally, the compensating currents in (14) are added to constant reference d-q current vector (i_{dq_ref}) from SMTPA in (11). The total reference d-q current vector (${\underset{\_}{i}}_{dq\_ref}^{\ast }$) is used for control as follows:

$${\underset{\_}{i}}_{dq\_ref}^{\ast }={\left[\begin{array}{ccccccc}{i}_{d1\_ref}^{\ast }& i_{q1\_ref}^{\ast }& i_{d9\_ref}^{\ast }& i_{q9\_ref}^{\ast }& i_{d3\_ref}^{\ast }& i_{q3\_ref}^{\ast }& 0\end{array}\right]}^{\mathrm{T}}={\underset{\_}{i}}_{dq\_ref}+{\underset{\_}{i}}_{dq\_com}$$

(15)

with

$$\begin{gathered} \{\begin{array}{l}{i}_{d1\_ref}^{*}=0\\ i_{q1\_ref}^{*}{}_{}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_ref}+T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n1}\end{array}\hspace{1em}\{\begin{array}{l}{i}_{d9\_ref}^{*}=0\\ i_{q9\_ref}^{*}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_ref}+T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n9}\end{array} \\ \{\begin{array}{l}{i}_{d3\_ref}^{*}=0\\ i_{q3\_ref}^{*}=\sqrt{\frac{7}{2}}\left(\frac{T_{em\_ref}+T_{em\_com}}{{\Vert {\underset{\_}{e}}_{sn}^{sim}\Vert }^2}\right)E_{n3}\end{array} \end{gathered}$$

Notably, from (15), reference d-axis currents ($i_{d1\_ref}^{\ast }$, $i_{d9\_ref}^{\ast }$, $i_{d3\_ref}^{\ast }$) that do not generate torque are kept zero. Only torque-generating q-axis currents ($i_{q1\_ref}^{\ast }$, $i_{q9\_ref}^{\ast }$, $i_{q3\_ref}^{\ast }$) are no longer time-constant to eliminate torque ripples. Therefore, the proposed control scheme using Adaline has three constant currents, facilitating current control with PI controllers. Meanwhile, study [20] applies Adalines to find reference currents but it has all reference d-q currents oscillating with high amplitudes like MTPA [10,11].

The proposed structure in Figure 2 can be applied to all electric machines with different phase numbers and NS-EMFs. Torque harmonics under healthy condition for a n-phase machine are multiples of nθ, specifically 2knθ if n is odd and knθ if n is even ($k\in \mathrm{N}$) [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. For example, a five-phase machine has torque ripples of 10kθ (10θ, 20θ…).

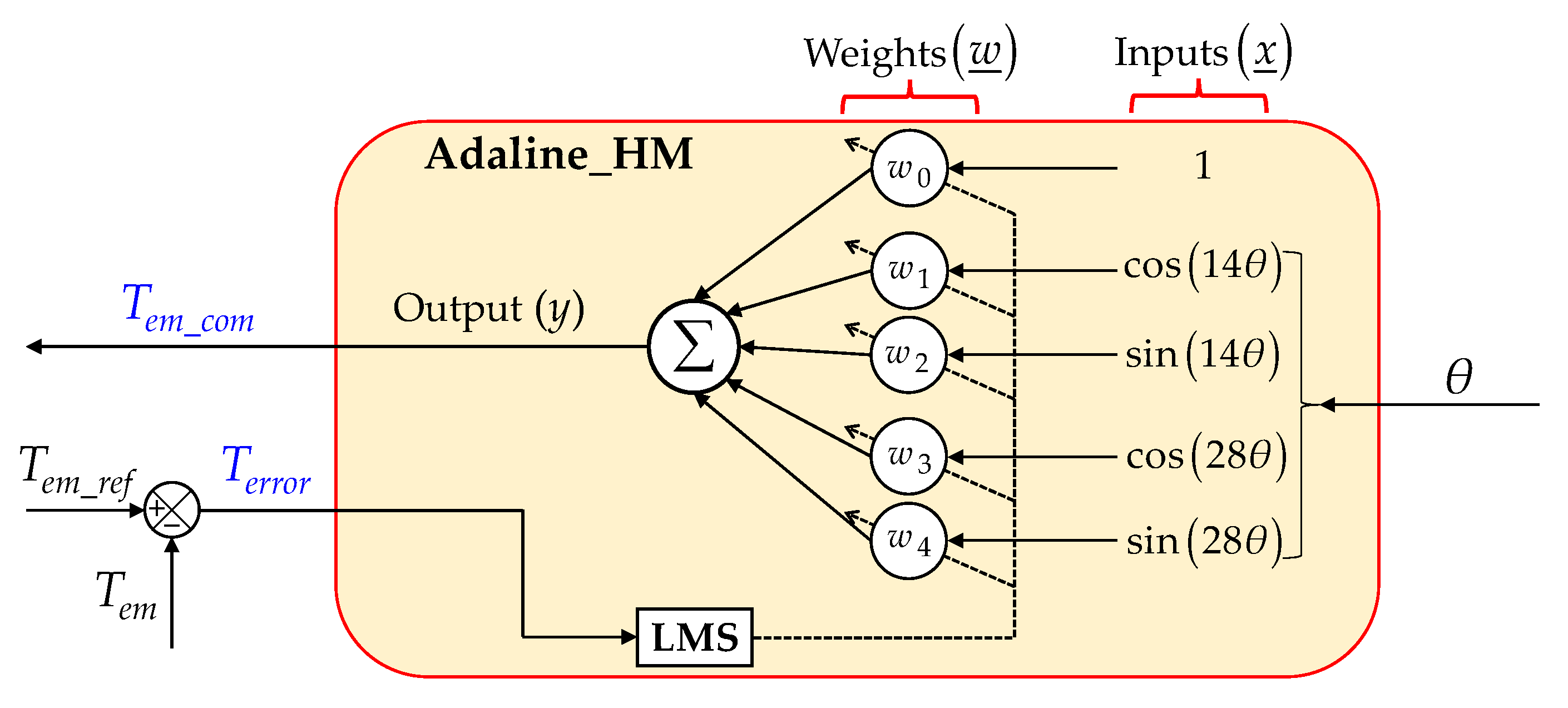
4.3. Structure of Proposed Adaline for Healthy Mode

As previously mentioned, the Adaline is used to adaptively determine compensating torque T_{em_com} as well as compensating currents i_com to make the total torque T_em properly track its reference value T_{em_ref}. It is assumed that the total torque with SMTPA in real time (experiments) $T_{em\_139}^{\ast }$ can be developed from (12) as follows:

$$\begin{array}{ll}{T}_{em\_139}^{*}& =T_{ave}^{*}+T_{14\theta }^{*}+T_{28\theta }^{*}\\ & =T_{ave}^{*}+\left[w_1^{\ast }\cos (14\theta )+w_2^{\ast }\sin (14\theta )\right]+\left[w_3^{\ast }\cos (28\theta )+w_4^{\ast }\sin (28\theta )\right]\end{array}$$

(16)

where $T_{ave}^{\ast }$ is the average torque; ($w_1^{\ast }$, $w_2^{\ast }$) and ($w_3^{\ast }$, $w_4^{\ast }$) are respectively coefficients representing torque harmonics $T_{14\theta }^{\ast }$ and $T_{28\theta }^{\ast }$, including their amplitudes and initial phase angles.

From (16), for a reference torque T_{em_ref}, the compensating torque T_{em_com} is given by:

$$\begin{array}{l}{T}_{em\_com}=T_{em\_ref}-T_{em\_139}^{*}=\left\{T_{em\_ref}-T_{ave}^{*}\right\}-\\ \left[w_1^{\ast }\cos (14\theta )+w_2^{\ast }\sin (14\theta )\right]-\left[w_3^{\ast }\cos (28\theta )+w_4^{\ast }\sin (28\theta )\right]\\ =w_0^{\ast }-\left[w_1^{\ast }\cos (14\theta )+w_2^{\ast }\sin (14\theta )\right]-\left[w_3^{\ast }\cos (28\theta )+w_4^{\ast }\sin (28\theta )\right]\end{array}$$

(17)

where $w_0^{\ast }$ is the error between T_{em_ref} and $T_{ave}^{\ast }$. Therefore, the compensating torque T_{em_com} is expressed by five coefficients ($w_0^{\ast }$, $w_1^{\ast }$, $w_2^{\ast }$, $w_3^{\ast }$, $w_4^{\ast }$). The torque $T_{em\_139}^{\ast }$ and its coefficients are not fixed and depend on the load and dead-time voltages of the drive [7,22].

Therefore, from (17), the structure of the Adaline used in Figure 2 is designed to minimize T_error (the error between reference torque T_{em_ref} and the total torque T_em) as presented in Figure 3.

The input and weight vectors of the Adaline are defined by:

$$\underset{\_}{x}={\left[1\begin{array}{ccccc}& \cos (14\theta )& \sin (14\theta )& \cos (28\theta )& \sin (28\theta )\end{array}\right]}^{\mathrm{T}}$$

(18)

$$\underset{\_}{w}={\left[\begin{array}{ccccc}{w}_0& w_1& w_2& w_3& w_4\end{array}\right]}^{\mathrm{T}}$$

(19)

where θ is the electrical position; (w₀, w₁, w₂, w₃, w₄) are five Adaline weights corresponding to the five coefficients of the compensating torque in (17).

The output of the Adaline representing the compensating torque (T_{em_com}) is the weighted sum of the inputs as follows:

$$y={\underset{\_}{w}}^{\mathrm{T}}\underset{\_}{x}=w_0+\left[w_1\cos (14\theta )+w_2\sin (14\theta )\right]+\left[w_3\cos (28\theta )+w_4\sin (28\theta )\right]$$

(20)

The five Adaline weights are updated by least mean square (LMS) rule at each sampled time k as:

$$\underset{\_}{w}(k+1)=\underset{\_}{w}(k)+\eta (T_{em\_ref}-T_{em}(k))\underset{\_}{x}(k)=\underset{\_}{w}(k)+\eta T_{error}(k)\underset{\_}{x}(k)$$

(21)

where η is the learning rate; T_error is the error between reference torque T_{em_ref} and the total torque T_em; T_em is calculated from measured phase currents and estimated NS-EMFs in (8).

To guarantee the system stability, the learning rate η is required to be between 0 and 1. Its value mainly depends on the sample time of calculations, and characteristics of the desired signal (T_{em_com}) such as amplitudes and phases of harmonics. An increase in η possibly results in faster convergence but it may lead to divergence. On each iteration, the Adaline weights are updated to converge to the coefficients of the compensating torque in (17). Weight convergence is obtained after a given number of iterations as:

$$\{\begin{array}{l}{w}_0(k)\underset{k\to \infty }{\to }{w}_0^{*}\\ w_1(k)\underset{k\to \infty }{\to }-w_1^{*}\\ w_2(k)\underset{k\to \infty }{\to }-w_2^{*}\\ w_3(k)\underset{k\to \infty }{\to }-w_3^{*}\\ w_4(k)\underset{k\to \infty }{\to }-w_4^{*}\end{array}\mathrm{then}y(k)\underset{k\to \infty }{\to }{T}_{em\_com}\mathrm{and}\{\begin{array}{l}{T}_{error}(k)\underset{k\to \infty }{\to }0\\ T_{em}(k)\underset{k\to \infty }{\to }{T}_{em\_ref}\end{array}$$

(22)

where ($w_0^{\ast }$, $w_1^{\ast }$, $w_2^{\ast }$, $w_3^{\ast }$, $w_4^{\ast }$) are the five coefficients of T_{em_com} as described in (17).

Finally, when η is properly chosen, T_error is minimized and the total torque T_em is equal to the constant reference torque T_{em_ref}. The proposed scheme using the Adaline can guarantee a smooth torque regardless of multi-harmonics existing in NS-EMFs.

Notably, the knowledge of torque harmonic rank and rotor position is used to optimize the Adaline training. The number of harmonics as well as the number of weights can be adapted to simplify calculations, improving the stability of the drives. If harmonics of torque ripples have very small amplitudes compared to those of the other harmonics as well as the average torque T_ave, these harmonics should be neglected in the Adaline inputs. Their corresponding weights are also removed. For example, the compensating torque in this study contains high-frequency components 14θ and 28θ. If absolute values of coefficients ($w_3^{\ast }$, $w_4^{\ast }$) are very small compared to those of ($w_1^{\ast }$, $w_2^{\ast }$, T_ave), harmonic component 28θ of the inputs and its corresponding weights should be removed from the Adaline. The Adaline can be designed by a S-function builder block MATLAB/Simulink.

5. Numerical and Experimental Results

5.1. Descriptions of Experimental Seven-Phase Test Bench

The proposed Adaline-based control scheme for healthy mode is validated with a seven-phase PMSM prototype as described in Figure 4 and

Table 2. Electrical parameters of the seven-phase PMSM drive.

Parameter	Unit	Value
Resistance of one phase R	Ω	1.4
Self-inductance L	mH	14.7
Mutual inductance M1	mH	3.5
Mutual inductance M2	mH	−0.9
Mutual inductance M3	mH	−6.1
Amplitude of 1st harmonic of NS-EMF En1	V/rad/s	1.27
Number of pole pairs p		3
Rated RMS current	A	5.1
Rated torque	N.m	33.5
Rated speed	rpm	750
Rated power	kW	2.5
Rated voltage	V	120
DC-bus voltage VDC	V	200
PWM frequency	kHz	10

. A DC-bus voltage (200 V) (XANTREX XDC Digital DC Power Supply) supplying an IGBT VSI is in parallel to a programmable resistive load (Chroma DC Electronic Load 63204) to absorb the regenerative energy. Seven of twelve legs of the IGBT VSI (SEMIKRON with DC supply up to 500 V and RMS current up to 7A) are used to supply the seven-phase NS-EMF PMSM. Switching signals for IGBTs are created by carrier-based PWM at 10 kHz. MATLAB Simulink is used to implement the algorithm. Especially, a S-function builder block in MATLAB Simulink is used to design the Adaline. A dSPACE 1005 processor and its I/O boards are used to execute the algorithm in real time (do calculations, transmit switching signals to the VSI, receive the rotor position signal from an encoder (DHM5 BEI) and phase current signals from current sensors). Notably, a load machine drive (PARVEX DIGIVEX DPD 50/80), with an industrial three-phase PMSM (Parker SSD PARVEX HD950VJR9000) mechanically connected to the shaft of the seven-phase PMSM, is used to adjust the speed of both machines.

The seven-phase PMSM with axial flux is composed of one stator and two permanent magnet rotors as shown in Figure 4. Its speed-normalized NS-EMF and electrical parameters are described in Figure 4 and Table 2, respectively. The harmonic spectrum of NS-EMF with THD = 38% is clearly described in Figure 5. The 1st harmonic accounts for the highest proportion while the 3rd harmonic accounts for the second highest proportion, followed by the 9th harmonic. The experimental NS-EMF consists of other harmonics with lower proportions. The details of experimental NS-EMF harmonics are described as follows:

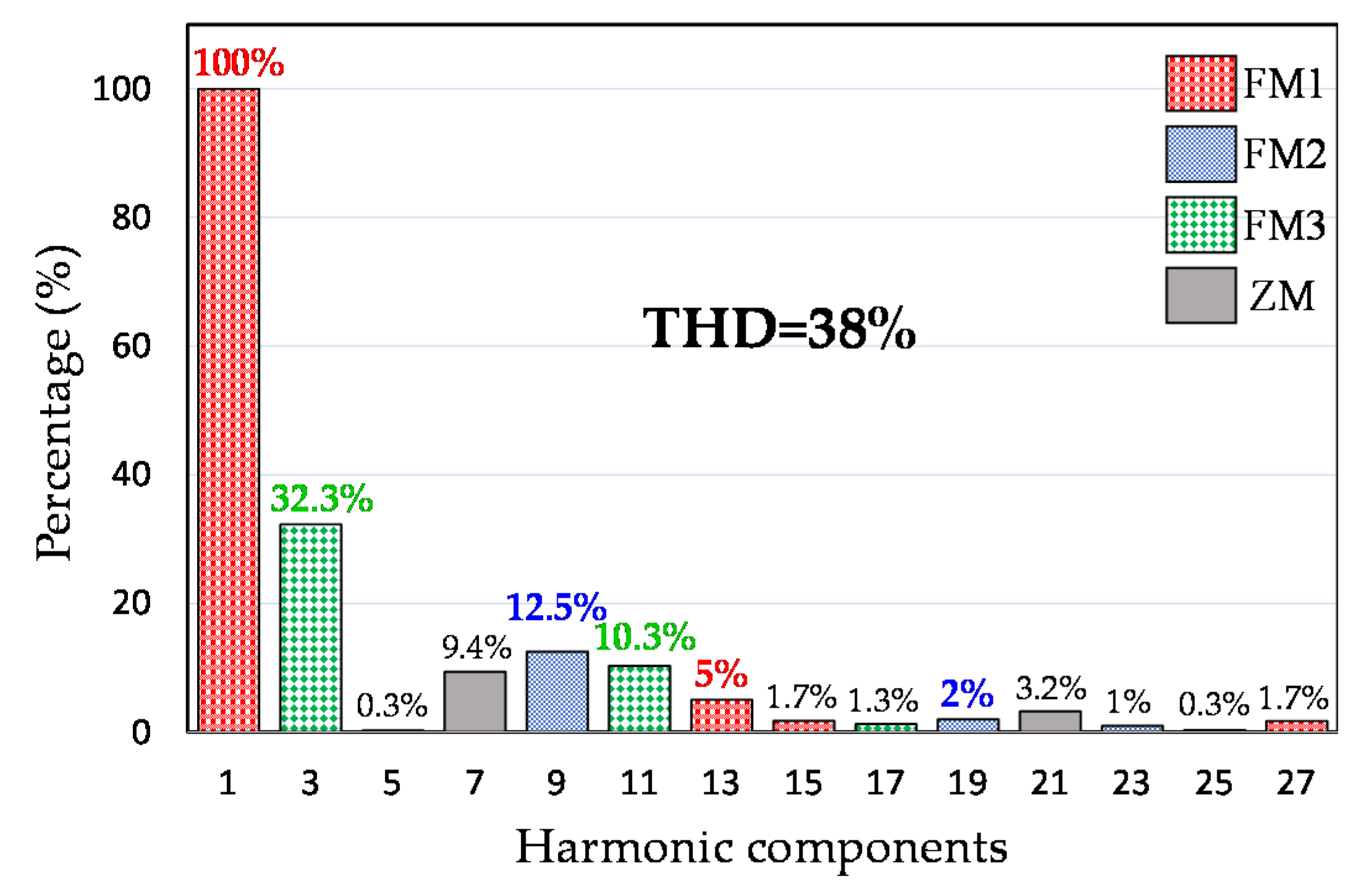
• FM1: The 1st (100%) and 13th (5% of the 1st);
• FM2: The 9th (12.5% of the 1st) and 19th (2% of the 1st);
• FM3: The 3rd (32.3% of the 1st) and 11th (10.3% of the 1st).

The 7th (9.4%) and 21st (3.2%) harmonics associated with the zero-sequence machine ZM do not have impact on the star-connected winding machine.

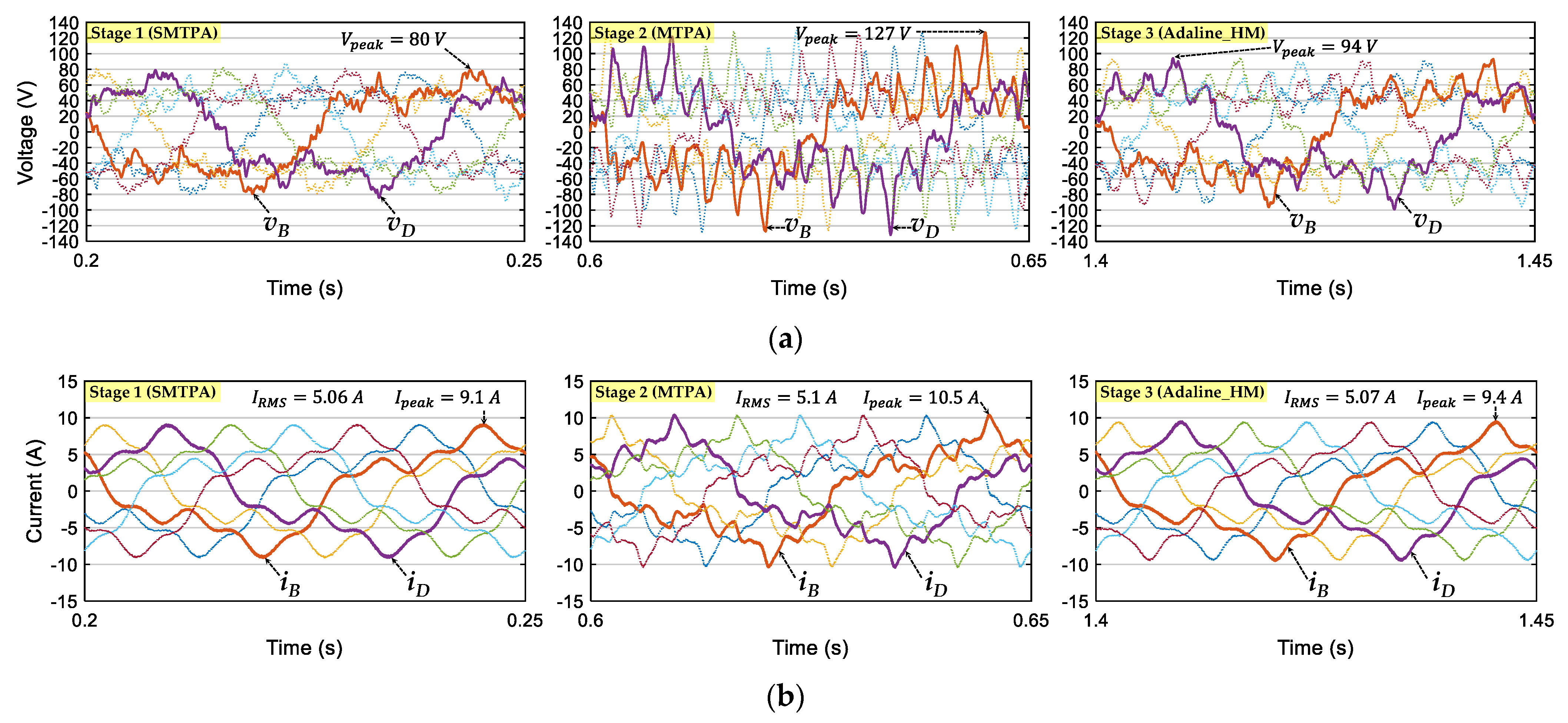
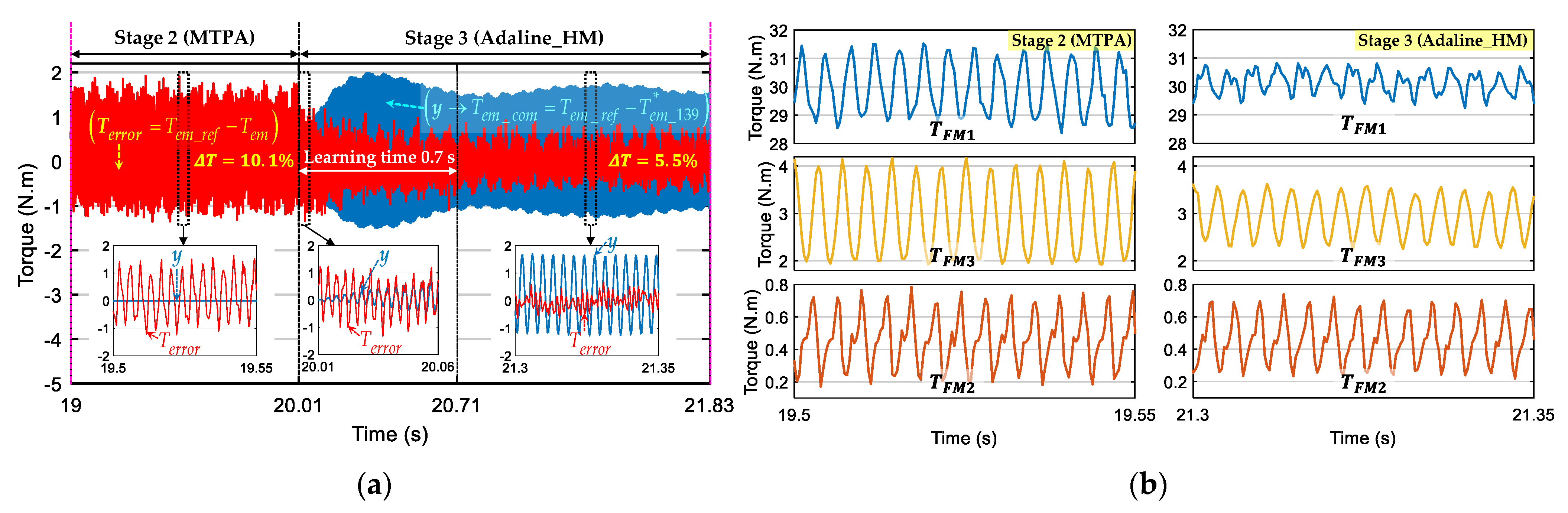
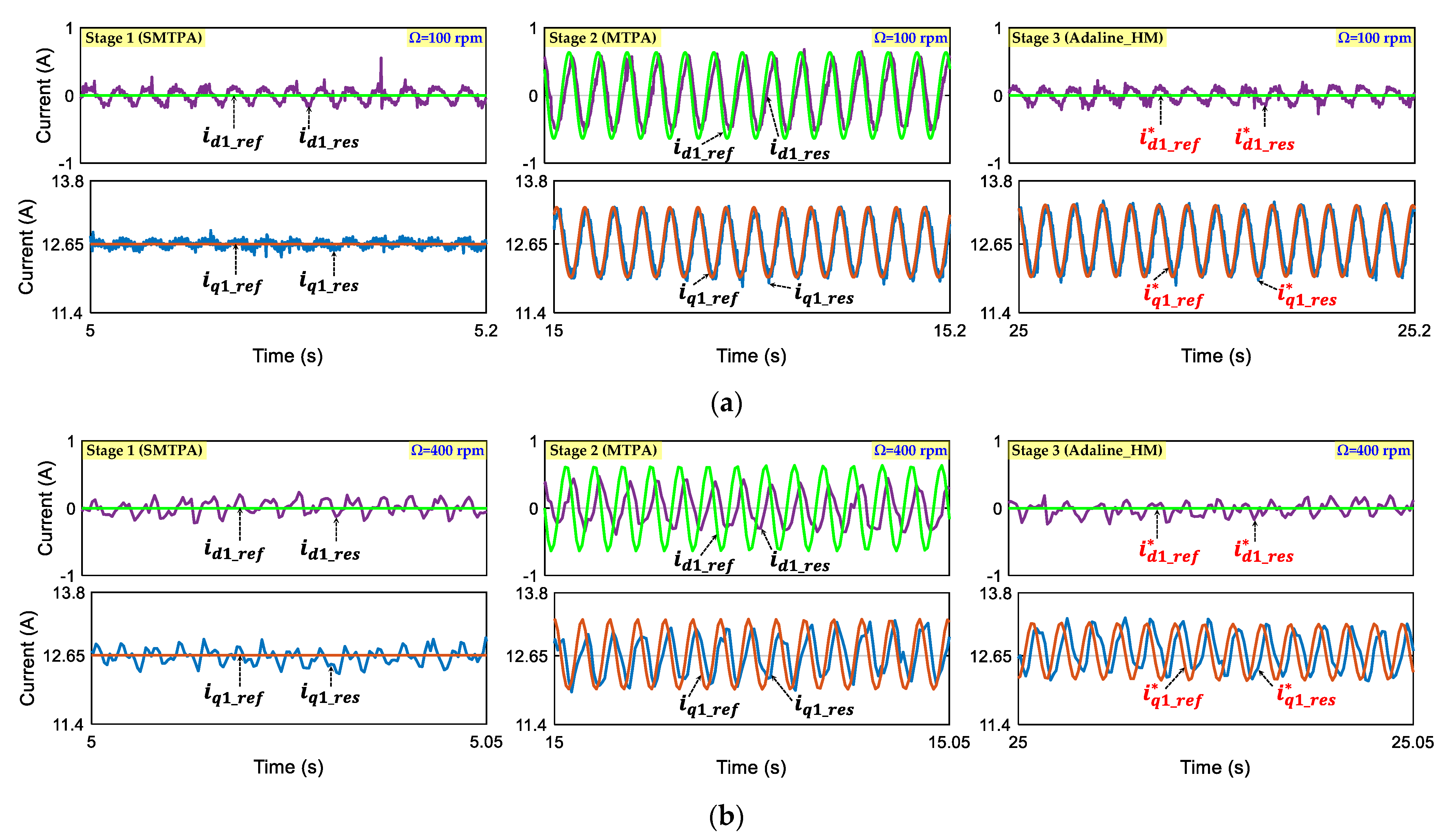
5.2. Numerical Results

The numerical results are obtained from MATLAB Simulink in which d-q currents are controlled by six PI controllers. As previously assumed, six harmonics (1st, 9th, 3rd, 13th, 19th, 11th) of NS-EMFs with the proportions described in Figure 5 are used to model the seven-phase machine. The reference torque T_{em_ref} is imposed at 33.5 N.m (rated torque) to obtain the rated RMS current of 5.1 A (Table 2).

Torque ripple ∆T for the torque quality evaluation can be calculated as

$$\Delta T=\frac{T_{em\_max}-T_{em\_min}}{T_{ave}}100\%$$

(23)

where T_{em_max} and T_{em_min} are maximum and minimum values of instantaneous torque T_em, respectively; T_ave is the average value of T_em.

To make comparisons between the proposed Adaline-based control scheme with the classical RFOC scheme using MTPA, three operating stages are described as follows:

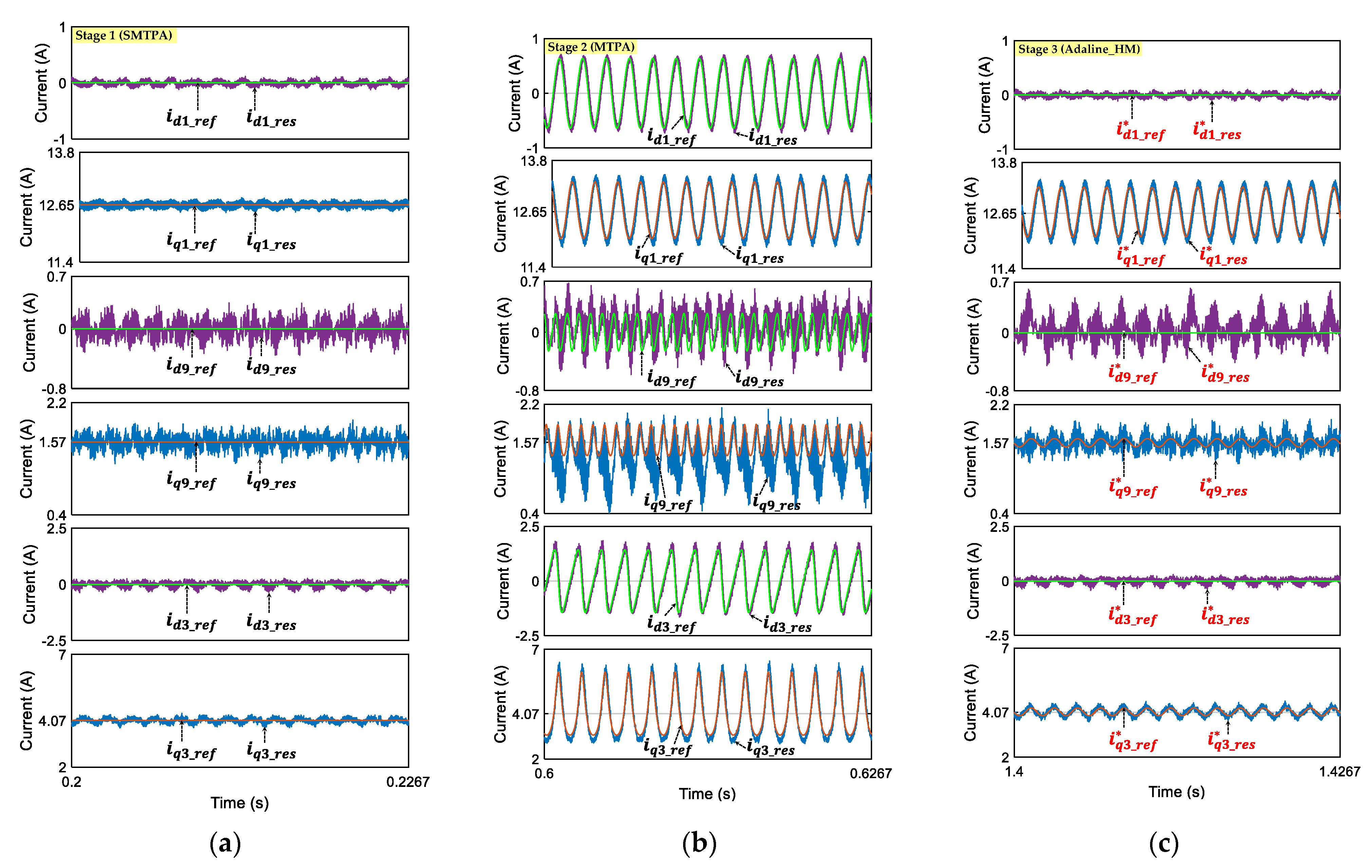
• Stage 1: The classical RFOC scheme (Figure 1) with SMTPA is used. Reference d-q currents are constant, but there are torque ripples as described in (12);
• Stage 2: The classical RFOC scheme (Figure 1) with MTPA is used. Reference d-q currents are no longer constant, but the torque ripples are theoretically eliminated;
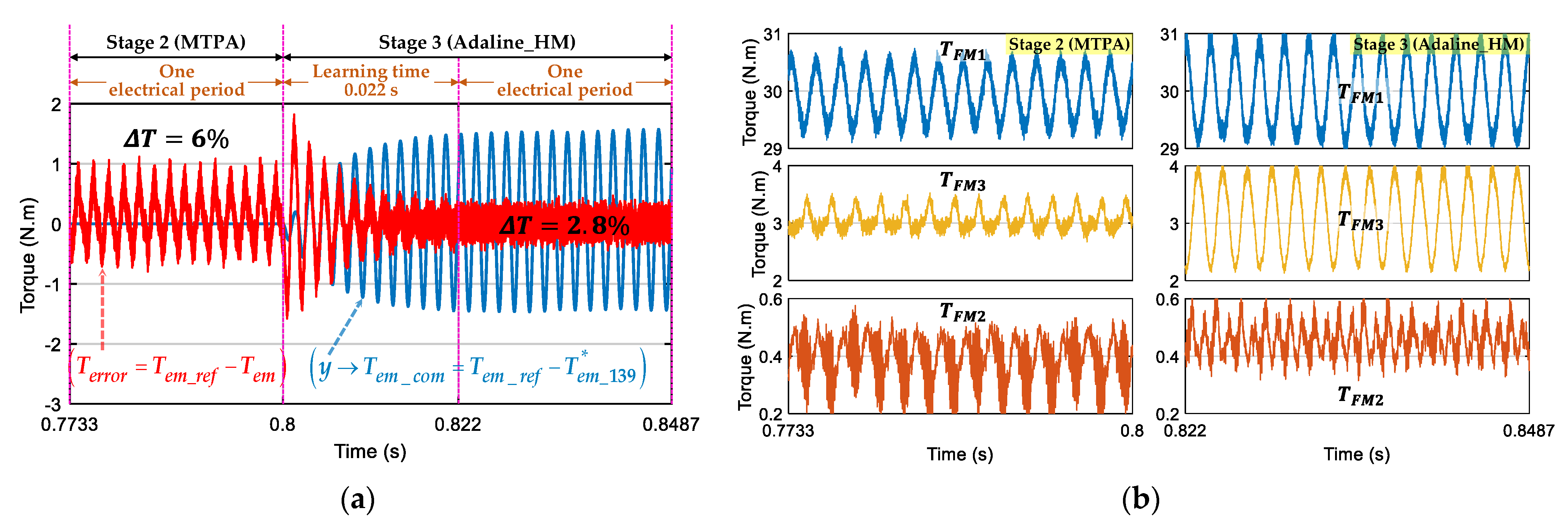
• Stage 3: The proposed Adaline-based control scheme (Figure 2) is used. Three reference d-axis currents are zero while three reference q-axis currents are no longer constant. The torque ripples are theoretically eliminated. The compensating torque T_{em_com} firstly contains both 14θ and 28θ (5 weights w₀, w₁, w₂, w₃, and w₄ are used), then T_{em_com} contains only 14θ (3 weights w₀, w₁, and w₂ are used).

Figure 6 presents the torque performance (at the rated value) in the three operating states at 100 rpm, 400 rpm, and 750 rpm (rated speed). With six constant reference d-q currents, the classical RFOC scheme using SMTPA has a torque ripple within 11% and 12% with harmonics 14θ and 28θ at different speeds (see stage 1 and zoom 1). MTPA has a higher quality torque compared to SMTPA, especially only 1.3% ripple at 100 rpm (see stage 2 and zoom 2). However, with six varying reference d-q currents for control, the torque ripple with MTPA increases to 6% at 750 rpm.

Meanwhile, by using the proposed control scheme with Adaline, the torque ripple slightly increases from 1.4% at 100 rpm to 2.6% at 750 rpm when 5 weights are used (see stage 3 and zoom 3). The proposed control scheme enables a higher quality torque compared to the classical RFOC scheme with MTPA.

With a learning rate of 0.001, the learning time to eliminate torque ripples is about 0.022 s at 750 rpm (see stage 3 and zoom 3 in Figure 6). It is noted that absolute values of weights w₃ and w₄ of harmonic 28θ are very small (<0.06) compared to those of w₁ (0.2), w₂ (1.49), and T_ave (33.5 N.m). Therefore, using only w₀, w₁, and w₂ to eliminate harmonic 14θ still guarantees a high-quality torque. Indeed, from 1.2 s of Figure 6, the torque ripple with 3 weights at the three speeds is 0.1% or 0.2% slightly higher than the case with 5 weights (see stage 3 and zoom 4 in Figure 6).

Figure 7a presents the learning process within 0.022 s at 750 rpm to eliminate T_error that is the difference between the reference torque T_{em_ref} and the total torque T_em. It is noted that the main harmonic of torque ripples in stage 2 is T_14θ due to 14 similar oscillations in one electrical period. When the output of the Adaline y converges to the compensating torque T_{em_com} with harmonic 14θ, T_error significantly reduces, and the torque ripple decreases from 6% to 2.8%. Torques generated by the three fictitious machines are presented in Figure 7b. In stages 2 and 3, the torque generated by FM2 (T_FM2) is much smaller than those of FM1 (T_FM1) and FM3 (T_FM3) due to the lower amplitude of NS-EMFs in FM2 (9th harmonic). T_FM2 with MTPA has higher ripples than those of the Adaline-based scheme. Notably, in stage 3, harmonic components of T_FM1 and T_FM3 are opposite with similar amplitudes. Therefore, total torque ripples are almost eliminated in stage 3. Indeed, reference currents in the proposed scheme are adaptively generated to eliminate torque ripples by using the online-trained Adaline.

The current control performance in the three operating stages at 750 rpm is described in Figure 8. Contrary to SMTPA, MTPA generates six reference d-q currents oscillating with high amplitudes. Especially, i_d9 and i_q9 with MTPA are no longer properly controlled at 750 rpm. Meanwhile, in the proposed Adaline-based scheme, three reference d-axis currents are null. Three q-axis reference currents oscillate with lower amplitudes compared to MTPA.

Figure 9 shows voltage references and phase currents in healthy mode at 400 rpm of the three operating stages. The performance at the speed of 400 rpm is chosen to verify the suitable maximum rotating speed with the DC-bus voltage limit (200 V) in experiments (see Table 2). SMTPA in stage 1 has the lowest peak voltage reference (80 V), the lowest RMS current (5.06 A), and the lowest peak current (9.1 A) among the three stages. The proposed scheme in stage 3 results in a lower peak voltage reference (94 V) compared to those of MTPA in stage 2 (127 V), possibly leading to a higher speed range. RMS and peak values of phase currents with the proposed scheme are respectively 5.07 and 9.4 A, slightly lower than those of MTPA with 5.1 A and 10.5 A.

From the numerical results, the proposed control scheme using Adaline has much better torque quality without increasing RMS and peak currents. In addition, its voltage references are smaller than those of the classical RFOC using MTPA.

5.3. Experimental Results

The rotating speed of the drive in healthy mode is limited to 400 rpm instead of 750 rpm because of the limit of DC-bus voltage (V_DC = 200 V). Indeed, with the star connection and classical PWM strategy, the maximum voltage of each phase should not be greater than V_DC/2 = 100 V. From Figure 9a, simulated voltage references at 400 rpm are about 100 V. If the speed could be higher (750 rpm in the numerical result section), the effectiveness of the proposed scheme will be clearer.

Figure 10 describes the torque performance at 100 rpm and 400 rpm. The proposed scheme in stage 3 has the best torque quality with lowest torque ripples. It is noted that torque quality with SMTPA does not change much in response to the speed increase. However, the torque ripple with MTPA almost doubles from 5% at 100 rpm to 10.1% at 400 rpm. Meanwhile, the ripple with the proposed scheme in stage 3 only increases from 3.9% to 5.5% for the same speed variation. The learning rate of 0.01 in experiments is higher than that of simulations (0.001) due to a longer sample time of calculations (350 µs in experiments compared to 3 µs in simulations). Thus, the learning time is longer within 0.6 s at 100 rpm and 0.7 s at 400 rpm as shown in Figure 10 (compared to only 0.022 s at 750 rpm in simulations in Figure 6). As discussed in the numerical result section, only three weights w₀, w₁, and w₂ are used to eliminate torque harmonic 14θ in experiments.

Experimental and numerical torque ripples at different speeds are summarized in

Table 3. Comparisons between the three operating stages (strategies) in terms of torque ripples at different speeds.

Speed Ω (rpm)	∆T with SMTPA (%)		∆T with MTPA (%)		∆T with Adaline_HM (%)
	sim1	exp2	sim1	exp2	sim1	exp2
100	11	11.8	1.3	5	1.5	3.9
400	11.5	9.5	3	10.1	2.3	5.5
750	12	-	6	-	2.8	-

¹ simulation (numerical) result; ² experimental result.

. In general, experimental torque ripples are higher than numerical results due to additional harmonics of NS-EMFs in the experimental seven-phase PMSM (see Figure 5). However, in general, the experimental results are in good accordance with the numerical results.

Figure 11a presents the learning process within 0.7 s at 400 rpm to eliminate T_error. It is noted that the main harmonic of torque ripples in stage 2 is T_14θ due to 14 oscillations in one electrical period. When y converges to T_{em_com}, T_error significantly reduces, and the torque ripple decreases from 10.1% to 5.5%. Torques generated by the three fictitious machines are presented in Figure 11b. In general, T_FM1 and T_FM3 are opposite with similar amplitudes in both stages 2 and 3. However, ripples of these torques with the Adaline-based scheme are lower than those of MTPA, leading to the lower total ripple in stage 3.

The current control performance of currents in (d₁-q₁) frame at 100 rpm and 400 rpm is described in Figure 12. At 100 rpm, all currents in the three stages are well controlled. At 400 rpm, with constant d₁-axis currents, SMTPA in stage 1 and the proposed scheme in stage 3 have better control quality than MTPA in stage 2. It is noted that the experimental control performance of q₁-axis current in stage 3 is not much better than that of stage 2. Indeed, there are current harmonics existing in d-q frames that are caused by the unwanted harmonics of NS-EMFs and the nonlinearity of VSI (e.g., dead-time voltages) as previously presented in [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. However, the proposed scheme with Adaline can automatically generate a proper torque in each fictitious machine (Figure 11b) to obtain the total torque with minimum ripples as presented in Figure 10b.

Measured phase currents in the three operating stages are described in Figure 13. These currents are similar in the three operating stages and in good accordance with the numerical results (see Figure 9b). The experimental values of RMS and peak currents, and peak voltage references at 400 rpm are compared with the numerical ones in

Table 4. Comparisons between the three operating stages (strategies) at 400 rpm in terms of RMS and peak currents, and peak voltage references.

Strategies	IRMS (A)		Ipeak (A)		Vpeak (V)
	sim1	exp2	sim1	exp2	sim1	exp2
SMTPA	5.06	5.09	9.1	10	80	93.5
MTPA	5.1	5.08	10.5	10.1	127	98
Adaline_HM	5.07	5.14	9.4	10.1	94	95

¹ simulation (numerical) result; ² experimental result.

. The experimental voltage reference with MTPA in stage 2 (98 V) is highest among the three stages. However, it is lower than the numerical result (127 V). Indeed, the presence of additional harmonics in NS-EMFs in the experimental machine (more than 6 harmonics as described in Figure 5) with different phase shift angles can change the peak voltage reference. Therefore, the agreement between numerical and experimental results of the torque, currents, and voltages can validate the mathematical model of the seven-phase PMSM.

The dynamic performance of the proposed scheme in response to speed and torque variations is presented in Figure 14. Different values of learning rate η (0.001, 0.005, 0.01, 0.05) are used to test the Adaline convergence of the proposed scheme. It is noted that different weights have different learning times.

The rotating variations between 200 rpm and 300 rpm have noticeable effects on torque quality as shown in Figure 14a with torque overshoots in transient states, especially with small values of learning rate. In steady states, the torque ripple is about 4%. When the learning rate increases to 0.05, the torque overshoots are almost eliminated. The weight variations can quickly compensate the effect of the speed variation on torque. An increase in learning rate generally results in faster weight convergence, except for w₀ due to weight oscillations.

When the reference torque varies between 20 N.m and 30 N.m at 300 rpm, the torque quality is guaranteed as shown in Figure 14b. The torque ripple slightly increases from 4.1% to 6% due to the decrease in the average torque. The Adaline weights are updated in each torque variation and remain almost constant at steady state. An increase in learning rate leads to faster weight convergence but slightly higher overshoots occur.

6. Conclusions

The first part of this study has proposed a control scheme for healthy mode in which torque quality of multi-harmonic NS-EMF multiphase drives is adaptively improved. Notably, numerous harmonics existing in NS-EMFs can be accepted with a high-quality control vector of the multiphase drives. The proposed scheme is based on only one specific simple Adaline, exploiting the torque harmonic rank and rotor position to automatically find compensating currents. Only one parameter (learning rate) needs to be properly chosen while other parameters are automatically updated. A smooth torque can be obtained without any increases in RMS currents (copper losses), peak currents, and peak voltages compared to MTPA. The proposed scheme has been tested on a seven-phase PMSM with a high THD of NS-EMFs. The numerical and experimental results are in good accordance, validating the effectiveness of the proposed scheme. It can be used for electric machines with other numbers of phases and arbitrary NS-EMF harmonic spectrums. The second part of this study will propose a control scheme using another Adaline for faulty mode.