Loss Investigation for Multiphase Induction Machine under Open-Circuit Fault Using Field–Circuit Coupling Finite Element Method
Abstract
:1. Introduction
2. Fault-Tolerant Current Design and Analysis
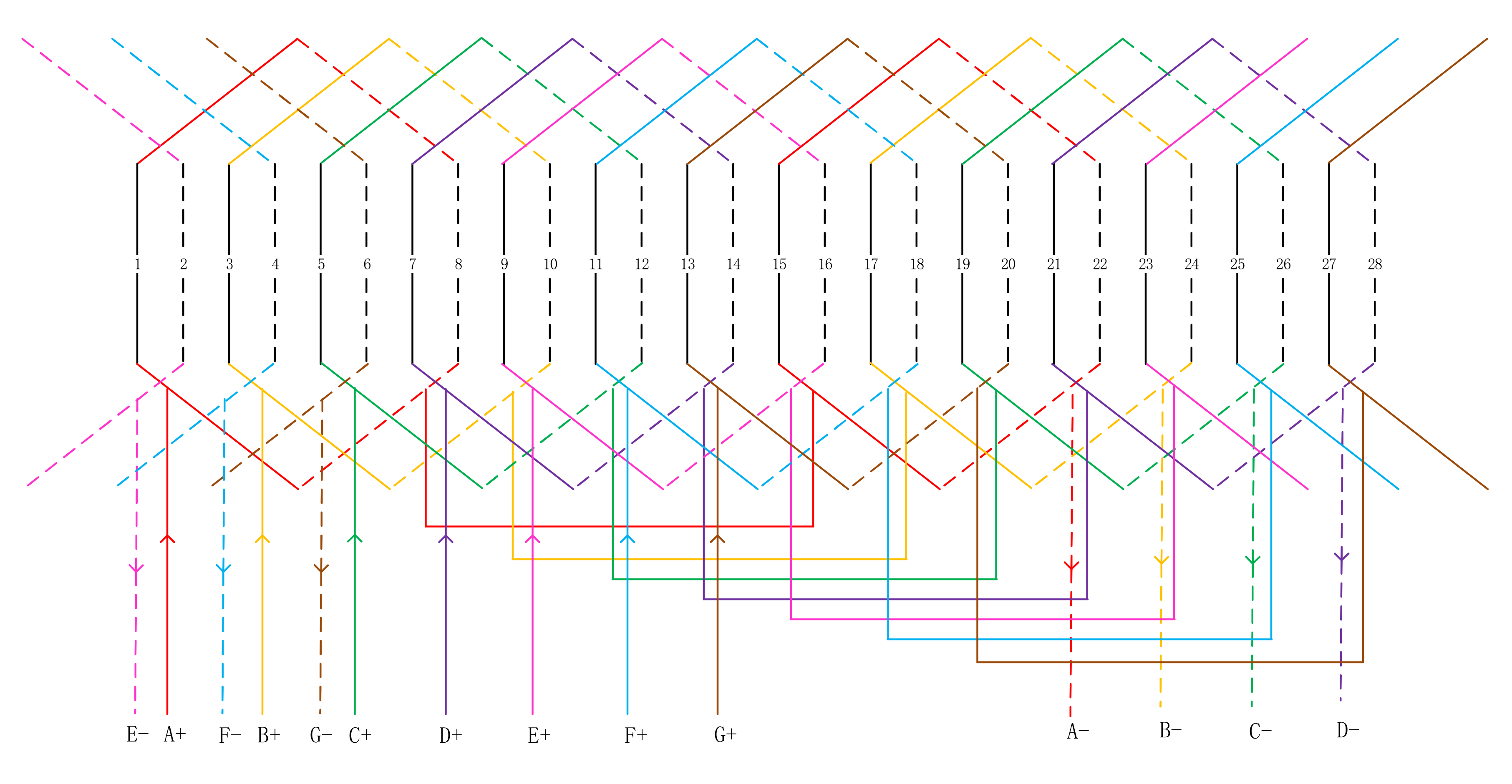
2.1. Residual Phase Currents Reconstitution
2.2. Coupling between the Fundamental and Harmonic Planes
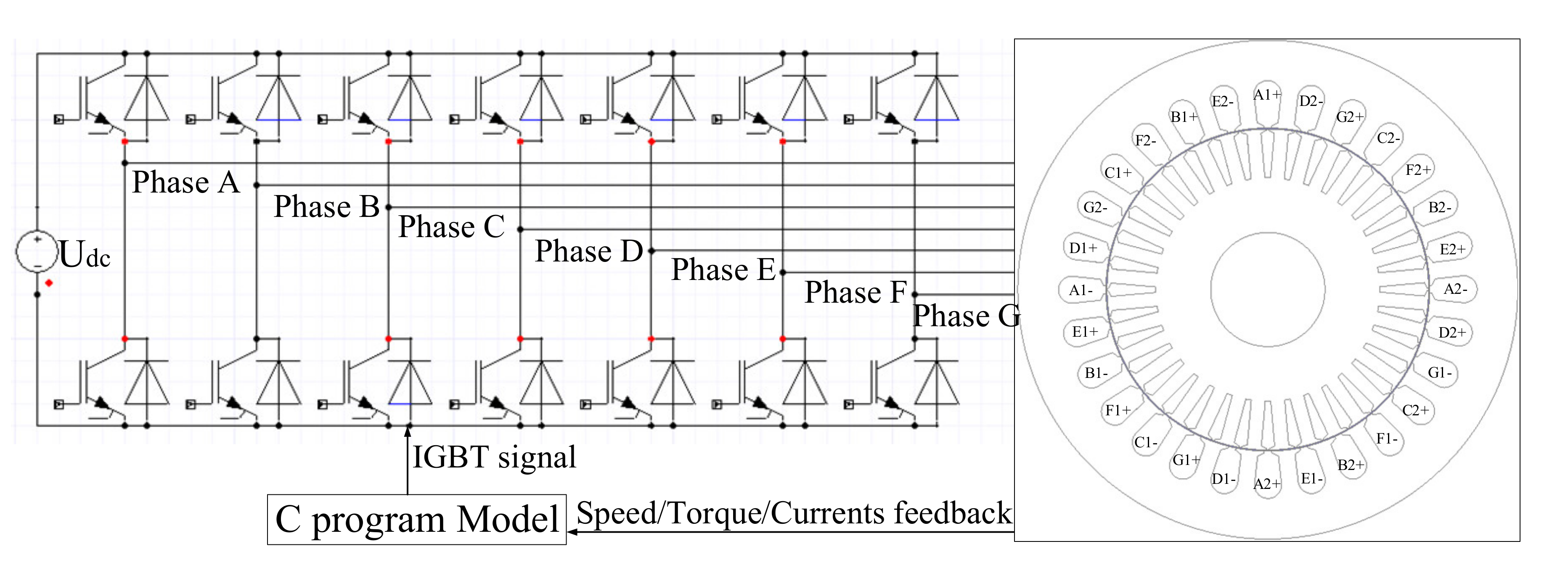
3. Time-Stepping FE Calculation
3.1. Field–Circuit Coupling FE Model
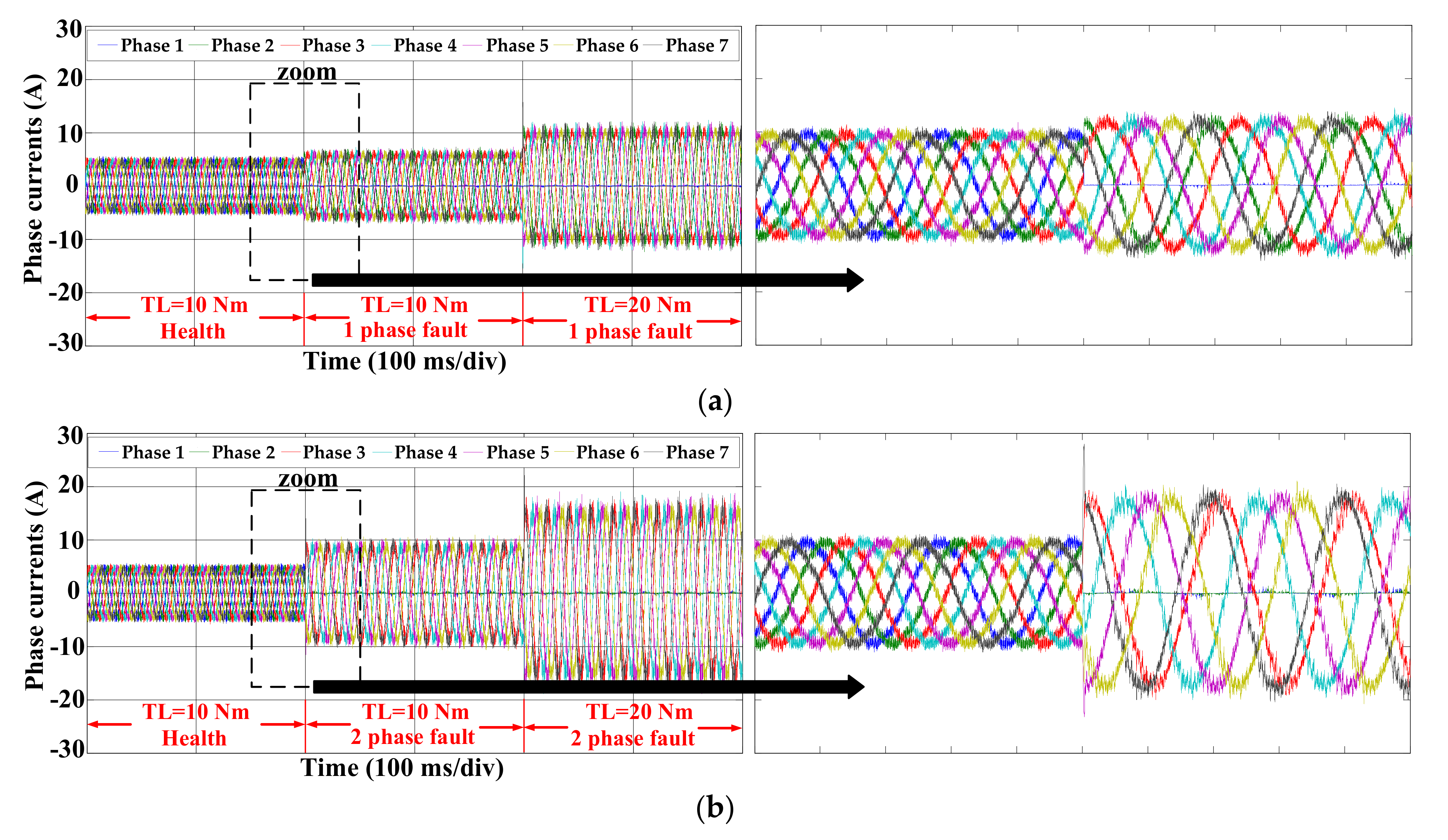
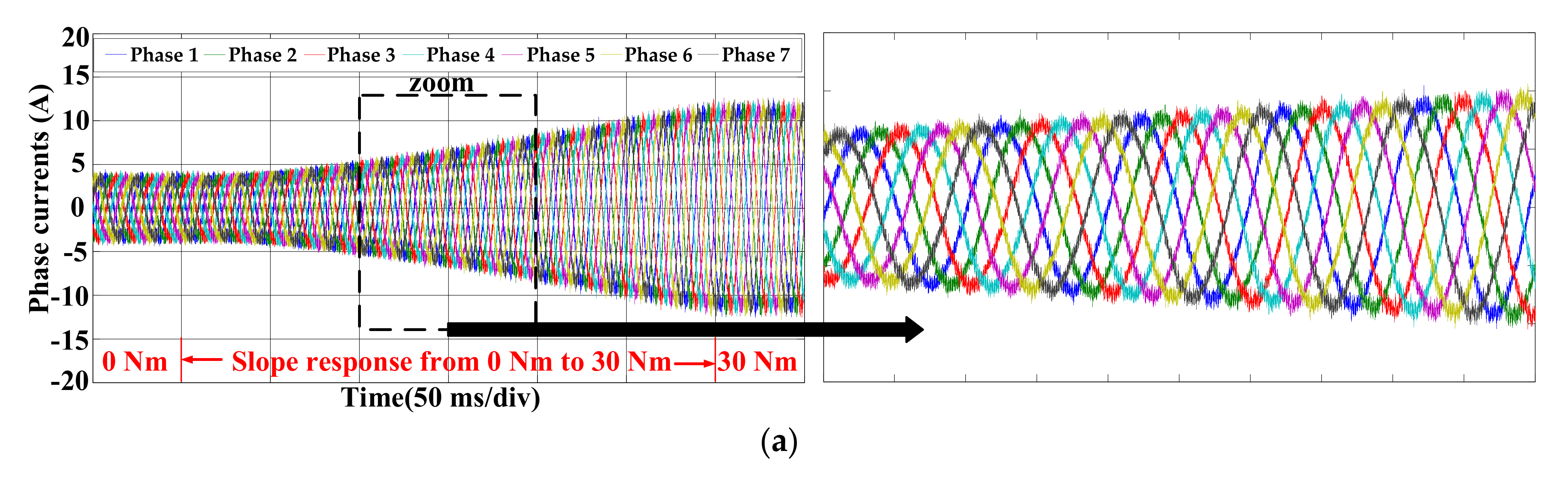
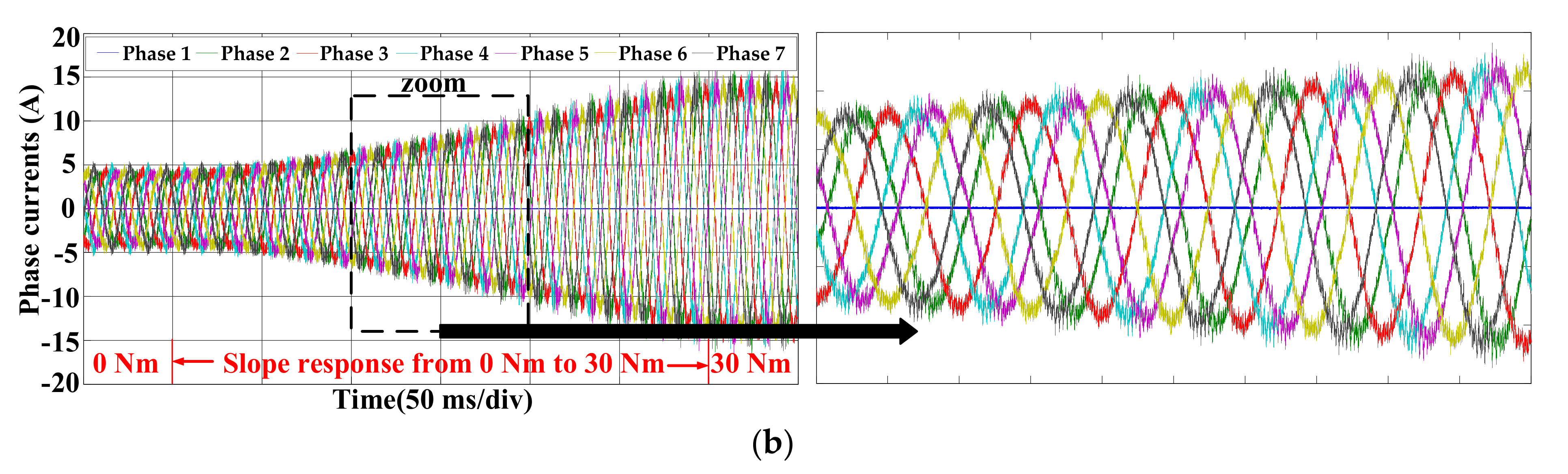
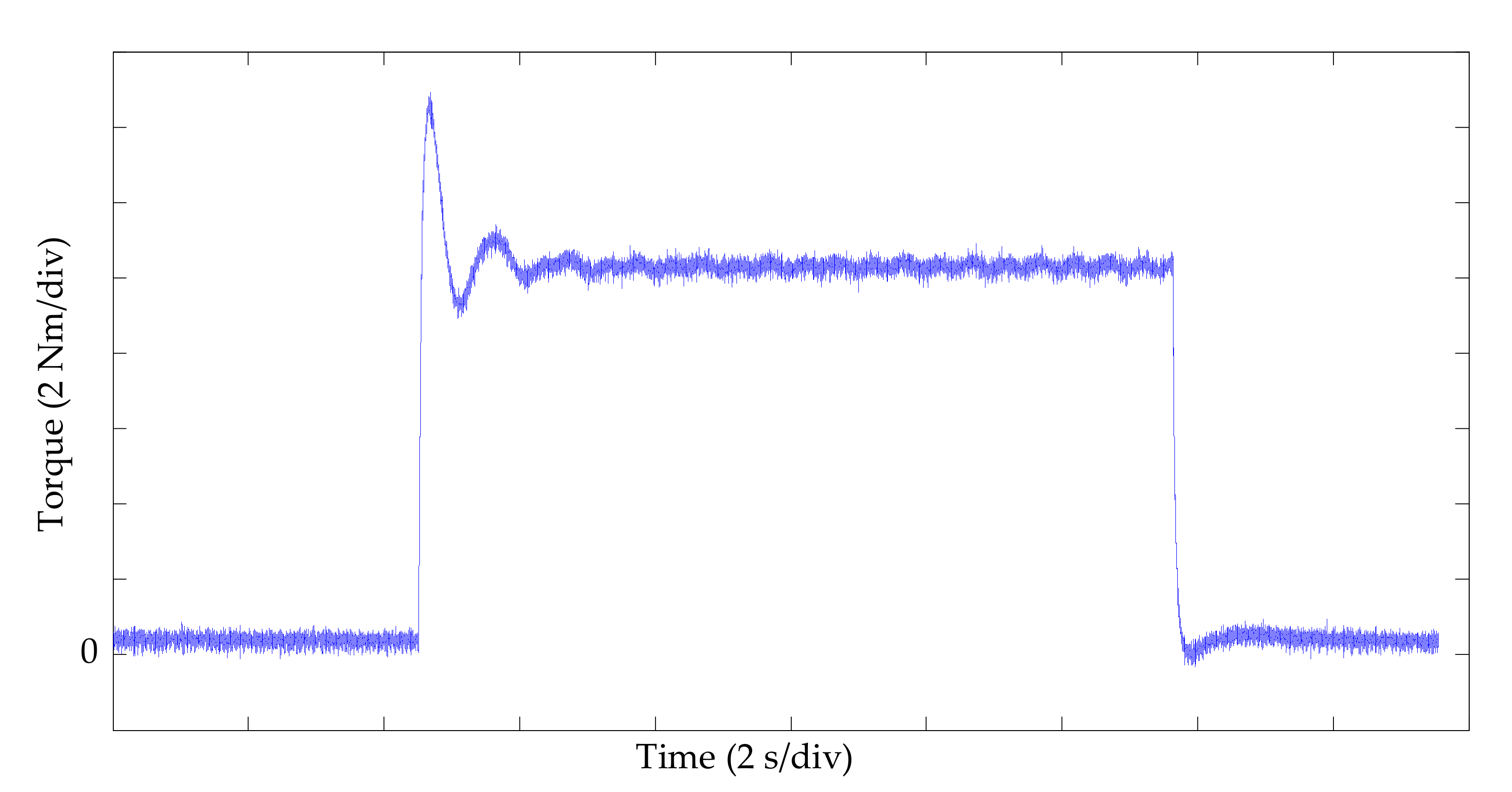
3.2. Transient and Steady Performance
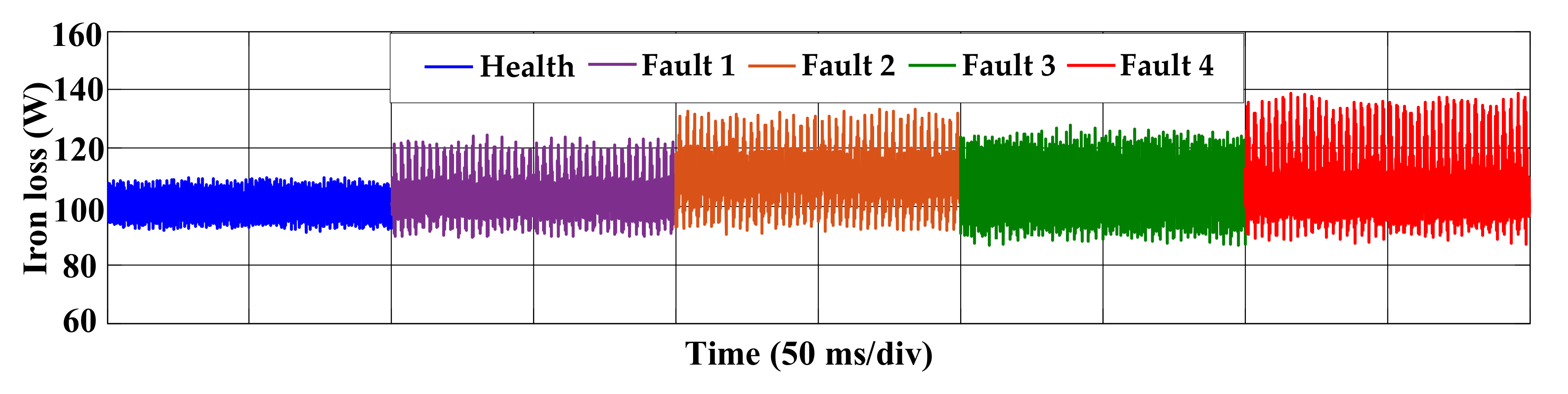
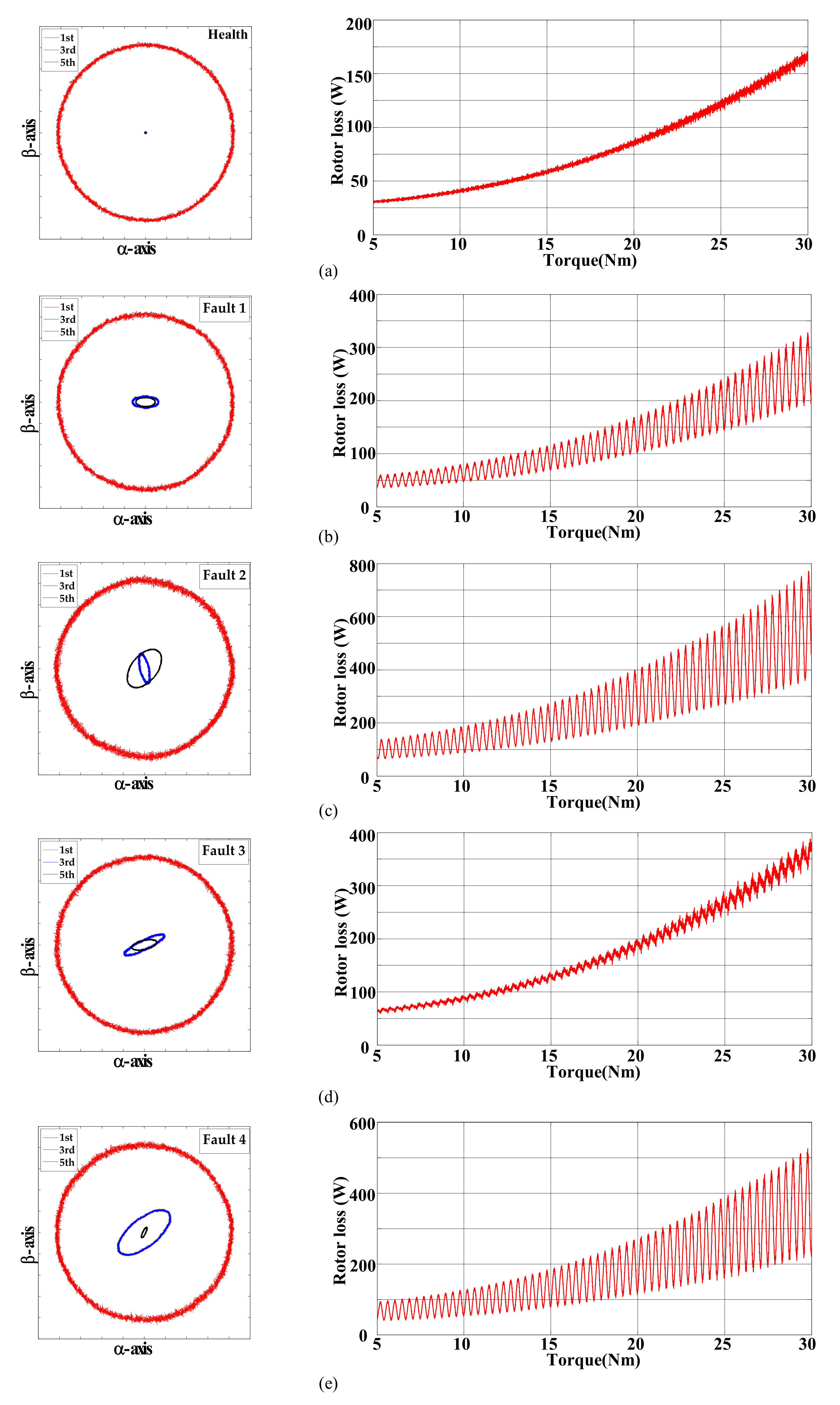
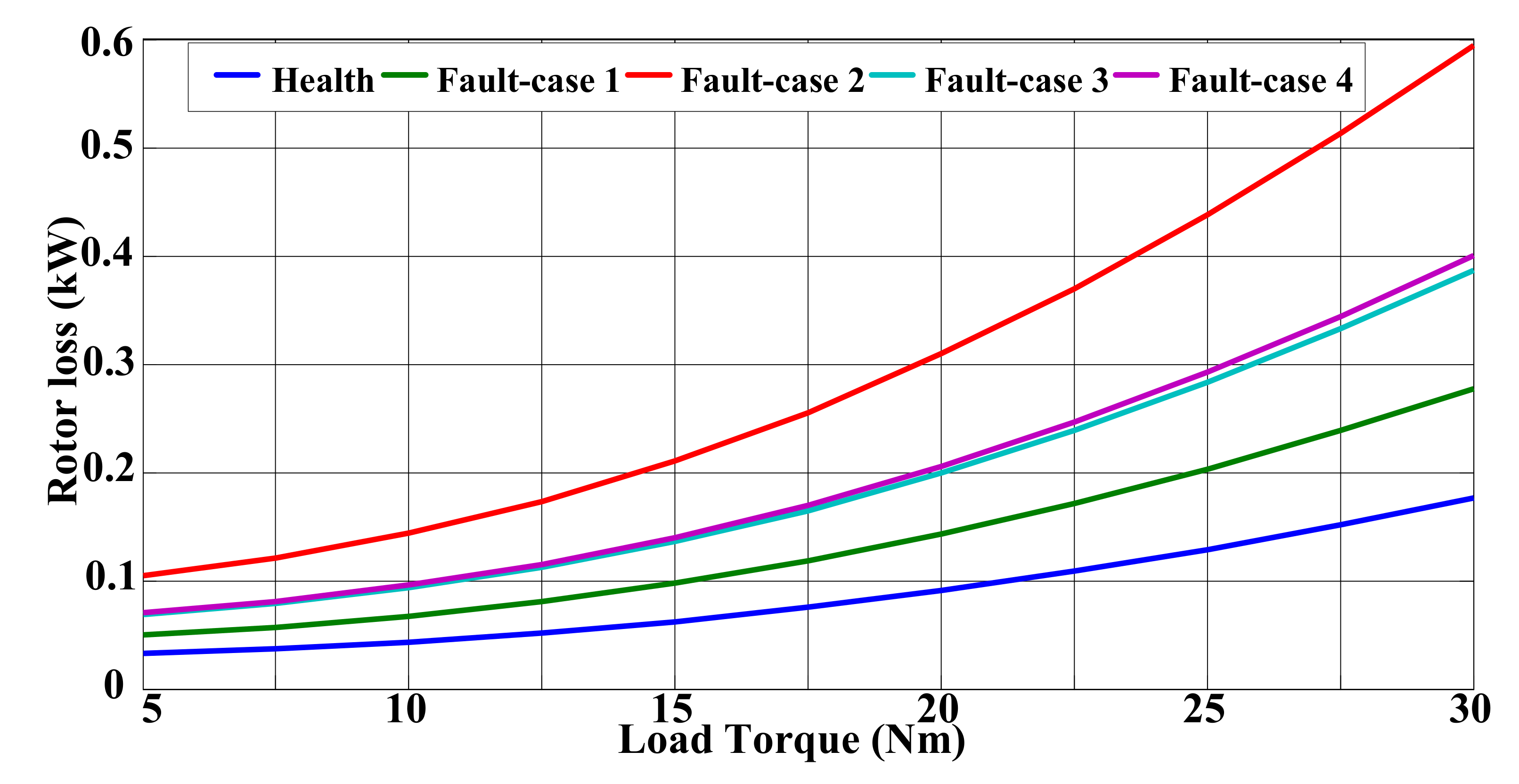
3.3. Loss Calculation and Analysis
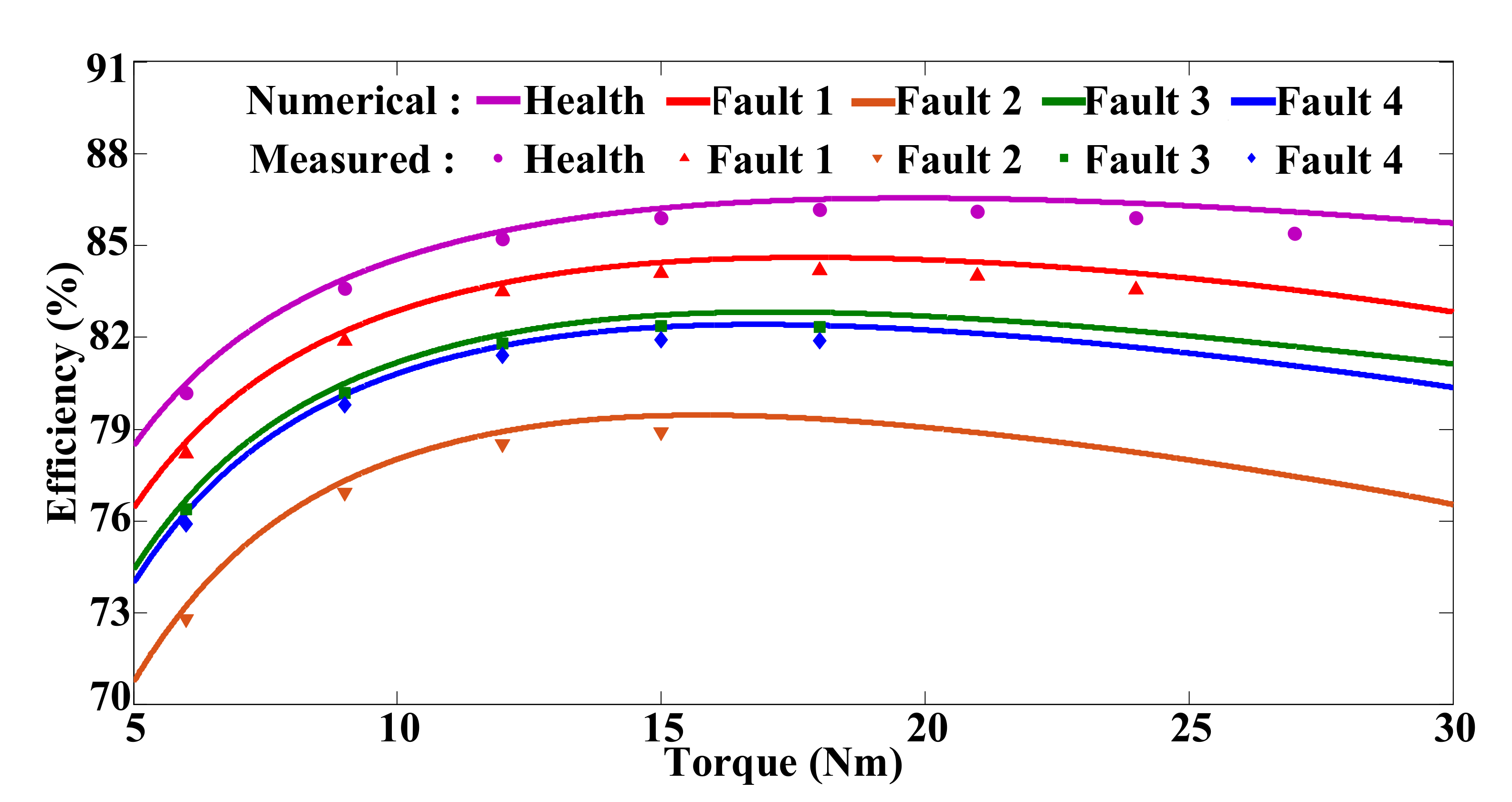
4. Experimental Validation and Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Levi, E.; Bojoi, R.; Profumo, F.; Toliyat, H.A.; Williamson, S. Multiphase induction motor drives—A technology status re-view. IET Elect. Power Appl. 2007, 1, 489–516. [Google Scholar] [CrossRef] [Green Version]
- Levi, E. Multiphase Electric Machines for Variable-Speed Applications. IEEE Trans. Ind. Electron. 2008, 55, 1893–1909. [Google Scholar] [CrossRef]
- Barrero, F.; Duran, M.J. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Duran, M.J.; Barrero, F. Recent Advances in the Design, Modeling, and Control of Multiphase Machines—Part II. IEEE Trans. Ind. Electron. 2016, 63, 459–468. [Google Scholar] [CrossRef]
- Zheng, L.; Fletcher, J.E.; Williams, B.W.; He, X. A Novel Direct Torque Control Scheme for a Sensorless Five-Phase Induction Motor Drive. IEEE Trans. Ind. Electron. 2010, 58, 503–513. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Yang, G.; Li, S.; Deng, R. Harmonic Currents Injection Strategy with Opti-mal Air-gap Flux Distribution for Multiphase Induction Machine. IEEE Trans. Power Electron. 2021, 36, 1054–1064. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J.; Li, S.; Yang, G.; Deng, R.; Hussain, H. Multiplane Rotor Resistance Online Estimation Strategy for Multiphase Induction Machine Under Nonsinusoidal Power Supply. IEEE Trans. Power Electron. 2021, 36, 9487–9500. [Google Scholar] [CrossRef]
- Fu, J.-R.; Lipo, T.A. Disturbance-free operation of a multiphase current-regulated motor drive with an opened phase. IEEE Trans. Ind. Appl. 1994, 30, 1267–1274. [Google Scholar] [CrossRef]
- Tani, A.; Mengoni, M.; Zarri, L.; Serra, G.; Casadei, D. Control of Multiphase Induction Motors with an Odd Number of Phases Under Open-Circuit Phase Faults. IEEE Trans. Power Electron. 2011, 27, 565–577. [Google Scholar] [CrossRef]
- Kianinezhad, R.; Nahid-Mobarakeh, B.; Baghli, L.; Betin, F.; Capolino, G.-A. Modeling and Control of Six-Phase Symmetrical Induction Machine Under Fault Condition Due to Open Phases. IEEE Trans. Ind. Electron. 2008, 55, 1966–1977. [Google Scholar] [CrossRef]
- Che, H.S.; Levi, E.; Jones, M.; Hew, W.-P.; Rahim, N.A. Current Control Methods for an Asymmetrical Six-Phase Induction Motor Drive. IEEE Trans. Power Electron. 2013, 29, 407–417. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Zheng, Z.; Xu, L.; Wang, K.; Li, Y. Current Balance Control for Symmetrical Multiphase In-verters. IEEE Trans. Ind. Electron. 2016, 31, 4005–4012. [Google Scholar]
- Kong, W.; Kang, M.; Li, D.; Qu, R.; Jiang, D.; Gan, C. Investigation of Spatial Harmonic Magnetic Field Coupling Effect on Torque Ripple for Multiphase Induction Motor Under Open Fault Condition. IEEE Trans. Power Electron. 2017, 33, 6060–6071. [Google Scholar] [CrossRef]
- Bermudez, M.; Gonzalez-Prieto, I.; Barrero, F.; Guzman, H.; Duran, M.J.; Kestelyn, X. An Experimental Assessment of Open-Phase Fault-Tolerant Virtual-Vector-Based Direct Torque Control in Five-Phase Induction Motor Drives. IEEE Trans. Power Electron. 2018, 33, 2774–2784. [Google Scholar] [CrossRef] [Green Version]
- Guzman, H.; Barrero, F.; Duran, M.J. IGBT-Gating Failure Effect on a Fault-Tolerant Predictive Cur-rent-Controlled Five-Phase Induction Motor Drive. IEEE Trans. Ind. Electron. 2015, 62, 15–20. [Google Scholar] [CrossRef] [Green Version]
- Duran, M.J.; Gonzalez-Prieto, I.; Rios-Garcia, N.; Barrero, F. A Simple, Fast, and Robust Open-Phase Fault Detection Technique for Six-Phase Induction Motor Drives. IEEE Trans. Power Electron. 2017, 33, 547–557. [Google Scholar] [CrossRef]
- Gonz´alez-Prieto, I.; Duran, M.J.; Rios-Garcia, N.; Barrero, F.; Mart´ın, C. Open-Switch Fault Detection in Five-Phase Induction Motor Drives Using Model Predictive Control. IEEE Trans. Ind. Electron. 2018, 65, 3045–3055. [Google Scholar] [CrossRef]
- Huangfu, Y.; Wang, S.; Qiu, J.; Zhang, H.; Wang, G.; Zhu, J. Transient Performance Analysis of Induction Motor Using Field-Circuit Coupled Finite-Element Method. IEEE Trans. Magn. 2014, 50, 873–876. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Gan, C.; Sun, Q.; Kong, W. Efficiency Optimization of PMSM Drives Using Field-Circuit Coupled FEM for EV/HEV Applications. IEEE Access 2018, 6, 15192–15201. [Google Scholar] [CrossRef]
- Wang, X.; Xie, D. Analysis of Induction Motor Using Field-Circuit Coupled Time-Periodic Finite Element Method Taking Account of Hysteresis. IEEE Trans. Magn. 2009, 45, 1740–1743. [Google Scholar] [CrossRef]
- Cheaytani, J.; Benabou, A.; Tounzi, A.; Dessoude, M. Stray Load Losses Analysis of Cage Induction Motor Using 3-D Fi-nite-Element Method with External Circuit Coupling. IEEE Trans. Magn. 2017, 53, 8202104. [Google Scholar] [CrossRef]
- Lee, J.-H.; Kim, Y.-K.; Nam, H.; Ha, K.-H.; Hong, J.-P.; Hwang, D.-H. Loss Distribution of Three-Phase Induction Motor Fed by Pulse width Modulated Inverter. IEEE Trans. Magn. 2004, 40, 762–765. [Google Scholar] [CrossRef]
- Dlala, E. Comparison of Models for Estimating Magnetic Core Losses in Electrical Machines Using the Finite-Element Method. IEEE Trans. Magn. 2009, 45, 716–725. [Google Scholar] [CrossRef]
- Dlala, E.; Bottauscio, O.; Chiampi, M.; Zucca, M.; Belahcen, A.; Arkkio, A. Numerical Investigation of the Effects of Loading and Slot Harmonics on the Core Losses of Induction Machines. IEEE Trans. Magn. 2012, 48, 1063–1066. [Google Scholar] [CrossRef]
- Fratila, M.; Benabou, A.; Tounzi, A.; Dessoude, M. Calculation of Iron Losses in Solid Rotor Induction Machine Using FEM. IEEE Trans. Magn. 2014, 50, 825–828. [Google Scholar] [CrossRef]
- Xue, S.; Feng, J.; Guo, S.; Chen, Z.; Peng, J.; Chu, W.Q.; Xu, P.L.; Zhu, Z.Q. Iron Loss Model for Electrical Machine Fed by Low Switching Frequency Inverter. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]





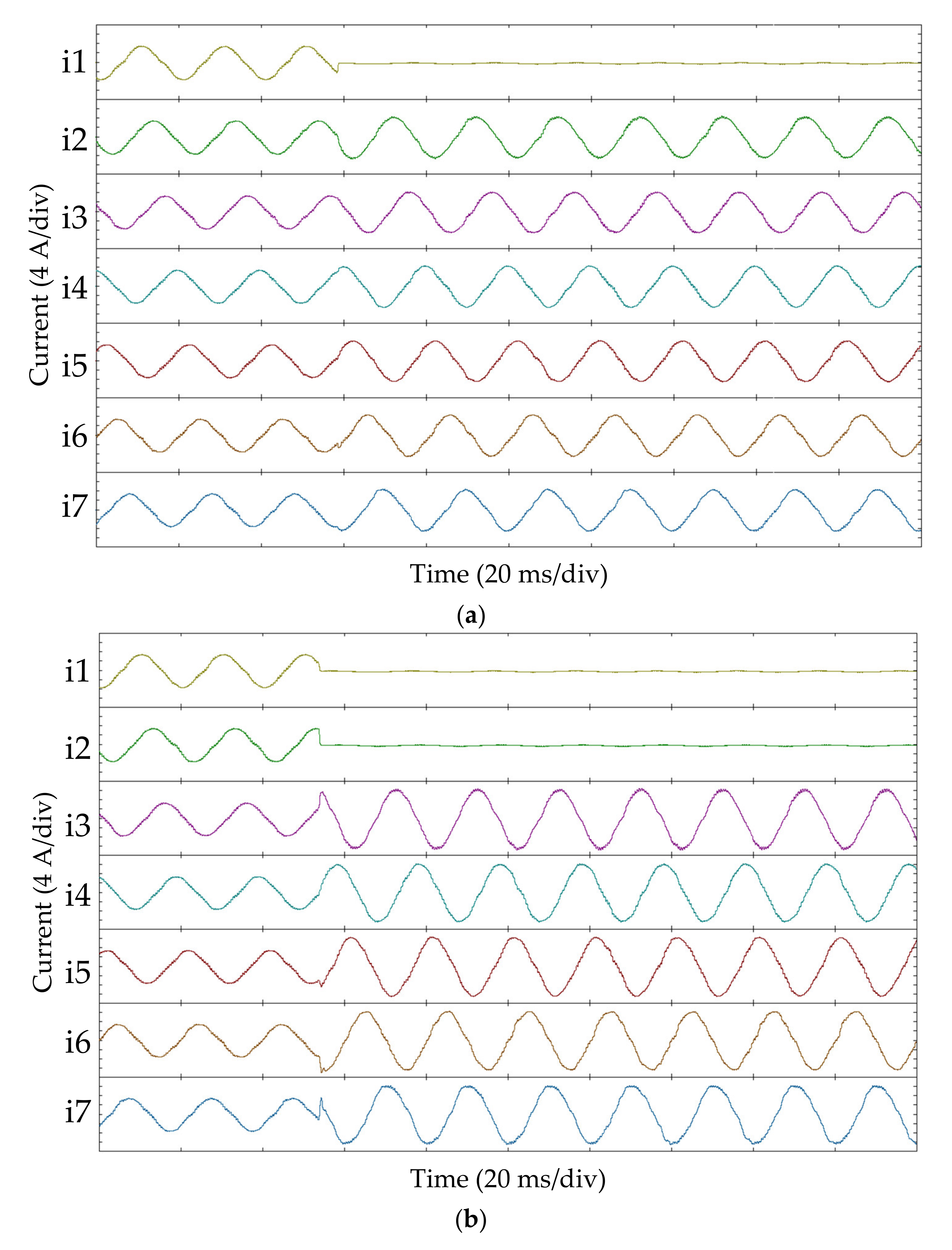
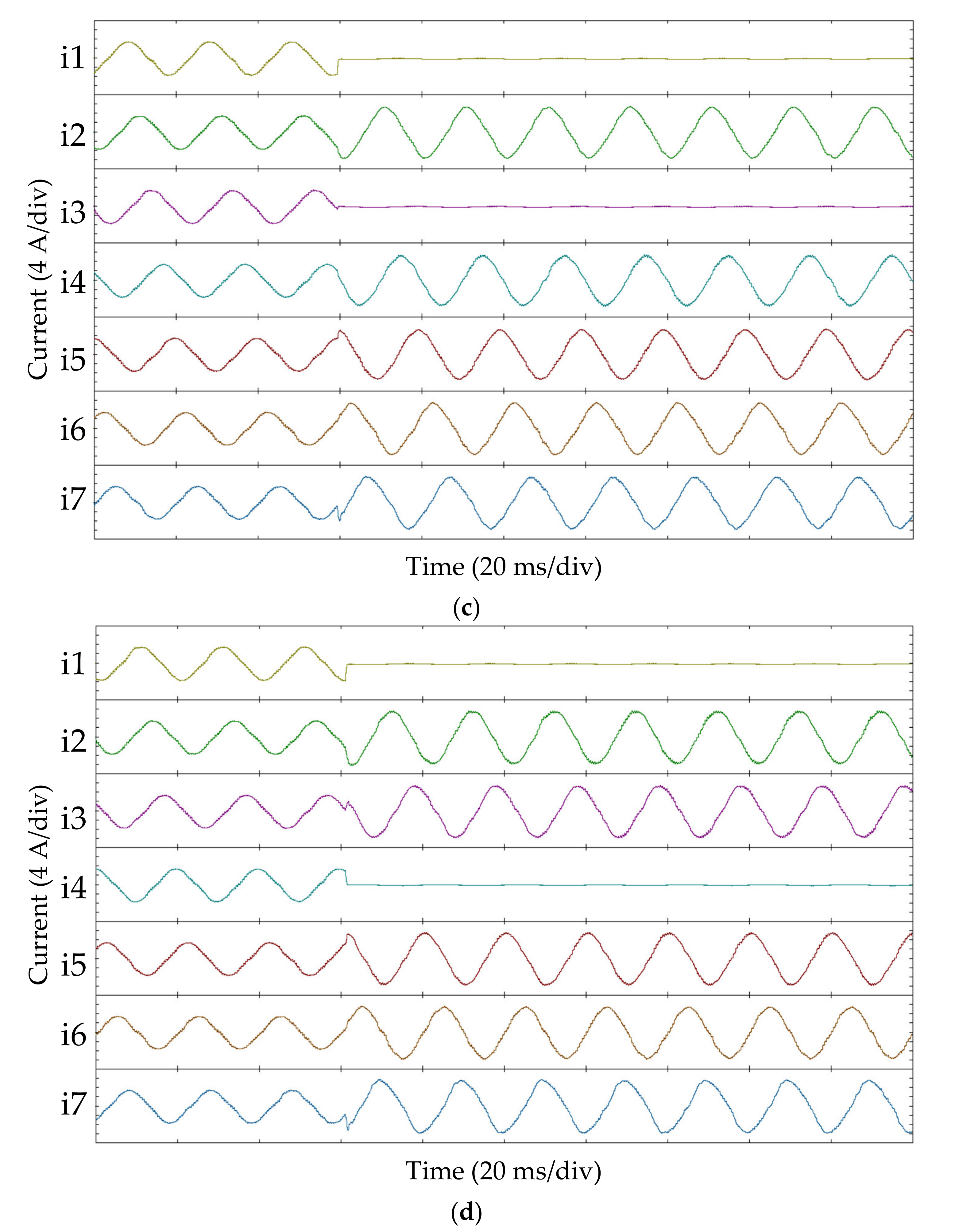
| Fault 1 | Fault 2 | Fault 3 | Fault 4 | |
|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 |
| i2 | 0 | |||
| i3 | 0 | |||
| i4 | 0 | |||
| i5 | ||||
| i6 | ||||
| i7 |
| Fault 1 | Fault 2 | Fault 3 | Fault 4 | |
|---|---|---|---|---|
| −1.108N3 | −0.387N3 | −0.233N3 | −2.446N3 | |
| 0 | 0.486N3 | −1.106N3 | −1.178N3 | |
| −0.449N3 | 0.255N3 | −1.443N3 | −0.650N3 | |
| 0 | 1.116N3 | −0.695N3 | −0.815N3 | |
| −0.523N3 | −0.204N3 | −0.743N3 | −0.250N3 | |
| 0 | 0.893N3 | −0.358N3 | −0.313N3 | |
| −1.419N3 | 3.164N3 | −1.081N3 | −0.154N3 | |
| 0 | 1.524N3 | −1.356N3 | −0.677N3 |
| Phase number | 7 | Pole number | 4 |
| Rated voltage (RMS) | 110 V | Rated current (RMS) | 8.5 A |
| Rated flux | 0.468 Wb | Rated magnetizing current | 3.6 A |
| Rated speed | 1460 pm | Number of turns | 76 |
| Number of stator slots | 28 | Number of rotor slots | 38 |
| Iron Loss (W/pu) | Stator Joule Loss (W/pu) | Rotor Joule Loss (W/pu) | Total Loss (W/pu) | |
|---|---|---|---|---|
| Fault 1 | 78.4/1.04 | 124.2/1.31 | 143.3/1.57 | 345.9/1.32 |
| Fault 2 | 82.2/1.09 | 212.5/2.24 | 309.8/3.40 | 604.5/2.31 |
| Fault 3 | 79.8/1.06 | 153.2/1.61 | 200.0/2.20 | 433.0/1.66 |
| Fault 4 | 81.6/1.08 | 166.6/1.75 | 205.8/2.26 | 454.0/1.74 |
| Rated Speed | Fault 1 (FEM/Test) | Fault 2 (FEM/Test) | Fault 3 (FEM/Test) | Fault 4 (FEM/Test) |
|---|---|---|---|---|
| 20% | (92%/91%) | (67%/66%) | (81%/80%) | (79%/78%) |
| 60% | (89%/88%) | (65%/64%) | (79%/78%) | (77%/76%) |
| 100% | (86%/85%) | (62%/61%) | (76%/75%) | (74%/73%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Yang, J.; Deng, R.; Wang, Y. Loss Investigation for Multiphase Induction Machine under Open-Circuit Fault Using Field–Circuit Coupling Finite Element Method. Energies 2021, 14, 5686. https://doi.org/10.3390/en14185686
Jia H, Yang J, Deng R, Wang Y. Loss Investigation for Multiphase Induction Machine under Open-Circuit Fault Using Field–Circuit Coupling Finite Element Method. Energies. 2021; 14(18):5686. https://doi.org/10.3390/en14185686
Chicago/Turabian StyleJia, Huili, Jiaqiang Yang, Rongfeng Deng, and Yan Wang. 2021. "Loss Investigation for Multiphase Induction Machine under Open-Circuit Fault Using Field–Circuit Coupling Finite Element Method" Energies 14, no. 18: 5686. https://doi.org/10.3390/en14185686
APA StyleJia, H., Yang, J., Deng, R., & Wang, Y. (2021). Loss Investigation for Multiphase Induction Machine under Open-Circuit Fault Using Field–Circuit Coupling Finite Element Method. Energies, 14(18), 5686. https://doi.org/10.3390/en14185686






