Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow
Abstract
1. Introduction
2. Numerical Methodology
2.1. Lattice Boltzmann Method
2.1.1. Octree Lattice Structure
2.1.2. Collision Operator
2.2. Turbulence Modeling
2.3. Near-Wall Treatment
Dynamic Geometries
3. Simulations
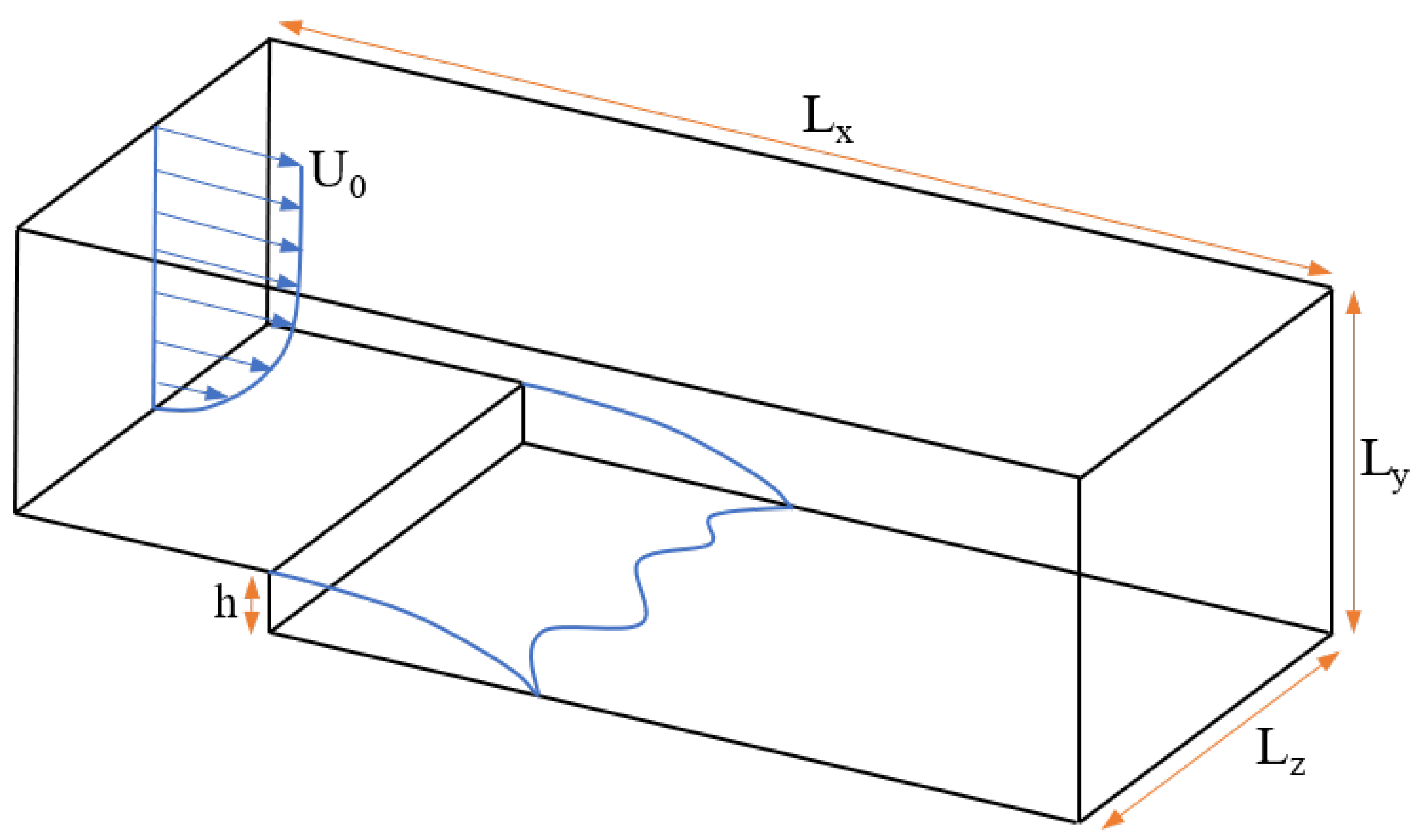
3.1. Backward-Facing Step
3.1.1. Introduction
3.1.2. Setup and Mesh Convergence
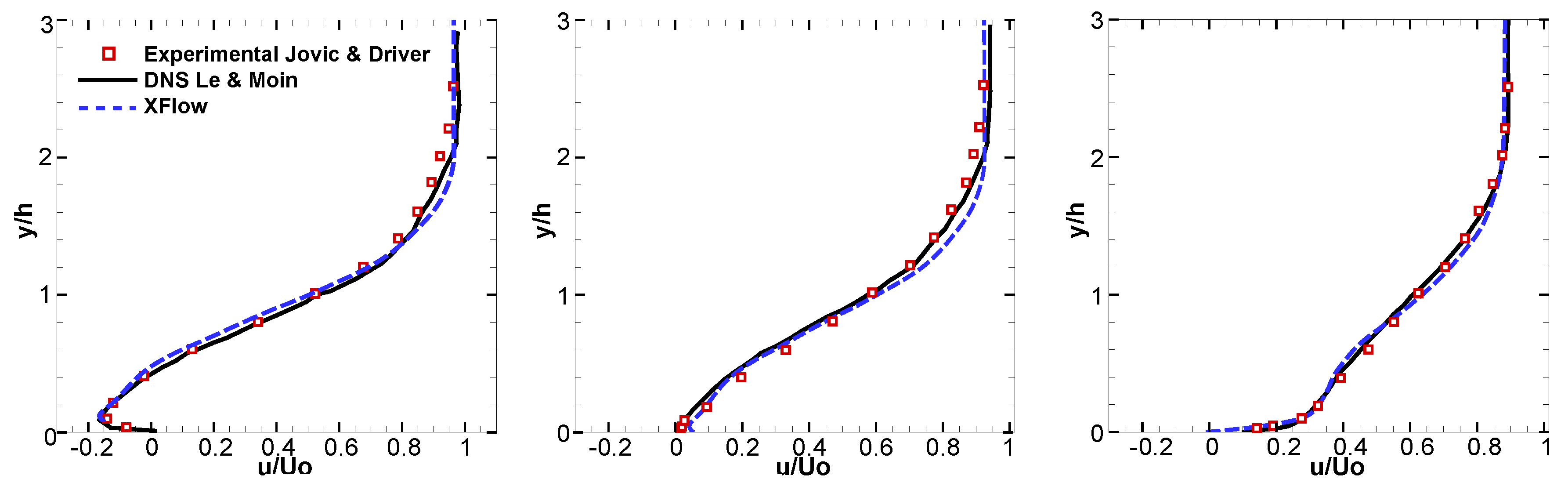
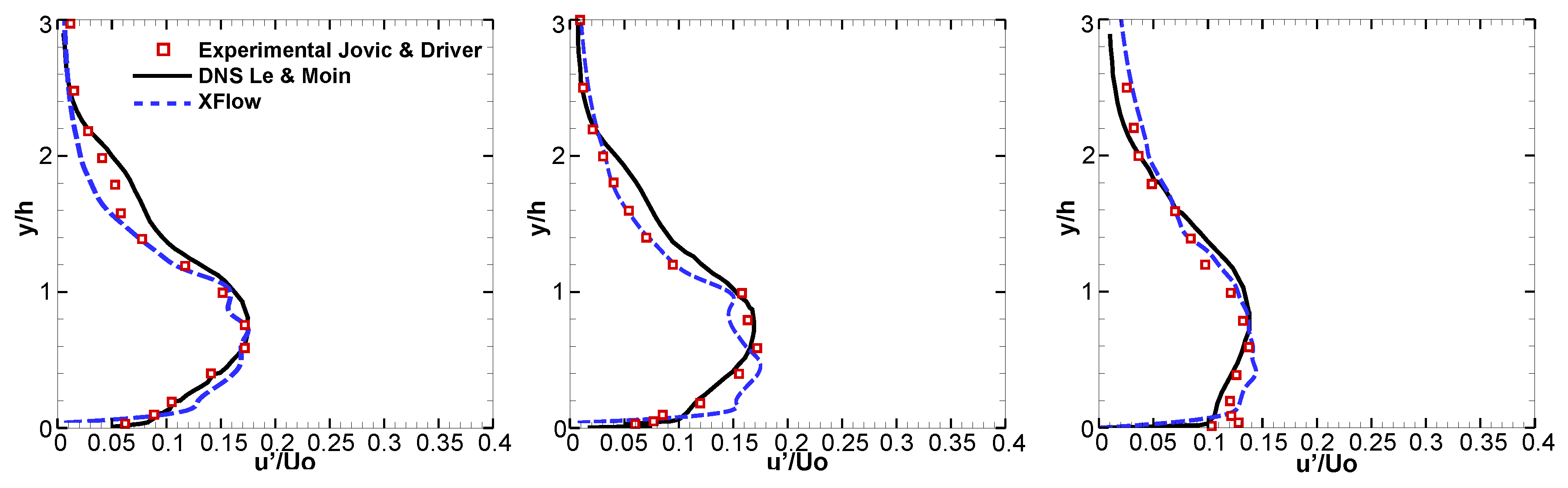
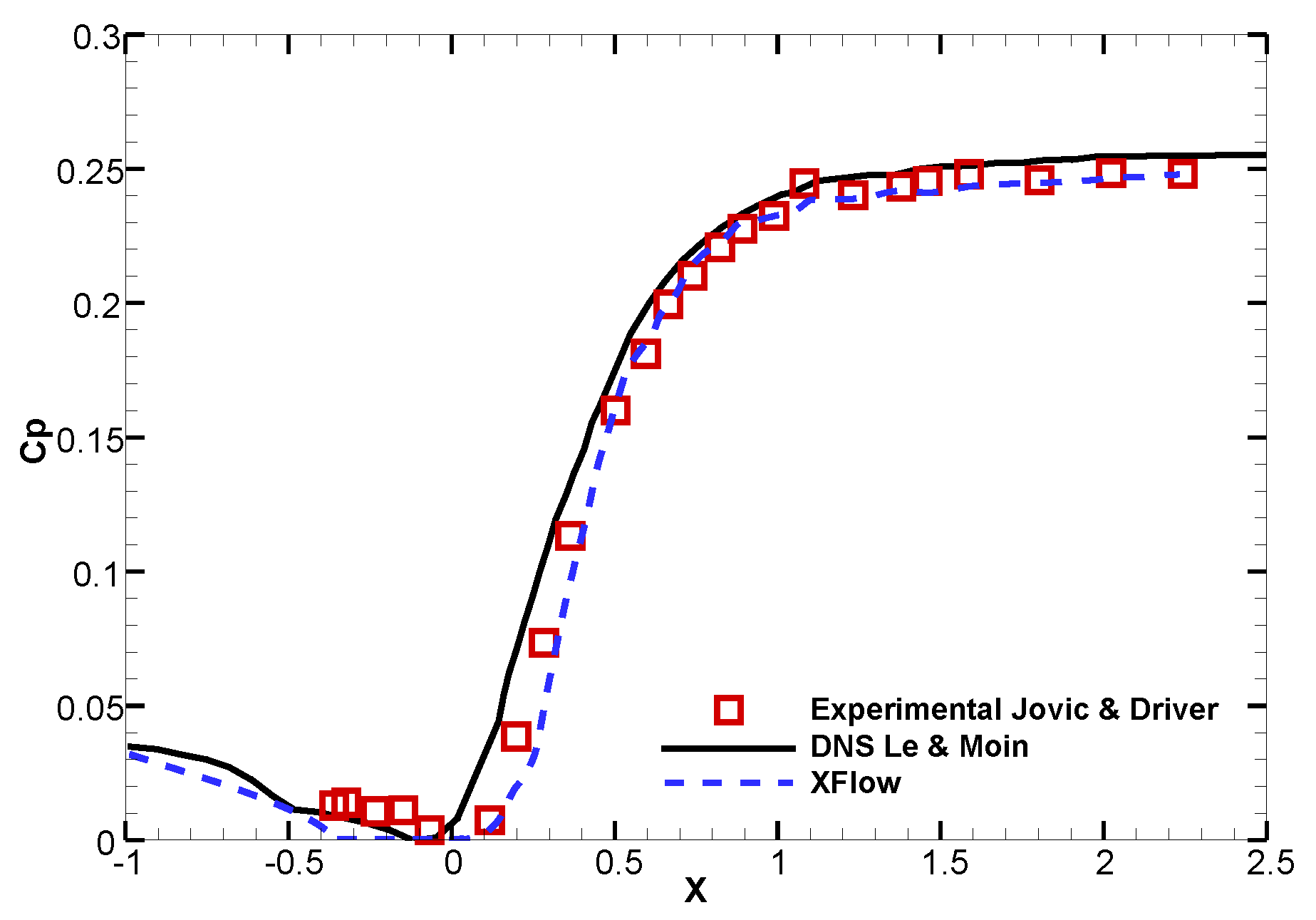
3.1.3. Results
3.2. Goldschmied Body
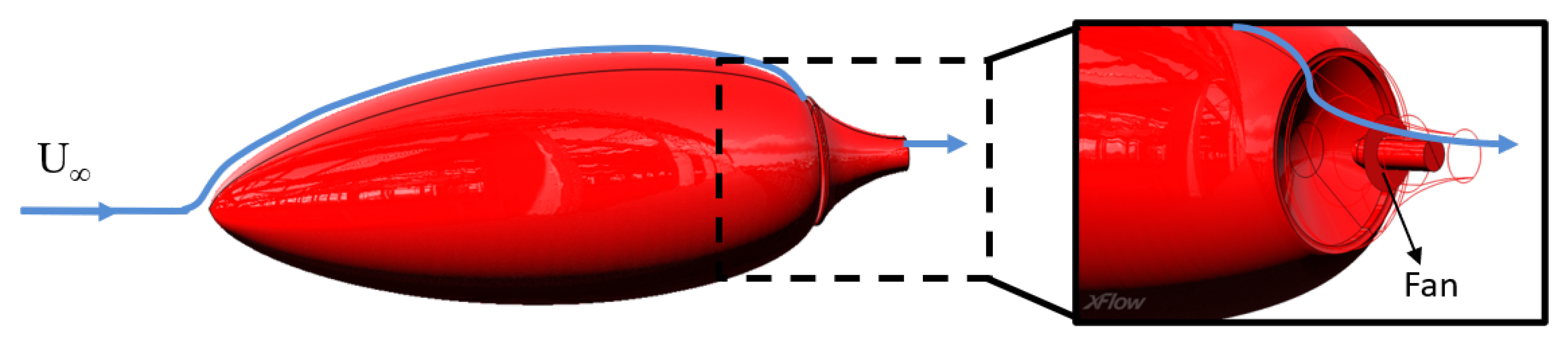
3.2.1. Introduction
3.2.2. Setup and Mesh Convergence
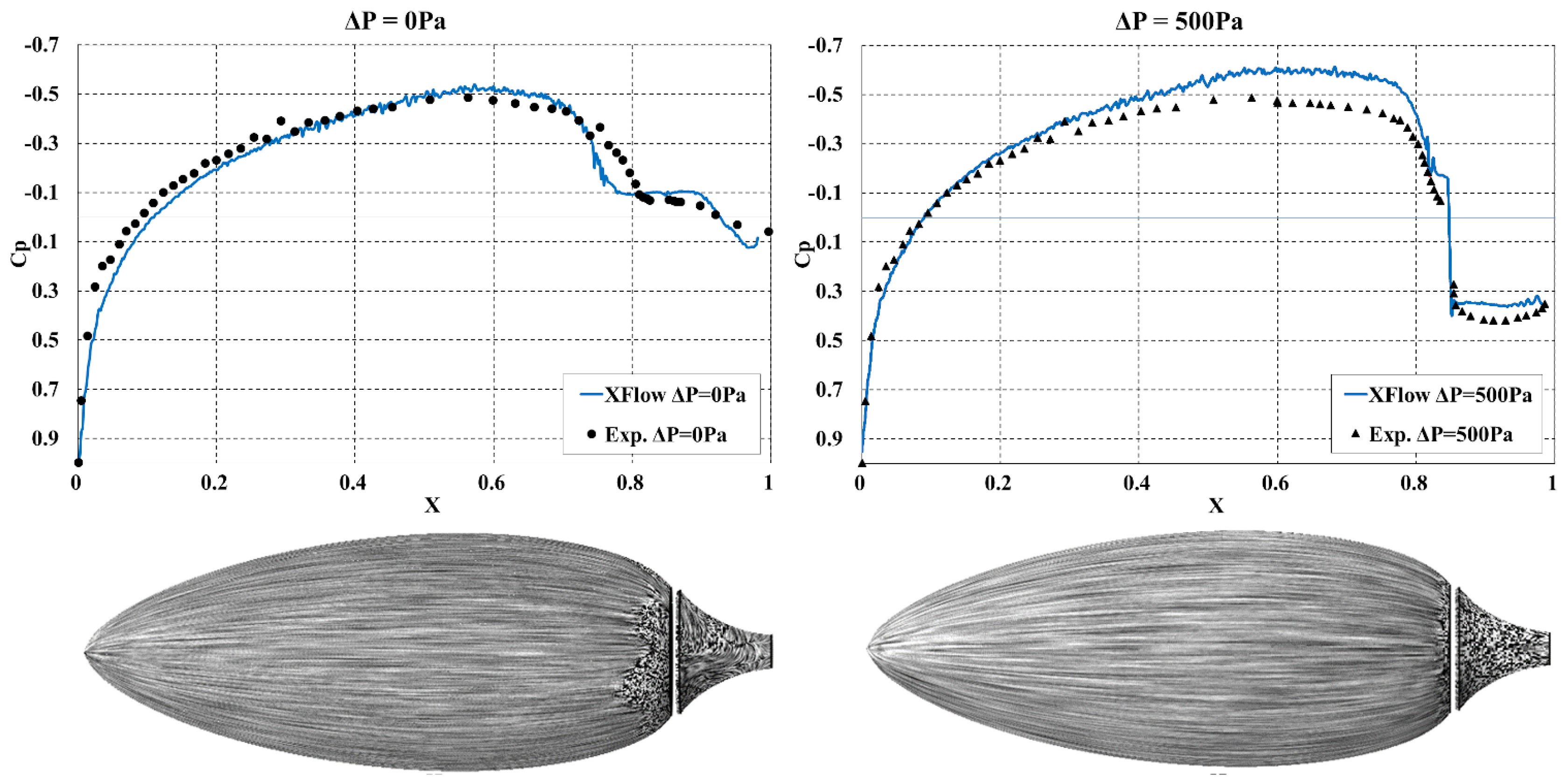
3.2.3. Results
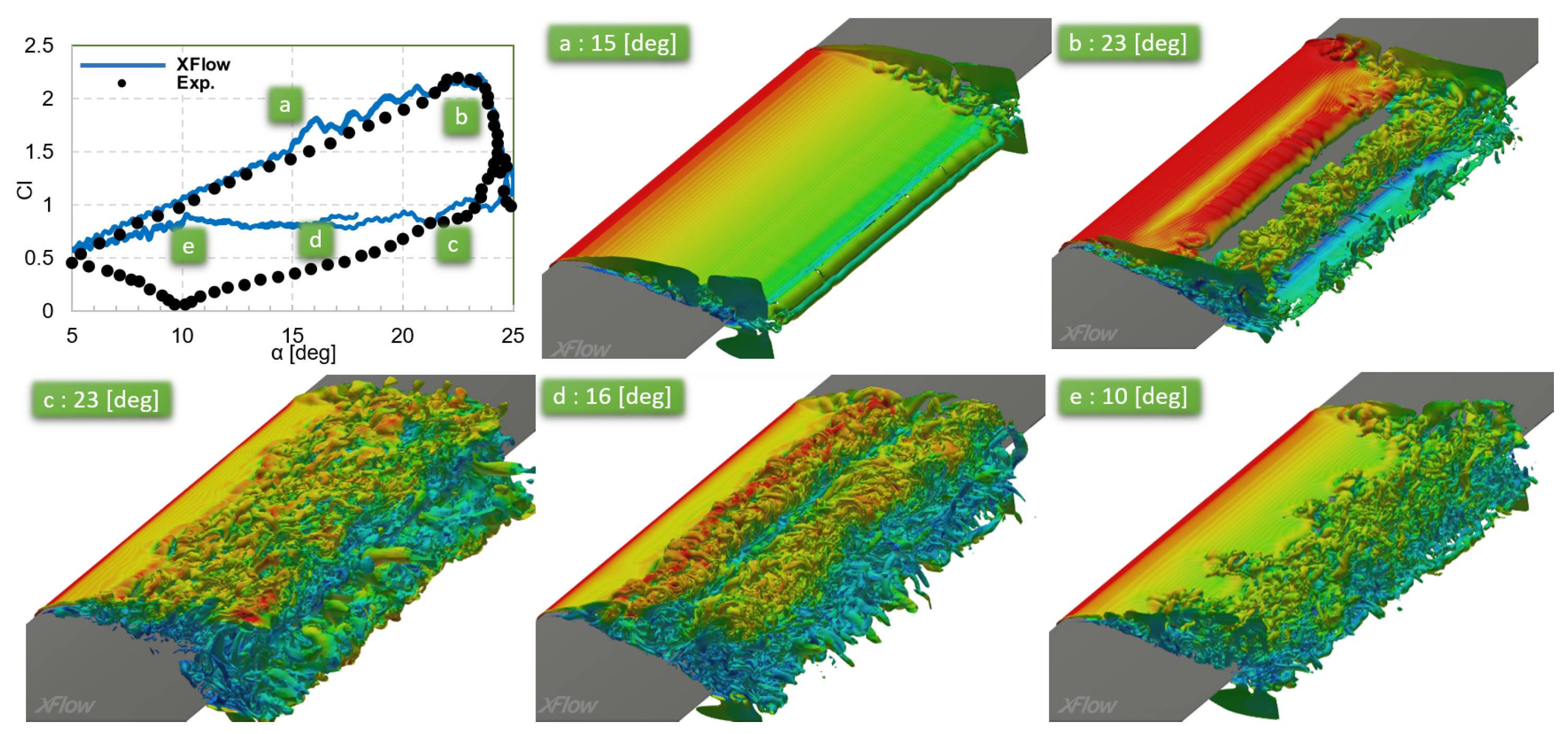
3.3. 2nd High-Lift Prediction Workshop
3.3.1. Introduction
3.3.2. Setup and Mesh Convergence
3.3.3. Results
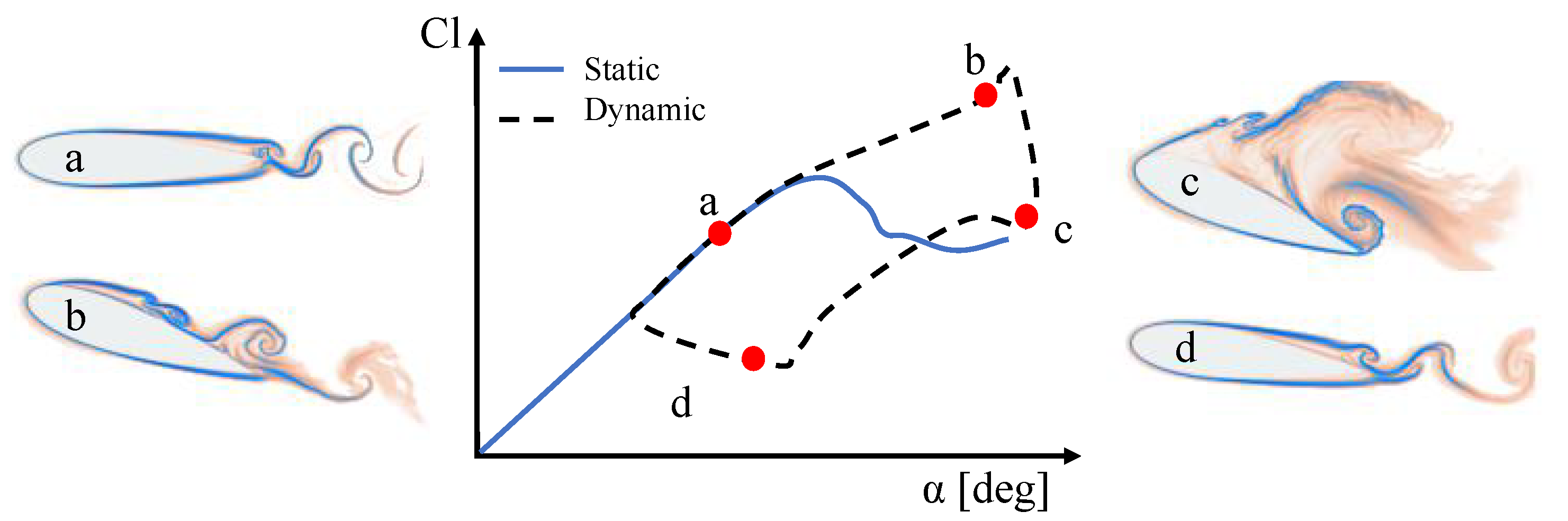
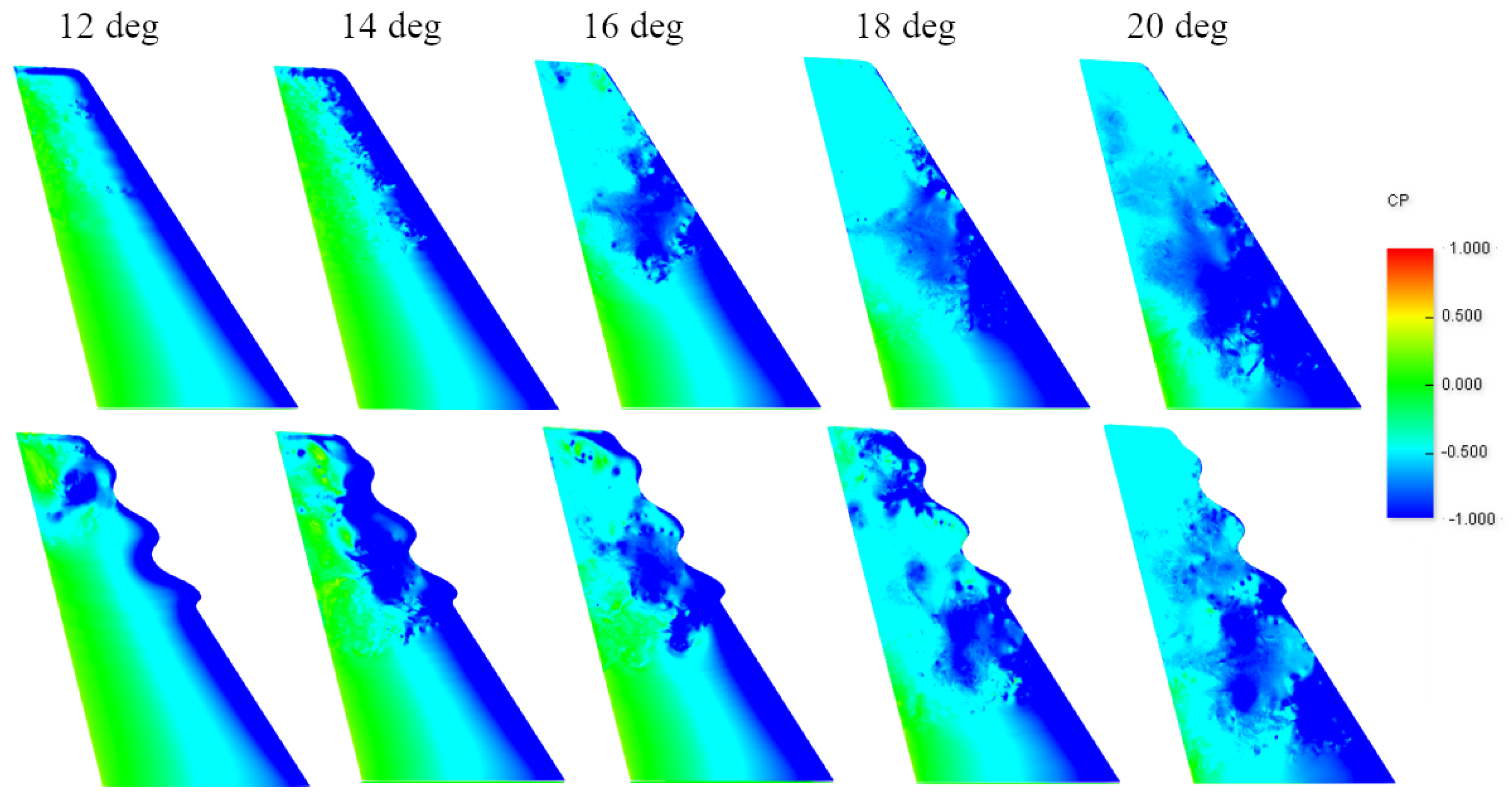
3.4. Dynamic Stall: NACA0012
3.4.1. Introduction
3.4.2. Setup and Mesh Convergence
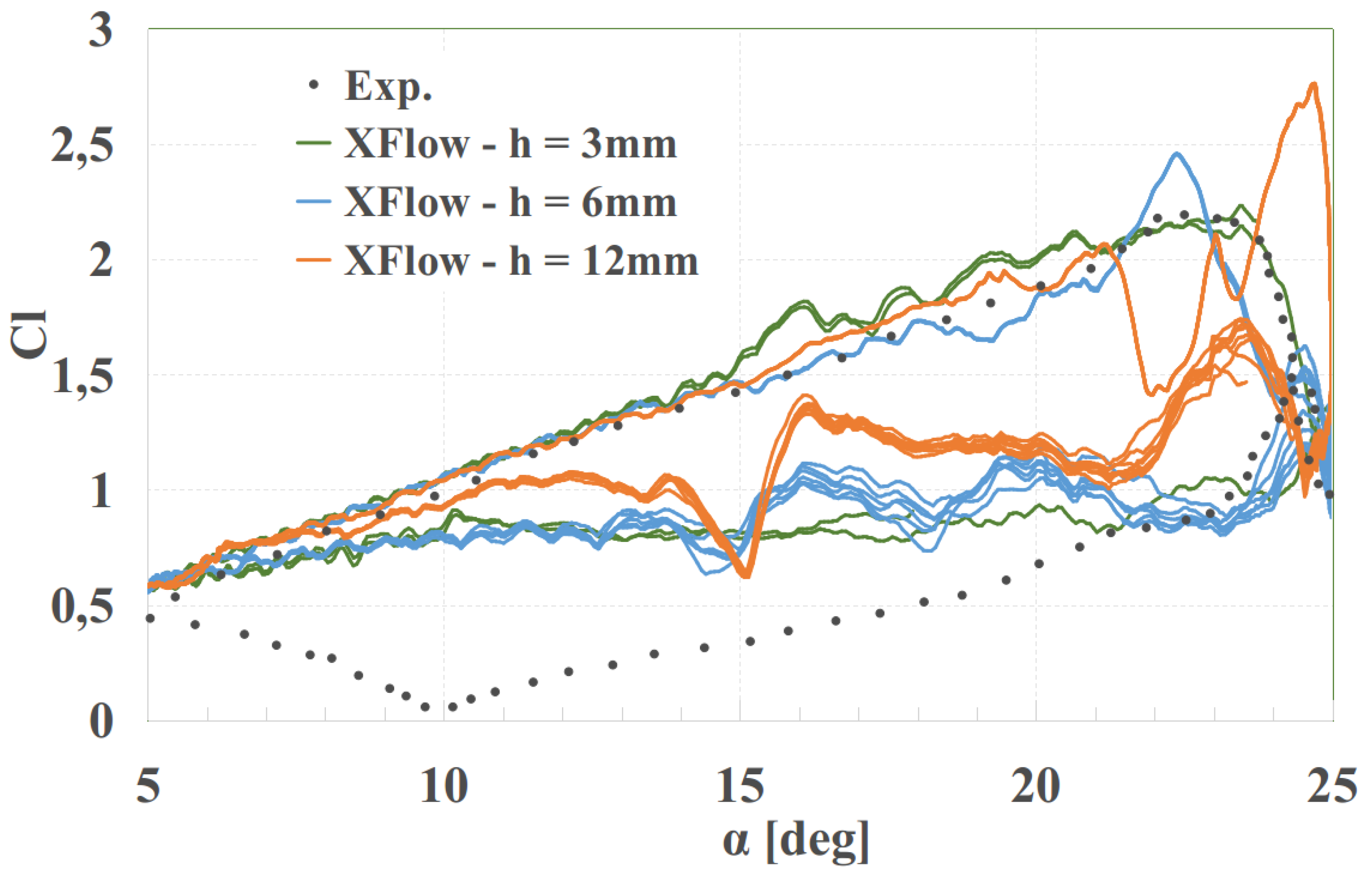
3.4.3. Results
3.5. Wing with Leading-Edge Tubercles
3.5.1. Introduction
- Wavelength, : defines the non-dimensional wavelength (or equivalently the spatial frequency) of the tubercles, with c being the local chord.
- Amplitude, : defines the amplitude of the tubercles. It is also made non-dimensional using the local chord c.
- Span section, : defines the wing span section where the tubercles start. Please note that b is the total wing span.
3.5.2. Setup and Mesh Convergence
3.5.3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vincent, P.E.; Jameson, A. Facilitating the adoption of unstructured high-order methods amongst a wider community of fluid dynamicists. Math. Model. Nat. Phenom. 2011, 6, 97–140. [Google Scholar] [CrossRef]
- Allahyari, M.; Esfahanian, V.; Yousefi, K. The Effects of Grid Accuracy on Flow Simulations: A Numerical Assessment. Fluids 2020, 5, 110. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. In Numerical Prediction of Flow, Heat Transfer, Turbulence and Combustion; Elsevier: Amsterdam, The Netherlands, 1983; pp. 54–73. [Google Scholar]
- Jacqmin, D. Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 1999, 155, 96–127. [Google Scholar] [CrossRef]
- Allahyari, M.; Mohseni, K. Numerical simulation of flows with shocks and turbulence using observable methodology. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 0066. [Google Scholar]
- Holman, D.M.; Brionnaud, R.M.; Chávez-Modena, M.; Sánchez, E.V. Lattice Boltzmann method contribution to the second high-lift prediction workshop. J. Aircr. 2015, 52, 1122–1135. [Google Scholar] [CrossRef]
- Brionnaud, R.; Chávez Modena, M.; Trapani, G.; Holman, M.D. Direct noise computation with a Lattice-Boltzmann method and application to industrial test cases. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; p. 2969. [Google Scholar]
- Sanders, L.; Manoha, E.; Murayama, M.; Yokokawa, Y.; Yamamoto, K.; Hirai, T. Lattice-Boltzmann flow simulation of a two-wheel landing gear. In Proceedings of the 22nd AIAA/CEAS Aeroacoustics Conference, Lyon, France, 30 May–1 June 2016; p. 2767. [Google Scholar]
- Trapani, G.; Brionnaud, R.; Holman, D. XFlow contribution to the third high-lift prediction workshop. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018; p. 2847. [Google Scholar]
- Thibault, S.; Holman, D.; Garcia, S.; Trapani, G. CFD Simulation of a quad-rotor UAV with rotors in motion explicitly modeled using an LBM approach with adaptive refinement. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0583. [Google Scholar]
- Grondeau, M.; Guillou, S.; Mercier, P.; Poizot, E. Wake of a Ducted Vertical Axis Tidal Turbine in Turbulent Flows, LBM Actuator-Line Approach. Energies 2019, 12, 4273. [Google Scholar] [CrossRef]
- Trapani, G.; Brionnaud, R.M.; Holman, D.M. Non-linear fluid-structure interaction using a partitioned lattice Boltzmann-FEA approach. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3636. [Google Scholar]
- Armaly, B.F.; Durst, F.; Pereira, J.; Schönung, B. Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 1983, 127, 473–496. [Google Scholar] [CrossRef]
- Goldschmied, F.R. On the aerodynamic optimization of mini-RPV and small GA aircraft. In Proceedings of the 2nd American Institute of Aeronautics and Astronautics, Applied Aerodynamics Conference, Seattle, WA, USA, 21–23 August 1984; Volume 21. [Google Scholar]
- Rudnik, R.; Huber, K.; Melber-Wilkending, S. EUROLIFT test case description for the 2nd high lift prediction workshop. In Proceedings of the 30th AIAA Applied Aerodynamics Conference, New Orleans, LA, USA, 25–28 June 2012; p. 2924. [Google Scholar]
- McCroskey, W.J.; McAlister, K.W.; Carr, L.W.; Pucci, S. An Experimental Study of Dynamic Stall on Advanced Airfoil Sections; Technical Report; Volume 1: Summary of the Experiment; NASA: Washington, DC, USA, 1982. [Google Scholar]
- Miklosovic, D.; Murray, M.; Howle, L.; Fish, F. Leading-edge tubercles delay stall on humpback whale (Megaptera novaeangliae) flippers. Phys. Fluids 2004, 16, L39–L42. [Google Scholar] [CrossRef]
- Boltzmann, L. Weitere studien über das wärmegleichgewicht unter gasmolekülen. In Kinetische Theorie II; Springer: Berlin/Heidelberg, Germany, 1970; pp. 115–225. [Google Scholar]
- Premnath, K.N.; Banerjee, S. Incorporating forcing terms in cascaded Lattice Boltzmann approach by method of central moments. Phys. Rev. E 2009, 80, 036702. [Google Scholar] [CrossRef]
- Chávez-Modena, M.; Ferrer, E.; Rubio, G. Improving the stability of multiple-relaxation lattice Boltzmann methods with central moments. Comput. Fluids 2018, 172, 397–409. [Google Scholar] [CrossRef]
- Coreixas, C.; Chopard, B.; Latt, J. Comprehensive comparison of collision models in the lattice Boltzmann framework: Theoretical investigations. Phys. Rev. E 2019, 100, 033305. [Google Scholar] [CrossRef]
- Geier, M.; Greiner, A.; Korvink, J.G. Bubble functions for the lattice Boltzmann method and their application to grid refinement. Eur. Phys. J. Spec. Top. 2009, 171, 173–179. [Google Scholar] [CrossRef]
- Imamura, T.; Suzuki, K.; Nakamura, T.; Yoshida, M. Acceleration of steady-state lattice Boltzmann simulations on non-uniform mesh using local time step method. J. Comput. Phys. 2005, 202, 645–663. [Google Scholar] [CrossRef]
- Arnone, A.; Liou, M.S.; Povinelli, L.A. Integration of Navier-Stokes equations using dual time stepping and a multigrid method. AIAA J. 1995, 33, 985–990. [Google Scholar] [CrossRef]
- Bhaskaran, R.; Lele, S.K. Large eddy simulation of free-stream turbulence effects on heat transfer to a high-pressure turbine cascade. J. Turbul. 2010, 11, N6. [Google Scholar] [CrossRef]
- Gardner, M. Taxicab geometry. In The Last Recreations; Springer: Berlin/Heidelberg, Germany, 1997; pp. 159–175. [Google Scholar]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- Guo, Z.; Zheng, C.; Zhao, T. A lattice BGK scheme with general propagation. J. Sci. Comput. 2001, 16, 569–585. [Google Scholar] [CrossRef]
- D’Humieres, D. Generalized lattice-Boltzmann equations. Prog. Astronaut. Aeronaut. 1994, 159, 450. [Google Scholar]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546. [Google Scholar] [CrossRef]
- Geier, M.; Greiner, A.; Korvink, J.G. Cascaded digital lattice Boltzmann automata for high Reynolds number flow. Phys. Rev. E 2006, 73, 066705. [Google Scholar] [CrossRef]
- Geier, M.; Greiner, A.; Korvink, J. A factorized central moment lattice Boltzmann method. Eur. Phys. J. Spec. Top. 2009, 171, 55–61. [Google Scholar] [CrossRef]
- Premnath, K.; Banerjee, S. On the Three-Dimensional Central Moment Lattice Boltzmann Method. J. Stat. Phys. 2011, 143, 747–794. [Google Scholar] [CrossRef]
- Chávez-Modena, M.; Martí-nez Cava, A.; Rubio, G.; Ferrer, E. Optimizing free parameters in the D3Q19 Multiple-Relaxation lattice Boltzmann methods to simulate under-resolved turbulent flows. J. Comput. Sci. 2020, 45, 101170. [Google Scholar] [CrossRef]
- Coreixas, C.; Wissocq, G.; Chopard, B.; Latt, J. Impact of collision models on the physical properties and the stability of lattice Boltzmann methods. arXiv 2020, arXiv:2002.05265. [Google Scholar] [CrossRef]
- Ducros, F.; Nicoud, F.; Poinsot, T. Wall-adapting local eddy-viscosity models for simulations in complex geometries. In Numerical Methods for Fluid Dynamics VI; 1998; Available online: https://www.researchgate.net/profile/Nicoud_Franck/publication/248366844_Wall-Adapting_Local_Eddy-Viscosity_Models_for_Simulations_in_Complex_Geometries/links/5501a2ea0cf2d60c0e5f946f.pdf (accessed on 2 October 2020).
- Chai, Z.; Shi, B.; Guo, Z.; Rong, F. Multiple-relaxation-time lattice Boltzmann model for generalized Newtonian fluid flows. J. Non-Newton. Fluid Mech. 2011, 166, 332–342. [Google Scholar] [CrossRef]
- Barad, M.F.; Kocheemoolayil, J.G.; Kiris, C.C. Lattice Boltzmann and navier-stokes Cartesian CFD approaches for airframe noise predictions. In Proceedings of the 23rd AIAA Computational Fluid Dynamics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Shih, T.; Povinelli, L.; Liu, N.; Potapczuk, M.; Lumley, J. A Generalized Wall Function; TM 113112 NASA Technical Report; Glenn Research Center: Cleveland, OH, USA, 1999. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Strack, O.E.; Cook, B.K. Three-dimensional immersed boundary conditions for moving solids in the lattice-Boltzmann method. Int. J. Numer. Methods Fluids 2007, 55, 103–125. [Google Scholar] [CrossRef]
- Jovic, S.; Driver, D.M. Backward-Facing Step Measurements at Low Reynolds Number, Reh = 5000; NASA Technical Reports Server (NTRS): Moffett Field, CA, USA, 1994. [Google Scholar]
- Le, H.; Moin, P. Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 1997, 330, 349–374. [Google Scholar] [CrossRef]
- Spalart, P.R. Direct simulation of a turbulent boundary layer up to Rθ = 1410. J. Fluid Mech. 1988, 187, 61–98. [Google Scholar] [CrossRef]
- Thomason, N.M. Experimental Investigation of Suction Slot Geometry on a Goldschmied Propulsor. Ph.D. Thesis, California Polytechnic State University, San Luis Obispo, CA, USA, 2012. [Google Scholar]
- Rumsey, C.L.; Slotnick, J.P. Overview and summary of the second AIAA High Lift Prediction Workshop. In Proceedings of the 52nd Aerospace Sciences Meeting, Harbor, MD, USA, 13–17 January 2014; p. 0747. [Google Scholar]
- Carr, L.W. Progress in analysis and prediction of dynamic stall. J. Aircr. 1988, 25, 6–17. [Google Scholar] [CrossRef]
- Ekaterinaris, J.A.; Platzer, M.F. Computational prediction of airfoil dynamic stall. Prog. Aerosp. Sci. 1998, 33, 759–846. [Google Scholar] [CrossRef]
- Ribeiro, A.F.; Casalino, D.; Fares, E. Lattice-Boltzmann simulations of an oscillating NACA0012 airfoil in dynamic stall. In Advances in Fluid-Structure Interaction; Springer: Berlin/Heidelberg, Germany, 2016; pp. 179–192. [Google Scholar]
- Aftab, S.; Razak, N.; Rafie, A.M.; Ahmad, K. Mimicking the humpback whale: An aerodynamic perspective. Prog. Aerosp. Sci. 2016, 84, 48–69. [Google Scholar] [CrossRef]
- Johari, H.; Henoch, C.W.; Custodio, D.; Levshin, A. Effects of leading-edge protuberances on airfoil performance. AIAA J. 2007, 45, 2634–2642. [Google Scholar] [CrossRef]
- Custodio, D.S. The Effect of Humpback Whale-like Protuberances on Hydrofoil Performance. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2007. [Google Scholar]
- Wei, Z.; New, T.H.; Cui, Y. Aerodynamic performance and surface flow structures of leading-edge tubercled tapered swept-back wings. AIAA J. 2018, 56, 423–431. [Google Scholar] [CrossRef]








| Lattice Resolution (mm) | Elements | Simulation Time (s) | Comp. Time (h) | Cores | ||
|---|---|---|---|---|---|---|
| Coarse | 78.1 | 0.5 | 9.16 | 0.3 | 8 | |
| Medium | 58.6 | 0.5 | 7.42 | 0.8 | 8 | |
| Fine | 48.8 | 0.5 | 6.81 | 2.1 | 8 | |
| Extra-Fine | 38.8 | 0.5 | 6.33 | 3.5 | 8 | |
| Le and Moin [43] | - | - | 6.28 | - | - | |
| Jovic and Driver [42] | - | - | - | 6.00 | - | - |
| Lattice Resolution (mm) | Elements | Simulation Time (s) | Cd | Comp. Time (h) | Cores | |
|---|---|---|---|---|---|---|
| Coarse | 4 | 0.5 | 0.24 | 3.2 | 16 | |
| Medium | 2 | 0.5 | 0.091 | 10 | 32 | |
| Fine | 1.5 | 0.5 | 0.066 | 25 | 64 | |
| Experimental | - | - | - | 0.055 | - | - |
| Grid | Fuselage (mm) | Wing (mm) | Elements | Sim. Time (s) | Cd | Cl | Comp. Time (h) | Cores |
|---|---|---|---|---|---|---|---|---|
| Extra-Coarse | 4 | 4 | 0.1 | 0.262 | 1.95 | 160 | ||
| Coarse | 2 | 2 | 0.1 | 0.295 | 2.16 | 5.2 | 160 | |
| Medium | 1 | 1 | 0.1 | 0.296 | 2.51 | 33.8 | 160 | |
| Fine | 2 | 0.5 | 0.1 | 0.310 | 2.67 | 84 | 256 | |
| Experimental | - | - | - | - | 0.275 | 2.68 | - | - |
| Lattice Resolution (mm) | Elements | Simulation Time (s) | Comp. Time (h) | Cores | |
|---|---|---|---|---|---|
| Coarse | 12 | 2 | 3.8 | 8 | |
| Medium | 6 | 2 | 24.5 | 8 | |
| Fine | 3 | 2 | 100 | 40 |
| Baseline | 2.702 m | 6.225 m | ||
|---|---|---|---|---|
| 0.025 | 0.05 | 0.1 | ||
| 0.1 | A02510 | A0510 | A1010 | |
| 0.2 | A02520 | A0520 | A1020 | |
| 0.4 | A02540 | A0540 | A1040 | |
| Lattice Resolution (mm) | Elements | Simulation Time (s) | Cd | Cl | Comp. Time (h) | Cores | |
|---|---|---|---|---|---|---|---|
| Extra Coarse | 40 | 3 | 0.254 | 0.780 | 19 | 8 | |
| Coarse | 20 | 3 | 0.242 | 0.872 | 28 | 8 | |
| Medium | 10 | 3 | 0.218 | 0.930 | 25 | 32 | |
| Fine | 5 | 3 | 0.215 | 0.941 | 155 | 32 |
| Baseline | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cd [%] | 0 | −8.3 | −4.9 | −3.5 | −4.9 | −2.6 | −1.8 | −1.7 | 2.8 | −1.9 |
| Cl [%] | 0 | −2.0 | 0.1 | −1.7 | 0.4 | 0.0 | 0.1 | 4.1 | 5.5 | 0.8 |
| L/D [%] | 0 | 6.8 | 5.2 | 1.8 | 5.5 | 2.7 | 2.0 | 5.9 | 2.7 | 2.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chávez-Modena, M.; Martínez, J.L.; Cabello, J.A.; Ferrer, E. Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow. Energies 2020, 13, 5146. https://doi.org/10.3390/en13195146
Chávez-Modena M, Martínez JL, Cabello JA, Ferrer E. Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow. Energies. 2020; 13(19):5146. https://doi.org/10.3390/en13195146
Chicago/Turabian StyleChávez-Modena, M., J. L. Martínez, J. A. Cabello, and E. Ferrer. 2020. "Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow" Energies 13, no. 19: 5146. https://doi.org/10.3390/en13195146
APA StyleChávez-Modena, M., Martínez, J. L., Cabello, J. A., & Ferrer, E. (2020). Simulations of Aerodynamic Separated Flows Using the Lattice Boltzmann Solver XFlow. Energies, 13(19), 5146. https://doi.org/10.3390/en13195146






