Voltage and Reactive Power Optimization Using a Simplified Linear Equations at Distribution Networks with DG
Abstract
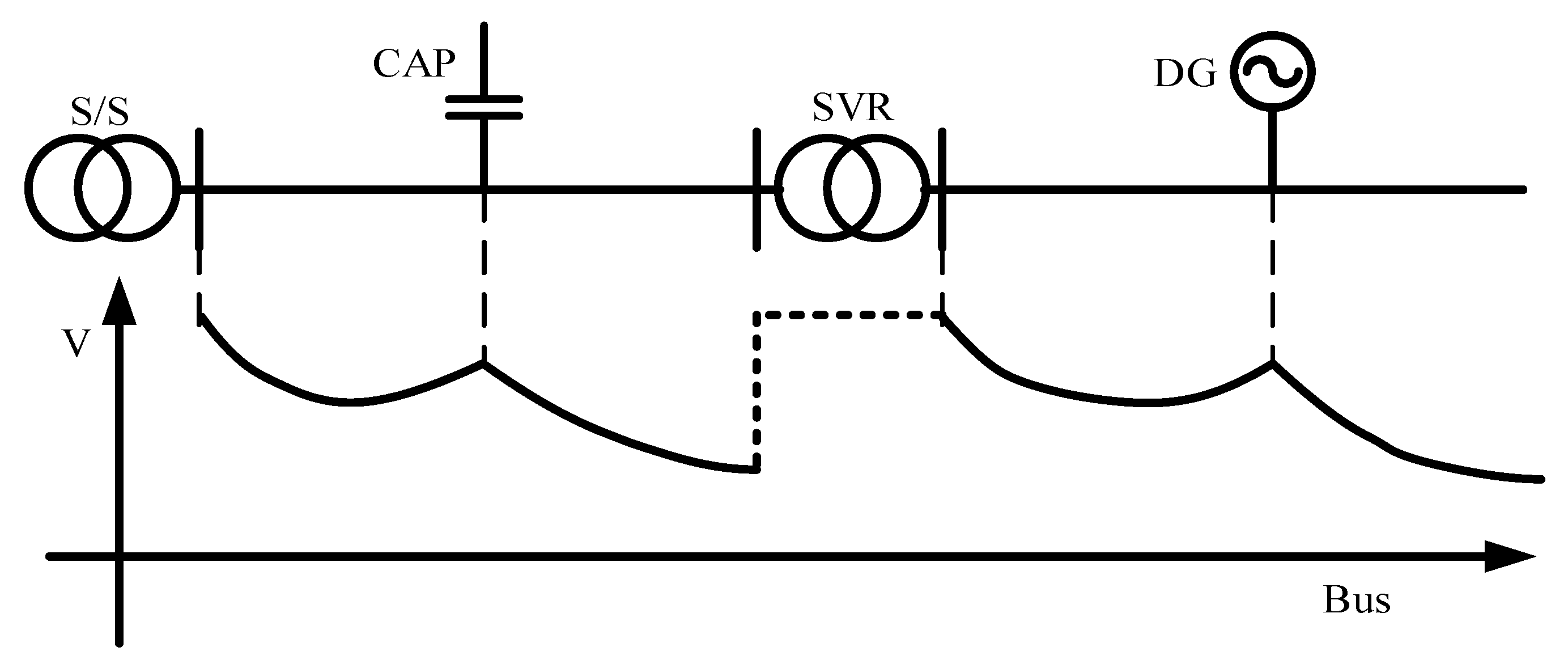
:1. Introduction
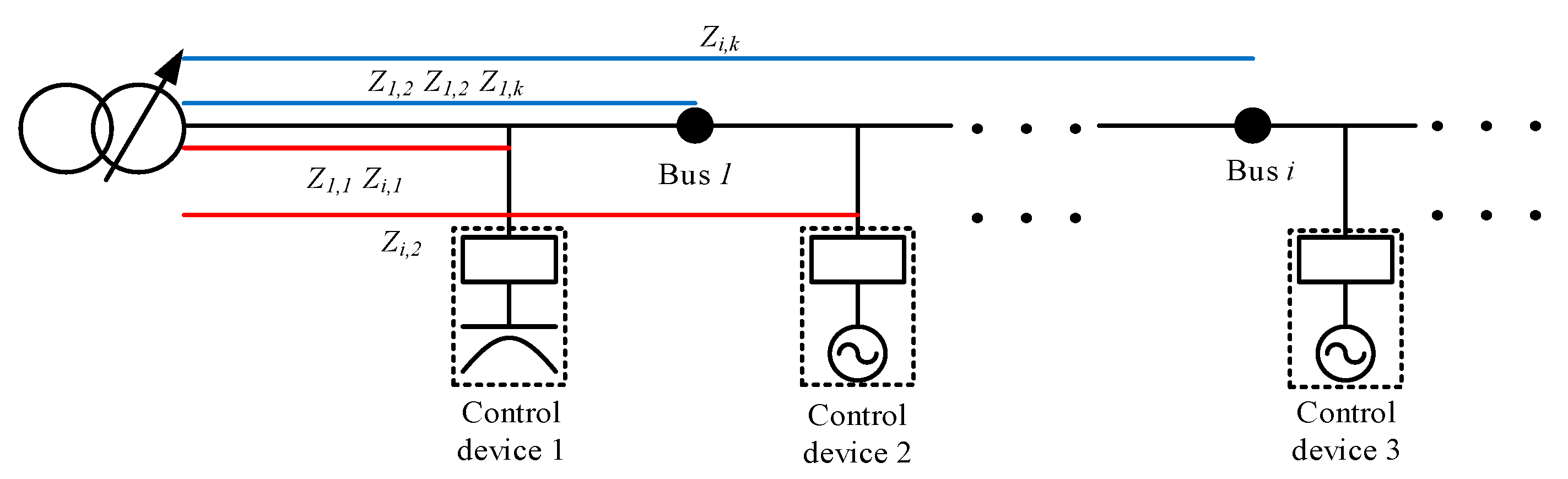
2. Voltage Equation Expressed as Simplified Linear Equation
2.1. Simplified Linear Equation
2.2. Formulation of Objective Function for Optimization
3. Quadratic Programming Formulation
3.1. Generalization of Objective Function
3.2. Generalization of Inequality Constraints
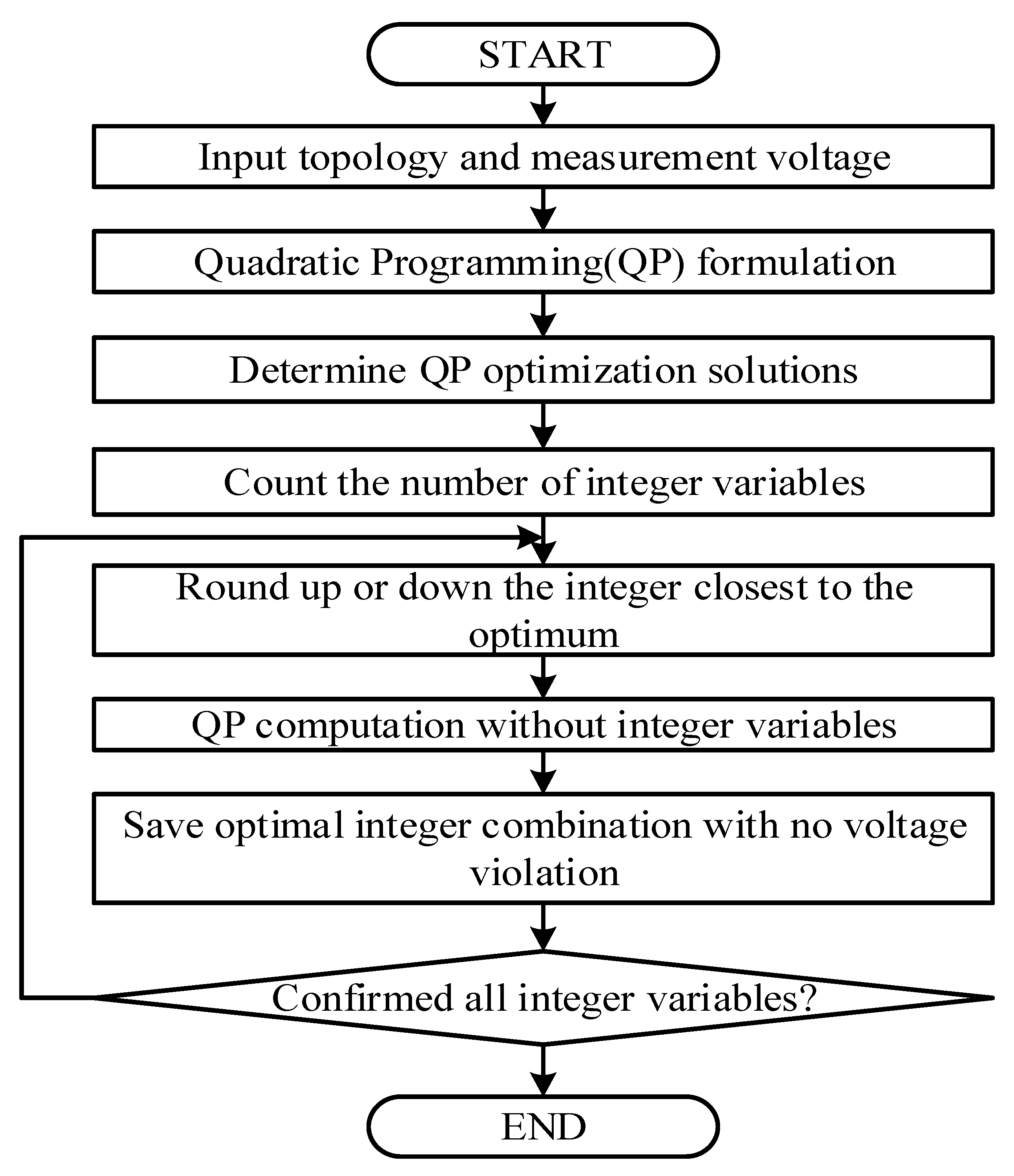
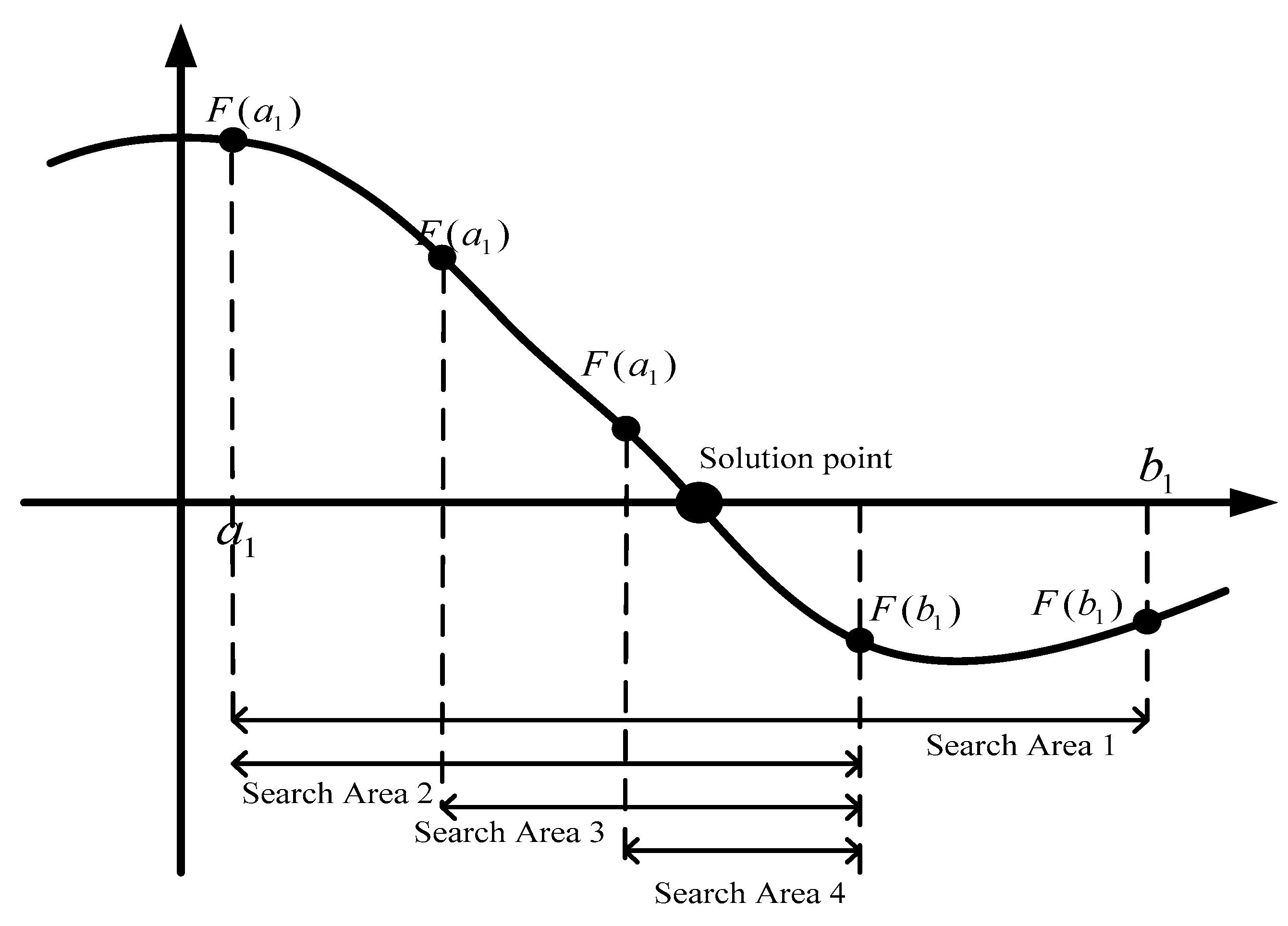
3.3. Approximation Method of MIQP
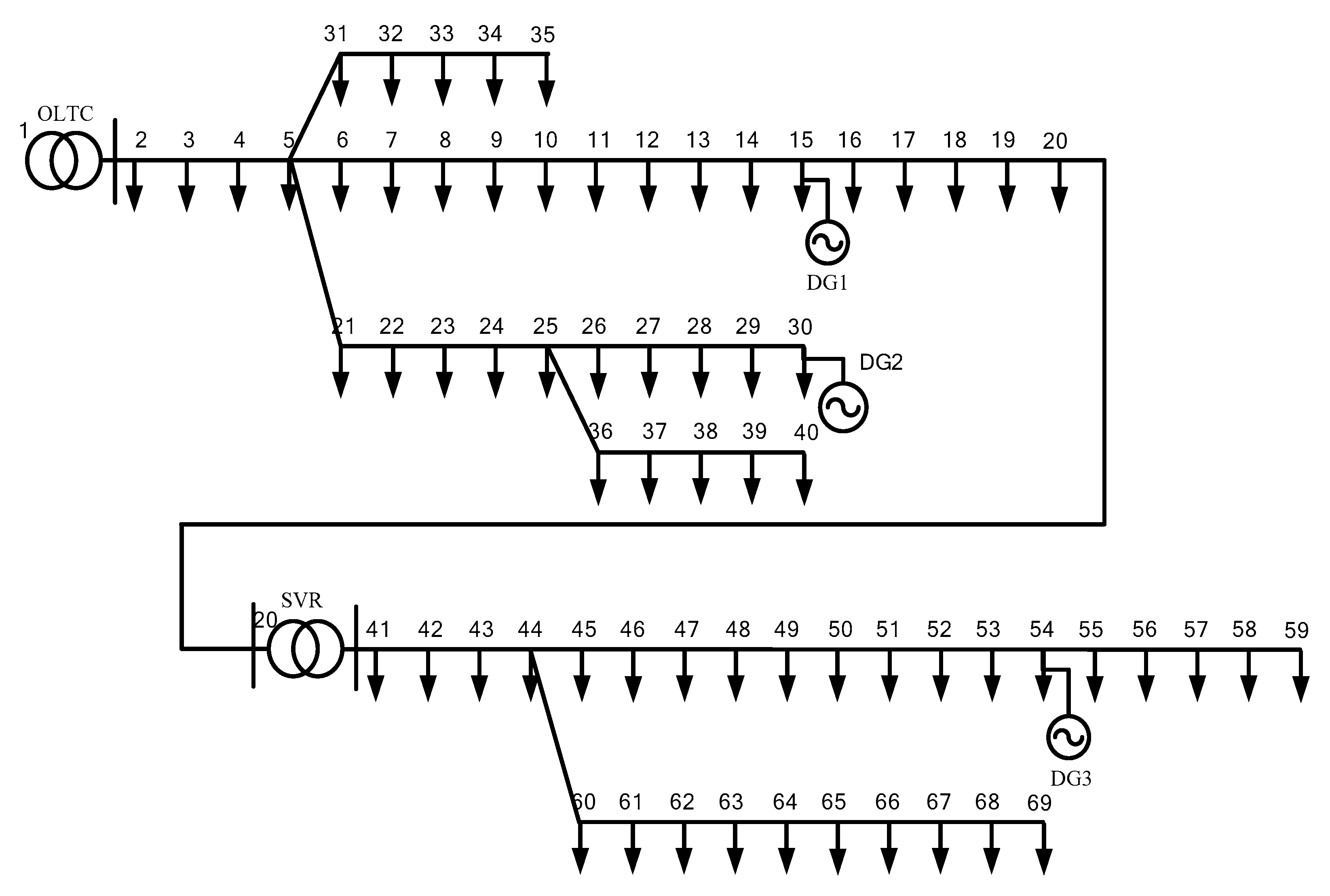
4. Case Studies
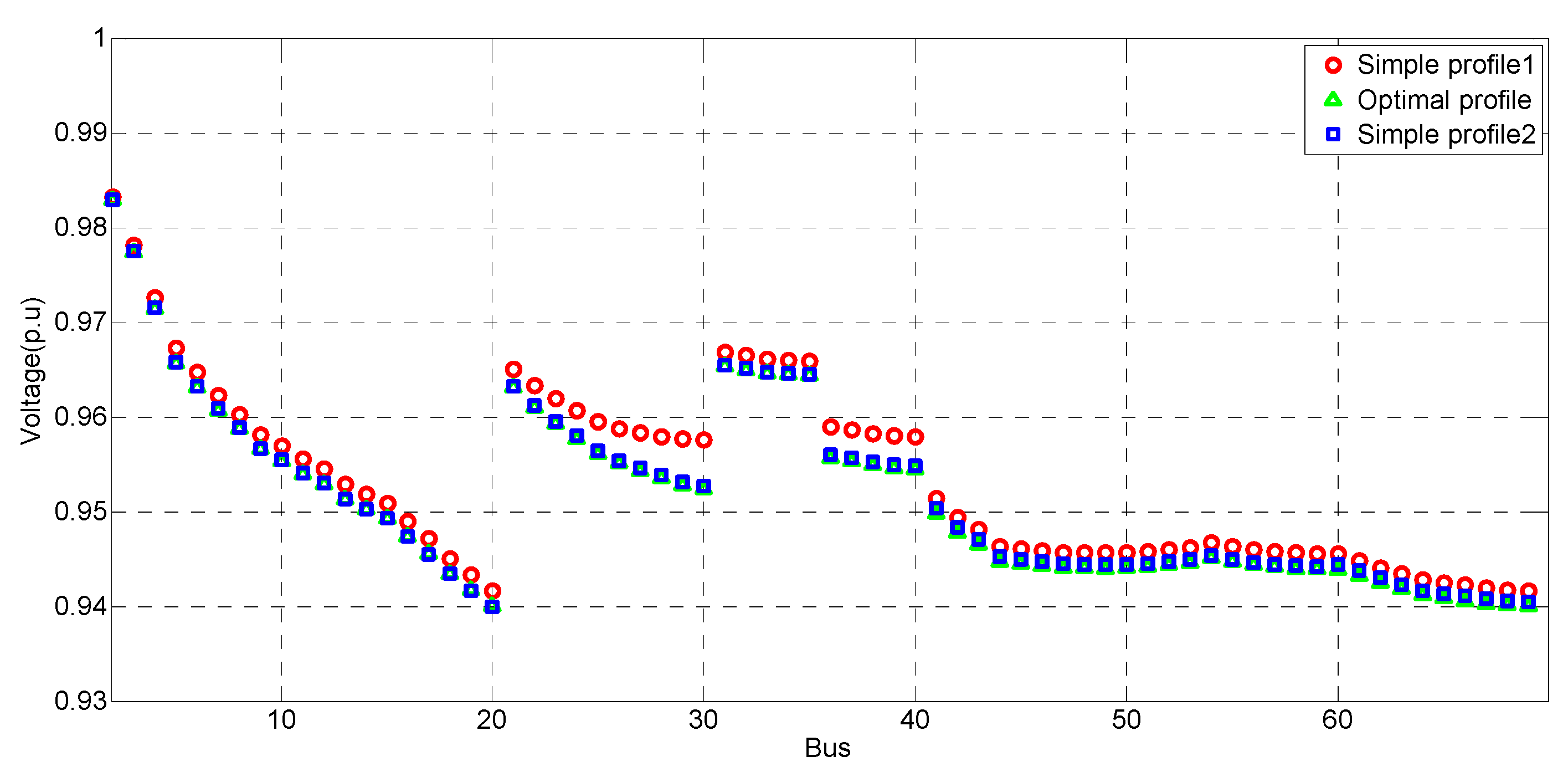
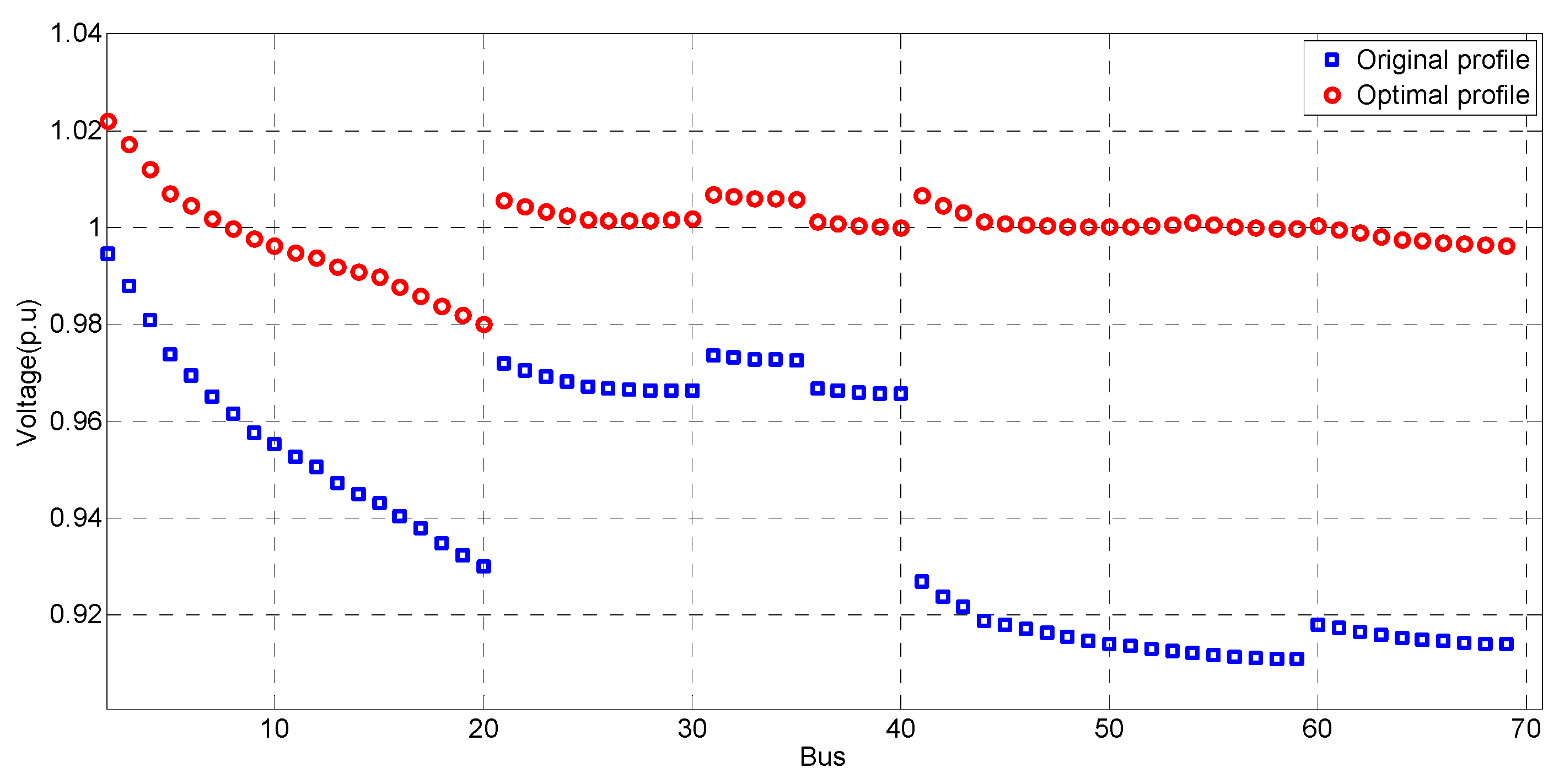
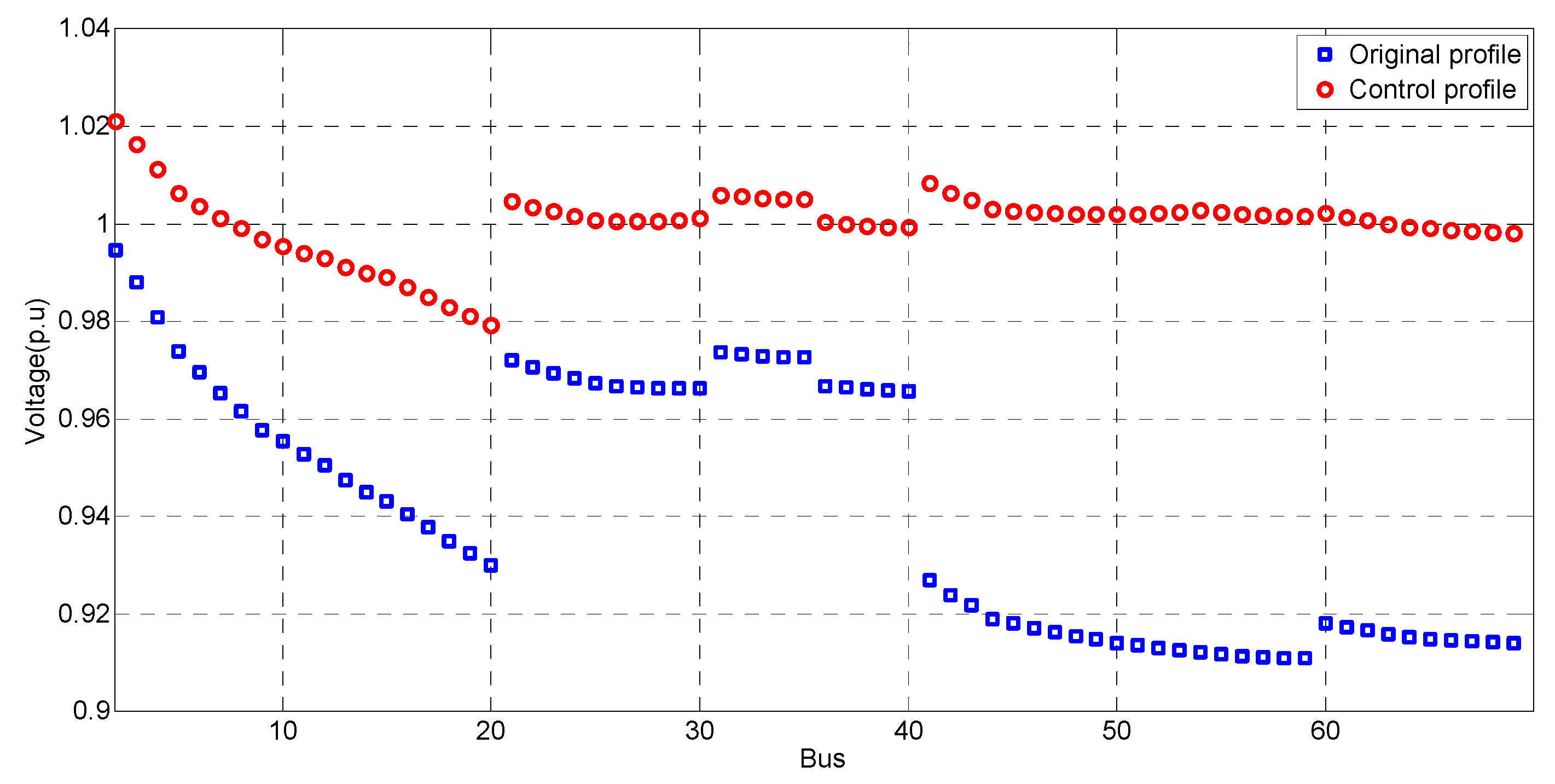
4.1. Simulation of Case Study 1
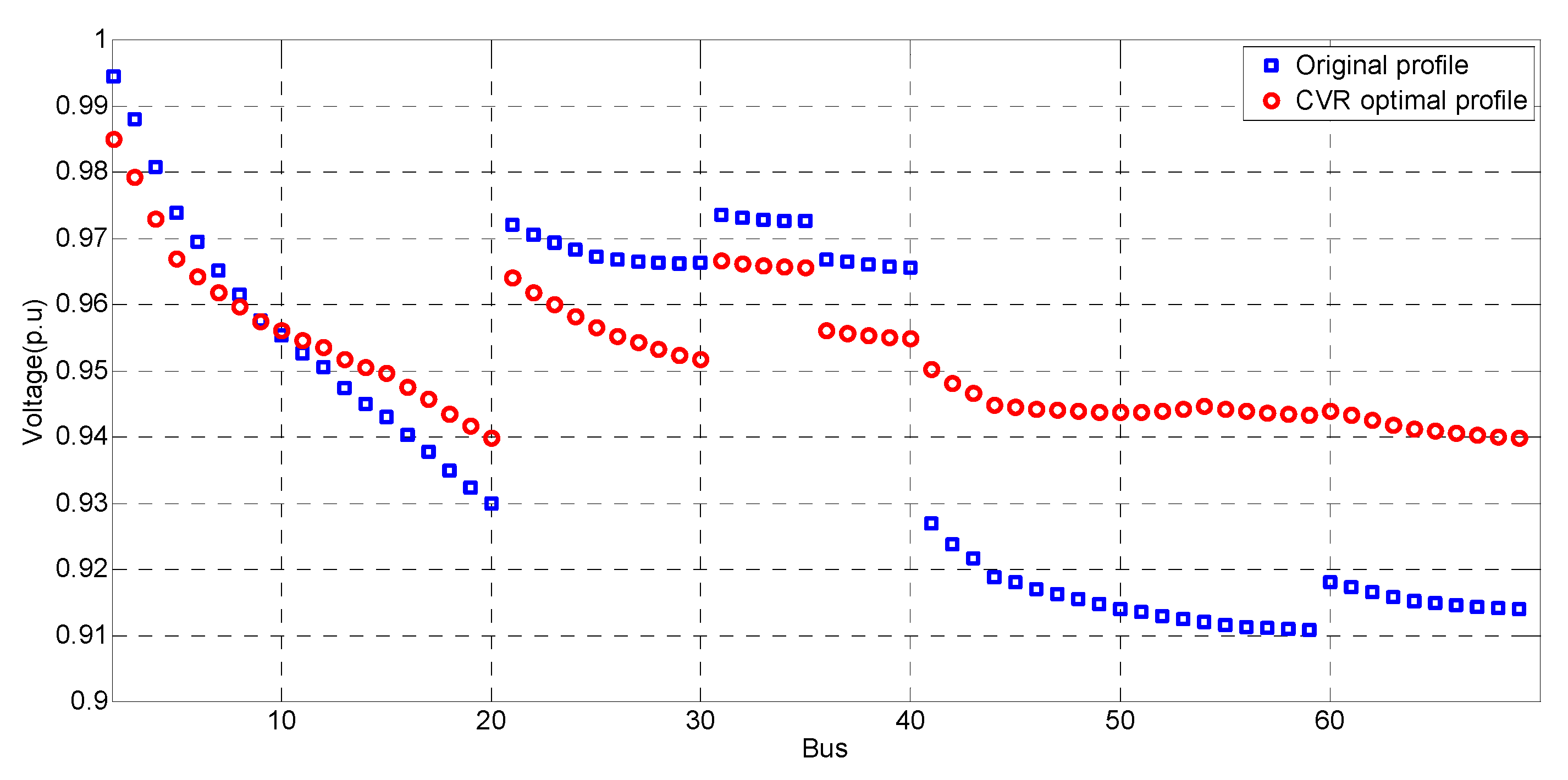
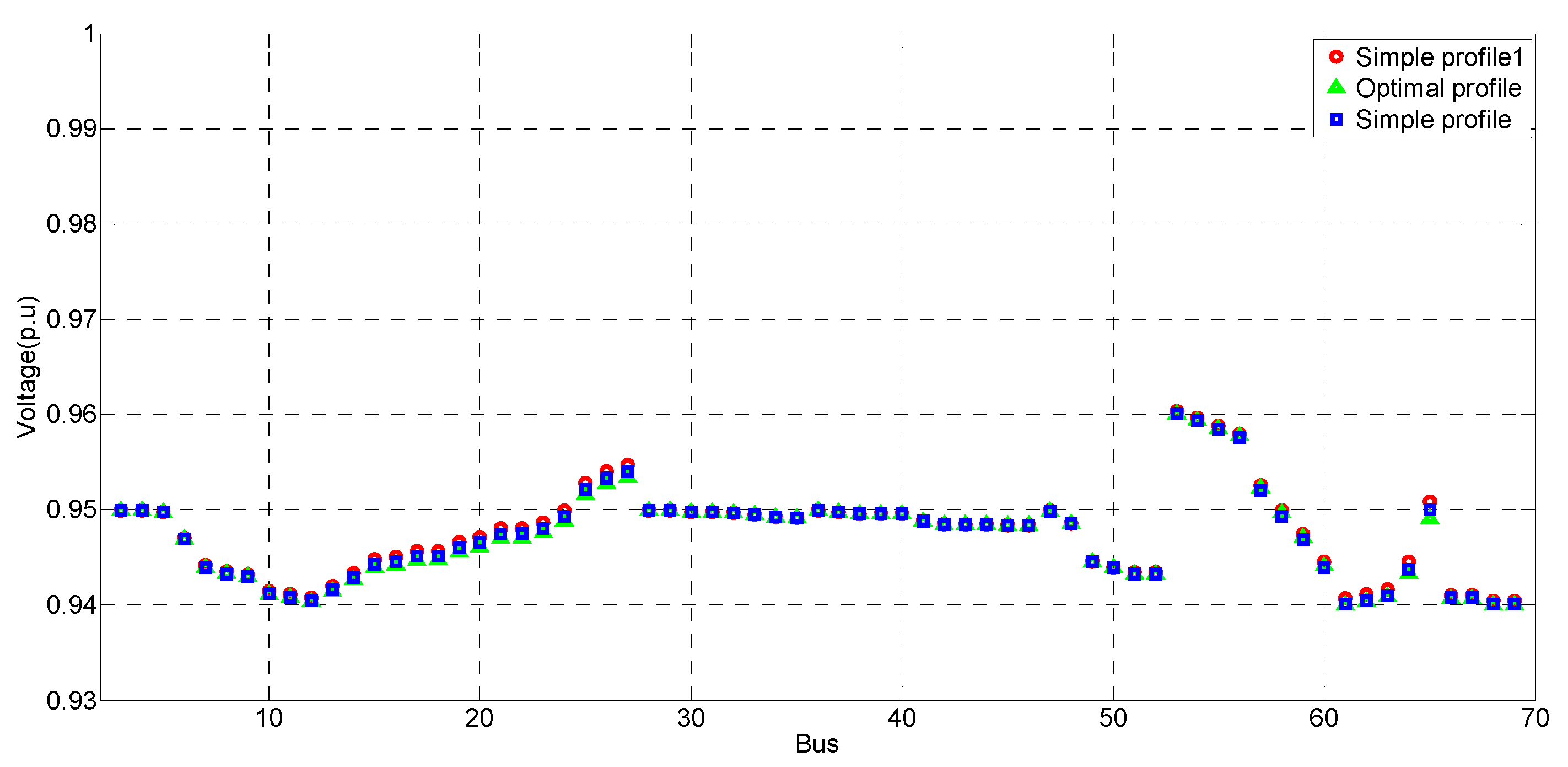
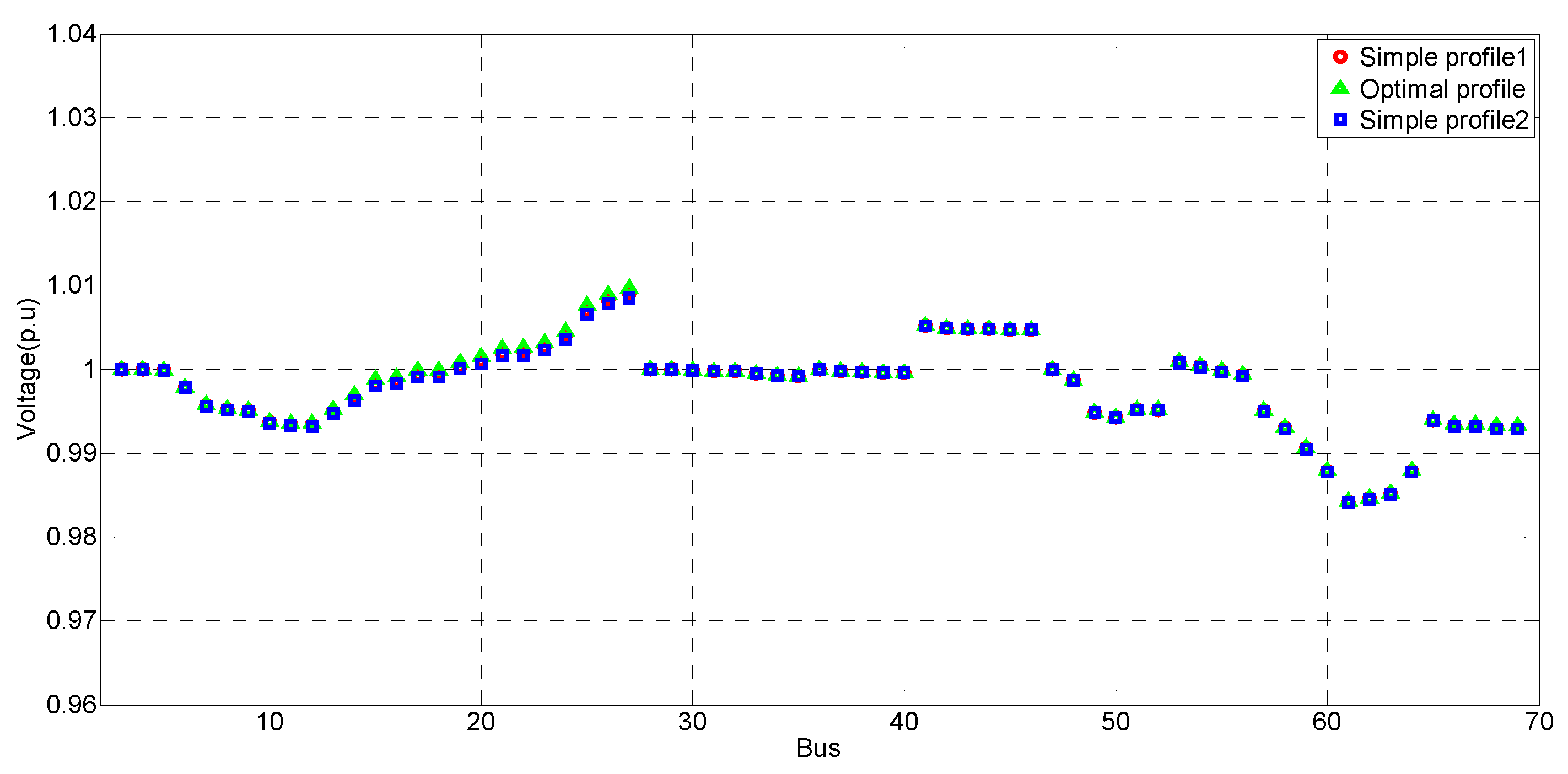
4.1.1. Voltage Control for CVR
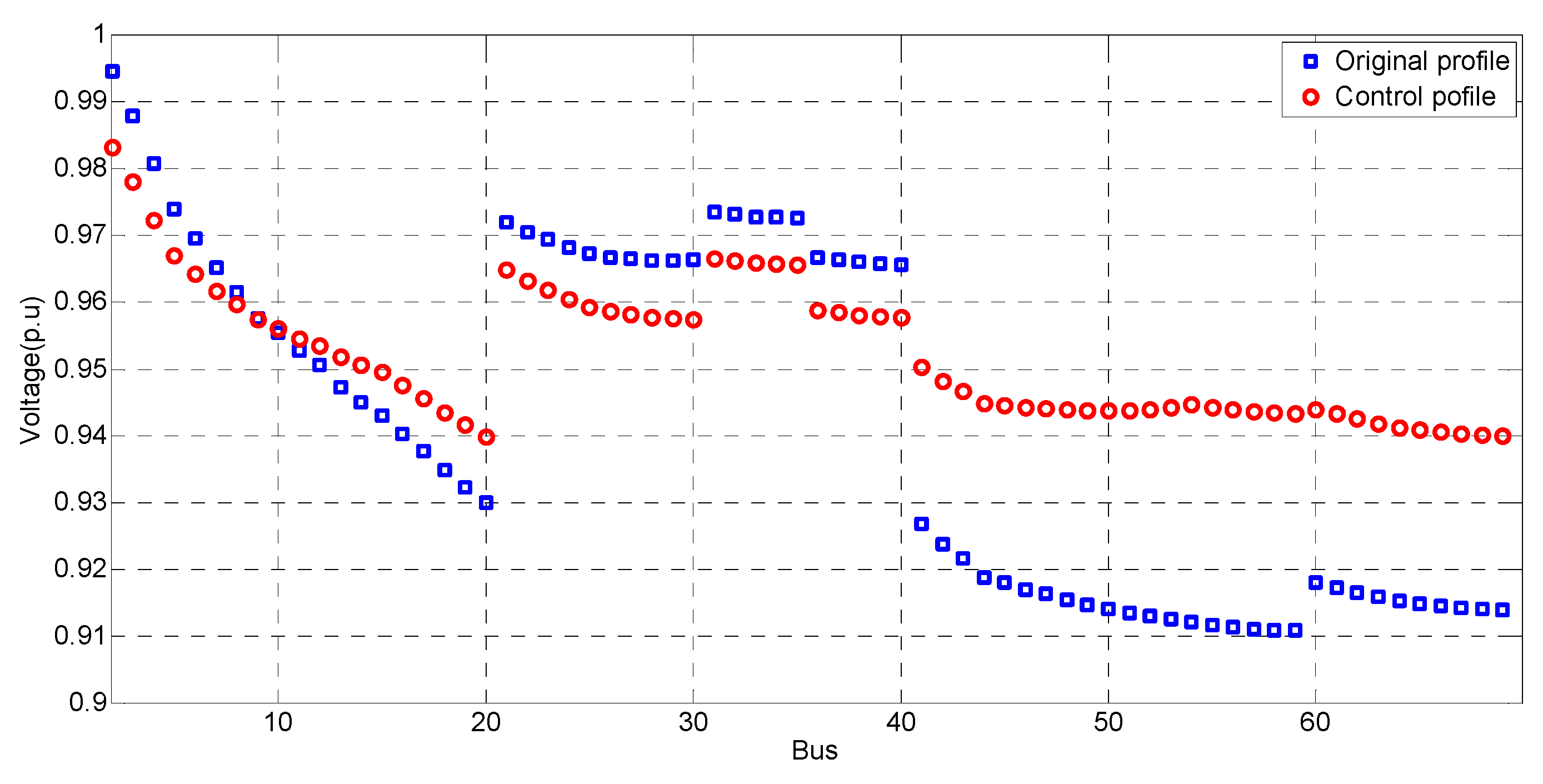
4.1.2. Voltage Control for Nominal Voltage
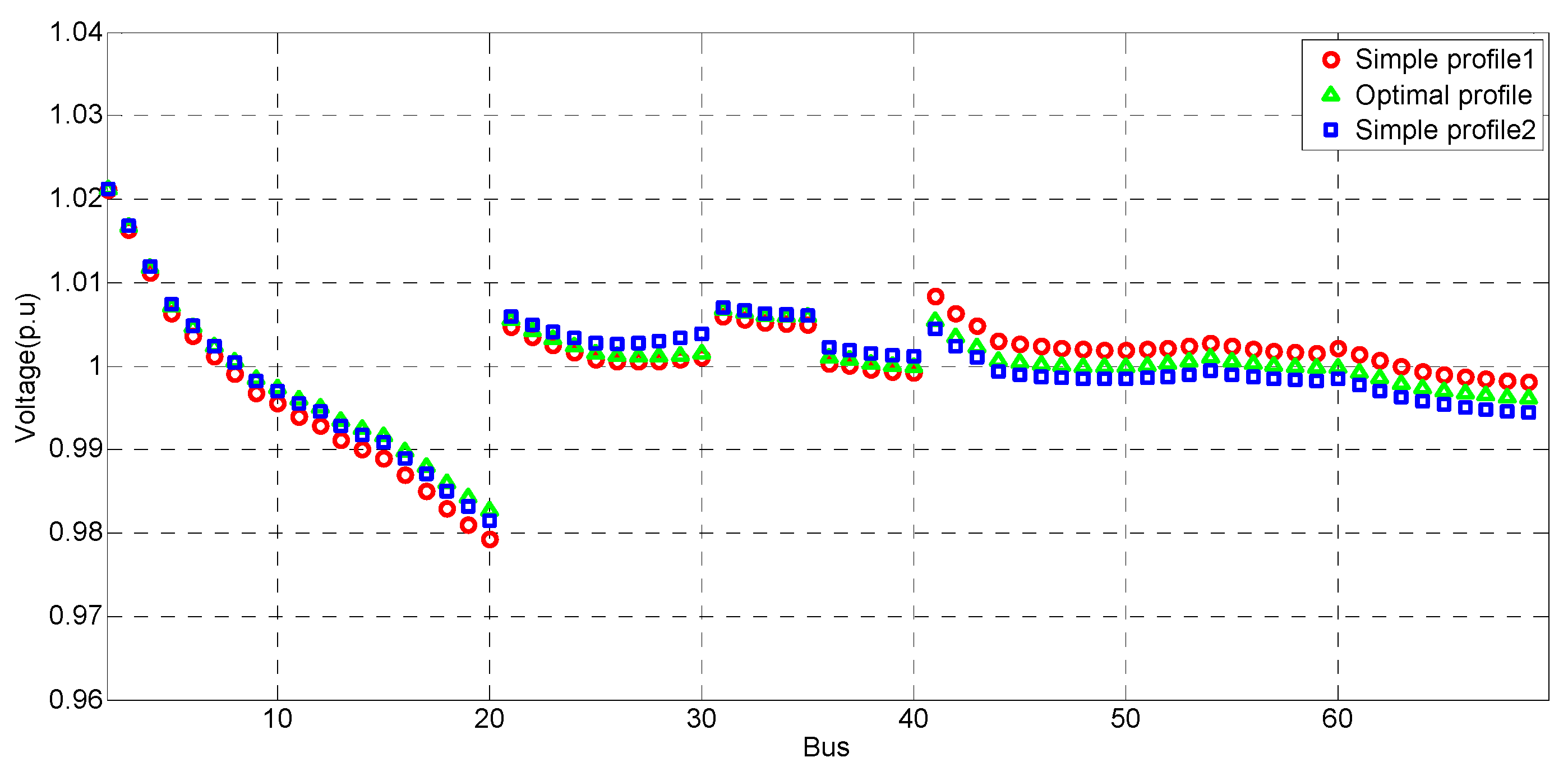
4.2. Simulation of Case Study 2
4.2.1. Voltage Control for CVR
4.2.2. Voltage Control for Nominal Voltage
4.3. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Nam-Koong, W.; Jang, M.J.; Lee, S.W.; Seo, D.W. A study on the operation of distribution system for increasing grid-connected distributed generation. J. Korean Inst. Illum. Electr. Install. Eng. 2014, 28, 83–88. [Google Scholar]
- Moon, W.S.; Cho, S.M.; Shin, H.S.; Lee, H.T.; Han, W.K.; Choo, D.W.; Kim, J.C. The study on permissible capacity of distributed generation considering voltage variation and load capacity at the LV distribution power system. KIEE Int. Trans. Power Eng. P 2010, 59, 100–105. [Google Scholar]
- Liu, X.; Aichhorn, A.; Liu, L.; Li, H. Coordinated control of distributed energy storage system with tap changer transformers for voltage rise mitigation under high photovoltaic penetration. IEEE Trans. Smart Grid 2012, 3, 897–906. [Google Scholar] [CrossRef]
- Comfort, R.; Mansoor, A.; Sundaram, A. Power quality impact of distributed generation: Effect on steady state voltage regulation. In Proceedings of the PQA 2001 North. America Conference, Pittsburgh, PA, USA, 12–14 June 2001. [Google Scholar]
- Li, Y.W.; Kao, C.N. An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid. IEEE Trans. Power Electr. 2009, 24, 2977–2988. [Google Scholar]
- Turitsyn, K.; Šulc, P.; Backhaus, S.; Chertkov, M. Local control of reactive power by distributed photovoltaic generators. In Proceedings of the 2010 First IEEE International Conference on Smart Grid Communications (SmartGridComm), Gaithersbury, MD, USA, 4–6 October 2010; IEEE: Piscataway, NL, USA, 2010. [Google Scholar]
- Elnashar, M.; Kazerani, M.; El Shatshat, R.; Salama, M.A. Comparative evaluation of reactive power compensation methods for a stand-alone wind energy conversion system. In Proceedings of the 2008. IEEE Power Electronics Specialists Conference PESC, Rhodes, Greece, 15–19 June 2008; IEEE: Piscataway, NL, USA, 2008. [Google Scholar]
- Thomson, M. Automatic voltage control relays and embedded generation. Power Eng. J. 2000, 14, 71–76. [Google Scholar] [CrossRef]
- Hiscock, J.; Hiscock, N.; Kennedy, A. Advanced voltage control for networks with distributed generation. In Proceedings of the19th International Conference on Electricity Distribution, Vienna, Austria, 21–24 May 2007. [Google Scholar]
- Viawan, F.A.; Sannino, A.; Daalder, J. Voltage control with on-load tap changers in medium voltage feeders in presence of distributed generation. Electr. Power Syst. Res. 2007, 77, 1314–1322. [Google Scholar] [CrossRef]
- Choi, J.H.; Kim, J.C. Advanced voltage regulation method of power distribution systems interconnected with dispersed storage and generation systems. IEEE Trans. Power Deliv. 2001, 16, 329–334. [Google Scholar] [CrossRef]
- Azzouz, M.A.; Farag, H.E.; El-Saadany, E.F. Fuzzy-based control of on-load tap changers under high penetration of distributed generators. In Proceedings of the 2013 3rd International Conference on Electric Power and Energy Conversion Systems (EPECS), Istanbul, Turkey, 2–4 October 2013; IEEE: Piscataway, NL, USA, 2013. [Google Scholar]
- Elkhatib, M.E.; Shatshat, R.E.; Salama, M.M.A. Decentralized reactive power control for advanced distribution automation systems. IEEE Trans. Smart Grid 2012, 3, 1482–1490. [Google Scholar] [CrossRef]
- Calderaro, V.; Conio, G.; Galdi, V.; Massa, G.; Piccolo, A. Optimal decentralized voltage control for distribution systems with inverter-based distributed generators. IEEE Trans. Power Syst. 2014, 29, 230–241. [Google Scholar] [CrossRef]
- Tsuji, T.; Hashiguchi, T.; Goda, T.; Horiuchi, K.; Kojima, Y. Autonomous decentralized voltage profile control using multi-agent technology considering time-delay. In Proceedings of the 2009 Transmission &Distribution Conference &Exposition: Asia and Pacific, Seoul, Korea, 20 June 2009; IEEE: Piscataway, NL, USA, 2009. [Google Scholar]
- Robbins, B.A.; Hadjicostis, C.N.; Domínguez-García, A.D. A two-stage distributed architecture for voltage control in power distribution systems. IEEE Trans. Power Syst. 2013, 28, 1470–1482. [Google Scholar] [CrossRef]
- Carvalho, P.M.S.; Correia, P.F.; Ferreira, L.A.F.M. Distributed reactive power generation control for voltage rise mitigation in distribution networks. IEEE Trans. Power Syst. 2008, 23, 766–772. [Google Scholar] [CrossRef]
- Zoka, Y.; Yorino, N.; Watanabe, M.; Kurushima, T. An optimal decentralized control for voltage control devices by means of a multi-agent system. In Proceedings of the 2014 Power Systems Computation Conference (PSCC 2014), Wroclaw, Poland, 18–22 August 2014; IEEE: Piscataway, NL, USA, 2014. [Google Scholar]
- Hatta, H.; Kobayashi, H. A study of centralized voltage control method for distribution system with distributed generation. In Proceedings of the 19th International Conference on Electricity Distribution (CIRED), Vienna, Austria, 21–24 May 2007. [Google Scholar]
- Thornley, V. Field experience with active network management of distribution networks with distributed generation. In Proceedings of the 19th International Conference on Electricity Distribution, Vienna, Austria, 21–24 May 2007. [Google Scholar]
- Thornley, V.; Hill, J.; Lang, P.; Reid, D. Active network management of voltage leading to increased generation and improved network utilisation. In Proceedings of the CIRED Seminar 2008, Frankfurt, Germany, 23–24 June 2008. [Google Scholar]
- Caldon, R.; Spelta, S.; Prandoni, V.; Turri, R. Co-ordinated voltage regulation in distribution networks with embedded generation. In Proceedings of the 18th International Conference on Electricity Distribution, Turin, Italy, 6–9 June 2005. [Google Scholar]
- Hird, C.M.; Leite, H.; Jenkins, N.; Li, H. Network voltage controller for distributed generation. IEE Proc.-Gener. Transm. Distrib. 2004, 151, 150–156. [Google Scholar] [CrossRef]
- Santoso, S.; Saraf, N.; Venayagamoorthy, G.K. Intelligent techniques for planning distributed generation systems. In Proceedings of the 2007 IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; IEEE: Piscataway, NL, USA, 2007. [Google Scholar]
- Sugimoto, J.; Yokoyama, R.; Fukuyama, Y.; Silva, V.V.R.; Sasaki, H. Coordinated allocation and control of voltage regulators based on reactive tabu search. In Proceedings of the 2005 IEEE Russia Power Tech, PowerTech, St. Peteersburg, Russia, 27–30 June 2005; IEEE: Piscataway, NL, USA, 2005. [Google Scholar]
- Hu, Z.; Wang, X.; Chen, H.; Taylor, G. Volt/VAr control in distribution systems using a time-interval based approach. IEE Proc.-Gener. Transm. Distrib. 2003, 150, 548–554. [Google Scholar] [CrossRef]
- Shalwala, R.A.; Bleijs, J.A.M. Voltage control scheme using Fuzzy Logic for residential area networks with PV generators in Saudi Arabia. In Proceedings of the 2010 Joint International Conference on Power Electronics, Drives and Energy Systems (PEDES) &2010 Power India, New Delhi, India, 20–23 December 2010; IEEE: Piscataway, NL, USA, 2010. [Google Scholar]
- Liang, R.H.; Liu, X.Z. Neuro-fuzzy based coordination control in a distribution system with dispersed generation system. In Proceedings of the 2007 International Conference on Intelligent Systems Applications to Power Systems, ISAP, Koahsiung, Taiwan, 5–8 November 2007; IEEE: Piscataway, NL, USA, 2007. [Google Scholar]
- Kim, G.W.; Lee, K.W. Coordination control of ULTC transformer and STATCOM based on an artificial neural network. IEEE Trans. Power Syst. 2005, 20, 580–586. [Google Scholar] [CrossRef]
- Ausavanop, O.; Chaitusaney, S. Coordination of dispatchable distributed generation and voltage control devices for improving voltage profile by Tabu Search. In Proceedings of the 2011 8th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Khon Kaen, Thailand, 17–19 May 2011; IEEE: Piscataway, NL, USA, 2011. [Google Scholar]
- Rahideh, A.; Gitizadeh, M.; Rahideh, A. Fuzzy logic in real time voltage/reactive power control in FARS regional electric network. Electr. Power Syst. Res. 2006, 76, 996–1002. [Google Scholar] [CrossRef]
- Spatti, D.H.; Usida, W.F.; Da Silva, I.N. Real-time voltage regulation in power distribution system using fuzzy control. IEEE Trans. Power Deliv. 2010, 25, 1112–1123. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, W.; Xiao, Z.; Hua, H. Reactive power optimization for transient voltage stability in energy internet via deep reinforcement learning approach. Energies 2019, 12, 1556. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Shi, C.; Shao, M.; An, R.; Zhu, X.; Huang, X.; Cai, R. Reactive power optimization of a distribution system based on scene matching and deep belief network. Energies 2019, 12, 3246. [Google Scholar] [CrossRef] [Green Version]
- Jiang, F.; Zhang, Y.; Zhang, Y.; Liu, X.; Chen, C. An adaptive particle swarm optimization algorithm based on guiding strategy and its application in reactive power optimization. Energies 2019, 12, 1690. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Wang, J. Review on implementation and assessment of conservation voltage reduction. IEEE Trans. Power Syst. 2014, 29, 1306–1315. [Google Scholar] [CrossRef]
- Jensen, P.A.; Bard, J.F. Operations Research Models and Methods; John Wiley & Sons Incorporated: Hoboken, NJ, USA, 2003; Volume 1. [Google Scholar]
- Wright, S.; Nocedal, J. Numerical Optimization; Springer: New York, NY, USA, 1999; Volume 35, p. 7. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis; Brooks/Cole: Boston, MA, USA, 2001. [Google Scholar]
- Baran, M.E.; Wu, F.F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
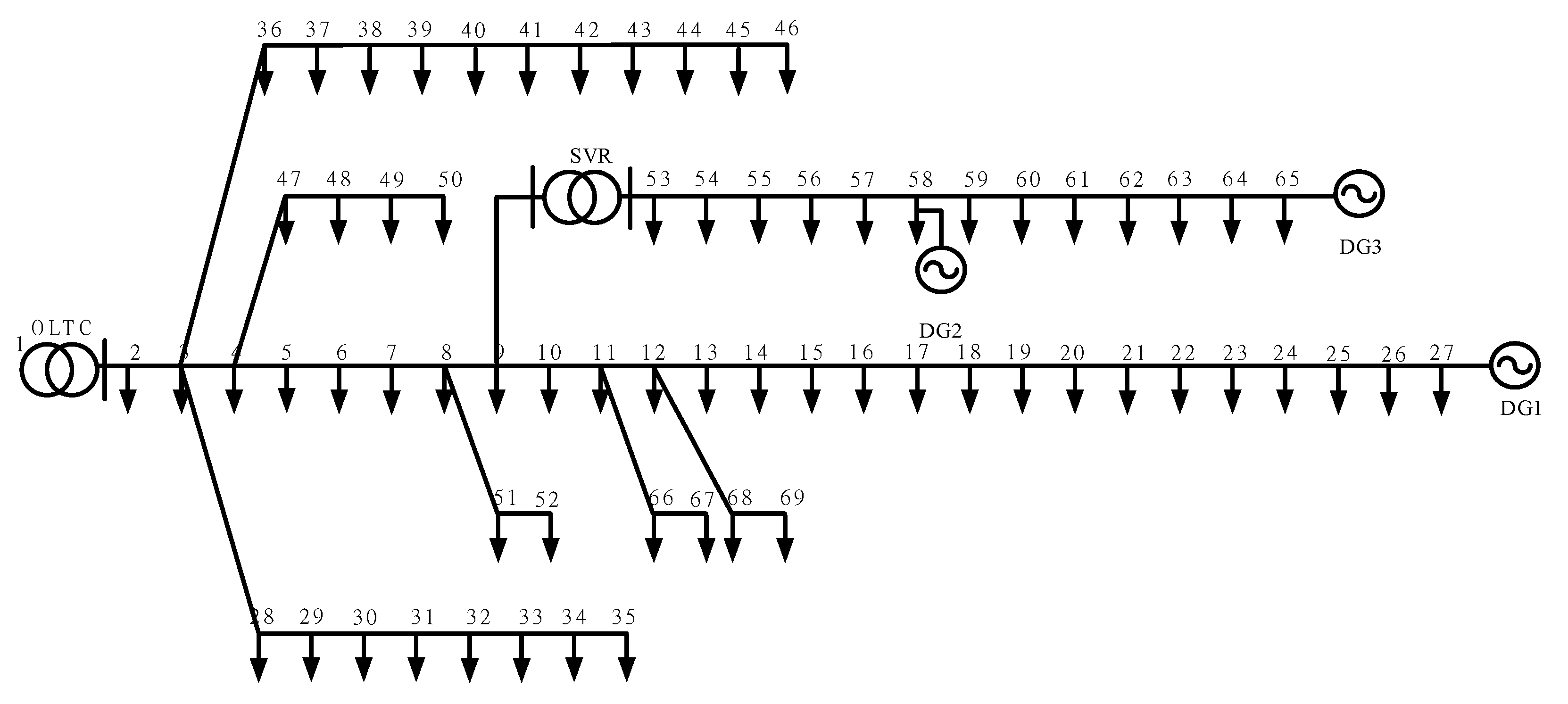
| Composition | Description | |
|---|---|---|
| Load | 10 MVA, 0.9 PF random distribution, 10% maximum voltage drop | |
| Tap changing device | OLTC | (−8–8) tap (initial position: 0) |
| SVR | (−16–16) tap (initial position: 0) | |
| Distributed generation | Initial condition 1 | Active power: 0.5 MW, reactive power: 0 MVAR |
| Initial condition 2 | Active power: 0.5 MW, reactive power: 0.5 MVAR | |
| Reactive power range | −1.0–1.0 MVAR | |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | −0.8108 |
| SVR | 1.9949 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | −1.0 | |
| DG3 | 1.0 | |
| Objective function index | 199.9426 | |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | −1 |
| SVR | 2 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | −0.2579 | |
| DG3 | 1.0 | |
| Objective function index | 212.1651 | |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | −1 |
| SVR | 2 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | −0.7524 | |
| DG3 | 1.0 | |
| Objective function index | 190.2078 | |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | −1 |
| SVR | 2 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | −0.7063 | |
| DG3 | 1.0 | |
| Objective function index | 187.0994 | |
| Objective | DG1 | DG2 | DG3 | OLTC | SVR | Objective Function Index |
|---|---|---|---|---|---|---|
| Proposed method (initial condition 1) | 1.0 | −0.2579 | 1.0 | −1 | 2 | 212.1651 |
| Proposed method (initial condition 2) | 1.0 | −0.7524 | 1.0 | −1 | 2 | 190.2078 |
| Global optimum | 1.0 | −0.7063 | 1.0 | −1 | 2 | 187.0994 |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | 2.0697 |
| SVR | 4.5818 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | 0.3138 | |
| DG3 | 1.0 | |
| Objective function index | 30.8997 | |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | 2 |
| SVR | 5 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | 0.3106 | |
| DG3 | 1.0 | |
| Objective function index | 32.0761 | |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | 2 |
| SVR | 4 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | 0.5109 | |
| DG3 | 1.0 | |
| Objective function index | 29.6959 | |
| Voltage Control Device | Control Reference | |
|---|---|---|
| Tap changing device | OLTC | 2 |
| SVR | 4 | |
| Reactive power device | DG1 | 1.0 |
| DG2 | 0.2195 | |
| DG3 | 1.0 | |
| Objective function index | 25.5613 | |
| Objective | DG1 | DG2 | DG3 | OLTC | SVR | Objective Function Index |
|---|---|---|---|---|---|---|
| Proposal method (initial condition 1) | 1.0 | 0.3106 | 1.0 | 2 | 5 | 32.0761 |
| Proposal method (initial condition 2) | 1.0 | 0.5109 | 1.0 | 2 | 4 | 29.6959 |
| Global optimum | 1.0 | 0.2195 | 1.0 | 2 | 4 | 25.5613 |
| Composition | Description | |
|---|---|---|
| Load | Total active power: 3801.89 kW Total reactive power: 2694.10 kVar | |
| Tap changing device | OLTC | (−8–8) tap (initial position: 0) |
| SVR | (−16–16) tap (initial position: 0) | |
| Distributed generation | Initial condition 1 | Active power: 0.5 MW, reactive power: 0 MVAR |
| Initial condition 2 | Active power: 0.5 MW, reactive power: 0.5 MVAR | |
| Reactive power range | −1.0–1.0 MVAR | |
| Objective | DG1 | DG2 | DG3 | OLTC | SVR | Objective Function Index |
|---|---|---|---|---|---|---|
| Proposed method (initial condition 1) | 0.3783 | 0.7117 | 1.0 | −4 | 3 | 90.1840 |
| Proposed method (initial condition 2) | 0.3518 | 0.6982 | 0.9683 | −4 | 3 | 87.6787 |
| Global optimum | 0.3143 | 0.8721 | 0.8311 | −4 | 3 | 86.7507 |
| Objective | DG1 | DG2 | DG3 | OLTC | SVR | Objective Function Index |
|---|---|---|---|---|---|---|
| Proposal method (initial condition 1) | 0.5436 | 1.0 | 1.0 | 0 | 1 | 21.2980 |
| Proposal method (initial condition 2) | 0.5769 | 1.0 | 1.0 | 0 | 1 | 21.2162 |
| Global optimum | 0.6120 | 1.0 | 1.0 | 0 | 1 | 21.1830 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Go, S.-I.; Yun, S.-Y.; Ahn, S.-J.; Choi, J.-H. Voltage and Reactive Power Optimization Using a Simplified Linear Equations at Distribution Networks with DG. Energies 2020, 13, 3334. https://doi.org/10.3390/en13133334
Go S-I, Yun S-Y, Ahn S-J, Choi J-H. Voltage and Reactive Power Optimization Using a Simplified Linear Equations at Distribution Networks with DG. Energies. 2020; 13(13):3334. https://doi.org/10.3390/en13133334
Chicago/Turabian StyleGo, Seok-Il, Sang-Yun Yun, Seon-Ju Ahn, and Joon-Ho Choi. 2020. "Voltage and Reactive Power Optimization Using a Simplified Linear Equations at Distribution Networks with DG" Energies 13, no. 13: 3334. https://doi.org/10.3390/en13133334
APA StyleGo, S.-I., Yun, S.-Y., Ahn, S.-J., & Choi, J.-H. (2020). Voltage and Reactive Power Optimization Using a Simplified Linear Equations at Distribution Networks with DG. Energies, 13(13), 3334. https://doi.org/10.3390/en13133334







