A Transformer Fault Diagnosis Model Based On Hybrid Grey Wolf Optimizer and LS-SVM

Abstract

Dissolved gas analysis (DGA) is a widely used method for transformer internal fault diagnosis. However, the traditional DGA technology, including Key Gas method, Dornenburg ratio method, Rogers ratio method, International Electrotechnical Commission (IEC) three-ratio method, and Duval triangle method, etc., suffers from shortcomings such as coding deficiencies, excessive coding boundaries and critical value criterion defects, which affect the reliability of fault analysis. Grey wolf optimizer (GWO) is a novel swarm intelligence optimization algorithm proposed in 2014 and it is easy for the original GWO to fall into the local optimum. This paper presents a new meta-heuristic method by hybridizing GWO with differential evolution (DE) to avoid the local optimum, improve the diversity of the population and meanwhile make an appropriate compromise between exploration and exploitation. A fault diagnosis model of hybrid grey wolf optimized least square support vector machine (HGWO-LSSVM) is proposed and applied to transformer fault diagnosis with the optimal hybrid DGA feature set selected as the input of the model. The kernel principal component analysis (KPCA) is used for feature extraction, which can decrease the training time of the model. The proposed method shows high accuracy of fault diagnosis by comparing with traditional DGA methods, least square support vector machine (LSSVM), GWO-LSSVM, particle swarm optimization (PSO)-LSSVM and genetic algorithm (GA)-LSSVM. It also shows good fitness and fast convergence rate. Accuracies calculated in this paper, however, are significantly affected by the misidentifications of faults that have been made in the DGA data collected from the literature.

1. Introduction

Transformer is one of the most critical equipment for power transmission and transformation and its safety and reliability is the basis to ensure continuous operation and power supply of power grid. Failures of transformer may bring huge losses to the power grid, and the repair and maintenance of the transformer is very expensive and difficult. Identifying the incipient faults of the transformer in time becomes very important which may avoid power outages and economic losses. DGA is an important and successful tool to detect incipient faults of oil-filled transformers. Based on the corresponding relationship between the type of dissolved gas in oil and internal fault, the abnormal state of the transformer can be identified by DGA method according to the composition and the content of various gases, and the fault type, severity and development trend of the fault can be determined. Several DGA interpretation methods [1], including key gas method [2,3], IEC three-ratio method [4,5], Duval triangle method [6], Rogers ratio method [7] and Dornenburg ratio method [8], Duval pentagon [9], Mansour pentagon method [10,11], etc., are available to identify the different types of faults occurring in operating transformers. Although the commonly used methods are simple and effective in transformer fault diagnosis, they suffer from defects such as coding deficiencies, excessive coding boundaries and critical value criterion defects, which will affect the reliability of fault analysis [12].

With the development of artificial intelligence (AI), machine learning and pattern recognition methods have been widely used in power transformer fault diagnosis, including artificial neural network (ANN) [13,14,15], support vector machine (SVM) [16,17,18,19,20,21,22,23,24], probabilistic neural network [25,26], Bayesian neural network [27], fuzzy logic [28,29,30], deep belief network [31], expert system [32,33], which make up for the shortcomings of the traditional DGA methods, directly or indirectly improve the accuracy of transformer fault diagnosis, and provide a new idea for high-precision transformer fault diagnosis. Although these methods have achieved good results, there are also some shortcomings. For example, the training speed of ANN is slow, it is easy to fall into local optimization, and a large number of training samples are needed, while it is very difficult to collect fault DGA sample of transformers. Expert system relies on knowledge and experience of the expert, and most of the experience is difficult to collect.

SVM is a new machine learning method proposed by Vapnik et al. in the 1990s [34], which is based on statistical theory and structural risk minimization, and fully guarantees its good generalization ability in theory. Compared with traditional machine learning methods, SVM can overcome the problems of small samples, the curse of dimensionality, local minimum and over-fitting. By constructing the optimal classification surface, the classification error of unknown samples is minimized, which means high generalization ability. SVM have been widely used in the field of fault diagnosis, such as fault diagnosis of analog circuits [35,36,37,38,39], fault diagnosis of rolling bearings [40,41,42], fault diagnosis of generator sets [43,44,45,46], etc. The Least Square-Support Vector Machine (LSSVM) is an extension of the SVM. It uses the least squares linear system as the loss function, and transforms the inequality constraints in the SVM into equality constraints. The process becomes an understanding of a set of equations, the solution speed is relatively faster. LSSVM has been applied to pattern recognition and nonlinear function estimation, and achieved good results.

In the field of power transformer fault diagnosis, a multi-layer SVM classifier was proposed and applied in power transformer fault diagnosis for the first time and showed fast training speed and reliability [16]. Fei [17] et al. applied support vector machine with genetic algorithm (SVMG) to power transformer fault diagnosis. The SVMG method showed higher diagnostic accuracy than the IEC three-ratio method, conventional SVM classifier and ANN. Khmais Bacha et al. [18] proposed a multi-layer SVM classifier for power transformer fault diagnosis which used combination ratios and graphical representation as the gas features. Compared with other AI approaches, the proposed method shows good performance. Wei [19] proposed a new approach for DGA feature prioritization and classification and the new gas features were used to train SVM optimized by PSO, which achieved the highest accuracy compared with other classification accuracies using different features. Selim Koroglu and Akif Demircali [20] developed a multi-layer SVM model optimized by grid search (GS), GA, DE, and PSO algorithms using Gaussian radial basis as kernel function and the result showed that the PSO optimized SVM achieved the highest classification accuracy and less computation time. The GA was used to perform DGA ratio selection from a total of 28 gas ratio combinations based on IEC TC 10 DGA data, combined with the traditional DGA ratio and the gas ratio combination proposed in [47,48] and optimize SVM parameter [21]. Nine feature ratios was selected as input vectors of the SVM and the diagnostic accuracy of 87.18% was obtained, which verified the robustness and generalization ability of optimal dissolved gas ratios (ODGR). Yuan et al. [22] proposed a transformer fault diagnosis model based on chemical reaction optimization (CRO) and twin support vector machine (TWSVM) which used restricted Boltzmann machine (RBM) for data preprocessing, cross-validation (CV) to ensure the reliability and generalization ability of the diagnostic model and CRO algorithm to select the optimal training parameters of the TWSVM classifier, and finally, the actual fault samples and random tests were used to verify the validity of the model. Hazlee Azil Illias and Wee Zhao Liang [23] proposed a transformer fault diagnosis model based on hybrid SVM and improved evolutionary particle swarm optimization (SVM-MEPSO), which used a stepwise regression approach for data reduction and the results show that the hybrid SVM-MEPSO time-varying acceleration coefficient (TVAC) technology can obtain the highest accuracy compared with other PSO algorithms. The optimal hybrid DGA feature subset (OHFS) was selected from three feature sets by using genetic algorithm-support vector machine-feature screen (GA-SVM-FS) model and used as input of the improved social group optimization (ISGO) optimized multi-SVM classifier to develop a transformer fault diagnosis model which achieved the highest fault diagnosis accuracy (92.86%) compared with other diagnostic models [24]. In addition, other scholars also used the SVM [49], relevance vector machine (RVM) [50] for transformer fault diagnosis and achieved good results.

The intelligent approaches mentioned above have directly or indirectly improved the accuracy of the transformer fault diagnosis methods based on DGA. However, there are deficiencies in the parameter optimization, the feature set selection and data preprocessing methods, which limit the practical application of AI algorithm in transformer fault diagnosis. A novel swarm intelligence algorithm proposed in 2014 by Mirjalili et al., the grey wolf optimization [51], which has the advantage of superior performance, few parameters and easy to implement, has attracted the attention of many scholars [52,53,54]. Compared with GA, PSO and DE, GWO shows superior performance in exploitation and exploration, high local optima avoidance and fast convergence. Due to its competitive performance, the GWO is employed for parameter optimization in this study. Because of a slow convergence rate and easy to fall into local optimum of the original GWO, various improved strategies for the GWO have been proposed, and achieved good results [55,56,57,58]. This paper proposes a hybrid grey wolf optimization algorithm (HGWO), combining the DE algorithm with the GWO, which uses the powerful search ability of the DE to update position of the grey wolf α, β, δ, and thus jump out stagnation and makes the GWO not to fall into the local optimum, which accelerates the convergence speed and improves the performance of the algorithm. In addition, the variation and selection of DE algorithm are used to generate the initial population, which can improve the diversity of the population. Then, the HGWO is applied as the optimizer of a transformer fault diagnosis model based on HGWO-LSSVM with the optimal hybrid DGA feature set selected as the input. The KPCA method is used for feature extraction. Finally, the proposed model is tested and compared with other models.

This paper is organized as follows: Section 2 introduces the basic theory of the HGWO-LSSVM model. In Section 3, the HGWO-LSSVM model is proposed and in Section 4 the performance of HGWO-LSSVM model is tested and compared with other diagnostic models, which proves the effectiveness of the proposed model. Finally, the conclusion is summarized and potential future work is discussed in Section 5.

2. Related Theory

2.1. Kernel Principal Component Analysis

Principal component analysis (PCA) is a linearly reduced method for data compression and can be used to extract the main components from high-dimensional variables, by which the dimension and complexity of the data are reduced. The extracted data, which can only characterize the linear state, loses the nonlinear components in the original data, which leads to the lack of valid information. The principle of KPCA is based on PCA. In the KPCA, the kernel function is used to realize the nonlinear variation of mapping the original data to the high-dimensional linear feature space, and then PCA is used to extract the features. The essence of KPCA is to perform PCA on the data mapped to the feature space.

Let $x_1$, $x_2$, $x_3$, …, $x_N\in \mathrm{R}$ as the data sample, and it is used as the input data which is mapped from the original space to the high-dimensional linear feature space F by the nonlinearity function $\mathsf{\varphi }(\cdot )$, and the covariance matrix $C$ of $\mathsf{\varphi }\left(x_j\right)$ is:

$$C^F=\frac{1}{N}{{\displaystyle \sum }}_{j=1}^N\mathsf{\varphi }\left(x_j\right)\mathsf{\varphi }{\left(x_j\right)}^T,$$

(1)

where the eigenvalue and eigenvector in the formula are: $\lambda V=C^{F}V$, and the eigenvalue $\lambda \ge 0$, $V$ is the eigenvector.

Defining N × N dimension matrix $K_{ij}=K\left(x_i, x_j\right)=\mathsf{\varphi }\left(x_j\right)\mathsf{\varphi }\left(x_j\right)$, and the eigenvectors $V^k$ is normalized, that is $\left(V^k, V^k\right)=1$. Then, the $k\left(k=1,2,\dots ,N\right)$ principal elements $t_k$ in the feature space is:

$$t_k=\left(V^k,\mathsf{\varphi }\left(x\right)\right)={{\displaystyle \sum }}_{i=1}^N{a}_i^{k}K\left(x,x_j\right),$$

(2)

As the same with the general principal component analysis algorithm, the input data needs to satisfy zero-mean conditions. This work can be done by replacing $K$ with the following:

$$\tilde{K}=K-LK-KL+LKL,$$

(3)

where $L_{i,j}=\frac{1}{N}.$

The KPCA has the same mathematical and statistical characteristics as the linear PCA in the $F$ space, such as each principal component is uncorrelated, the principal component can represent the maximum variance of the sample data, and the principal component is used to reconstruct the sample data, which can gain a minimum mean square error. In addition, it extracts more sample information than linear PCA. Under the premise of achieving the same classification performance, the number of principals required by KPCA is less than that of linear PCA. Compared with other nonlinear feature extraction methods, it does not need to solve the nonlinear optimization problem and only involves the eigenvalue decomposition calculation of the matrix. KPCA has been widely used in feature extraction [42] and has achieved good results.

2.2. Differential Evolution

Storn and Price [59] proposed a powerful method for global optimization, differential evolution, DE mainly produces a new population through the mechanisms of population variation, crossover and selection to obtain the optimal solution, which can improve the diversity of population. Because of its simple principle, few controlled parameters and strong robustness, DE has been widely used in constrained optimization [60,61,62], nonlinear control optimization [63], feature selection [64] and other optimization problems [65,66,67,68].

DE is used to solve the optimization problem, which mainly includes the following operations:

2.2.1. Initialization of Population

Like other swarm intelligence optimization algorithms, DE also needs to initialize the population:

$$\left\{x_i\left(0\right)|x_{i,j}^L\le x_{i,j}\left(0\right)\le x_{i,j}^U;i=1,2,\dots ,NP;j=1,2,\dots ,D\right\},$$

(4)

where $x_i\left(0\right)$ is the ith individual, $j$ is the dimension.

$$x_{i,j}\left(0\right)=x_{i,j}^L+rand\left(0,1\right)\left(x_{i,j}^U-x_{i,j}^L\right),$$

(5)

where $x_{i,j}^L$ and $x_{i,j}^U$ are the lower bound and the upper bound of the j dimension, respectively, $rand\left(0,1\right)$ is a random number in the range of $\left[0,1\right]$.

2.2.2. Mutation

DE realizes individual variation through differential strategy. The common differential strategy is to randomly select two different individuals in the population, and scale the vector difference and synthesize the vector with the individual to be mutated.

$$v_i\left(\mathrm{g}+1\right)=x_{r1}\left(\mathrm{g}\right)+F\left(x_{r2}\left(\mathrm{g}\right)-x_{r3}\left(\mathrm{g}\right)\right),$$

(6)

where $r1$, $r2$ and $r3$ are random numbers in the range of $\left[0,NP\right]$, $F$ is scaling factor, $x_i\left(\mathrm{g}\right)$ represents the $i$th individual in the g generation population.

2.2.3. Crossover

The crossover operation is carried out on the $\mathrm{g}$th generation population $\left\{x_i\left(\mathrm{g}\right)\right\}$ and its variant intermediate $\left\{v_i\left(\mathrm{g}+1\right)\right\}$.

$$u_{i,j}\left(\mathrm{g}+1\right)=\{\begin{array}{c}{v}_{i,j}\left(\mathrm{g}+1\right) if rand\left(0,1\right)\le CR\\ x_{i,j}\left(\mathrm{g}\right) otherwise\end{array},$$

(7)

where $CR$ is crossover probability.

2.2.4. Selection

The strategy of greedy selection is adopted in DE, that is, the better individual is selected as the new one.

$$x_i\left(\mathrm{g}+1\right)=\{\begin{array}{c}{u}_i\left(\mathrm{g}+1\right) if f\left(u_i\left(\mathrm{g}+1\right)\right)\le f\left(x_i\left(\mathrm{g}+1\right)\right)\\ x_i\left(\mathrm{g}\right)\end{array},$$

(8)

2.3. Grey Wolf Optimizer

Grey wolf optimizer, a newly swarm intelligence algorithm introduced by Mirjalili et al. [51], is a powerful meta-heuristic algorithm, which has the ability to compete with other algorithms including PSO, GA, DE and many other algorithms in terms of solution accuracy, minimum computational effort, and aversion of premature convergence [69,70]. Because of these advantages, it has been gained a very big research interest by tremendous audiences from several domains and successfully applied in the fields of global optimization [71], control engineering [72,73], feature selection [74], scheduling problems [75,76] in recent years.

Based on the physical behavior and social behavior of grey wolves, the mathematical model of the GWO algorithm contains five parts, including social hierarchy, encircling, hunting, attacking and searching, and a brief introduction is presented as follows.

2.3.1. Social Hierarchy

In GWO, a hierarchical model is constructed according to social hierarchy of the grey wolf, and the fitness of each individual is calculated, and the three grey wolves with the best fitness are sequentially labeled as $\alpha$, $\beta$, $\delta$, and the rest grey wolf is marked as $\omega$. The optimization process of GWO is mainly guided by the best three solutions in each generation (i.e., $\alpha$, $\beta$, $\delta$).

2.3.2. Encircling Prey

When the grey wolf hunts the prey, it gradually approaches the prey and surrounds it. The mathematical model of this behavior is as follows:

$$D=C·X_p\left(t\right)-X\left(t\right),$$

(9)

$$X\left(t+1\right)=X_p\left(t\right)-A·D,$$

(10)

$$A=2a·r_1-a,$$

(11)

$$C=2r_2,$$

(12)

where $t$ is number of iterations, $A$ and $C$ are the coefficient vectors; $X_p$ is the position vector of the prey, $X\left(t\right)$ is the position vector of the wolf, $a$ is linearly reduced from 2 to 0 during the iteration; $r_1$ and $r_2$ is a random vector in $\left[0,1\right]$.

2.3.3. Hunting

In order to simulate the search behavior of grey wolves, it is assumed that $\alpha$, $\beta$, $\delta$ have strong ability to identify the potential prey and during each iteration, the best three wolves ($\alpha$, $\beta$, $\delta$) are retained, and then the locations of other search agents are updated based on their location. The mathematical model can be expressed as follows:

$$D_{\alpha }=C_1·X_{\alpha }-X, D_{\beta }=C_1·X_{\beta }-X,D_{\delta }=C_1·X_{\delta }-X,$$

(13)

$$X_1=X_{\alpha }-A_1·D_{\alpha }, X_2=X_{\beta }-A_2·D_{\beta },X_3=X_{\delta }-A_3·D_{\delta },$$

(14)

$$X\left(t+1\right)=\frac{X_1+X_2+X_3}{3}$$

(15)

where $X_{\alpha }$, $X_{\beta }$, $X_{\delta }$ are the positions of $\alpha$, $\beta$, $\delta$, $X$ represents the position of the wolf, $D_{\alpha }$, $D_{\beta }$, $D_{\delta }$ respectively represent the distance between the current candidate and the optimal three wolves, when $\left|A\right|>1$, the grey wolves are scattered among the regions to search for prey and when $\left|A\right|<1$, the grey wolves will focus on hunting for prey in the search areas.

2.3.4. Attacking Prey

According to the formula of encircling prey, the decrease of a causes a fluctuation of $A$ accordingly. And $A$ is a random vector in [−2a, 2a], where a decreases linearly during the iteration. When $A$ is in the [−1, 1], the position of the search agent in next moment can be anywhere between the current grey wolf and the prey. Parameter $a$ is linearly updated in each iteration to range from 2 to 0 as follows:

$$a=2-t\times \frac{2}{Ma{x}_{Iter}}$$

(16)

where $t$ is the iteration number and $Ma{x}_{Iter}$ is the total number of iterations allowed for the optimization.

2.3.5. Searching Prey

Grey wolves rely mainly on $\alpha$, $\beta$, $\delta$ to find the prey. They search for prey location in the beginning and then concentrate to attack prey. In the model, $A>1$ makes the search agent far away from the prey, enabling GWO to perform global search. C is another search coefficient of the GWO algorithm. As can be seen from the formula of encircling prey, the C is a random vector in the range of [0, 2], which provides a random weight for the prey to add ($C>1$) or decrease ($C<1$). This helps GWO to exhibit random search behavior during the optimization process to avoid the algorithm falling into local optimum. The pseudo-code of the GWO (Algorithm 1) is presented in the following form:

Algorithm 1. GWO pseudo-code

(1) Initialize the positions of grey wolf population Xi (i = 1,2,3…, n) randomly. (2) Initialize a, A, C. (3) Find α, β, and δ as the first three best solutions based on their fitness values. (4) t = 0.  while t ≤ MaxIter do   for each Wolfi $\in$ pack do    Update current wolf’s position according to Equation (15).   end  - Update a, A, and C as in Equations (16), (11) and (12).  - Evaluate the positions of individual wolves.  - Update α, β, and δ positions as the first best three solutions in the current population.  - t = t + 1.  end (5) Select the optimal grey wolf position.

Although the GWO algorithm shows the superiority in many fields, when the training sample is a big data, it will face problems of local optimum, slow computation speed, and low accuracy. Therefore, this paper uses DE combined with the GWO to improve the performance of the original GWO algorithm, which uses the DE with the powerful search ability to force the GWO to jump out of the stagnation when attacking the prey to avoid the local optimum and achieve the appropriate compromise between exploration and exploitation for further accelerating the convergence speed and improving the accuracy of GWO. In addition, the variation and selection of DE algorithm are used to generate the initial population, which can improve the diversity of the population.

2.4. Least Square Support Vector Machine

SVM is a new machine learning theory based on V-dimensional theory and structural risk minimization principle proposed by Bell Labs researcher Vapnik in the 1990s [34]. which has excellent learning performance and generalization ability. Compared with other machine learning algorithms, SVM has significant advantages in dealing with overfitting and local optimum. Since SVM was proposed, it has been successfully applied in many fields, such as regression analysis, pattern recognition and so on. Least squares support vector machine LS-SVM (Least Square-Support Vector Machine) is an extension of standard SVM, which transforms quadratic programming problem into linear equations and a much faster solution speed and strong real-time performance is obtained.

Let $\mathrm{D}=\left\{\left(x_i, y_i\right)|i=1,2,3,\dots ,N\right\}$ be the training sample set, where $x_i$ is the input and $y_i$ is the output. For nonlinear regression, LS-SVM is modeled as follows:

$$y\left(x\right)={\omega }^T\phi \left(x_i\right)+b+e_i,$$

(17)

where $\omega$ represents the weight vector, $\phi \left(x_i\right)$ is a nonlinear function, which is used to complete the mapping from the input space to the high dimensional feature space. $b$ is the deviation, and $e_i$ represents the fitting error, which is the error between the actual training output and the estimated output of the data group $i$. $\omega$ and $b$ can be obtained from the following optimization problems:

$$\min J\left(w,e\right)=\frac{1}{2}{\omega }^T\omega +\gamma \frac{1}{2}{\displaystyle \sum }_{i=1}{e}_i^2,$$

(18)

Equation (18) satisfies the equation constraint:

$$y_i={\omega }^T\phi \left(x_i\right)+b+e_i,i=1,2,3,\dots ,N,$$

(19)

In the Equation (18), the first part is to adjust the weight and punish the large weight, and the second part represents the training error. For Equation (18), define the Lagrange function $L$:

$$L\left(w,b,e,\alpha \right)=J\left(w,e\right)-{\displaystyle \sum }_{i=1}^N{\alpha }_i\left\{{\omega }^T\phi \left(x_i\right)+b+e_i-y_i\right\},$$

(20)

In Equation (20), ${\alpha }_i$ is the Lagrange multiplier and $\gamma$ is the penalty parameter, which balances the complexity of the LS-SVM model, such as $y\left(x\right)$ and training error. According to the KKK (Karush-Kuhn-Tucker) optimization condition, Equation (20) is used to obtain the partial derivatives of $w$, $b$, $e$ and ${\alpha }_i$ respectively and make them all 0, and the optimization conditions are obtained.

$$\{\begin{array}{c}\frac{\partial L}{\partial w}=0\to w={\displaystyle {\displaystyle \sum }_{i=1}^N}{\alpha }_i\phi \left(x_i\right)\\ \frac{\partial L}{\partial b}=0\to {\displaystyle {\displaystyle \sum }_{i=1}^N}{\alpha }_i=0\\ \begin{array}{c}\frac{\partial L}{\partial e_i}=0\to {\alpha }_i=\lambda e_i\\ \frac{\partial L}{\partial {\alpha }_i}=0\to {\omega }^T\phi \left(x_i\right)+b+e_i-y_i=0\end{array}\end{array}$$

(21)

The $\omega$ is eliminated and the LS-SVM regression model was obtained.

$$y\left(x\right)={\displaystyle \sum }_{i=1}^N{\alpha }_{i}K\left(x,x_i\right)+b,$$

(22)

where $K\left(x,x_i\right)$ is the kernel function, $x$ represents the input vector of the training sample, and $x_i$ is the center of the kernel function. $\alpha$ and $b$ is the solution of Equation (21). Because there is a nonlinear relationship between the transformer fault and the DGA data, the radial basis kernel function (RBF), which is suitable to solve the nonlinear problem and has few kernel parameters, is selected as the kernel function for the research.

$$K\left(x,x_i\right)=\exp \left(-\frac{\Vert x-x_2\Vert {}^2}{2{\sigma }^2}\right),$$

(23)

where ${\sigma }^2$ is the kernel parameter. Penalty parameter $\gamma$ and kernel parameter ${\sigma }^2$ have great effect on the accuracy of LS-SVM model. The generalization ability of the model increases with the decrease of $\gamma$, while the training error increases. The smaller of kernel parameter, the higher of the model complexity, and a larger kernel parameter is easy to lead to lack of learning. So reasonable $\gamma$ and ${\sigma }^2$ values are the key to the success of the model.

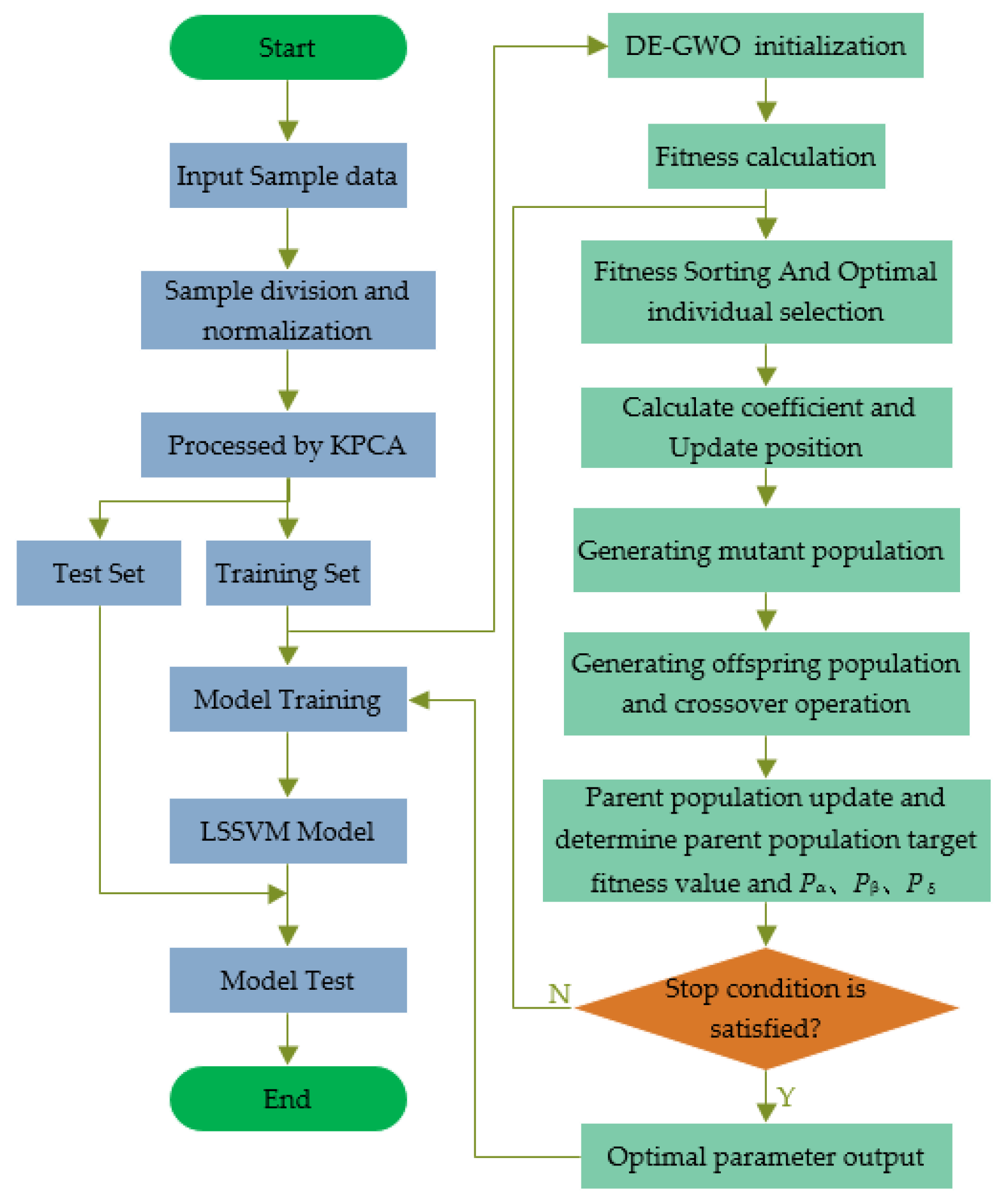
3. Fault Diagnosis Model Based on HGWO-LSSVM

In the proposed fault diagnosis method based on HGWO-LSSVM model, the HGWO is used to optimize the parameter of LSSVM algorithm. The construction of the model includes the following parts:

(1) Sample collection. The DGA data of various fault modes are collected to form the fault sample set, which is used as the training set of the fault diagnosis model.

(2) Feature set selection. Select commonly used feature set and optimal hybrid feature set as the input of the model, respectively.

(3) Sample division. The sample is divided into two groups: training data and test data. The training data is used in the simulation to establish the mathematical model, and the test data is used to validate the model.

(4) Sample normalization. After normalization, all the sample data values are in the range of [0,1], which makes the calculation speed of the model faster. The conversion function of normalization is as follows:

$$x_i^{\ast }=\frac{x_i-x_{min}}{x_{max}-x_{min}},$$

(24)

where: $x_i$ represents the actual value; $x_{max}$ and $x_{min}$ represent the maximum and minimum value, respectively.

(5) Feature extraction. The KPCA method is used for feature extraction to reduce the dimensions of the sample data and the number of principal components is selected with a cumulative contribution rate greater than 90%.

(6) Model construction. The steps of the transformer fault diagnosis algorithm based on HGWO-LSSVM model are as follows:

Step 1: Set each initial parameter including population size, maximum number of iterations, dimension, the scaling factors and the crossover probability factor CR.

Step 2: Initialize the population according to Equation (4), where $X$ consists of a kernel width parameter $\sigma$ and a regularization parameter $C$ of the least squares vector machine.

Step 3: Calculate the individual fitness values and arrange them in descending order, with the top three individual $X_{\alpha }$, $X_{\beta }$, $X_{\delta }$ as the upper wolves.

Step 4: Update the position of the parent population individual using Equation (15).

Step 5: According to Equations (6) and (7), the differential algorithm is used to perform mutation and cross-update to generate new children.

Step 6: Update the parent population according to Equation (8), and then update $C$, $A$, and $a$ according to Equations (11) and (12).

Step 7: Update the parental $P_{\alpha }$, $P_{\beta }$, $P_{\delta }$, and sort the grey wolf father population again. The algorithm termination condition is judged. When the condition is satisfied, the parents $P_{\alpha }$ and $f(P_{\alpha )}$ are returned, and the obtained optimal solutions $C$ and $\sigma$ are output.

Step 8: Establish an LSSVM model based on $\sigma$ and $C$.

The fault diagnosis model based on LSSVM integrated with KPCA and HGWO is shown in Figure 1. It includes two main parts. One is that the transformer DGA data is preprocessed by KPCA. The other is that the parameter of LSSVM model is optimized by HGWO.

Figure 1. Flowchart of Fault Diagnosis Model Based on hybrid grey wolf optimized least square support vector machine (HGWO-LSSVM).

4. Case study and Analysis

The MATLAB toolkit (R2018b, MathWorks, Natick, Massachusetts, USA) is used to implement the LSSVM fault diagnosis model using HGWO optimization mentioned above. At the same time, a large number of transformer DGA data were collected, and the data was preprocessed and classified to verify the effectiveness of the fault diagnosis model.

4.1. Fault Sample Collection

During the operation of the power transformer, internal heat or discharge failure will cause the transformer oil to decompose and generate gases, mainly including H₂, C₂H₄, C₂H₆, C₂H₄, C₂H₂, CO and CO₂. When faults of different type and degrees occur, the content of the seven gases will vary significantly. Therefore, the content of these seven gases can be selected as the feature set.

In this paper, transformer DGA data have been collected from many literatures. These literatures analyze the transformer fault condition and the processing process, and finally determine the specific fault cause and fault type through the disintegration inspection. The fault types of the transformer include low temperature overheating T1 (<300 °C), medium and low overheating T2 (300~700 °C), and high temperature overheating T3 (> 700 °C), low energy discharge (D1), high energy discharge (D2), partial discharge (PD), including normal mode (N). The distribution of the sample DGA data used in this study are shown in Table 1. In addition, part of the field DGA data with actual faults and the fault type diagnosed by the IEC ratio method are shown in Table 2.

Table 1. Distribution of transformer sample data.

	Fault Type	Total	N	T1	T2	T3	PD	D1	D2
Voltage Level
110 kV		244	56	0	16	121	1	8	42
220 kV		734	184	2	63	222	55	63	145
500 kV		191	30	1	12	54	8	57	29
750 kV		112	10	2	1	0	0	5	94
Total		1281	280	5	92	397	64	133	310

Table 2. Partial field dissolved gas analysis (DGA) data with actual faults.

No.	H2	CH4	C2H2	C2H4	C2H6	CO	CO2	Actual Fault	IEC Ratio
1	96	20.61	38.57	15.82	5.4	367	854	D1	D2
2	89	20.01	39.4	16.36	6.16	354	874	D1	D2
3	134.78	34.7	94.1	40.54	4.5	53.1	89.76	D2	D2
4	207.6	44.14	139	80.9	3.8	29.62	331.7	D2	D2
5	292.58	38.39	0	0.84	3.87	161.54	523.68	PD	N
6	522.2	43.21	1.01	1.02	16.73	158.6	2251.3	PD	D2
7	529.75	58.96	1.27	5.06	18.12	160.5	2263.98	PD	D2
8	2525.3	130.55	0	1.53	14.25	612.17	2687.13	PD	PD
9	3417.62	131.42	0	1.22	14.36	428.03	2770.29	PD	PD
10	5869.58	175.21	0	1.45	16.45	624.47	3684.56	PD	PD
11	4966.14	145.66	0	1.28	15.33	503.42	3397.51	PD	PD
12	6.82	10.13	0	74.85	3.81	662.43	5871.86	T2	T3
13	14	33.3	0	20.1	8	101	654	T2	T2
14	87	223.6	0	121.1	49.6	62	498	T2	T2
15	78	196.3	0	109.3	46.1	51	384	T2	T2
16	22.04	171.05	0	182.04	91.29	1651.57	16,390.39	T2	T2
17	82.74	108.92	3.91	249.8	28.06	809.04	2053.72	T3	T3
18	3.11	6.61	0.26	36.43	3.23	296.54	2367.99	T3	T3
19	3.05	5.84	0.27	37.28	3.38	256.61	2970.88	T3	T3
20	3.82	7.93	0.13	52.68	3.37	406.24	2770.54	T3	T3

Considering that the fault sample data of the low temperature overheating is relatively few, the two types of faults, low temperature overheating and medium temperature overheating, are regarded as one category. Thus, the failure types involved in this paper include five categories, namely, low to medium temperature overheating (T2), high temperature overheating (T3), low energy discharge (D1), high energy discharge (D2) and partial discharge (PD), including normal mode (N), a total of 6 categories.

4.2. Feature Set Selection

Feature selection is crucial for a classification mathematical model. It is necessary to select features that reflect the core characteristics of the sample and consider reducing the computational errors caused during the model training. In a transformer fault diagnosis model, the DGA data are used as inputs of the diagnostic model. The feature sets that have been widely used so far include two categories: dissolved gases concentration and dissolved gas ratios [77], as shown in Table 3.

Table 3. Common feature set of transformer fault diagnosis.

Feature Set		Content
DGA gases	Total	H2, CH4, C2H2, C2H4, C2H6, CO, CO2
	Common	H2, CH4, C2H2, C2H4, C2H6
DGA gas ratios	Doernenberg	CH4/H2, C2H2/C2H4, C2H2/CH4, C2H6/C2H2
	Roger	C2H6/CH4, C2H2/C2H4, CH4/H2, C2H4/C2H6
	IEC 60599	C2H2/C2H4, CH4/H2, C2H4/C2H6
	CIGRE gas ratio	C2H2/C2H6, H2/CH4, C2H4/C2H6, C2H2/H2, CO/CO2

Studies have shown that [24,47,48,78], using a hybrid feature set including DGA gas and gas ratios as input is preferred over using only DGA gas or gas ratios. The optimal hybrid feature set selected in this paper consists of CH₄/H₂, CH₄/C₂H₄, CH₄/C₂H₆, CH₄/CO₂, H₂/C₂H₂, H₂/CO, H₂/CO₂, H₂/TH, C₂H₂/CO, C₂H₂/TH, C₂H₄/TH, C₂H₆/TH, C₂H₂ and C₂H₆, which has been proved that high diagnostic accuracy can be obtained [24].

4.3. Multi-Class Classification Model

The fault diagnosis process of the transformer is essentially a multi-class classification problem. As a two-classifier, LS-SVM cannot be directly used for multi-class classification. In the diagnosis model proposed in this paper, a multi-class binary tree based on LS-SVM is developed.

The model includes a total of 5 sub-classifiers, which are proposed to identify the six fault types: low to medium temperature overheating (T2), high temperature overheating (T3), low energy discharge (D1), high energy discharge (D2), partial discharge (PD) and normal mode. LS-SVM1 separates the normal state from the fault state while LS-SVM2 separates discharge faults from thermal faults. The third and fourth LS-SVM classify the thermal faults as either low to medium temperature overheating or high temperature overheating, and discharge faults as either partial discharge or low energy discharge and high energy discharge, respectively, while the fifth LS-SVM is used to classify the low energy discharge and high energy discharge. Meanwhile, to improve training and diagnostic efficiency, the input of each sub-classifier contains the most effective feature parameters for identifying the fault, which are optimized by HGWO. The multi-class binary tree constructed in this paper is shown in Figure 2.

Figure 2. Binary tree of transformer fault diagnosis model.

4.4. Results and Discussion

HGWO is used to optimize the parameters of the LS-SVM in the multi-classification model. The relevant initial parameters of the HGWO algorithm are set as: population size is 50, maximum iteration number is 200, and variable dimension is 2. In the differential evolution algorithm, the scaling factors $M_{max}$ and $M_{min}$ are 0.8 and 0.2, respectively, and the crossover probability factor CR is 0.2. The HGWO-LSSVM fault diagnosis model has been implemented by the MATLAB simulation platform on an 8-core Lenovo laptop (T470P, Lenovo, Beijing, China) with 8 GB memory and 2.8 GHz clock, running Windows 10 enterprise operating system (64-bit).

4.4.1. Example 1

The training and test results of the proposed model are summarized in Table 4. The diagnostic accuracy of the transformer fault diagnosis model proposed in this paper is 97.45%, and the diagnostic time is 2225 ms.

Table 4. Training results HGWO-LSSVM fault diagnosis model.

Model	Training Sample	Test Sample	Classification Accuracy (%)	C	σ	Training Time (ms)
LS-SVM1	900	381	98.7	5.8263	1.8523	3264
LS-SVM2	700	299	97.0	2.3560	2.6530	2646
LS-SVM3	346	148	96.62	3.6382	1.8635	2235
LS-SVM4	355	152	97.37	1.8693	0.9685	2024
LS-SVM5	310	123	97.56	1.0635	0.8625	1956

Traditional DGA methods, including the IEC three-ratio method, Rogers ratio method, Duval triangle method, Dornenburg ratio method, are adopted to diagnose the testing data set for comparison. Table 5 shows the fault diagnosis accuracy for different methods using the same sample. The Dornenburg ratio method shows the lowest accuracy. The accuracy of Rogers ratio method is 63.84%, lower than the three ratio method and Duval triangle method. The accuracy of three ratio method is better than Duval triangle method. Because three-ratio and Duval triangle methods are obtained from typical faults, they will fail in dealing with some complex faults. The accuracy of the proposed method is 97.45%. Compared with the traditional DGA methods, the LSSVM method shows a relatively good diagnosis accuracy rate. When the LSSVM parameters are optimized by HGWO, the accuracy of the fault diagnosis improves substantially. However, misclassifications of the original DGA data collected from the literatures may lead to errors in the accuracy in this paper.

Table 5. Accuracy rate for the different diagnostic methods.

Method	IEC Three-Ratio	Rogers Ratio	Duval Triangle	Dornenburg Ratio	LSSVM	HGWO-LSSVM
Accuracy Rate	75.41%	63.84%	73.73%	53.26%	88.75%	97.45%

4.4.2. Example 2

In order to verify the superiority of the proposed method, the sample data is used to construct the fault diagnosis model by using LSSVM, GWO-LSSVM, PSO-LSSVM, GA-LSSVM, etc. The results are compared with the method in this paper, as shown in Table 6 and Figure 3. To further verify the improvement of using the optimal hybrid feature set to the model accuracy, we applied dissolved gases concentration and the optimal hybrid feature set as inputs, respectively. And the results are shown in Table 7.

Table 6. Comparison of different fault diagnosis model.

Model	Average	Classification Accuracy		Training Time (ms)
		Upper Limit(%)	Lower Limit(%)
LSSVM	88.75	90.25	86.75	3654
PSO-LSSVM	89.38	91.6	87.16	3562
GA-LSSVM	92.25	92.6	91.9	4526
GWO-LSSVM	94.6	95.25	93.95	2615
HGWO-LSSVM	97.45	98.7	96.62	2135

Figure 3. Comparison of accuracy for different fault diagnosis model.

Table 7. Comparison of using dissolved gases concentration and optimal hybrid DGA feature subset (OHFS) as input, respectively.

Model	Classification Accuracy (%)
	Dissolved Gases Concentration	OHFS
LSSVM	80.35	90.25
PSO-LSSVM	82.63	91.6
GA-LSSVM	83.55	92.6
GWO-LSSVM	85.28	95.25
HGWO-LSSVM	87.53	98.7

It can be seen from Table 6:

(1) The average training time of the classifier in the proposed method is far less than the training time of the classifiers constructed by several other methods, indicating that training time of the transformer fault diagnosis model can be greatly shortened according to the method of this paper, which can improve the efficiency of fault diagnosis and increase the online diagnostic capabilities.

(2) Under the same fault sample set, the proposed method achieves a higher average classification accuracy in the diagnosis of various types of faults. In addition, compared with other optimization algorithms, GWO-LSSVM achieves higher classification accuracy and fast convergence speed, which proves that the good performance of GWO algorithm in parameter optimization.

(3) Compared with GWO-LSSVM, the fault diagnosis model proposed by HGWO-LSSVM achieves higher fault classification accuracy and faster training speed, indicating that after the combined with DE algorithm, population diversity is improved through operations such as crossover and mutation. At the same time, the DE algorithm forces GWO to jump out of the stagnation state when attacking the prey, thus improving the local optimum avoidance.

It can be seen from Table 7 that while using the optimal hybrid feature set as the inputs, the accuracy of the fault diagnosis model can be significantly improved, which means data preprocessing and feature selection play an important role in the construction of fault diagnosis model.

According to the results above, the fault diagnosis model proposed in this paper not only has higher diagnostic accuracy, but also consumes less time and has higher efficiency. However, misclassifications of the raw data may affect the accuracies in this paper.

5. Conclusions

In this paper, a transformer fault diagnosis model based on HGWO-LSSVM is proposed. First, transformer DGA data from many literatures are collected and the optimal hybrid feature set is selected as the input of the model. KPCA is used for feature selection. The hybrid grey wolf optimizer, combined GWO with DE, is proposed to optimize the LSSVM to develop a fault diagnosis model. The proposed model is compared with traditional DGA methods and other models such as LSSVM, GWO-LSSVM, PSO-LSSVM and GA-LSSVM. The major conclusions in this paper are listed as follows:

(1) Compared with traditional DGA methods, the model proposed in this paper has achieved better performance on transformer fault diagnosis, indicating the effectiveness of the proposed model.

(2) Compared with other optimization algorithms, GWO-LSSVM achieves higher classification accuracy and fast convergence speed, which proves that the good performance of GWO algorithm in parameter optimization than PSO and GA.

(3) The model proposed by HGWO-LSSVM achieves higher fault classification accuracy and faster training speed than GWO-LSSVM, which verifies the effectiveness of combining DE with GWO.

(4) The dissolved gases and hybrid DGA features are used as DGA feature sets, respectively. The accuracy of the fault diagnosis model based on the optimal hybrid feature set has been improved by nearly 10% than DGA gases. It is proved that the optimal hybrid feature set can indeed improve the accuracy of fault diagnosis model.

(5) Accuracies calculated in this paper, however, are significantly affected by the misidentifications of faults that have been made in the DGA data collected from the literature. Therefore, in order to ensure the reliability of the accuracy for the model, it is very important to ensure the accuracy of the raw data.

At present, most of the transformer fault diagnosis model are rarely taking the correlation between transformer faults and other factors other than DGA data into consideration, which lead to a low generalization ability of the model and the accuracy of fault diagnosis will decrease for a new data set. In fact, the failure of the transformer, in addition to the relationship with the DGA data, may also be related to insulating oil type [79], voltage levels, operating oil temperature, load, operating years, and so on [80]. In this paper, the DGA data are arranged according to the voltage level, including four voltage levels of 110 kV, 220 kV, 500 kV, and 750 kV. Therefore, in the future work, the DGA data will be classified by the voltage level to develop fault diagnosis models, from which the relationship between the voltage level and the fault type of the DGA data can be analyzed. Based on the results of the study, a more generalized model can be proposed which can further improve the accuracy of transformer fault diagnosis.