The Application of Building Physics in the Design of Roof Windows
Abstract
:1. Introduction
2. Problem Analysis
3. Methods
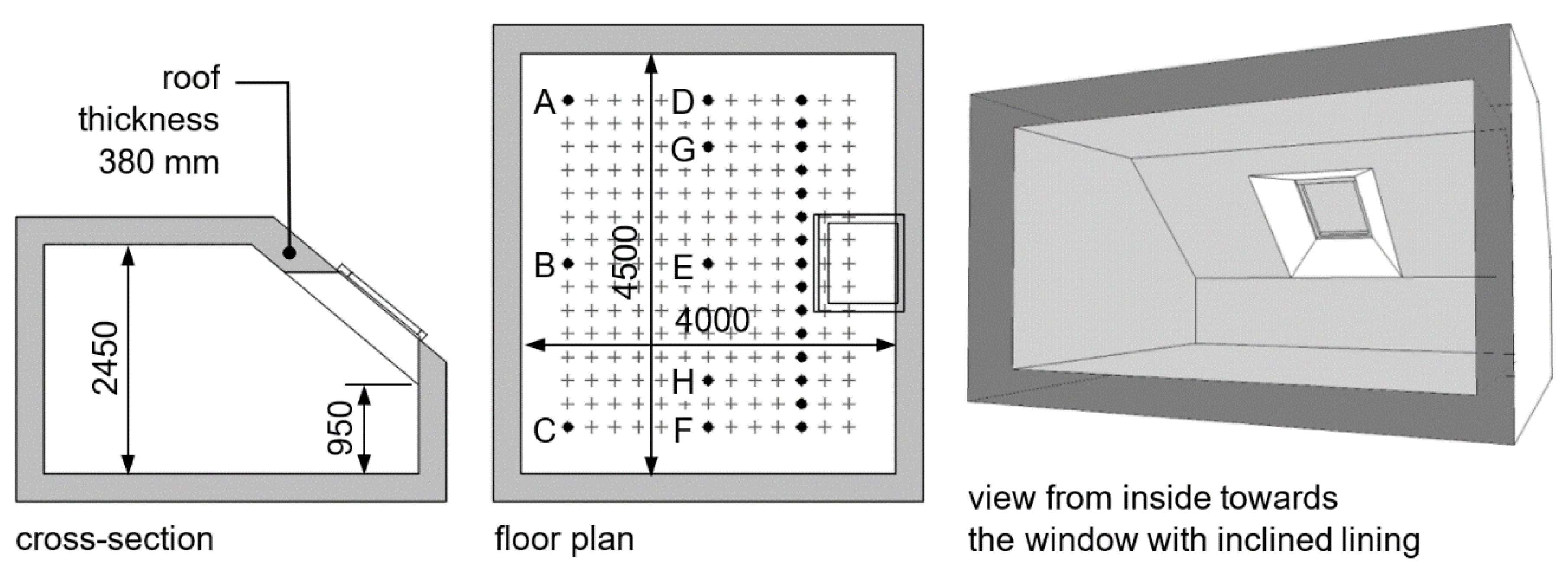
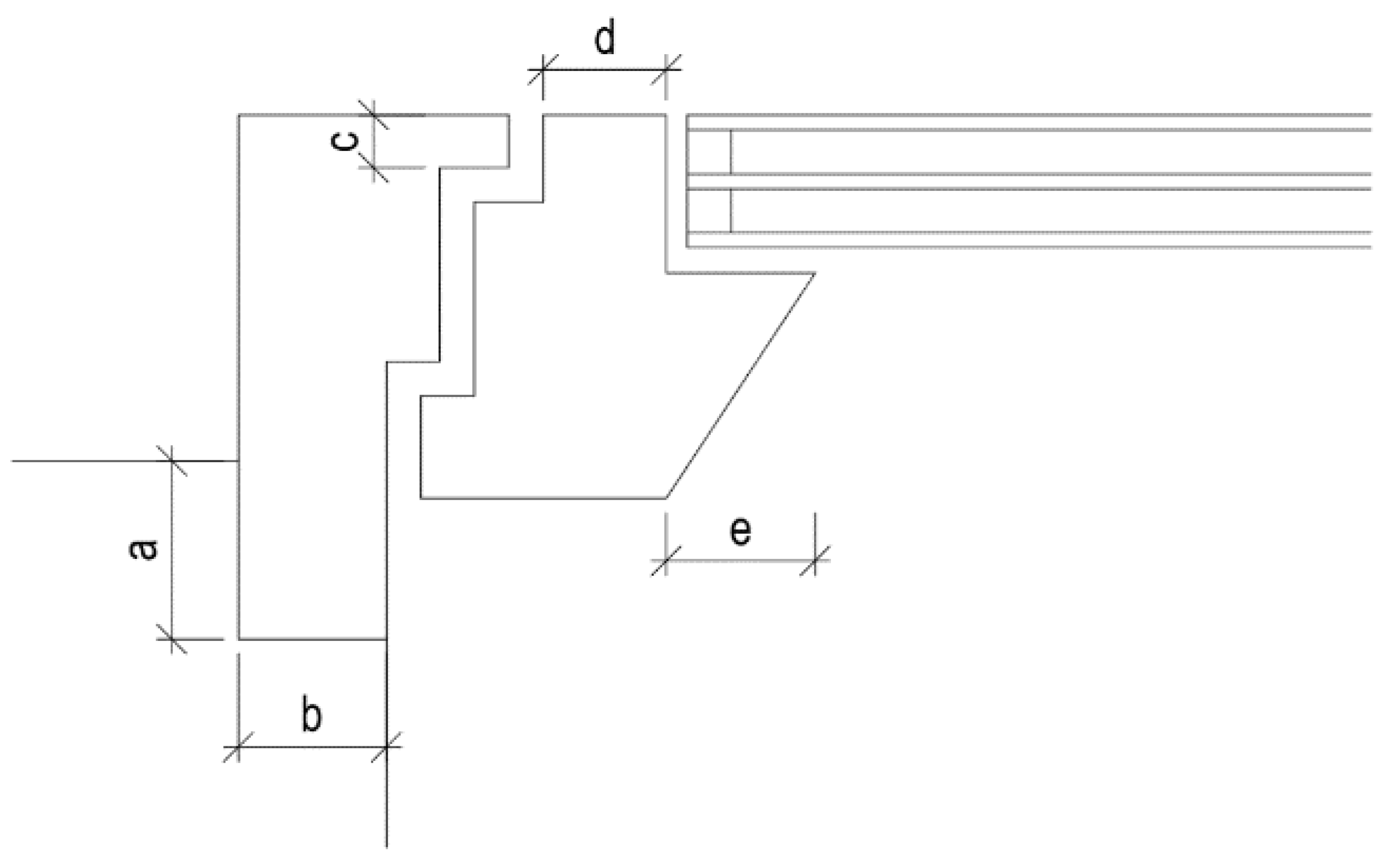
3.1. Parametric Studies
3.2. Real Design Solution
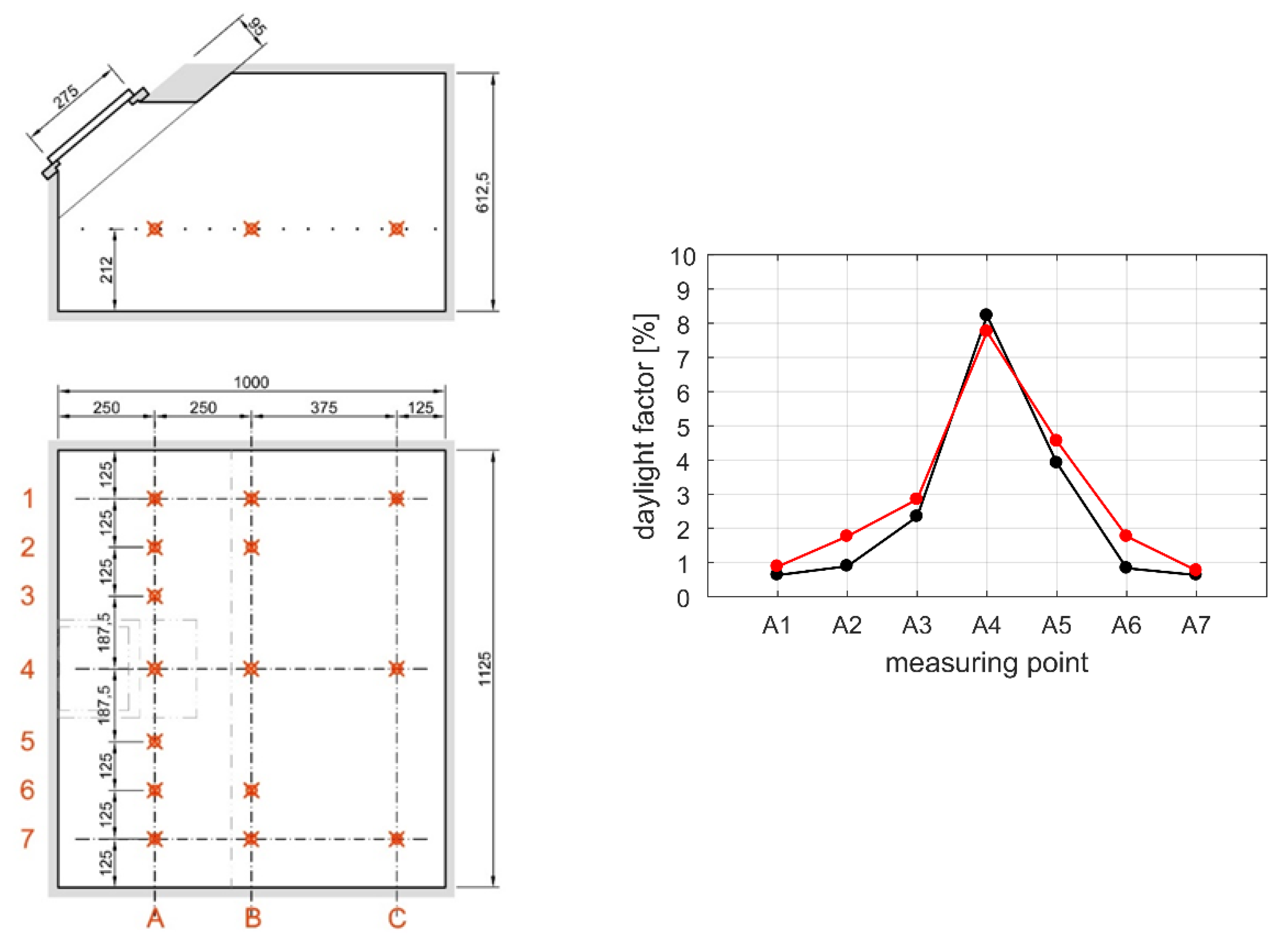
3.3. Daylight Simulation
3.4. Daylight Measurements
3.5. Formulation of General and Detailed Recommendations
4. Results
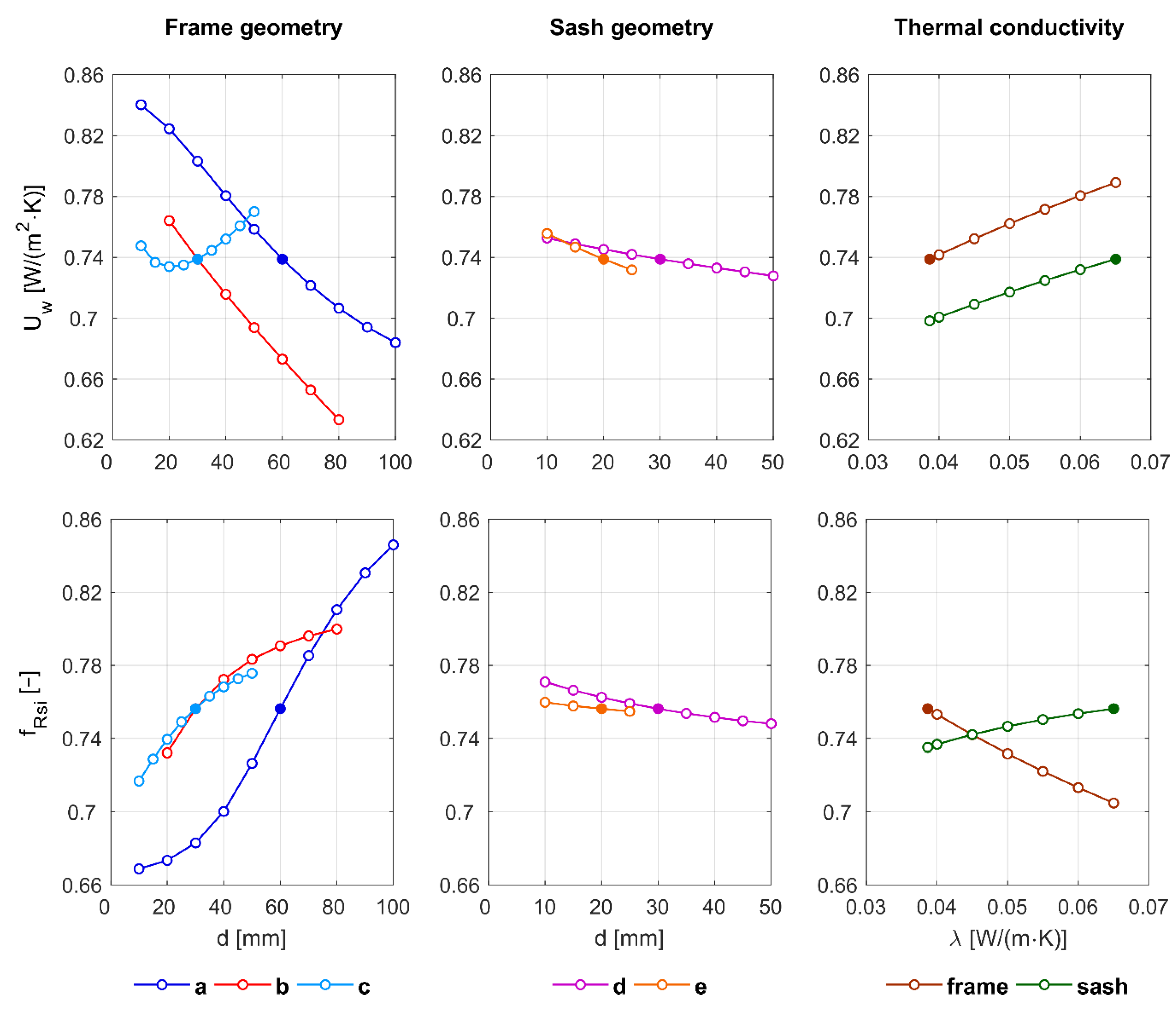
4.1. Parametric Studies
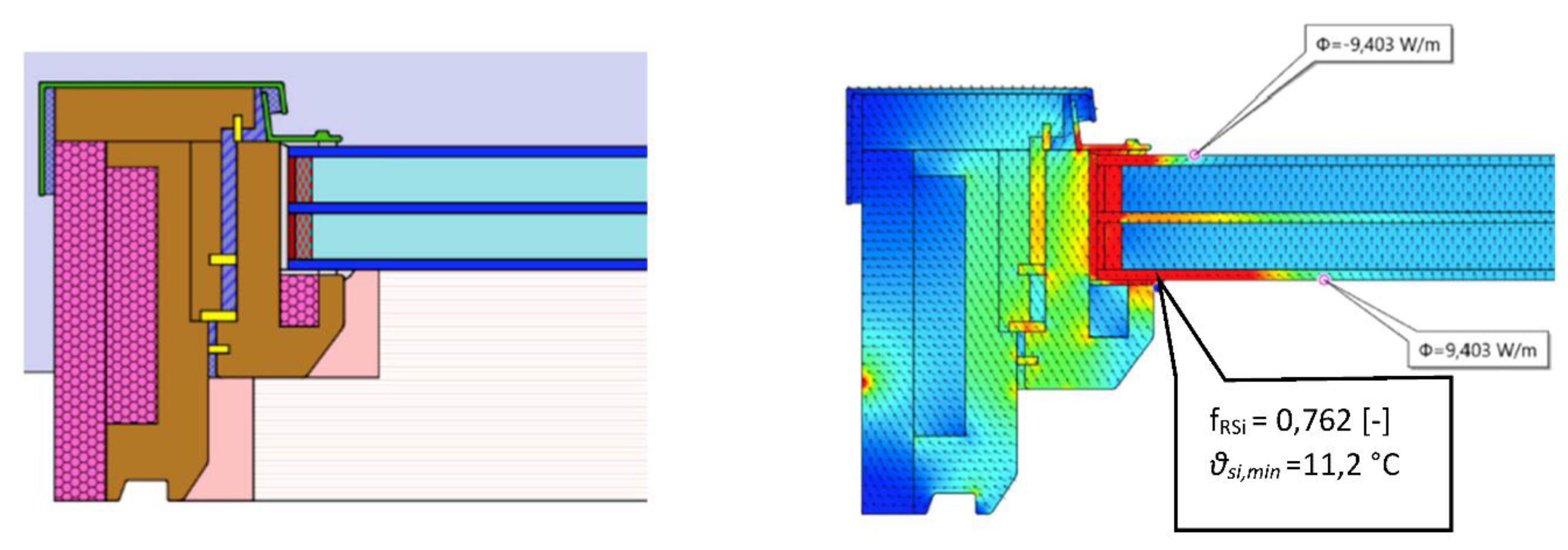
4.2. Real Design Solution
4.3. Daylight Simulations
4.4. Daylighting Measurements
5. Discussion
- (a)
- The risk of overheating. Overheating and/or cooling energy demand of attic rooms and, in this context, the possibility of advanced controlled shading of roof windows [30].
- (b)
- 3D heat transfer models. Due to the fact that windows contain parts for which it is not possible to perform a 2D calculation, especially in corners, it might be useful to use the 3D calculation of a whole window including coupling, taking advantage of the symmetry. However, to achieve this, some simplifications would have to be made, for example, for the opening mechanism, handle, and eventually ventilation flaps.
- (c)
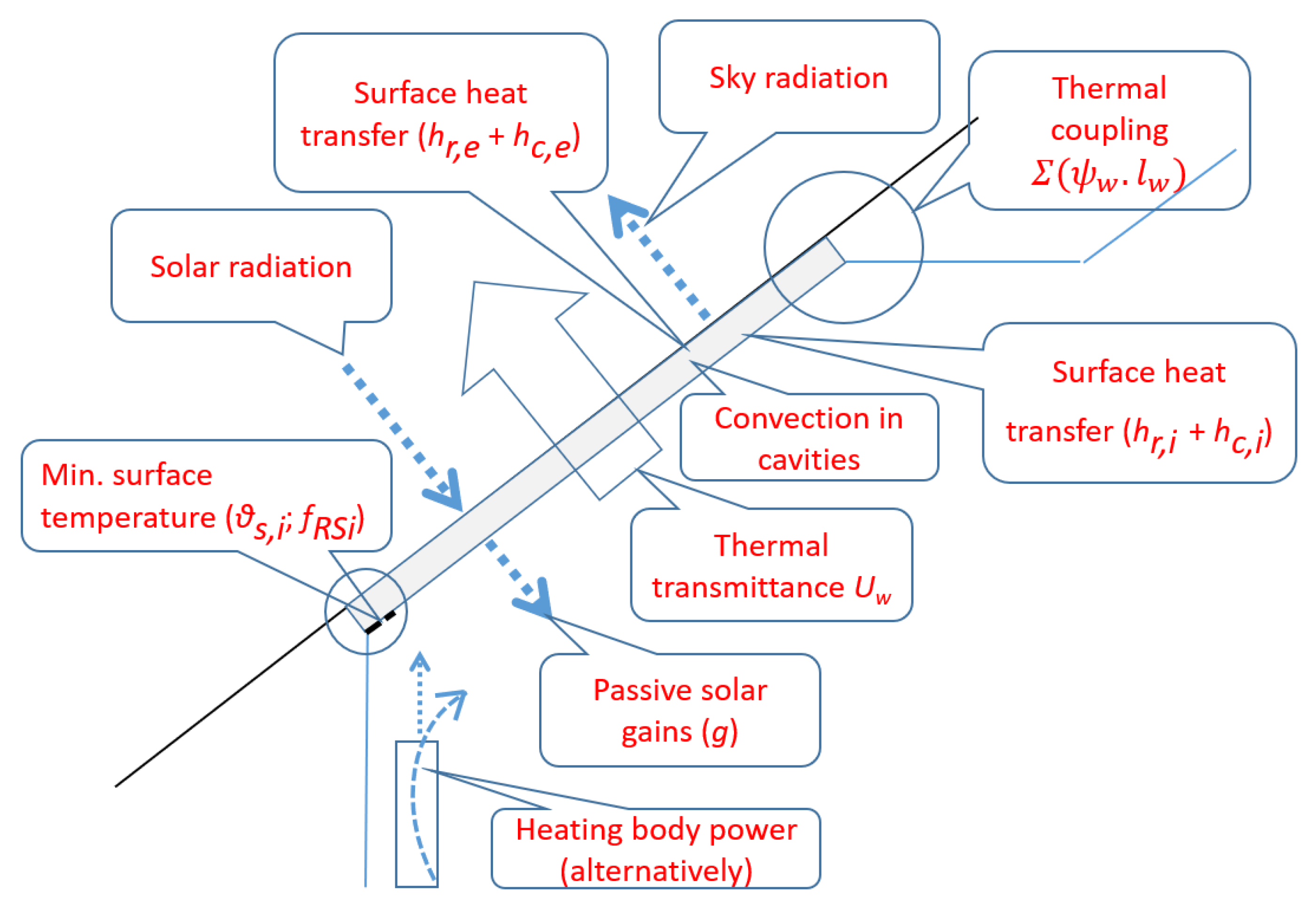
- Values of the heat transfer between the local surface and surroundings. Aside from the complexity of the calculations, the results were further burdened by uncertainties regarding the boundary conditions. Very detailed studies of heat transfer near to the surfaces of roof windows are needed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Area, m2 |
| D | Daylight factor, % |
| U | Thermal transmittance, W/(m2·K) |
| f | Surface temperature factor, dimensionless |
| g | Solar factor, dimensionless |
| h | Surface heat transfer coefficient, W/(m2·K) |
| l | Length, m |
| ψ | Linear thermal transmittance, W/(m·K) |
| ρ | Light reflectance, dimensionless |
| τ | Light transmittance, dimensionless |
| Indices | |
| a | Air |
| c | Convection |
| g | Glazing |
| e | Exterior |
| f | Frame |
| i | Interior |
| inst | Installed |
| r | Radiation |
| s, S | Surface |
| R | Required |
| w | Window |
Appendix A
| Thermal Transmittance | Heat Transfer Coefficient | Increased Heat Transfer (%) (100% = No Windows) | |||
|---|---|---|---|---|---|
| (W/K) | (%) | ||||
| A | |||||
| Roof | 0.3 W/(m2·K) | 40.2 | 69 | 69 | |
| Roof windows | 1.8 W/(m2·K) | 10.8 | 19 | 31 | |
| Window–roof thermal coupling | 0.3 W/(m·K) | 7.2 | 12 | ||
| Total | 58.2 | 100 | 139 | ||
| B | |||||
| Roof | 0.1 W/(m2·K) | 13.4 | 49 | 49 | |
| Roof windows | 1.5 W/(m2·K) | 9.0 | 33 | 51 | |
| Window–roof thermal coupling | 0.2 W/(m·K) | 4.8 | 18 | ||
| Total | 27.2 | 100 | 194 | ||
| C | |||||
| Roof | 0.1 W/(m2·K) | 13.4 | 71 | 71 | |
| Roof windows | 0.6 W/(m2·K) | 3.6 | 19 | 29 | |
| Window–roof thermal coupling | 0.08 W/(m·K) | 1.9 | 10 | ||
| Total | 18.9 | 100 | 135 | ||
Appendix B. Results of Observations of Heat Transfer at an Internal Surface under Real Conditions—Preliminary Comparison of a Large Vertical Window and a Small Roof Window (Case Study)
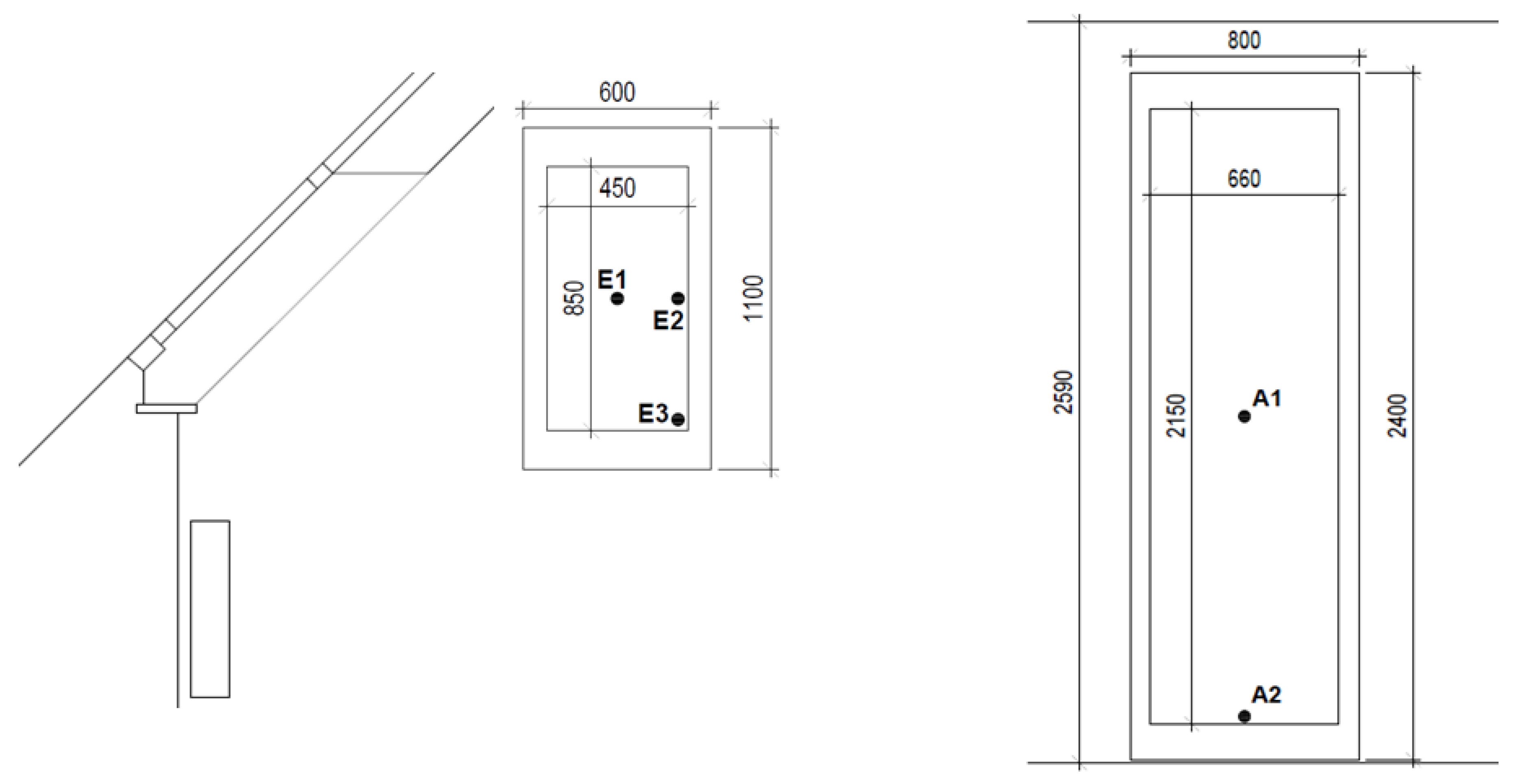


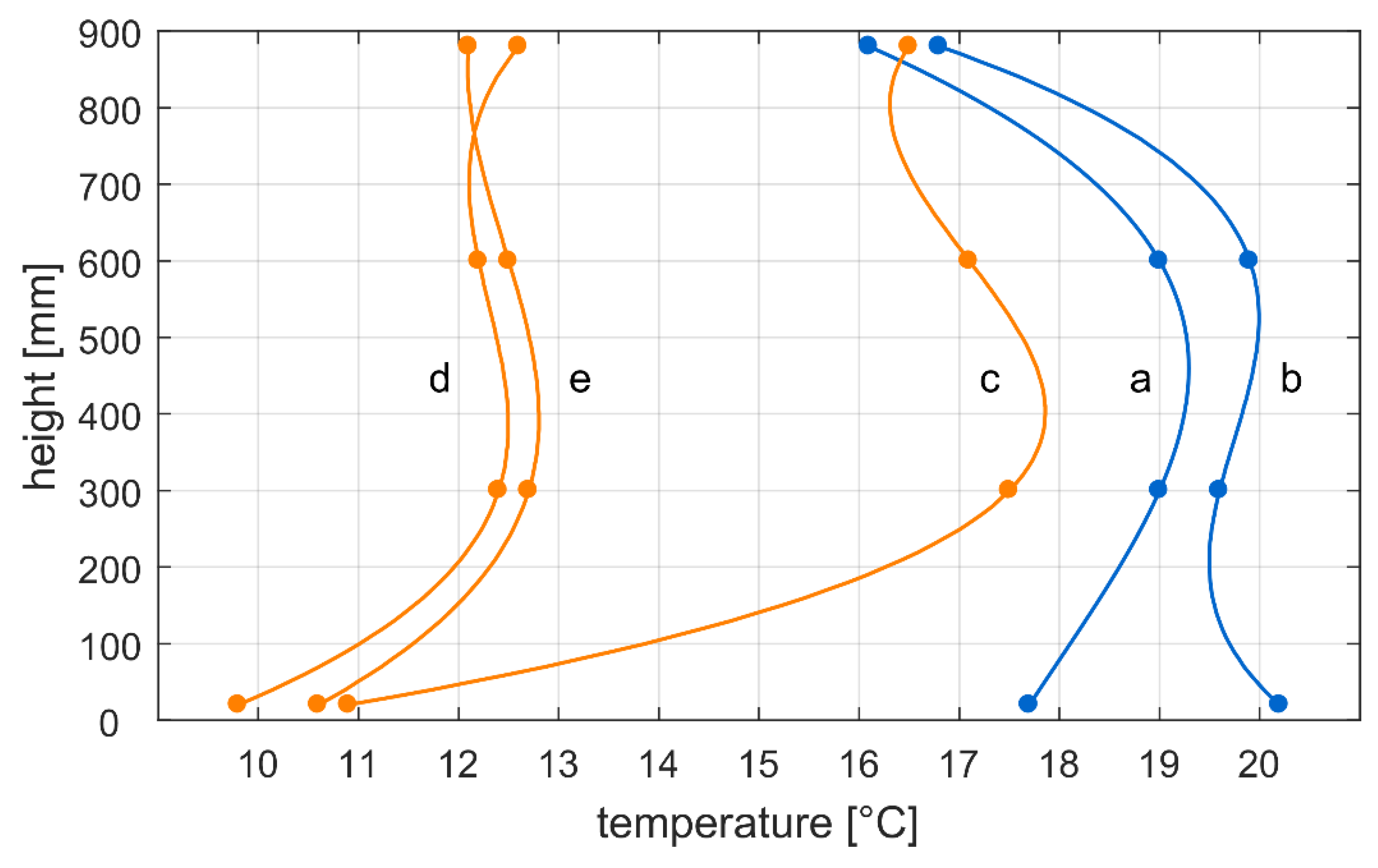

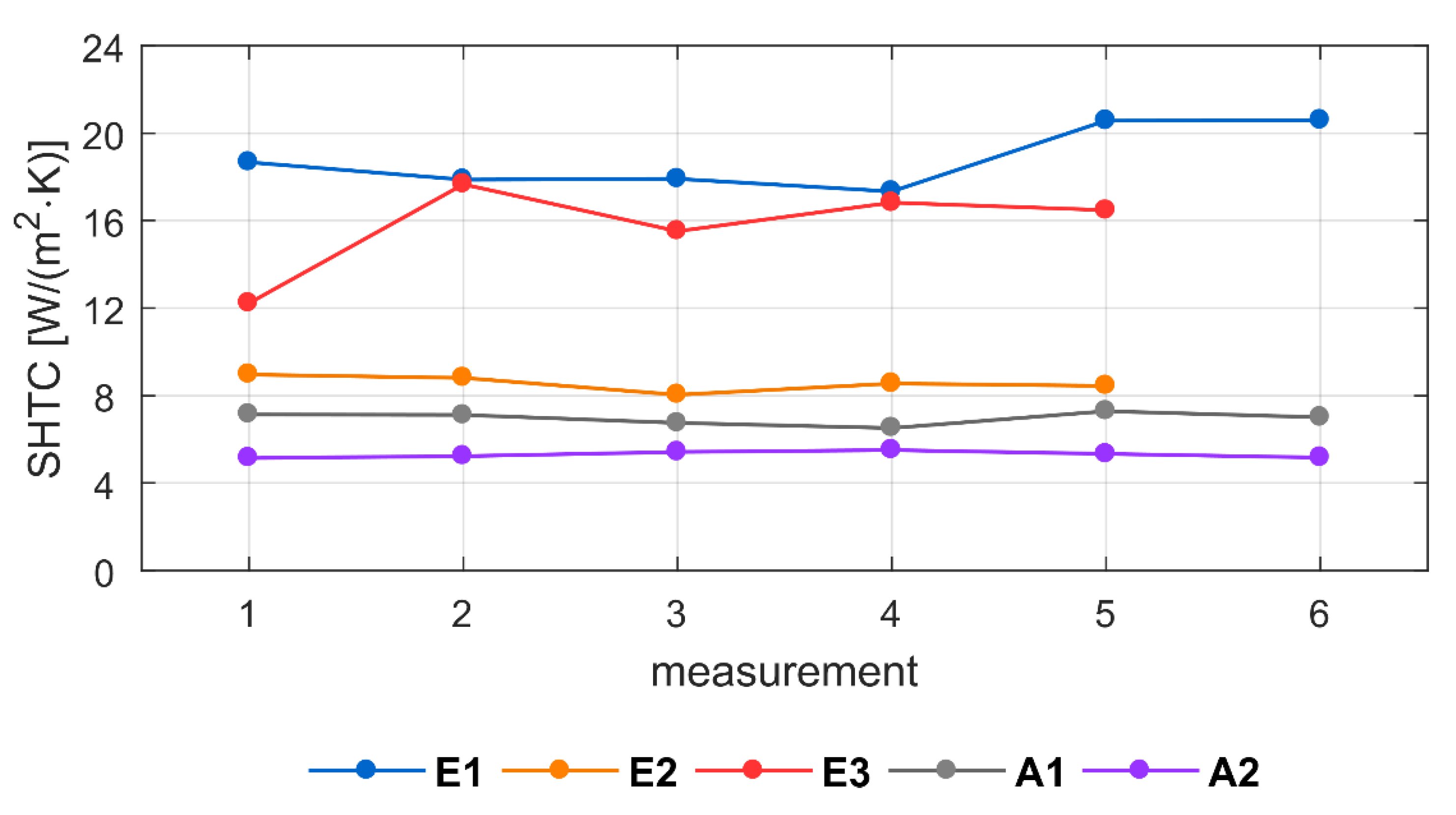
| Window | Position | Mean Value hsi W/(m2·K) | |
|---|---|---|---|
| Glazed balcony door | Center | A1 | 7.0 |
| Bottom | A2 | 5.3 | |
| Roof window | Center | E1 | 18.8 |
| Center, right | E2 | 8.6 | |
| Bottom, right edge | E3 | 15.7 | |
References
- Hens, H. Building Physics. Heat, Air and Moisture. Fundamentals and Engineering Methods with Examples and Exercises; Wilhelm Ernst & Sohn: Berlin, Germany, 2012. [Google Scholar]
- European Committee for Standardization. Set of European Standards in Responsibility of CEN TC89 Thermal Performance of Buildings and Building Components; European Committee for Standardization (CEN): Brussels, Belgium, 2019. [Google Scholar]
- Technological Agency of the Czech Republic. Project TH01021120 SONG—Střešní Okna Nové Generace (Skylights of New Generation). Technological Agency of the Czech Republic: Prague, Czech Republic; Available online: https://www.uceeb.cz/projekty/stresni-okna-nove-generace (accessed on 16 June 2019).
- Schnieders, J.; Feist, W.; Rongen, L. Passive Houses for different climate zones. Energy Build. 2015, 105, 71–87. [Google Scholar] [CrossRef]
- Kriterien für den Passivhaus-, EnerPHit- und PHI-Energiesparhaus-Standard. Passivhaus Institut. Available online: https://passiv.de/downloads/03_zertifizierungskriterien_gebaeude_de.pdf (accessed on 1 March 2019).
- Grove-Smith, J.; Aydin, V.; Feist, W.; Schnieders, J.; Thomas, S. Standards and policies for very high energy efficiency in the urban building sector towards reaching the 1.5 degrees C target. Curr. Opin. Environ. Sustain. 2018, 30, 103–114. [Google Scholar] [CrossRef]
- The New Passive House Classes. Available online: https://passipedia.org/certification/passive_house_categories (accessed on 1 March 2019).
- D’Agostino, D.; Mazzarella, L. What is a nearly zero energy building? Overview, implementation and comparison of definitions. J. Build. Eng. 2019, 21, 200–212. [Google Scholar] [CrossRef]
- Erhorn-Kluttig, H.; Erhorn, H.; Reiss, J. Plus energy—A new energy performance standard in Germany for both residential and non-residential buildings. Adv. Build. Energy Res. 2015, 9, 73–88. [Google Scholar] [CrossRef]
- Informationen, Kriterien und Algorithmen für Zertifizierte Passivhaus Komponenten: Transparente Bauteile und Öffnungselemente in der Gebäudehülle. Available online: http://www.passiv.de/downloads/03_zertifizierungskriterien_transparente_bauteile.pdf (accessed on 1 March 2019).
- Gustavsen, A.; Arasteh, D.; Jelle, B.P.; Curcija, C.; Kohler, C. Developing low conductance window frames: Capabilities and limitations of current window heat transfer design tools—State-of-the-art review. J. Build. Phys. 2008, 32, 131–153. [Google Scholar] [CrossRef]
- Okna stresni, zateplovací sada thermos. Available online: https://www.oknastresni.cz/zatepleni-oken/zateplovaci-sada-thermos (accessed on 20 October 2018).
- Component Database. Roof Windows. Passivhaus Institut. Available online: https://database.passivehouse.com/de/components/list/roof_window (accessed on 1 March 2019).
- European Committee for Standardization. EN 673 Glass in Buildings; European Committee for Standardization (CEN): Brussels, Belgium, 2011. [Google Scholar]
- Van de Bossche, N.; Buffe, L.; Janssens, A. Thermal optimization of window frames. In Proceedings of the 6th International Building Physics Conference, IBPC 2015, Torino, Italy, 14–17 June 2015; Volume 78. [Google Scholar]
- Misiopecki, C.; Bouquin, M.; Gustavsen, A.; Jelle, B.P. Thermal modeling and investigation of the most energy-efficient window position. Energy Build. 2018, 158, 1079–1086. [Google Scholar] [CrossRef]
- European Committee for Standardization. EN ISO 13789 Thermal Performance of Buildings—Transmission and Ventilation Heat Transfer Coefficients—Calculation Method; European Committee for Standardization (CEN): Brussels, Belgium, 2018. [Google Scholar]
- UNMZ. CSN 73 0540-2 2011 Thermal Protection of Buildings. Part 2—Requirements; UNMZ: Prague, Czech Republic, 2011. [Google Scholar]
- Tywoniak, J.; Staněk, K.; Calta, V. Roof windows for passive houses what can be improved? In Proceedings of the 7th International Building Physics Conference IBPC 2018, Syracuse, NY, USA, 23–26 September 2018; Syracuse University: Syracuse, NY, USA, 2018; pp. 1449–1454. [Google Scholar]
- European Committee for Standardization. EN 14351-1 Windows and EXTERNAL Pedestrian Doorsets without Resistance to Fire and/or Smoke Leakage; European Committee for Standardization (CEN): Brussels, Belgium, 2018. [Google Scholar]
- European Committee for Standardization. EN ISO 12567-2. Thermal Performance of Windows and Doors—Determination of Thermal Transmittance by Hot Box Method—Part 2: Roof Windows and other Projecting Windows; European Committee for Standardization (CEN): Brussels, Belgium, 2006. [Google Scholar]
- COMSOL Multiphysics 4.4. Available online: https://www.comsol.com (accessed on 5 March 2016).
- European Committee for Standardization. EN ISO 10077-2 Thermal Performance of Windows, Doors and Shutters—Calculation of Thermal Transmittance—Part 2: Numerical Method for Frames; European Committee for Standardization (CEN): Brussels, Belgium, 2017. [Google Scholar]
- Svend, S.; Lautsen, J.B.; Kragh, J. Linear thermal transmittance of the assembly of the glazing and the frame in windows. In Proceedings of the 7th Symposium on Building Physics in the Nordic, Reykjavik, Iceland, 13–15 June 2005; IBRI: Reykjavik, Iceland, 2005; pp. 995–1002. [Google Scholar]
- Compacfoam. Available online: http://www.compacfoam.at (accessed on 20 April 2019).
- Software HTflux. Available online: https://www.htflux.com (accessed on 20 January 2019).
- European Committee for Standardization. EN ISO 10211 Thermal Bridges in Building Construction—Heat Flows and Surface Temperatures—Detailed Calculations; European Committee for Standardization (CEN): Brussels, Belgium, 2018. [Google Scholar]
- Velux Daylight Visualiser. Available online: https://www.velux.com/article/2016/daylight-visualizer (accessed on 20 January 2019).
- European Committee for Standardization. EN ISO 12667 Thermal Performance of Building Materials and Products. Determination of Thermal Resistance by Means of Guarded Hot Plate and Heat Flow Meter Methods. Products of High and Medium Thermal Resistance; European Committee for Standardization (CEN): Brussels, Belgium, 2001. [Google Scholar]
- Intellectual Property Office. Exterior Shading System with Integrated Functions for Roof Windows; Utility Model CZ 32088; Intellectual Property Office: Prague, Czech Republic, 2018. [Google Scholar]

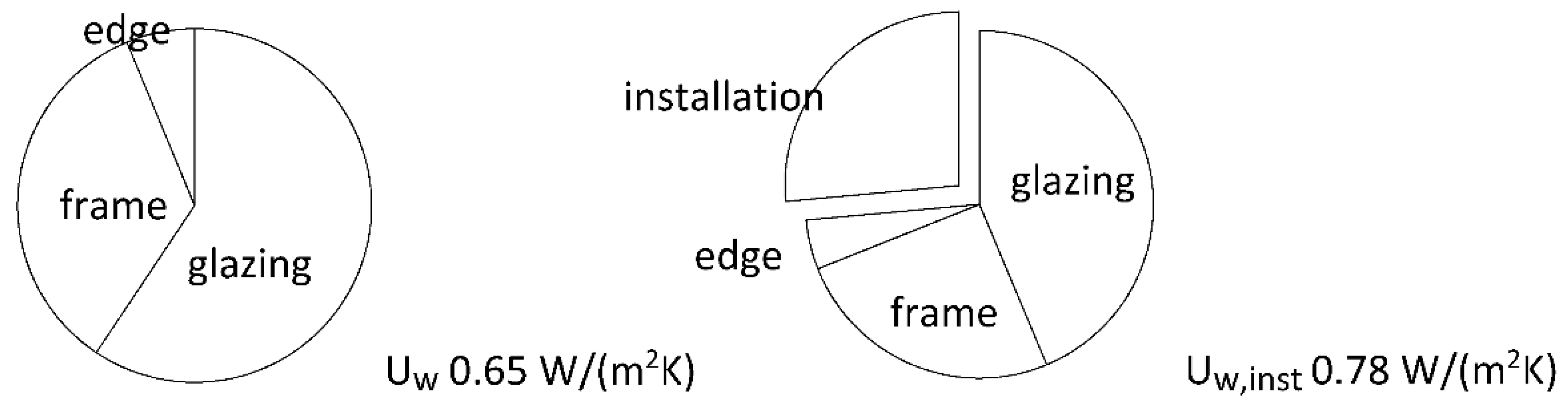
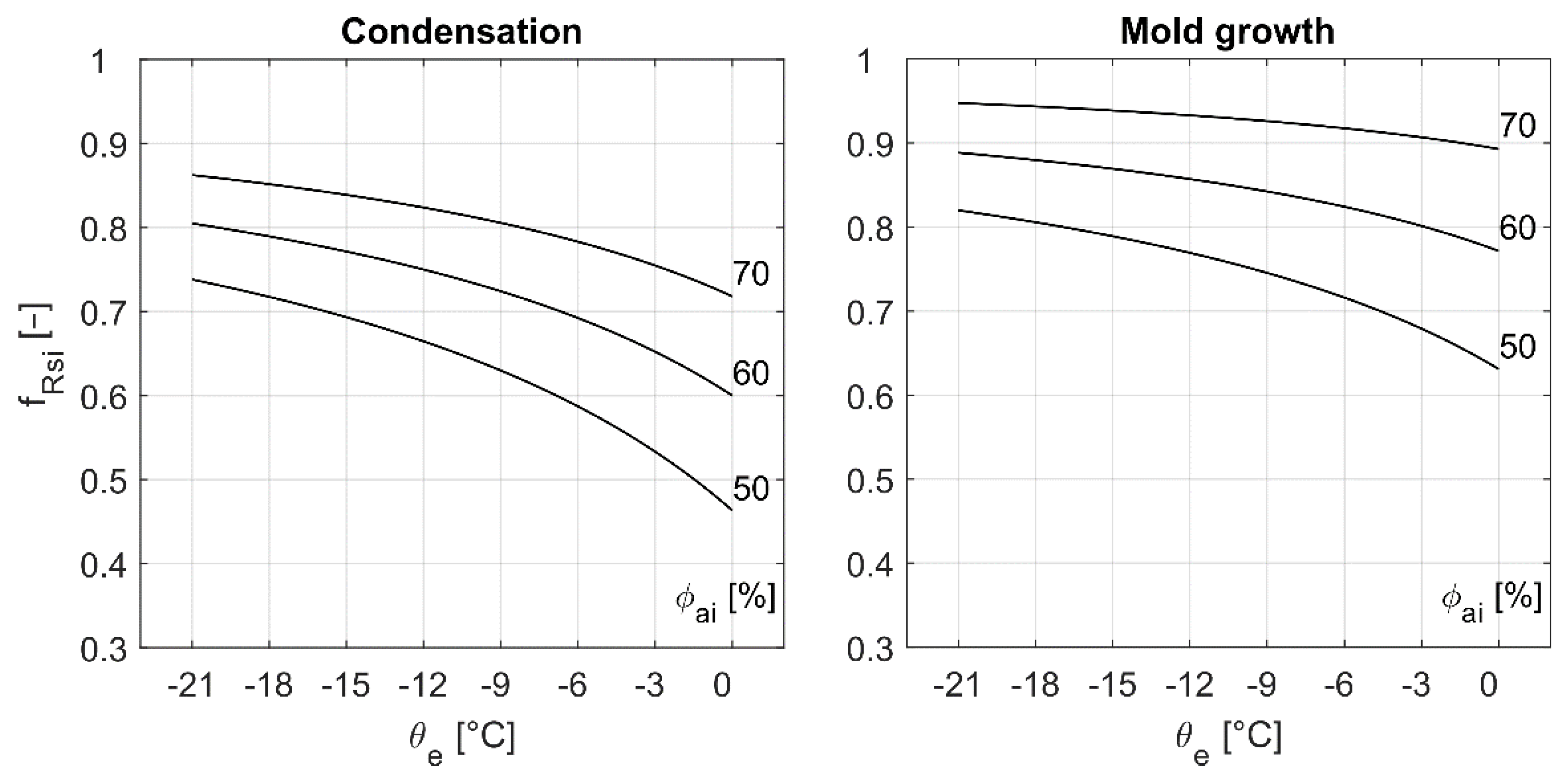
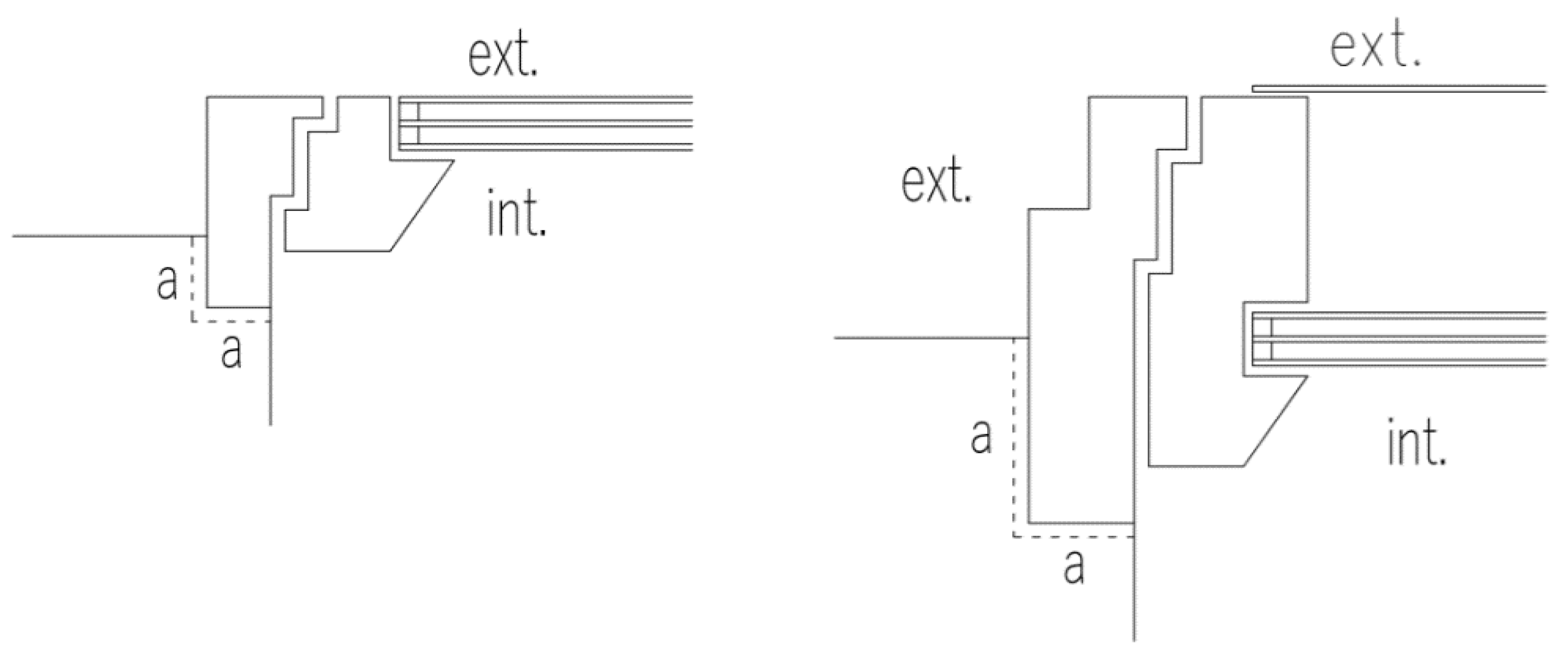
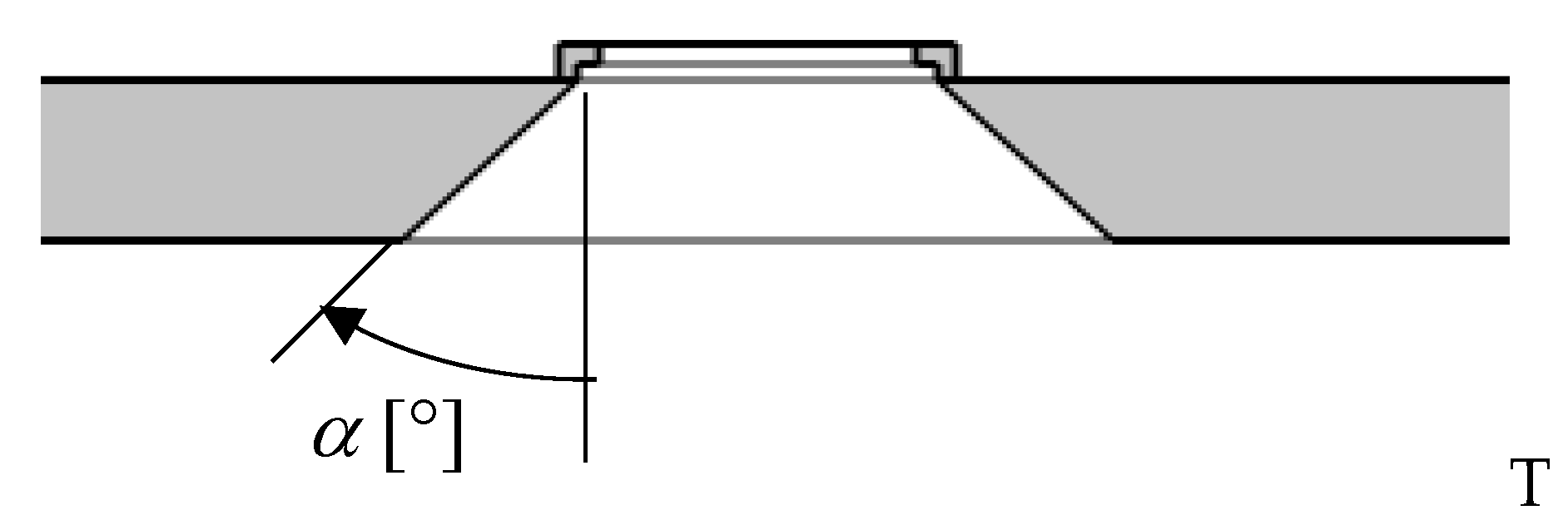




| Required | Recommended | Recommended for Passive Buildings | |
|---|---|---|---|
| Window in wall | 0.1 | 0.03 | 0.01 |
| Window in pitched roof | 0.3 | 0.1 | 0.02 |
| Required | Recommended | Recommended for Passive Buildings | |
|---|---|---|---|
| Window in wall | 1.5 | 1.2 | Range: 0.8–0.6 |
| Window in pitched roof | 1.4 | 1.1 | 0.9 |
| Material | Thermal Conductivity, λ (W/(m·K)) | Pattern According to Figure 13 and Figure 14 |
|---|---|---|
| Glazing pane | 1.00 |  |
| Seals (EPDM profiles) | 0.25 |  |
| Wood (soft) | 0.12 |  |
| Compacfoam | 0.039 |  |
| Aerogel | 0.014 |  |
| Extruded polystyrene | 0.032 |  |
| Boundary Condition | Air Temperature θ (°C) | Surface Heat Transfer Resistance Rsi (m2K/W) |
|---|---|---|
| Interior—Building construction | 20 | 0.10 |
| Interior—Window | 20 | 0.13 |
| Interior—Edges of window | 20 | 0.20 |
| Interior—Edges of window for the evaluation of minimum surface temperature | 20 | 0.25 |
| Exterior | −17 | 0.04 |
| Ventilated cavity connected to the exterior (under roof covering) | −17 | 0.10 |
| Variant | Heat Transfer Coefficient (W/K) | Mean Linear Thermal Transmittance for Glazing Edge (W/m·K) ψg | Thermal Transmittance for Reference Window Size (W/(m2·K)) | |||
|---|---|---|---|---|---|---|
| Glazing HT,g | Frame HT,f | Edge HT,ψ,g | ||||
| UF | UW | |||||
| I | 0.530 | 0.503 | 0.103 | 0.025 | 0.94 | 0.71 |
| II | 0.303 | 0.344 | 0.148 | 0.037 | 0.59 | 0.50 |
| Perpendicular Lining | Slanted Lining (α = 45°) | ||||
|---|---|---|---|---|---|
| ψw (W/(m·K)) | Uw,inst (W/(m2·K)) | ΔU (W/(m2·K)) | ψw (W/(m·K)) | Uw,inst (W/(m2·K)) | ΔU (W/(m2·K)) |
| 0.071 | 0.72 | 0.22 | 0.093 | 0.79 | 0.29 |
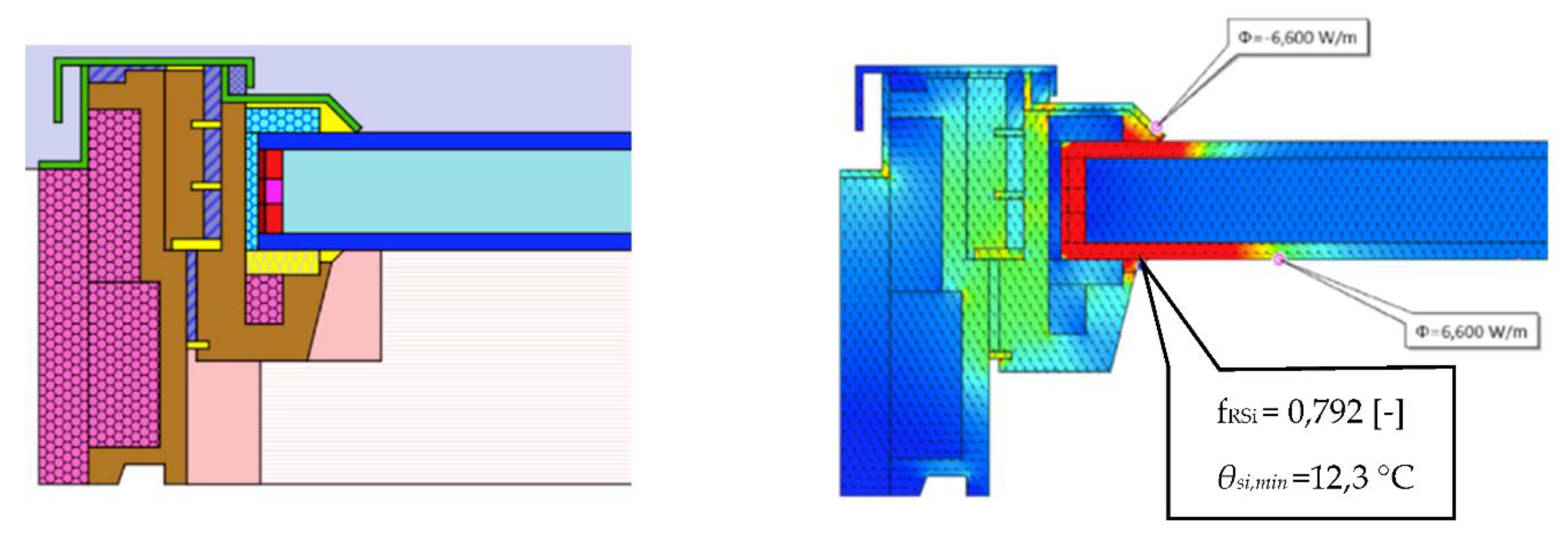
| Area | Minimum Surface Temperature θsi,min (°C) | Surface Temperature Factor fRsi (-) |
|---|---|---|
| Sill | 10.8 | 0.752 |
| Head | 11.0 | 0.756 |
| Side lining | 10.9 | 0.755 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tywoniak, J.; Calta, V.; Staněk, K.; Novák, J.; Maierová, L. The Application of Building Physics in the Design of Roof Windows. Energies 2019, 12, 2300. https://doi.org/10.3390/en12122300
Tywoniak J, Calta V, Staněk K, Novák J, Maierová L. The Application of Building Physics in the Design of Roof Windows. Energies. 2019; 12(12):2300. https://doi.org/10.3390/en12122300
Chicago/Turabian StyleTywoniak, Jan, Vítězslav Calta, Kamil Staněk, Jiří Novák, and Lenka Maierová. 2019. "The Application of Building Physics in the Design of Roof Windows" Energies 12, no. 12: 2300. https://doi.org/10.3390/en12122300





