Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems
Abstract
1. Introduction
2. Methods
2.1. Multi-Energy System Model
2.1.1. System Constraints
2.1.2. Conversion and Generation Technologies
2.1.3. Storage Processes
2.1.4. Software
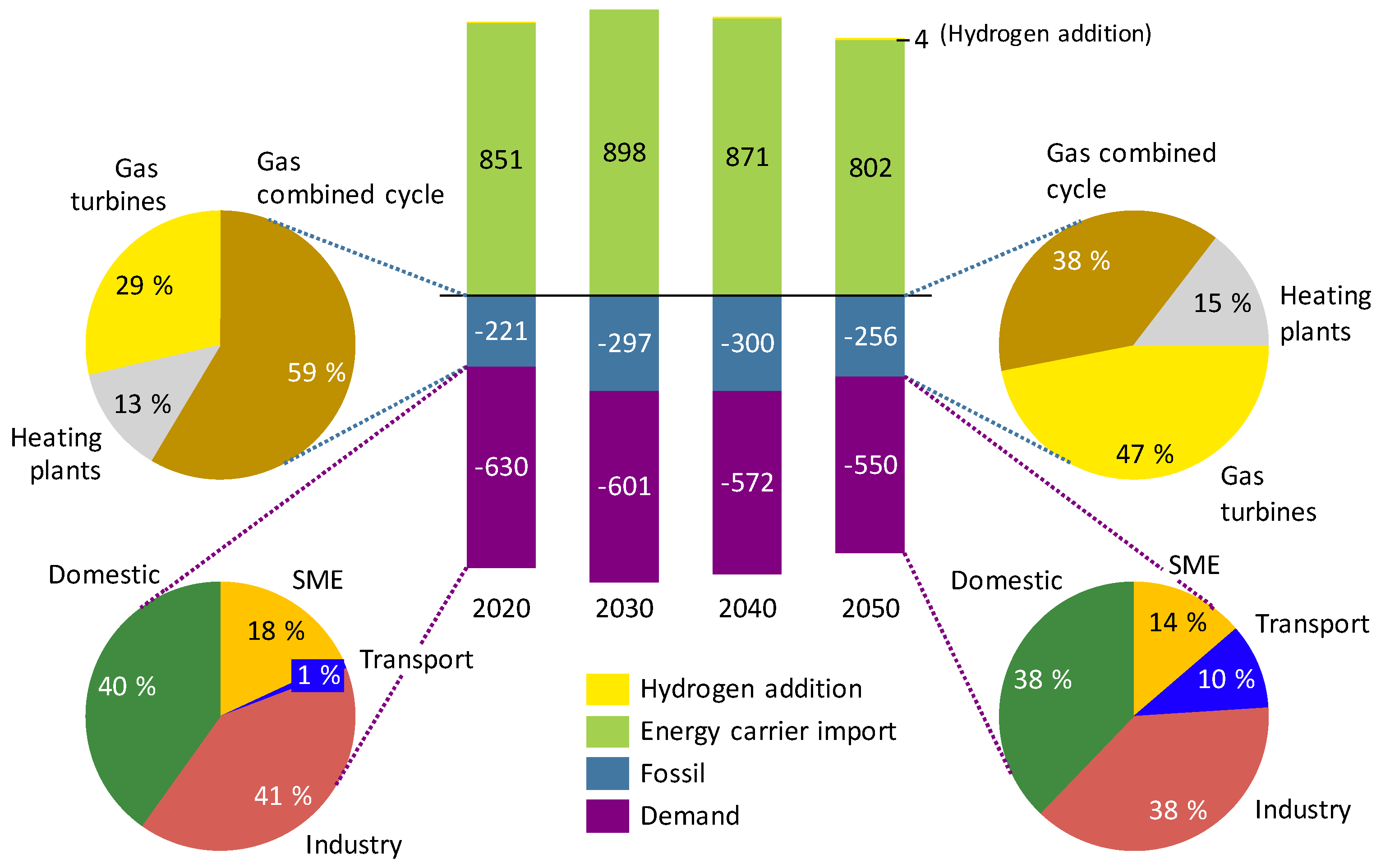
2.2. Energy System Scenario
2.2.1. Electricity
2.2.2. District Heating
2.2.3. Hydrogen
2.2.4. Methane
2.2.5. Biomass
2.3. Emissions Accounting
2.3.1. Mix Method
2.3.2. Marginal Method
2.4. Marginal Cost Calculation
3. Results
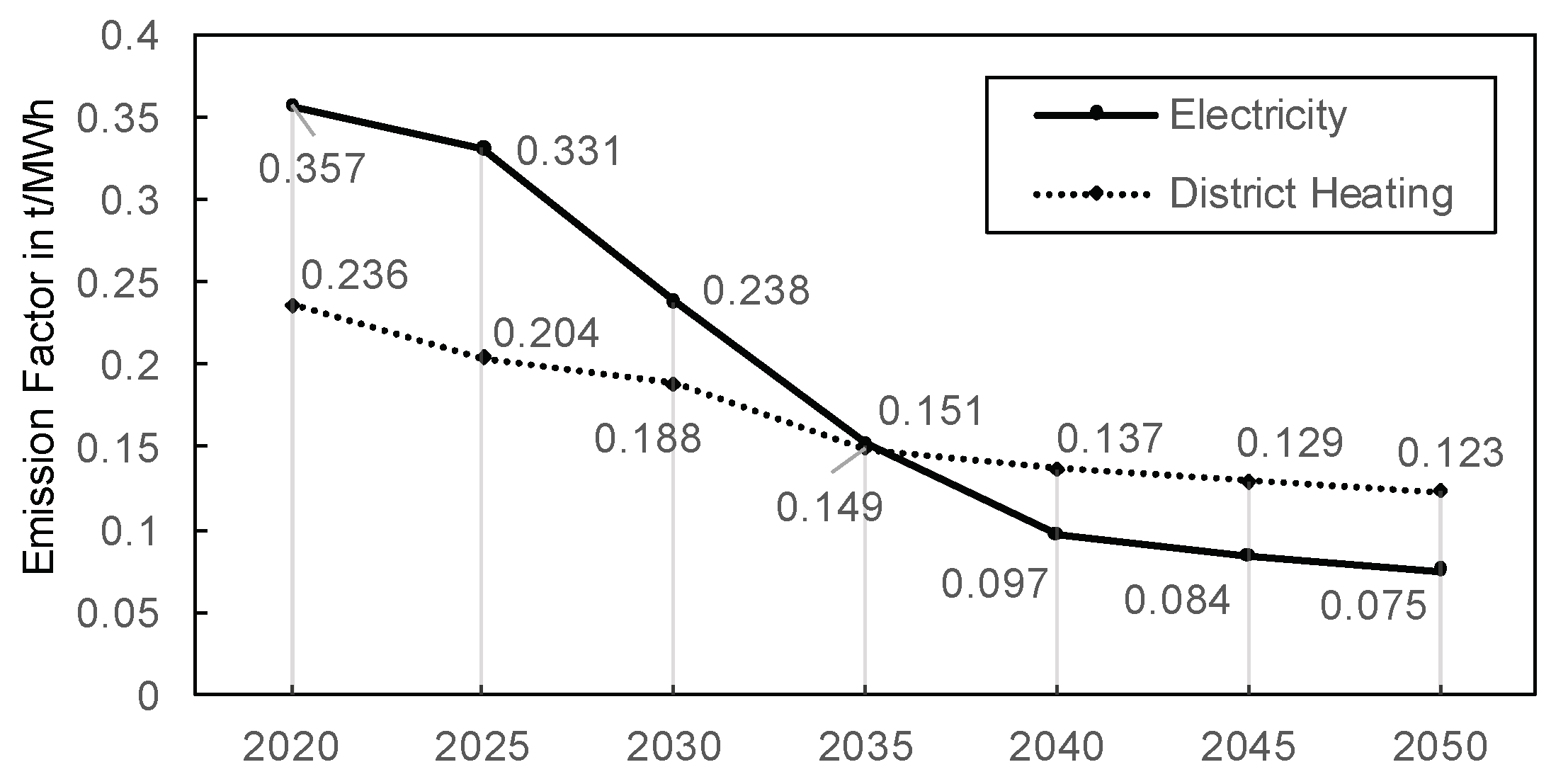
3.1. Emission Factors: Mix Method, Load Weighted Annual Average
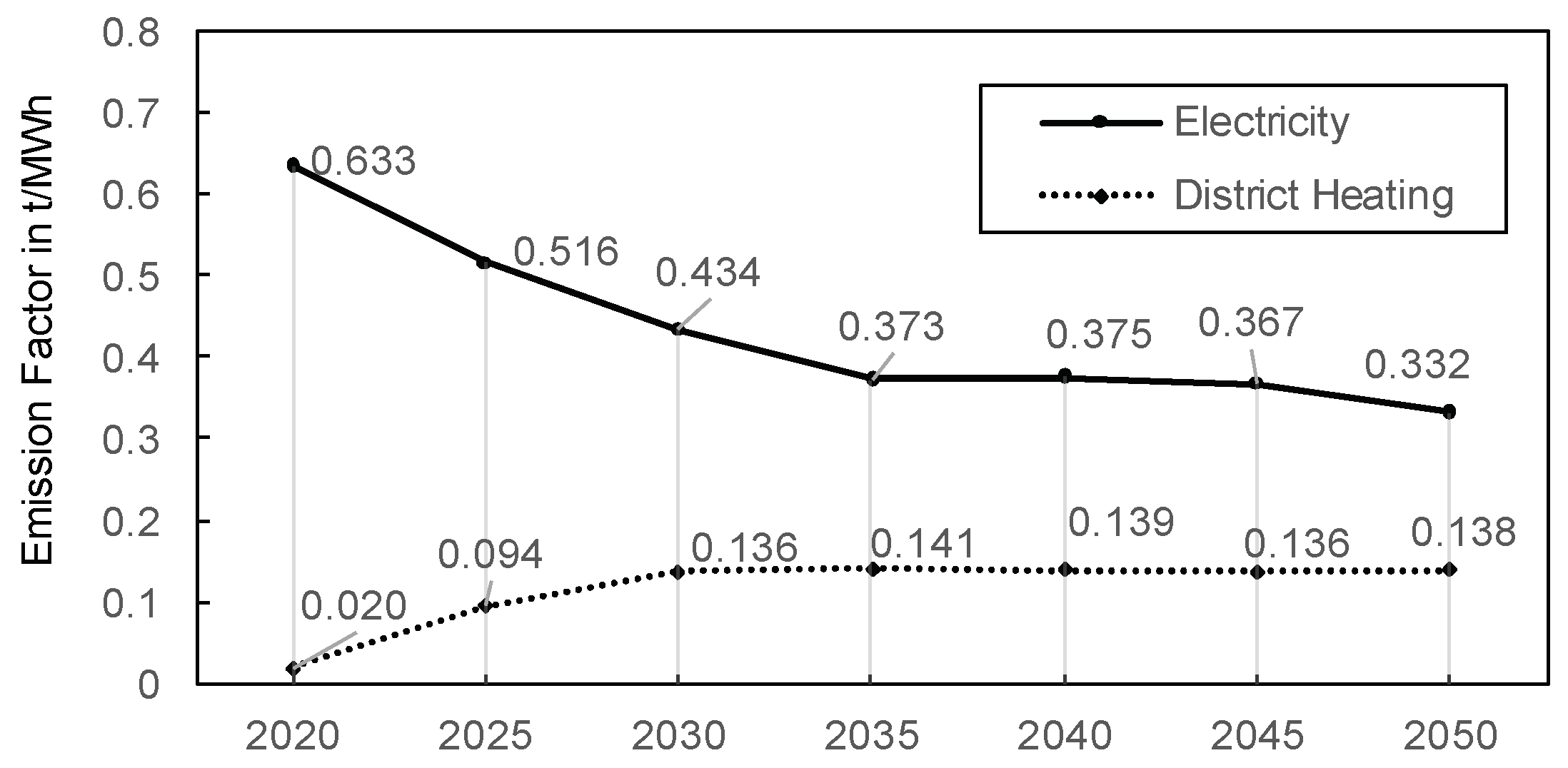
3.2. Emission Factors: Marginal Method, Load Weighted Annual Average
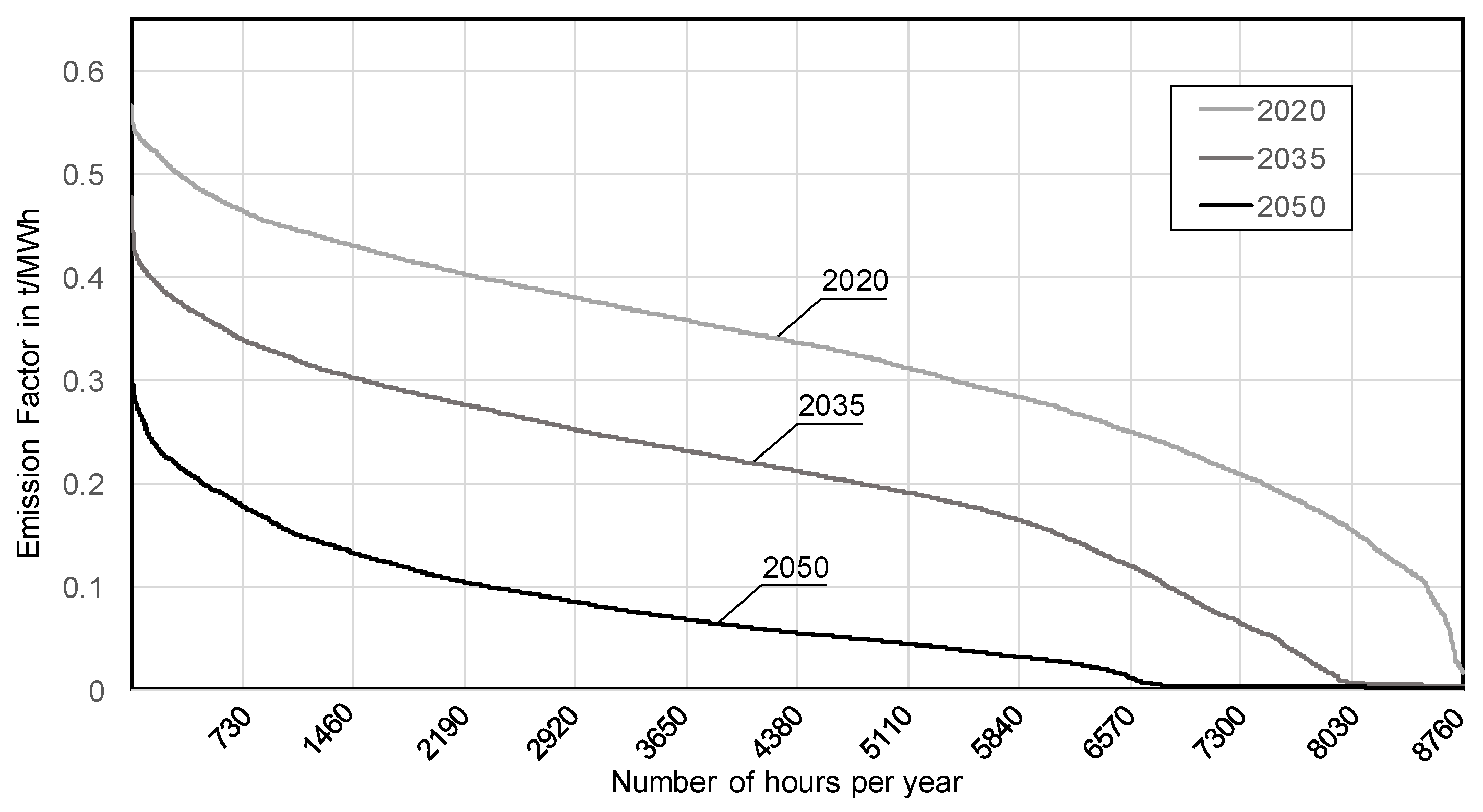
3.3. Emission Factors: Mix Method, Hourly Resolution
3.4. Emission Factors: Marginal Method, Hourly Resolution
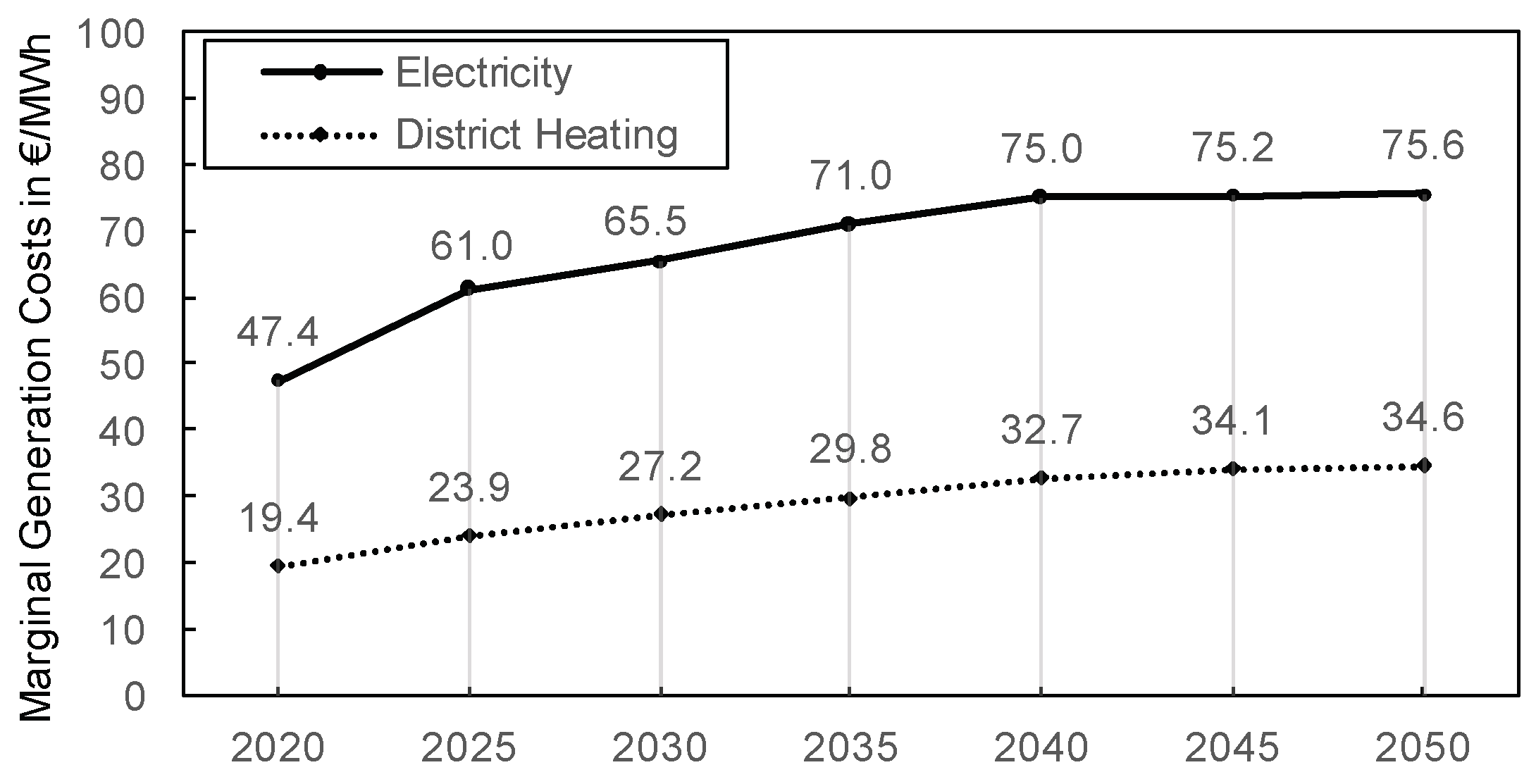
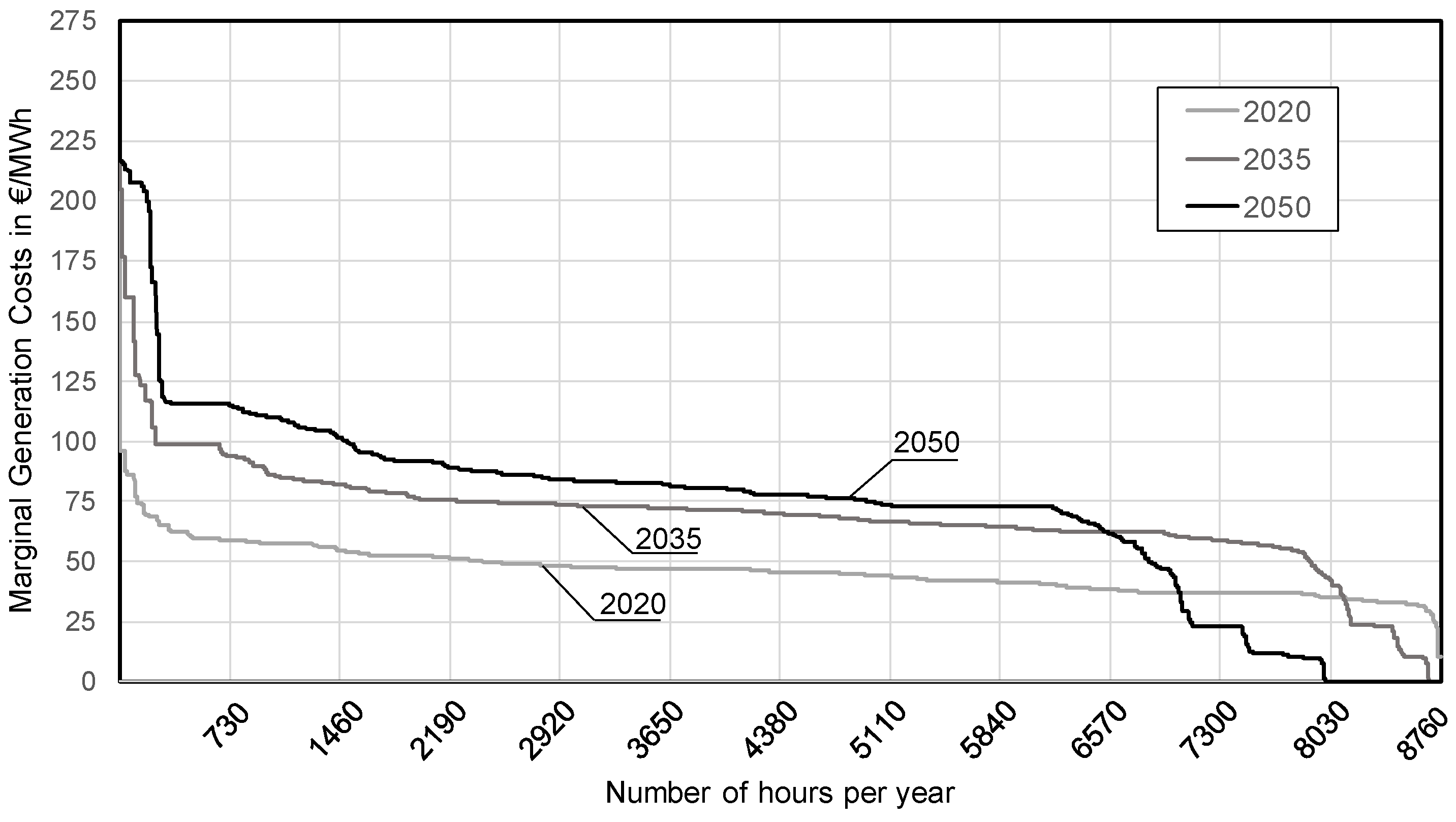
3.5. Marginal Costs
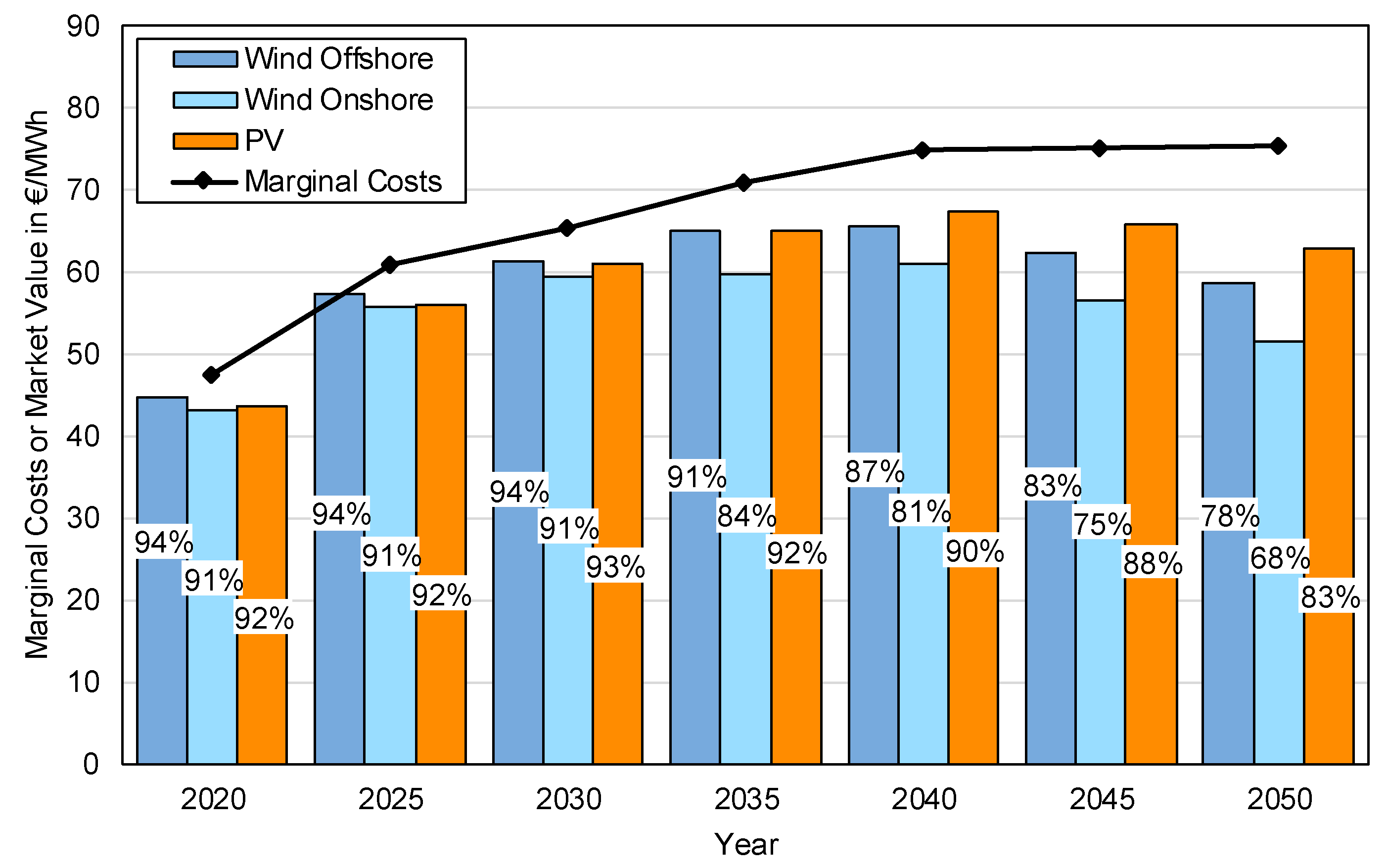
3.6. Marginal Costs: Market Values of Variable Renewable Energy Sources (vRES)
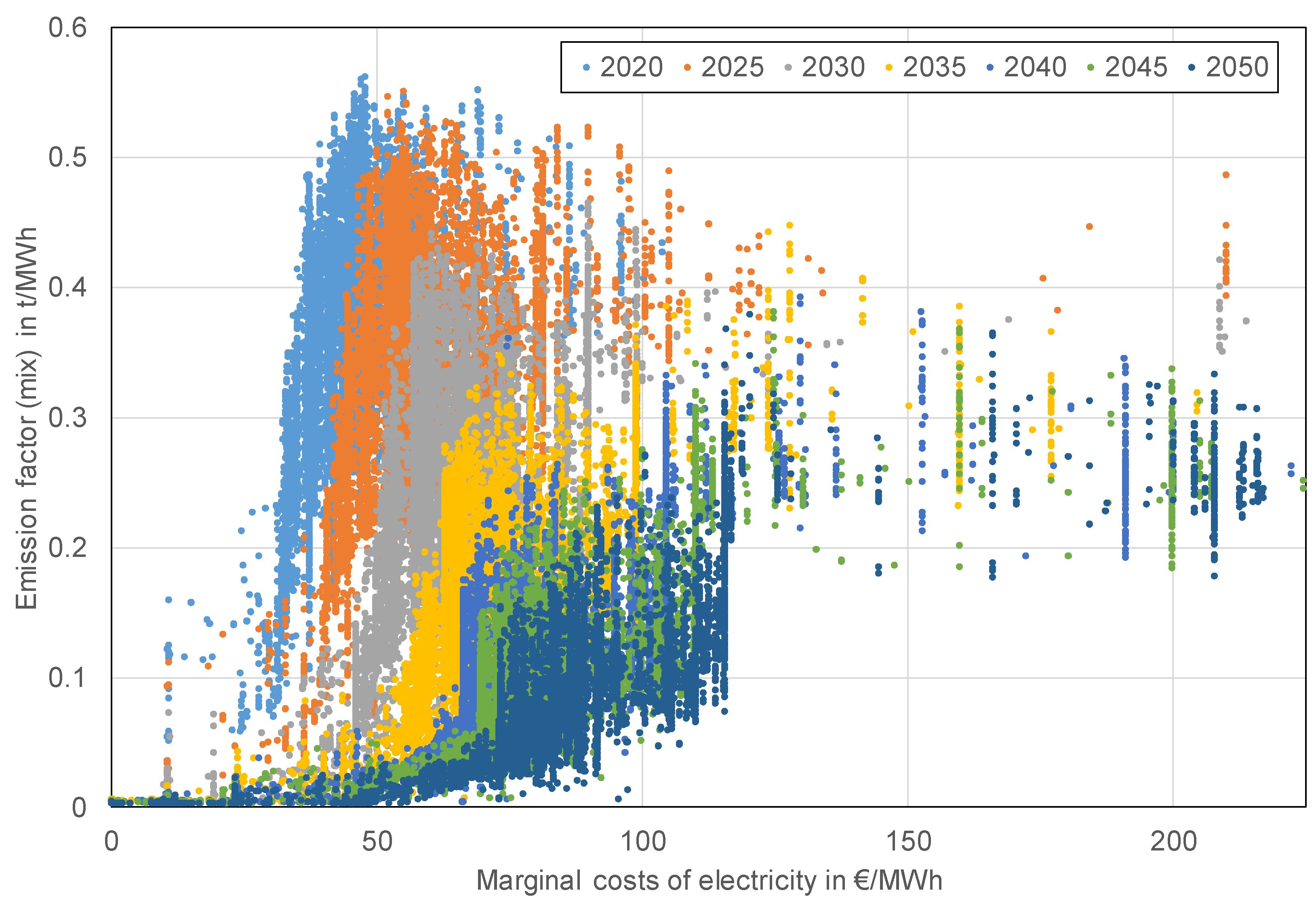
3.7. Comparison: Emission Factors and Marginal Costs
4. Discussion
4.1. Emission Factors
4.2. Marginal Costs
4.3. Energy System Scenario
5. Conclusions
6. Data Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
| Fuel: | Hard Coal | Lignite | Methane | Oil | Uranium | CO2 Price | |
|---|---|---|---|---|---|---|---|
| Unit: | €/MWh | €/MWh | €/MWh | €/MWh | €/MWh | €/t | |
| Costs: | 2015 | 8.3 | 3.0 | 20.2 | 30.1 | 3.6 | 5.4 |
| 2020 | 8.4 | 4.3 | 22.7 | 40.0 | 3.3 | 20.1 | |
| 2025 | 8.5 | 5.6 | 25.2 | 49.9 | 3.3 | 31.0 | |
| 2030 | 8.4 | 5.6 | 26.4 | 48.3 | 3.3 | 41.8 | |
| 2035 | 8.5 | 5.6 | 27.9 | 53.0 | 3.3 | 52.7 | |
| 2040 | 8.9 | 5.6 | 28.0 | 53.0 | 3.3 | 63.5 | |
| 2045 | 9.3 | 5.6 | 28.0 | 53.0 | 3.3 | 74.4 | |
| 2050 | 9.8 | 5.6 | 28.1 | 53.0 | 3.3 | 85.2 | |
| Fuel: | Hard Coal | Lignite | Oil | Methane |
|---|---|---|---|---|
| Unit: | t/MWh | t/MWh | t/MWh | t/MWh |
| Emission factor: | 0.337 | 0.399 | 0.264 | 0.199 |
Appendix D
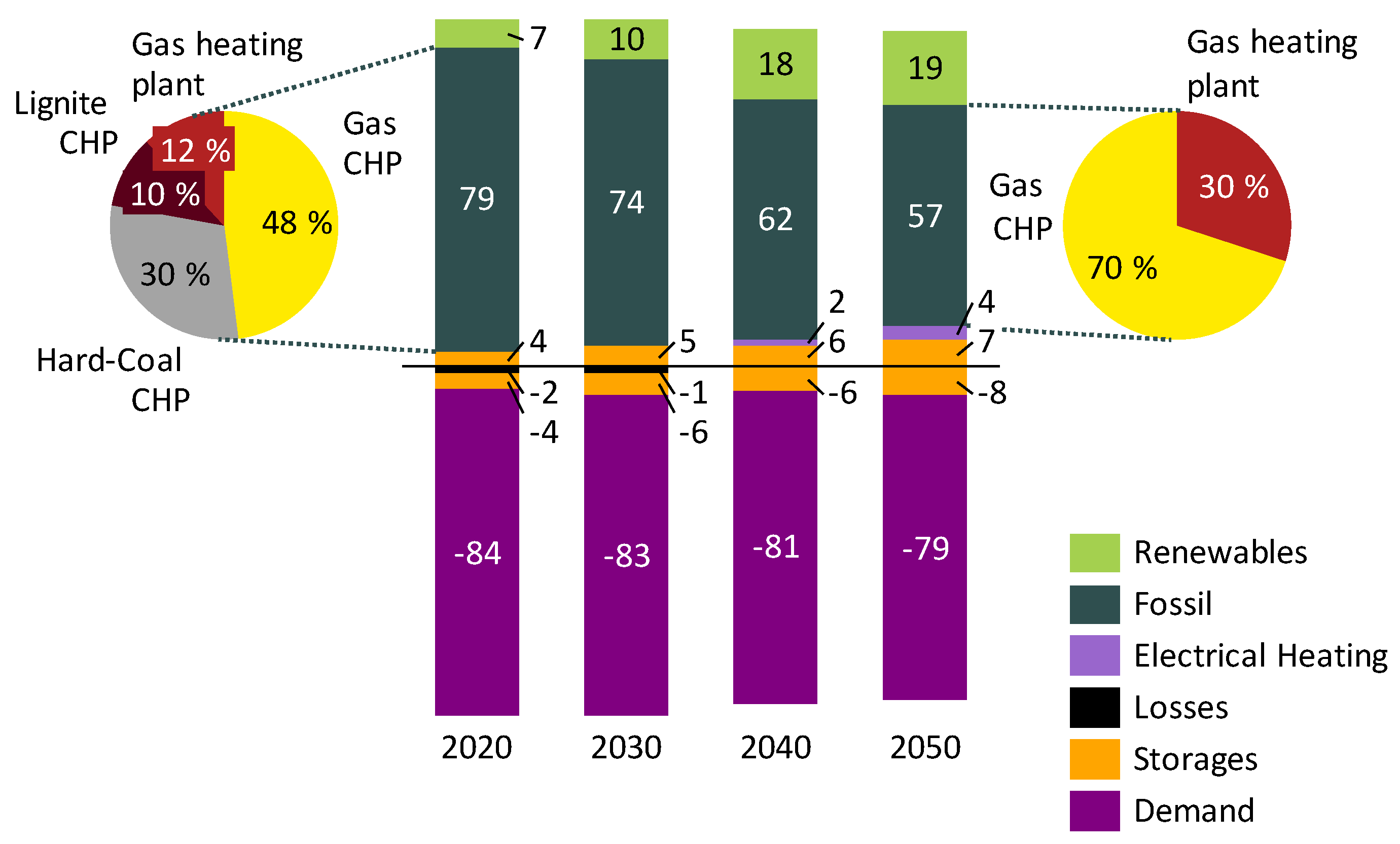
References
- Mancarella, P.; Andersson, G.; Pecas-Lopes, J.A.; Bell, K.R.W. Modeling of integrated multi-energy systems: Drivers, requirements, and opportunities. In Proceedings of the Power Systems Computation Conference (PSCC), Genua, Italy, 20–24 June 2016; IEEE: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Bründlinger, T.; König, J.E.; Frank, O.; Gründig, D.; Jugel, C.; Kraft, P.; Krieger, O.; Mischinger, S.; Prein, P.; Seidl, H.; et al. Dena-Leitstudie Integrierte Energiewende—Impulse für die Gestaltung des Energiesystems bis 2050; Deutsche Energie-Agentur GmbH (dena), ewi Energy Research & Scenarios gGmbH: Berlin/Köln, Germany, 2018. [Google Scholar]
- Günther, J.; Lehmann, H.; Lorenz, U.; Purr, K. Den Weg zu Einem Treibhausgasneutrale Deutschland Ressourcenschonend Gestalten; Umweltbundesamt: Dessau-Roßlau, Germany, 2017. [Google Scholar]
- Gebert, P.; Herhold, P.; Burchardt, J.; Schönberger, S.; Rechenmacher, F.; Kirchner, A.; Kemmler, A.; Wünsch, M. Klimapfade für Deutschland, Studie im Auftrag des Bundesverbandes der Deutschen Industrie e.V. (BDI); The Boston Consultung Group und Prognos: München/Berlin, Germany, 2018. [Google Scholar]
- Pfluger, B.; Tersteegen, B.; Franke, B. Langfristszenarien für die Transformation des Energiesystems in Deutschland, Studie im Auftrag des Bundesministeriums für Wirtschaft und Energie (BMWi); Fraunhofer Institut für System- und Innovationsforschung (ISI): Karlsruhe, Germany; Consentec GmbH: Aachen, Germany; Insitut für Energie- und Umweltforschung GmbH (ifeu): Heidelberg, Germany, 2017. [Google Scholar]
- Capros, P.; Höglund-Isaksson, L.; Frank, S.; Witzke, H.P. EU Reference Scenario 2016; European Commission: Brussles, Belgium, 2016. [Google Scholar]
- Ryan, N.A.; Johnson, J.X.; Keoleian, G.A. Comparative assessment of models and methods to calculate grid electricity emissions. Environ. Sci. Technol. 2016, 50, 8937–8953. [Google Scholar] [CrossRef] [PubMed]
- Ripp, C.; Steinke, F. A first shot at time-dependent CO2 intensities in multi-modal energy systems. In Proceedings of the 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; IEEE: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Regett, A.; Böing, F.; Conrad, J. Emission assessment of electricity: Mix vs. marginal power plant method. In Proceedings of the 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; IEEE: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Böing, F.; Murmann, A.; Guminski, A. Electrification and coal phase-out in Germany: A scenario analysis. In Proceedings of the 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; IEEE: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Böing, F.; Bruckmeier, A.; Murmann, A.; Pellinger, C.; Kern, T. Relieving the German transmission grid with regulated wind power development. In Proceedings of the 15th IAEE European Conference, Vienna, Austria, 3–6 September 2017; IAEE: Cleveland, OH, USA, 2017. [Google Scholar]
- Guminski, A.; Böing, F.; Murmann, A.; Roon, S. System effects of high demand-side electrification rates: A scenario analysis for Germany in 2030. WIREs Energy Environ. 2019, 8, e327. [Google Scholar] [CrossRef]
- Böing, F.; Murmann, A.; Pellinger, C.; Bruckmeier, A.; Kern, T.; Mongin, T. Assessment of grid optimisation measures for the German transmission grid using open source grid data. J. Phys. Conf. Ser. 2018, 977, 012002. [Google Scholar] [CrossRef]
- Pellinger, C.; Schmid, T. Merit Order der Energiespeicherung im Jahr 2030—Hauptbericht; Forschungsstelle für Energiewirtschaft (FfE): München, Germany, 2016. [Google Scholar]
- Pellinger, C. Mehrwert Funktionaler Energiespeicher aus System- und Akteurssicht. Ph.D. Thesis, Technical University Munich, Munich, Germany, July 2016. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bazaraa, M.S.; Jarvis, J.J.; Sherali, H.D. Linear Programming and Network Flows; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Netzentwicklungsplan Strom. Szenariorahmen für den Netzentwicklungsplan Strom 2030 (Version 2019)—Entwurf der Übertragungsnetzbetreiber; 50Hertz Transmission GmbH: Berlin, Germany; Amprion GmbH: Dortmund, Germany; TenneT TSO GmbH: Bayreuth, Germany; TransnetBW GmbH: Stuttgart, Germany, 2018. [Google Scholar]
- Weber, C. Uncertainty in the Electric Power Industry; Springer: Berlin, Germany, 2005. [Google Scholar] [CrossRef]
- Müller-Syring, G.; Henel, M.; Köppel, W.; Mlaker, H.; Sterner, M.; Höcher, T. Entwicklung von Modularen Konzepten zur Erzeugung, Speicherung und Einspeisung von Wasserstoff und Synthetischem Methan in das Erdgasnetz, Studie im Auftrag der DVGW; DBI Gas- und Umwelttechnik GmbH: Leipzig, Germany; DVGW: Bonn, Germany; E.ON: Essen, Germany; Fraunhofer IWES: Kassel, Germany, 2013. [Google Scholar]
- Fishbone, L.; Abilock, H. Markal, a linear-programming model for energy systems analysis: Technical description of the Bnl version. Int. J. Energy Res. 1981, 5, 353–375. [Google Scholar] [CrossRef]
- ENTSO-E. TYNDP—Ten Year Net Developing Plan; ENTSO-E: Brussles, Belgium, 2018; Available online: http://tyndp.entsoe.eu/maps-data/ (accessed on 4 February 2019).
- Schlesinger, M.; Lindenberger, D.; Lutz, C. Entwicklung der Energiemärkte—Energiereferenzprognose, Studie im Bundesministeriums für Wirtschaft und Technologie (BMWi); BMWi: Berlin, Germany, 2014. [Google Scholar]
- Federal Ministry for Economic Affairs and Energy (BMWi). Final Report: Commission on Growth, Structural Change and Employment; Federal Ministry for Economic Affairs and Energy (BMWi): Berlin, Germany, 2018; Available online: https://www.bmwi.de/Redaktion/EN/Publikationen/commission-on-growth-structural-change-and-employment.pdf?__blob=publicationFile&v=3 (accessed on 4 February 2019).
- Platts. WEPP Database (Europe); Platts: Washington, DC, USA, 2018. [Google Scholar]
- Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BNetzA). Kraftwerksliste der Bundesnetzagentur—Stand November 2018; Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BNetzA): Bonn, Germany, 2018; Available online: https://www.bundesnetzagentur.de/DE/Sachgebiete/ElektrizitaetundGas/Unternehmen_Institutionen/Versorgungssicherheit/Erzeugungskapazitaeten/Kraftwerksliste/kraftwerksliste-node.html (accessed on 13 December 2018).
- Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BNetzA). Veröffentlichung Zu- und Rückbau—Kraftwerksliste der Bundesnetzagentur—Stand November 2018; Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BNetzA): Bonn, Germany, 2018; Available online: https://www.bundesnetzagentur.de/DE/Sachgebiete/ ElektrizitaetundGas/Unternehmen_Institutionen/Versorgungssicherheit/Erzeugungskapazitaeten/Kraftwerksliste/kraftwerksliste-node.html (accessed on 13 December 2018).
- Umweltbundesamt (UBA). Kraftwerke in Deutschland (ab 100 Megawatt elektrischer Leistung); Umweltbundesamt (UBA): Dessau-Roßlau, Germany, 2018; Available online: https://www.umweltbundesamt.de/dokument/datenbank-kraftwerke-in-deutschland (accessed on 13 December 2018).
- Von Roon, S.; Dossow, P.; Kern, T.; Hinterstocker, M.; Pellinger, C. Relevance and chances for industrial self-generation of electricity for high market shares of renewable energies. In Proceedings of the 11th Internationale Energiewirtschaftstagung an der TU Wien, Vienna, Austria, 13–15 February 2019; Available online: https://iewt2019.eeg.tuwien.ac.at/download/contribution/fullpaper/261/261_fullpaper_20190218_225307.pdf (accessed on 23 April 2019).
- Schluss-be-Richt. Langfristszenarien und Strategien für den Ausbau der Erneuerbaren Energien in Deutschland bei Berücksichtigung der Entwicklung in Europa und global Datenanhang II zum Schlussbericht, Studie im Auftrag des Bundesministeriums für Umwelt, Naturschutz und Reaktorsicherheit; Fraunhofer-Institut für Windenergie und Energiesystemtechnik (IWES): Stuttgart, Germany; Ingenieurbüro für neue Energien (IfnE): Kassel, Germany; Deutsches Zentrum für Luft- und Raumfahrt e. V. (DLR): Teltow, Germany, 2012; Available online: https://www.dlr.de/tt/Portaldata/41/Resources/dokumente/institut/system/publications/Leitstudie_2011_-_Tabellen_Datenanhang_II.xls (accessed on 23 April 2019).
- Henning, H.-M.; Palzer, A. Was kostet die Energiewende?—Wege zur Transformation des deutschen Energiesystems bis 2050; Fraunhofer Institut für Solare Energiesystem (ISE): Freiburg, Germany, 2015; Available online: https://www.fraunhofer.de/content/dam/zv/de/Forschungsfelder/Energie-Rohstoffe/Fraunhofer-ISE_Transformation-Energiesystem-Deutschland_final_19_11%20(1).pdf (accessed on 4 June 2014).
- ASUE. BHKW-Kenndaten 2014/2015—Module, Anbieter, Kosten; Arbeitsgemeinschaft für Sparsamen und Umweltfreundlichen Energieverbrauch e.V. (ASUE): Berlin, Germany, 2014. [Google Scholar]
- Kesicki, F.; Ekins, P. Marginal abatement cost curves: A call for caution. Clim. Policy 2012, 12, 219–236. [Google Scholar] [CrossRef]
- Schroedter-Homscheidt, M.; Hoyer-Klick, C.; Killius, N.; Lefèvre, M.; Wald, L.; Wey, E.; Saboret, L. User’s Guide to the CAMS Radiation Service—Status December 2016; ECMWF: Shinfield Park, Reading, UK, 2016. [Google Scholar]
- Schulz, J.-P.; Schättler, U. Beschreibung des Lokal-Modells Europa COSMO-EU (LME) und seiner Datenbanken auf dem Datenserver des DWD; Deutscher Wetterdienst (DWD): Offenbach, Germany, 2011. [Google Scholar]
- Müller, M.; Reinhard, J.; Ostermann, A.; Estermann, T.; Köppl, S. Regionales flexibilitäts-potenzial dezentraler anlagen—modellierung und bewertung des regionalen flexibilitäts-potenzials von dezentralen flexibilitäts-typen im verteilnetz. In Proceedings of the Konferenzband der Konferenz Zukünftige Stromnetze, Berlin, Germany, 30–31 Januar 2019; Connexio GmbH: Pforzheim, Germany, 2019. [Google Scholar]
- Figgener, J.; Haberschusz, D.; Kairies, K.-P.; Tepe, B.; Ebbert, M.; Herzog, R.; Sauer, D.U. Wissenschaftliches Mess- und Evaluierungsprogramm Solarstromspeicher 2.0—Jahresbericht 2017; Institut für Stromrichtertechnik und Elektrische Antriebe der RWTH Aachen: Aachen, Germany, 2017. [Google Scholar]
- Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BnetzA). Genehmigung des Szenariorahmens für die Netzentwicklungsplanung 2019–2030; Bundesnetzagentur für Elektrizität, Gas, Telekommunikation, Post und Eisenbahnen (BNetzA): Bonn, Germany, 2018. [Google Scholar]
- Hecker, C.; Zauner, E.; Pellinger, C.; Carr, L.; Hötzl, S. Modellierung der flexiblen Energiebereitstellung von Wasserkraftwerken in Europa. In Proceedings of the Konferenzband der 17th Internationale Energiewirtschaftstagung an der TU Wien, Vienna, Austria, 15–17 February 2015; AAEE: Sycamore, IL, USA, 2015. [Google Scholar]
- ENTSO-E. Net Transfer Capacity (NTC) and Available Transfer Capacities (ATC) in the Internal Market of Electricity in Europe (IEM); ENTSO-E: Brussles, Belgium, 2000; Available online: https://www.entsoe.eu/fileadmin/user_upload/_library/ntc/entsoe_NTCusersInformation.pdf (accessed on 24 April 2019).
- ENTSO-E. Transparency Plattform; ENTSO-E: Brussles, Belgium, 2016; Available online: https://transparency.entsoe.eu (accessed on 20 March 2016).
- Conrad, J.; Greif, S. Modeling the Private Households Sector and the Impact on the Energy System. In Proceedings of the 41st IAEE Conference, Groningen, The Netherlands, 10–13 June 2018; IAEE: Cleveland, OH, USA, 2018. [Google Scholar]
- Conrad, J.; Greif, S. Modeling load profiles of heat pumps. Energies 2019, 12, 766. [Google Scholar] [CrossRef]
- Pichlmaier, S.; Bayer, C. Modelling the transport sector in the context of a dynamic energy system. In Proceedings of the 41st IAEE Conference, Groningen, The Netherlands, 10–13 June 2018; IAEE: Cleveland, OH, USA, 2018. [Google Scholar]
- Öffentliche Nettostromerzeugung in Deutschland—Erneuerbare Energiequellen erreichen über 40 Prozent, Pressemitteilung des Fraunhofer ISE. Available online: https://www.ise.fraunhofer.de/de/presse-und-medien/news/2018/nettostromerzeugung-2018.html (accessed on 9 January 2019).
- AGFW. AGFW—Hauptbericht 2016; AGFW: Frankfurt am Main, Germany, 2017; Available online: https://www.agfw.de/index.php?eID=tx_securedownloads&p=436&u=0&g=0&t=1556182285&hash=3253fea8235754ef2787f657b4379ea4260cf62f&file=fileadmin/user_upload/Zahlen_und_Statistiken/Version_1_HB2016.pdf (accessed on 24 April 2019).
- Conrad, J.; Greif, S.; Kleinertz, B.; Pellinger, C. Flexibilisierung der Kraft-Wärme- Kopplung—Kurzgutachten im Auftrag der Übertragungsnetzbetreiber in Deutschland; Forschungsstelle für Energiewirtschaft e.V. (FfE): München, Germany, 2017; Available online: https://www.ffe.de/attachments/article/761/Flexibilisierung%20der%20Kraft-Waerme-Kopplung.pdf (accessed on 24 April 2019).
- BAFA. Zulassung von KWK-Anlagen nach dem Kraft-Wärme-Kopplungsgesetz (KWKG); Bundesamt für Wirtschaft und Ausfuhrkontrolle (BAFA): Eschborn, Germany, 2014. [Google Scholar]
- Kail, C.; Spahn, K.; Grupczynski, M. Die Brennstoff-Frage—Energieversorgungslösungen für Industrie und Kommunen. BWK 2010, 62, 58–66. [Google Scholar]
- Kail, C.; Haberberger, G. Kenngrößen zur optimalen Auslegung großer KWK-Anlagen. VDI-Berichte 2001, 1594, 99–112. [Google Scholar]
- Pehnt, M. Energieeffizienz—Ein Lehr- und Handbuch; Springer: Berlin, Germany, 2010. [Google Scholar] [CrossRef]
- Estermann, T.; Pichlmaier, S.; Guminski, A.; Pellinger, C. Kurzstudie Power-to-X—Ermittlung des Potenzials von PtX-Anwendungen im Auftrag der Übertragungsnetzbetreiber in Deutschland; Forschungsstelle für Energiewirtschaft e.V. (FfE): München, Germany, 2017; Available online: https://www.ffe.de/attachments/article/761/Kurzstudie%20Power-to-X.pdf (accessed on 24 April 2019).
- Kern, T.; Buchwitz, K.; Guminski, A.; von Roon, S. The impact of electrification on the gas sector. In Proceedings of the 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; IEEE: New York, NY, USA, 2018. [Google Scholar] [CrossRef]
- Kern, T.; Eberl, B.; Böing, F.; von Roon, S. Coupling of electricity and gas market models. In Proceedings of the 14th International Conference on the European Energy Market (EEM), Dresden, Germany, 6–9 June 2017; IEEE: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- ENTSO-G Transmission Capacity Map. Available online: https://www.entsog.eu/maps/transmission-capacity-map (accessed on 1 April 2018).
- AGSI+ Transparency Plattform. Available online: https://agsi.gie.eu/ (accessed on 5 June 2018).
- Heijungs, R.; Suh, S. The Computational Structure of Life Cycle Assessment; Springer: Amsterdam, The Netherlands, 2002. [Google Scholar] [CrossRef]
- Tereshchenko, T.; Nord, N. Uncertainty of the allocation factors of heat and electricity production of combined cycle power plant. Appl. Therm. Eng. 2015, 76, 410–422. [Google Scholar] [CrossRef]
- IEA Sankey Diagramm. Available online: https://www.iea.org/Sankey/#?c=Germany&s=Balance (accessed on 24 April 2019).
- Tranberg, B.; Corradi, O.; Lajoie, B.; Gibon, T.; Staffell, I.; Andresen, G.B. Real-time carbon accounting method for the European electricity markets. In Energy Strategy Reviews; Howells, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; Available online: https://arxiv.org/abs/1812.06679 (accessed on 23 April 2019).
- Kleinertz, B.; Pellinger, C.; von Roon, S.; Hübner, T.; Kaestle, G. EU Displacement Mix—A Simplified Marginal Method to Determine Environmental Factors for Technologies Coupling Heat and Power in the European Union; Forschungsstelle für Energiewirtschaft (FfE): Munich, Germany, 2018. [Google Scholar]
- Schweppe, F.C.; Caramanis, M.C.; Tabors, R.D.; Bohn, R.E. Spot Pricing of Electricity; Springer: New York, NY, USA, 1988. [Google Scholar] [CrossRef]
- Müsgens, F. Quantifying market power in the german wholesale electricity market using a dynamic multi-regional dispatch model. J. Ind. Econ. 2006, 54, 471–498. [Google Scholar] [CrossRef]
- Mann, N.; Tsai, C.-H.; Gülen, G.; Schneider, E.; Chuevas, P.; Dyer, J.; Butler, J.; Zhang, T.; Baldick, R.; Deetjen, T.; et al. Capacity Expansion and Dispatch Modeling: Model Documentation and Results for ERCOT Scenarios; The University of Texas at Austin: Austin, TX, USA, 2017; Available online: https://energy.utexas.edu/sites/default/files/UTAustin_FCe_ERCOT_2017.pdf (accessed on 24 April 2019).
- Umweltbundesamt (UBA). Submission under the United Nations Framework Convention on Climate Change and the Kyoto Protocol 2016—National Inventory Report for the German Greenhouse Gas Inventory 1990–2014; Umweltbundesamt (UBA): Dessau-Roßlau, Germany, 2016. [Google Scholar]
- Burger, B. Stromerzeugung in Deutschland im Jahr 2016; Fraunhofer-Institut für Solare Energiesysteme (ISE): Freiburg, Germany, 2017; Available online: https://www.ise.fraunhofer.de/content/dam/ise/de/documents/publications/studies/Stromerzeugung_2016.pdf (accessed on 24 April 2019).
- Hirth, L. The market value of variable renewables. Energy Econ. 2013, 38, 218–236. [Google Scholar] [CrossRef]
- Phelix-DE Futures European Energy Exchange (EEX). Available online: https://www.eex.com/de/marktdaten/strom/futures/phelix-de-futures#!/2019/04/11 (accessed on 24 April 2019).
- Steurer, M.; Fahl, U.; Eberl, T.; Voß, A. Identifikation und Bewertung des intelligenten Lastmanagementpotenzials in der Industrie in Baden-Württemberg, Studie im Auftrag der EnBW Vertrieb GmbH; Institut für Energiewirtschaft und Rationelle Energieanwendung (IER): Stuttgart, Germany, 2013. [Google Scholar]
- Heilek, C. Modellgestützte Optimierung des Neubaus und Einsatzes von Erzeugungsanlagen und Speichern für elektrische und thermische Energie im deutschen Energiesystem. Ph.D.Thesis, Technical University Munich, Munich, Germany, March 2015. [Google Scholar]
- Bundesministerium für Wirtschaft und Energie (BMWi). Zahlen und Fakten Energiedaten 2016–Nationale und internationale Entwicklung; Bundesministerium für Wirtschaft und Energie (BMWi): Berlin, Germany, 2017. [Google Scholar]
- Bundesministerium für Wirtschaft und Energie (BMWi). Zahlen und Fakten Energiedaten 2017—Nationale und internationale Entwicklung; Bundesministerium für Wirtschaft und Energie (BMWi): Berlin, Germany, 2018. [Google Scholar]
- Industrie- und Handelskammer (IHK). Projektionsbericht 2017 für Deutschland—Gemäß Verordnung (EU) Nr. 525/2013; Industrie- und Handelskammer (IHK): Karlsruhe, Germany, 2017. [Google Scholar]
- Intercontinental Exchange (ICE). Market. Data; Intercontinental Exchange (ICE): Atlanta, GA, USA, 2017; Available online: https://www.theice.com/market-data (accessed on 10 September 2017).
- Energiewirtschaftliches Institut an der Universität zu Köln (EWI). Techno-ökonomische Kennwerte für den Forschungsverbund—Systemanalyse Energiespeicher; Energiewirtschaftliches Institut an der Universität zu Köln (EWI): Köln, Germany, 2014. [Google Scholar]

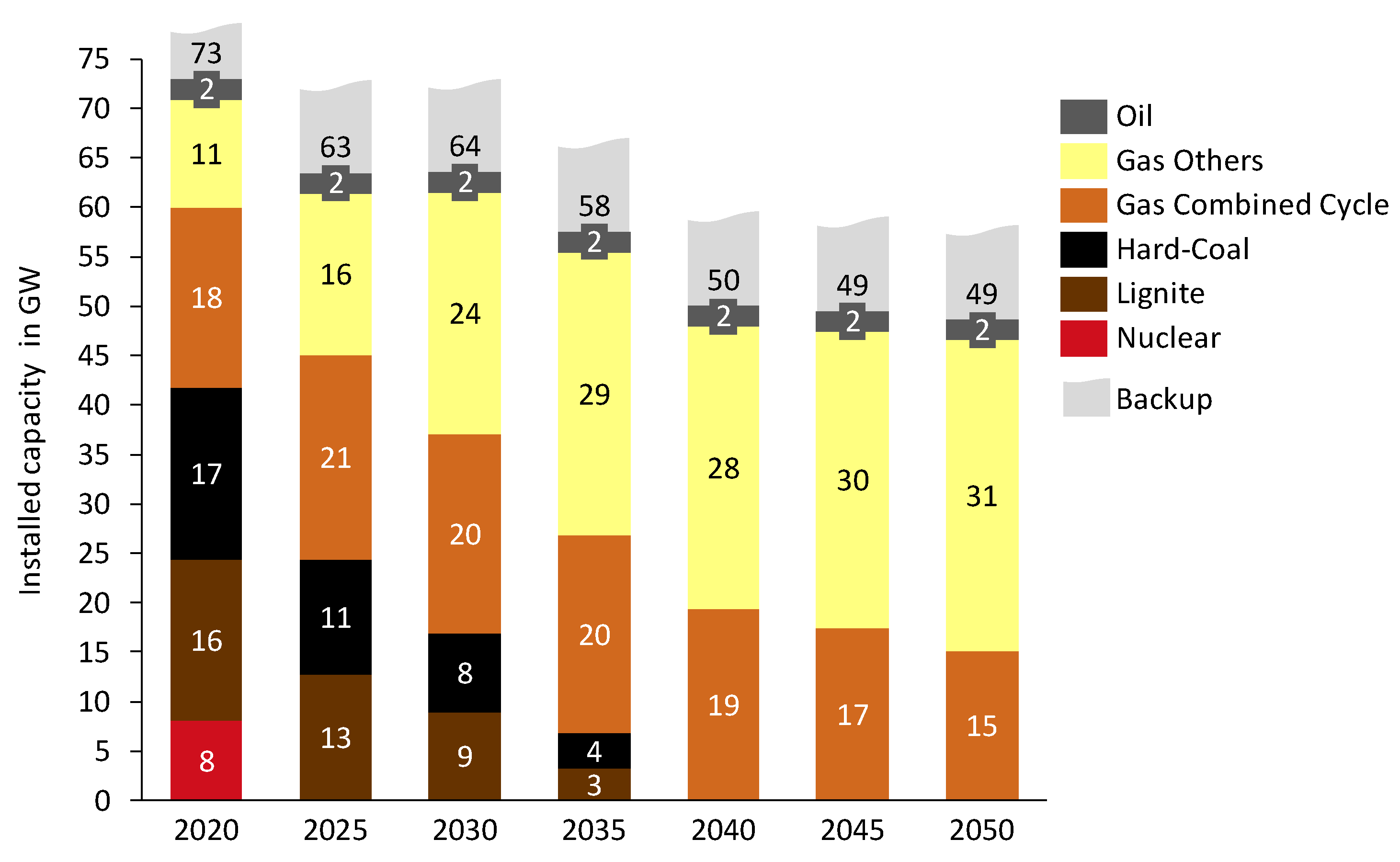
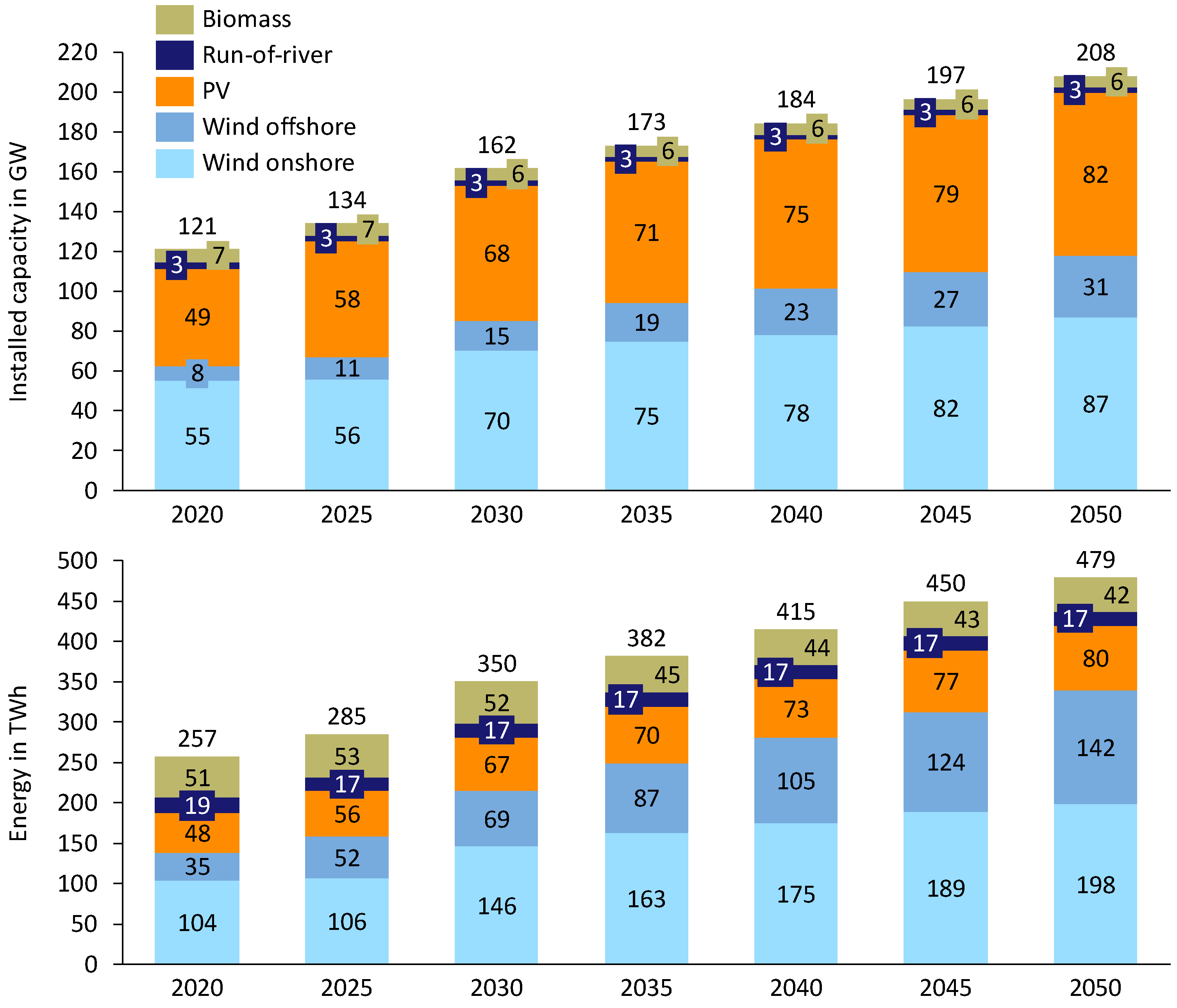


| Source: | TYNDP 2018 1 | ERP 2 | NEP 2019 3 |
|---|---|---|---|
| Scenario Attributes ↓ Scenario Names → | “Sustainable Transition” | “Trend-Szenario” | “Szenario B” |
| Consistent representation of developments in neighboring European countries | yes | no | no |
| Sufficient level of detail for bottom-up modeling of German final energy consumption | no | yes | no |
| Scenario until 2050? | until 2040 | yes | until 2035 |
| Development of renewable energy capacities in the highest possible regional resolution | Countries/ENTSO-E-regions | Country (GER) | Federal States (GER) |
| High differentiation of electricity generation technologies | Yes | No | Yes |
| Detailed consideration of the German conventional power plant fleet | No | No | Yes |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Böing, F.; Regett, A. Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems. Energies 2019, 12, 2260. https://doi.org/10.3390/en12122260
Böing F, Regett A. Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems. Energies. 2019; 12(12):2260. https://doi.org/10.3390/en12122260
Chicago/Turabian StyleBöing, Felix, and Anika Regett. 2019. "Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems" Energies 12, no. 12: 2260. https://doi.org/10.3390/en12122260
APA StyleBöing, F., & Regett, A. (2019). Hourly CO2 Emission Factors and Marginal Costs of Energy Carriers in Future Multi-Energy Systems. Energies, 12(12), 2260. https://doi.org/10.3390/en12122260





