Coupling Methodology for Studying the Far Field Effects of Wave Energy Converter Arrays over a Varying Bathymetry
Abstract
:1. Introduction
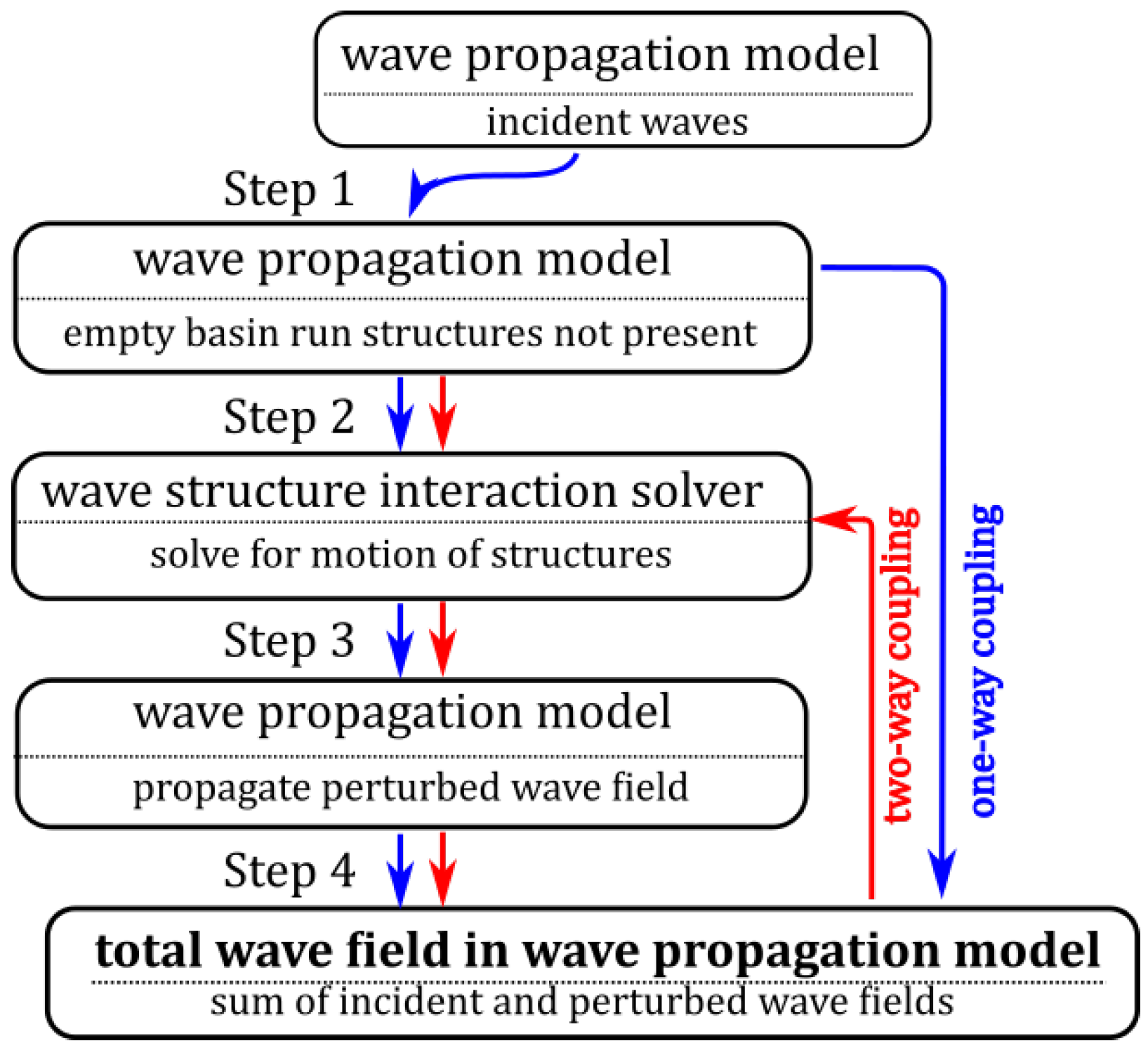
2. Generic Coupling Methodology
- Any wave-structure interaction solver that describes the perturbed wave field is suitable for obtaining the input parameters for the internal wave generation boundary. Models based on potential flow theory (e.g., BEM [17,22,23]) or analytical models based on analytical calculation of coefficients or numerical models based on resolving the Navier–Stokes equations (e.g., CFD [6] or SPH) are all suitable in obtaining the perturbed wave field around the WEC array [20].
- Any wave propagation model can be used. A wave propagation boundary can be implemented in both phase-resolving and phase-averaging models.
- The methodology applies to any kind of oscillating or floating structure. In this paper, a WEC array of heaving point absorber WECs is modelled using a phase-resolving model (in order to demonstrate this numerical coupling methodology). However, it can be applied to oscillating water column WECs, overtopping WECs, wave surge WECs, floating breakwaters or platforms.
3. Application of the Coupling Methodology between the Wave Propagation Model, MILDwave, and the BEM Solver, NEMOH
3.1. Numerical Background
3.1.1. Linear Potential Flow
- The flow is inviscid.
- The flow is irrotational.
- The flow is incompressible.
3.1.2. Wave Propagation Model MILDwave
3.1.3. Wave-Structure Interaction Solver NEMOH
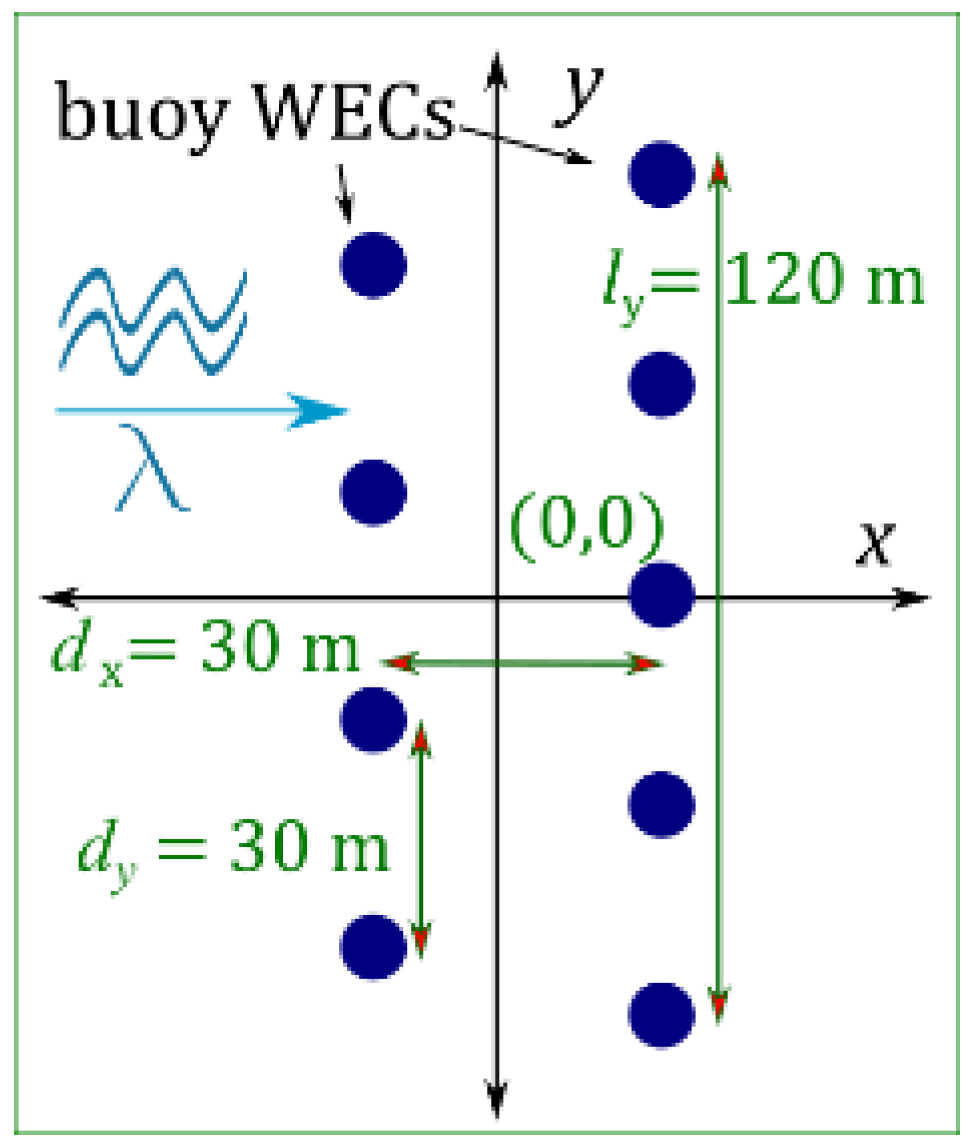
3.1.4. Modelled WECs
3.1.5. Wave Characteristics
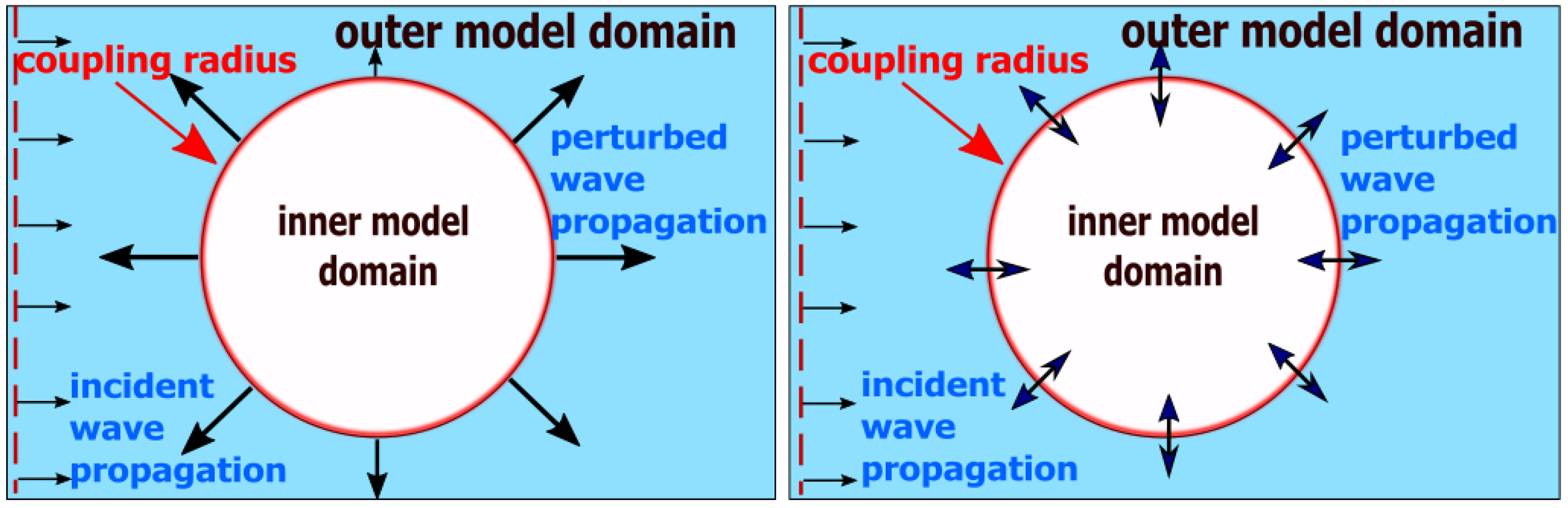
3.2. Coupling Methodology Implementation
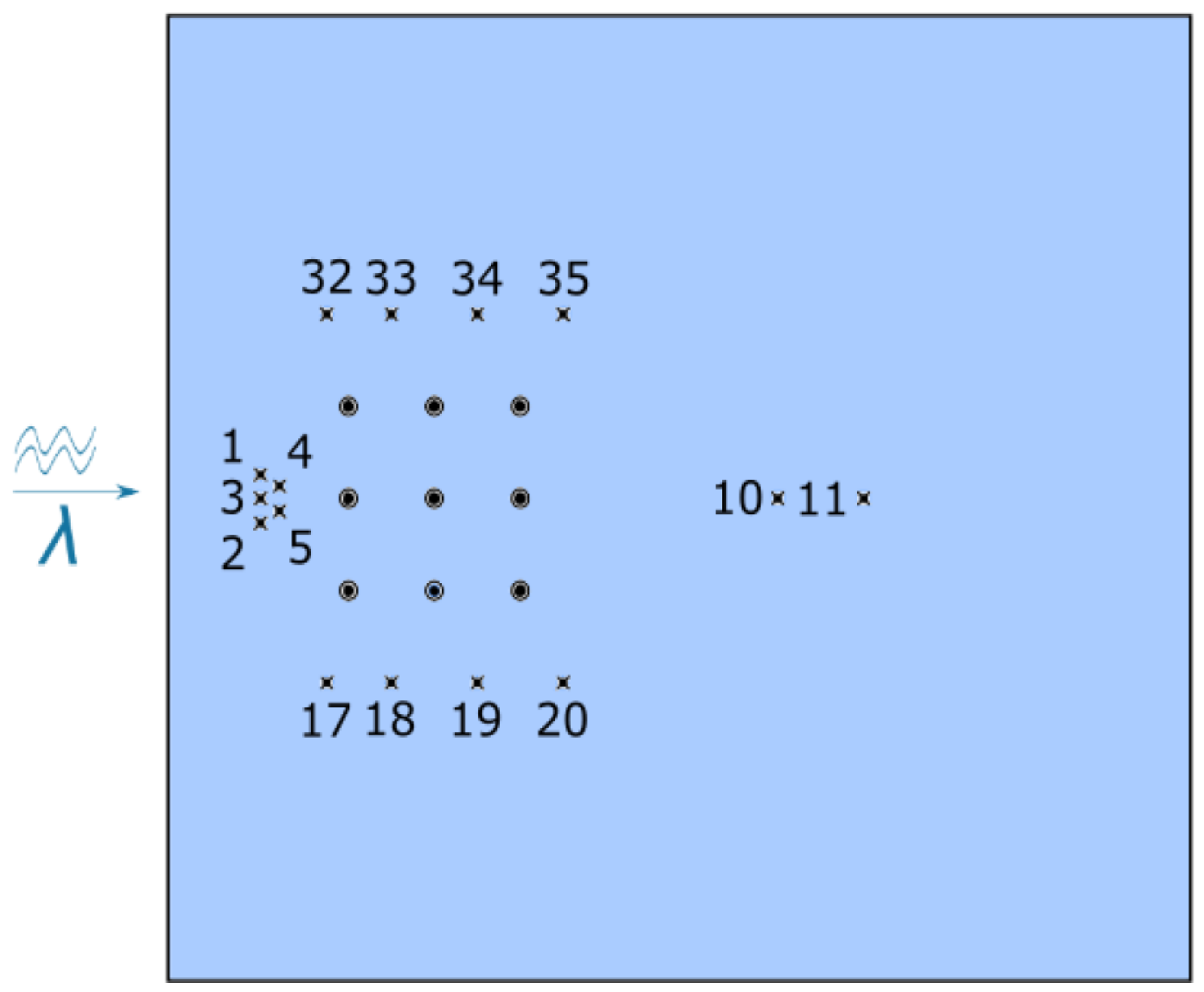
3.3. Experimental Data-Set Used for Numerical Validation Purposes
3.4. Test Program
3.4.1. Coupling Methodology Implementation for Constant Bottom Bathymetry
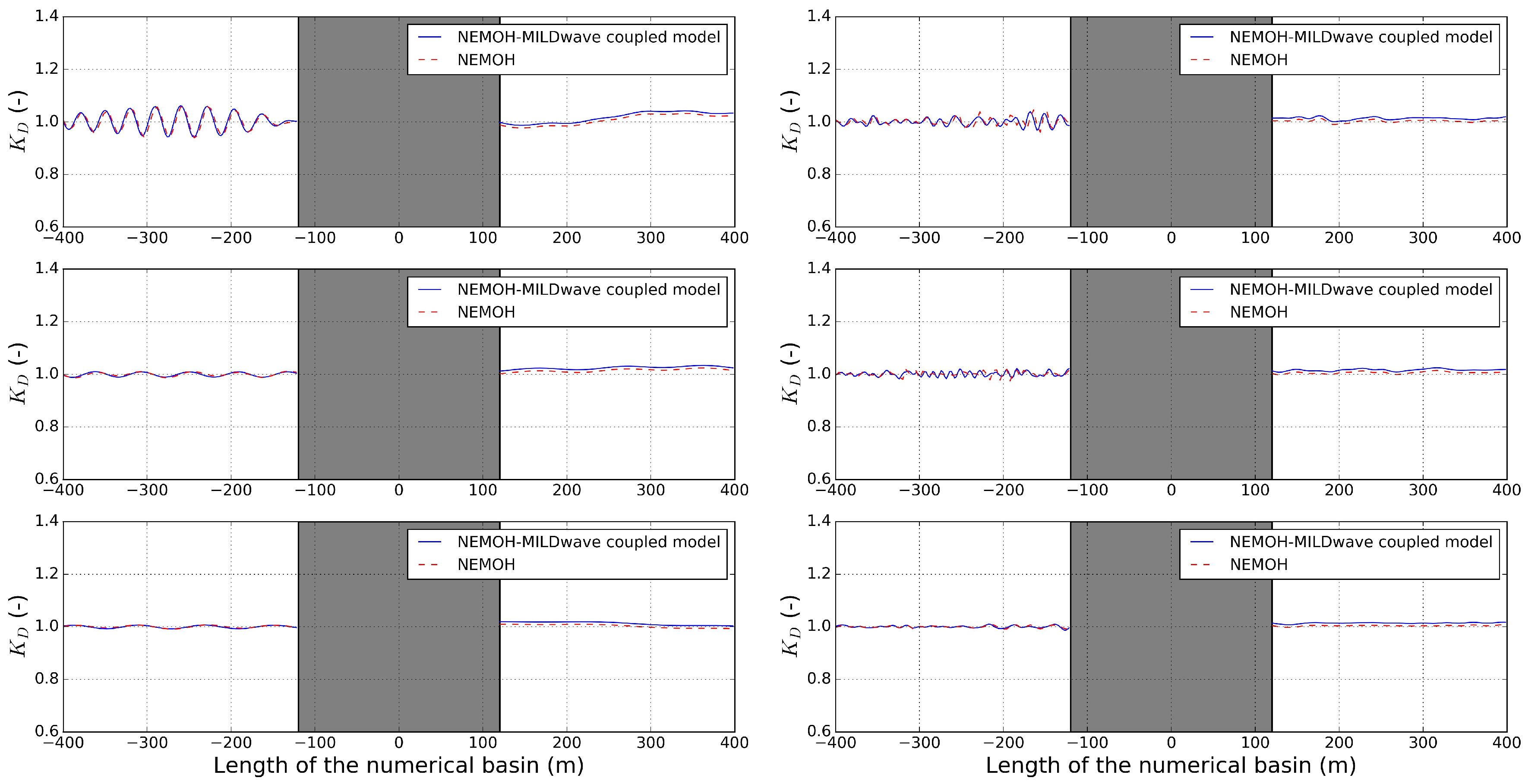
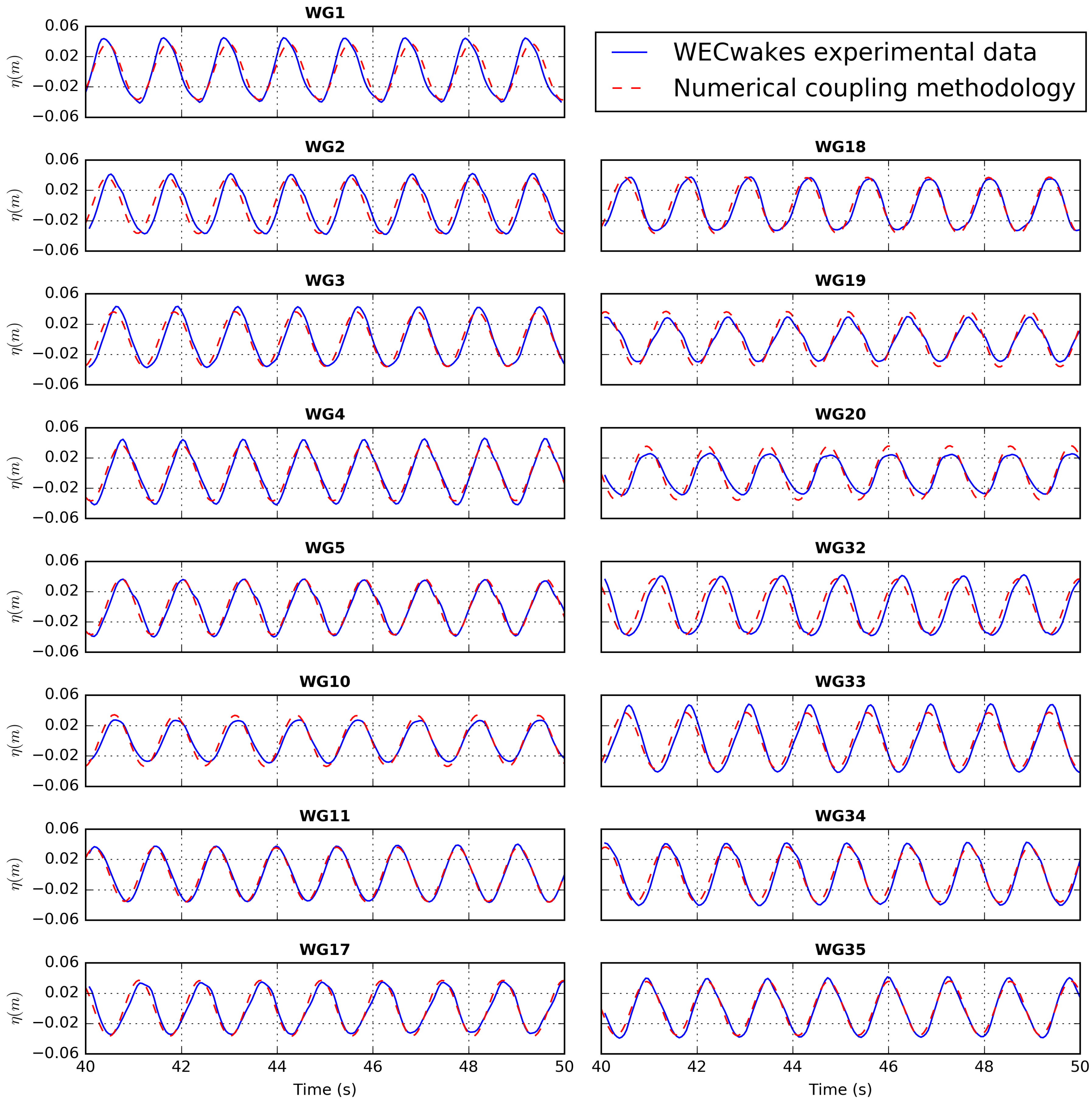
3.4.2. Coupling Methodology Validation for Constant Bottom Bathymetry against Experimental Data
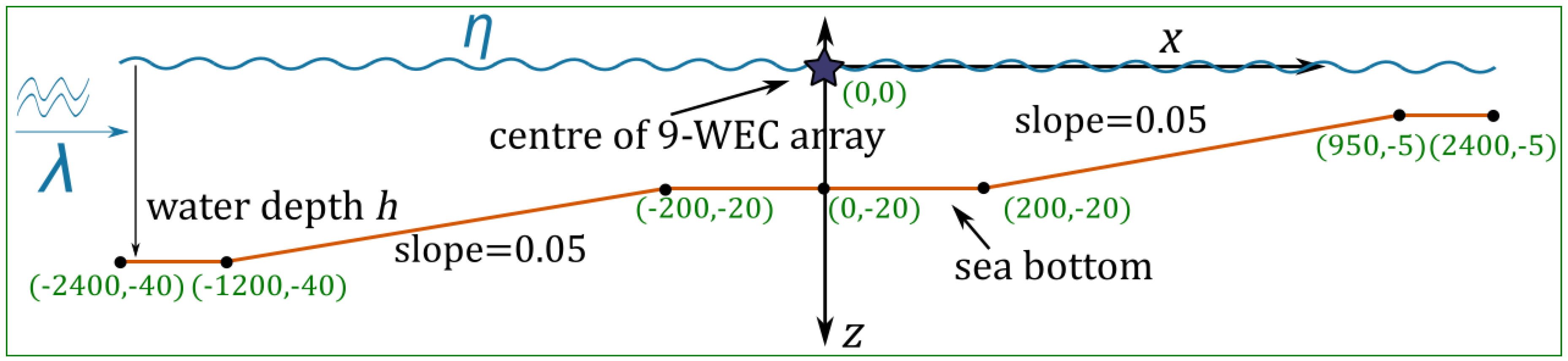
3.4.3. Coupling Methodology Implementation for Varying Bathymetry
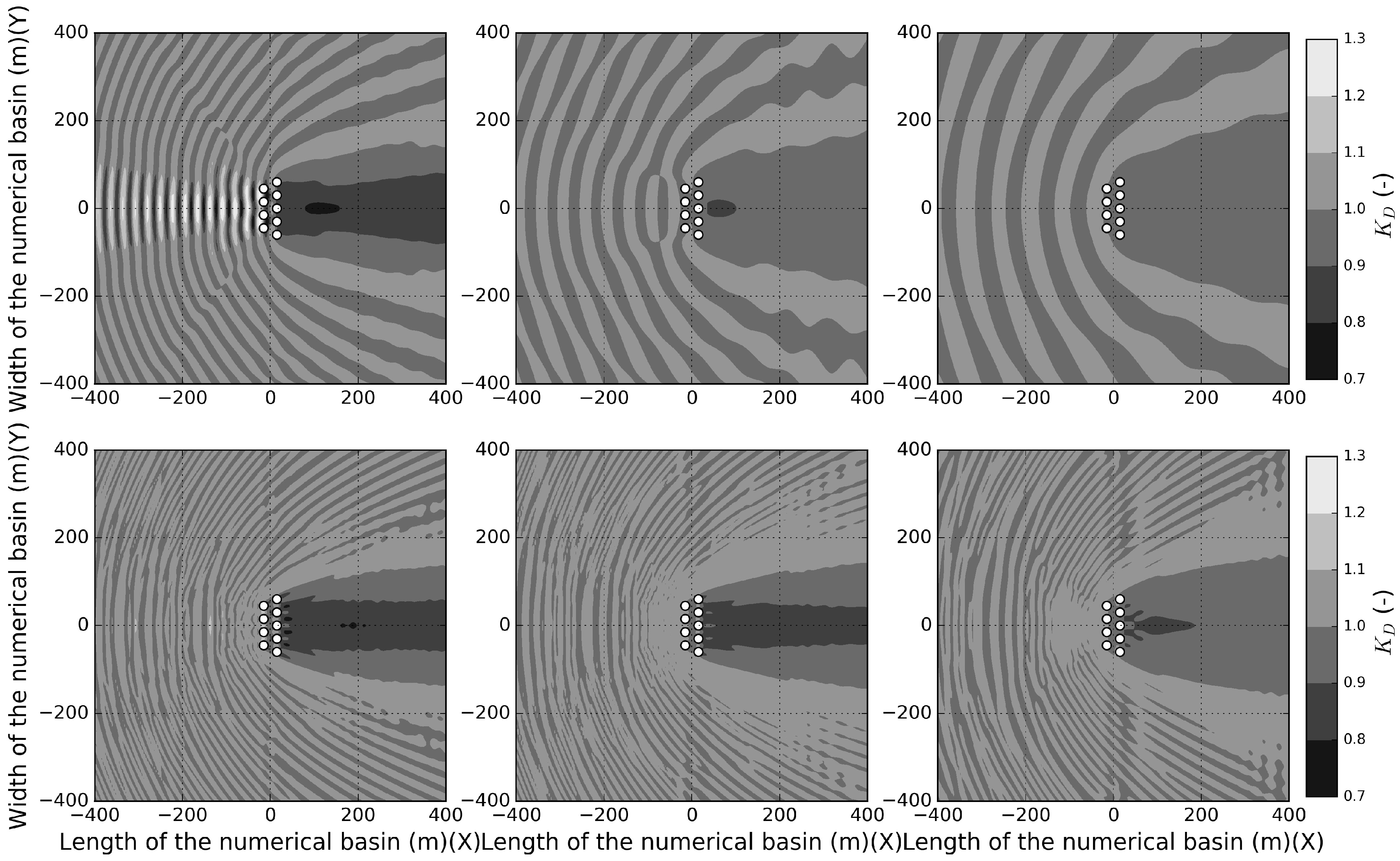
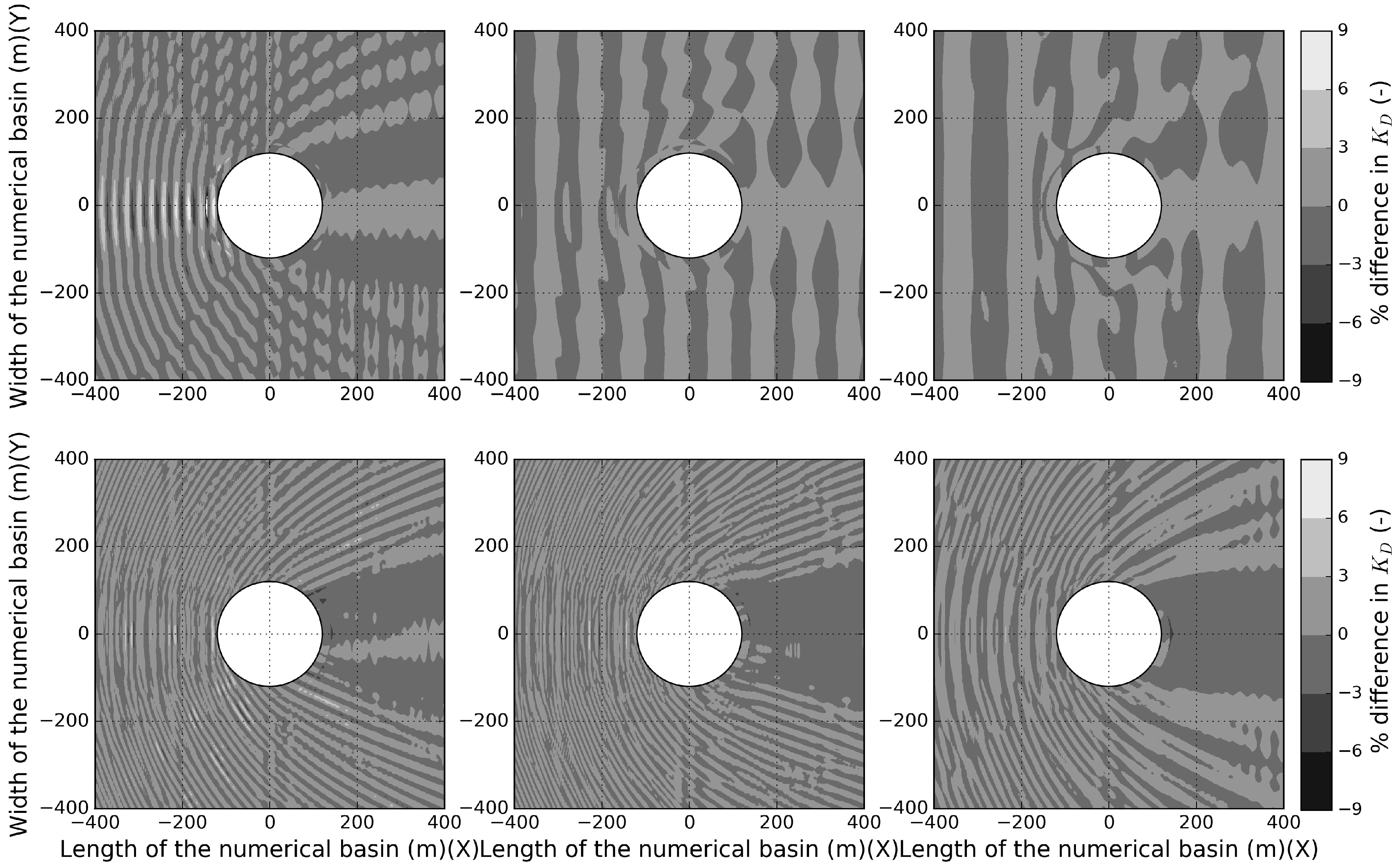
4. Results
4.1. Coupling Methodology Implementation for Constant Bottom Bathymetry
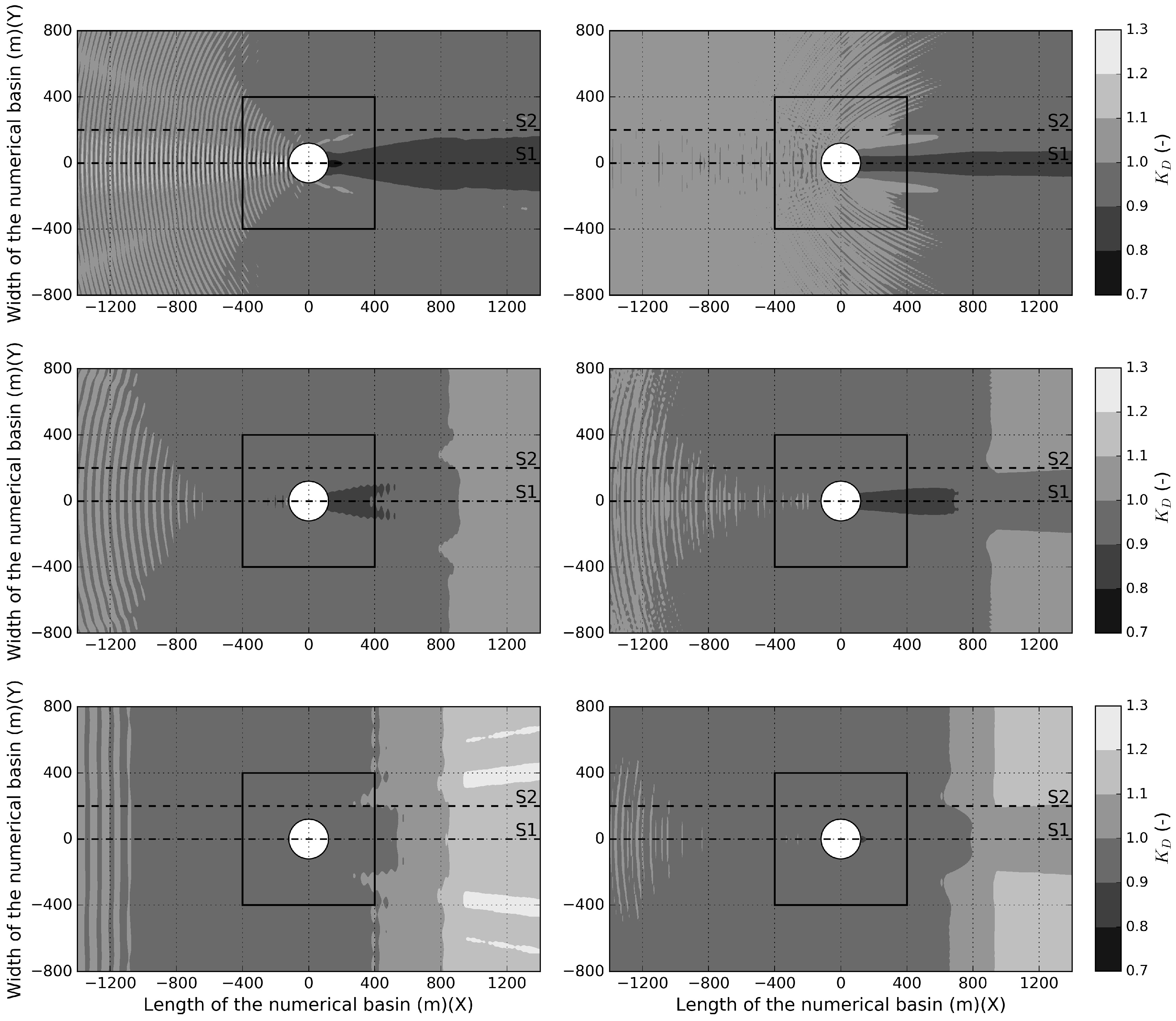
4.1.1. NEMOH Wave Field
4.1.2. NEMOH-MILDwave Coupled Model Wave Field
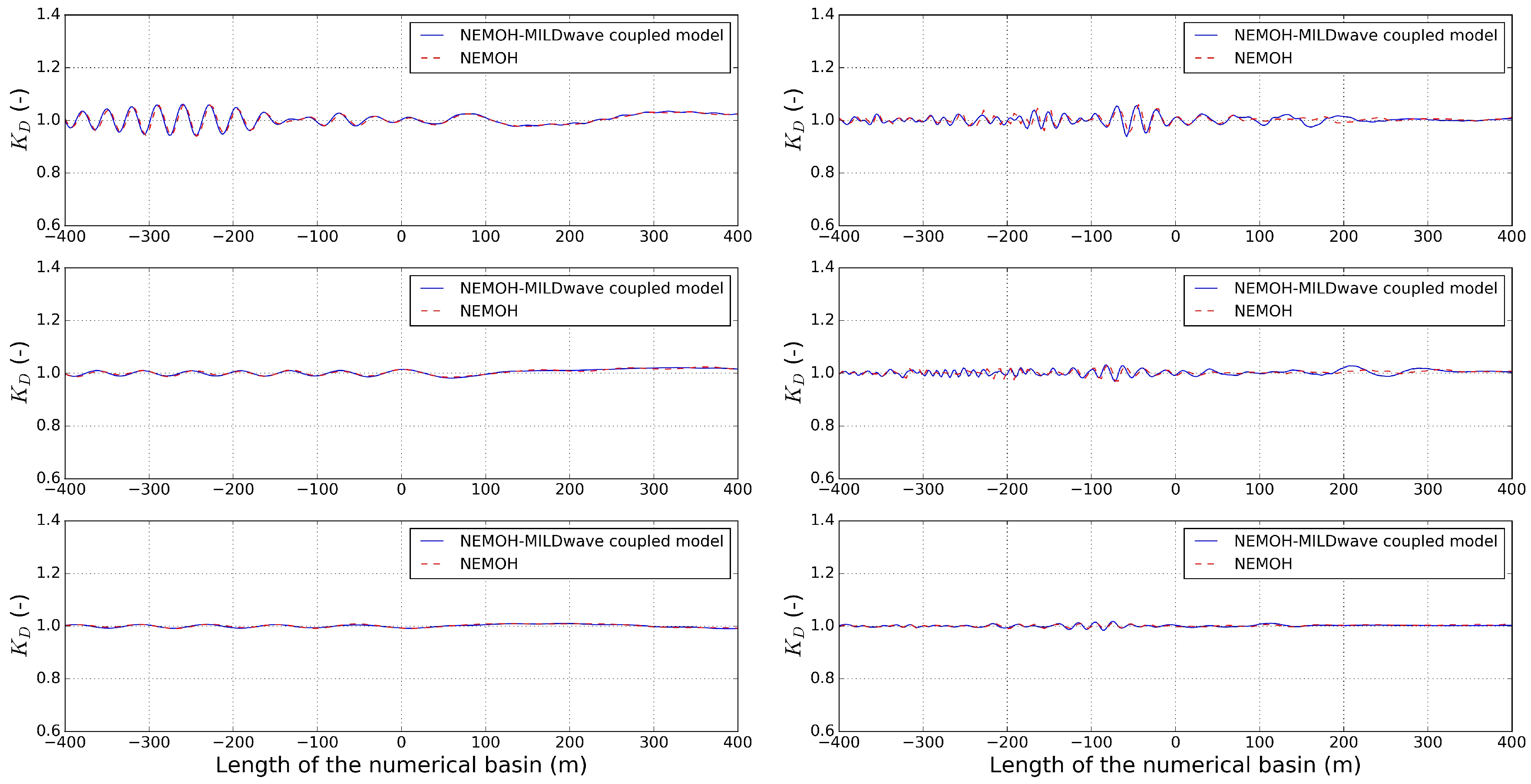
4.1.3. Comparison of the Total Wave Field Generated by NEMOH and the NEMOH-MILDwave Coupled Model
4.2. Coupling Methodology Validation for Constant Bottom Bathymetry against Experimental Data
4.3. Coupling Implementation for Varying Bathymetry
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| WEC | Wave Energy Converter |
| BEM | Boundary Element Method |
| CFD | Computer Fluid Dynamics |
| SPH | Smoothed Particle Hydrodynamics |
| PTO | Power Take-Off |
| RAO | Response Amplitude Operator |
| DHI | Danish Hydraulic Institute |
| WG | Wave Gauge |
| RMSE | Root-Mean-Square-Error |
References
- Stratigaki, V. Experimental Study and Numerical Modelling of Intra-Array Interactions and Extra-Array Effects of Wave Energy Converter Arrays. Ph.D. Thesis, Ghent University, Gent, Belgium, 2014. [Google Scholar]
- Child, B.M.F.; Venugopal, V. Optimal Configurations of wave energy devices. Ocean Eng. 2010, 37, 1402–1417. [Google Scholar] [CrossRef]
- Garcia-Rosa, P.B.; Bacelli, G.; Ringwood, J. Control-Informed Optimal Array Layout for Wave Farms. IEEE Trans. Sustain. Energy 2015, 6, 575–582. [Google Scholar] [CrossRef] [Green Version]
- Babarit, A. On the park effect in arrays of oscillating wave energy converters. Renew. Energy 2013, 58, 68–78. [Google Scholar] [CrossRef]
- Borgarino, B.; Babarit, A.; Ferrant, P. Impact of wave interaction effects on energy absorbtion in large arrays of Wave Energy Converters. Ocean Eng. 2012, 41, 79–88. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Towards the numerical simulation of 5 Floating Point Absorber Wave Energy Converters installed in a line array using OpenFOAM. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC 2017), Cork, Ireland, 27 August–1 September 2017; pp. 739–749. [Google Scholar]
- Abanades, J.; Greaves, D.; Iglesias, G. Wave farm impact on the beach profile: A case study. Coast. Eng. 2014, 86, 36–44. [Google Scholar] [CrossRef]
- Iglesias, G.; Carballo, R. Wave farm impact: The role of farm-to-coast distance. Renew. Energy 2014, 69, 375–385. [Google Scholar] [CrossRef]
- Millar, D.L.; Smith, H.C.M.; Reeve, D.E. Modelling analysis of the sensitivity of shoreline change to a wave farm. Ocean Eng. 2007, 34, 884–901. [Google Scholar] [CrossRef]
- Venugopal, V.; Smith, G. Wave Climate Investigation for an Array of Wave Power Devices. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007; p. 10. [Google Scholar]
- Smith, H.C.M.; Millar, D.L.; Reeve, D.E. Generalisation of wave farm impact assessment on inshore wave climate. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007. [Google Scholar]
- Beels, C.; Troch, P.; De Backer, G.; Vantorre, M.; De Rouck, J. Numerical implementation and sensitivity analysis of a wave energy converter in a time-dependent mild-slope equation model. Coast. Eng. 2010, 57, 471–492. [Google Scholar] [CrossRef]
- Folley, M.; Babarit, A.; Child, B.; Forehand, D.; O’Boyle, L.; Silverthorne, K.; Spinneken, J.; Stratigaki, V.; Troch, P. A Review of Numerical Modelling of Wave Energy Converter Arrays. In Proceedings of the ASME 2012 31st International Conference on Ocean, Offshore and Arctic Engineering (OMAE), Rio de Janeiro, Brazil, 1–6 July 2012. [Google Scholar]
- Lee, C.H.; Newman, J.N. WAMIT User Manual, Versions 6.4, 6.4 PC, 6.3, 6.3S-PC; WAMIT, Inc.: Chestnut Hill, MA, USA, 2006. [Google Scholar]
- Babarit, A.; Delhommeau, G. Theoretical and numerical aspects of the open source BEM solver NEMOH. In Proceedings of the 11th European Wave and Tidal Energy Conference, Nantes, France, 6–11 September 2015. [Google Scholar]
- Balitsky, P.; Verao Fernandez, G.; Stratigaki, V.; Troch, P. Coupling methodology for modelling the near-field and far-field effects of a Wave Energy Converter. In Proceedings of the ASME 36th International Conference on Ocean, Offshore and Arctic Engineering (OMAE2017), Trondheim, Norway, 25–30 June 2017. [Google Scholar]
- Verbrugghe, T.; Stratigaki, V.; Troch, P.; Rabussier, R.; Kortenhaus, A. A comparison study of a generic coupling methodology for modeling wake effects of wave energy converter arrays. Energies 2017, 10, 1697. [Google Scholar] [CrossRef]
- Charrayre, F.; Peyrard, C.; Benoit, M.; Babarit, A. A Coupled Methodology for Wave-Body Interactions at the Scale of a Farm of Wave Energy Converters Including Irregular Bathymetry. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, San Francisco, CA, USA, 8–13 June 2014. [Google Scholar]
- Tomey-Bozo, N.; Murphy, J.; Lewis, T.; Troch, P.; Thomas, G. Flap type wave energy converter modelling into a time-dependent mild-slope equation model. In Proceedings of the 2nd International Conference on Offshore Renewable Energies, Lisbon, Portugal, 24–26 October 2016; pp. 277–284. [Google Scholar]
- Verbrugghe, T.; Devolder, B.; Dominguez, J.; Kortenhaus, A.; Troch, P. Feasibility study of applying SPH in a coupled simulation tool for wave energy converter arrays. In Proceedings of the 12th European Wave and Tidal Energy Conference (EWTEC 2017), Cork, Ireland, 27 August–1 September 2017; pp. 679–689. [Google Scholar]
- Troch, P. MILDwave—A Numerical Model for Propagation and Transformation of Linear Water Waves; Technical Report; Department of Civil Engineering, Ghent University: Ghent, Belgium, 1998. [Google Scholar]
- Alves, M. Wave Energy Converter modelling techniques based on linear hydrodynamic theory. Numer. Model. Wave Energy Convert. 2016, 1, 11–65. [Google Scholar]
- Verbrugghe, T.; Troch, P.; Kortenhaus, A.; Stratigaki, V.; Engsig-Karup, A.P. Development of a numerical modelling tool for combined near field and far field wave transformations using a coupling of potential flow solvers. In Proceedings of the 2nd International Conference on Renewable Energies Offshore, Lisbon, Portugal, 24–26 October 2016. [Google Scholar]
- Stratigaki, V.; Troch, P.; Stallard, T.; Forehand, D.; Kofoed, J.P.; Folley, M.; Benoit, M.; Babarit, A.; Kirkegaard, J. Wave Basin Experiments with Large Wave Energy Converter Arrays to Study Interactions between the Converters and Effects on Other Users. Energies 2014, 7, 701–734. [Google Scholar] [CrossRef] [Green Version]
- Stratigaki, V.; Troch, P.; Stallard, T.; Forehand, D.; Folley, M.; Kofoed, J.P.; Benoit, M.; Babarit, A.; Vantorre, M.; Kirkegaard, J. Sea-state modification and heaving float interaction factors from physical modelling of arrays of wave energy converters. J. Renew. Sustain. Energy 2015, 7, 061705. [Google Scholar] [CrossRef]
- Penalba, M.; Touzón, I.; Lopez-Mendia, J.; Nava, V. A numerical study on the hydrodynamic impact of device slenderness and array size in wave energy farms in realistic wave climates. Ocean Eng. 2017, 142, 224–232. [Google Scholar] [CrossRef]
- Troch, P.; Stratigaki, V. Phase-Resolving Wave Propagation Array Models. Numer. Model. Wave Energy Convert. 2016, 10, 191–216. [Google Scholar]
- Radder, A.C.; Dingemans, M.W. Canonical equations for almost periodic, weakly nonlinear gravity waves. Wave Motion 1985, 7, 473–485. [Google Scholar] [CrossRef]
- Beels, C.; Troch, P.; Kofoed, J.P.; Frigaard, P.; Kringelum, J.V.; Kromann, P.C.; Donovan, M.H.; De Rouck, J.; De Backer, G. A methodology for production and cost assessment of a farm of wave energy converters. Renew. Energy 2011, 36, 3402–3416. [Google Scholar] [CrossRef]
- Stratigaki, V.; Troch, P.; Baelus, L.; Keppens, Y.U. Introducing wave generation by wind in a mild-slope wave propagation model MILDwave, to investigate the wake effects in the lee of a farm of wave energy converters. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar]
- Brorsen, M.; Helm-Petersen, J. On the Reflection of Short-Crested Waves in Numerical Models. In Proceedings of the 26th International Conference on Coastal Engineering, Copenhagen, Denmark, 22–26 June 1998; pp. 394–407. [Google Scholar]
- National Renewable Energy Laboratory. Marine and Hydrokinetic Technology Database. Available online: https://openei.org/wiki/Marine_and_Hydrokinetic_Technology_Database_759 (accessed on 1 June 2018).
- Faltinsen, O.M. Sea Loads on Ships and Offshore Structures; Cambridge University Press: Cambridge, UK, 1990; p. 328. [Google Scholar]
- Sismani, G.; Babarit, A.; Loukogeorgaki, E. Impact of Fixed Bottom Offshore Wind Farms on the Surrounding Wave Field. Int. J. Offshore Polar Eng. 2017, 27, 357–365. [Google Scholar] [CrossRef]
- Devolder, B.; Rauwoens, P.; Troch, P. Numerical simulation of a single floating point absorber wave energy converter using OpenFOAM. In Proceedings of the 2nd International Conference on Renewable energies Offshore, Lisbon, Portugal, 24–26 October 2016; pp. 197–205. [Google Scholar]
- Devolder, B.; Stratigaki, V.; Troch, P.; Rauwoens, P. CFD simulations of floating point absorber wave energy converter arrays subjected to regular waves. Energies 2018, 11, 641. [Google Scholar] [CrossRef]
- Child, B.M.F. On the Configuration of Arrays of Floating Wave Energy Converters. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2011. [Google Scholar]






| Regular Waves | |||
| Case Name | T(s) | H(m) | = 0 |
| A | 6 | 2 | 0 |
| B | 8 | 2 | 0 |
| C | 10 | 2 | 0 |
| Irregular Waves | |||
| Case Name | (s) | (m) | = 0 |
| D | 6 | 2 | 0 |
| E | 8 | 2 | 0 |
| F | 10 | 2 | 0 |
| Test Number | Numerical Models | Wave Type | H (m) | T (s) | Water Depth d (m) |
|---|---|---|---|---|---|
| 1 | NEMOH | REG | 2 | 6 | 40 |
| 2 | NEMOH | REG | 2 | 8 | 40 |
| 3 | NEMOH | REG | 2 | 10 | 40 |
| 4 | NEMOH-MILDwave | REG | 2 | 6 | 40 |
| 5 | NEMOH-MILDwave | REG | 2 | 8 | 40 |
| 6 | NEMOH-MILDwave | REG | 2 | 10 | 40 |
| 7 | NEMOH | IRREG | 2 | 6 | 40 |
| 8 | NEMOH | IRREG | 2 | 8 | 40 |
| 9 | NEMOH | IRREG | 2 | 10 | 40 |
| 10 | NEMOH-MILDwave | IRREG | 2 | 6 | 40 |
| 11 | NEMOH-MILDwave | IRREG | 2 | 8 | 40 |
| 12 | NEMOH-MILDwave | IRREG | 2 | 10 | 40 |
| Test Number | Numerical Models | Wave Type | H (m) | T (s) | Water Depth d (m) |
|---|---|---|---|---|---|
| 13 | NEMOH-MILDwave | REG | 2 | 6 | VAR |
| 14 | NEMOH-MILDwave | REG | 2 | 8 | VAR |
| 15 | NEMOH-MILDwave | REG | 2 | 10 | VAR |
| 16 | NEMOH-MILDwave | IRREG | 2 | 6 | VAR |
| 17 | NEMOH-MILDwave | IRREG | 2 | 8 | VAR |
| 18 | NEMOH-MILDwave | IRREG | 2 | 10 | VAR |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verao Fernandez, G.; Balitsky, P.; Stratigaki, V.; Troch, P. Coupling Methodology for Studying the Far Field Effects of Wave Energy Converter Arrays over a Varying Bathymetry. Energies 2018, 11, 2899. https://doi.org/10.3390/en11112899
Verao Fernandez G, Balitsky P, Stratigaki V, Troch P. Coupling Methodology for Studying the Far Field Effects of Wave Energy Converter Arrays over a Varying Bathymetry. Energies. 2018; 11(11):2899. https://doi.org/10.3390/en11112899
Chicago/Turabian StyleVerao Fernandez, Gael, Philip Balitsky, Vasiliki Stratigaki, and Peter Troch. 2018. "Coupling Methodology for Studying the Far Field Effects of Wave Energy Converter Arrays over a Varying Bathymetry" Energies 11, no. 11: 2899. https://doi.org/10.3390/en11112899
APA StyleVerao Fernandez, G., Balitsky, P., Stratigaki, V., & Troch, P. (2018). Coupling Methodology for Studying the Far Field Effects of Wave Energy Converter Arrays over a Varying Bathymetry. Energies, 11(11), 2899. https://doi.org/10.3390/en11112899







