Abstract
This work is located in a growing sector within the field of renewable energies, wave energy converters (WECs). Specifically, it focuses on one of the point absorber waves (PAWs) of the hybrid platform W2POWER. With the aim of maximizing the mechanical power extracted from the waves by these WECs and reducing their mechanical fatigue, the design of five different model predictive controllers (MPCs) with hard and soft constraints has been carried out. As a contribution of this paper, two of the MPCs have been designed with the addition of an embedded integrator. In order to analyze and compare the MPCs with conventional PI type control, an exhaustive study about performance and robustness is realized through the computer simulations carried out, in which uncertainties in the WEC dynamics and JONSWAP spectrum are considered. The results obtained show how the MPCs with embedded integrator improve power production of the WEC system studied in this work.
1. Introduction
Nowadays, the main motivation for the research and development of wave energy converters (WECs) is the advantages offered by waves: a clean and abundant source of energy. As evidence, the authors in [1] compared a global study of net wave power (estimated at about 3 TW) with the electrical power consumed globally in 2008 (equivalent to an average power of 2.3 TW). However, it should be noted that currently, there is not a clear line of development, but a great diversity of systems based on different approaches to extract energy from the waves. In particular, the ocean energy systems collaboration program [2] classifies three kinds of WEC systems: oscillating water columns, overtopping and wave-activated bodies (WABs). This work focuses on a type of WAB system, a point absorber wave (PAW) energy converter from the W2POWER (Wind and Wave Power) platform [3]. These systems are characterized because their extension is significantly smaller than the predominant wavelengths. In addition, PAWs extract the maximum mechanical power from the sea when they are in resonance with the excitation force caused by the waves [4]. In order to favor this situation, it is necessary to enlarge the bandwidth of these devices. For this reason, several control systems are used, and the most common are: passive loading control, reactive loading control and latching control [5,6]. Although, since the last decade, more complex controllers like MPC (model predictive control) are being employed. The interest in implementing MPCs in WEC systems is motivated by the need to increase the productive/economic viability of these systems; due to the fact that these controllers allow them to minimize mechanical fatigue in their structures (limiting the operating ranges) and to focus the control strategy on the maximization of the extracted power directly.
Actually, several authors have developed predictive controllers for WECs [7,8,9,10,11,12,13,14,15,16,17]. These MPCs can be grouped according to the characteristics of the cost function optimized. On the one hand, the authors in [8,10,11,12,13,14,15,16] used a cost function in which the extraction of mechanical power was directly maximized. Whereas, on the other hand, in [9,17], the authors proposed a cost function to maximize power extraction by minimizing the error between the speed of oscillation of the system and a setpoint for it. In addition to the above classification, MPCs can be distinguished according to the mathematical model used for their design. On one side, in [9,10,11,13,14], a reduced model was used for the design, which did not consider the dynamics of the radiation force. Meanwhile, in [7,8,12,13,15,16,17], such dynamics were considered in the design model. Moreover, the previous works did not consider the dynamics of the power take-off system (PTO), neither in the evaluation, nor in the design of the MPCs. In this aspect, the authors in [11,14], although they did not consider the PTO dynamics, optimized the cost function for the increment of the control signal, thus limiting the slew rate of the actuator. Finally, the treatment carried out in the case of non-feasibility when solving the cost functions with restrictions should be highlighted. In this aspect, the works in [9,10,13] considered a more complete approach by adding soft constrains in the case of non-feasibility.
This paper analyses the main approaches of MPCs applied to PAW systems [8,9,10,11,12,13,14,15,16,17]. In addition, a new design is proposed: MPC based on a model with an embedded integrator for controllers that follow a setpoint for the speed of oscillation of the PAW. This approach is recommended in the theory of predictive control in the space of states [18,19], and it is proposed as an alternative method to the one carried out in [9,17] for PAW systems. Moreover, all predictive controllers of this work consider soft and hard constraints. On the other hand, the PTO dynamics is taken into account to validate the MPC controllers, as well as in the design of some of these controllers. After an exhaustive fine-tuning for all MPCs, the main contribution of this work is obtained, and an in-depth study about performance and robustness of all MPCs through simulations is carried out. The results obtained for a sea state defined by the JONSWAP spectrum [15,16] are compared with conventional controllers: I-P control and resistive damping (RD). Furthermore, the mathematical model of the WEC system is obtained using a software simulation based on the boundary element method, such as openWEC [20].
The rest of the article is organized as follows: Section 2 presents the generic mathematical model of a PAW, the standard identification methodology applied in this paper and the treatment applied to the model identified for its later use in the design of the MPCs. Section 3 details the five MPC controllers designed with hard and soft restrictions. Section 4 presents a performance and robustness comparison analysis for the MPCs and conventional (P, PI) controllers. Finally, in Section 5, the main conclusions are indicated.
2. Mathematical Model
Given the importance of mathematical modeling in the design of MPC controllers, this section begins by describing the generic model of a PAW. This is followed by the standard identification process realized in this paper for the study system, one of the WEC systems of the platform W2POWER [3]. Later, the treatment of the model is detailed for its later use in the design of MPC controllers.
2.1. Generic Mathematical Model for Point Absorber Wave
The modeling of the forces affecting a PAW that extracts power from the waves using a single degree of freedom (heave) is widely used in the literature [4,7,8,9,21,22,23,24,25,26,27]; see Figure 1. The main dynamic interactions between the buoy and the waves are collected by:
where m is the mass of the system, z the vertical displacement of the buoy, the excitation force caused by the wave, the radiation force, the hydrostatic restoring force and the control force realized by the PTO system.
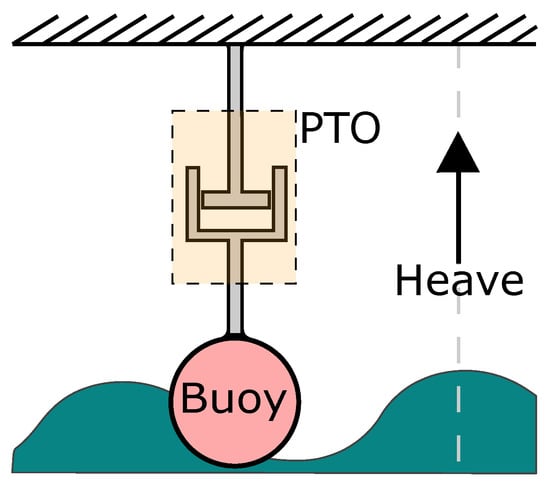
Figure 1.
Illustrative scheme: point absorber wave (PAW) system of the W2POWER platform.
The force of radiation is due to the effect produced on the system by the waves it radiates when oscillating. It is modeled by the Cummins equation [28] as (2), where the radiation force is composed of two terms: and . The first is a function of the acceleration of the system and the mass of water added ; while the second defines a radiation force as a function of the speed of oscillation as an integral of convolution.
The convolution term represents the impulse response that relates the speed of the oscillation system with the force of radiation, where represents the radiation impulse response function (RIRF). To avoid convolution calculations [21,24,26], an approximation is made based on ordinary differential equations (ODE) or as a transfer function in the Laplace domain (3).
The hydrostatic restoring force represents the effect of Archimedes and gravity on the buoy (4). By linearizing Equation (4), the hydrostatic force is approximated as (5).
where is the volume of water displaced, is the density of seawater, g is the gravity constant, is the hydrostatic restoring coefficient and is the area of the buoy on its waterline.
For the excitation force caused by the waves, the components with the highest frequency are negligible. For this reason, authors such as [7,8,11,12,15,16,24,25,26,27] have defined the excitation force as a low pass filter of first/second order at wave height (6). This modeling is used later in the performance study.
On the other hand, in order to model the force on a buoy, the Morison equation [29] can be used, which is habitually employed to estimate the wave loads in the design of offshore structures. By linearizing the Morison equation for a point absorber wave in heave, the excitation force is defined according to Equation (7). This modeling is used later in the robustness study.
where is the height of the incoming wave and represents the damping of the system, which can be obtained as the stationary gain of the transfer function (3).
The PTO dynamics can be approximated as a linear second order system with a force limitation. The linear relation between the demanded force by the control system, (), and the force applied to the buoy, (), is given by (8).
2.2. Forces Identification Using Simulation Based on BEM
A common approach to determine the hydrodynamic forces of interaction between the wave and buoy is to use the linear wave theory, which assumes that waves are the sum of incident, radiated and diffracted wave components [21]. These components can be modeled using linear coefficients obtained from the frequency-domain potential flow BEM (boundary element method) solver Nemoh [30]. The BEM solutions are obtained by solving the Laplace equation for the velocity potential, which assumes that the flow is inviscid, incompressible and irrotational. In this work, openWEC software is employed. It is an open-source tool to simulate the hydrodynamic behavior and energy yield from single-body wave energy converters [20]. Two software packages are coupled in openWEC, a frequency domain solver Nemoh and a time domain solver. In particular, this numerical tool is applied to solve the fluid equation for a submerged body. The equations are solved for the following effects in the heave direction on a buoy: excitation force , radiation force and restoring force . Thus, the frequency domain modeling is performed with the Nemoh BEM solver. For each panel of a mesh (see Figure 2a), the hydrodynamic parameters are calculated for a frequency range. The pressures caused by the incoming wave are integrated into resulting forces on the buoy; see Figure 2b. From these data in the frequency domain, a filter is established to convert a wave into an exciting force (9). A magnitude diagram of the resulting filter is also shown in Figure 2b. The magnitude response resembles a second order filter with a cut-off frequency of rad/s.

Figure 2.
(a) Mesh defined by openWEC for a cylindrical buoy (11 m long and m in diameter). Comparison of the identified transfer functions: (b) Bode diagram for excitation force ; (c) impulse response for radiation force .
An advanced function of Nemoh can be enabled to calculate the impulse response function (IRF). A comparison between the IRF identified and that provided by openWEC is shown in Figure 2c. To avoid convolution calculations in (2), it is replaced as ordinary differential equations (ODE) or as a transfer function in the Laplace domain (3). This can be performed using Prony’s method [21,31,32], which is implemented in MATLAB 2016b [33]. Different orders of ODEs have been tested to fit the impulse response. By comparing these responses, it was observed that for orders above eighth, the improvement in the system response was not significant.
where the coefficients and are listed in Table 1.

Table 1.
Model coefficients identified for the WEC system.
2.3. Treatment of the Mathematical Model for the Design of MPCs
In order to ensure safe behavior and reduce mechanical fatigue in PAW systems, a model that allows them to constrain the oscillation speed and the position of the buoy is necessary. For this reason, a brief study of the identified model (11) is realized. By representing it in the state space, it can be verified that the system obtained is not completely controllable, and therefore, it is not a minimal realization [34]. Furthermore, it is not enough to reduce the model (11) to its minimum order. This is because, except for the system output (z), the other state variables lack physical sense, and this does not allow it to impose speed constraints (w) directly. As a solution, we study the transfer function (10) that defines the dynamics of the radiation force. Representing (10) in the state space, it can be seen how the model obtained is not of minimum order, so the system is minimized to get (12). Note that the state variables of this model () will not be controlled, so it is not necessary that they have physical sense.
where the matrices , , and are given by (13).
A complete model must consider the dynamics of the power take-off system. Given the similarity between the Wavestar system and the WEC studied in this work, the PTO model proposed in [24] is used, where the PTO dynamics are modeled according to (8). By representing this model in the state space, with the parameters indicated in [24], the matrices (14) have been obtained. For this purpose, the observable canonical form has been chosen. Thus, one of the state variables corresponds to the output of the PTO system, so MPCs may impose restrictions on the output of the actuator.
After that, in this paper, we propose (15) as one of the design models, and the MPCs can impose restrictions on the following state variables: force applied by the PTO (), oscillation speed (w) and buoy position (z). This model is similar to the one proposed in [8,12], but also considers the PTO dynamics.
where and the matrices I (unit matrix) and zero have the required size according to their location, and the parameters not yet presented are listed in Table 2.
Simplified Model for the Design
In this paper, as in others works [9,10,11,13,14], a simplified model (16) is used for the design of some MPCs. It differs from the previous model (15) in that it does not take into account the dynamic of the radiation force or the PTO dynamics. Figure 3 shows a comparison of the outputs of the simplified model and the complete model.
where , and the parameter values are listed in Table 2.
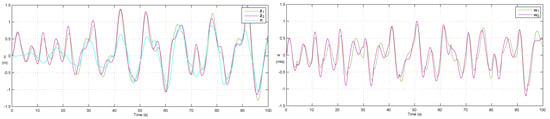
Figure 3.
Comparison of models: complete (, ) vs. simplified (, ). The height of the wave is n.
3. Model Predictive Control for the Point Absorber WEC
This section details the design of the commonly-used MPCs for PAWs. Moreover, in this work, two MPCs are proposed based on the addition of an embedded integrator. In order to make a complete design, all the MPCs take into account constraints and the possibility of relaxing them, in the case of non-feasibility, in their cost functions. In particular, these constraints are applied to the control force of the PTO system, the position of the buoy and its oscillation speed. However, in the case of non-feasibility, only soft-constraints are applied to the position and oscillation speed of the system; due to the PTO being an actuator whose physical limit cannot be exceeded. Finally, for each controller, a sampling period of is set, which is used to discretize the mathematical model using the zero order hold (ZOH) approximation.
3.1.
The cost function that minimizes this controller considers the maximization of extracted power directly; as the design model is used (16), for which the state vector estimated for a prediction horizon M and a control horizon N is defined according to Equation (17) [18,19].
where X represents the estimated state vector for a prediction horizon M, represents the state vector at the current instant, the matrices A and B are obtained from the model (16) discretized (ZOH), n is the order of the model and and are vectors that contain the force applied by the PTO and the excitation force for whole control horizon N, respectively.
In a more compact form, the above equation can be expressed as:
On the other side, as defined in [10,12,26], the mechanical power generated is given by (19). The expression of the power generated for the whole prediction horizon is obtained (20).
where W and are vectors with length M, which represent the oscillation speed and control force for the whole prediction horizon, respectively.
Developing (21) and grouping in terms of least squares, the cost function is obtained:
where the matrix R weights the control effort.
In addition, constraints are imposed to: force demanded for the PTO position and oscillation speed of the buoy (24). Therefore, the cost function (22) with constraints is defined as:
where and ; see Equation (24).
where is a selector matrix for position (size ), the vectors and (size ) define the nominal limits of the force applied by the PTO and the vectors , , and (size ) define the nominal limits of the buoy position and oscillation speed, respectively. In addition, the matrices I (unit matrix) and 0 have the required size according to their location.
In the case of non-feasibility, soft constraints to the position and oscillation speed of the system are applied. Thus, the cost function (22) would be defined as:
where and represent the relaxation applied to position and speed along the prediction horizon M and the matrices and (size ) weight these slacks.
By regrouping terms and adding soft restrictions, the cost function (25) can be expressed as:
where , with size , and ; see Equation (27). Matrices 0 have the required size according to their location.
where and are vectors (size ) that represent the maximum slack allowed for position and oscillation speed, respectively. The matrices I (unit matrix) and 0 have the required size according to their location.
3.2.
This controller uses the simplified model (16). Its cost function is based on maximizing the extracted power by tracking a setpoint for the oscillation speed () along a prediction horizon M,
where Q and R are diagonal matrices of size and that weight the tracking error and the control effort, respectively.
By developing the cost function (29) and grouping terms, the following expression is obtained:
Note that the term l can be ignored when the cost function is minimized, because it does not depend on the variable to be optimized (),
3.3.
This approach is a contribution made in this work. This controller uses the simplified model (16) to which an embedded integrator has been added according to the theory of predictive controllers in the state space [18,19]. Its cost function is based on the maximization of the extracted power through the tracking of a setpoint for the oscillation speed. To add the integrator, it is necessary to multiply the model (16) discretized by the operator . Regrouping terms, an extended state vector is defined as:
where the output vector is formed by the position and oscillation speed of the WEC system, represents the state vector increment, the matrices A, B and C are from the model (16) discretized (ZOH) and the matrices 0 have the required size according to their location.
Using the extended model (32), the prediction of the outputs (z, w) is defined for a prediction horizon M and a control horizon N according to:
where represents the order of the extended model and j its number of outputs. In the matrices A, B and C, the sub-index e has been omitted to get a clearer notation.
By adding the embedded integrator, this controller minimizes a cost function that gets the optimal increase in control force () for the full control horizon N,
where Q and R are diagonal matrices of size and that weigh the tracking error and the control effort, respectively.
In addition, constraints are added to the demanded force on the PTO, position and oscillation speed of the system. Therefore, the cost function (35) subject to the restrictions is defined as:
where and ; see Equation (37).
where and are selector matrices for z and w (size ), T is a lower triangular matrix (size ), the vectors and (size ) define the nominal limits of the force applied by the PTO and the vectors , , and (size ) define the nominal limits of the buoy position and oscillation speed, respectively. The matrices I (unit matrix) and 0 have the required size according to their location.
In the case of non-feasibility in the cost function (36), soft constraints are applied,
where and ; see Equation (38).
where and are vectors (size ) that represent the maximum slack allowed for z and w, respectively. The matrices I (unit matrix) and 0 have the required size according to their location.
3.4.
This controller is made using the model (15). The cost function that minimizes this controller is focused on the maximization of extracted power directly. The matrix development needed to express this controller as a least squares problem is analogous to that presented for controller . Although, when the PTO dynamics are taken into account, Equation (18) should be redefined as:
where is a matrix already defined in Equation (17), while the matrices and are given by:
where A, and are obtained by discretizing (ZOH) , and of the model (15).
The cost function to be minimized by this controller can be expressed according to (42). Its development is analogous to that carried out for the controller .
In addition, the nominal constraints imposed on the system must be added, which are defined in the same way as in the controller , Equation (24). However, in this case, it must be considered that the state vector prediction is given by Equation (40). Therefore, the cost function (42) subject to the constraints is defined as:
where and ; see Equation (24).
Finally, in the case of non-feasibility in the function (48), soft constraints will be applied to the system. These can be expressed in a similar way to the development shown for , Equation (27). However, in this case, it must be considered that the prediction of the state vector is given by Equation (40). Therefore, the cost function of this controller subject to soft constraints is given by:
where and ; see Equation (27).
3.5. MPC5
This controller is another contribution of this work. It uses the model (15), to which an embedded integrator has been added according to the theory of predictive controllers in the state space [18,19]. Its cost function to minimize is based on the maximization of the extracted power through the tracking of a setpoint for the oscillation speed of the system . As in the , the state vector is extended by adding an embedded integrator (32). Despite taking into account the PTO dynamics, the prediction of the output vector for the full prediction horizon M is defined by:
where F is a matrix already defined in Equation (33), and the matrices and are given by:
where and are obtained by discretizing the matrices that define the inputs of (15) extended.
Analogous to controller , the cost function to be minimized can be expressed according to:
In addition, it is necessary to add nominal constraints to the system, which are defined as in the controller . However, in this case, it must be considered that the prediction of the system outputs is given by (45). Thus, the cost function (47) subject to the constraint is defined as:
where and ; see Equation (37).
Furthermore, in the case of the non-feasibility in the function (47), soft constraints are used. The soft constraints are expressed analogously to the development made for controller , Equation (39). However, in this case, the prediction of the system output is given by (45). Therefore, the cost function of this controller subject to soft constraints is defined as:
where and ; see Equation (39).
3.6. Conventional Controllers
In order to make a comparative analysis of the proposed predictive controllers, this section presents the design of two of the controllers most commonly used in WEC systems [5,6]. Firstly, a resistive damping (RD) controller (or proportional control) has been tuned for the PTO system, whose control law is given by:
where k is the current sampling time and is a proportional gain (), which must be tuned to maximize the power generated.
On the other hand, an I-P control has been designed whose control law is defined by Equation (51). A compromise between generated power and keeping the system within its nominal limits of operation is maintained by tuning the gains and .
where k is the current moment. The backward Euler method has been used to discretize the controller for a sampling period .
4. Study about Performances and Robustness
This section presents the results obtained from an in-depth study of the performance and robustness of the five MPCs designs. This study assumes that the system state vector and the excitation force () for the whole prediction horizon (M) are known. The computer simulations have been carried out using Simulink, employing a fourth order Runge–Kutta integration method with a fixed step of one millisecond. In order to solve the optimization problems with constraints, associated with MPCs’ design, the MATLAB quadprog function has been employed [35]. Note that although the quadprog function provides for the whole control horizon N, only the setpoint obtained for the current instant k is applied [18,19].
Due to the fact that the WEC system of the W2POWER platform has not yet been built, its operating limits and physical limits are not available. Therefore, these limits have been chosen on the basis of [12,15,16,24], whose WEC systems are similar to the system studied in this paper; see Table 3.

Table 3.
Hard and soft constraints for the WEC system.
4.1. Performance Comparison
This section shows a comparison between the seven controllers designed. The controllers’ performances are compared in terms of: average power generated, reduction of instantaneous power peaks, overshoot of nominal limits and control effort. A sea state defined by the JONSWAP spectrum [15,16], with a significant wave height of three meters and a peak period of 11 s, has been chosen as a realistic scenario for evaluating these characteristics. In order to obtain a truthful performance comparison, all predictive controllers must have the same information about the incoming wave, which is recorded in the prediction time . To set the prediction horizon, two factors have been taken into account. Firstly, in [7,8,10], the authors used realistic sea states, and they set the prediction times between two and four seconds. Furthermore, in [8], the authors checked that could also be reduced to three or four seconds without significant reduction of the harvested energy. Secondly, in [36], the authors showed how short-term wave forecasting models maintain good performance up to five seconds of prediction for wide wave spectra. Therefore, in this work, the prediction time chosen was three seconds, the same as the one set in [10]. With this , a prediction horizon , a control horizon and a sampling period s has been set for all MPCs. The RD and I-P controllers have the same sampling period. On the other hand, as a result of a fine-tuning for this realistic sea state, the parameters of the controllers are listed in Table 4.

Table 4.
Control parameter set for the sea state defined by the JONSWAP spectrum (3 m of significant wave height and 11 s of peak period).
Figure 4 shows a comparison of the instantaneous mechanical powers generated by applying the seven controllers to the mathematical model (15). In this comparison, it can be seen how MPCs with an embedded integrator (MPC3 and MPC5) achieve more regular power than the MPCs most used for WEC systems, those whose optimization criteria maximize the extracted power directly (MPC1 and MPC4). In addition, Figure 5 shows how MPCs with embedded integrators achieve less overshoot in the control force applied by the PTO system than all other MPCs (reducing actuator overstress).
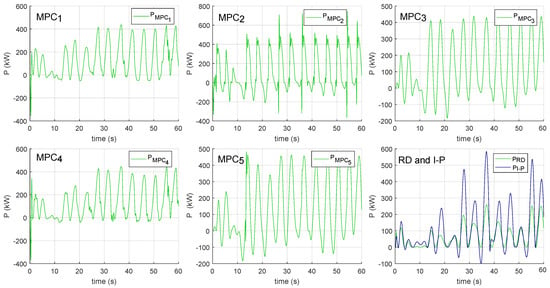
Figure 4.
Simulation of the instantaneous mechanical powers generated by the WEC system when applying the seven controllers to the mathematical model (15).
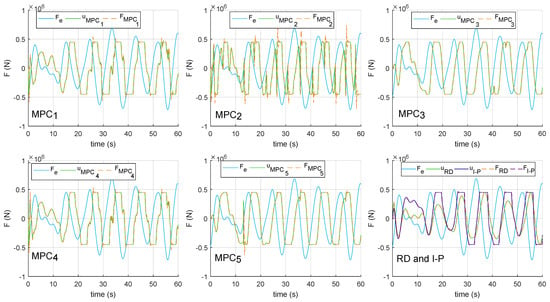
Figure 5.
Simulation of: wave force, force setpoint demanded for the PTO and real force produced by the PTO, when applying the seven controllers to the mathematical model (15).
By applying the MPC2 to the system, it gives the most irregular power; while the power generated with the MPC3, designed from the same model and following the same optimization criteria, is much cleaner, with fewer occasional peaks. This is due to the fact that the MPC1 is continuously applying soft constraints to the oscillation speed, because it does not carry out a good control of the force that the PTO system exerts on the WEC during the time (see Figure 5). On the other hand, Table 5 shows how the addition of the embedded integrator (MPC3) considerably improves the behavior of the system with respect to that obtained by applying the MPC2. Since, the MPC3 does not exceed nominal limits of the position and oscillation speed on any occasion. Furthermore, the MPC3 controller generates a clearer control signal than the MPC2 (see Figure 5), and as a consequence, the underdamped response of the PTO system decreases greatly.

Table 5.
Results obtained in the application of the seven controllers to the WEC system. The powers are expressed in kW. Note that indicates overshoot of nominal limits for position and indicates overshoot of nominal limits for speed.
Table 5 records the most significant quality indicators of the control performed by each controller. First, this table shows the average mechanical powers generated by the WEC system when applying each controller. In this aspect, the MPC5 controller is the one that generates more power, followed very closely by the MPC1, MPC4 and, with a bit more distance, the MPC3. On the other side, the indicators and quantify the area of overshoot from the nominal limits of the position and oscillation speed, respectively. In this sense, the MPC3 (together with the RD control) provides the best behavior, since it does not apply slack to the nominal limits on any occasion, then it is followed by MPC1. This can be verified in Figure 6 and Figure 7, which show a comparison between the positions and oscillation speeds obtained by applying the designed controllers to the mathematical model (15). As can be seen, all controllers keep the WEC system within its physical operating limits. Finally, the last two columns of Table 5 show the maximum and minimum power peaks obtained when applying each controller. In this aspect, ignoring the resistive damping control, MPCs with embedded integrators are once again the best performers. Note that these power peaks will cause an oversizing of: electrical machines, power electronics, accumulators, etc.
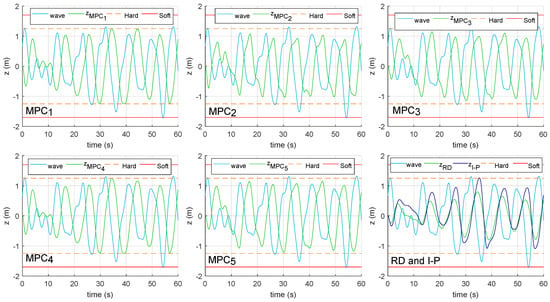
Figure 6.
Simulation of the positions obtained in the WEC system when applying the seven controllers to the mathematical model (15).
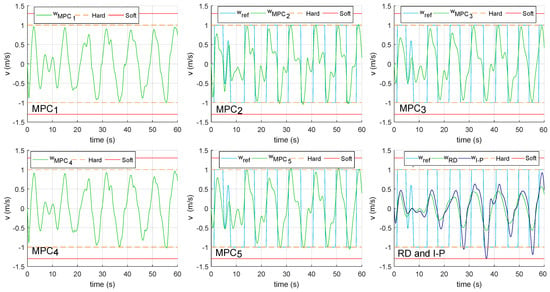
Figure 7.
Simulation of the oscillation speeds obtained in the WEC system when applying the seven controllers to the mathematical model (15).
With respect to the two optimization criteria compared in this paper, it can be concluded that the MPCs that employ an optimization criterion based on the minimization of the error between w and should only be used if they are designed from a model with an embedded integrator. Thus, this approach achieves better performance (in terms of diminution of instantaneous power peaks and reduction of mechanical fatigue due to exceeding nominal limits) than the standard optimization criteria based on maximizing the extracted power directly. On the other hand, with respect to the use of a complete model or a simplified model, it can be concluded that (in terms of instantaneous power generated and reduction of mechanical fatigue) the use of a complete model does not improve the performance of MPCs for this WEC significantly. This is because, the increase in the average power generated is minimal, and only in the case of the MPC1 and MPC4, the use of a complete model reduces the overshoot of the PTO system a bit. Finally, the variation of the extracted mechanical power as a function of the prediction time is studied. In particular, Figure 8 shows a comparison between MPC3 and MPC1. As can be seen, in both cases, after a prediction time of 3 s, the power generation does not improve significantly, while the computation effort increases. In addition, it should be pointed that MPC3 does not have a monotonously increasing behavior that relates to the power generated, as would be expected. Nevertheless, in this aspect, the MPC3 is better than the MPC1, because it can generate more power with less information of the future excitation force (up to s).
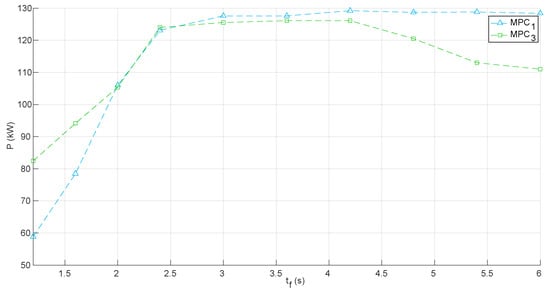
Figure 8.
Variation of the extracted mechanical power as a function of the prediction time for and (control parameters listed in Table 4).
To conclude the performance study, by comparing the previous figures and the values recorded in Table 5, it can be seen how the MPCs almost double the average power generated by the WEC system with respect to that obtained by tuning an adequate resistive damping for the PTO system (RD control). In addition, like the RD control, the MPC3 keeps the system within its nominal operating limits. On the other hand, it is also verified that the MPCs are superior in performances than the conventional I-P controller, in terms of: average mechanical powers generated, diminution of instantaneous power peaks and reduction of mechanical fatigue (due to exceeding nominal limits).
4.2. Robustness Comparison
Another contribution of this work, searching for the greatest realism in the comparative of the designed controllers, is that uncertainty is added to the complete system model (15) to the most significant identified parameters (52): added mass and dynamics of the radiation force, which have been obtained through the openWEC software, and the hydrostatic restoring coefficient (a nonlinear parameter that has been linearized during the modeling of the WEC system).
where Δ represents the added uncertainty in each parameter.
Note that when modifying the physical parameters of the WEC system, the frequency response of the filter (9) is affected. Therefore, looking for a truthful comparison, it would be necessary to identify a new filter (6) for each added uncertainty. Given the high number of simulations required, applying different levels of uncertainty to each of the parameters, this is not feasible. For this reason, in this work, the Morison model (7) is used to define , allowing one to modify the excitation force caused by the wave as a function of the added uncertainty more easily. Thus, when modifying the physical parameters of the system, the external force that the wave causes on the system also varies. Therefore, Equation (7) is redefined for this analysis as:
It should be noted that Equation (53) uses a first and a second derivative of wave height. As a consequence, if the Morison model is used for the excitation force in a realistic sea state, it will amplify the high-frequency harmonics that are part of the wave. This is the opposite of the bandwidth of the WEC system provided by the openWEC software (see Figure 2b). For this reason, in this part of the paper, the simulations are performed in an irregular sea state formed by the fifteen sinusoidal components listed in Table 6.

Table 6.
Sinusoidal components used for sea-state (values expressed in international units).
In order to create an unfavorable test scenario for the MPCs, two factors have been adjusted. In the first place, the sea state recorded in Table 6 is not favorable to the controllers, because the wave force becomes more than twice the stationary force that the PTO system can apply (recorded in Table 3). Moreover, the prediction time has been limited to a maximum of s. After this, a fine-tuning has been made to all the MPCs looking for a balance between the generated power and the overshoot of the nominal limits of the WEC system. The result of this fine-tuning is listed in Table 7.

Table 7.
Control parameters set for the sea state recorded in Table 7.
Note that for the same wave height, the excitation force can increase or decrease according to the uncertainty added in each parameter. Therefore, there will be situations where, for the sea state defined in Table 6, the controller cannot keep the system within its physical limits. This is because, the actuation force of the PTO system will be much lower than the excitation force. In this paper, this non-feasibility situation will be considered as the robustness limit that the controller can support. This limit is defined for the uncertainty added in each of the parameters (52). This non-feasibility situation with soft constraints does not mean that the closed-loop system becomes unstable, but that the controller cannot keep the WEC system within the physical limits defined in Table 3. Furthermore, in order to obtain a more complete analysis of how this uncertainty affects the closed-loop system, the average powers generated for each value of added uncertainty to each parameter are recorded. A large number of simulations has been carried out for this purpose; all of them have a duration of 120 s and use fourth order Runge–Kutta (RK4) integration method with an integration step of 1 ms.
Once the robustness study has been defined, Figure 9 shows the results obtained as a function of the added uncertainties; feasible limits obtained for the five MPCs and the variation of their mean power generated. With respect to the added uncertainty in , the MPC2 is the least robust. Meanwhile, the MPC1 offers the best features in a power-robustness ratio. However, it should be noted that when considering more reasonable added uncertainty values (interval ), the MPC5 extracts significantly more power than the others. It should also be noted that the controllers that directly maximize power in their cost function (MPC1 and MPC4) have the most predictable behavior with respect to the added uncertainty in . On the other hand, the MPC5 offers the best features with respect to the uncertainty added to the dynamics of the radiation force (up to ). In contrast, the MPC2 gives very bad results in this respect. The MPC1 also gets good results, because it achieves a practically constant power production despite variations of .
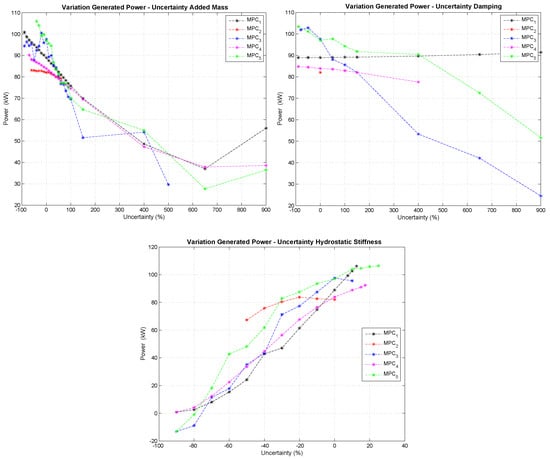
Figure 9.
Variations of the average mechanical power generated as a function of the added uncertainty to: added mass, damping coefficient and hydrostatic restoring coefficient.
Finally, Figure 9 shows how the power generated by the different controllers varies according to the uncertainty added to the hydrostatic restoring coefficient of the system. In this aspect, it can be appreciated how the robustness of all the controllers is more limited. If the value of the coefficient increases, the excitation force that the wave exerts on the system (53) increases proportionally. Therefore, the margin of action of the PTO system decreases noticeably. Even so, the MPC5 supports an added uncertainty of , again being the one that provides the best robustness results even with the smallest prediction time . Note that, for such added uncertainty, the excitation force becomes more than three-times the force that the PTO system can apply to the buoy; see Figure 10. After the MPC5, the MPC4 and MPC1 get the best results, in this order.
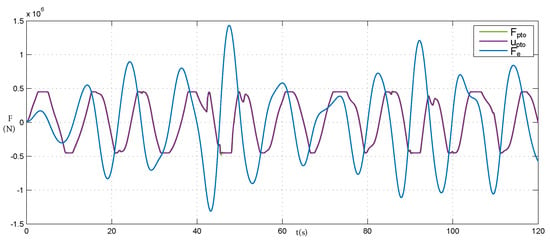
Figure 10.
Wave force, force setpoint demanded and real force produced by the PTO, by applying the MPC5 to the model (15), which has an added uncertainty to the hydrostatic restoring coefficient of .
5. Conclusions
The interest in implementing MPCs in WEC systems is motivated by the need to increase the productive/economic viability of these systems. For this reason, in this work, five different predictive controllers have been designed. All these controllers allow minimizing mechanical fatigue by limiting the operating range of the WEC system by means of hard and soft constraints. The main contribution of this work is the study of performance and robustness carried out for the five MPCs designed. This study demonstrates how the addition of an embedded integrator to the design model improves the performance of the WEC device referring to: average power generated, diminution of instantaneous power peaks, reduction of mechanical fatigue and robustness of the closed-loop system, in comparison with the other MPCs. In addition, the MPCs have been compared with two conventional controllers for WEC systems (resistive damping and I-P control) in a realistic sea state defined by the JONSWAP spectrum. Predictive controllers have proven that, compared to these conventional controllers, they minimize mechanical fatigue due to overshoot of nominal limits and increase the mechanical power generated by this type of WEC system.
Author Contributions
R.G. was responsible for designing the predictive controllers, studying them and writing most of the paper. A.C. and M.J.L. performed the modeling of the WEC system, proposed the identification methodology for PAW systems and the comparative robustness, reviewed all the work done and wrote part of the document. Furthermore, M.J.L. and A.C. proposed the control problems to solve using the model predictive control strategy and participated in the design and analysis of the controllers.
Funding
This project is funded by the Spanish Ministry of Economy, Industry and Competitiveness within the framework of the State Plan for Scientific and Technical Research and Innovation 2013-2016/State Programme for R+D+I aimed at the challenges of society.
Acknowledgments
Thanks to all ORPHEO (Optimización de la Rentabilidad de Plataformas Híbridas de energía Eólica y de las Olas) project partners for giving us the opportunity and funds to research in this promising field.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy; Sprinder Open: Boca Raton, FL, USA, 2016; ISBN 978-3-319-39888-4. [Google Scholar]
- The Ocean Energy Systems Technology Collaboration Programme. Available online: www.ocean-energy-systems.org/index.php (accessed on 4 May 2017).
- Pelagic Power. Available online: www.pelagicpower.no/about.html (accessed on 6 May 2017).
- Falnes, J. Ocean Waves and Oscillating Systems; Cambridge University Press: New York, NY, USA, 2002; ISBN 0-521-78211-2. [Google Scholar]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef]
- Valério, D.; Beirao, P.; Mendes, M.J.G.C.; da Costa, J.S. Comparison of control strategies performance for a Wave Energy Converter. In Proceedings of the 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 773–778. [Google Scholar]
- Li, G. Predictive control of a wave energy converter with wave prediction using differential flatness. In Proceedings of the 54th IEEE Conference on Decision and Control, Osaka, Japan, 15–18 December 2015; pp. 3230–3235. [Google Scholar]
- Andersen, P.; Pedersen, T.S.; Nielsen, K.M.; Vidal, E. Model Predictive Control of a Wave Energy Converter. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA 2015), Sydney, Australia, 21–23 September 2015; pp. 1540–1545. [Google Scholar]
- Brekken, T.K. On Model Predictive Control for a point absorber Wave Energy Converter. In Proceedings of the IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011; pp. 1–8. [Google Scholar]
- Richter, M.; Magana, M.E.; Sawodny, O.; Brekken, T.K.A. Nonlinear Model Predictive Control of a Point Absorber Wave Energy Converter. IEEE Trans. Sustain. Energy 2013, 4, 118–126. [Google Scholar] [CrossRef]
- Li, G.; Belmont, M.R. Model predictive control of sea wave energy converters—Part I: A convex approach for the case of a single device. Renew. Energy 2014, 69, 453–463. [Google Scholar] [CrossRef]
- Cavaglieri, D.; Bewley, T.R.; Previsic, M. Model Predictive Control leveraging Ensemble Kalman forecasting for optimal power take-off in wave energy conversion systems. In Proceedings of the American Control Conference, Chicago, IL, USA, 1–3 July 2015; Volume 2015, pp. 5224–5230. [Google Scholar]
- Oetinger, D.; Magaña, M.E.; Member, S.; Sawodny, O. Decentralized Model Predictive Control for Wave Energy Converter Arrays. IEEE Trans. Sustain. Energy 2014, 5, 1099–1107. [Google Scholar] [CrossRef]
- Li, G.; Belmont, M.R. Model predictive control of a sea wave energy converter: A convex approach. In Proceedings of the International Federation of Automatic Control (IFAC 2014), Cape Town, South Africa, 24–29 August 2014; Volume 19, pp. 11987–11992. [Google Scholar]
- Soltani, M.N.; Sichani, M.T.; Mirzaei, M. Model Predictive Control of Buoy Type Wave Energy Converter. In Proceedings of the International Federation of Automatic Control (IFAC 2014), Cape Town, South Africa, 24–29 August 2014; Volume 47, pp. 11159–11164. [Google Scholar]
- Starrett, M.; So, R.; Brekken, T.K.A.; McCall, A. Increasing power capture from multibody wave energy conversion systems using model predictive control. In Proceedings of the 2015 IEEE Conference on Technologies for Sustainability (SusTech), Ogden, UT, USA, 30 July–1 August 2015; pp. 20–26. [Google Scholar]
- Lagoun, M.S.; Benalia, A.; Benbouzid, M.E.H. A predictive power control of Doubly fed induction generator for wave energy converter in irregular waves. In Proceedings of the 1st International Conference on Green Energy, Sfax, Tunisia, 25–27 March 2014; pp. 26–31. [Google Scholar]
- Camacho, E.F.; Bordons, C. Model Predictive Control; Sprinder: Sevilla, Spain, 1998; ISBN 978-1-85233-694-3. [Google Scholar]
- Wang, L. Model Predictive Control System Desing and Implementation Using MATLAB; Sprinder: Melbourne, Australia, 2009; ISBN 978-1-84882-330-3. [Google Scholar]
- Openore. Available online: https://openore.org/2016/04/28/openwec/ (accessed on 14 May 2017).
- Ricci, P. Time-Domain Models. In Numerical Modelling of Wave Energy Converters; Elsevier Inc.: New York, NY, USA, 2016; pp. 31–66. ISBN 978-0-12-803210-7. [Google Scholar]
- Bozzi, S.; Miquel, A.M.; Antonini, A.; Passoni, G.; Archetti, R. Modeling of a point absorber for energy conversion in Italian seas. Energies 2013, 6, 3033–3051. [Google Scholar] [CrossRef]
- Hong, Y.; Eriksson, M.; Boström, C.; Waters, R. Impact of generator stroke length on energy production for a direct drivewave energy converter. Energies 2016, 9, 730. [Google Scholar] [CrossRef]
- Hansen, R.H.; Kramer, M.M. Modelling and Control of the Wavestar Prototype. In Proceedings of the 9th European Wave and Tidal Energy Conference, Southampton, UK, 5–9 September 2011; pp. 1–10. [Google Scholar]
- Kovaltchouk, T.; Multon, B.; BenAhmed, H.; Glumineau, A.; Aubry, J. Influence of control strategy on the global efficiency of a Direct Wave Energy Converter with electric Power Take-Off. In Proceedings of the Eighth International Conference and Exhibition on Ecological Vehicles and Renewable Energies, Monte Carlo, Monaco, 27–30 March 2013; pp. 1–10. [Google Scholar]
- Fusco, F.; Ringwood, J.V. A study of the prediction requirements in real-time control of wave energy converters. IEEE Trans. Sustain. Energy 2012, 3, 176–184. [Google Scholar] [CrossRef]
- Tedeschi, E.; Carraro, M.; Molinas, M.; Mattavelli, P. Effect of control strategies and power take-off efficiency on the power capture from sea waves. IEEE Trans. Energy Convers. 2011, 26, 1088–1098. [Google Scholar] [CrossRef]
- Cummins, W. The Impulse Response Function and Ship Motions. Schiffstechnick 1962, 9, 101–109. [Google Scholar]
- Morison, J.R.; O’Brien, M.P.; Johnson, J.W.; Schaaf, S.A. The forces exerted by surface waves on piles. Soc. Pet. Eng. 1950, 189, 149–154. [Google Scholar] [CrossRef]
- Openore. Available online: https://openore.org/2014/01/21/nemoh-open-source-bem/ (accessed on 13 October 2018).
- Armesto, J.A.; Guanche, R.; Jesus, F.; Iturrioz, A.; Losada, I.J. Comparative analysis of the methods to compute the radiation term in Cummins’ equation. J. Ocean Eng. Mar. Energy 2015, 1, 377–393. [Google Scholar] [CrossRef]
- Duarte, T.; Sarmento, A.; Alves, M.; Jonkman, J. State-Space Realization of the Wave-Radiation Force within FAST. In Proceedings of the ASME 2013 32nd International Conference on Ocean, Offshore and Arctic Engineering, Nantes, France, 9–14 June 2013; pp. 1–12. [Google Scholar]
- Mathworks. Available online: https://es.mathworks.com/help/signal/ref/prony.html (accessed on 2 February 2017).
- Ogata, K. Ingeniería de Control Moderna; Pearson Educación S.A.: Madrid, Spain, 2010; ISBN 9788483226605. [Google Scholar]
- Mathworks. Available online: https://es.mathworks.com/help/optim/ug/quadprog.html (accessed on 17 May 2017).
- Fusco, F.; Ringwood, J.V. Short-Term Wave Forecasting for Real-Time Control of Wave Energy Converters. IEEE Trans. Sustain. Energy 2010, 1, 99–106. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).