Stabilization of Zwitterionic Versus Canonical Glycine by DMSO Molecules
Abstract
1. Introduction
2. Results
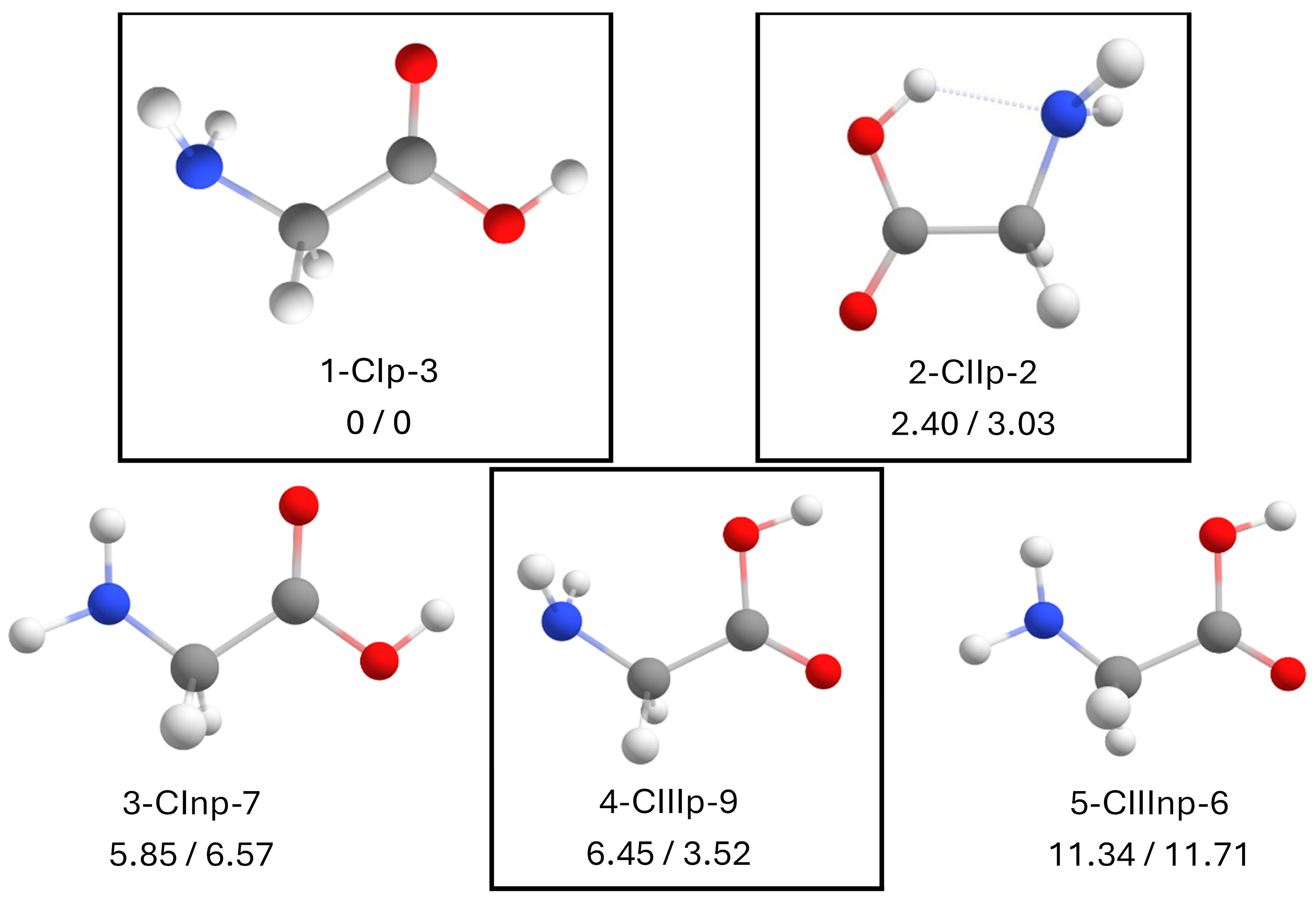
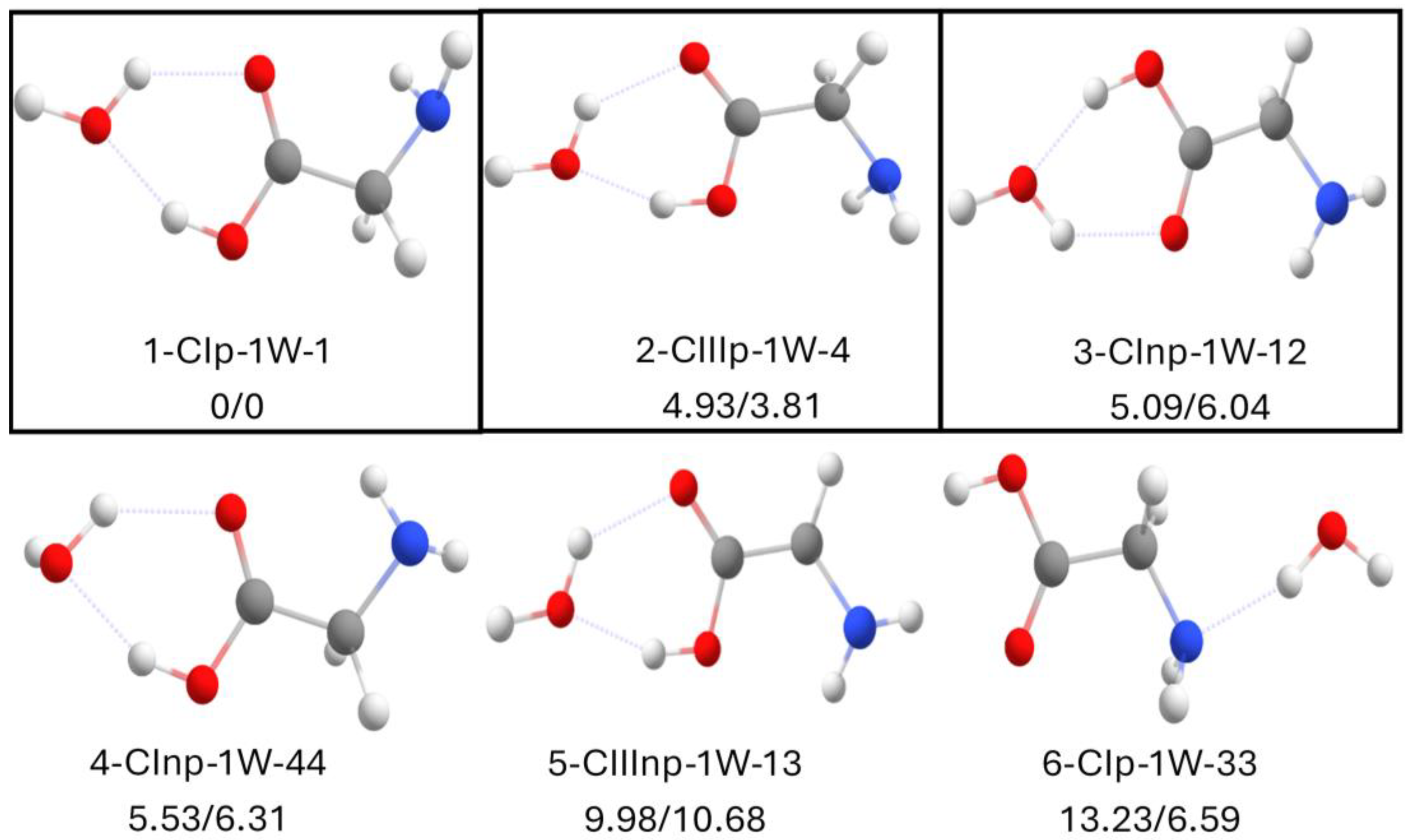
2.1. Conformational Search
- N is the energetic position of the conformer relative to the global minimum starting from 1.
- In the case of a canonical structure, C will be used, and Z will be used when it is zwitterionic instead.
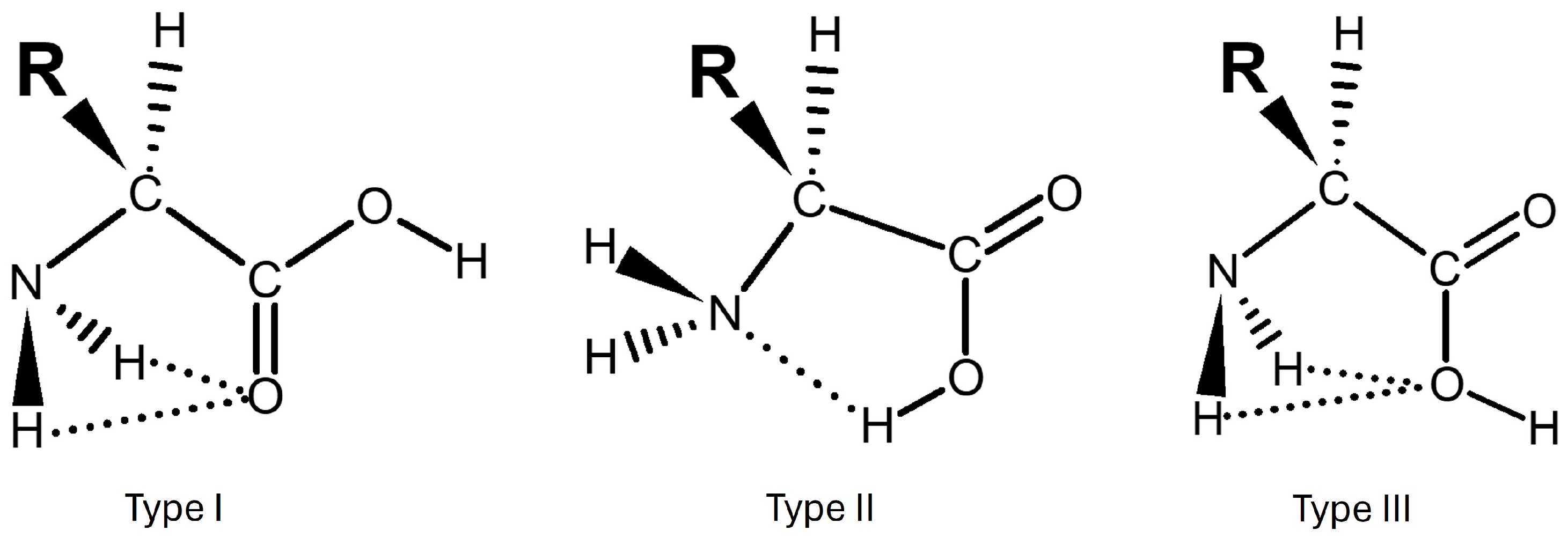
- Tp is the type of intramolecular interaction of glycine. There are three possible types of interactions, ranging from I to III and planar (p) or non-planar (np). A detailed description is given in Section 2.2.
- n is the number of molecules besides glycine that form the cluster.
- M is the molecule that will form the cluster, either water (W) or DMSO.
- X is the conformer number ordered by stability as determined by molecular mechanics.
2.2. Isolated Canonical Glycine
2.3. Canonical Glycine with 1 Water Molecule
2.4. Canonical Glycine with 2 Water Molecules
2.5. Zwitterionic Glycine with 1 Water Molecule
2.6. Zwitterionic Glycine with 2 Water Molecules
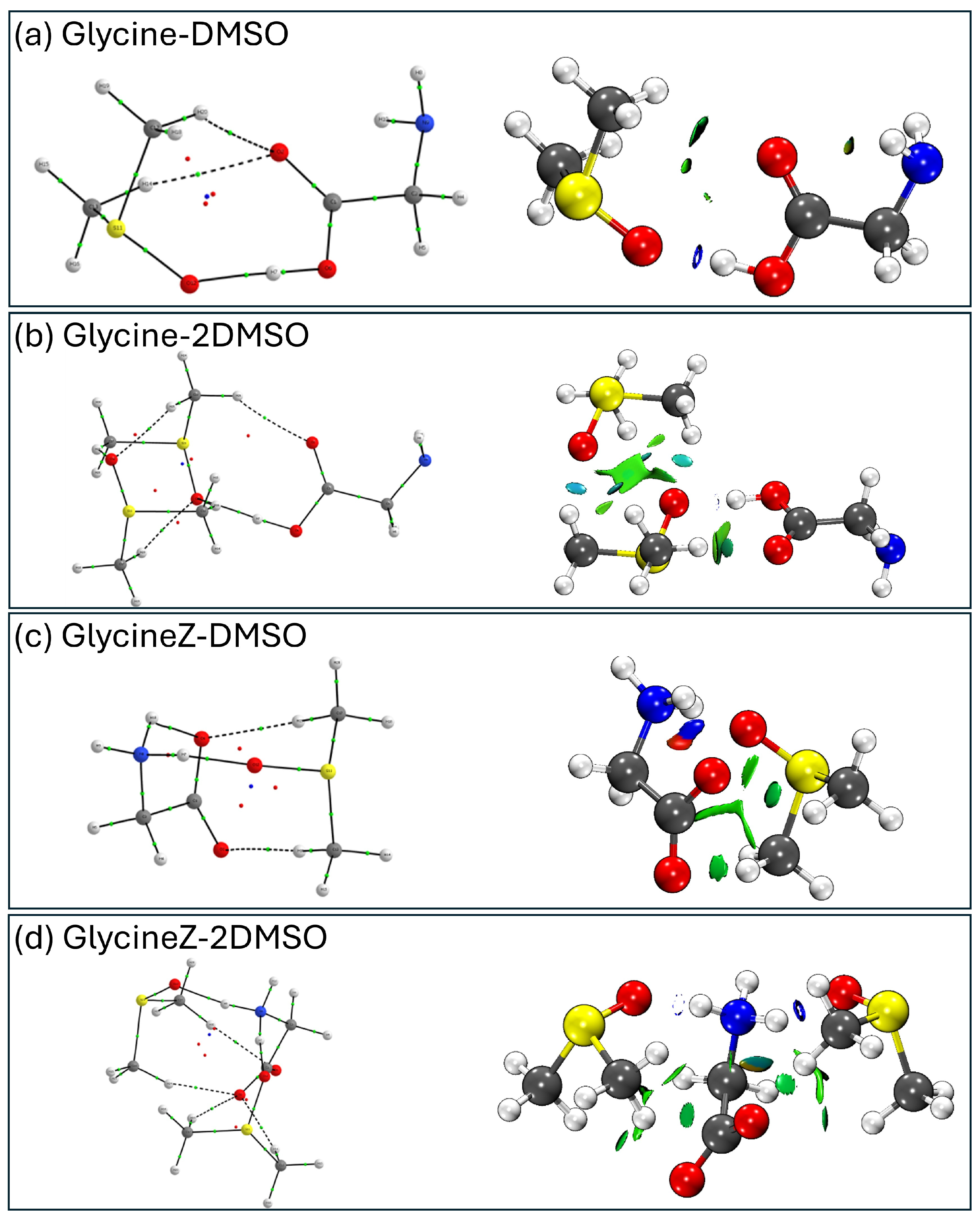
2.7. Canonical Glycine with 1 DMSO Molecule
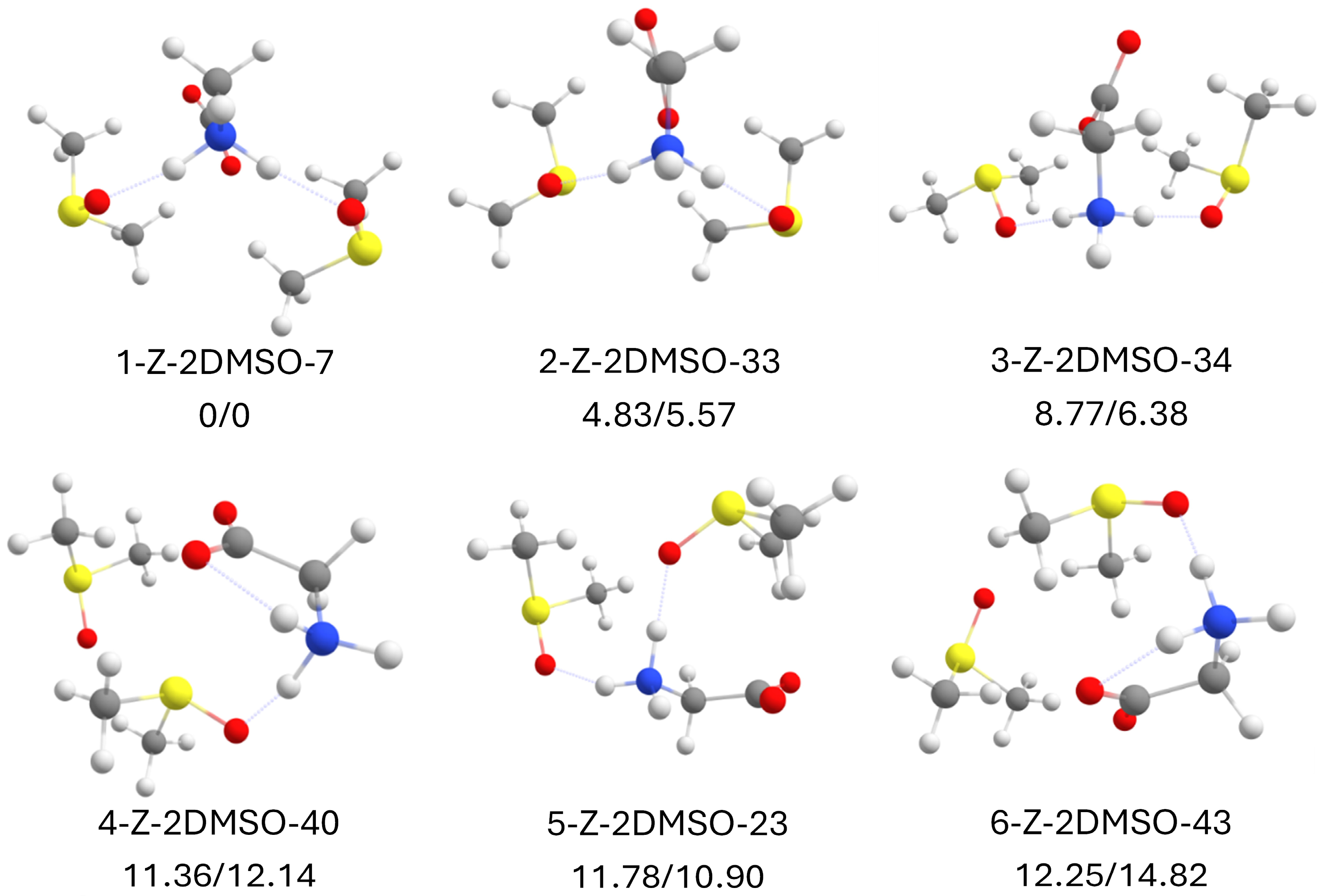
2.8. Canonical Glycine with 2 DMSO Molecules
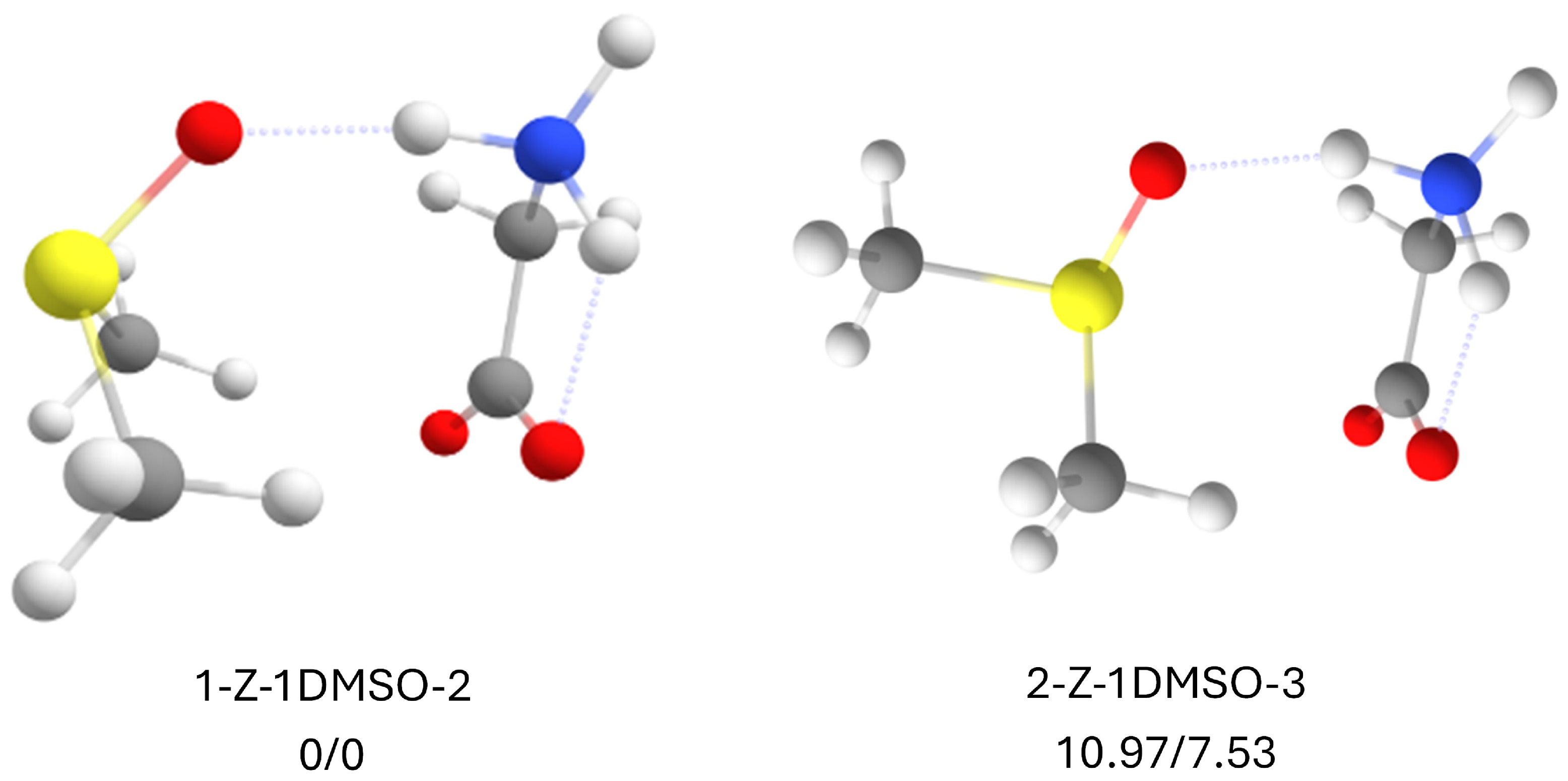
2.9. Zwitterionic Glycine with 1 DMSO Molecule
2.10. Zwitterionic Glycine with 2 DMSO Molecules
2.11. Explicit Solvent Model
2.12. Implicit Solvent Model
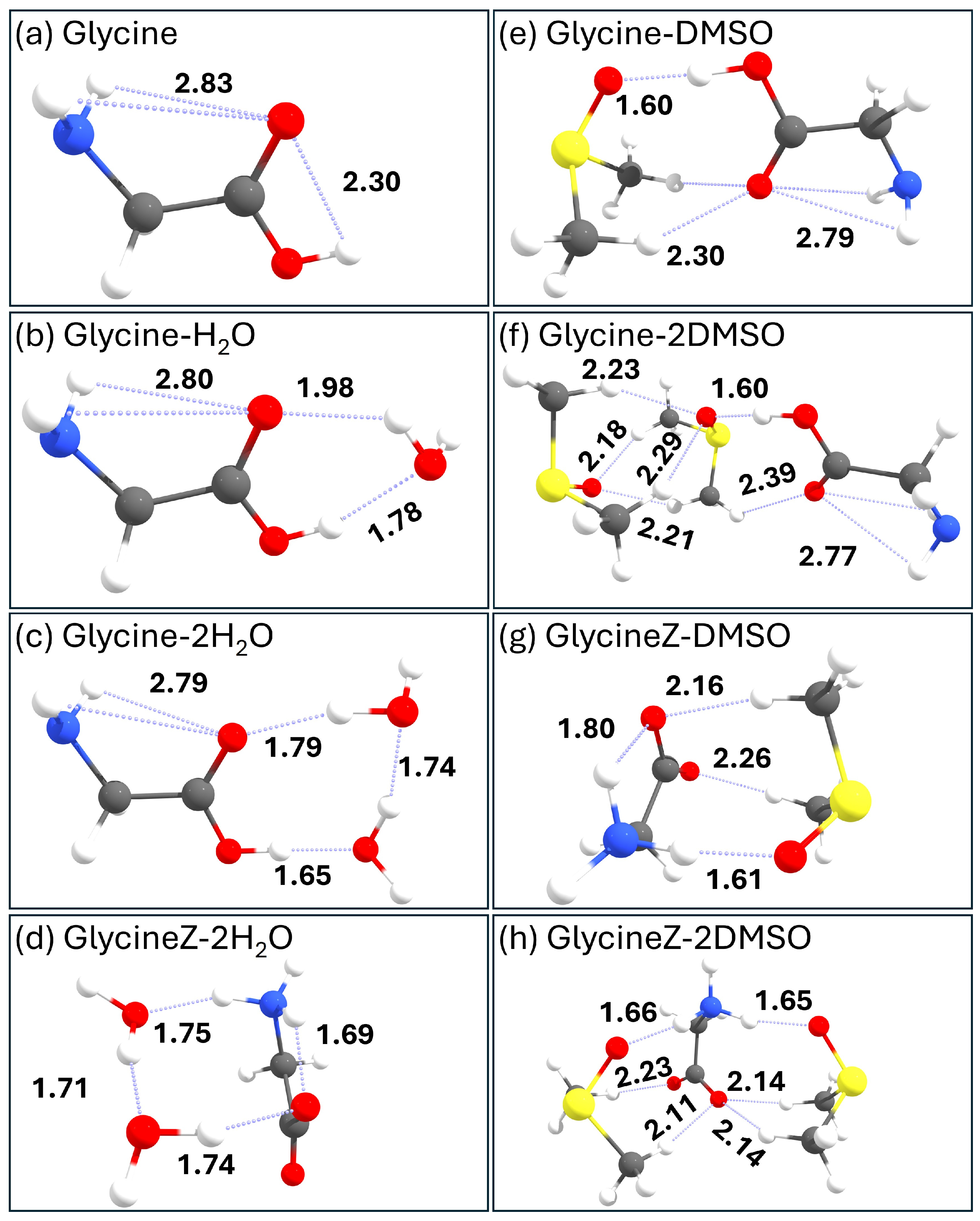
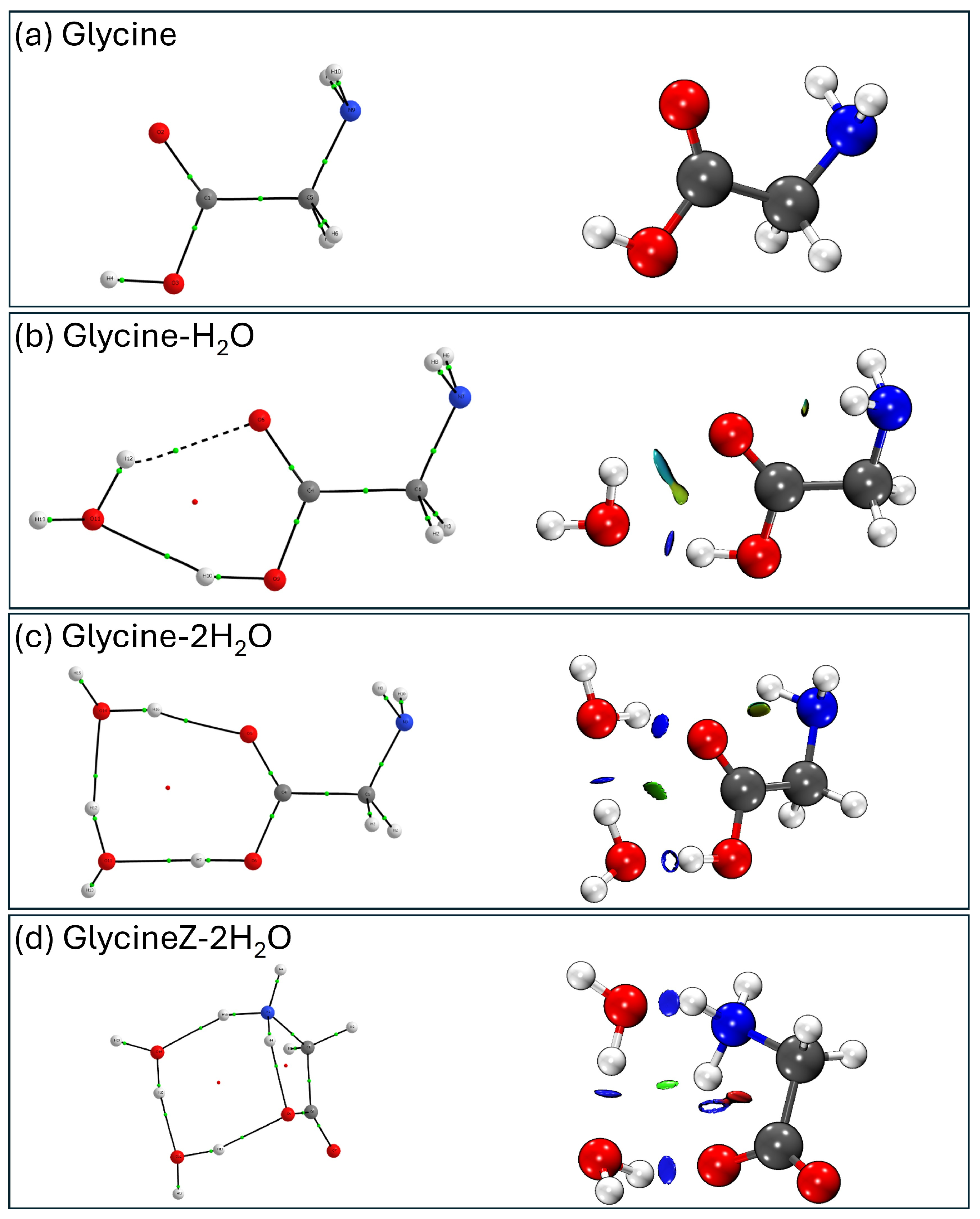
2.13. Analysis of Intramolecular Interactions: NCI and QTAIM
3. Discussion
4. Materials and Methods
4.1. Computational Methods
4.2. Analysis of Non-Covalent Interactions
- -
- Quantum Theory of Atoms in Molecules (QTAIM): This analysis was performed using the AIMAll program [47] to identify bond critical points (BCPs), ring critical points (RCPs) and cage critical points (CCPs) and determine the nature of the interactions based on the electron density (ρ), its Laplacian (∇2ρ), the total energy density (H), and the ratio between potential and kinetic energy densities (|V|/G). When ρ takes a high value and ∇2ρ < 0, the electronic charge is concentrated in the internuclear region, and it is said to be a shared interaction (characteristic of covalent bonds). In addition, in this type of interaction, the total energy density H(r) is negative and the ratio |V(r)|/G(r) > 2. When ρ is small and ∇2ρ > 0, we talk about closed-shell interaction, characteristic of ionic bonds, hydrogen bonds, or van der Waals molecules. In this type of interaction, the total energy density H(r) > 0 and the ratio |V(r)|/G(r) < 1.
- -
- Non-covalent interaction (NCI) analysis: Using the NCIPlot program(3.0) [48,49] and VMD for visualization, we mapped the regions of non-covalent interactions in the molecular complexes, distinguishing between attractive interactions (hydrogen bonds), weak van der Waals forces, and repulsive interactions. The NCI analysis uses electron density to locate different types of intermolecular forces in the molecule. We can thus see the interactions that will stabilize or destabilize our conformer. We can distinguish 3 types of interactions: strong attractive interactions, such as hydrogen bonds (in blue color); strong repulsive interactions, such as steric repulsions (in red color); and van der Waals interactions, which are those weaker attractive interactions with lower electron density (in green color).
5. Conclusions
- -
- The zwitterionic form of glycine cannot be stabilized with a single water molecule using conventional quantum chemical levels such as B3LYP-D3BJ/6-311++G(d,p). In contrast, one DMSO molecule successfully stabilizes the zwitterionic form of glycine, demonstrating DMSO’s unique solvation properties. This stabilization occurs through specific interactions where the S=O group of DMSO acts as a hydrogen bond acceptor from the NH3+ group, while the methyl groups interact with the carboxylate group.
- -
- QTAIM and NCI analyses reveal that some of these interactions have partial covalent character, particularly in the bonds formed between the NH3+ hydrogens and the O atom of DMSO, contributing to the enhanced stabilization of the zwitterionic form.
- -
- In explicit solvation models, the canonical form of glycine remains more stable than the zwitterionic form with both water and DMSO molecules. However, two DMSO molecules significantly reduce this energy gap to approximately 12 kJ/mol, suggesting that additional DMSO molecules might eventually invert this stability.
- -
- In implicit solvent models, the zwitterionic form becomes more stable than the canonical form in both water and DMSO at 0 K. However, temperature-dependent analysis reveals that in DMSO, the canonical form becomes more stable above 150 K, while in water, the zwitterionic form predominates up to about 375 K.
- -
- DMSO exhibits remarkable versatility in forming hydrogen bonds, not only through its S=O group acting as a hydrogen bond acceptor but also through its methyl groups forming C-H•••O interactions with carbonyl groups of glycine.
- -
- The self-aggregation patterns differ significantly between water and DMSO clusters: water molecules strongly interact with each other regardless of whether glycine is in its canonical or zwitterionic form, while DMSO shows different preferences depending on the glycine form.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| B3LYP | Becke Three-Parameter Hybrid Functional |
| BCP | Bond critical point |
| CCP | Cage critical point |
| HF | Hartree–Fock |
| NCI | Non-covalent interactions |
| PES | Potential energy surface |
| QTAIM | Quantum Theory of Atoms In Molecules |
| RCP | Ring critical point |
| RGB | Red green blue |
| MM | Molecular mechanics |
| DMSO | Dimethyl sulfoxide |
| ZPE | Zero-point energy |
| MMFFs | Merck Molecular Force Field Static |
| PCM | Polarizable continuum model |
| SMD | Solvation model based on electron density |
| Gly | Glycine |
References
- Rand, R.P.; Ho, M.W.; Littlechild, J.A.; Finney, J.L.; Cupane, A.; Engberts, J.B.F.N. Probing the role of water in protein conformation and function. Philos. Trans. R. Soc. B Biol. Sci. 2004, 359, 1277–1285. [Google Scholar] [CrossRef]
- Timasheff, S.N. Protein-Solvent Interactions and Protein Conformation. Acc. Chem. Res. 1970, 3, 62–68. [Google Scholar] [CrossRef]
- Levy, Y.; Onuchic, J.N. Water Mediation In Protein Folding And Molecular Recognition. Annu. Rev. Biophys. Biomol. Struct. 2006, 35, 389–415. [Google Scholar] [CrossRef]
- Canchi, D.R.; García, A.E. Cosolvent effects on protein stability. Annu. Rev. Phys. Chem. 2013, 64, 273–293. [Google Scholar] [CrossRef]
- Panuszko, A.; Pastwa, P.; Gajewski, J.; Bruździak, P. Characterizing Interactions Between Small Peptides and Dimethyl Sulfoxide Using Infrared Spectroscopy and Computational Methods. Molecules 2024, 29, 5869. [Google Scholar] [CrossRef]
- Levy, H.A.; Corey, R.B. The crystal structure of dl-alanine. J. Am. Chem. Soc. 1941, 63, 2095–2108. [Google Scholar] [CrossRef]
- Donohue, J. The Crystal Structure of dl-Alanine. II. Revision of Parameters by Three-Dimensional Fourier Analysis. J. Am. Chem. Soc. 1950, 72, 949–953. [Google Scholar] [CrossRef]
- Albrecht, G.; Corey, R.B. The Crystal Structure of Glycine. J. Am. Chem. Soc. 1939, 61, 1087–1103. [Google Scholar] [CrossRef]
- Marsh, R.E.; Donohue, J. Crystal Structure Studies of Amino Acids and Peptides. Adv. Protein Chem. 1967, 22, 235–256. [Google Scholar] [CrossRef] [PubMed]
- Kieffer, W.F. Dimethyl sulfoxide. Vol.1: Basic concepts of DMSO (Jacob, Stanley W.; Rosenbaum, Edward E.; Wood, Don C.). J. Chem. Educ. 1972, 49, A114. [Google Scholar] [CrossRef][Green Version]
- Huang, A.; Liu, C.; Ma, L.; Tong, Z.; Lin, R. Effects of clustering structure on volumetric properties of amino acids in (DMSO + water) mixtures. J. Chem. Thermodyn. 2012, 49, 95–103. [Google Scholar] [CrossRef]
- Arakawa, T.; Kita, Y.; Timasheff, S.N. Protein precipitation and denaturation by dimethyl sulfoxide. Biophys. Chem. 2007, 131, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Voets, I.K.; Cruz, W.A.; Moitzi, C.; Lindner, P.; Arêas, E.P.G.; Schurtenberger, P. DMSO-induced denaturation of hen egg white lysozyme. J. Phys. Chem. B 2010, 114, 11875–11883. [Google Scholar] [CrossRef] [PubMed]
- Tjernberg, A.; Markova, N.; Griffiths, W.J.; Hallén, D. DMSO-related effects in protein characterization. J. Biomol. Screen. 2006, 11, 131–137. [Google Scholar] [CrossRef]
- Chaudhari, A.; Lee, S.L. Computational study of glycine-(water)3 complex by density functional method. Chem. Phys. 2005, 310, 281–285. [Google Scholar] [CrossRef]
- Vener, M.V.; Medvedev, A.G.; Churakov, A.V.; Prikhodchenko, P.V.; Tripol’Skaya, T.A.; Lev, O. H-bond network in amino acid cocrystals with H2O or H2O2. the DFT study of serine—H2O and Serine—H2O2. J. Phys. Chem. A 2011, 115, 13657–13663. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Yang, G.; Zhou, L.; Chen, Y. Stabilization of zwitterionic versus canonical proline by water molecules. Springerplus 2016, 5, 19. [Google Scholar] [CrossRef]
- Kim, J.Y.; Ahn, D.S.; Park, S.W.; Lee, S. Gas phase hydration of amino acids and dipeptides: Effects on the relative stability of zwitterion vs. canonical conformers. RSC Adv. 2014, 4, 16352–16361. [Google Scholar] [CrossRef]
- Ulman, K.; Busch, S.; Hassanali, A.A. Quantum mechanical effects in zwitterionic amino acids: The case of proline, hydroxyproline, and alanine in water. J. Chem. Phys. 2018, 148, 222826. [Google Scholar] [CrossRef]
- Kokpol, S.U.; Doungdee, P.B.; Hannongbua, S.V.; Rode, B.M.; Limtrakul, J.P. Ab initio study of the hydration of the glycine zwitterion. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1988, 84, 1789–1792. [Google Scholar] [CrossRef]
- Ding, Y.; Krogh-Jespersen, K. The 1: 1 glycine zwitterion-water complex: An ab initio electronic structure study. J. Comput. Chem. 1996, 17, 338–349. [Google Scholar] [CrossRef]
- Langlet, J.; Caillet, J.; Evleth, E.; Kassab, E. Studies in Physical and Theoretical Chemistry; Rivail, J.L., Ed.; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Wanga, W.; Pu, X.; Zhenga, W.; Wong, N.B.; Tian, A. Some theoretical observations on the 1:1 glycine zwitterion-water complex. J. Mol. Struct. THEOCHEM 2003, 626, 127–132. [Google Scholar] [CrossRef]
- Luzar, A.; Soper, A.K.; Chandler, D. Combined neutron diffraction and computer simulation study of liquid dimethyl sulphoxide. J. Chem. Phys. 1993, 99, 6836–6847. [Google Scholar] [CrossRef]
- McLain, S.E.; Soper, A.K.; Luzar, A. Investigations on the structure of dimethyl sulfoxide and acetone in aqueous solution. J. Chem. Phys. 2007, 127, 174515. [Google Scholar] [CrossRef]
- Soper, A.K. Computer simulation as a tool for the interpretation of total scattering data from glasses and liquids. Mol. Simul. 2012, 38, 1171–1185. [Google Scholar] [CrossRef]
- Onthong, U.; Megyes, T.; Bakó, I.; Radnai, T.; Grósz, T.; Hermansson, K.; Probst, M. X-ray and neutron diffraction studies and molecular dynamics simulations of liquid DMSO. Phys. Chem. Chem. Phys. 2004, 6, 2136–2144. [Google Scholar] [CrossRef]
- Di Mino, C.; Clancy, A.J.; Sella, A.; Howard, C.A.; Headen, T.F.; Seel, A.G.; Skipper, N.T. Weak Interactions in Dimethyl Sulfoxide (DMSO)-Tertiary Amide Solutions: The Versatility of DMSO as a Solvent. J. Phys. Chem. B 2023, 127, 1357–1366. [Google Scholar] [CrossRef] [PubMed]
- Halgren, T.A. MMFF VI. MMFF94s option for energy minimization studies. J. Comput. Chem. 1999, 20, 720–729. [Google Scholar] [CrossRef]
- Schrödinger Release 2018-3, Maestro Schrödinger, LLC: New York, NY, USA, 2018.
- Hu, C.H.; Shen, M.; Schaefer, H.F. Glycine Conformational Analysis. J. Am. Chem. Soc. 1993, 115, 2923–2929. [Google Scholar] [CrossRef]
- Ke, H.W.; Rao, L.; Xu, X.; Yan, Y.J. Theoretical study of glycine conformers. J. Theor. Comput. Chem. 2008, 7, 889–909. [Google Scholar] [CrossRef]
- Barone, V.; Biczysko, M.; Bloino, J.; Puzzarini, C. Glycine conformers: A never-ending story? Phys. Chem. Chem. Phys. 2013, 15, 1358–1363. [Google Scholar] [CrossRef]
- Lovas, F.J.; Kawashima, Y.; Grabow, J.-U.; Suenram, R.D.; Fraser, G.T.; Hirota, E. Microwave spectra, hyperfine structure, and electric dipole moments for conformers I and II of glycine. Astrophys. J. 1995, 455, L201–L204. [Google Scholar] [CrossRef]
- Schafer, L.; Sellers, H.L.; Lovas, F.J.; Suenram, R.D. Theory versus Experiment: The Case of Glycine. J. Am. Chem. Soc. 1980, 102, 6566–6568. [Google Scholar] [CrossRef]
- Suenram, R.D.; Lovas, F.J. Millimeter Wave Spectrum of Glycine. A New Conformer. J. Am. Chem. Soc. 1980, 102, 7180–7184. [Google Scholar] [CrossRef]
- Stepanian, S.G.; Reva, I.D.; Radchenko, E.D.; Rosado, M.T.S.; Duarte, M.L.T.S.; Fausto, R.; Adamowicz, L. Matrix-isolation infrared and theoretical studies of the glycine conformers. J. Phys. Chem. A 1998, 102, 1041–1054. [Google Scholar] [CrossRef]
- Ruoff, R.S.; Klots, T.D.; Emilsson, T.; Gutowsky, H.S. Relaxation of conformers and isomers in seeded supersonic jets of inert gases. J. Chem. Phys. 1990, 93, 3142–3150. [Google Scholar] [CrossRef]
- Godfrey, P.D.; Brown, R.D.; Rodgers, F.M. The missing conformers of glycine and alanine: Relaxation in seeded supersonic jets. J. Mol. Struct. 1996, 376, 65–81. [Google Scholar] [CrossRef]
- Alonso, J.L.; Cocinero, E.J.; Lesarri, A.; Sanz, M.E.; López, J.C. The glycine-water complex. Angew. Chemie—Int. Ed. 2006, 45, 3471–3474. [Google Scholar] [CrossRef] [PubMed]
- Balabin, R.M. The first step in glycine solvation: The glycine-water complex. J. Phys. Chem. B 2010, 114, 15075–15078. [Google Scholar] [CrossRef] [PubMed]
- Brown, G.G.; Dian, B.C.; Douglass, K.O.; Geyer, S.M.; Shipman, S.T.; Pate, B.H. A broadband Fourier transform microwave spectrometer based on chirped pulse excitation. Rev. Sci. Instrum. 2008, 79, 053103. [Google Scholar] [CrossRef] [PubMed]
- Alonso, J.L.; López, J.C. Microwave Spectroscopy of Biomolecular Building Blocks. Top. Curr. Chem. 2014, 364, 335–401. [Google Scholar]
- Alonso, J.L.; Peña, I.; Sanz, M.E.; Vaquero, V.; Mata, S.; Cabezas, C.; López, J.C. Observation of dihydrated glycine. Chem. Commun. 2013, 49, 3443–3445. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll, Version 19.10.12; TK Gristmill Software: Overland Park, KS, USA, 2019. Available online: https://aim.tkgristmill.com/ (accessed on 4 June 2025).
- Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.P.; Beratan, D.N.; Yang, W. NCIPLOT: A program for plotting noncovalent interaction regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian, Gaussian 09 Rev. D01.; Gaussian, Inc.: Wallingford, CT, USA, 2012. Available online: http://www.gaussian.com (accessed on 28 June 2025).
- Halgren, T.A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Density functionals for noncovalent interaction energies of biological importance. J. Chem. Theory Comput. 2007, 3, 289–300. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A.; Binkley, J.S. Self-consistent molecular orbital methods 25. Supplementary functions for Gaussian basis sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Schwabe, T.; Grimme, S. Double-hybrid density functionals with long-range dispersion corrections: Higher accuracy and extended applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef]
- Mennucci, B.; Tomasi, J. Continuum solvation models: A new approach to the problem of solute’s charge distribution and cavity boundaries. J. Chem. Phys. 1997, 106, 5151–5158. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to Isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Cossi, M.; Barone, V.; Mennucci, B.; Tomasi, J. Ab initio study of ionic solutions by a polarizable continuum dielectric model. Chem. Phys. Lett. 1998, 286, 253–260. [Google Scholar] [CrossRef]
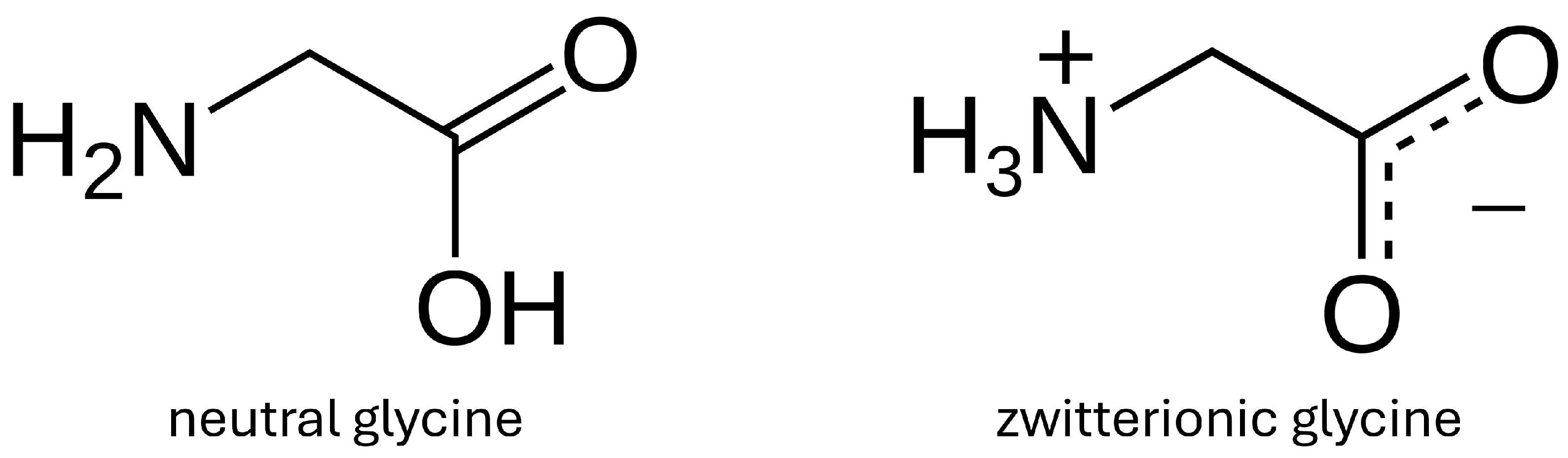
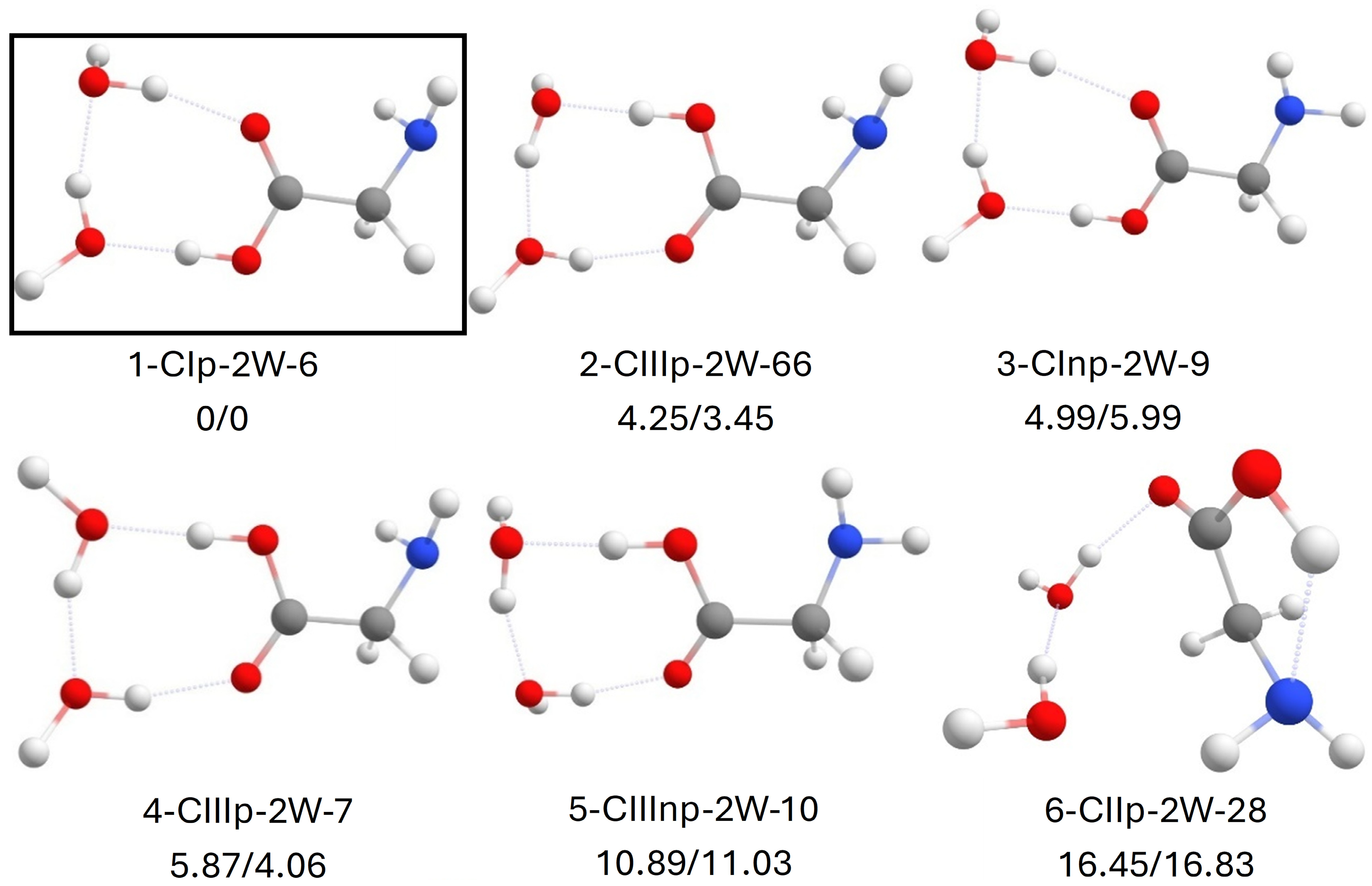
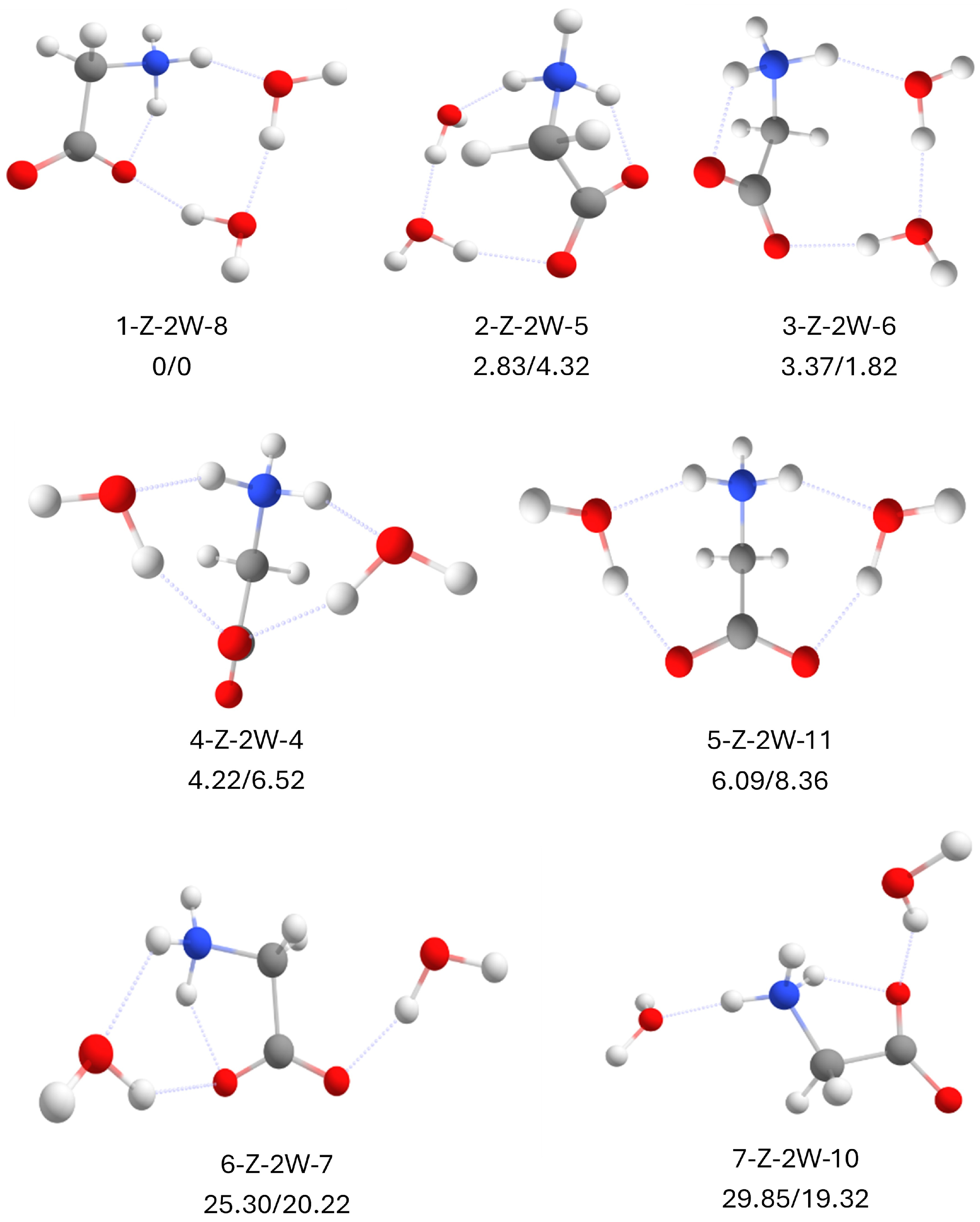
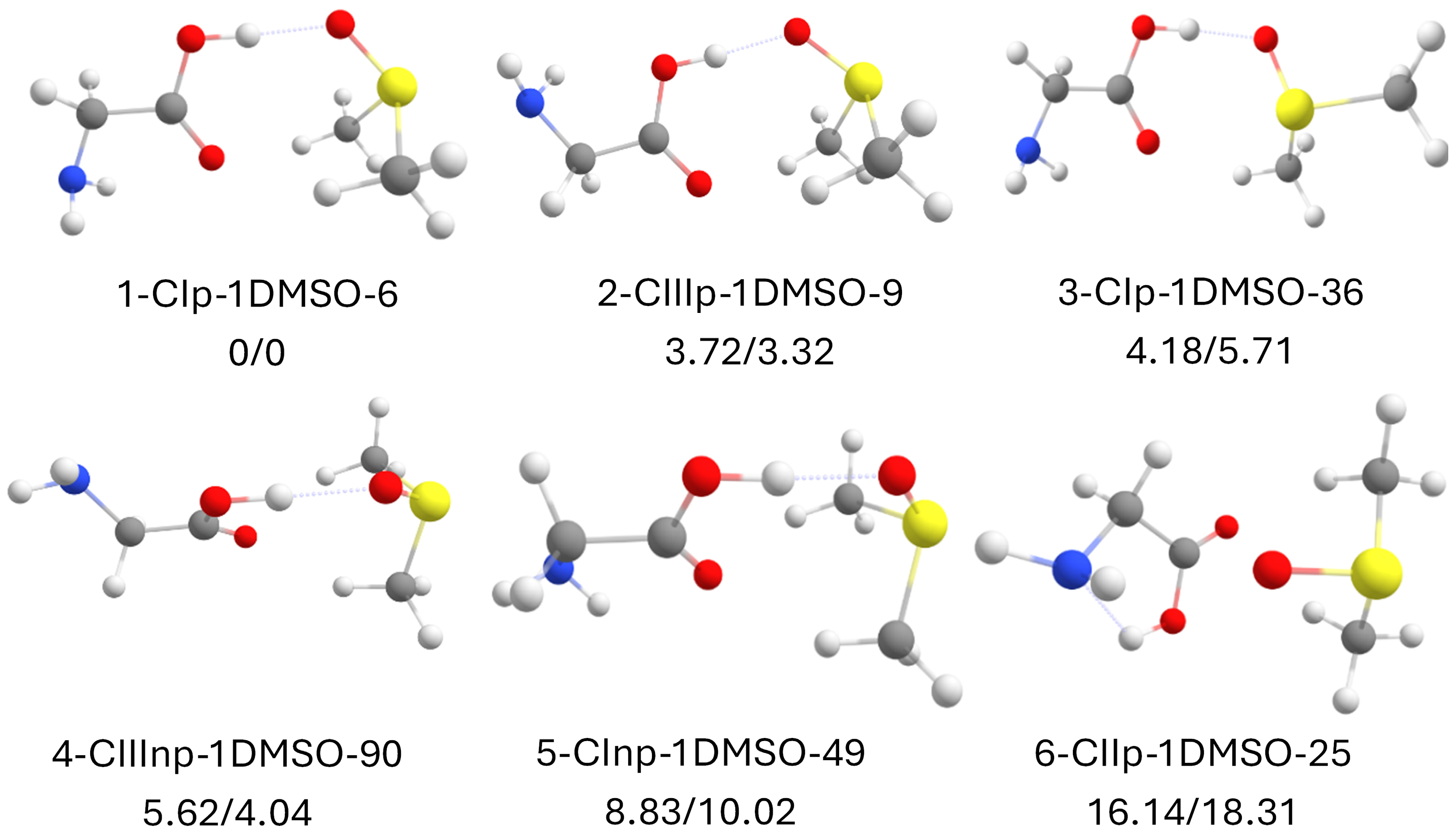
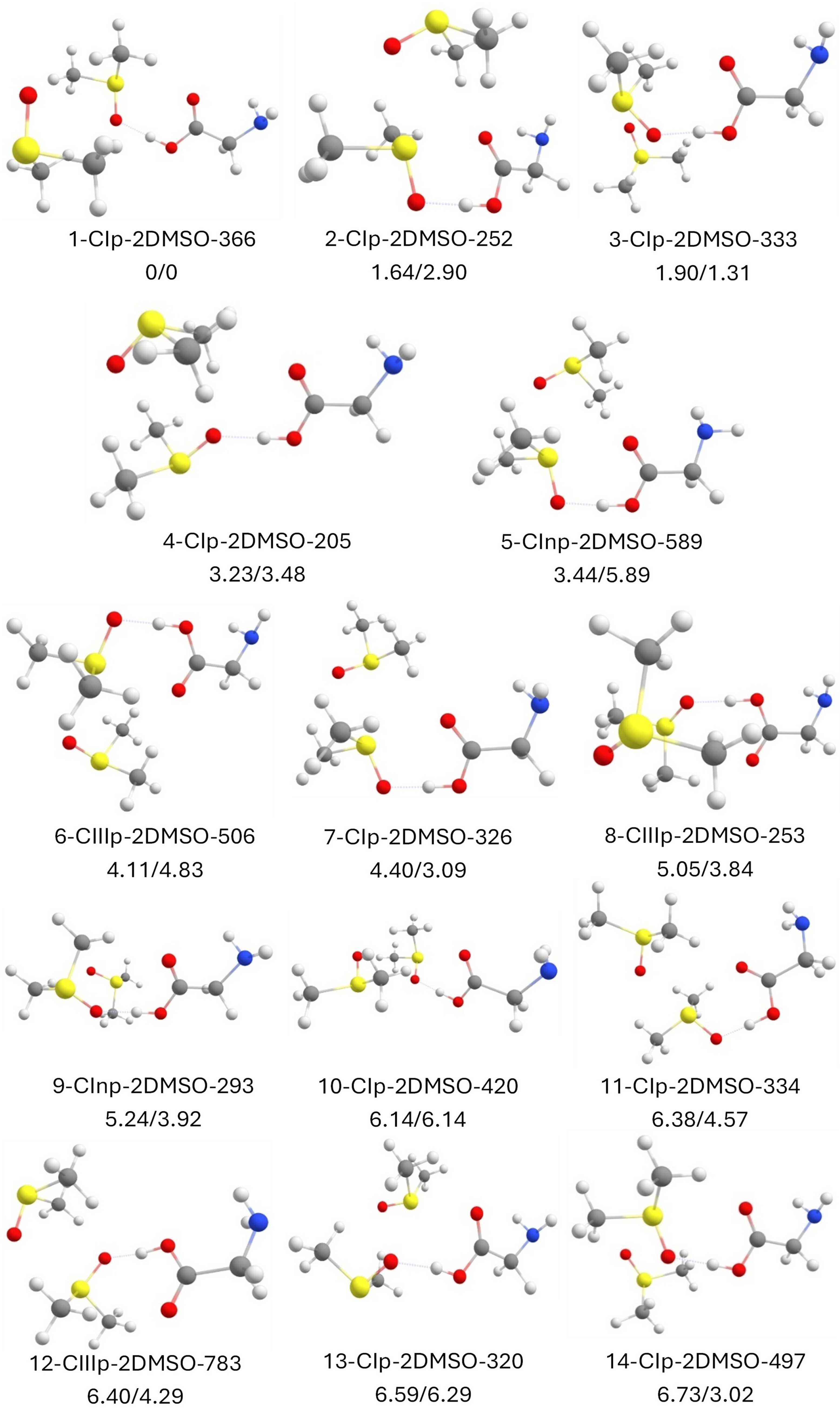

| System | Canonical | Zwitterionic |
|---|---|---|
| Gly | 9 | 3 |
| Gly—H2O | 47 | 4 |
| Gly—2 H2O | 71 | 13 |
| Gly—DMSO | 110 | 4 |
| Gly—2 DMSO | 616 | 45 |
| H2O | 2H2O | DMSO | 2DMSO | |||||
|---|---|---|---|---|---|---|---|---|
| Parameter | Can. | Zwitt. | Can. | Zwitt. | Can. | Zwitt. | Can. | Zwitt. |
| ΔE 1 | - | - | 0 | 45.15 | - | 40.89 | 0 | 7.09 |
| ΔEZPE 2 | - | - | 0 | 46.57 | - | 43.74 | 0 | 12.13 |
| ΔG 3 | - | - | 0 | 49.19 | - | 48.98 | 0 | 19.06 |
| H2O | DMSO | |||
|---|---|---|---|---|
| Parameter | Canonical | Zwitterionic | Canonical | Zwitterionic |
| ΔE 1 | 6.09/27.25 | 0/0 | 4.83/9.78 | 0/0 |
| ΔEZPE 2 | 1.47/22.30 | 0/0 | 0.25/5.43 | 0/0 |
| ΔG 3 | 0.39/22.99 | 0/0 | 0/4.64 | 0.90/0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín, V.; Colón, A.; Barrientos, C.; León, I. Stabilization of Zwitterionic Versus Canonical Glycine by DMSO Molecules. Pharmaceuticals 2025, 18, 1168. https://doi.org/10.3390/ph18081168
Martín V, Colón A, Barrientos C, León I. Stabilization of Zwitterionic Versus Canonical Glycine by DMSO Molecules. Pharmaceuticals. 2025; 18(8):1168. https://doi.org/10.3390/ph18081168
Chicago/Turabian StyleMartín, Verónica, Alejandro Colón, Carmen Barrientos, and Iker León. 2025. "Stabilization of Zwitterionic Versus Canonical Glycine by DMSO Molecules" Pharmaceuticals 18, no. 8: 1168. https://doi.org/10.3390/ph18081168
APA StyleMartín, V., Colón, A., Barrientos, C., & León, I. (2025). Stabilization of Zwitterionic Versus Canonical Glycine by DMSO Molecules. Pharmaceuticals, 18(8), 1168. https://doi.org/10.3390/ph18081168








