Role of Non-Covalent Interactions in Carbonic Anhydrase I—Topiramate Complex Based on QM/MM Approach
Abstract
1. Introduction
- (i)
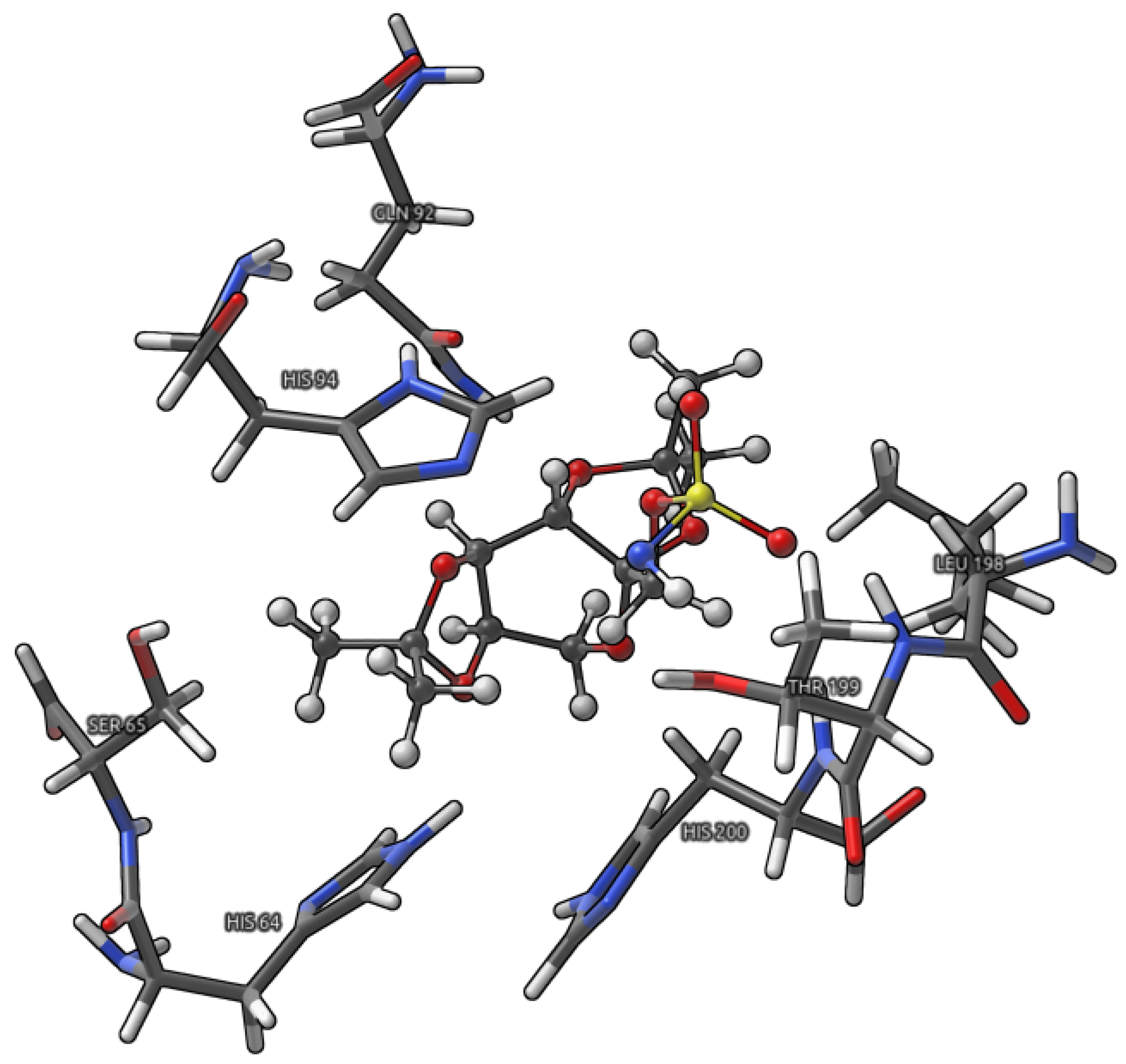
- Large model (Figure 2), where the interactions between Topiramate (TPM) and the binding site, excluding the ones involved in the coordination of the zinc ion, were studied;
- (ii)
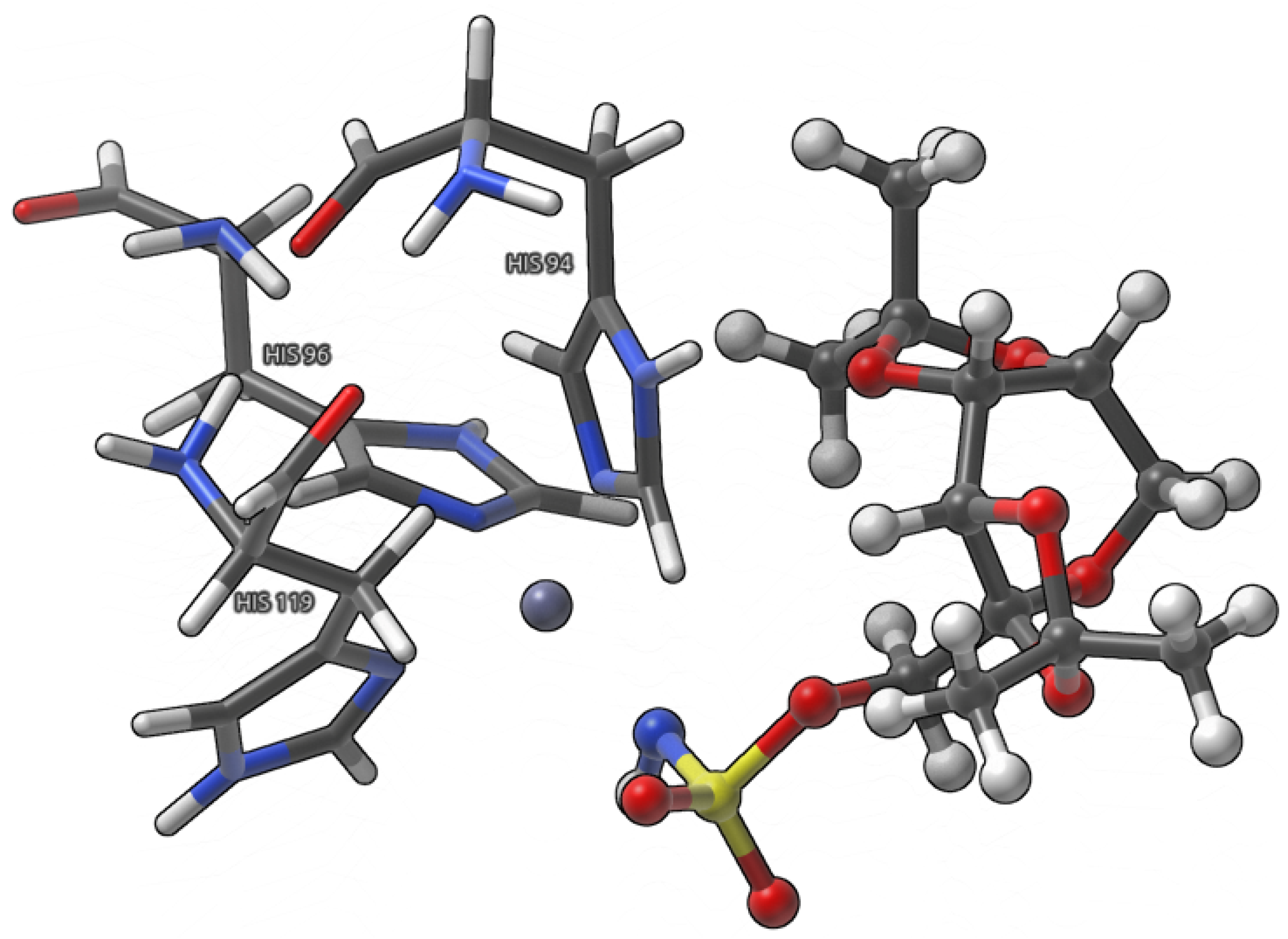
- Small model (Figure 3), where the interactions between Topiramate (TPM) and amino acids involved in zinc coordination, as well as the zinc coordination itself, were analyzed.

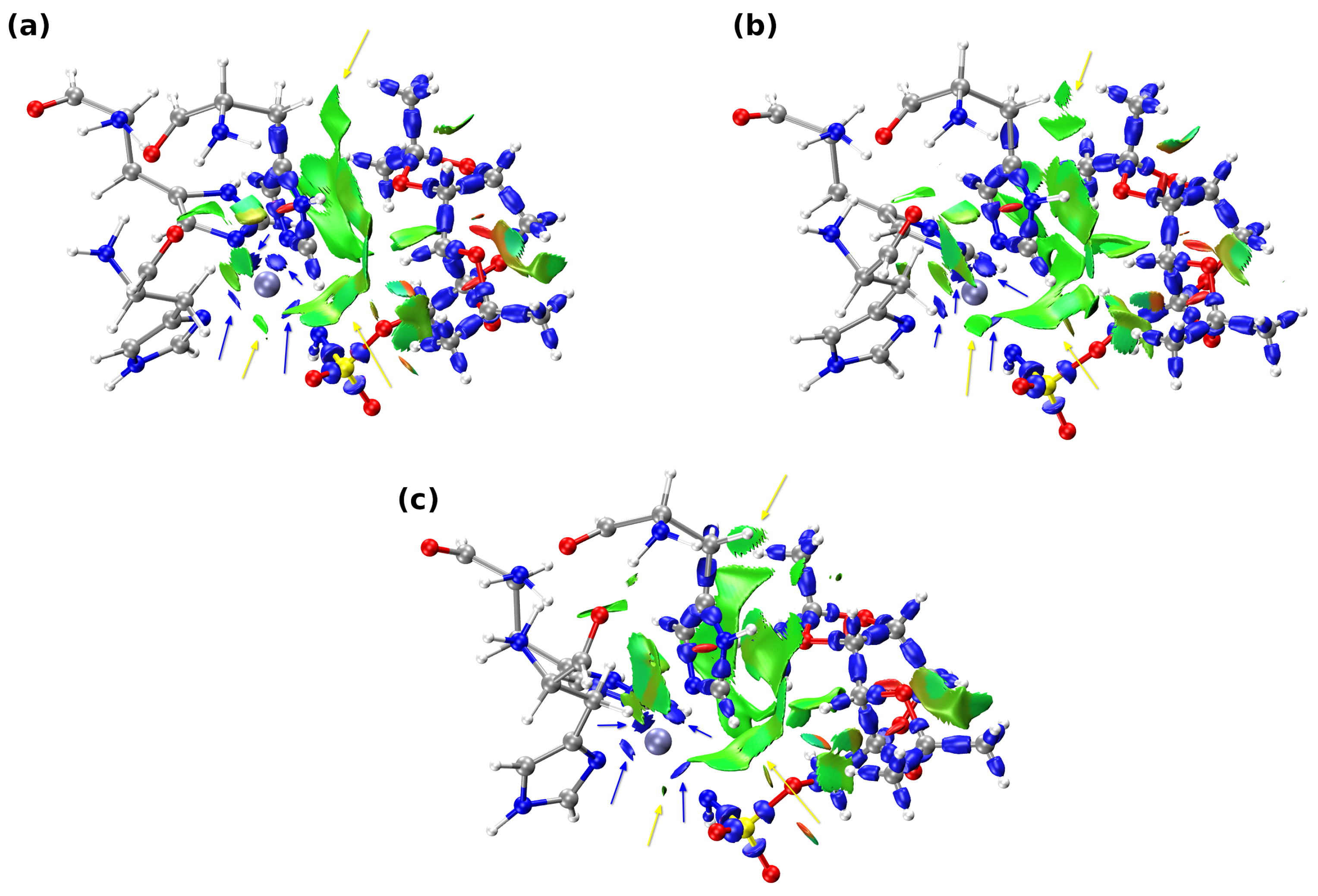
2. Results and Discussion
2.1. Analysis of Non-Covalent Interactions Present in a Large Model
| Snapshot [ps] | System | BCP | BCP | VBCP | HBCP | BCP | E1 |
|---|---|---|---|---|---|---|---|
| 5 | THR199 | H-O…H-N− | 0.0334 | −0.0264 | 0.0027 | 0.1270 | −8.2895 |
| GLN92 | HN-H…O | 0.0322 | −0.0239 | 0.0021 | 0.1128 | −7.5059 | |
| HIS64 | N-H…O | 0.0225 | −0.0173 | 0.0004 | 0.0722 | −5.4147 | |
| THR199 | N-H…O=S | 0.0104 | −0.0079 | 0.0005 | 0.0359 | −2.4824 | |
| LEU198 | C-H…O=S | 0.0104 | −0.0077 | 0.0007 | 0.0360 | −2.4119 | |
| HIS200 | N-H…O=S | 0.0094 | −0.0067 | 0.0002 | 0.0280 | −2.0951 | |
| 10 | HIS64 | N-H…O | 0.0236 | −0.0186 | 0.0005 | 0.0782 | −5.8295 |
| THR199 | H-O…H-N− | 0.0234 | −0.0172 | 0.0009 | 0.0765 | −5.4111 | |
| GLN92 | HN-H…O | 0.0184 | −0.0137 | 0.0002 | 0.0558 | −4.2838 | |
| THR199 | N-H…O=S | 0.0145 | −0.0106 | −0.0001 | 0.0418 | −3.3396 | |
| LEU198 | C-H…O=S | 0.0119 | −0.0092 | 0.0007 | 0.0424 | −2.8745 | |
| GLN92 | C=O…H-C | 0.0072 | −0.0050 | 0.0012 | 0.0297 | −1.5717 | |
| 15 | THR199 | N-H…O=S | 0.0225 | −0.0157 | 0.0010 | 0.0709 | −4.9365 |
| THR199 | H-O…H-N− | 0.0196 | −0.0143 | 0.0004 | 0.0604 | −4.4977 | |
| HIS64 | N-H…O | 0.0141 | −0.0103 | 0.0001 | 0.0418 | −3.2406 | |
| GLN92 | HN-H…O | 0.0120 | −0.0086 | 0.0001 | 0.0350 | −2.7019 | |
| GLN92 | C=O…H-C | 0.0101 | −0.0070 | 0.0001 | 0.0291 | −2.2096 | |
| LEU198 | HC-H…O=S | 0.0086 | −0.0064 | 0.0010 | 0.0335 | −2.0209 |
| Snapshot [ps] | System | Interacting Pair | LP1(O) (X–H) | LP2(O) (X–H) | (X–H) → LP1(O) | (X–H) → LP2(O) | ENBO |
|---|---|---|---|---|---|---|---|
| 5 | THR199 | H-O…H-N− | −3.95 | −12.78 | 2.69 | 9.81 | −4.23 |
| GLN92 | HN-H…O | −5.51 | −14.05 | 2.45 | 9.51 | −7.60 | |
| HIS64 | N-H…O | −7.15 | −1.04 | 5.24 | 1.56 | −1.39 | |
| THR199 | N-H…O=S | −0.99 | −0.20 | 0.86 | 0.22 | −0.11 | |
| LEU198 | C-H…O=S | −0.63 | −0.39 | 2.11 | 0.18 | 1.27 | |
| HIS200 | N-H…O=S | −1.95 | −2.24 | 0.73 | 0.65 | −2.81 | |
| 10 | HIS64 | N-H…O | −6.32 | −1.39 | 4.51 | 1.75 | −1.45 |
| THR199 | H-O…H-N− | −3.41 | −6.99 | 2.00 | 4.61 | −3.79 | |
| GLN92 | HN-H…O | −4.64 | −2.10 | 2.88 | 1.90 | −1.96 | |
| THR199 | N-H…O=S | −2.88 | −3.81 | 1.63 | 1.40 | −3.66 | |
| LEU198 | C-H…O=S | −0.93 | −0.15 | 2.95 | — | 1.87 | |
| GLN92 | C=O…H-C | −0.35 | −0.14 | 0.91 | 0.50 | 0.92 | |
| 15 | THR199 | N-H…O=S | −6.68 | −4.49 | 3.41 | 1.89 | −5.87 |
| THR199 | H-O…H-N− | −3.94 | −4.52 | 2.24 | 3.06 | −3.16 | |
| HIS64 | N-H…O | −3.36 | −1.22 | 2.27 | 0.64 | −1.67 | |
| GLN92 | HN-H…O | −3.74 | −0.40 | 1.82 | 0.27 | −2.05 | |
| GLN92 | C=O…H-C | −0.41 | −0.93 | 0.69 | 1.09 | 0.44 | |
| LEU198 | HC-H…O=S | −0.75 | — | 1.86 | — | 1.11 |
2.2. Analysis of Non-Covalent Interactions and Dative Covalent Bonds of a Small Model
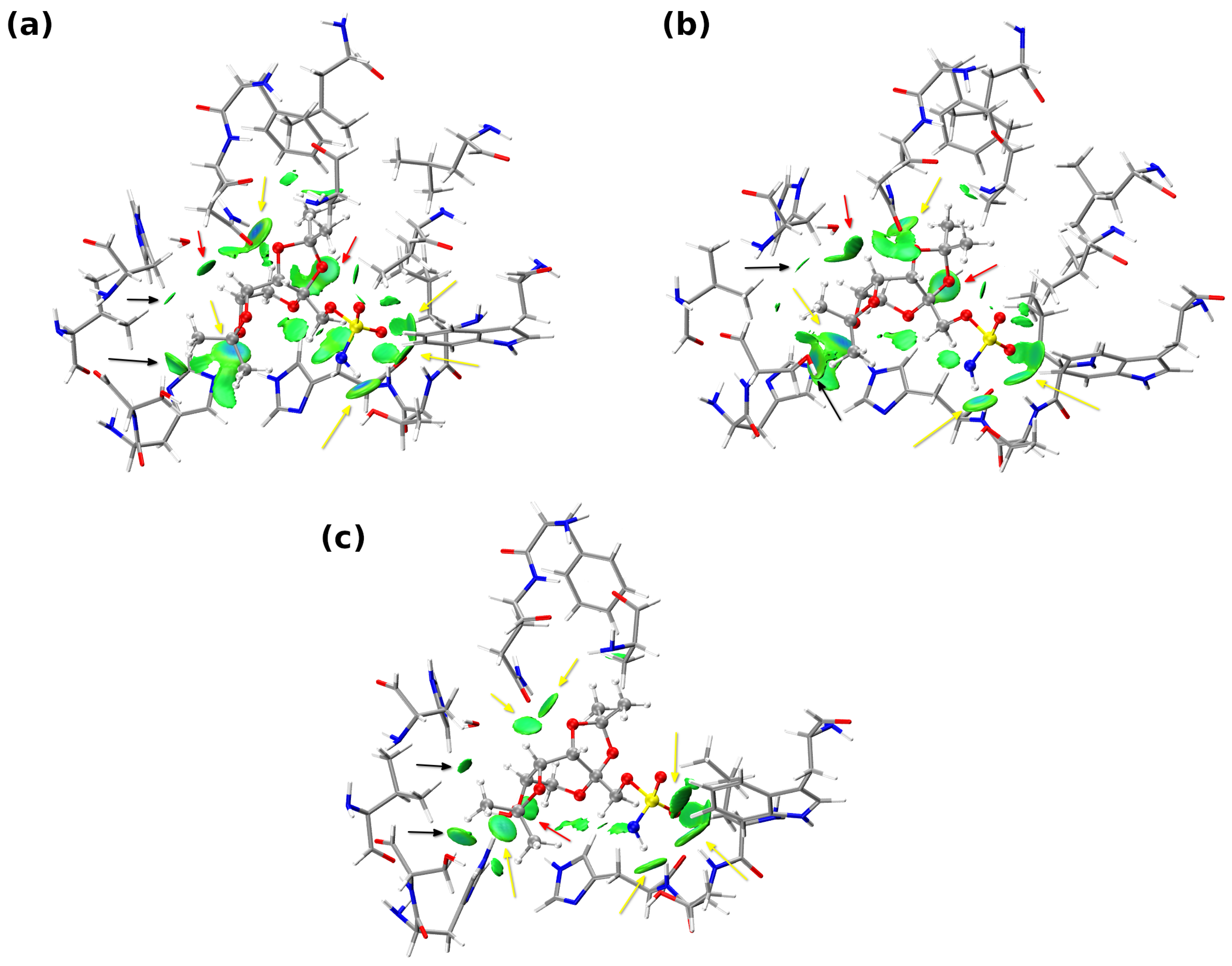
2.3. Topiramate-CA I Binding Pocket Interaction Energy Estimation and Its Decomposition
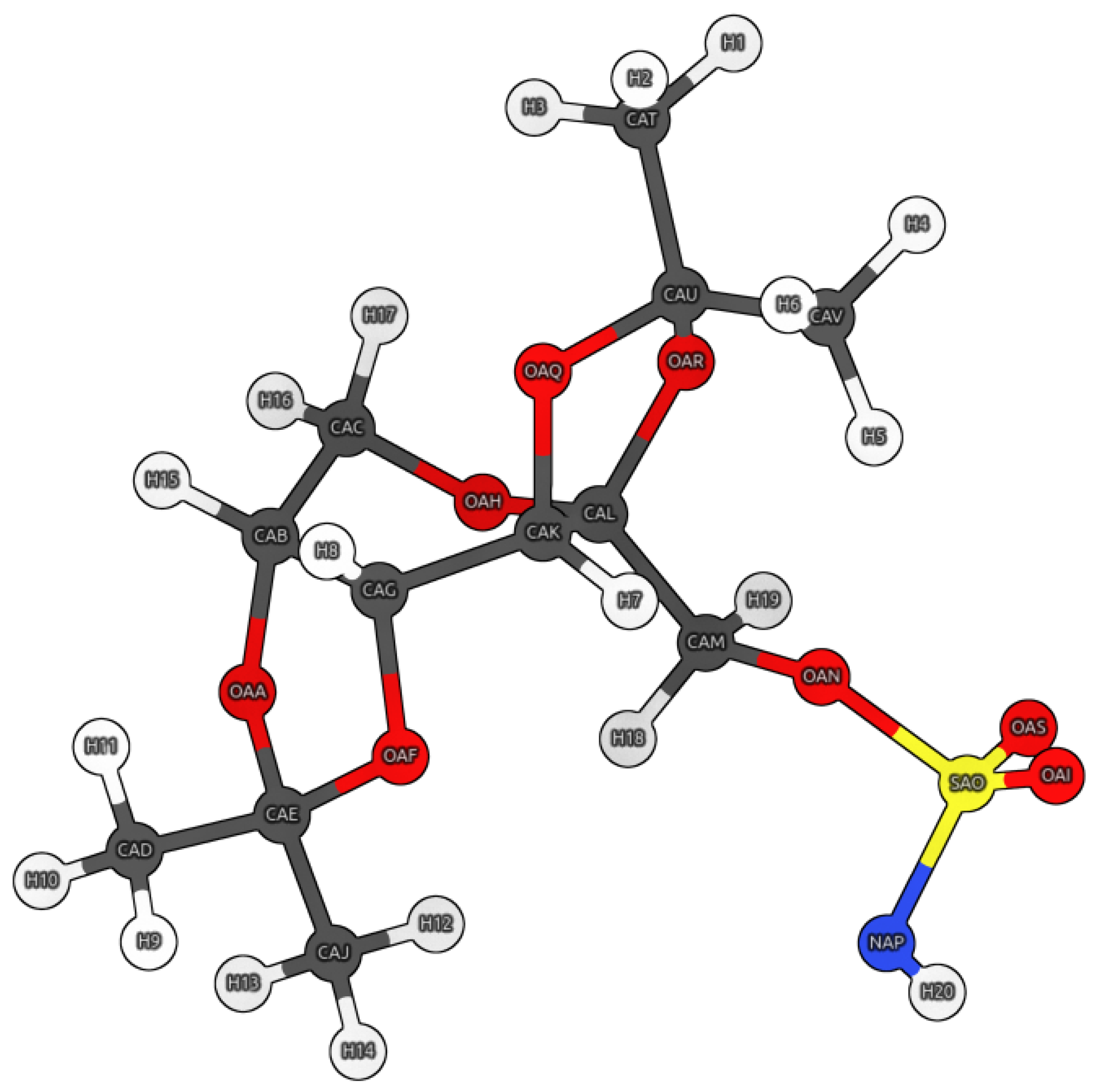
3. Materials and Methods
3.1. Molecular Dynamics in a Hybrid QM/MM Scheme
3.2. Density Functional Theory (DFT) and Wavefunction Analysis
- (i)
- Larger one, which included the ligand molecule as well as the nearest amino acids (within 3.5 Å) with two water molecules;
- (ii)
- Smaller one, which included ligand molecule as well as zinc atoms and the amino acids involved in its coordination.
3.3. Symmetry-Adapted Perturbation Theory (SAPT) Decomposition of the Interaction Energy
4. Conclusions
- (i)
- The physical quantities at BCPs and acceptor–donor properties of the studied interactions (as well as the donors of interactions) were reorganizing throughout the course of the MD; nonetheless, the ligand was firmly kept in the binding site for all the simulation time;
- (ii)
- The application of IGMH, IRI, QTAIM, and NBO methods allowed for obtaining a complementary and detailed picture of the particular secondary bonds of interest—notably, the NBO analysis enabled us to reveal the nature (attractive or repulsive) of the examined non-covalent interactions;
- (iii)
- The energy decomposition supported the observations about the binding site reorganization from other analyses and it showed that the most pronounced components to the interaction energy of the TPM-CA I binding site are electrostatics and dispersion.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BCP | Bond Critical Point |
| BOMD | Born–Oppenheimer Molecular Dynamics |
| BSSE | Basis Set Superposition Error |
| CPMD | Car–Parrinello Molecular Dynamics |
| DFT | Density Functional Theory |
| ED | Electron density |
| EDA | Energy Decomposition Analysis |
| HB | Hydrogen Bond |
| IGM | Independent Gradient Model |
| IGMH | Independent Gradient Model based on Hirshfeld partitioning |
| IMOMM | Integrated Molecular Orbital Molecular Mechanics |
| IRI | Interaction Region Indicator |
| MD | Molecular Dynamics |
| MEP | Molecular Electrostatic Potential |
| NBO | Natural Bond Orbitals |
| NCI | Non-Covalent Interaction |
| NMR | Nuclear Magnetic Resonance |
| RDG | Reduced Density Gradient |
| QM/MM | Quantum Mechanics/Molecular Mechanics |
| QTAIM | Quantum Theory of Atoms in Molecules |
| SAPT | Symmetry-Adapted Perturbation Theory |
| WBI | Wiberg Bond Index |
References
- Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Interrelation between H-Bond and Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3513–3560. [Google Scholar] [CrossRef] [PubMed]
- Denisov, G.S.; Mavri, J.; Sobczyk, L. Hydrogen Bonding-New Insights (Challenges and Advances in Computational Chemistry and Physics, 3); Grabowski, S.J., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 377–416. [Google Scholar]
- Grabowski, S.J. What Is the Covalency of Hydrogen Bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef] [PubMed]
- Michalczyk, M.; Zierkiewicz, W.; Wysokiński, R.; Scheiner, S. Theoretical Studies of IR and NMR Spectral Changes Induced by Sigma-Hole Hydrogen, Halogen, Chalcogen, Pnicogen, and Tetrel Bonds in a Model Protein Environment. Molecules 2019, 24, 3329. [Google Scholar] [CrossRef]
- Müller-Dethlefs, K.; Hobza, P. Noncovalent Interactions: A Challenge for Experiment and Theory. Chem. Rev. 2000, 100, 143–167. [Google Scholar] [CrossRef]
- Yamauchi, O. Noncovalent interactions in biocomplexes. Phys. Sci. Rev. 2016, 1, 20160001. [Google Scholar] [CrossRef]
- Pauling, L.; Corey, R.B.; Branson, H.R. The structure of proteins: Two hydrogen-bonded helical configurations of the polypeptide chain. Proc. Natl. Acad. Sci. USA 1951, 37, 205–211. [Google Scholar] [CrossRef]
- Pauling, L.; Corey, R.B. A Proposed Structure For The Nucleic Acids. Proc. Natl. Acad. Sci. USA 1953, 39, 84–97. [Google Scholar] [CrossRef]
- Desiraju, G.R. C-H…O and other weak hydrogen bonds. From crystal engineering to virtual screening. Chem. Comm. 2005, 24, 2995–3001. [Google Scholar] [CrossRef]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond; Oxford University Press: Oxford, UK, 2009. [Google Scholar] [CrossRef]
- Takahashi, O.; Kohno, Y.; Nishio, M. Relevance of Weak Hydrogen Bonds in the Conformation of Organic Compounds and Bioconjugates: Evidence from Recent Experimental Data and High-Level ab Initio MO Calculations. Chem. Rev. 2010, 110, 6049–6076. [Google Scholar] [CrossRef]
- Taylor, R.; Kennard, O. Crystallographic evidence for the existence of CH…O, CH…N and CH…Cl hydrogen bonds. J. Am. Chem. Soc. 1982, 104, 5063–5070. [Google Scholar] [CrossRef]
- Alterio, V.; Monti, S.M.; Truppo, E.; Pedone, C.; Supuran, C.T.; Simone, G.D. The first example of a significant active site conformational rearrangement in a carbonic anhydrase-inhibitor adduct: The carbonic anhydrase I–topiramate complex. Org. Biomol. Chem. 2010, 8, 3528. [Google Scholar] [CrossRef]
- Maresca, A.; Temperini, C.; Vu, H.; Pham, N.B.; Poulsen, S.A.; Scozzafava, A.; Quinn, R.J.; Supuran, C.T. Non-Zinc Mediated Inhibition of Carbonic Anhydrases: Coumarins Are a New Class of Suicide Inhibitors. J. Am. Chem. Soc. 2009, 131, 3057–3062. [Google Scholar] [CrossRef] [PubMed]
- Fiore, A.D.; Monti, S.M.; Hilvo, M.; Parkkila, S.; Romano, V.; Scaloni, A.; Pedone, C.; Scozzafava, A.; Supuran, C.T.; Simone, G.D. Crystal structure of human carbonic anhydrase XIII and its complex with the inhibitor acetazolamide. Proteins Struct. Funct. Genet. 2009, 74, 164–175. [Google Scholar] [CrossRef] [PubMed]
- Mboge, M.; Mahon, B.; McKenna, R.; Frost, S. Carbonic Anhydrases: Role in pH Control and Cancer. Metabolites 2018, 8, 19. [Google Scholar] [CrossRef] [PubMed]
- Supuran, C.T. Carbonic anhydrases: Novel therapeutic applications for inhibitors and activators. Nat. Rev. Drug Discov. 2008, 7, 168–181. [Google Scholar] [CrossRef]
- Lionetto, M.; Caricato, R.; Giordano, M.; Schettino, T. The Complex Relationship between Metals and Carbonic Anhydrase: New Insights and Perspectives. Int. J. Mol. Sci. 2016, 17, 127. [Google Scholar] [CrossRef] [PubMed]
- Uhlen, M.; Oksvold, P.; Fagerberg, L.; Lundberg, E.; Jonasson, K.; Forsberg, M.; Zwahlen, M.; Kampf, C.; Wester, K.; Hober, S.; et al. Towards a knowledge-based Human Protein Atlas. Nat. Biotechnol. 2010, 28, 1248–1250. [Google Scholar] [CrossRef]
- Uhlén, M.; Fagerberg, L.; Hallström, B.M.; Lindskog, C.; Oksvold, P.; Mardinoglu, A.; Sivertsson, Å.; Kampf, C.; Sjöstedt, E.; Asplund, A.; et al. Tissue-based map of the human proteome. Science 2015, 347, 1260419. [Google Scholar] [CrossRef]
- Hassan, M.I.; Shajee, B.; Waheed, A.; Ahmad, F.; Sly, W.S. Structure, function and applications of carbonic anhydrase isozymes. Bioorg. Med. Chem. 2013, 21, 1570–1582. [Google Scholar] [CrossRef]
- Sly, W.S.; Hewett-Emmett, D.; Whyte, M.P.; Yu, Y.S.; Tashian, R.E. Carbonic anhydrase II deficiency identified as the primary defect in the autosomal recessive syndrome of osteopetrosis with renal tubular acidosis and cerebral calcification. Proc. Natl. Acad. Sci. USA 1983, 80, 2752–2756. [Google Scholar] [CrossRef] [PubMed]
- Lyseng-Williamson, K.A.; Yang, L.P.H. Topiramate. Drugs 2007, 67, 2231–2256. [Google Scholar] [CrossRef] [PubMed]
- Casucci, G.; Villani, V.; Frediani, F. Central mechanism of action of antimigraine prophylactic drugs. Neurol. Sci. 2008, 29, 123–126. [Google Scholar] [CrossRef]
- Çelebisoy, N.; Gökçay, F.; Şirin, H.; Akyürekli, O. Treatment of idiopathic intracranial hypertension: Topiramate vs acetazolamide, an open-label study. Acta Neurol. Scand. 2007, 116, 322–327. [Google Scholar] [CrossRef] [PubMed]
- McElroy, S.L.; Guerdjikova, A.I.; Martens, B.; Keck, P.E.; Pope, H.G.; Hudson, J.I. Role of Antiepileptic Drugs in the Management of Eating Disorders. CNS Drugs 2009, 23, 139–156. [Google Scholar] [CrossRef] [PubMed]
- Hollander, E.; Dell’Osso, B. Topiramate plus paroxetine in treatment-resistant obsessive–compulsive disorder. Int. Clin. Psychopharmacol. 2006, 21, 189–191. [Google Scholar] [CrossRef]
- Vasudev, K.; Macritchie, K.; Geddes, J.; Watson, S.; Young, A.H. Topiramate for Acute Affective Episodes in Bipolar Disorder; Young, A.H., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM Methods for Biomolecular Systems. Angew. Chem. Int. Ed. Engl. 2009, 48, 1198–1229. [Google Scholar] [CrossRef]
- Lefebvre, C.; Khartabil, H.; Boisson, J.C.; Contreras-García, J.; Piquemal, J.P.; Hénon, E. The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations. ChemPhysChem 2018, 19, 724–735. [Google Scholar] [CrossRef]
- Lu, T.; Chen, Q. Independent gradient model based on Hirshfeld partition: A new method for visual study of interactions in chemical systems. J. Comput. Chem. 2022, 43, 539–555. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Lu, T.; Chen, Q. Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions. Chem.-Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Szatyłowicz, H.; Sadlej-Sosnowska, N. Characterizing the Strength of Individual Hydrogen Bonds in DNA Base Pairs. J. Chem. Inf. Model. 2010, 50, 2151–2161. [Google Scholar] [CrossRef]
- Szatylowicz, H.; Jezierska, A.; Sadlej-Sosnowska, N. Correlations of NBO energies of individual hydrogen bonds in nucleic acid base pairs with some QTAIM parameters. Struct. Chem. 2015, 27, 367–376. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Gilli, G.; Gilli, P. Towards an unified hydrogen-bond theory. J. Mol. Struct. 2000, 552, 1–15. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Case, D.A.; Walker, R.C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 3, 198–210. [Google Scholar] [CrossRef]
- Case, D.A.; Aktulga, H.M.; Belfon, K.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cisneros, G.A.; Cruzeiro, V.W.D.; Darden, T.A.; et al. Amber 2021; University of California: San Francisco, CA, USA, 2021. [Google Scholar]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L. Quantum and statistical mechanical studies of liquids. 10. Transferable intermolecular potential functions for water, alcohols, and ethers. Application to liquid water. J. Am. Chem. Soc. 1981, 103, 335–340. [Google Scholar] [CrossRef]
- Li, P.; Merz, K.M. MCPB.py: A Python Based Metal Center Parameter Builder. J. Chem. Inf. Model. 2016, 56, 599–604. [Google Scholar] [CrossRef] [PubMed]
- Lippert, G.; Hutter, J.; Parrinello, M. A hybrid Gaussian and plane wave density functional scheme. Mol. Phys. 1997, 92, 477–487. [Google Scholar] [CrossRef]
- VandeVondele, J.; Hutter, J. An efficient orbital transformation method for electronic structure calculations. J. Chem. Phys. 2003, 118, 4365–4369. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Ben, M.D.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An electronic structure and molecular dynamics software package—Quickstep: Efficient and accurate electronic structure calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef]
- Available online: https://www.cp2k (accessed on 29 September 2022).
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable dual-space Gaussian pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- VandeVondele, J.; Borštnik, U.; Hutter, J. Linear Scaling Self-Consistent Field Calculations with Millions of Atoms in the Condensed Phase. J. Chem. Theory Comput. 2012, 8, 3565–3573. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865, Erratum in Phys. Rev. Lett. 1997, 78, 1396–1396. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed]
- Maseras, F.; Morokuma, K. IMOMM: A new integrated ab initio molecular mechanics geometry optimization scheme of equilibrium structures and transition states. J. Comput. Chem. 1995, 16, 1170–1179. [Google Scholar] [CrossRef]
- Case, D.; Belfon, K.; Ben-Shalom, I.; Brozell, S.; Cerutti, D.; Cheatham, T.C., III; Cruzeiro, V.; Darden, T.; Duke, R.; Giambasu, G.; et al. Amber 2020; University of California: San Francisco, CA, USA, 2020. [Google Scholar]
- Chai, J.D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Rappoport, D.; Furche, F. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA quantum chemistry program package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Koch, U.; Popelier, P.L.A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Gálvez, O.; Gómez, P.C.; Pacios, L.F. Variation with the intermolecular distance of properties dependent on the electron density in hydrogen bond dimers. J. Chem. Phys. 2001, 115, 11166–11184. [Google Scholar] [CrossRef]
- Pacios, L.F. Change with the intermolecular distance of electron properties of hydrogen bond dimers at equilibrium and non-equilibrium geometries. Struct. Chem. 2005, 16, 223–241. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Weinhold, F.; Landis, C.R. Natural Bond Orbitals and extensions of localized bonding concepts. Chem. Educ. Res. Pract. 2001, 2, 91–104. [Google Scholar] [CrossRef]
- Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 6.0: Natural bond orbital analysis program. J. Comput. Chem. 2013, 34, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- OneAngstrom. SAMSON 2022 R2. Available online: https://www.samson-connect.net/ (accessed on 15 December 2022).
- Szalewicz, K. Symmetry-adapted perturbation theory of intermolecular forces. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 2, 254–272. [Google Scholar] [CrossRef]
- Papajak, E.; Truhlar, D.G. Convergent Partially Augmented Basis Sets for Post-Hartree-Fock Calculations of Molecular Properties and Reaction Barrier Heights. J. Chem. Theory Comput. 2010, 7, 10–18. [Google Scholar] [CrossRef]
- Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Smith, D.G.A.; Burns, L.A.; Simmonett, A.C.; Parrish, R.M.; Schieber, M.C.; Galvelis, R.; Kraus, P.; Kruse, H.; Di Remigio, R.; Alenaizan, A.; et al. PSI4 1.4: Open-source software for high-throughput quantum chemistry. J. Chem. Phys. 2020, 152, 184108. [Google Scholar] [CrossRef] [PubMed]

| Snapshot [ps] | Acceptor | BCP | BCP | VBCP | HBCP | BCP |
|---|---|---|---|---|---|---|
| 5 | TPM | Zn-N− | 0.0987 | −0.1583 | −0.0271 | 0.4166 |
| HIS96 | Zn-N | 0.0787 | −0.1186 | −0.0152 | 0.3529 | |
| HIS119 | Zn-N | 0.0867 | −0.1364 | −0.0197 | 0.3875 | |
| HIS94 | Zn-N | 0.1024 | −0.1769 | −0.0292 | 0.4738 | |
| 10 | TPM | Zn-N− | 0.0979 | −0.1584 | −0.0261 | 0.4251 |
| HIS96 | Zn-N | 0.0794 | −0.1190 | −0.0157 | 0.3504 | |
| HIS119 | Zn-N | 0.0757 | −0.1092 | −0.0143 | 0.3223 | |
| HIS94 | Zn-N | 0.0807 | −0.1206 | −0.0168 | 0.3482 | |
| 15 | TPM | Zn-N− | 0.0919 | −0.1449 | −0.0222 | 0.4017 |
| HIS96 | Zn-N | 0.0851 | −0.1337 | −0.0183 | 0.3880 | |
| HIS119 | Zn-N | 0.0938 | −0.1538 | −0.0238 | 0.4250 | |
| HIS94 | Zn-N | 0.0749 | −0.1083 | −0.0139 | 0.3221 |
| Snapshot | Eelst | % | Eexch | Eind | % | Edisp | % | Totala |
|---|---|---|---|---|---|---|---|---|
| 5 ps | −41.710 | 37.00 | 77.113 | −24.036 | 21.30 | −47.009 | 41.70 | −35.642 |
| 10 ps | −33.281 | 34.10 | 65.338 | −20.362 | 20.90 | −43.874 | 45.00 | −32.179 |
| 15 ps | −27.195 | 32.80 | 46.730 | −18.667 | 22.50 | −37.056 | 44.70 | −36.188 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wojtkowiak, K.; Jezierska, A. Role of Non-Covalent Interactions in Carbonic Anhydrase I—Topiramate Complex Based on QM/MM Approach. Pharmaceuticals 2023, 16, 479. https://doi.org/10.3390/ph16040479
Wojtkowiak K, Jezierska A. Role of Non-Covalent Interactions in Carbonic Anhydrase I—Topiramate Complex Based on QM/MM Approach. Pharmaceuticals. 2023; 16(4):479. https://doi.org/10.3390/ph16040479
Chicago/Turabian StyleWojtkowiak, Kamil, and Aneta Jezierska. 2023. "Role of Non-Covalent Interactions in Carbonic Anhydrase I—Topiramate Complex Based on QM/MM Approach" Pharmaceuticals 16, no. 4: 479. https://doi.org/10.3390/ph16040479
APA StyleWojtkowiak, K., & Jezierska, A. (2023). Role of Non-Covalent Interactions in Carbonic Anhydrase I—Topiramate Complex Based on QM/MM Approach. Pharmaceuticals, 16(4), 479. https://doi.org/10.3390/ph16040479






