Detection and Localization of Rotor Winding Inter-Turn Short Circuit Fault in DFIG Using Zero-Sequence Current Component Under Variable Operating Conditions
Abstract
1. Introduction
- This paper analytically validates the rotor winding ITSC fault detection in DFIG under variable operating conditions by using a detailed mathematical model that offers a strong theoretical foundation for practical applications.
- This paper introduces a fault detection algorithm that validates fault detection under both sub-synchronous and super-synchronous modes of DFIG operation with rotor-side dynamic low-frequency conditions, whereas previous research has largely overlooked the super-synchronous mode and dynamic low-frequency conditions.
- This paper uses the FC in rotor currents and ZSC under rotor dynamic frequency for detecting the ITSC fault and identifying the fault location which simplifies the implementation and enhances the sensitivity and accuracy of the rotor winding ITSC fault detection in DFIG.
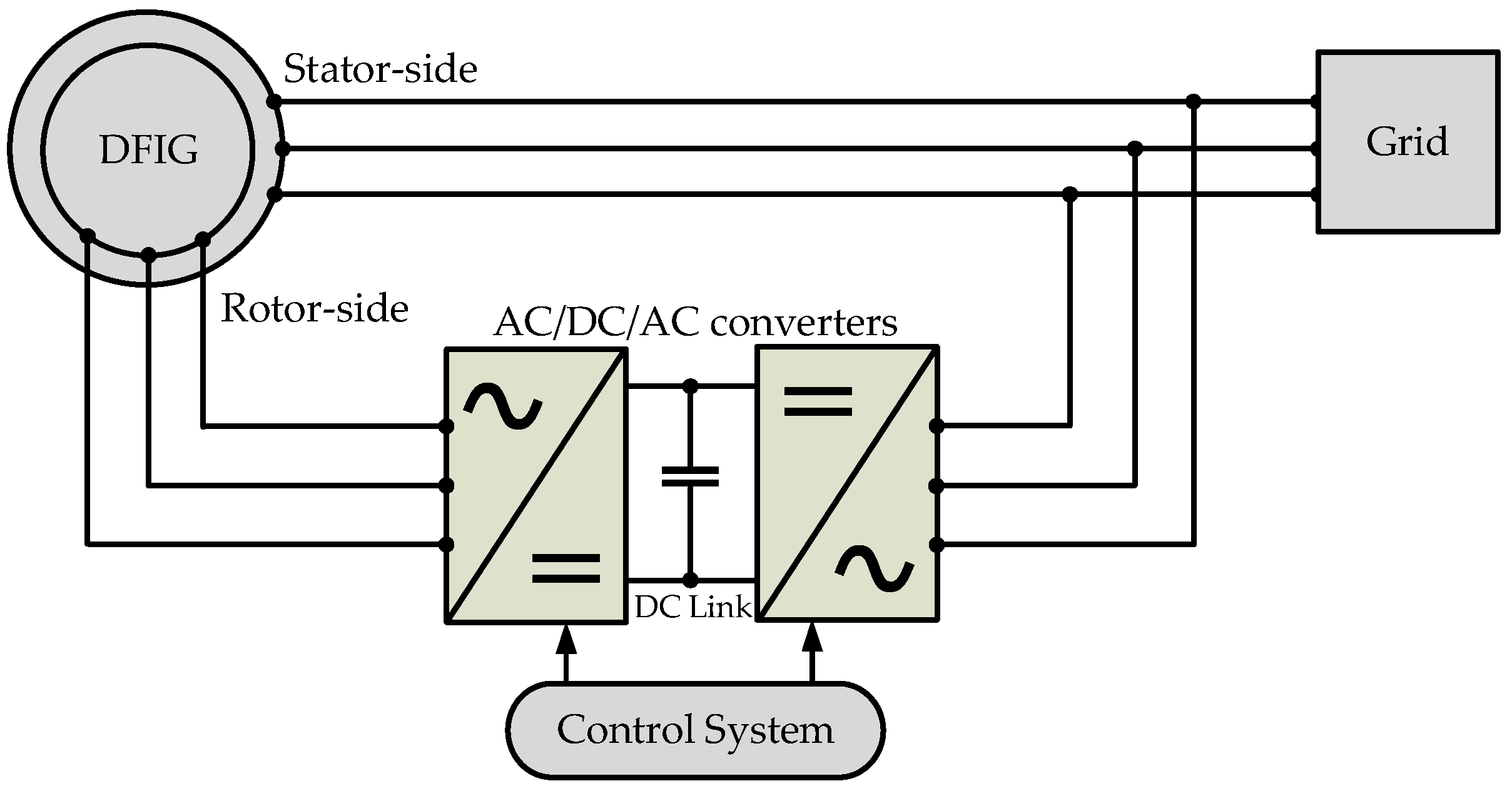
2. Modeling
2.1. Inter-Turn Short Circuit Fault
2.2. Mathematical Model of DFIG with Rotor ITSC
3. Methodology
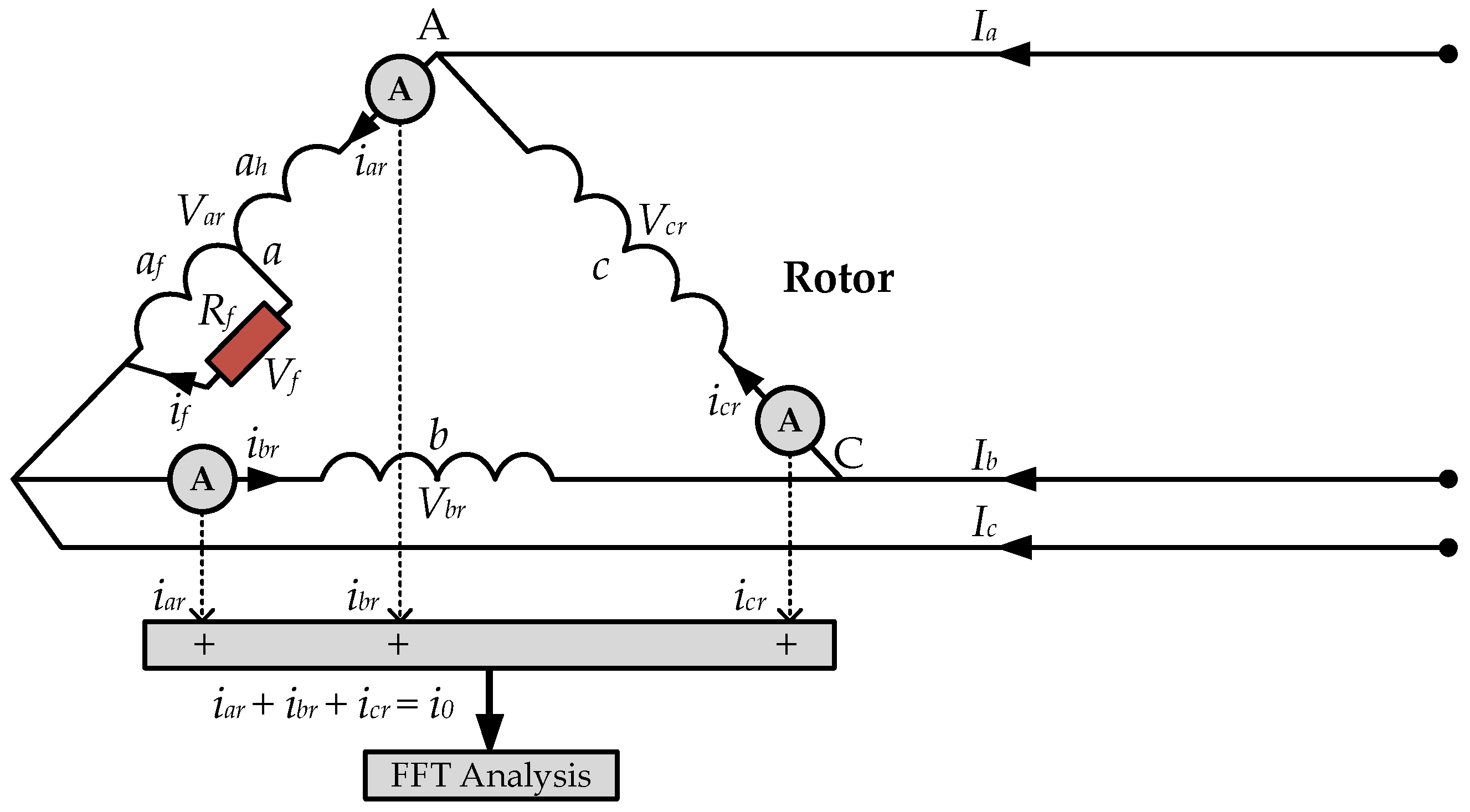
3.1. Expression for ZSC Signal
3.2. Fault Indicator
Fault Indicator Under Dynamic Conditions
3.3. Fault Position Indicator
Fault Position Indicator Under Dynamic Conditions
- (1)
- Sub-synchronous mode
- (2)
- Super-synchronous mode
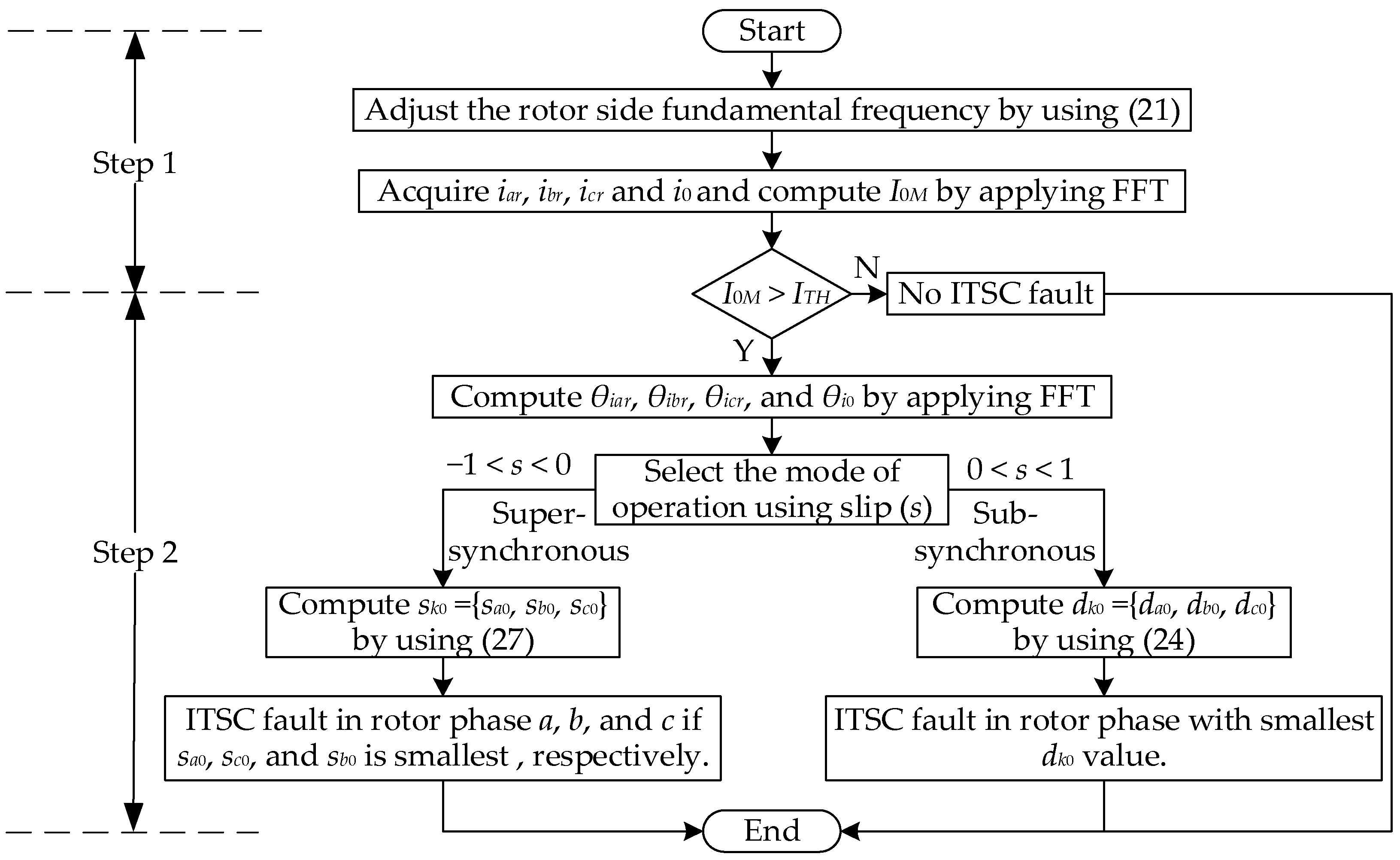
3.4. Algorithm for Rotor ITSC Fault Diagnosis
4. Simulations
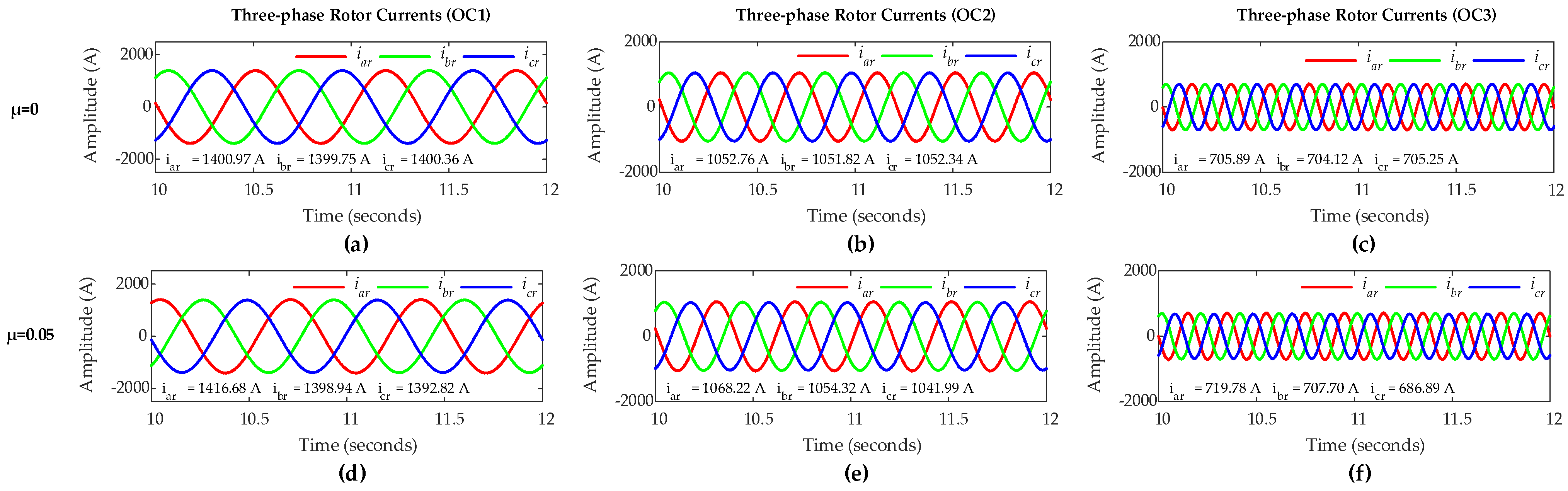
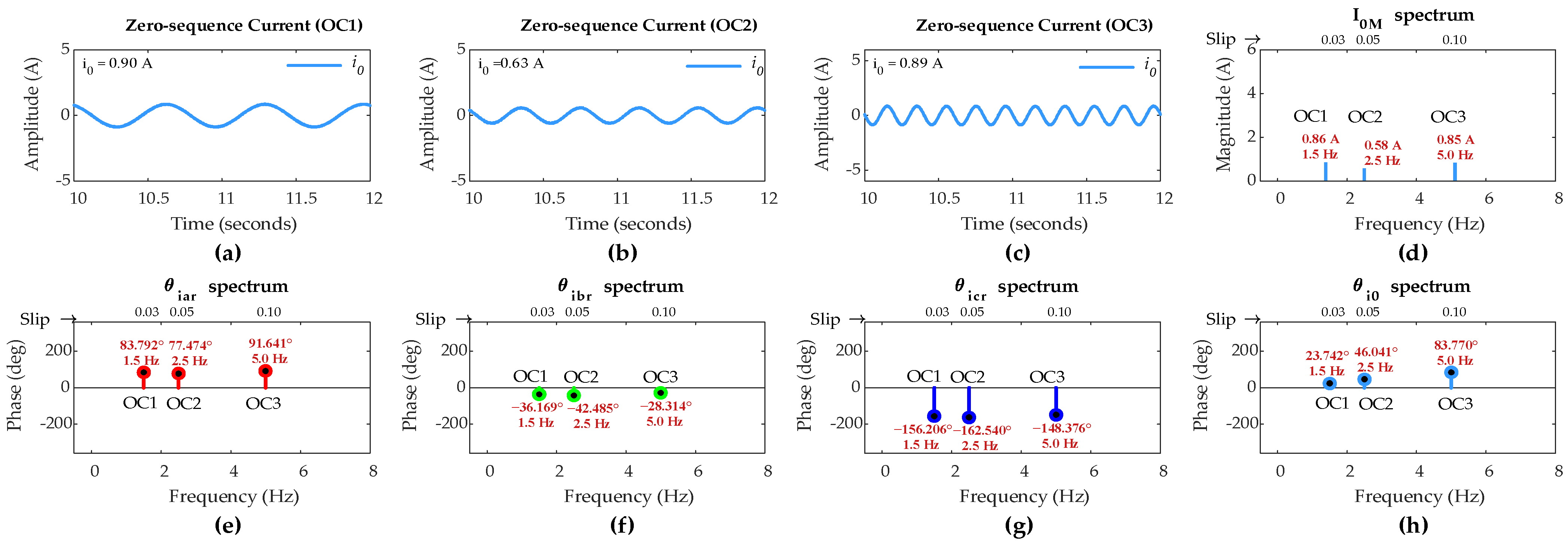
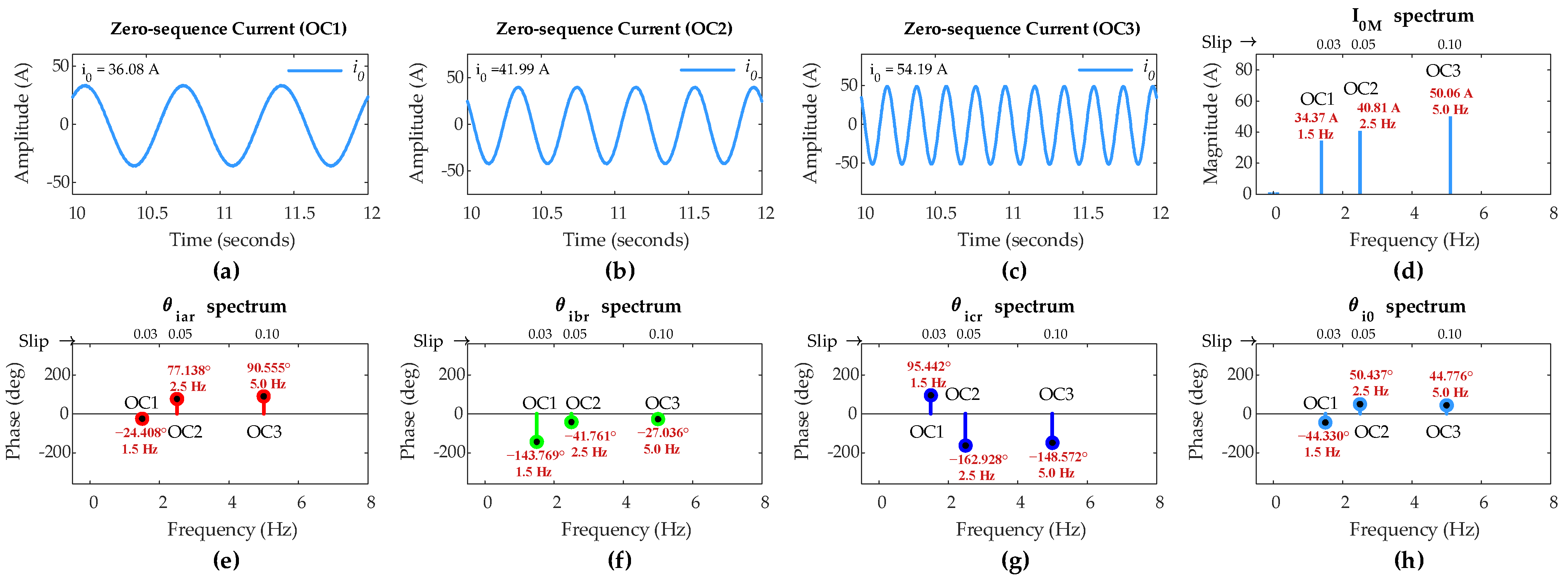
4.1. Simulation Under Sub-Synchronous Mode of Operation
- OC1: DFIG operation with slip s = 0.03 and load= 100%.
- OC2: DFIG operation with slip s = 0.05 and load= 75%.
- OC3: DFIG operation with slip s = 0.1 and load= 50%.
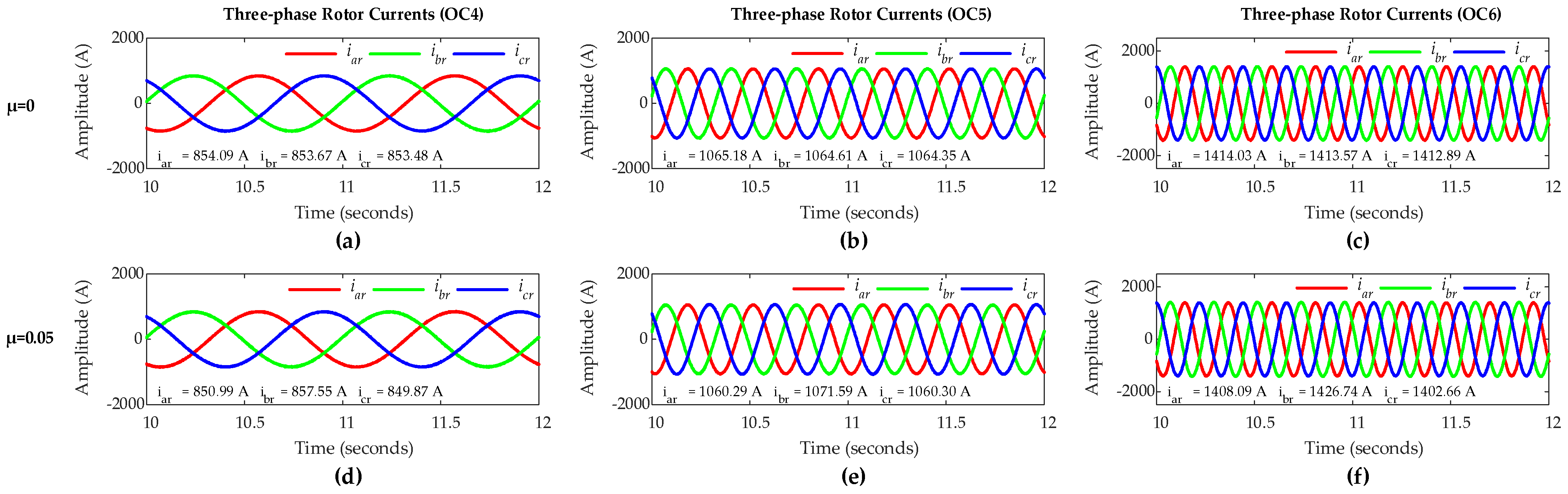
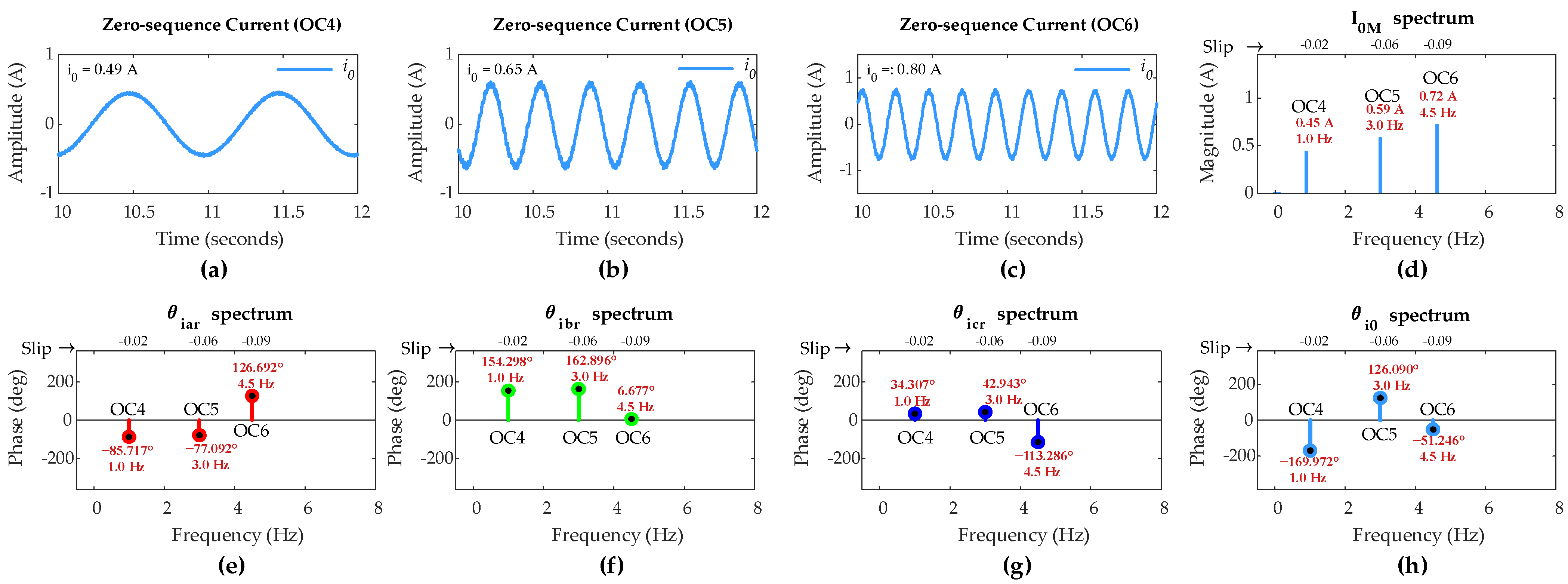
4.2. Simulation Under Super-Synchronous Mode of Operation
- OC4: DFIG operation with slip s = −0.02 and load = 60%.
- OC5: DFIG operation with slip s = −0.06 and load = 75%.
- OC6: DFIG operation with slip s = −0.09 and load = 100%.
4.3. Comparitive Analysis with the Existing Method
4.3.1. Comparative Analysis of Fault Indicator (I0M)
4.3.2. Comparative Analysis of Fault Location Indicators (dk0 and sk0)
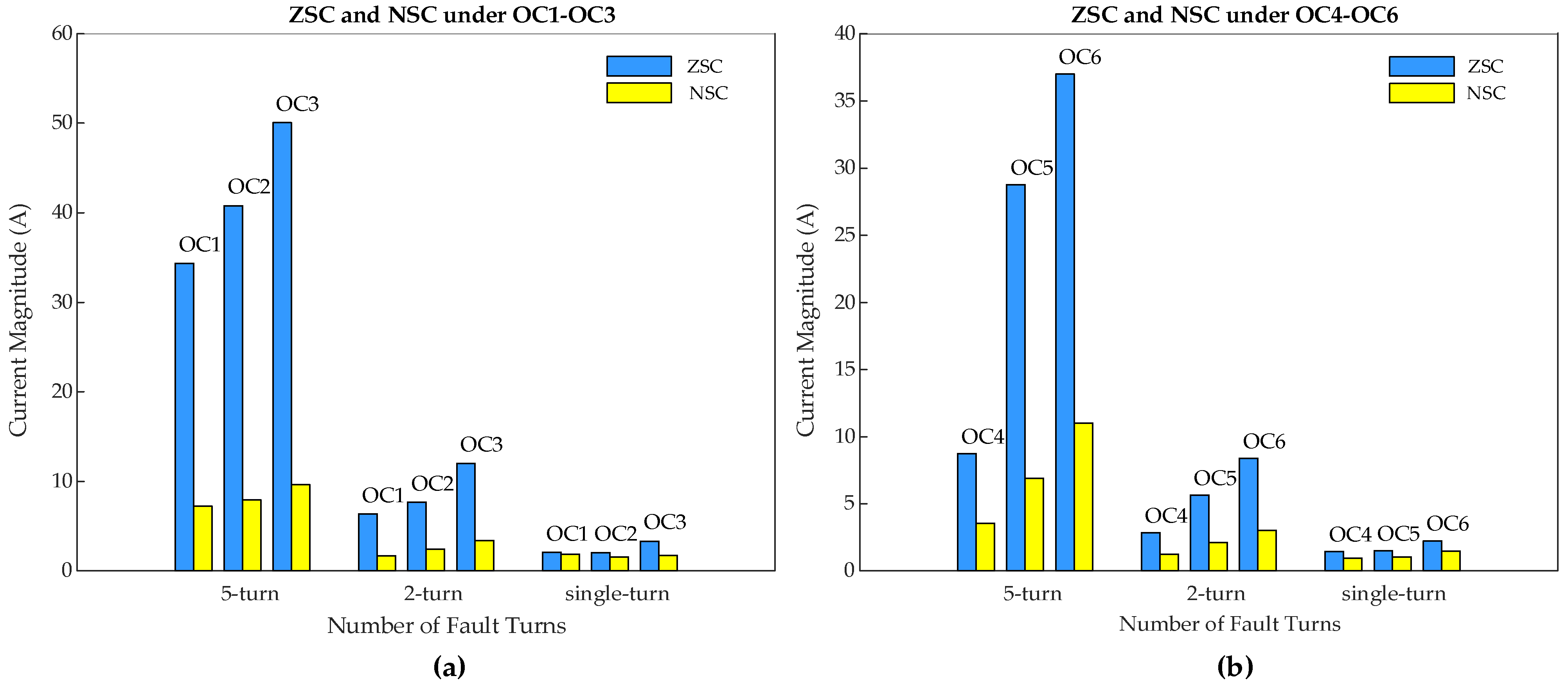
- The FC magnitude in ZSC increases as the fault severity level µ increases and decreases as the value of µ decreases, under all OC1–OC6 scenarios.
- IPAs of the FCs in rotor three-phase currents are only a little affected by the fault severity level µ, whereas IPA of the FC in ZSC is greatly affected by the value of µ under all OC1–OC6 scenarios.
- Hence, ZSC offers high sensitivity to the severity and location of fault which makes it a reliable feature for low-severity fault detection under variable operating conditions.
5. Discussion
6. Conclusions
- (1)
- While previous research has largely overlooked the super-synchronous mode and rotor-side dynamic low-frequency conditions, the proposed methodology remains effective for rotor ITSC fault detection and faulty phase identification under both sub-synchronous and super-synchronous modes of DFIG operation with rotor-side dynamic low-frequency conditions, ensuring its reliability in practical applications.
- (2)
- The FC magnitude in ZSC signal is large and highly sensitive to ITSC fault severity levels in DFIG rotor windings, enabling the effective fault detection even at an early stage with low-severity level. However, ZSC signal is not inherently available, and an auxiliary arrangement is required on the rotor side. As a result, this approach is most appropriate for large-scale and high-cost DFIG applications.
- (3)
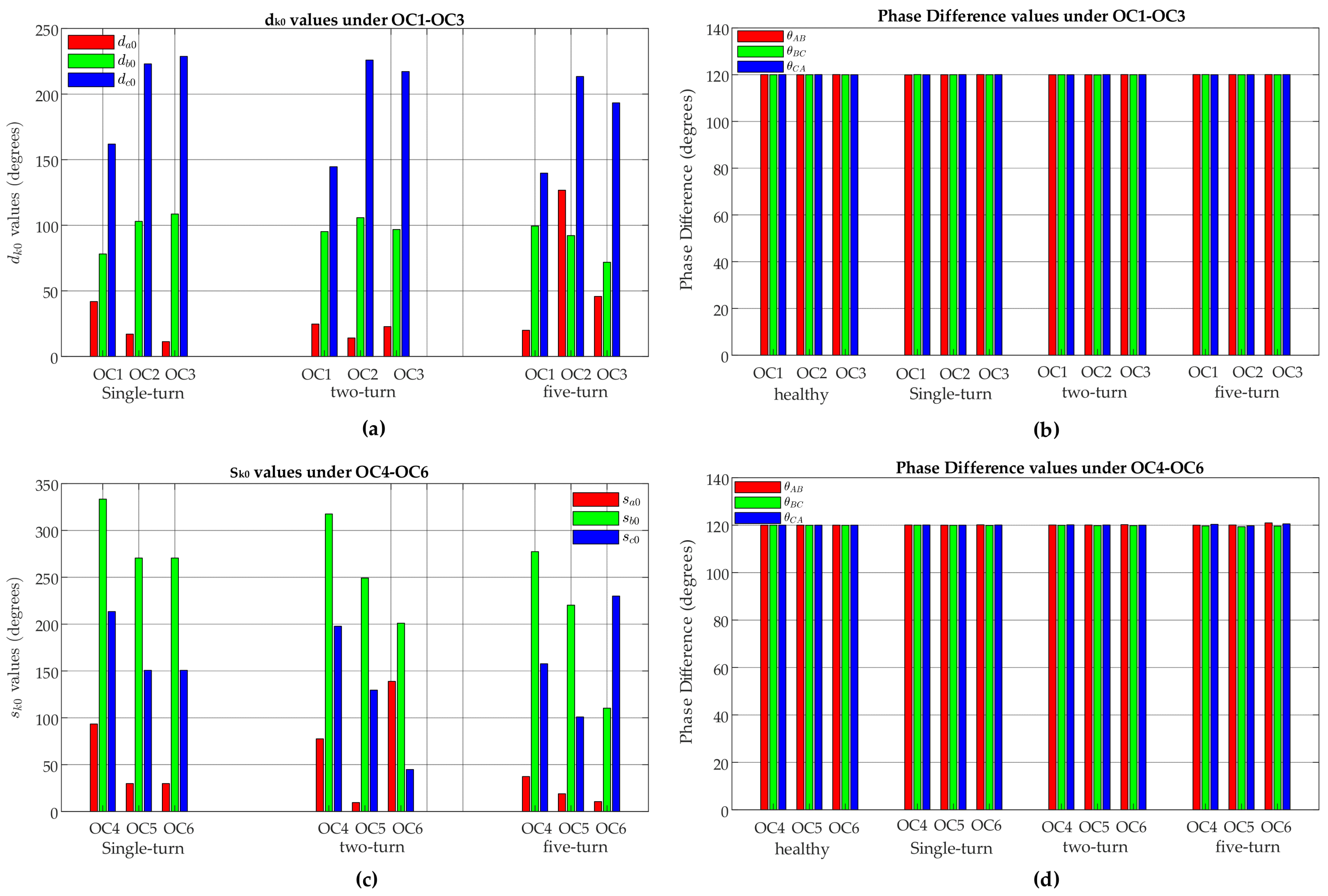
- IPA of the FC in ZSC is highly sensitive to ITSC fault severity levels and the faulty phase location in DFIG rotor windings. On the other hand, IPAs of the FCs in rotor three-phase currents are only a little sensitive to faults. Therefore, the correlation between these angles is effective for the faulty phase location. When the DFIG operates under the sub-synchronous mode, rotor three-phase currents have positive phase sequence (abc), and the difference between the IPA of the FC in ZSC and the IPA of the FC in rotor faulty phase current (dk0) is the smallest angle. Hence, da0, db0, and dc0 are the smallest values when an ITSC occurs in rotor phase ‘a’, ‘b’, and ‘c’, respectively. However, when the DFIG operates under the super-synchronous mode, rotor three-phase currents have the negative phase sequence (acb), and the sum of the IPA of the FC in ZSC and the IPA of the FC in rotor-phase current (sk0) is the smallest angle for phases ‘a’, ‘b’, and ‘c’ when the fault occurs in phases ‘a’, ‘c’, and ‘b’, respectively. Hence, sa0, sb0, and sc0 are the smallest values when an ITSC occurs in rotor phases ‘a’, ‘c’, and ‘b’, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| DFIG | Doubly fed induction generator |
| ITSC | Inter-turn short circuit |
| ZSC | Zero-sequence current |
| FFT | Fast Fourier transform |
| FC | Fundamental component |
| FCs | Fundamental components |
| IPA | Initial phase angle |
| IPAs | Initial phase angles |
References
- Torkaman, G.H.; Keyhani, A. A review of design consideration for Doubly Fed Induction Generator based wind energy system. Electr. Power Syst. Res. 2018, 160, 128–141. [Google Scholar] [CrossRef]
- Aziz, M.S.; Ahmed, S.; Saleem, U.; Mufti, G.M. Wind-hybrid power generation systems using renewable energy sources—A review. Int. J. Renew. Energy Res. 2017, 7, 111–127. [Google Scholar]
- Artigao, E.; Honrubia-Escribano, A.; Gómez-Lázaro, E. In-Service Wind Turbine DFIG Diagnosis using Current Signature Analysis. IEEE Trans. Ind. Electron. 2020, 67, 2262–2271. [Google Scholar] [CrossRef]
- Maldonado-Correa, J.; Martín-Martínez, S.; Artigao, E.; Gómez-Lázaro, E. Using SCADA Data for Wind Turbine Condition Monitoring: A Systematic Literature Review. Energies 2020, 13, 3132. [Google Scholar] [CrossRef]
- Kumar, K.K.; Kumar, P.G.S.; Reddy, K.M. Premature failure of modern turbine generator rotor windings. In Proceedings of the 2016 IEEE 7th Power India International Conference (PIICON), Bikaner, India, 25–27 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Yakhni, M.F.; Cauet, S.; Sakout, A.; Assoum, H.; Etien, E.; Rambault, L.; El-Gohary, M. Variable speed induction motors’ fault detection based on transient motor current signatures analysis: A review. Mech. Syst. Signal Process. 2023, 184, 109737. [Google Scholar] [CrossRef]
- Yousefi Kia, M.; Khedri, M.; Najafi, H.R.; Nejad, M.A.S. Hybrid modelling of doubly fed induction generators with inter-turn stator fault and its detection method using wavelet analysis. IET Gener. Transm. Distrib. 2013, 7, 982–990. [Google Scholar] [CrossRef]
- He, S.; Shen, X.; Jiang, Z. Detection and Location of Stator Winding Interturn Fault at Different Slots of DFIG. IEEE Access 2019, 7, 89342–89353. [Google Scholar] [CrossRef]
- Joksimovic, G.M.; Penman, J. The detection of inter-turn short circuits in the stator windings of operating motors. IEEE Trans. Ind. Electron. 2000, 47, 1078–1084. [Google Scholar] [CrossRef]
- Jung, J.-H.; Lee, J.-J.; Kwon, B.-H. Online Diagnosis of Induction Motors Using MCSA. IEEE Trans. Ind. Electron. 2006, 53, 1842–1852. [Google Scholar] [CrossRef]
- Junqing, L.; Long, H.; Dong, W. Rotor winding inter-turn fault analysis of doubly-fed induction generator based on negative sequence component. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Republic of Korea, 26–29 October 2013; pp. 785–788. [Google Scholar] [CrossRef]
- Shah, D.; Nandi, S.; Neti, P. Stator-Interturn Fault Detection of Doubly Fed Induction Generators using Rotor-Current and Search-Coil-Voltage Signature Analysis. IEEE Trans. Ind. Appl. 2009, 45, 1831–1842. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, Y.; Jia, W.; Han, B.; Liu, Y.; Tanaka, T.; Cheng, Y.; Chen, Y. Fault diagnosis based on current signature analysis for stator winding of Doubly Fed Induction Generator in wind turbine. In Proceedings of the 2014 International Symposium on Electrical Insulating Materials, Niigata, Japan, 1–5 June 2014; pp. 233–236. [Google Scholar] [CrossRef]
- Gritli, Y.; Stefani, A.; Filippetti, F.; Chatti, A. Stator fault analysis based on wavelet technique for wind turbines equipped with DFIG. In Proceedings of the IEEE International Conference on Clean Electrical Power (ICCEP), Capri, Italy, 9–11 June 2009; pp. 485–491. [Google Scholar] [CrossRef]
- Junqing, L.; Dong, W.; Long, H. Study of rotor winding inter-turn short circuit fault in doubly fed induction generator based on current signal spectrum analysis. In Proceedings of the International Conference on Electrical Machines and Systems (ICEMS), Busan, Republic of Korea, 26–29 October 2013; pp. 789–792. [Google Scholar] [CrossRef]
- Qin, P.; Zhang, Z.; Sun, Y.; Liu, H.; Ren, H. Vibration Analysis of DFIG Stator Winding Inter-turn Short Circuit Fault. In Proceedings of the 2018 International Conference on Information Systems and Computer Aided Education (ICISCAE), Changchun, China, 6–8 July 2018; pp. 436–442. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Y.; Liang, F.; Zhang, S.; Shahbaz, N.; Wang, S.; Zhao, Y.; Deng, W.; Cheng, Y. Incipient Fault Detection and Condition Assessment in DFIGs Based on External Leakage Flux Sensing and Modified Multiscale Poincare Plots Analysis. Meas. Sci. Technol. 2023, 35, 025007. [Google Scholar] [CrossRef]
- Vu, H.; Hammouri, H.; Yahoui, H. An experimental investigation of new electromagnetic field signal for stator asymmetric fault detection of doubly fed induction generators. Int. Trans. Electr. Energy Syst. 2019, 29, 12019. [Google Scholar] [CrossRef]
- Tavner, P. Review of condition monitoring of rotating electrical machines. IET Electr. Power Appl. 2008, 2, 215–247. [Google Scholar] [CrossRef]
- Abadi, M.B.; Cruz, S.M.A.; Gonçalves, A.P.; Gonçalves, P.F.C.; Mendes, A.M.S.; Ribeiro, A. Detection of stator and rotor faults in a DFIG based on the stator reactive power analysis. In Proceedings of the IECON 2014—40th Annual Conference of the IEEE Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2037–2043. [Google Scholar] [CrossRef]
- Rehman, A.U.; Jiao, W.; Sun, J.; Sohaib, M.; Jiang, Y.; Shahzadi, M.; Khan, M.I. Efficient fault detection of rotor minor inter-turn short circuit in induction machines using wavelet transform and empirical mode decomposition. Sensors 2023, 23, 7109. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, J.; Xu, Z.; Wang, S.; Fu, H. Feature Extraction and Applicability Comparisons for Fault Detection of Inter-Turn Short-Circuited PMSM. IEEE Trans. Instrum. Meas. 2024, 73, 3523810. [Google Scholar] [CrossRef]
- Wei, D.; Liu, K.; Huang, J.; Wang, J.; Zhou, S.; Cai, H.; Chen, J. Instantaneous Phase Estimation Based Single-Signal Diagnosis for Inter-Turn Short Circuit Fault in PMSMs. IEEE Trans. Energy Convers. 2024, 1–15. [Google Scholar] [CrossRef]
- Wei, D.; Liu, K.; Zhu, Z.Q.; Zhou, S.; Wang, J.; Chen, Y. Rotor speed signature analysis-based inter-turn short circuit fault detection for permanent magnet synchronous machines. IET Electr. Power Appl. 2024, 18, 1187–1199. [Google Scholar] [CrossRef]
- Singh, G.; Kumar, T.C.A.; Naikan, V.N.A. Induction motor inter-turn fault detection using infrared thermographic analysis. Infrared Phys. Technol. 2016, 77, 277–282. [Google Scholar] [CrossRef]
- Lopez-Perez, D.; Antonino-Daviu, J. Application of infrared thermography to failure detection in industrial induction motors: Case stories. IEEE Trans. Ind. Appl. 2017, 53, 1901–1908. [Google Scholar] [CrossRef]
- Garcia-Ramirez, A.G.; Morales-Hernandez, L.A.; Osornio-Rios, R.A.; Benitez-Rangel, J.P.; Garcia-Perez, A.; de Jesus Romero-Troncoso, R. Fault detection in induction motors and the impact on the kinematic chain through thermographic analysis. Electr. Power Syst. Res. 2014, 114, 1–9. [Google Scholar] [CrossRef]
- Antonino-Daviu, J.; Zamudio-Ramírez, I.; Osornio-Ríos, R.A.; Fuster-Roig, V.; Romero-Troncoso, R.J.; Dunai, L.D. Stray Flux Analysis for the Detection of Rotor Failures in Wound Rotor Induction Motors. In Proceedings of the IECON 2019—45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; pp. 3704–3709. [Google Scholar] [CrossRef]
- Kia, S.H. Monitoring of wound rotor induction machines by means of discrete wavelet transform. Electr. Power Compon. Syst. 2018, 46, 2021–2035. [Google Scholar] [CrossRef]
- Wang, M.; Song, Q.; Lai, W. On Model-Based Transfer Learning Method for the Detection of Inter-Turn Short Circuit Faults in PMSM. Sensors 2023, 23, 9145. [Google Scholar] [CrossRef] [PubMed]
- Urresty, J.C.; Riba, J.R.; Romeral, L. Application of the zero-sequence voltage component to detect stator winding inter-turn faults in PMSMs. Electr. Power Syst. Res. 2012, 89, 38–44. [Google Scholar] [CrossRef]
- Bellini, A.; Filippetti, F.; Franceschini, G.; Tassoni, C. Closed-loop control impact on the diagnosis of induction motor faults. IEEE Trans. Ind. Appl. 2000, 36, 1318–1329. [Google Scholar] [CrossRef]
- Kang, Y.; Kang, H.; Lee, J. D-q equivalent circuit-based protection algorithm for a doubly-fed induction generator in the time domain. J. Electr. Eng. Technol. 2010, 5, 371–378. [Google Scholar] [CrossRef]
- Stefani, A.; Yazidi, A.; Rossi, C.; Filippetti, F.; Casadei, D.; Capolino, G.-A. Doubly Fed Induction Machines Diagnosis Based on Signature Analysis of Rotor Modulating Signals. IEEE Trans. Ind. Appl. 2008, 44, 1711–1721. [Google Scholar] [CrossRef]
- Zaggout, M.; Tavner, P.J.; Crabtree, C.J.; Ran, L. Detection of rotor electrical asymmetry in wind turbine doubly-fed induction generators. IET Renew. Power Gener. 2014, 8, 878–886. [Google Scholar] [CrossRef]
- Hamatwi, E.; Barendse, P.; Khan, A. Evaluating the Interturn and Eccentricity Fault Indices in the Stator Current and the Embedded Controller Signals of a Micro-DFIG. IEEE Trans. Ind. Appl. 2024, 61, 25–36. [Google Scholar] [CrossRef]
- Kamarzarrin, M.; Refan, M.H.; Amiri, P.; Dameshghi, A. Fault diagnosis of wind turbine double-fed induction generator based on multi-level fusion and measurement of back-to-back converter current signal. Iran. J. Electr. Electron. Eng. 2022, 18, 26–34. [Google Scholar]
- Urresty, J.-C.; Riba, J.-R.; Saavedra, H.; Romeral, L. Detection of inter-turns short circuits in permanent magnet synchronous motors operating under transient conditions by means of the zero sequence voltage. In Proceedings of the 2011 14th European Conference on Power Electronics and Applications, Birmingham, UK, 30 August–1 September 2011; pp. 1–9. [Google Scholar]
- Ma, H.; Zhang, Y.; Li, S.; Tang, Z.; Zhang, Z. Research on fault diagnosis of asymmetric stator winding for doubly-fed induction generators. In IOP Conference Series: Earth and Environmental Science, Proceedings of the International Conference on Energy Engineering and Environmental Protection (EEEP2017), Sanya, China, 20–22 November 2017; IOP Publishing: Bristol, UK, 2017; Volume 121, p. 042024. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Y.; Liang, F.; Zhang, S.; Shahbaz, N.; Wang, S.; Zhao, Y.; Deng, W.; Cheng, Y. Identifying Early Stator Fault Severity in DFIGs based on Adaptive Feature Mode Decomposition and Multiscale Complex Component Current Trajectories. IEEE Trans. Instrum. Meas. 2024, 73, 1–16. [Google Scholar] [CrossRef]
- Dongare, U.V.; Umre, B.S.; Ballal, M.S. Rotor winding inter-turn short-circuit fault detection in wound rotor induction motors using Wing Technique. J. Power Electron. 2022, 22, 614–628. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Cheng, M.; Huang, J. Online Interturn Fault Diagnosis of Permanent Magnet Synchronous Machine Using Zero-Sequence Components. IEEE Trans. Power Electron. 2015, 30, 6731–6741. [Google Scholar] [CrossRef]
- Schmidt, E.; Sušić, M.; Eilenberger, A. Design Studies on a Permanent Magnet Synchronous Machine with Y- and Δ-Connected Stator Winding. In Proceedings of the Digests of the 2010 14th Biennial IEEE Conference on Electromagnetic Field Computation, Chicago, IL, USA, 9–12 May 2010. [Google Scholar]
- Rehman, A.U.; Chen, Y.; Wang, L.; Zhao, Y.; Cheng, Y.; Tanaka, T. Simulation using MATLAB/Simulink on rotor winding inter-turn short circuit fault in DFIG. In Proceedings of the 2016 IEEE International Conference on Dielectrics (ICD), Montpellier, France, 3–7 July 2016; pp. 506–509. [Google Scholar]
- Dinkhauser, V.; Fuchs, F.W. Rotor turn-to-turn faults of doubly-fed induction generators in wind energy plants—Modelling, simulation and detection. In Proceedings of the 2008 IEEE 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 1819–1826. [Google Scholar]
- Bebars, A.D.; Eladl, A.A.; Abdulsalam, G.M.; Badran, E.A. Internal electrical fault detection techniques in DFIG-based wind turbines: A review. Prot. Control Mod. Power Syst. 2022, 7, 1–22. [Google Scholar] [CrossRef]
- Hernández-Mayoral, E.; Iracheta-Cortez, R.; Lecheppe, V.; Salgado, O.A.J. Modelling and Validation of a Grid-Connected DFIG by Exploiting the Frequency-Domain Harmonic Analysis. Appl. Sci. 2020, 10, 9014. [Google Scholar] [CrossRef]



| Method | Machine | ITSC Winding | Analytical Evaluation | Fault Position | Super-Synch. Mode | Frequency |
|---|---|---|---|---|---|---|
| Stator current analysis [3,7,15] | DFIG | stator | No | No | No | Fixed |
| Rotor current analysis [12,14] | DFIG | stator | No | No | No | Fixed |
| Currents/torque signal analysis [21] | DFIG | rotor | No | No | No | Fixed |
| Vibration signal analysis [16] | DFIG | stator | Yes | No | No | Fixed |
| Stator reactive power analysis [20] | DFIG | stator | Yes | No | No | Fixed |
| winding temperature analysis [25,27] | IM | stator | No | No | No | Fixed |
| Embedded control signal analysis [23,24] | PMSM | stator | Yes | No | No | Fixed |
| Embedded control signal analysis [36,37] | DFIG | rotor | Yes | No | Yes | dynamic |
| NSC * analysis [8,13] | DFIG | stator | Yes | Yes | No | Fixed |
| ZSV ** analysis [38] | PMSM | stator | No | No | No | Fixed |
| ZSC/NSC analysis [40] | DFIG | stator | No | No | No | Fixed |
| ZSV/ZSC analysis [42] | PMSM | stator | Yes | Yes | No | Fixed |
| ZSC analysis (present study) | DFIG | rotor | Yes | Yes | Yes | dynamic |
| Mode | Faulty Phase | dk0 = {da0, db0, dc0} | Position Indicator |
|---|---|---|---|
| Sub-synchronous (1 > s > 0) | Phase ‘a’ | {|δ|, |δ + 2π/3|, |δ + 2π/3|} | smallest da0 |
| Phase ‘b’ | {|δ + 2π/3|, |δ|, |δ + 4π/3|} | smallest db0 | |
| Phase ‘c’ | {|δ + 2π/3|, |δ + 4π/3|, |δ|} | smallest dc0 |
| Mode | Faulty Phase | sk0 = {sa0, sb0, sc0} | Position Indicator |
|---|---|---|---|
| Super-synchronous (0 > s > −1) | Phase ‘a’ | {|δ|, |δ + 2π/3|, |δ + 2π/3|} | smallest sa0 |
| Phase ‘b’ | {|δ + 2π/3|, |δ + 4π/3|, |δ|} | smallest sc0 | |
| Phase ‘c’ | {|δ + 2π/3|, |δ|, |δ + 4π/3|} | smallest sb0 |
| Property | Value | Property | Value |
|---|---|---|---|
| Rated power | 2 MW | Stator resistance | 0.00261 Ω |
| RMS stator voltage (L-L) | 690 V | Rotor resistance | 0.00292 Ω |
| RMS rotor voltage (L-L) | 207 V | Magnetizing inductance | 2.5 mH |
| RMS stator current | 1760 A | Stator leakage inductance | 87 µH |
| RMS rotor current | 1420 A | Rotor leakage inductance | 783 µH |
| Stator/rotor winding | Star/delta | Grid-side frequency | 50 Hz |
| Synchronous speed | 1500 r/min | Pole pairs | 2 |
| Stator-phase series turns | 333 | Rotor-phase series turns | 100 |
| µ | OC Scenario | Mag. and IPA of FC in ZSC | IPAs of FCs in Three-Phase Rotor Currents | dk0 = |θikr0 − θikr| | Diagnosis Result | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| I0M (A) | θi0 (deg.) | θiar (deg.) | θibr (deg.) | θicr (deg.) | da0 | db0 | dc0 | |||
| 0 | OC1 | 0.86 | 23.74 | 83.80 | −36.17 | −156.21 | I0M < ITH | Healthy rotor winding | ||
| OC2 | 0.58 | 46.04 | 77.47 | −42.49 | −162.54 | |||||
| OC3 | 0.85 | 83.78 | 91.64 | −28.31 | −148.38 | |||||
| 0.05 | OC1 | 34.37 | −44.33 | −24.41 | −143.77 | 95.44 | 19.92 | 99.44 | 139.77 | da0 is smallest; ITSC in phase ‘a’ |
| OC2 | 40.81 | 50.44 | 77.14 | −41.76 | −162.93 | 26.70 | 92.20 | 213.37 | ||
| OC3 | 50.06 | 44.78 | 90.56 | −27.04 | −148.57 | 45.78 | 71.81 | 193.35 | ||
| 0.02 | OC1 | 6.33 | −48.97 | −24.28 | −144.15 | 95.69 | 24.69 | 95.17 | 144.67 | da0 is smallest; ITSC in phase ‘a’ |
| OC2 | 7.67 | 63.39 | 77.45 | −42.37 | −162.63 | 14.06 | 105.75 | 226.01 | ||
| OC3 | 12.01 | 68.77 | 91.48 | −28.04 | −148.50 | 22.71 | 96.81 | 217.27 | ||
| 0.01 | OC1 | 2.06 | −66.13 | −24.27 | −144.20 | 95.73 | 41.86 | 78.07 | 161.86 | da0 is smallest; ITSC in phase ‘a’ |
| OC2 | 2.02 | 60.50 | 77.47 | −42.46 | −162.56 | 16.98 | 102.95 | 223.05 | ||
| OC3 | 3.31 | 80.31 | 91.62 | −28.26 | −148.40 | 11.31 | 108.57 | 228.71 | ||
| µ | OC Scenario | Mag. and IPA of FC in ZSC | IPAs of FCs in Three Phase Rotor Currents | sk0 = |θikr0 + θikr| | Diagnosis Result | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| I0M (A) | θi0 (deg.) | θiar (deg.) | θibr (deg.) | θicr (deg.) | sa0 | sb0 | sc0 | |||
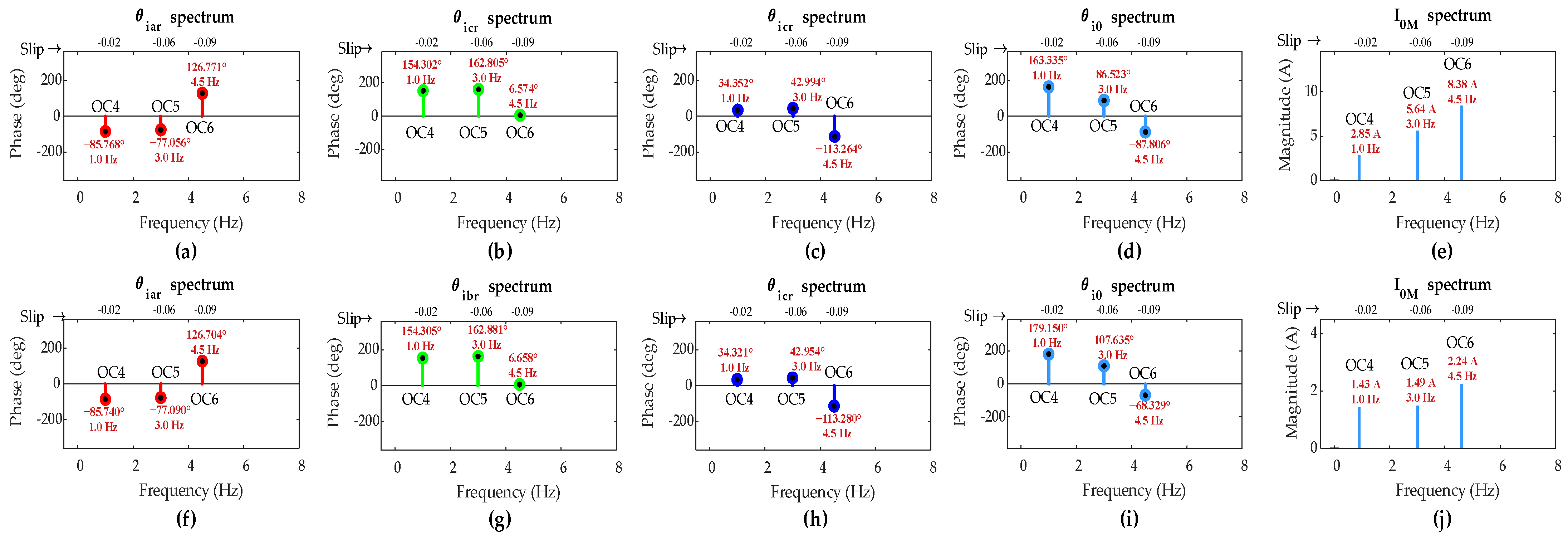
| 0 | OC4 | 0.45 | −169.97 | −85.72 | 154.30 | 34.31 | I0M < ITH | Healthy rotor winding | ||
| OC5 | 0.59 | 126.09 | −77.09 | 162.90 | 42.94 | |||||
| OC6 | 0.72 | −51.25 | 126.69 | 6.68 | −113.29 | |||||
| 0.05 | OC4 | 8.74 | 123.09 | −85.81 | 154.19 | 34.50 | 37.29 | 277.28 | 157.59 | sa0 is smallest; ITSC in phase ‘a’ |
| OC5 | 28.78 | 57.80 | −76.71 | 162.40 | 43.04 | 18.90 | 220.20 | 100.85 | ||
| OC6 | 36.99 | −116.62 | 127.18 | 6.25 | −113.35 | 10.56 | 110.35 | 229.97 | ||
| 0.02 | OC4 | 2.85 | 163.34 | −85.77 | 154.30 | 34.35 | 77.57 | 317.64 | 197.69 | sa0 is smallest; ITSC in phase ‘a’ |
| OC5 | 5.64 | 86.52 | −77.06 | 162.81 | 42.99 | 9.47 | 249.33 | 129.52 | ||
| OC6 | 8.38 | −87.81 | 126.77 | 6.57 | −113.26 | 38.97 | 201.07 | 44.81 | ||
| 0.01 | OC4 | 1.43 | 179.15 | −85.74 | 154.31 | 34.32 | 93.41 | 333.46 | 213.47 | sa0 is smallest; ITSC in phase ‘a’ |
| OC5 | 1.49 | 107.63 | −77.09 | 162.88 | 42.95 | 29.74 | 270.52 | 150.59 | ||
| OC6 | 2.24 | −68.33 | 126.70 | 6.58 | −113.28 | 58.38 | 61.67 | 181.61 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aziz, M.S.; Zhang, J.; Ruzimov, S.; Huang, X. Detection and Localization of Rotor Winding Inter-Turn Short Circuit Fault in DFIG Using Zero-Sequence Current Component Under Variable Operating Conditions. Sensors 2025, 25, 2815. https://doi.org/10.3390/s25092815
Aziz MS, Zhang J, Ruzimov S, Huang X. Detection and Localization of Rotor Winding Inter-Turn Short Circuit Fault in DFIG Using Zero-Sequence Current Component Under Variable Operating Conditions. Sensors. 2025; 25(9):2815. https://doi.org/10.3390/s25092815
Chicago/Turabian StyleAziz, Muhammad Shahzad, Jianzhong Zhang, Sarvarbek Ruzimov, and Xu Huang. 2025. "Detection and Localization of Rotor Winding Inter-Turn Short Circuit Fault in DFIG Using Zero-Sequence Current Component Under Variable Operating Conditions" Sensors 25, no. 9: 2815. https://doi.org/10.3390/s25092815
APA StyleAziz, M. S., Zhang, J., Ruzimov, S., & Huang, X. (2025). Detection and Localization of Rotor Winding Inter-Turn Short Circuit Fault in DFIG Using Zero-Sequence Current Component Under Variable Operating Conditions. Sensors, 25(9), 2815. https://doi.org/10.3390/s25092815






