Misalignment Effects on Power Gathered by Optical Fiber Pyrometer
Highlights
- A model to ensure proper pyrometer alignment and avoid errors in off-axis pyrometers, based on analyzing the power gathered by the optical fiber.
- The limits on lateral displacements and required tilting angle on off-axis pyrometers for proper measurements.
- High-temperature measurements are crucial in advanced manufacturing requiring non-contact measurement techniques capable of withstanding harsh conditions.
- The new model will be key in future installations to obtain accurate measurements in many applications, including additive manufacturing.
Abstract
1. Introduction
2. Theoretical Basis and Model Development
3. Simulation and Discussion
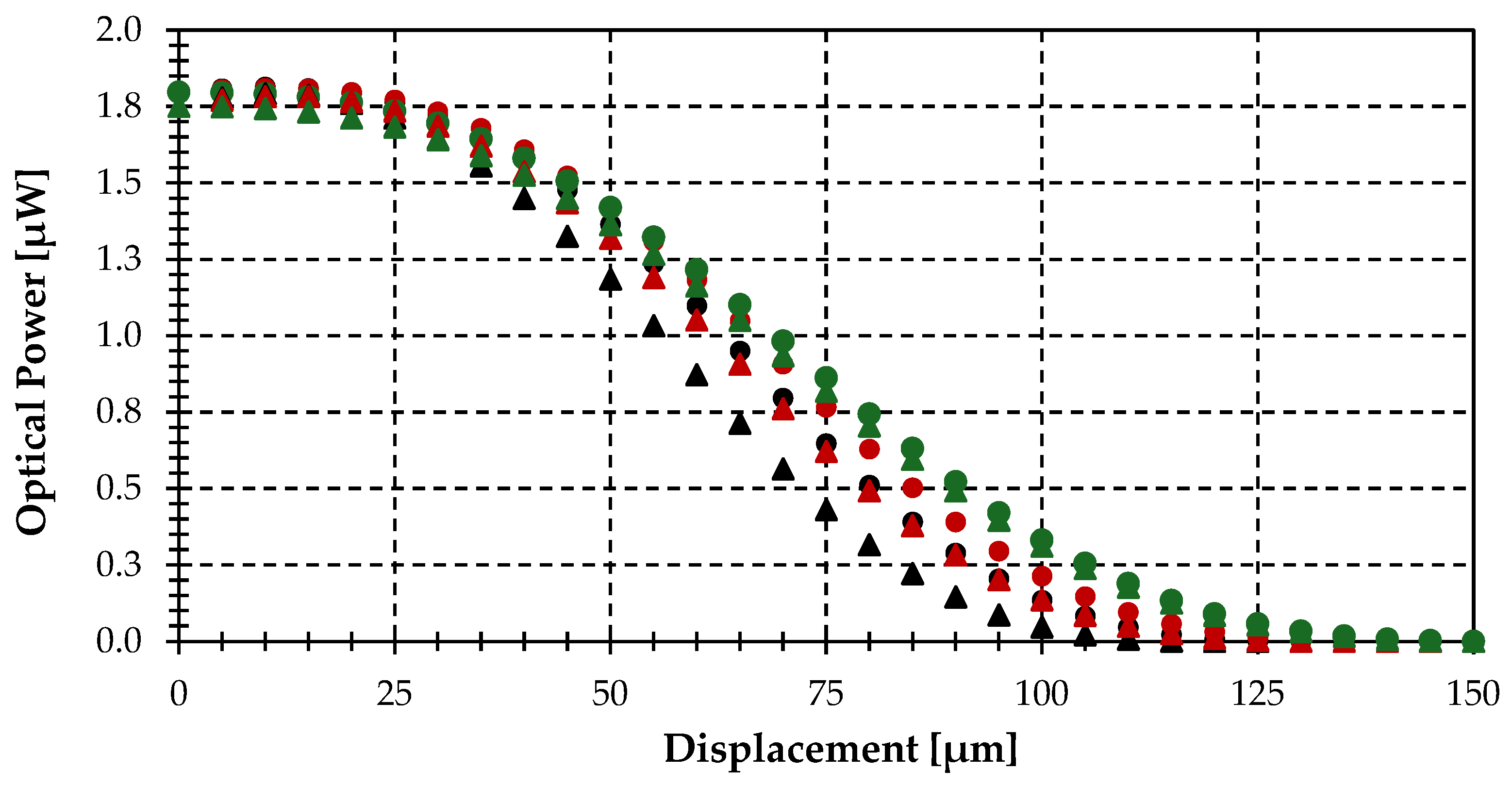
3.1. Robustness of the Misalignment Model
3.2. Combined Tilting and Lateral Misalignment Effects
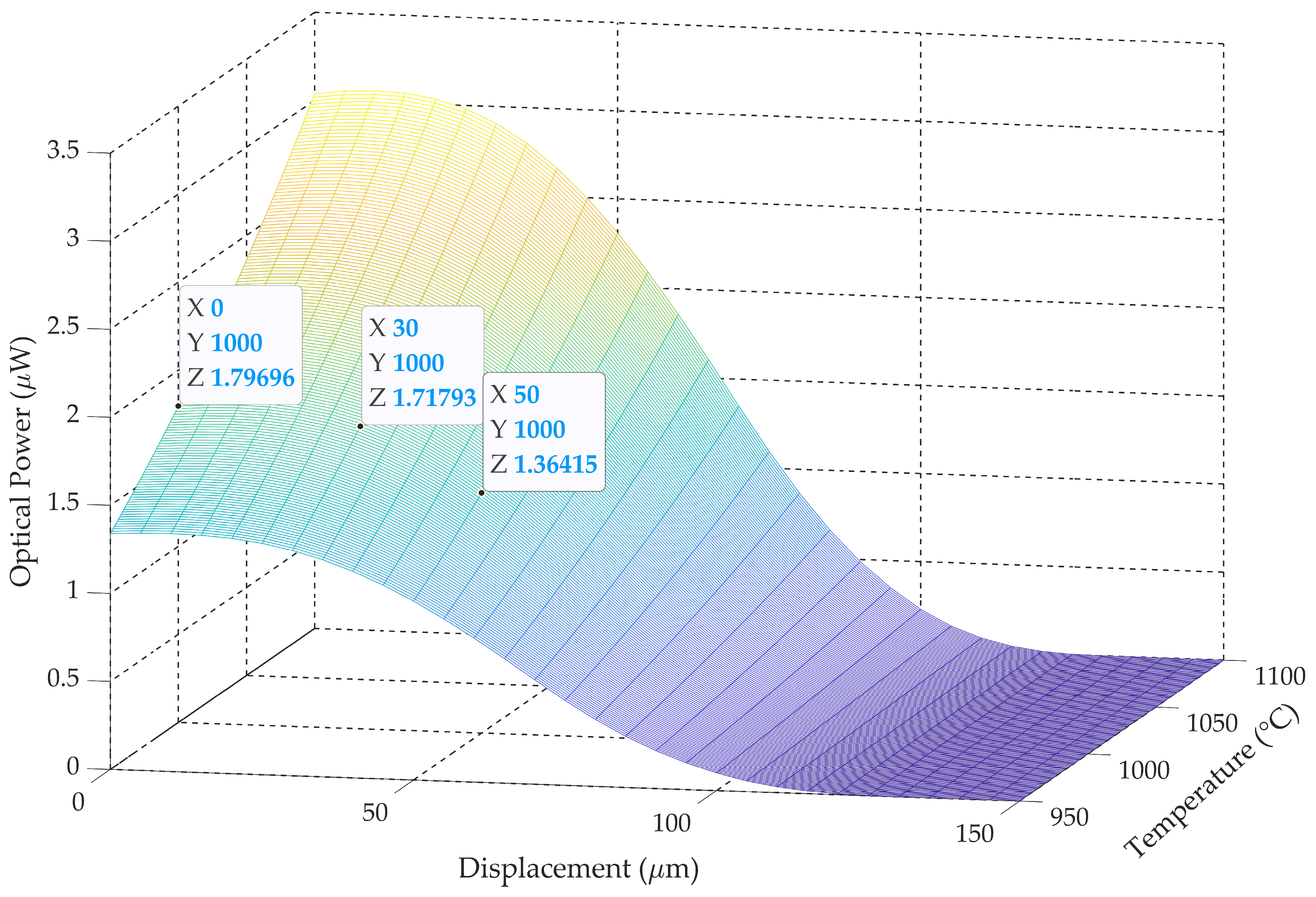
3.3. Temperature Error Analysis and Model Limitations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, P.; Lin, B.; Zhou, J.; Lv, B.; Li, J.; Zhang, J.; Wang, L.; Sui, T. Review of grinding temperature theory and measurement for the needs of the times: Promoting the development of advanced manufacturing. J. Mater. Process. Technol. 2025, 337, 118744. [Google Scholar] [CrossRef]
- Mitrašinović, A.; Đurđević, T.; Nešković, J.; Radosavljević, M. Temperature Monitoring in Metal Additive Manufacturing in the Era of Industry 4.0. Technologies 2025, 13, 317. [Google Scholar] [CrossRef]
- Usamentiaga, R.; Garcia, D.F.; Pérez, J.M. High-Speed Temperature Monitoring for Steel Strips Using Infrared Line Scanners. IEEE Trans. Ind. Appl. 2020, 56, 3261–3271. [Google Scholar] [CrossRef]
- Tapetado, A.; Díaz-Álvarez, J.; Miguélez, M.H.; Vázquez, C. Two-Color Pyrometer for Process Temperature Measurement During Machining. J. Lightw. Technol. 2016, 34, 1380–1386. [Google Scholar] [CrossRef]
- Öner, B.; Pomeroy, J.W.; Kuball, M. Submicrometer Resolution Hyperspectral Quantum Rod Thermal Imaging of Microelectronic Devices. ACS Appl. Electron. Mater. 2019, 2, 93–102. [Google Scholar] [CrossRef]
- Usamentiaga, R.; García, D.F.; Molleda, J.; Bulnes, F.G.; Pérez, J.M. Temperature Measurement Using the Wedge Method: Comparison and Application to Emissivity Estimation and Compensation. IEEE Trans. Instrum. Meas. 2011, 60, 1768–1778. [Google Scholar] [CrossRef]
- Misra, S.; Mohanty, I.; Raza, M.S.; Chakraborty, R.; Chatterjee, P.; Gopal, M.; Ponkshe, S.; Saha, P.; Kumar, C.S. Investigation of IR pyrometer-captured thermal signatures and their role on microstructural evolution and properties of Inconel 625 tracks in DED-based additive manufacturing. Surf. Coat. Technol. 2022, 447, 128818. [Google Scholar] [CrossRef]
- Herzog, T.; Brandt, M.; Trinchi, A.; Sola, A.; Molotnikov, A. Process monitoring and machine learning for defect detection in laser-based metal additive manufacturing. J. Intell. Manuf. 2024, 35, 1407–1437. [Google Scholar] [CrossRef]
- Wu, J.; Li, J.; Li, J.; Zhou, X.; Weng, J.; Liu, S.; Tao, T.; Ma, H.; Tang, L.; Gao, Z.; et al. A sub-nanosecond pyrometer with broadband spectral channels for temperature measurement of dynamic compression experiments. Measurement 2022, 195, 111147. [Google Scholar] [CrossRef]
- Traunecker, D.; Jarwitz, M.; Michalowski, A. Correcting the Influence of the Angle-Dependent Emissivity on Pyrometric Temperature Measurements for Laser Processes. Lasers Manuf. Mater. Process. 2025, 12, 98–111. [Google Scholar] [CrossRef]
- Warren, T.J.; Bowles, N.E.; Hanna, K.D.; Bandfield, J.L. Modeling the angular dependence of emissivity of randomly rough surfaces. J. Geophys. Res. Planets 2019, 124, 585–601. [Google Scholar] [CrossRef]
- Núñez-Cascajero, A.; Tapetado, A.; Vázquez, C. High spatial resolution optical fiber two colour pyrometer with fast response. IEEE Sens. J. 2021, 21, 2942. [Google Scholar] [CrossRef]
- Núñez-Cascajero, A.; Tapetado, A.; Vargas, S.; Vázquez, C. Optical Fiber Pyrometer Designs for Temperature Measurements Depending on Object Size. Sensors 2021, 21, 646. [Google Scholar] [CrossRef] [PubMed]
- Safarloo, S.; Tapetado, A.; Vázquez, C. Experimental Validation of High Spatial Resolution of Two-Color Optical Fiber Pyrometer. Sensors 2023, 23, 4320. [Google Scholar] [CrossRef]
- Vargas, S.; Tapetado, A.; Vázquez, C. Influence of Tilting Angle on Temperature Measurements of Different Object Sizes Using Fiber-Optic Pyrometers. Sensors 2023, 23, 8119. [Google Scholar] [CrossRef]
- Aretusini, S.; Núñez-Cascajero, A.; Spagnuolo, E.; Tapetado, A.; Vázquez, C.; Di Toro, G. Fast and Localized Temperature Measurements During Simulated Earthquakes in Carbonate Rocks. Geophys. Res. Lett. 2021, 48, e2020GL091856. [Google Scholar] [CrossRef] [PubMed]
- Aydogan, B.; Chou, K. Review of In Situ Detection and Ex Situ Characterization of Porosity in Laser Powder Bed Fusion Metal Additive Manufacturing. Metals 2024, 14, 669. [Google Scholar] [CrossRef]
- Li, T.; Long, H.; Shi, T.; Yang, J.; Duan, J. Cutting temperature measurement using a novel near-infrared two-color pyrometer under dry and wet cutting of Ti-6Al-4V alloy. J. Mater. Process. Technol. 2022, 309, 117751. [Google Scholar] [CrossRef]
- Koyano, T.; Takahashi, T.; Tsurutani, S.; Hosokawa, A.; Furumoto, T.; Hashimoto, Y. Temperature Measurement of Wire Electrode in Wire EDM by Two-color Pyrometer. Procedia CIRP 2018, 68, 96–99. [Google Scholar] [CrossRef]
- Opielka, D.; Rittich, D. Transmission loss caused by an angular misalignment between two multimode fibers with arbitrary profile exponents. Appl. Opt. 1983, 22, 991–994. [Google Scholar] [CrossRef]
- Gao, C.; Farrell, G. Power coupling between two step-index multimode fibers of different numerical apertures with an angular misalignment. Microw. Opt. Technol. Lett. 2004, 43, 231–234. [Google Scholar] [CrossRef][Green Version]
- Horiguchi, K.; Iikubo, T.; Hyakutake, Y.; Kobayashi, S.; Sugihara, O. Launch Light Design for Coupling Loss Measurement of Step-Index Multimode Fiber Connections. J. Lightw. Technol. 2021, 39, 2505–2513. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, X.; Hurley, J.E.; Dong, H.; Chen, H.; Li, M.J.; Liu, G.N. Large Core Multimode Fiber with High Tolerance to Coupling Misalignment and Dust Contamination in Intra-Vehicle Networks. Opt. Commun. 2024, 564, 130575. [Google Scholar] [CrossRef]
- Kam, W.; Ong, Y.S.; O’Keeffe, S.; Mohammed, W.S.; Lewis, E. An Analytical Model for Describing the Power Coupling Ratio between Multimode Fibers with Transverse Displacement and Angular Misalignment in an Optical Fiber Bend Sensor. Sensors 2019, 19, 4968. [Google Scholar] [CrossRef]
- Liu, J.; Wu, Z.; Zeng, Q.; Zhang, B.; Chen, J.; Xiao, J.; Ye, H.; Chen, Y.; Liu, J.; Zhou, X.; et al. Efficient Dynamic Free-Space-to-Fiber Coupling of Cylindrical Vector Beams via Twisted Moiré Meta-Devices. Commun. Phys. 2025, 8, 409. [Google Scholar] [CrossRef]
- Ramakrishnan, M.; Zhou, H.; Jiang, Z.; Su, X.; Duan, Y.; Alhaddad, A.; Ko, W.; Zeng, R.; Wang, Y.; Minoofar, A.; et al. Demonstration of Simultaneous Mitigation of Turbulence and Misalignment in a Free-Space Mode-Division-Multiplexed Optical Link Using Beam Shaping. J. Lightw. Technol. 2025, 43, 7551–7557. [Google Scholar] [CrossRef]
- Korzhyk, V.; Strohonov, D.; Gao, S.; Tereshchenko, O.; Demianov, O.; Ganushchak, O.; Wang, X. Production of spherical Inconel 625 powder for additive manufacturing by plasma-arc wire atomization: Influence of non-transferred and transferred arc modes on fine powder yield. Adv. Sci. Technol. Res. J. 2025, 19, 109–123. [Google Scholar] [CrossRef]
- Wang, M.; Salter, P.S.; Payne, F.P.; Shipley, A.; Dyson, I.N.; Liu, T.; Wang, T.; Zhang, K.; Zhang, J.; Jia, Z.; et al. Single-Mode Sapphire Fiber Temperature Sensor. J. Lightw. Technol. 2024, 42, 6409–6416. [Google Scholar] [CrossRef]
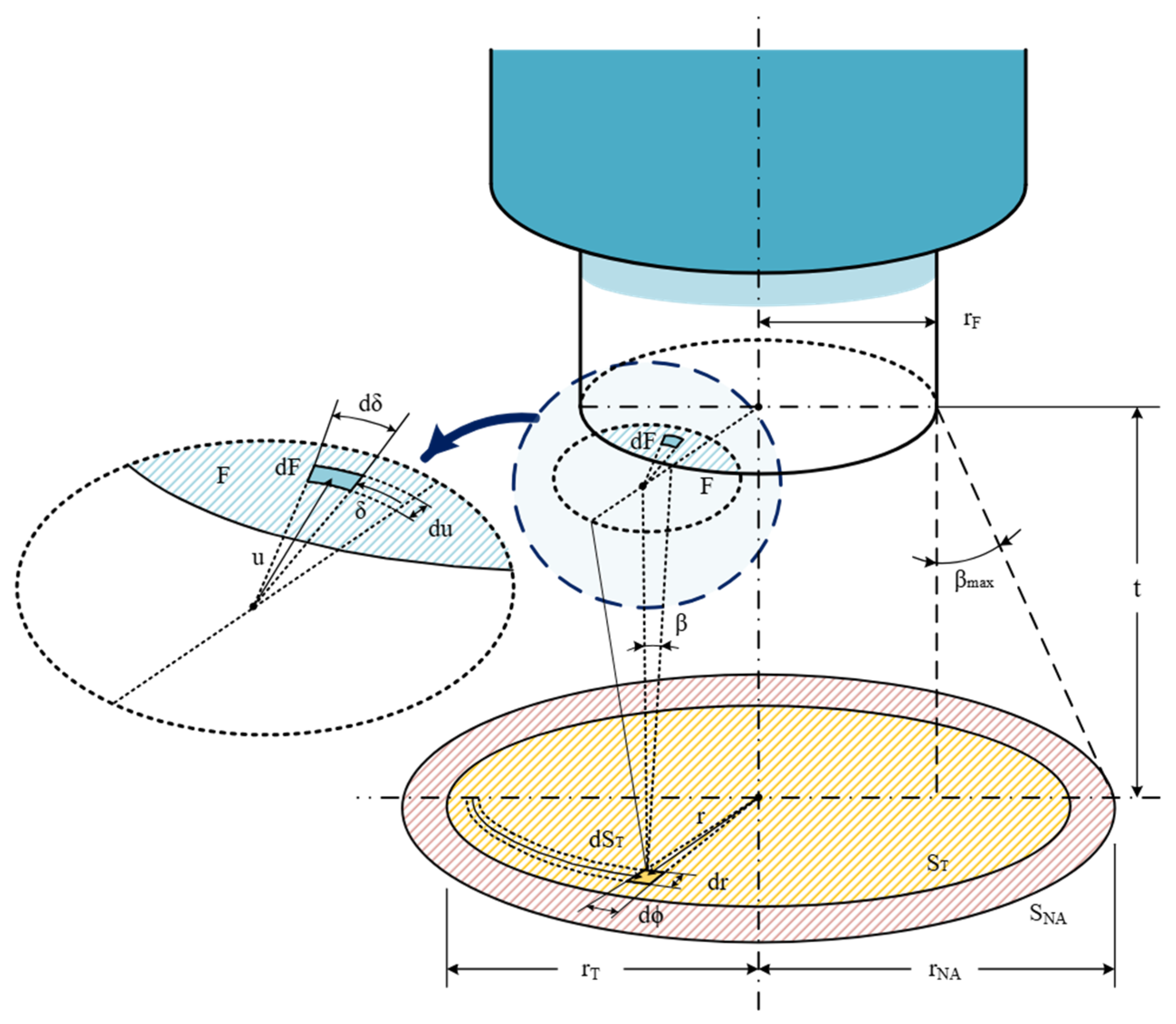
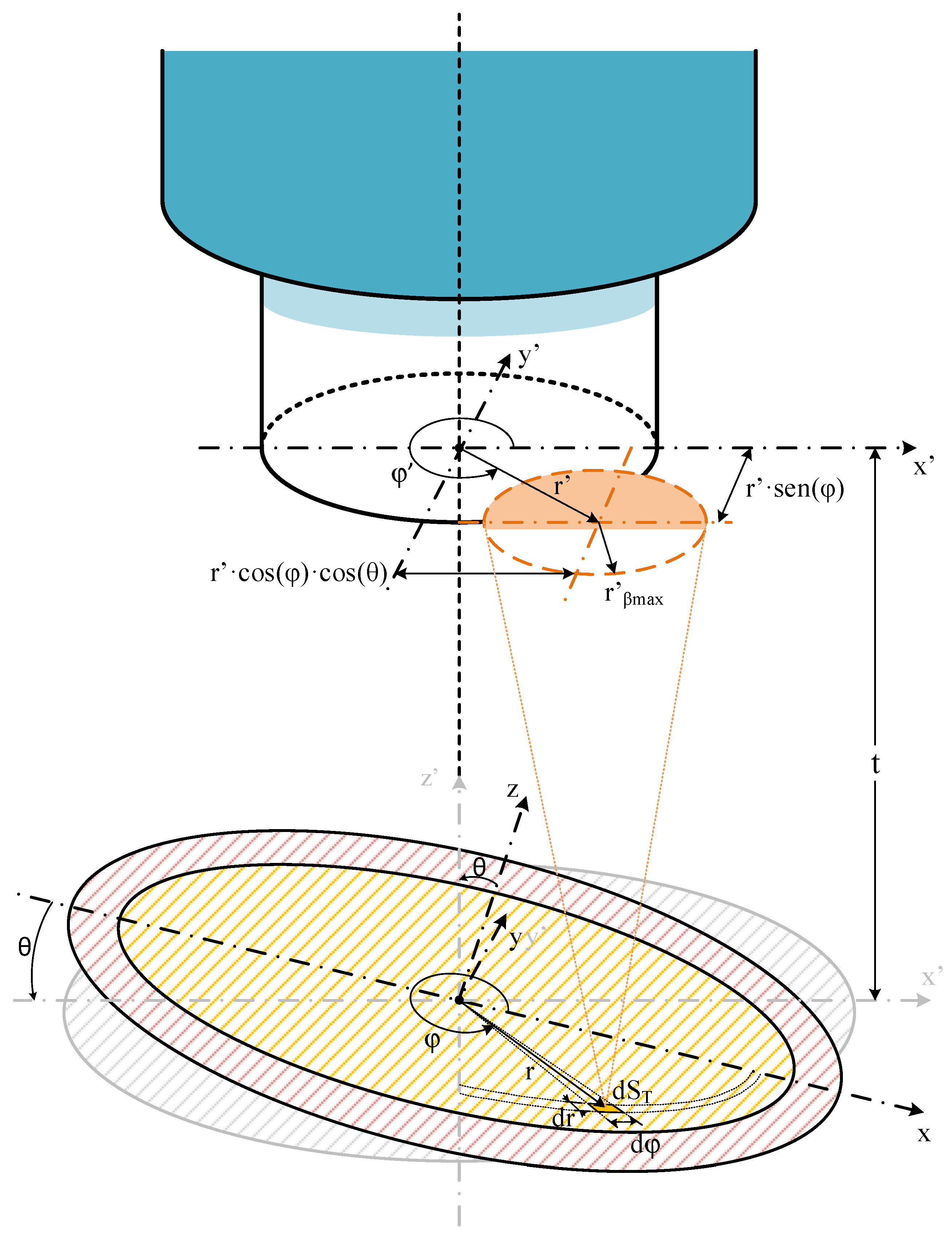
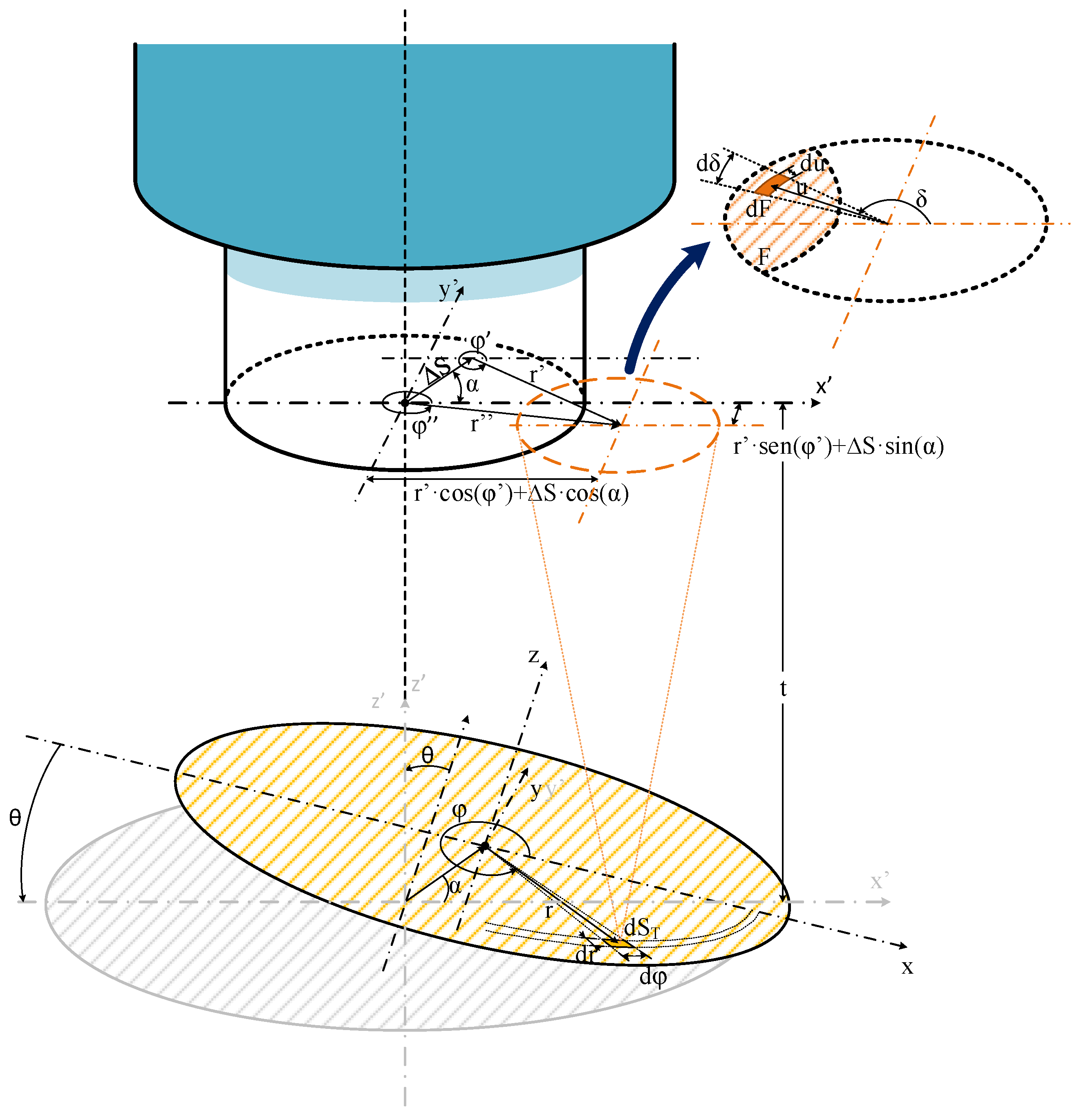

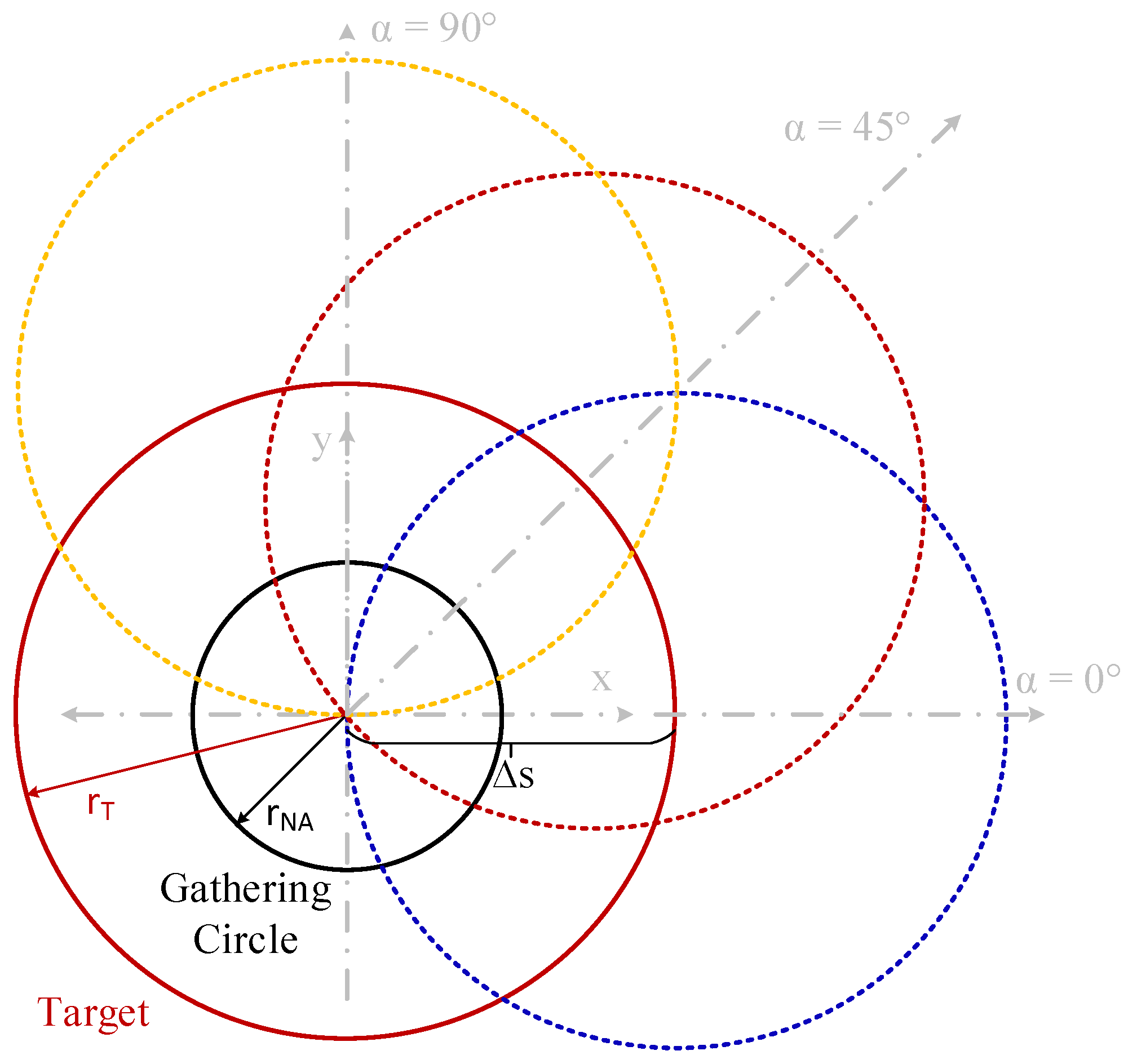
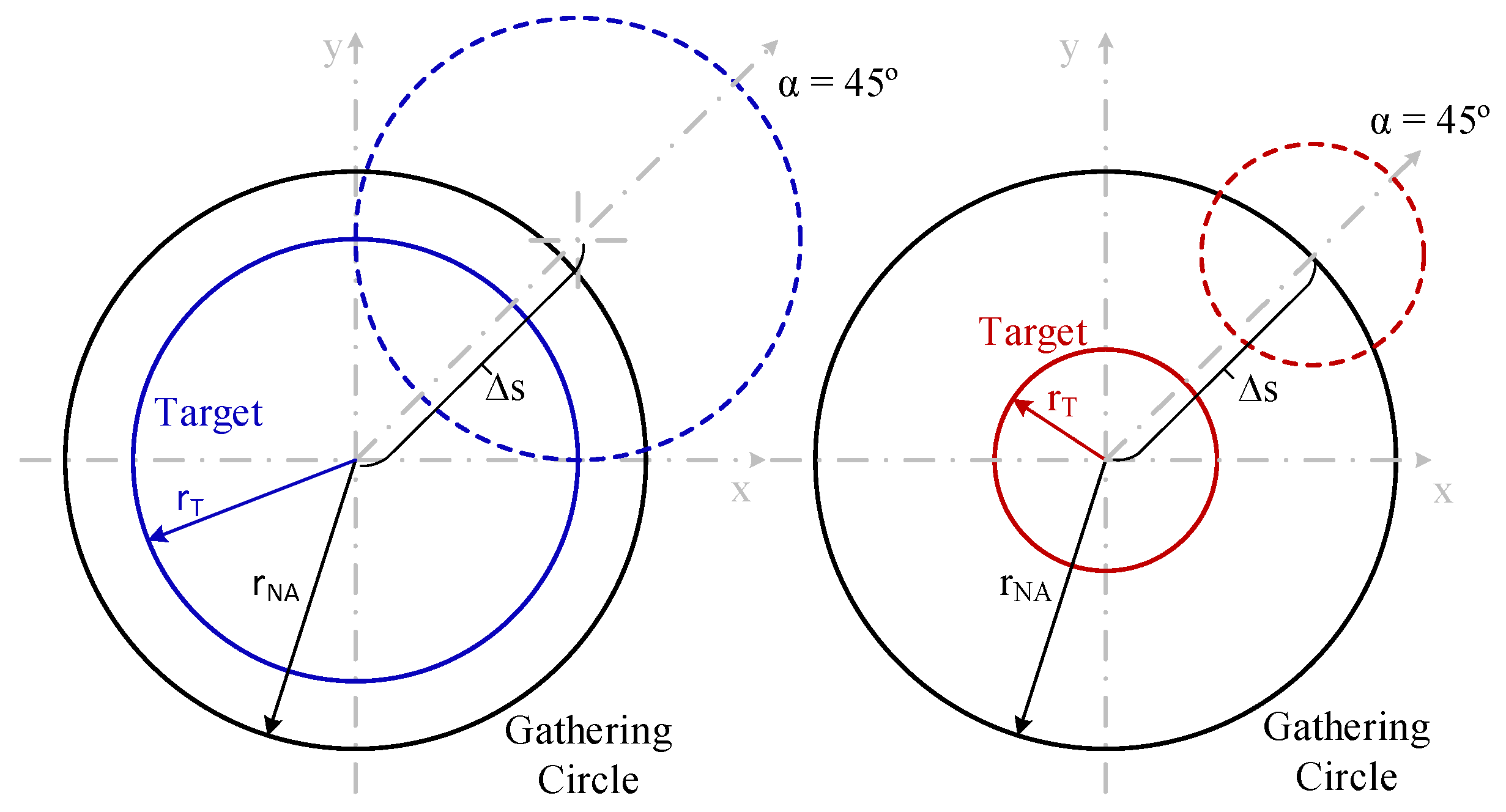

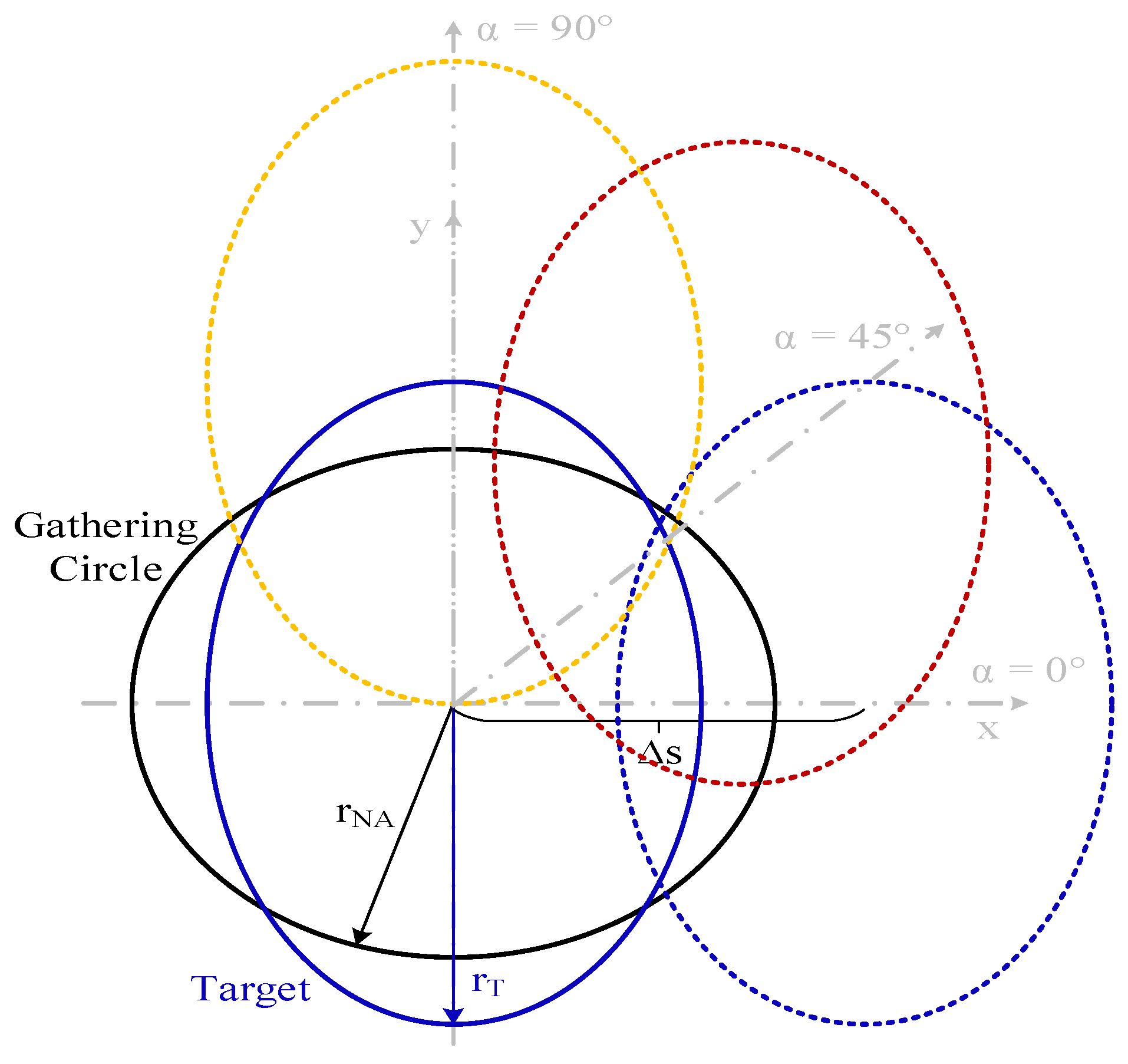
| Variable | Meaning | Variable | Meaning |
|---|---|---|---|
| dST | Differential element of the target surface | rT | Radius of the target |
| rF | Optical fiber (OF) core radius | β | Angle between the normal to dST and the vector from dST to each solid angle differential in the intersection of the circles with radii rF and rβmax or r′βmax |
| rβmax, r′βmax * | Radius of the circle defined by the light cone projection, due to OF NA | dF | Differential element of area of circle with radius rβmax or r′βmax |
| t, t′ * | Minimum distance from dST to fiber end plane on each model | u | Radial coordinate of each differential element of area dF |
| r | Radial coordinate of dST on the plane of the target | δ | Azimuthal coordinate of each differential element of area dF |
| r′ | Distance of the projected object center on the fiber end plane, to the center of a circle with radius rβmax or r′βmax | θ | Angle between the fiber axis and the normal to the emitting target surface |
| r″ | Distance between the centers of the circles with radii rF and r′βmax | ΔS | Displacement of the center of the target object, in a parallel plane to the fiber end plane (x′–y′) |
| φ | Azimuthal coordinate of dST on the target plane on each model | α | Angle of the direction of displacement of vector ΔS |
| φ′ | Angle between r′ and x-axis on the fiber end plane | rNA | Radius of the gathering circle defined by the OF field of view due to NA, on the target plane |
| φ″ | Angle between r″ and x-axis on the fiber end plane | βmax | Maximum acceptance angle OF |
| 0 < r″ < rF − r′βmax | rF − r′βmax < r″ < rF | rF < r″ < rF + r′βmax | ||||
|---|---|---|---|---|---|---|
| r′βmax < rF | Int. Sit. | Circum. | Circum. | Arcs | Arcs | |
| umin | 0 | 0 | rF − r″ | r″ − rF | ||
| umax | r′βmax | rF − r″ | r′βmax | r′βmax | ||
| rF < r′βmax < 2rF | Int. Sit. | Circum. | Arcs | Circum. | Arcs | Arcs |
| umin | 0 | rF − r″ | 0 | rF − r″ | r″ − rF | |
| umax | rF − r″ | rF + r″ | rF − r″ | r′βmax | r′βmax | |
| 2rF < r′βmax | Int. Sit. | Circum. | Arcs | Arcs | Arcs | |
| umin | 0 | rF − r″ | r″ − rF | r″ − rF | ||
| umax | rF − r″ | rF + r″ | r″ + rF | r′βmax | ||
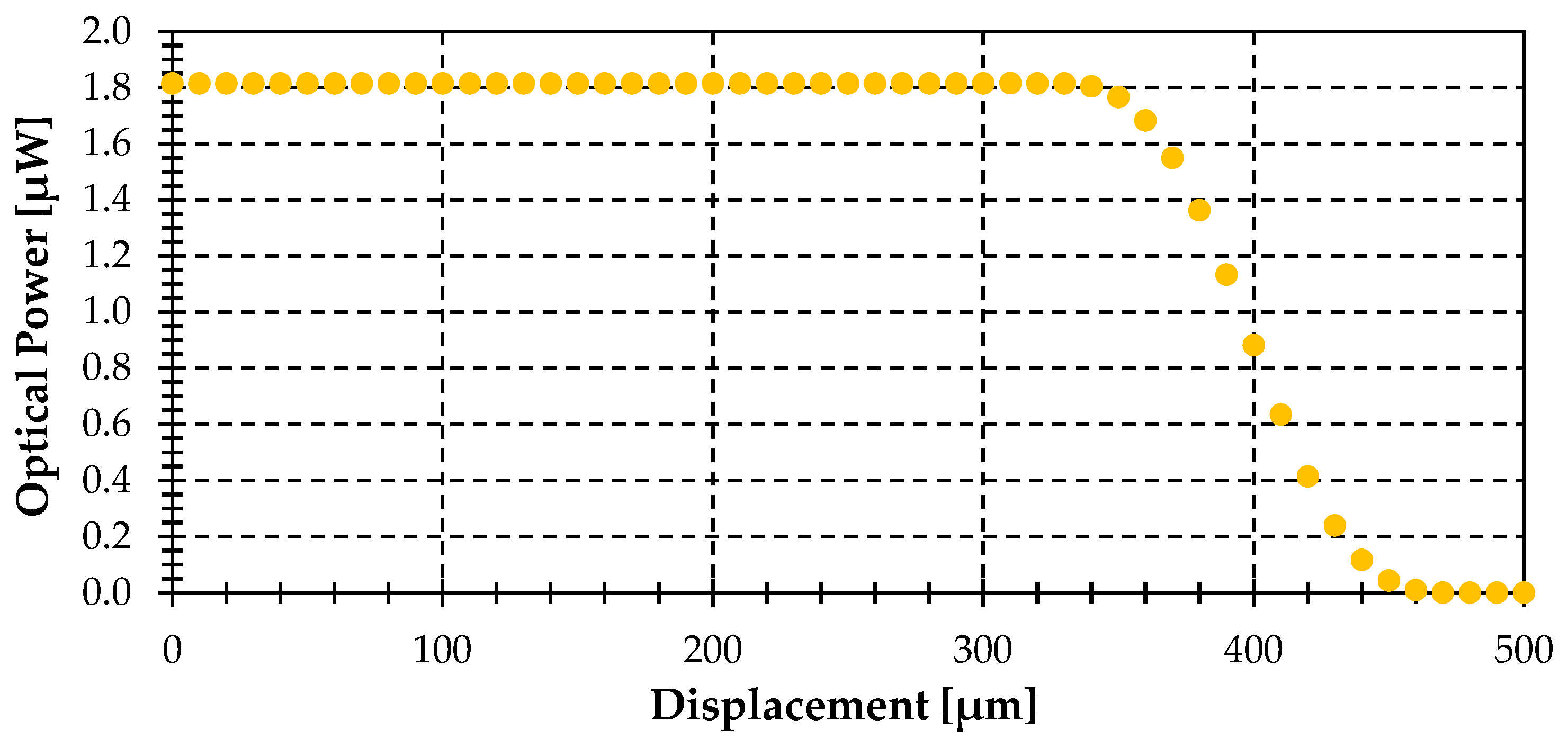
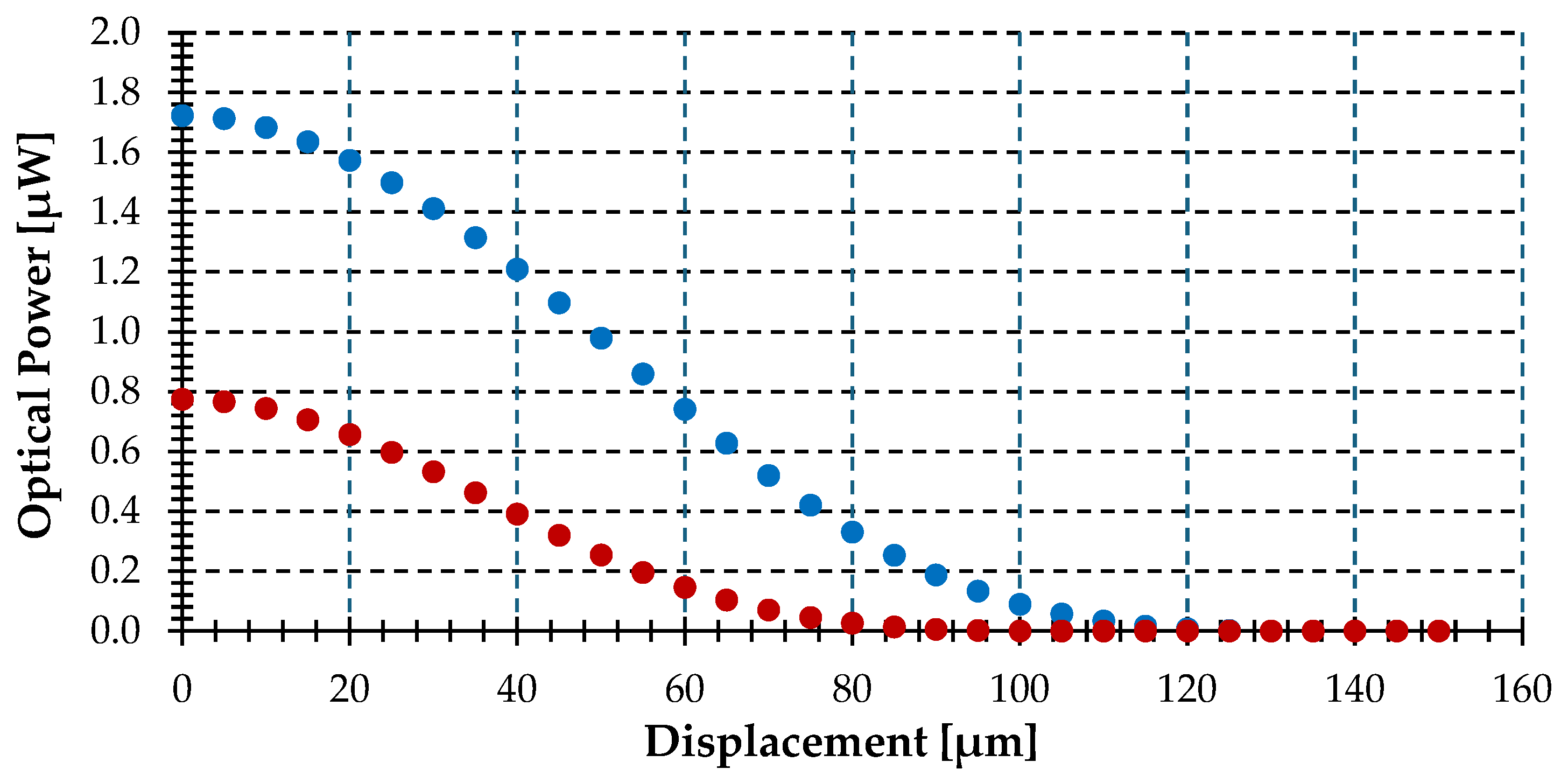
| Temperature (°C) | 998 | 990 | 951 |
|---|---|---|---|
| Optical power (μW) | 1.796 | 1.718 | 1.364 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas, S.; Tapetado, A.; Vázquez, C. Misalignment Effects on Power Gathered by Optical Fiber Pyrometer. Sensors 2025, 25, 7011. https://doi.org/10.3390/s25227011
Vargas S, Tapetado A, Vázquez C. Misalignment Effects on Power Gathered by Optical Fiber Pyrometer. Sensors. 2025; 25(22):7011. https://doi.org/10.3390/s25227011
Chicago/Turabian StyleVargas, Salvador, Alberto Tapetado, and Carmen Vázquez. 2025. "Misalignment Effects on Power Gathered by Optical Fiber Pyrometer" Sensors 25, no. 22: 7011. https://doi.org/10.3390/s25227011
APA StyleVargas, S., Tapetado, A., & Vázquez, C. (2025). Misalignment Effects on Power Gathered by Optical Fiber Pyrometer. Sensors, 25(22), 7011. https://doi.org/10.3390/s25227011








