Application of Optical Measurements to Assess Form Deviations of Cylindrical Parts Made Using FDM Additive Technology
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
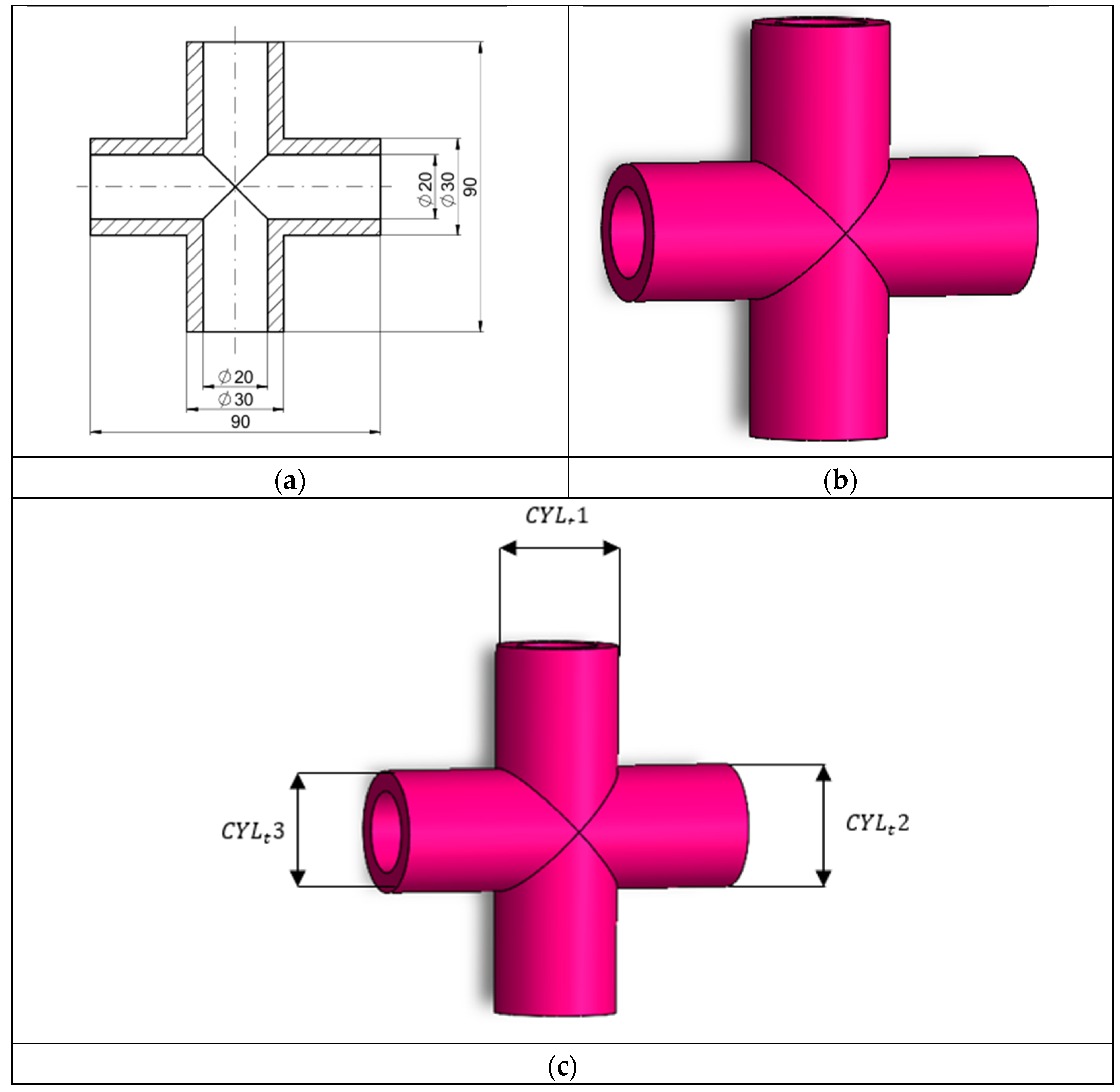
2.3. Research Model
2.4. Three-Dimensional Printing Technology
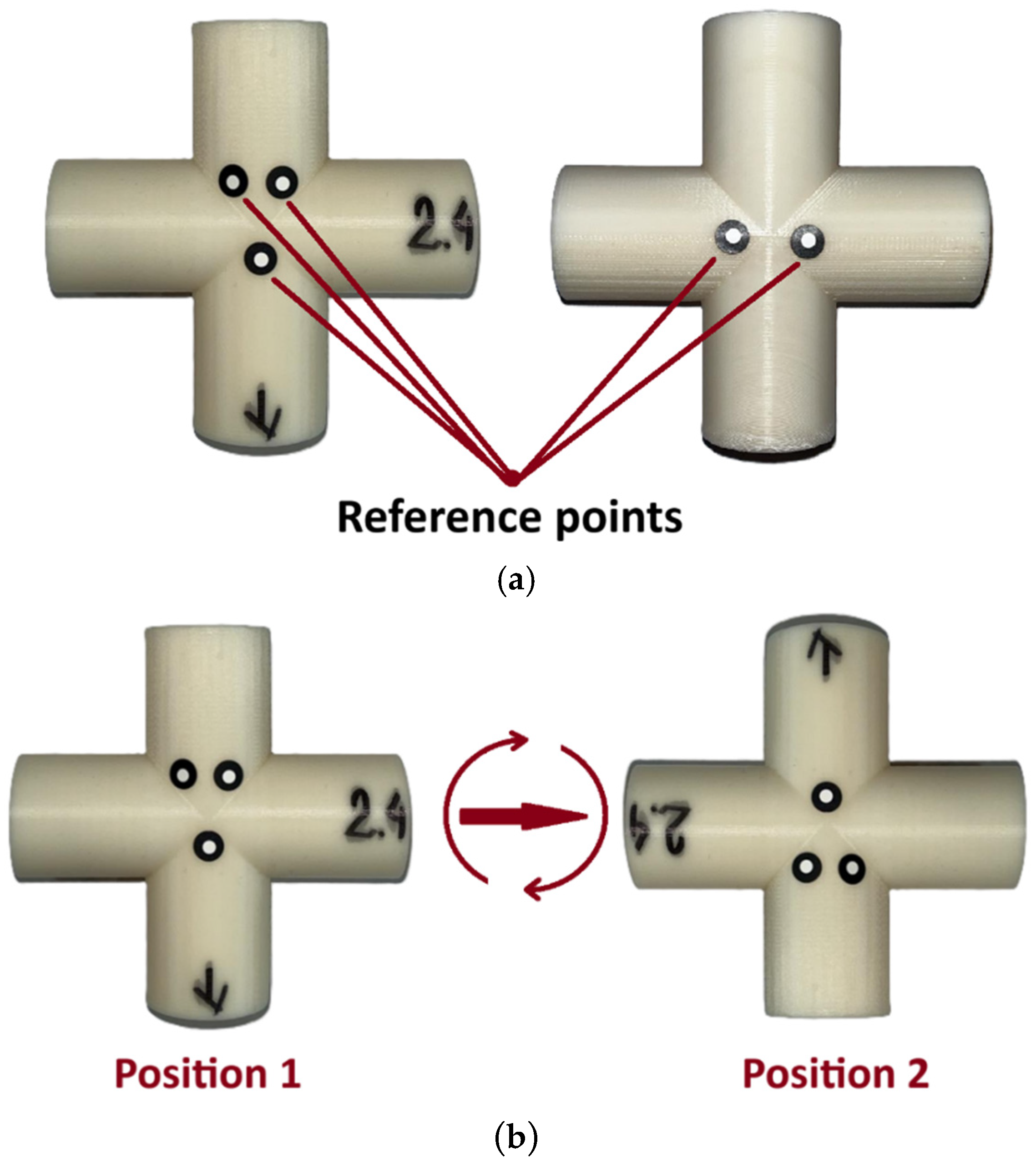
2.5. Measurement of Cylindricity and Roundness Deviation
3. Results and Discussion
4. Summary and Conclusions
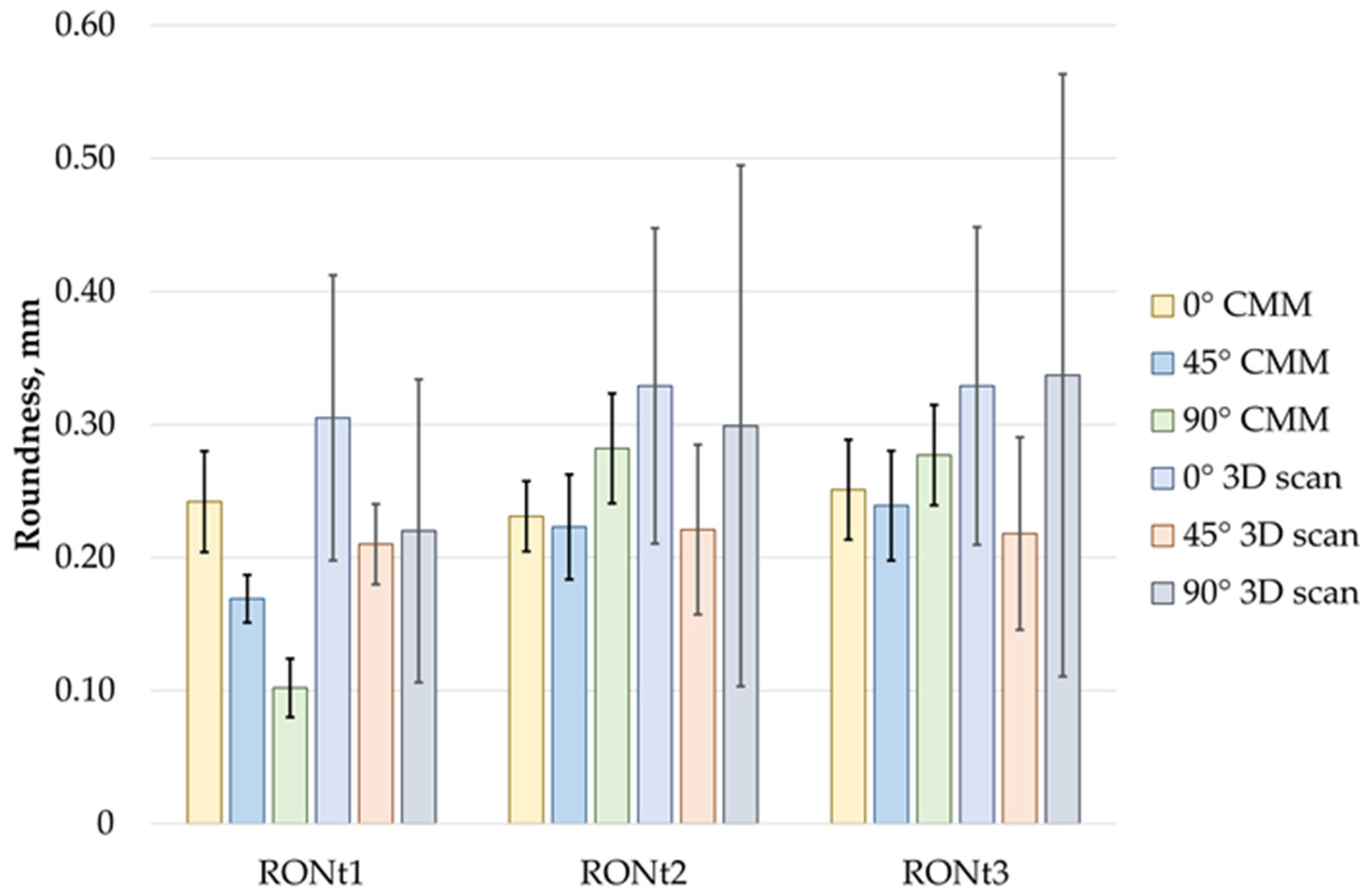
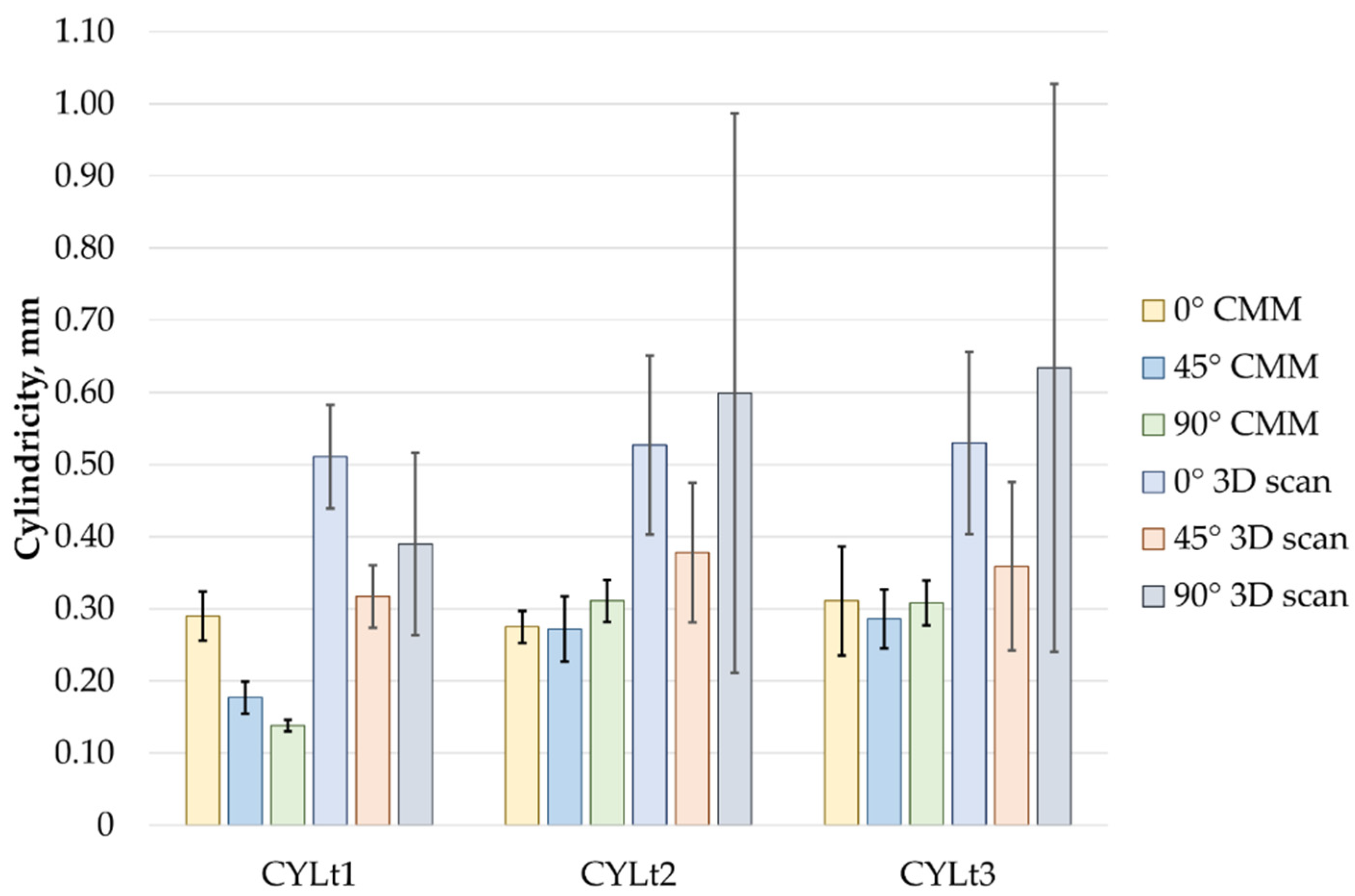
- Measurements obtained using the CMM were characterized by lower values compared to those obtained with 3D scanning.
- Analyzing roundness and cylindricity deviations of cylindrical components made using FDM technology in three different printing orientations (0°, 45°, 90°) clearly shows a dependence of geometric quality on the printing orientation. The largest deviations in both roundness and cylindricity were observed for the 90° printing direction, likely due to deformations resulting from the layer-by-layer material deposition and settling of successive layers.
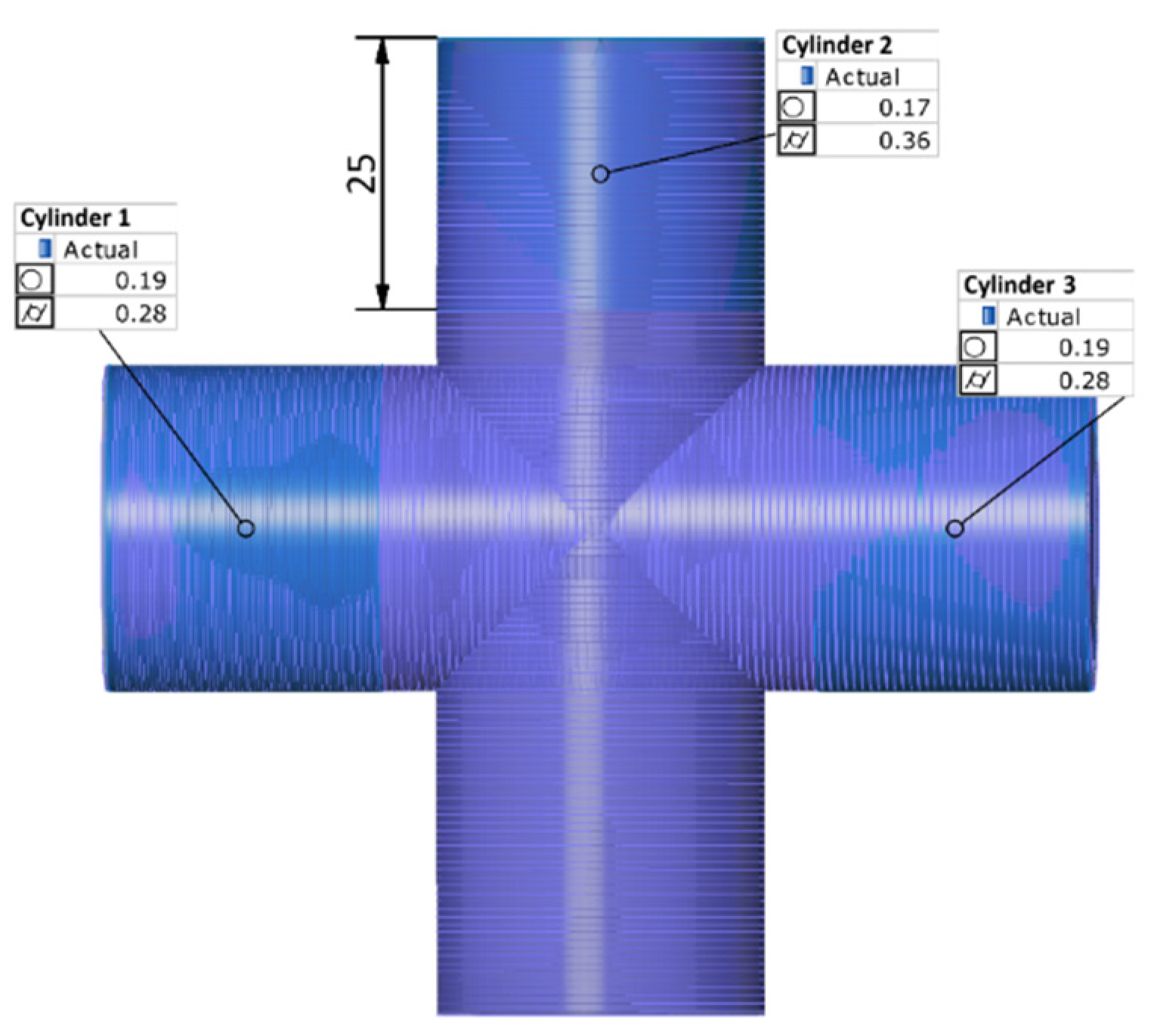
- Roundness and cylindricity measurements of cylindrical components produced by FDM technology clearly indicate that surface 3 exhibited the highest values for roundness and cylindricity deviations, regardless of the printing direction (0°, 45°, 90°) and the measurement method (CMM and 3D scanner). The smallest deviations were recorded for Feature 1, with minor exceptions that did not significantly impact the overall trend.
- Summarizing the results, it can be concluded that contact measurements with a CMM provide greater accuracy and repeatability than 3D scanning, which, in turn, offers faster and more comprehensive surface quality analysis, albeit with noticeably overestimated deviation values.
- The choice of measurement method should depend on the quality requirements for the intended application of the manufactured part. For high-accuracy requirements, contact measurements are recommended, while for parts with larger tolerances, optical measurements can be an effective alternative.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- PN-EN ISO/ASTM 52900:2022-05; Additive Manufacturing-General Rules-Basics and Vocabulary. Polish Committee for Standardization: Warsaw, Poland, 2022.
- Zhou, L.; Miller, J.; Vezza, J.; Mayster, M.; Raffay, M.; Justice, Q.; Tamimi, Z.A.; Hansotte, G.; Sunkara, L.D.; Bernat, J. Additive Manufacturing: A Comprehensive Review. Sensors 2024, 24, 2668. [Google Scholar] [CrossRef] [PubMed]
- Patel, R.; Desai, C.; Kushwah, S.; Mangrola, M.H. A review article on FDM process parameters in 3D printing for composite materials. Mater. Proc. 2022, 60 Pt 3, 2162–2166. [Google Scholar] [CrossRef]
- Minhaz, A.; Mohd, J.; Abid, H. A study on fused deposition modeling (FDM) and laser-based additive manufacturing (LBAM) in the medical field. Intell. Pharm. 2024, 2, 381–391. Available online: https://www.sciencedirect.com/science/article/pii/S2949866X24000339 (accessed on 14 July 2025).
- Sukindar, A.A.; Azhar, M.A.; Shaharuddin, S.I.S.; Kamaruddin, S.; Azhar, A.Z.A.; Choong, Y.C.; Adesta, E.Y.T. A review study on the effect of printing parameters of fused deposition modelling (fdm) metal polymer composite parts on mechanical properties and surface roughness. Malays. J. Microsc. 2022, 18, 281–297. [Google Scholar]
- Rouf, S.; Raina, A.; Haq, M.I.U.; Naveed, N.; Jeganmohan, S.; Kichloo, A.F. 3D printed parts and mechanical properties: Influencing parameters, sustainability aspects, global market scenario, challenges and applications. Adv. Ind. Eng. Polym. Res. 2022, 5, 143–158. Available online: https://www.sciencedirect.com/science/article/pii/S254250482200001X (accessed on 14 July 2025). [CrossRef]
- Mirza, F.; Shenoy, S.B.; Nunna, S.; Creighton, C. Effect of material extrusion process parameters on tensile performance of pristine and discontinuous fibre reinforced PLA composites: A review. Prog. Addit. Manuf. 2025, 10, 3251–3265. Available online: https://link.springer.com/article/10.1007/s40964-024-00825-4 (accessed on 14 July 2025). [CrossRef]
- Tofail, S.A.M.; Koumoulos, E.P.; Bandyopadhyay, A.; Bose, S.; O’Donoghue, L.; Charitidis, C. Additive manufacturing: Scientific and technological challenges, market uptake and opportunities. Mater. Today 2018, 21, 22–37. Available online: https://www.sciencedirect.com/science/article/pii/S1369702117301773 (accessed on 14 July 2025). [CrossRef]
- Minettoa, R.; Volpatob, N.; Stolfic, J.; Gregoria, R.M.M.H.; Silvaa, M.V.G. Anoptimal algorithm for 3D triangle mesh slicing. Comput.-Aided Des. 2017, 92, 1–10. Available online: https://www.sciencedirect.com/science/article/pii/S0010448517301215 (accessed on 14 July 2025). [CrossRef]
- Husiev, V.O.; Nikiforova, T.D. Research of the converting stages for the volume model of the product into the control code for a 3D printer in the context of automated construction of 3D printing technology. Ukr. J. Civ. Eng. Archit. 2024, 4, 38–45. [Google Scholar]
- Benamira, M.; Benhassine, N.; Ayad, A.; Dekhane, A. Investigation of printing parameters effects on mechanical and failure properties of 3D printed PLA. Eng. Fail. Anal. 2023, 148, 107218. Available online: https://www.sciencedirect.com/science/article/pii/S1350630723001723 (accessed on 14 July 2025). [CrossRef]
- Domingo-Espin, M.; Travieso-Rodriguez, J.A.; Jerez-Mesa, R.; Lluma-Fuentes, J. Fatigue Performance of ABS Specimens Obtained by Fused Filament Fabrication. Materials 2018, 11, 2521. Available online: https://www.mdpi.com/1996-1944/11/12/2521 (accessed on 14 July 2025). [CrossRef] [PubMed]
- Lokesh, N.; Praveena, B.A.; Sudheer Reddy, J.; Vasu, V.K.; Vijaykumar, S. Evaluation on effect of printing process parameter through Taguchi approach on mechanical properties of 3D printed PLA specimens using FDM at constant printing temperature. Mater. Proc. 2022, 52, 1288–1293. [Google Scholar] [CrossRef]
- Petruse, R.E.; Simion, A.; Bondrea, I. Geometrical and Dimensional Deviations of Fused DepositionModelling (FDM) Additive-Manufactured Parts. Metrology 2024, 4, 411–429. Available online: https://www.researchgate.net/publication/383020751_Geometrical_and_Dimensional_Deviations_of_Fused_Deposition_Modelling_FDM_Additive-Manufactured_Parts (accessed on 14 July 2025). [CrossRef]
- Vardy, K.; Softić, A.; Zaimović-Uzunović, N.; Bešlagić, E. Comparison of dimensions, shapes and positions controlusing cmm and 3d scanner. In Proceedings of the IMEKO TC11 & TC24 Joint Hybrid Conference, Dubrovnik, Croatia, 17–19 October 2022. [Google Scholar]
- Stojkic, Z.; Culjak, E.; Saravanja, L. 3D measurement—Comparison of CMM and 3D scanner. In Proceedings of the 31st DAAAM International Symposium On Intelligent Manufacturing and Automation, Mostar, Bosnia, 21–24 October 2020, ISSN 1726-9679. [Google Scholar]
- Bhagia, S.; Ragauskas, S.Z.J.; Satlewa, A.; Durković, J.; Lagana, R.; Yoo, C.G.; Zhao, X.; Kunc, V.; Pu, Y.; Ozcan, S.; et al. Critical review of FDM 3D printing of PLA biocomposites filled with biomass resources, characterization, biodegradability, upcycling and opportunities for biorefineries. Appl. Mater. Today 2021, 24, 101078. Available online: https://www.researchgate.net/publication/352260606_Critical_review_of_FDM_3D_printing_of_PLA_biocomposites_filled_with_biomass_resources_characterization_biodegradability_upcycling_and_opportunities_for_biorefineries (accessed on 14 July 2025). [CrossRef]
- ABSplus-P430 Production-Grade Thermoplastic for 3D Printers. Available online: https://www.prosolutions.pl/wp-content/uploads/2019/11/MSS_FDM_ABSplusP430_1117a.pdf (accessed on 15 July 2025).
- PN-EN ISO 1101:2017-05; Geometrical Product Specifications (GPS)—Geometrical Tolerancing—Tolerances of Form, Orientation, Location and Run-Out. Polish Committee for Standardization: Warsaw, Poland, 2017.
- Stepień, K.; Kmiecik-Sołtysiak, U.; Cepova, L.; Zuperl, U. Problems of measurements of roundness deviations with the use of coordinate measuring machines. MM Sci. J. 2024, 7203–7209, Special Issue | VRBA100 International Conference on Modern Manufacturing Technologies 4. 10. 2023, Ostrava, Czech Republic. [Google Scholar] [CrossRef]
- Ratajczyk, E.; Woźniak, A. Współrzędnościowe Systemy Pomiarowe; Publishing House of the Warsaw University of Technology: Warsaw, Poland, 2016. [Google Scholar]
- Vozár, M.; Pätoprstý, B.; Hrušecký, R. Comparison of Tactile and Optical Measurement Methods Using Precise Geometrical Shape. Int. J. Precis. Eng. Manuf. 2024, 5, 565–570. [Google Scholar] [CrossRef]





| Mechanical Properties | Value | Unit | Test Standard |
|---|---|---|---|
| Tensile Strength, Ultimate (Type 1, 0.125″, 0.2″/min) | 33 | MPa | ASTM D638 |
| Tensile Strength, Yield (Type 1, 0.125″, 0.2″/min) | 31 | MPa | ASTM D638 |
| Tensile Modulus (Type 1, 0.125″, 0.2″/min) | 2200 | MPa | ASTM D638 |
| Tensile Elongation at Break (Type 1, 0.125″, 0.2″/min) | 6 | % | ASTM D638 |
| Tensile Elongation at Yield (Type 1, 0.125″, 0.2″/min) | 2 | % | ASTM D638 |
| IZOD Impact, notched (Method A, 23 °C) | 106 | J/m | ASTM D256 |
| Parameter | Value |
|---|---|
| Measurement range | X = 900 mm; Y = 1200 mm, Z = 700 mm |
| Max. permissible error/spindle error | 0.9 + L/350 µm |
| Camera Pixels | Measuring Area (mm2) | Point Spacing (mm) | Recording of Measured Points | Working Distance (mm) | Operating Temperature (°C) | Rotary Table | Permissible Measurement Limit Error (mm) |
|---|---|---|---|---|---|---|---|
| 2 × 5,000,000 | 38 × 29–2000 × 1500 | 0.02–0.79 | up to 1,400,000 | 490–2000 | 5–40 (non-condensing) | Yes | ±0.01 |
| RONt CMM | RONt 3D Scan | Percentage Difference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample no. | RONt 1 mm | RONt2 mm | RONt3 mm | RONt1 mm | RONt2 mm | RONt3 mm | RONt1 % | RONt2 % | RONt3 % | |
| print direction 0° | ||||||||||
| 1_1 | 0.29 | 0.24 | 0.28 | 0.25 | 0.29 | 0.29 | 13.79 | 17.24 | 3.45 | |
| 1_2 | 0.24 | 0.24 | 0.24 | 0.4 | 0.25 | 0.25 | 40.00 | 4.00 | 4.00 | |
| 1_3 | 0.17 | 0.27 | 0.24 | 0.16 | 0.29 | 0.29 | 5.88 | 6.90 | 17.24 | |
| 1_4 | 0.23 | 0.26 | 0.34 | 0.18 | 0.26 | 0.26 | 21.74 | 0.00 | 23.53 | |
| 1_5 | 0.22 | 0.19 | 0.24 | 0.5 | 0.66 | 0.66 | 56.00 | 71.21 | 63.64 | |
| 1_6 | 0.3 | 0.22 | 0.26 | 0.31 | 0.32 | 0.33 | 3.23 | 31.25 | 21.21 | |
| 1_7 | 0.25 | 0.19 | 0.23 | 0.33 | 0.29 | 0.27 | 24.24 | 34.48 | 14.81 | |
| 1_8 | 0.27 | 0.22 | 0.25 | 0.26 | 0.32 | 0.33 | 3.70 | 31.25 | 24.24 | |
| 1_9 | 0.22 | 0.24 | 0.20 | 0.25 | 0.30 | 0.30 | 12.00 | 20.00 | 33.33 | |
| 1_10 | 0.23 | 0.24 | 0.23 | 0.41 | 0.31 | 0.31 | 43.90 | 22.58 | 25.81 | |
| print direction 45° | ||||||||||
| 2_1 | 0.18 | 0.22 | 0.23 | 0.19 | 0.28 | 0.29 | 5.26 | 21.43 | 20.69 | |
| 2_2 | 0.16 | 0.23 | 0.27 | 0.26 | 0.18 | 0.19 | 38.46 | 21.74 | 29.63 | |
| 2_3 | 0.17 | 0.21 | 0.23 | 0.18 | 0.22 | 0.21 | 5.56 | 4.55 | 8.70 | |
| 2_4 | 0.19 | 0.13 | 0.13 | 0.17 | 0.19 | 0.19 | 10.53 | 31.58 | 31.58 | |
| 2_5 | 0.2 | 0.29 | 0.24 | 0.18 | 0.18 | 0.18 | 10.00 | 37.93 | 25.00 | |
| 2_6 | 0.15 | 0.24 | 0.27 | 0.24 | 0.19 | 0.19 | 37.50 | 20.83 | 29.63 | |
| 2_7 | 0.16 | 0.22 | 0.26 | 0.22 | 0.38 | 0.38 | 27.27 | 42.11 | 31.58 | |
| 2_8 | 0.17 | 0.24 | 0.24 | 0.24 | 0.22 | 0.23 | 29.17 | 8.33 | 4.17 | |
| 2_9 | 0.14 | 0.22 | 0.26 | 0.21 | 0.19 | 0.11 | 33.33 | 13.64 | 57.69 | |
| 2_10 | 0.17 | 0.23 | 0.26 | 0.21 | 0.18 | 0.21 | 19.05 | 21.74 | 19.23 | |
| print direction 90° | ||||||||||
| 3_1 | 0.1 | 0.28 | 0.31 | 0.17 | 0.84 | 0.94 | 41.18 | 66.67 | 67.02 | |
| 3_2 | 0.11 | 0.22 | 0.21 | 0.19 | 0.24 | 0.45 | 42.11 | 8.33 | 53.33 | |
| 3_3 | 0.16 | 0.26 | 0.26 | 0.18 | 0.21 | 0.25 | 11.11 | 19.23 | 3.85 | |
| 3_4 | 0.1 | 0.3 | 0.28 | 0.17 | 0.2 | 0.2 | 41.18 | 33.33 | 28.57 | |
| 3_5 | 0.1 | 0.26 | 0.29 | 0.18 | 0.2 | 0.2 | 44.44 | 23.08 | 31.03 | |
| 3_6 | 0.08 | 0.27 | 0.22 | 0.18 | 0.26 | 0.26 | 55.56 | 3.70 | 15.38 | |
| 3_7 | 0.1 | 0.3 | 0.31 | 0.16 | 0.24 | 0.25 | 37.50 | 20.00 | 19.35 | |
| 3_8 | 0.09 | 0.28 | 0.3 | 0.54 | 0.36 | 0.37 | 83.33 | 22.22 | 18.92 | |
| 3_9 | 0.09 | 0.27 | 0.32 | 0.22 | 0.21 | 0.22 | 59.09 | 22.22 | 31.25 | |
| 3_10 | 0.09 | 0.38 | 0.27 | 0.21 | 0.23 | 0.23 | 57.14 | 39.47 | 14.81 | |
| CYLt, CMM | CYTt 3D Scan | Percentage Difference | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample no. | CYLt1 mm | CYLt2 mm | CYLt3 mm | CYLt1 mm | CYLt2 mm | CYLt3 mm | CYLt1 % | CYLt2 % | CYLt3 % | |
| print direction 0° | ||||||||||
| 1_1 | 0.32 | 0.28 | 0.31 | 0.51 | 0.47 | 0.47 | 37.25 | 40.43 | 34.04 | |
| 1_2 | 0.30 | 0.29 | 0.29 | 0.59 | 0.46 | 0.46 | 49.15 | 36.96 | 36.96 | |
| 1_3 | 0.23 | 0.29 | 0.27 | 0.37 | 0.45 | 0.45 | 37.84 | 35.56 | 40.00 | |
| 1_4 | 0.30 | 0.31 | 0.51 | 0.46 | 0.41 | 0.41 | 34.78 | 24.39 | 19.61 | |
| 1_5 | 0.26 | 0.23 | 0.28 | 0.64 | 0.85 | 0.85 | 59.38 | 72.94 | 67.06 | |
| 1_6 | 0.34 | 0.28 | 0.32 | 0.51 | 0.49 | 0.51 | 33.33 | 42.86 | 37.25 | |
| 1_7 | 0.30 | 0.25 | 0.34 | 0.52 | 0.49 | 0.50 | 42.31 | 48.98 | 32.00 | |
| 1_8 | 0.32 | 0.27 | 0.28 | 0.52 | 0.52 | 0.52 | 38.46 | 48.08 | 46.15 | |
| 1_9 | 0.27 | 0.27 | 0.24 | 0.51 | 0.54 | 0.50 | 47.06 | 50.00 | 52.00 | |
| 1_10 | 0.26 | 0.28 | 0.27 | 0.48 | 0.59 | 0.63 | 45.83 | 52.54 | 57.14 | |
| print direction 45° | ||||||||||
| 2_1 | 0.19 | 0.27 | 0.27 | 0.36 | 0.39 | 0.39 | 47.22 | 30.77 | 30.77 | |
| 2_2 | 0.20 | 0.26 | 0.28 | 0.30 | 0.28 | 0.29 | 33.33 | 7.14 | 3.45 | |
| 2_3 | 0.17 | 0.26 | 0.27 | 0.26 | 0.30 | 0.30 | 34.62 | 13.33 | 10.00 | |
| 2_4 | 0.22 | 0.16 | 0.20 | 0.36 | 0.28 | 0.28 | 38.89 | 42.86 | 28.57 | |
| 2_5 | 0.18 | 0.26 | 0.27 | 0.25 | 0.31 | 0.31 | 28.00 | 16.13 | 12.90 | |
| 2_6 | 0.16 | 0.30 | 0.30 | 0.30 | 0.50 | 0.49 | 46.67 | 40.00 | 38.78 | |
| 2_7 | 0.14 | 0.28 | 0.31 | 0.36 | 0.46 | 0.46 | 61.11 | 39.13 | 32.61 | |
| 2_8 | 0.17 | 0.31 | 0.36 | 0.37 | 0.52 | 0.47 | 54.05 | 40.38 | 23.40 | |
| 2_9 | 0.17 | 0.31 | 0.29 | 0.30 | 0.45 | 0.13 | 43.33 | 31.11 | 55.17 | |
| 2_10 | 0.17 | 0.31 | 0.31 | 0.31 | 0.29 | 0.47 | 45.16 | 6.45 | 34.04 | |
| print direction 90° | ||||||||||
| 3_1 | 0.14 | 0.33 | 0.33 | 0.47 | 1.67 | 1.67 | 70.21 | 80.24 | 80.24 | |
| 3_2 | 0.15 | 0.25 | 0.23 | 0.31 | 0.55 | 0.55 | 51.61 | 54.55 | 58.18 | |
| 3_3 | 0.13 | 0.29 | 0.30 | 0.31 | 0.44 | 0.84 | 58.06 | 34.09 | 64.29 | |
| 3_4 | 0.14 | 0.30 | 0.33 | 0.30 | 0.38 | 0.38 | 53.33 | 21.05 | 13.16 | |
| 3_5 | 0.15 | 0.33 | 0.30 | 0.31 | 0.37 | 0.37 | 51.61 | 10.81 | 18.92 | |
| 3_6 | 0.14 | 0.30 | 0.31 | 0.32 | 0.47 | 0.45 | 56.25 | 36.17 | 31.11 | |
| 3_7 | 0.13 | 0.31 | 0.33 | 0.31 | 0.51 | 0.53 | 58.06 | 39.22 | 37.74 | |
| 3_8 | 0.13 | 0.32 | 0.30 | 0.67 | 0.70 | 0.70 | 80.60 | 54.29 | 57.14 | |
| 3_9 | 0.14 | 0.32 | 0.31 | 0.37 | 0.43 | 0.39 | 62.16 | 25.58 | 20.51 | |
| 3_10 | 0.13 | 0.36 | 0.34 | 0.53 | 0.47 | 0.46 | 75.47 | 23.40 | 26.09 | |
| Print Direction 0° | CMM | Scanner | Print Direction 0° | CMM | Scanner | ||||
|---|---|---|---|---|---|---|---|---|---|
| , mm | SD, mm | , mm | SD, mm | , mm | SD, mm | , mm | SD, mm | ||
| RONt1 | 0.24 | 0.04 | 0.31 | 0.11 | CYLt1 | 0.29 | 0.03 | 0.51 | 0.07 |
| RONt2 | 0.23 | 0.03 | 0.33 | 0.12 | CYLt2 | 0.28 | 0.02 | 0.53 | 0.12 |
| RONt3 | 0.25 | 0.04 | 0.33 | 0.12 | CYLt3 | 0.31 | 0.08 | 0.53 | 0.13 |
| print direction 45° | print direction 45° | ||||||||
| RONt1 | 0.17 | 0.02 | 0.21 | 0.03 | CYLt1 | 0.18 | 0.02 | 0.32 | 0.04 |
| RONt2 | 0.22 | 0.04 | 0.22 | 0.06 | CYLt2 | 0.27 | 0.04 | 0.38 | 0.10 |
| RONt3 | 0.24 | 0.04 | 0.22 | 0.07 | CYLt3 | 0.29 | 0.04 | 0.36 | 0.12 |
| print direction 90° | print direction 90° | ||||||||
| RONt1 | 0.10 | 0.02 | 0.22 | 0.11 | CYLt1 | 0.14 | 0.01 | 0.39 | 0.13 |
| RONt2 | 0.28 | 0.04 | 0.30 | 0.20 | CYLt2 | 0.31 | 0.03 | 0.60 | 0.39 |
| RONt3 | 0.28 | 0.04 | 0.34 | 0.23 | CYLt3 | 0.31 | 0.03 | 0.63 | 0.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bujarska, A.; Zmarzły, P.; Szczygieł, P. Application of Optical Measurements to Assess Form Deviations of Cylindrical Parts Made Using FDM Additive Technology. Sensors 2025, 25, 5855. https://doi.org/10.3390/s25185855
Bujarska A, Zmarzły P, Szczygieł P. Application of Optical Measurements to Assess Form Deviations of Cylindrical Parts Made Using FDM Additive Technology. Sensors. 2025; 25(18):5855. https://doi.org/10.3390/s25185855
Chicago/Turabian StyleBujarska, Anna, Paweł Zmarzły, and Paweł Szczygieł. 2025. "Application of Optical Measurements to Assess Form Deviations of Cylindrical Parts Made Using FDM Additive Technology" Sensors 25, no. 18: 5855. https://doi.org/10.3390/s25185855
APA StyleBujarska, A., Zmarzły, P., & Szczygieł, P. (2025). Application of Optical Measurements to Assess Form Deviations of Cylindrical Parts Made Using FDM Additive Technology. Sensors, 25(18), 5855. https://doi.org/10.3390/s25185855








