Cooperative Schemes for Joint Latency and Energy Consumption Minimization in UAV-MEC Networks †
Abstract
1. Introduction
1.1. Related Works
1.2. Motivations and Contributions
- We introduce cost functions to balance the latency and energy consumption for both the whole system and individual UDs. Then, we formulate a long-term cost minimization problem that has discrete association constraints and continuous offloading and computing frequency constraints. We further formulate this long-term problem into a POMDP and propose a cooperative multi-agent DRL framework. All UDs are agents and each of them makes its own decision based on its local observation and individual reward function.
- We propose a MAPPO-based scheme that adopts centralized training and decentralized execution to tackle the POMDP. In the training stage, the global observations and the system reward function are used to train the actor and the critic networks for all UDs. In the execution stage, each UD agent uses its local observation and individual reward function for decision-making and network updates. Simulation results validate the MAPPO-based scheme and show its superiority in reducing system cost.
- We decouple the association from the task offloading and the computing resource allocation and propose a lightweight scheme based on closed-form enhanced multi-armed bandit (CF-MAB). In the CF-MAB-based scheme, each UD agent selects its association to maximize its long-term achievable rate and then the optimal offloading and computing resource allocation can be obtained in closed form given the association. Simulation results validate the CF-MAB-based scheme and show its superiority regarding its complexity and task completion rate.
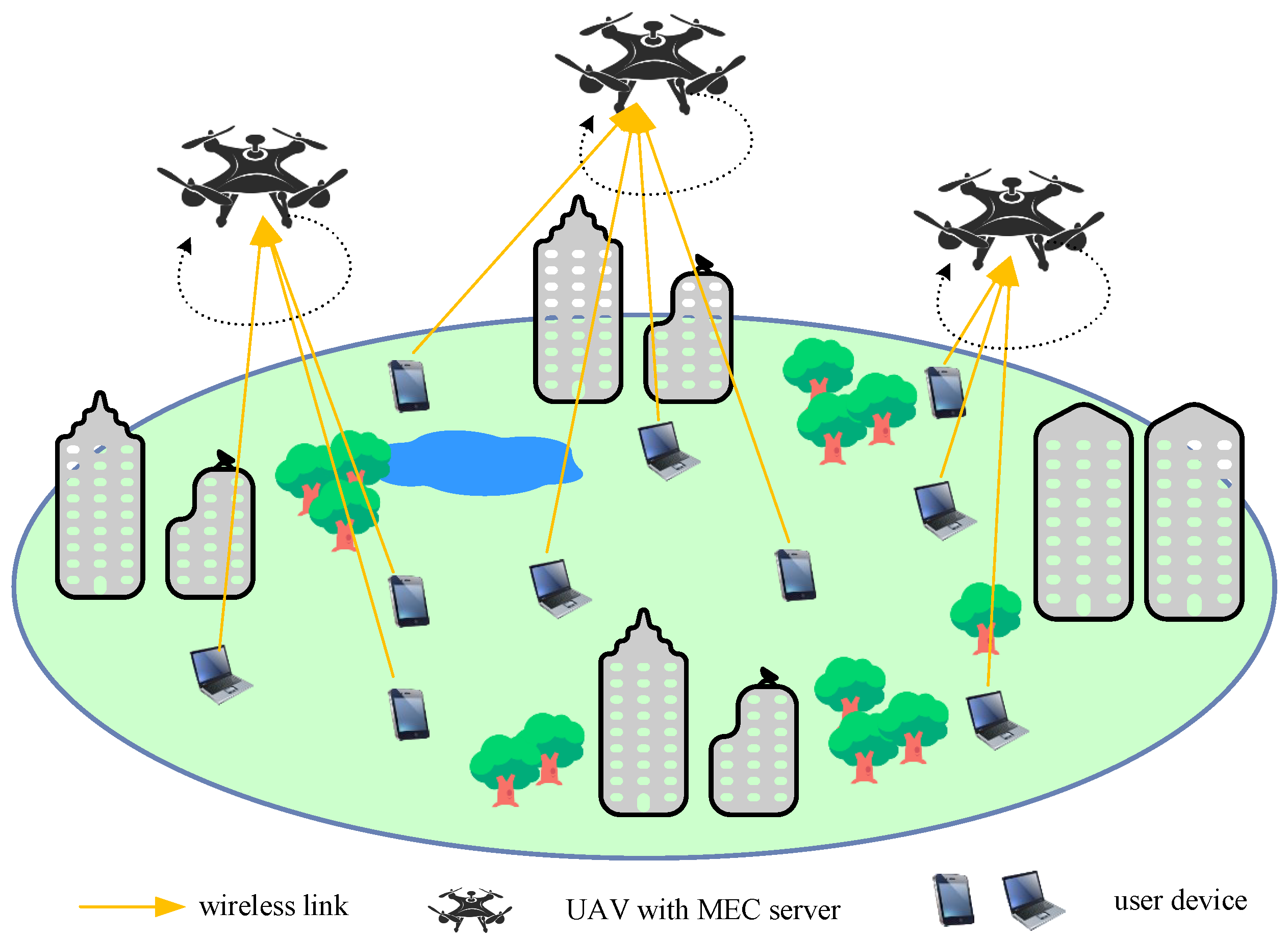
2. System Model
2.1. Association
2.2. Communication Model
2.3. Computation Model
2.3.1. Edge Computing
2.3.2. Local Computing
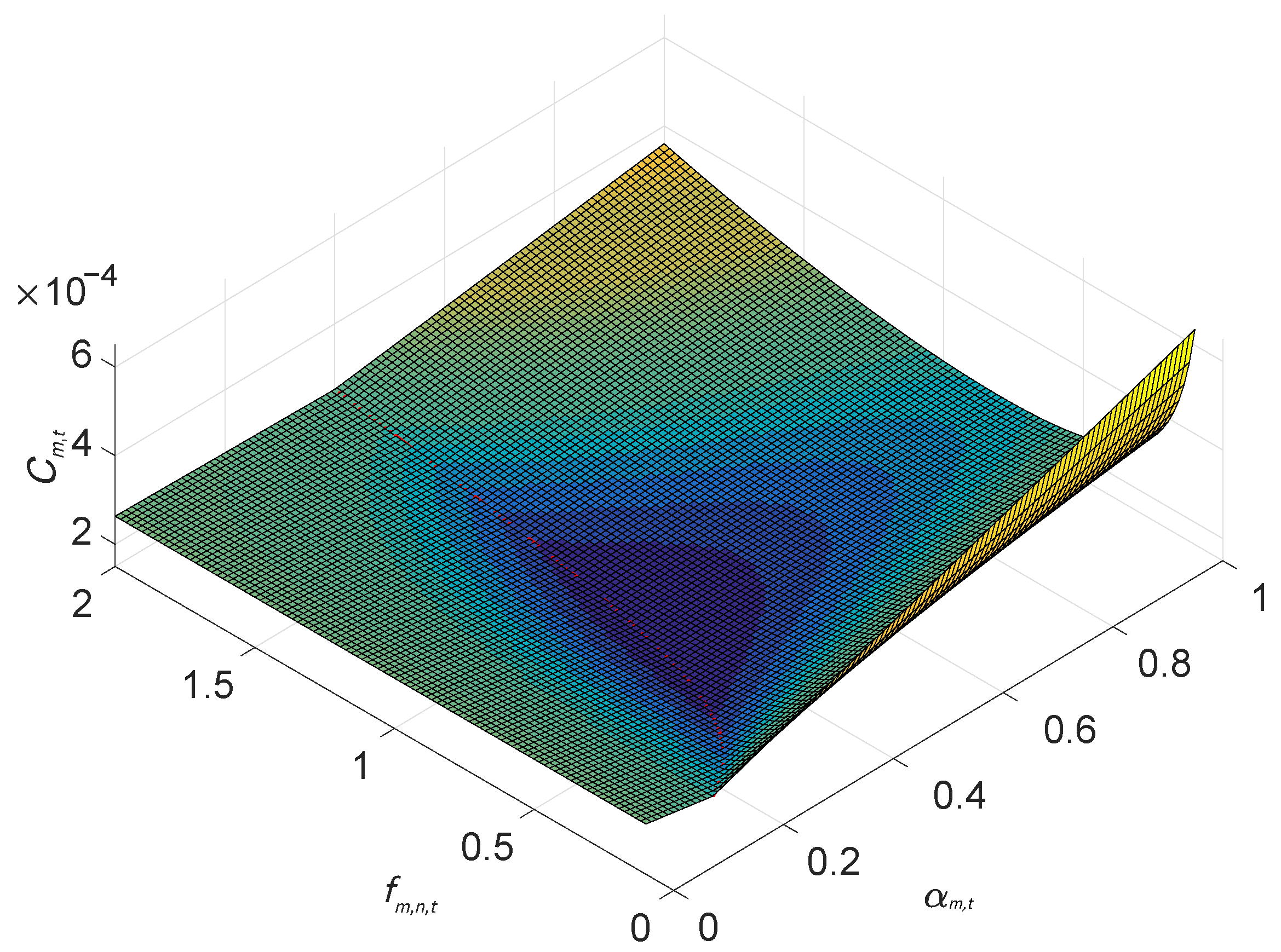
2.4. System Energy Consumption and Latency
2.5. Problem Formulation
3. Multi-Agent DRL-Based Association, Offloading, and Resource Allocation Schemes
3.1. Multi-Agent RL Framework
3.2. MAPPO-Based Scheme for Long-Term Consumption Minimization
3.2.1. Typical MAPPO Procedure
3.2.2. Centralized Training and Decentralized Execution
3.2.3. MAPPO-Based Algorithm
| Algorithm 1 MAPPO-Based algorithm | |
| 1: | Initialize parameter of the actor network and parameter of the critic network. |
| 2: | for each episode do |
| 3: | Initialize experience reply buffer U; |
| 4: | for each timeslot do |
| 5: | for each UD do |
| 6: | Execute action according to ; |
| 7: | Get the reward and the next observation ; |
| 8: | end for |
| 9: | end for |
| 10: | Get trajectory ; |
| 11: | Compute the cumulative discounted reward , the state-value function , and the advantage (According to (24)). |
| 12: | Split , , and into chunks of length , and store them in U. |
| 13: | for mini-batch do |
| 14: | Randomly select a chunk from U as mini-batch b; |
| 15: | Compute gradients of (25) and (26) on and , respectively, using mini-batch b; |
| 16: | Update and using by Adam. |
| 17: | end for |
| 18: | end for |
3.3. CF-MAB-Based Scheme for Long-Term Consumption Minimization
3.3.1. Closed-Form Offloading and Computing Resource Allocation for a Given Association
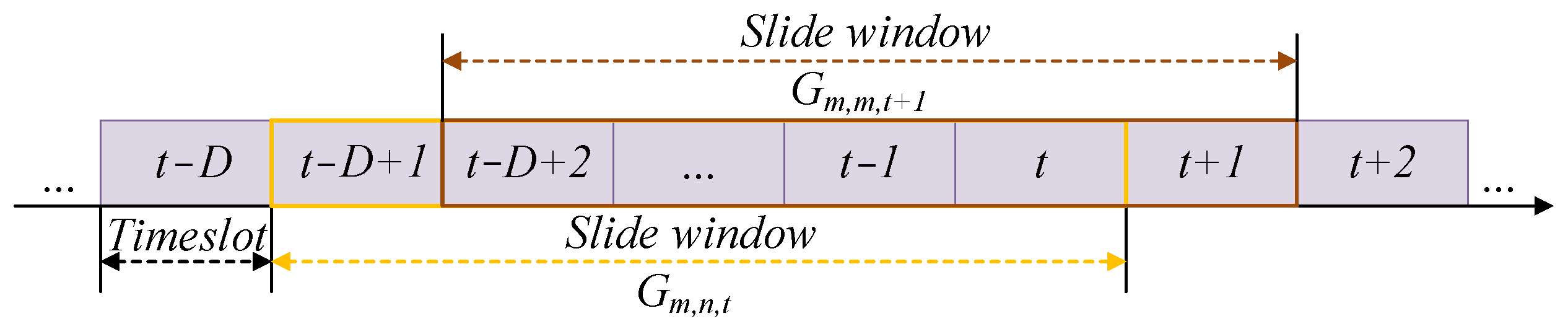
3.3.2. MAB-Based Long-Term Association
3.3.3. CF-MAB-Based Algorithm
| Algorithm 2 CF-MAB-based algorithm | |
| Require: , | |
| 1: | Initialize , for and ; |
| 2: | for each timeslot do |
| 3: | for each UD do |
| 4: | Calculate probability distribution with (40); |
| 5: | Make action randomly according to the probabilities ; |
| 6: | Calculate the achieved rate ; |
| 7: | Obtain the optimal offloading proportion , computing resource allocation and , and the minimum cost ; |
| 8: | Calculate rewards with (41) and cumulative rewards with (45) or (47); |
| 9: | Update the weights ; |
| 10: | end for |
| 11: | end for |
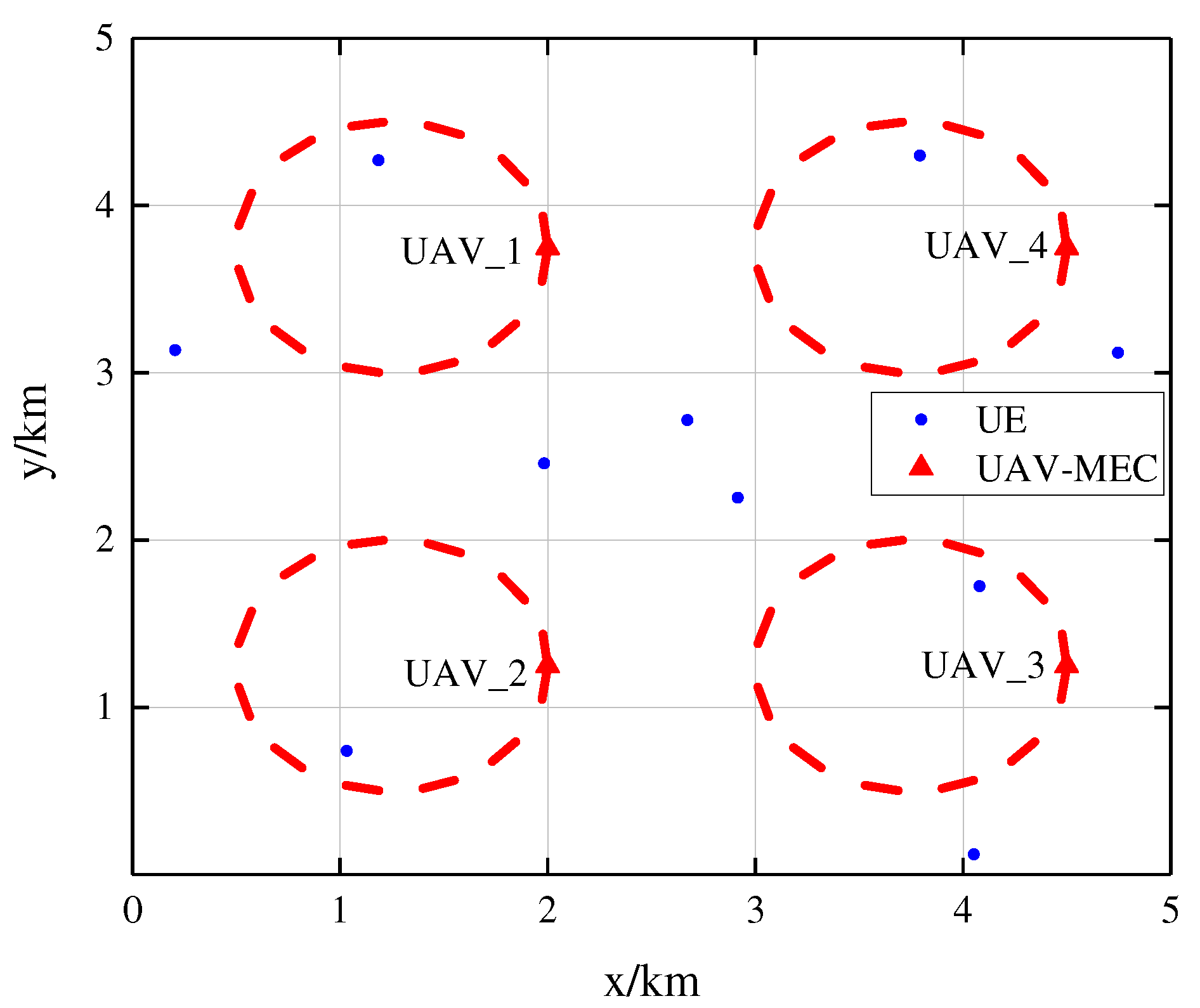
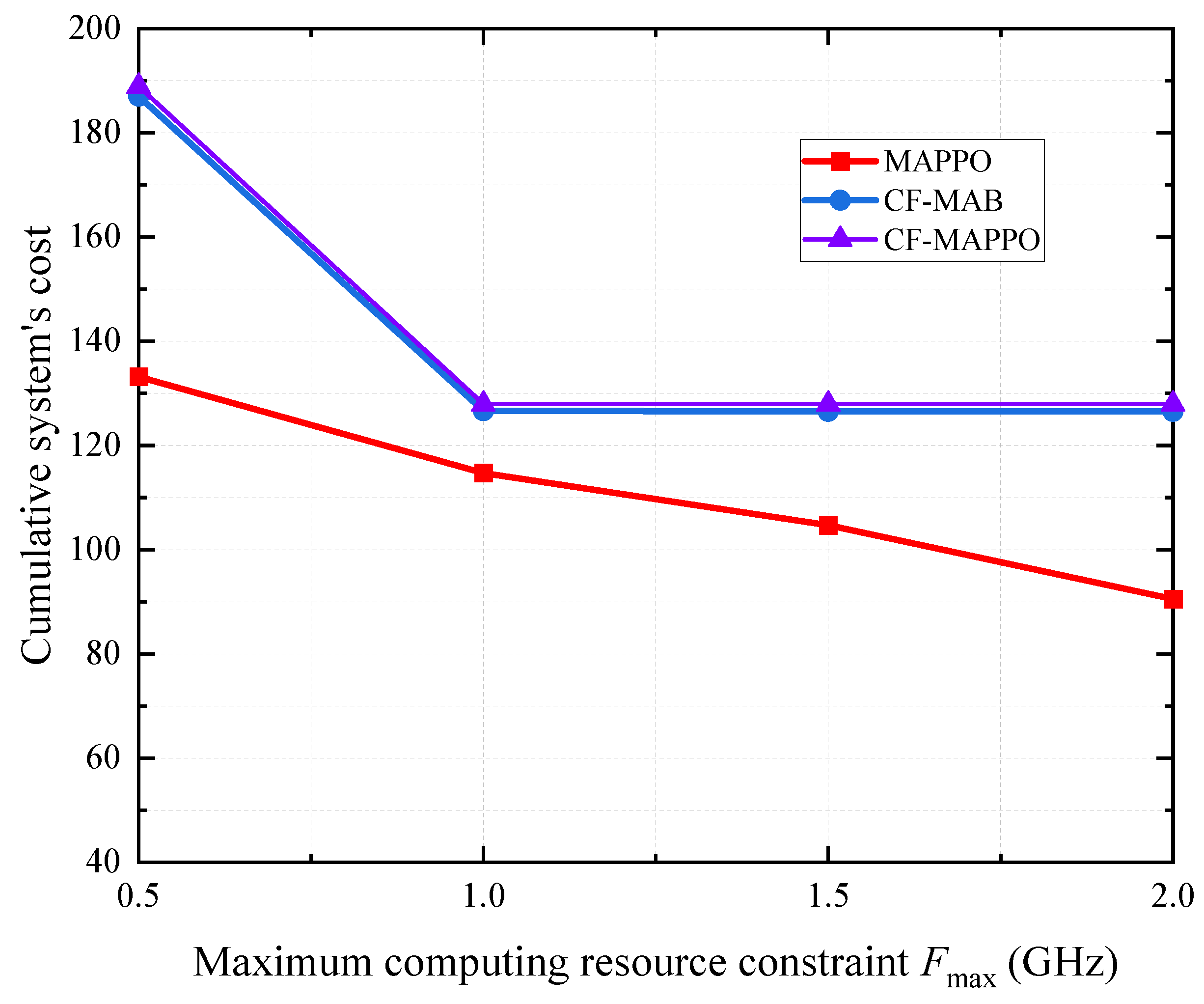
4. Performance Evaluation
- CF-MAPPO scheme: The UDs’ association is determined via a simplified MAPPO-based scheme to maximize the total achievable rate. Then, the offloading and computing resource allocation are obtained through a closed-form solution;
- RSS + Remote-only scheme: Each UD associates to the UAV with maximum RSS and all its tasks are executed at the UAV server;
- Local-only scheme: Each UD computes its tasks locally;
- Random + Random means: Each UD associates with a random UAV and a random part of its tasks are executed at the UAV server.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nguyen, D.C.; Ding, M.; Pathirana, P.N.; Seneviratne, A.; Li, J.; Niyato, D.; Dobre, O.; Poor, H.V. 6G Internet of Things: A Comprehensive Survey. IEEE Internet Things J. 2022, 9, 359–383. [Google Scholar] [CrossRef]
- Aouedi, O.; Vu, T.H.; Sacco, A.; Nguyen, D.C.; Piamrat, K.; Marchetto, G.; Pham, Q.V. A Survey on Intelligent Internet of Things: Applications, Security, Privacy, and Future Directions. IEEE Commun. Surv. Tutor. 2025, 27, 1238–1292. [Google Scholar] [CrossRef]
- McEnroe, P.; Wang, S.; Liyanage, M. A Survey on the Convergence of Edge Computing and AI for UAVs: Opportunities and Challenges. IEEE Internet Things J. 2022, 9, 15435–15459. [Google Scholar] [CrossRef]
- Spinelli, F.; Mancuso, V. Toward Enabled Industrial Verticals in 5G: A Survey on MEC-Based Approaches to Provisioning and Flexibility. IEEE Commun. Surv. Tutor. 2021, 23, 596–630. [Google Scholar] [CrossRef]
- Azari, M.M.; Solanki, S.; Chatzinotas, S.; Kodheli, O.; Sallouha, H.; Colpaert, A.; Mendoza Montoya, J.F.; Pollin, S.; Haqiqatnejad, A.; Mostaani, A.; et al. Evolution of Non-Terrestrial Networks From 5G to 6G: A Survey. IEEE Commun. Surv. Tutor. 2022, 24, 2633–2672. [Google Scholar] [CrossRef]
- Mahboob, S.; Liu, L. Revolutionizing Future Connectivity: A Contemporary Survey on AI-Empowered Satellite-Based Non-Terrestrial Networks in 6G. IEEE Commun. Surv. Tutor. 2024, 26, 1279–1321. [Google Scholar] [CrossRef]
- Panahi, F.H.; Panahi, F.H. Reliable and Energy-Efficient UAV Communications: A Cost-Aware Perspective. IEEE Trans. Mobile Comput. 2024, 23, 4038–4049. [Google Scholar] [CrossRef]
- Kirubakaran, B.; Vikhrova, O.; Andreev, S.; Hosek, J. UAV-BS Integration with Urban Infrastructure: An Energy Efficiency Perspective. IEEE Commun. Mag. 2025, 63, 100–106. [Google Scholar] [CrossRef]
- Peng, H.; Shen, X. Multi-Agent Reinforcement Learning Based Resource Management in MEC- and UAV-Assisted Vehicular Networks. IEEE J. Sel. Areas Commun. 2021, 39, 131–141. [Google Scholar] [CrossRef]
- Ullah, S.A.; Hassan, S.A.; Abou-Zeid, H.; Qureshi, H.K.; Jung, H.; Mahmood, A.; Gidlund, M.; Imran, M.A.; Hossain, E. Convergence of MEC and DRL in Non-Terrestrial Wireless Networks: Key Innovations, Challenges, and Future Pathways. IEEE Commun. Surv. Tutor. 2025, 1–39, early access. [Google Scholar]
- Tun, Y.K.; Park, Y.M.; Tran, N.H.; Saad, W.; Pandey, S.R.; Hong, C.S. Energy-Efficient Resource Management in UAV-Assisted Mobile Edge Computing. IEEE Commun. Lett. 2021, 25, 249–253. [Google Scholar] [CrossRef]
- Liu, B.; Wan, Y.; Zhou, F.; Wu, Q.; Hu, R.Q. Resource Allocation and Trajectory Design for MISO UAV-Assisted MEC Networks. IEEE Trans. Veh. Technol. 2022, 71, 4933–4948. [Google Scholar] [CrossRef]
- Xu, B.; Kuang, Z.; Gao, J.; Zhao, L.; Wu, C. Joint Offloading Decision and Trajectory Design for UAV-Enabled Edge Computing With Task Dependency. IEEE Trans. Wireless Commun. 2023, 22, 5043–5055. [Google Scholar] [CrossRef]
- Li, Y.; Gao, X.; Shi, M.; Kang, J.; Niyato, D.; Yang, K. Dynamic Weighted Energy Minimization for Aerial Edge Computing Networks. IEEE Internet Things J. 2025, 12, 683–697. [Google Scholar] [CrossRef]
- Wang, C.; Zhai, D.; Zhang, R.; Cai, L.; Liu, L.; Dong, M. Joint Association, Trajectory, Offloading, and Resource Optimization in Air and Ground Cooperative MEC Systems. IEEE Trans. Veh. Technol. 2024, 73, 13076–13089. [Google Scholar] [CrossRef]
- Li, C.; Gan, Y.; Zhang, Y.; Luo, Y. A Cooperative Computation Offloading Strategy With On-Demand Deployment of Multi-UAVs in UAV-Aided Mobile Edge Computing. IEEE Trans. Network Serv. Manag. 2024, 21, 2095–2110. [Google Scholar] [CrossRef]
- Hu, Q.; Cai, Y.; Yu, G.; Qin, Z.; Zhao, M.; Li, G.Y. Joint Offloading and Trajectory Design for UAV-Enabled Mobile Edge Computing Systems. IEEE Internet Things J. 2019, 6, 1879–1892. [Google Scholar] [CrossRef]
- Zhang, L.; Ansari, N. Latency-Aware IoT Service Provisioning in UAV-Aided Mobile-Edge Computing Networks. IEEE Internet Things J. 2020, 7, 10573–10580. [Google Scholar] [CrossRef]
- Nasir, A.A. Latency Optimization of UAV-Enabled MEC System for Virtual Reality Applications Under Rician Fading Channels. IEEE Wireless Commun. Lett. 2021, 10, 1633–1637. [Google Scholar] [CrossRef]
- Sabuj, S.R.; Asiedu, D.K.P.; Lee, K.-J.; Jo, H.-S. Delay Optimization in Mobile Edge Computing: Cognitive UAV-Assisted eMBB and mMTC Services. IEEE Trans. Cogn. Commun. Netw. 2022, 8, 1019–1033. [Google Scholar] [CrossRef]
- Han, Z.; Zhou, T.; Xu, T.; Hu, H. Joint User Association and Deployment Optimization for Delay-Minimized UAV-Aided MEC Networks. IEEE Wirel. Commun. Lett. 2023, 12, 1791–1795. [Google Scholar] [CrossRef]
- Zhang, J.; Luo, H.; Chen, X.; Shen, H.; Guo, L. Minimizing Response Delay in UAV-Assisted Mobile Edge Computing by Joint UAV Deployment and Computation Offloading. IEEE Trans. Cloud Comput. 2024, 12, 1372–1386. [Google Scholar] [CrossRef]
- Yu, Z.; Gong, Y.; Gong, S.; Guo, Y. Joint Task Offloading and Resource Allocation in UAV-Enabled Mobile Edge Computing. IEEE Internet Things J. 2020, 7, 3147–3159. [Google Scholar] [CrossRef]
- Zhao, L.; Yang, K.; Tan, Z.; Li, X.; Sharma, S.; Liu, Z. A Novel Cost Optimization Strategy for SDN-Enabled UAV-Assisted Vehicular Computation Offloading. IEEE Trans. Intell. Transp. Syst. 2021, 22, 3664–3674. [Google Scholar] [CrossRef]
- Pervez, F.; Sultana, A.; Yang, C.; Zhao, L. Energy and Latency Efficient Joint Communication and Computation Optimization in a Multi-UAV-Assisted MEC Network. IEEE Trans. Wirel. Commun. 2024, 23, 1728–1741. [Google Scholar] [CrossRef]
- Kuang, Z.; Pan, Y.; Yang, F.; Zhang, Y. Joint Task Offloading Scheduling and Resource Allocation in Air–Ground Cooperation UAV-Enabled Mobile Edge Computing. IEEE Trans. Veh. Technol. 2024, 73, 5796–5807. [Google Scholar] [CrossRef]
- Yuan, H.; Wang, M.; Bi, J.; Shi, S.; Yang, J.; Zhang, J.; Zhou, M.; Buyya, R. Cost-Efficient Task Offloading in Mobile Edge Computing With Layered Unmanned Aerial Vehicles. IEEE Internet Things J. 2024, 11, 30496–30509. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Sun, Z.; Wu, Q.; Kang, J.; Niyato, D.; Leung, V.C.M. Multi-Objective Optimization for Multi-UAV-Assisted Mobile Edge Computing. IEEE Trans. Mobile Comput. 2024, 23, 14803–14820. [Google Scholar] [CrossRef]
- Zhang, L.; Wen, F.; Zhang, Q.; Gui, G.; Sari, H.; Adachi, F. Constrained Multiobjective Decomposition Evolutionary Algorithm for UAV-Assisted Mobile Edge Computing Networks. IEEE Internet Things J. 2024, 11, 36673–36687. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, L.; Tang, Q.; Ngai, E.C.H.; Hu, X.; Zhao, H.; Wei, J. Stochastic Computation Offloading and Trajectory Scheduling for UAV-Assisted Mobile Edge Computing. IEEE Internet Things J. 2019, 6, 3688–3699. [Google Scholar] [CrossRef]
- Zeng, Y.; Chen, S.; Li, J.; Cui, Y.; Du, J. Online Optimization in UAV-Enabled MEC System: Minimizing Long-Term Energy Consumption Under Adapting to Heterogeneous Demands. IEEE Internet Things J. 2024, 11, 32143–32159. [Google Scholar] [CrossRef]
- Liu, B.; Peng, M. Online Offloading for Energy-Efficient and Delay-Aware MEC Systems with Cellular-Connected UAVs. IEEE Internet Things J. 2024, 11, 22321–22336. [Google Scholar] [CrossRef]
- Wang, J.; Wang, L.; Zhu, K.; Dai, P. Lyapunov-Based Joint Flight Trajectory and Computation Offloading Optimization for UAV-Assisted Vehicular Networks. IEEE Internet Things J. 2024, 11, 22243–22256. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, R.; He, Z.; Li, K. Joint Optimization of Trajectory, Offloading, Caching, and Migration for UAV-Assisted MEC. IEEE Trans. Mob. Comput. 2025, 24, 1981–1998. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, Z.; Yang, C.; Cao, X. Latency Optimization in UAV-Assisted Mobile Edge Computing Empowered by Caching Mechanisms. IEEE J. Miniat. Air Space Syst. 2024, 5, 228–236. [Google Scholar] [CrossRef]
- Li, C.; Wu, J.; Zhang, Y.; Wan, S. Energy-Latency Tradeoff for Joint Optimization of Vehicle Selection and Resource Allocation in UAV-Assisted Vehicular Edge Computing. IEEE Trans. Green Commun. Netw. 2025, 9, 445–458. [Google Scholar] [CrossRef]
- Seid, A.M.; Boateng, G.O.; Anokye, S.; Kwantwi, T.; Sun, G.; Liu, G. Collaborative Computation Offloading and Resource Allocation in Multi-UAV-Assisted IoT Networks: A Deep Reinforcement Learning Approach. IEEE Internet Things J. 2021, 8, 12203–12218. [Google Scholar] [CrossRef]
- Wang, Y.; Farooq, J.; Ghazzai, H.; Setti, G. Joint Positioning and Computation Offloading in Multi-UAV MEC for Low Latency Applications: A Proximal Policy Optimization Approach. IEEE Trans. Mobile Comput. 2025, 1–15, early access. [Google Scholar]
- He, Y.; Xiang, K.; Cao, X.; Guizani, M. Task Scheduling and Trajectory Optimization-based on Fairness and Communication Security for Multi-UAV-MEC System. IEEE Internet Things J. 2021, 11, 30510–30523. [Google Scholar] [CrossRef]
- Yan, M.; Zhang, L.; Jiang, W.; Chan, C.A.; Gygax, A.F.; Nirmalathas, A. Energy Consumption Modeling and Optimization of UAV-Assisted MEC Networks Using Deep Reinforcement Learning. IEEE Sens. J. 2024, 24, 13629–13639. [Google Scholar] [CrossRef]
- Liu, Y.; Lin, P.; Zhang, M.; Zhang, Z.; Yu, F.R. Mobile-Aware Service Offloading for UAV-Assisted IoV: A Multiagent Tiny Distributed Learning Approach. IEEE Internet Things J. 2024, 11, 21191–21201. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, H.; Liu, L.; Sun, E.; Zhang, H.; Li, Z.; Fang, C.; Li, M. Dynamic Trajectory Design for Multi-UAV-Assisted Mobile Edge Computing. IEEE Trans. Veh. Technol. 2025, 74, 4684–4697. [Google Scholar] [CrossRef]
- Kang, H.; Chang, X.; Mišić, J.; Mišić, V.B.; Fan, J.; Liu, Y. Cooperative UAV resource allocation and task offloading in hierarchical aerial computing systems: A MAPPO based approach. IEEE Internet Things J. 2023, 10, 10497–10509. [Google Scholar] [CrossRef]
- Cheng, M.; Zhu, C.; Lin, M.; Wang, J.B.; Zhu, W.P. An O-MAPPO scheme for joint computation offloading and resources allocation in UAV assisted MEC systems. Comp. Commun. 2023, 208, 190–199. [Google Scholar] [CrossRef]
- Cheng, M.; Zhu, C.; Lin, M.; Zhu, W.-P. A MAPPO Based Scheme for Joint Resource Allocation in UAV Assisted MEC Networks. In Proceedings of the IEEE/CIC International Conference on Communications in China (ICCC), Hangzhou, China, 7–9 August 2024. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar] [CrossRef]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of PPO in cooperative multi-agent games. In Proceedings of the 36th International Conference on Neural Information Processing Systems (NIPS ’22), New Orleans, LA, USA, 28 November–9 December 2022. [Google Scholar]
- Guo, D.; Tang, L.; Zhang, X.; Liang, Y.-C. Joint Optimization of Handover Control and Power Allocation Based on Multi-Agent Deep Reinforcement Learning. IEEE Trans. Veh. Tech. 2020, 69, 13124–13138. [Google Scholar] [CrossRef]
- He, S.; Cheng, M.; Pan, Y.; Lin, M.; Zhu, W.-P. Distributed access and offloading scheme for multiple UAVs assisted MEC network. In Proceedings of the IEEE 98th Vehicular Technology Conference (VTC2023-Fall), Hong Kong, China, 10–13 October 2023. [Google Scholar]
- Pokkunuru, A.; Zhang, Q.; Wang, P. Capacity analysis of aerial small cells. In Proceedings of the IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017. [Google Scholar]
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv 2018, arXiv:1506.02438. [Google Scholar] [CrossRef]
- Auer, P.; Cesa-Bianchi, N.; Freund, Y.; Schapire, R.E. Gambling in a rigged casino: The adversarial multi-armed bandit problem. In Proceedings of the IEEE 36th Annual Foundations of Computer Science, Milwaukee, WI, USA, 23–25 October 1995; pp. 322–331. [Google Scholar]
- Cheng, M.; He, S.; Lin, M.; Zhu, W.-P.; Wang, J. RL and DRL Based Distributed User Access Schemes in Multi-UAV Networks. IEEE Trans. Veh. Tech. 2025, 74, 5241–5246. [Google Scholar] [CrossRef]


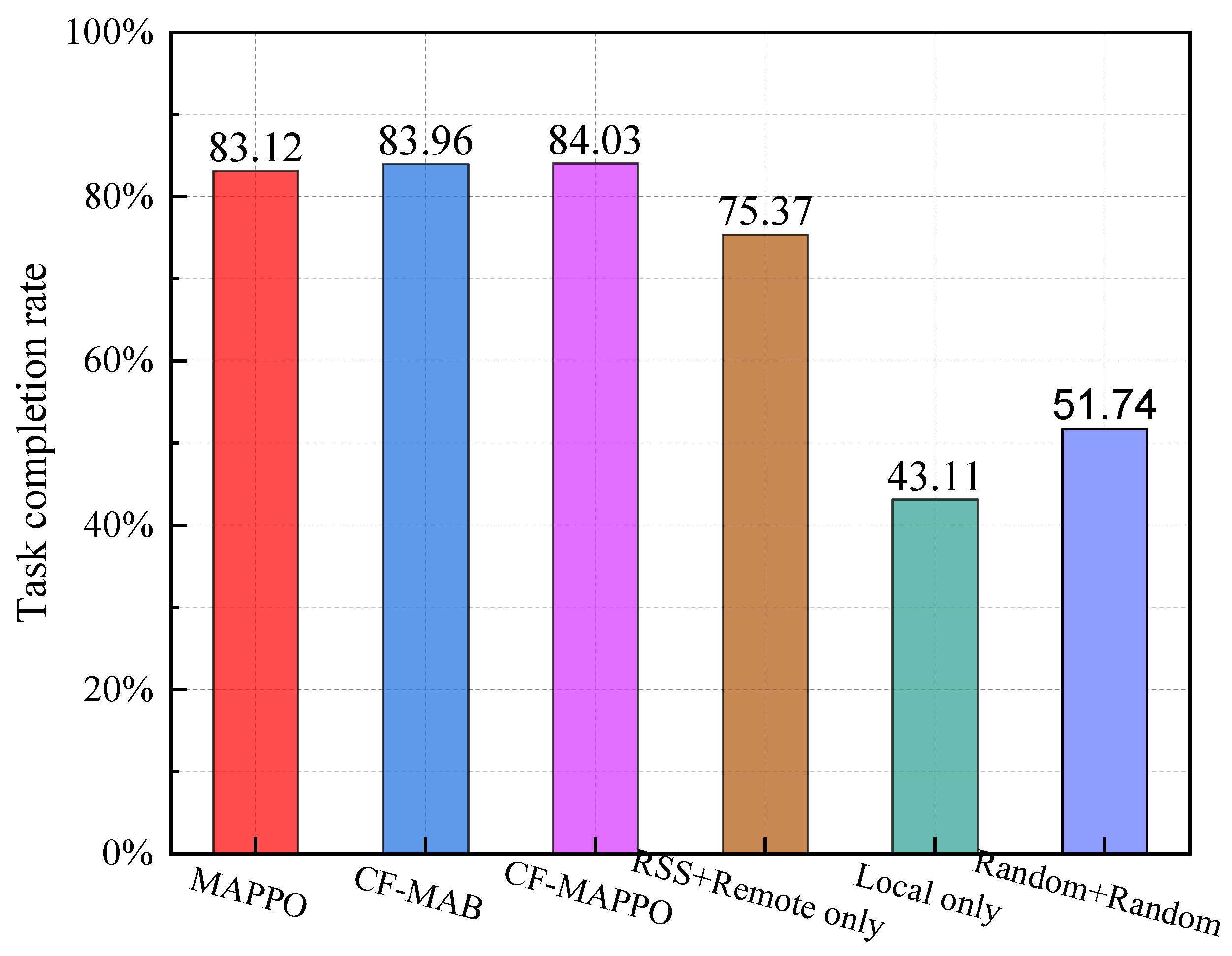
| Work | Objective | Method | |||
|---|---|---|---|---|---|
| Energy | Latency | ||||
| [11,12,13,14,15,16] | ✓ | short-term | Convex Optimization | ||
| [17,18,19,20,21,22] | ✓ | ||||
| [23,24,25,26,27,28,29] | ✓ | ✓ | |||
| [30,31] | ✓ | long-term | Lyapunov | ||
| [32,33] | ✓ | ✓ | |||
| [34] | Service quantity | ||||
| [35] | ✓ | AC | Single agent | ||
| [36] | ✓ | ✓ | DDQN | ||
| [37] | ✓ | ✓ | DDPG | ||
| [38] | ✓ | PPO | |||
| [39,42] | ✓ | ✓ | MADDPG | Multiple agents | |
| [40] | ✓ | ||||
| [41] | ✓ | ||||
| [43] | Task amount | MAPPO | |||
| [44] | Energy efficiency | ||||
| [45] | ✓ | ||||
| Notation | Description |
|---|---|
| Offloading task proportion of UD m at timeslot t | |
| , | Path loss exponent for LOS and NLOS links |
| Discount factor for rewards | |
| Parameter that adjusts the exploitation and exploration | |
| SNR between UD m and UAV n in timeslot t | |
| TD residual to calculate GAE in (24) | |
| Determines the interval of clip function | |
| Parameter that determines how aggressively to learn and update | |
| Parameter of actor network | |
| , | Weights of energy consumption by UAVs and UDs |
| Probability ratio between the current and the updated policy | |
| Adjusts the weights of energy consumption and latency | |
| Balances the bias and variance in GAE | |
| , | Attenuation factor for LOS and NLOS links |
| Policy of agent m | |
| Latency | |
| Parameter of critic network | |
| Association between UD m and UAV n in timeslot t | |
| Action of agent m in timeslot t | |
| , | System’s cost and individual cost in timeslot t |
| Volume of tasks | |
| E | Energy consumption |
| , | Computing frequencies at UD and UAV |
| Observation of UD m at timeslot t | |
| Achievable rate between UD m and UAV n in timeslot t | |
| Reward of UD m at timeslot t | |
| Individual reward function of UD m at timeslot t | |
| System’s reward function at timeslot t |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, M.; He, S.; Pan, Y.; Lin, M.; Zhu, W.-P. Cooperative Schemes for Joint Latency and Energy Consumption Minimization in UAV-MEC Networks. Sensors 2025, 25, 5234. https://doi.org/10.3390/s25175234
Cheng M, He S, Pan Y, Lin M, Zhu W-P. Cooperative Schemes for Joint Latency and Energy Consumption Minimization in UAV-MEC Networks. Sensors. 2025; 25(17):5234. https://doi.org/10.3390/s25175234
Chicago/Turabian StyleCheng, Ming, Saifei He, Yijin Pan, Min Lin, and Wei-Ping Zhu. 2025. "Cooperative Schemes for Joint Latency and Energy Consumption Minimization in UAV-MEC Networks" Sensors 25, no. 17: 5234. https://doi.org/10.3390/s25175234
APA StyleCheng, M., He, S., Pan, Y., Lin, M., & Zhu, W.-P. (2025). Cooperative Schemes for Joint Latency and Energy Consumption Minimization in UAV-MEC Networks. Sensors, 25(17), 5234. https://doi.org/10.3390/s25175234






