Achievable Rate Optimization for Reconfigurable Intelligent Surface-Aided Multi-User Movable Antenna Systems
Abstract
1. Introduction
1.1. Related Work
1.2. Contribution
- We model the RIS-aided multi-input single-output (MISO) downlink MA system and propose a novel and efficient joint optimization framework for it.
- We propose the fixed-point iteration (FPI) for the formulated problem in RIS-aided MA systems to efficiently solve the passive reflection phase, which can iteratively recover the phase at low complexity.
- We address an RIS-aided MA system by reformulating the BS antenna position optimization as an SQP problem. This formulation enables efficient handling of both nonlinearity and spatial constraints via iterative quadratic programming (QP). To jointly optimize RIS coefficients, beamforming, and antenna positions, we propose an alternating optimization framework that alternates between fixed-point iteration for RIS and beamforming, and SQP for antenna placement.
2. System Model
3. Problem Formulation
- The unit-modulus constraint on the RIS reflection coefficients ;
- A total transmit power constraint on the precoding vector ;
- A minimum spacing constraint between any two BS antenna elements to prevent spatial correlation.
3.1. Optimization of and
3.2. Optimization of
- Approximates the original problem by a quadratic model of the Lagrangian;
- Linearizes the nonlinear constraints;
- Solves the resulting QP to obtain a search direction;
- Performs a line search to determine an appropriate step size;
- Updates the current solution.
| Algorithm 1 SQP for Antenna Position Optimization |
|
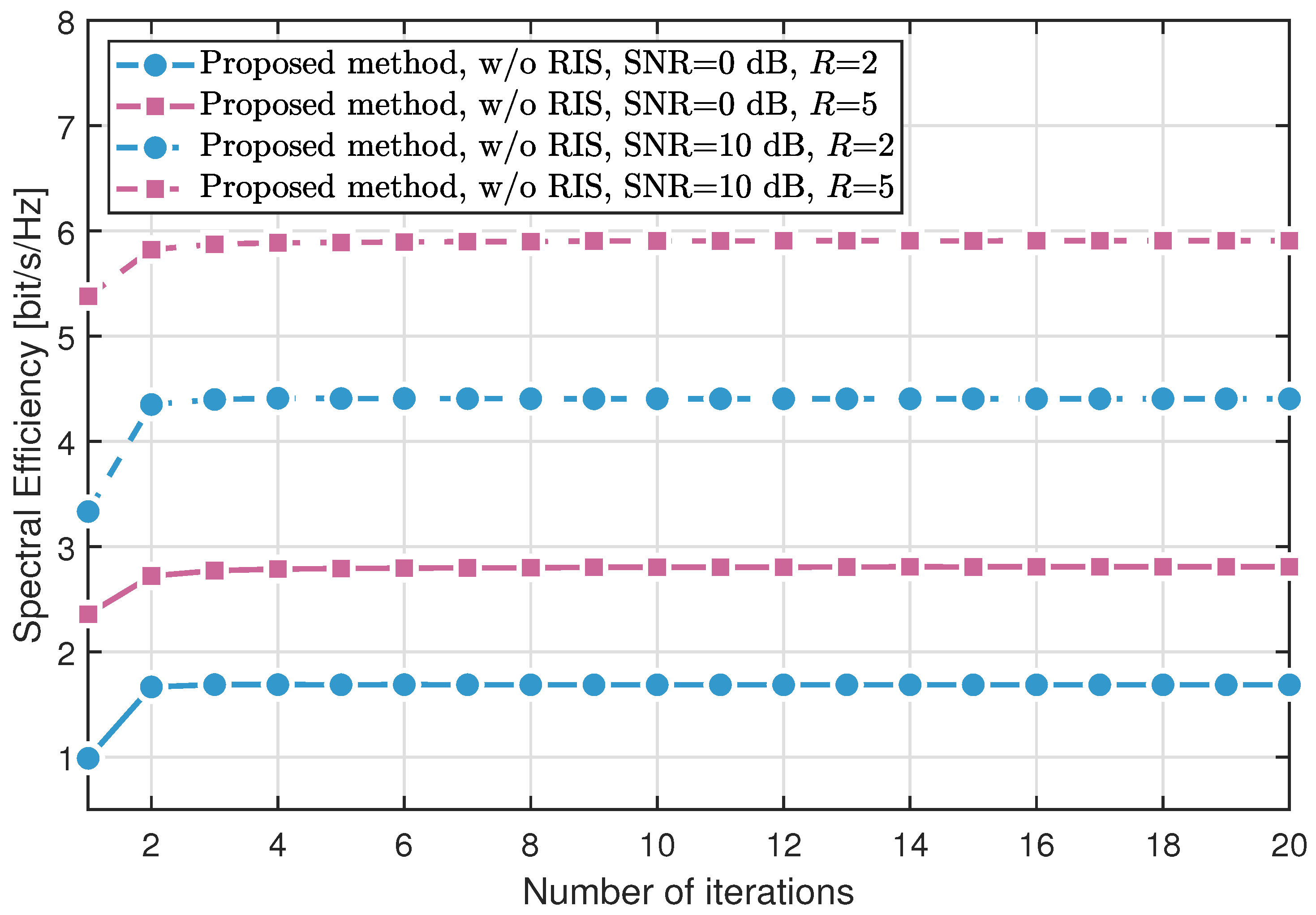
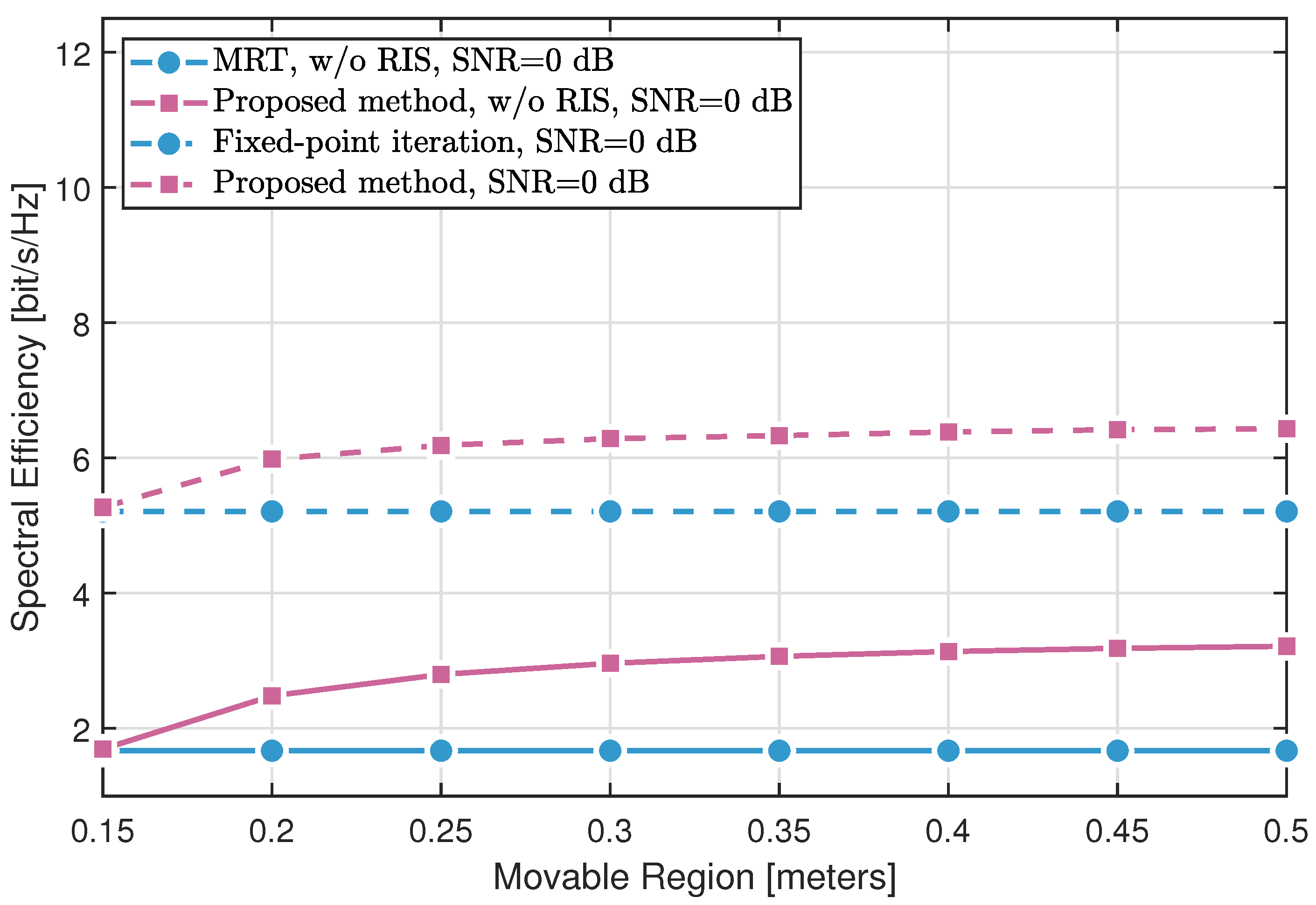
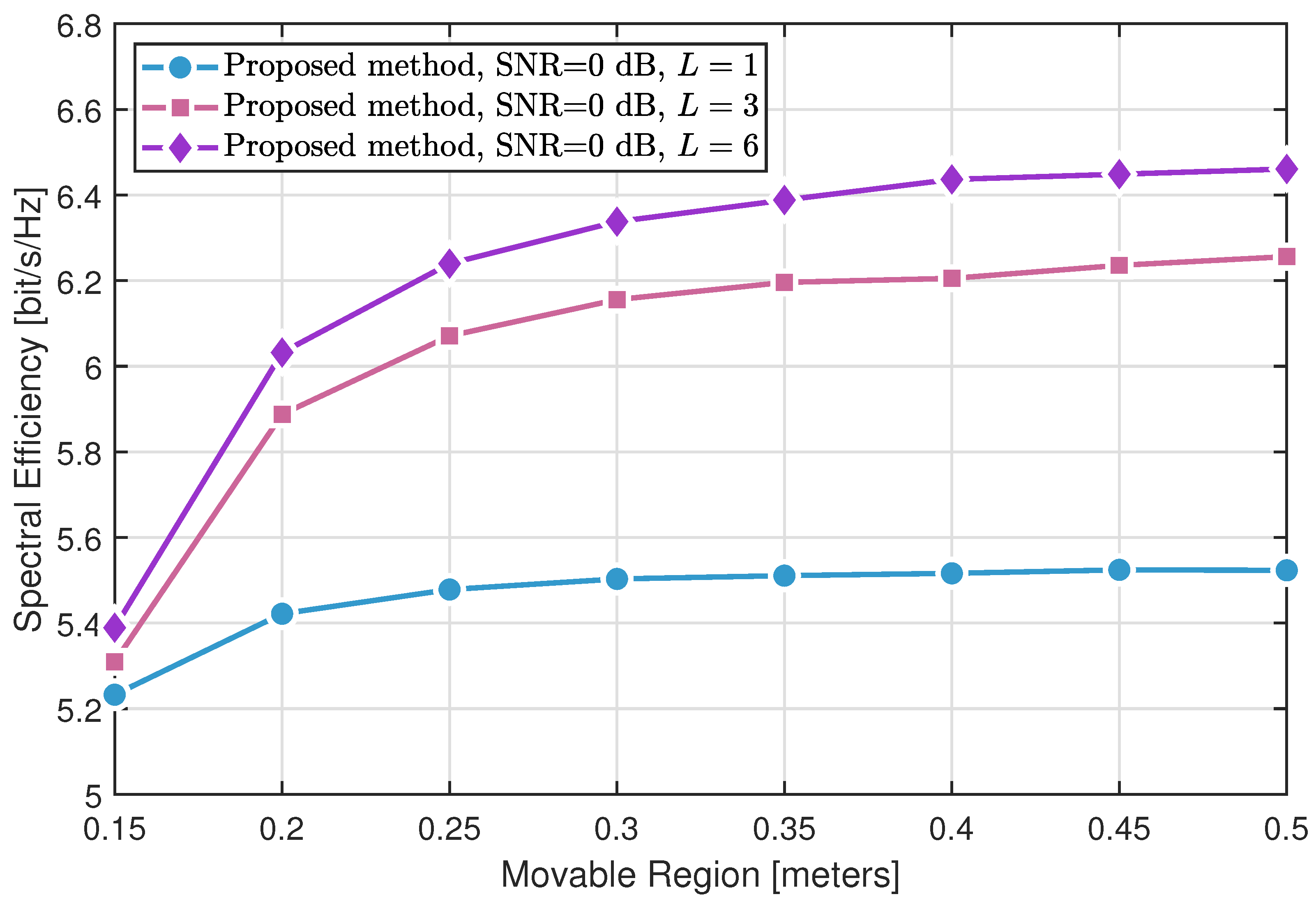
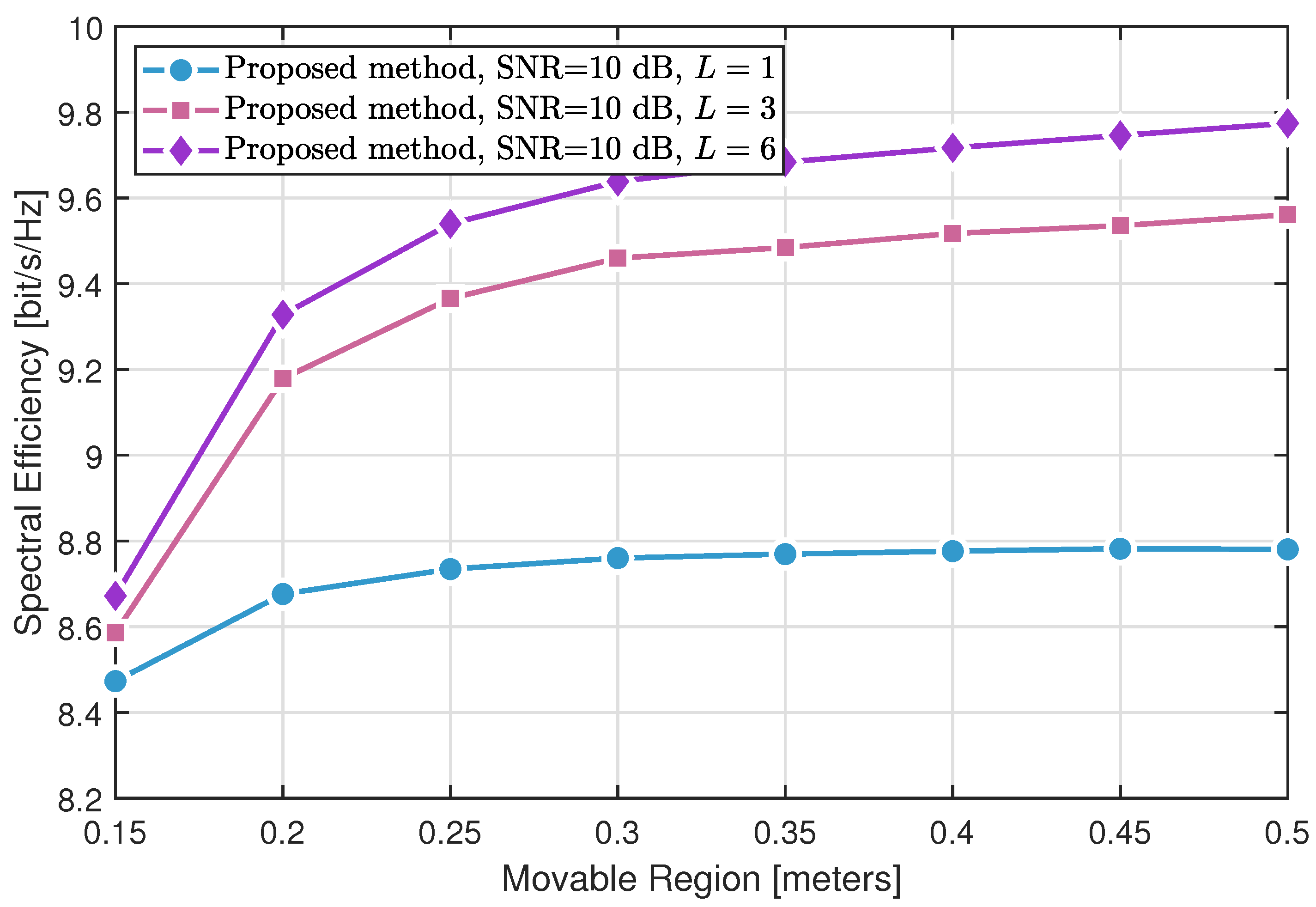
4. Results
- The fixed-point iteration method with RIS assistance significantly outperforms conventional MRT with fixed BS antennas, validating the effectiveness of RIS in enhancing the propagation environment.
- The proposed MA optimization approach without RIS yields notable gains over MRT by exploiting antenna position diversity through SQP-based optimization. When combined with RIS, the proposed method further surpasses the fixed-point RIS design, highlighting the synergistic benefits of joint MA and RIS optimization.
5. Conclusions
- BS beamforming via MRT;
- RIS beamforming via fixed-point iteration;
- BS antenna positions via SQP.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, R.; Ai, B.; Wang, G.; Yang, M.; Huang, C.; Zhong, Z. Wireless Channel Sparsity: Measurement, Analysis, and Exploitation in Estimation. IEEE Wirel. Commun. 2021, 28, 113–119. [Google Scholar] [CrossRef]
- Yang, S.; Xie, C.; Wang, D.; Zhang, Z. Fast Multibeam Training for mmWave MIMO Systems With Subconnected Hybrid Beamforming Architecture. IEEE Syst. J. 2023, 17, 2939–2949. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable Intelligent Surfaces for Energy Efficiency in Wireless Communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent Reflecting Surface Enhanced Wireless Network via Joint Active and Passive Beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Lyu, W.; Yang, S.; Xiu, Y.; Li, Y.; He, H.; Yuen, C.; Zhang, Z. CRB Minimization for RIS-Aided mmWave Integrated Sensing and Communications. IEEE Internet Things J. 2024, 11, 18381–18393. [Google Scholar] [CrossRef]
- Meng, K.; Masouros, C.; Petropulu, A.P.; Hanzo, L. Cooperative ISAC Networks: Opportunities and Challenges. IEEE Wirel. Commun. 2024, 32, 212–219. [Google Scholar] [CrossRef]
- Lu, H.; Zeng, Y. Near-Field Modeling and Performance Analysis for Multi-User Extremely Large-Scale MIMO Communication. IEEE Commun. Lett. 2022, 26, 277–281. [Google Scholar] [CrossRef]
- Yang, S.; Lyu, W.; Hu, Z.; Zhang, Z.; Yuen, C. Channel Estimation for Near-Field XL-RIS-Aided mmWave Hybrid Beamforming Architectures. IEEE Trans. Veh. Technol. 2023, 72, 11029–11034. [Google Scholar] [CrossRef]
- Yang, S.; Chen, H.; Liu, W.; Zhang, X.-P.; Yuen, C. Near-Field Channel Estimation and Localization: Recent Developments, Cooperative Integration, and Future Directions. IEEE Signal Process. Mag. 2025, 42, 60–73. [Google Scholar] [CrossRef]
- Pan, C.; Zhou, G.; Zhi, K.; Hong, S.; Wu, T.; Pan, Y.; Ren, H.; Di Renzo, M.; Swindlehurst, A.L.; Zhang, R.; et al. An Overview of Signal Processing Techniques for RIS/IRS-Aided Wireless Systems. IEEE J. Sel. Top. Signal Process. 2022, 16, 883–917. [Google Scholar] [CrossRef]
- Jung, M.; Saad, W.; Debbah, M.; Hong, C.S. On the Optimality of Reconfigurable Intelligent Surfaces (RISs): Passive Beamforming, Modulation, and Resource Allocation. IEEE Trans. Wirel. Commun. 2021, 20, 4347–4363. [Google Scholar] [CrossRef]
- Chen, J.; Wu, K.; Niu, J.; Li, Y. Joint Active and Passive Beamforming in RIS-Assisted Secure ISAC Systems. Sensors 2024, 24, 289. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Deng, F.; Li, S. Jointly Active/Passive Beamforming Optimization for Intelligent-Reflecting Surface-Assisted Cognitive-IoT Networks. Electronics 2024, 13, 299. [Google Scholar] [CrossRef]
- Peng, C.; Deng, H.; Xiao, H.; Qian, Y.; Zhang, W.; Zhang, Y. Two-Stage Channel Estimation for Semi-Passive RIS-Assisted Millimeter Wave Systems. Sensors 2022, 22, 5908. [Google Scholar] [CrossRef]
- Yang, S.; Lyu, W.; Xiu, Y.; Zhang, Z.; Yuen, C. Active 3D Double-RIS-Aided Multi-User Communications: Two-Timescale-Based Separate Channel Estimation via Bayesian Learning. IEEE Trans. Commun. 2023, 71, 3605–3620. [Google Scholar] [CrossRef]
- Wang, B.; Pan, C.; Ren, H.; Yu, Z.; Zhang, Y.; Liu, M.; Zhou, G. Beamforming Design for Double-Active-RIS-aided Communication Systems with Inter-Excitation. IEEE Trans. Wirel. Commun. 2025, 24, 5855–5870. [Google Scholar] [CrossRef]
- Do, T.N.; Kaddoum, G.; Nguyen, T.L.; da Costa, D.B.; Haas, Z.J. Multi-RIS-Aided Wireless Systems: Statistical Characterization and Performance Analysis. IEEE Trans. Commun. 2021, 69, 8641–8658. [Google Scholar] [CrossRef]
- Castillo-Soria, F.R.; Macias-Velasquez, S.; Kumaravel, V.B.; Ramos, V.; Azurdia-Meza, C.A. Multiple Parallel RIS-Assisted MU-MIMO-DQSM System: Blind and Intelligent Approaches. China Commun. 2024, 21, 1–16. [Google Scholar]
- Lyu, W.; Xiu, Y.; Yang, S.; Yuen, C.; Zhang, Z. Energy-Efficient Cell-Free Network Assisted by Hybrid RISs. IEEE Wirel. Commun. Lett. 2023, 12, 718–722. [Google Scholar] [CrossRef]
- Yang, S.; Xie, C.; Lyu, W.; Ning, B.; Zhang, Z.; Yuen, C. Near-Field Channel Estimation for Extremely Large-Scale Reconfigurable Intelligent Surface (XL-RIS)-Aided Wideband mmWave Systems. IEEE J. Sel. Areas Commun. 2024, 42, 1567–1582. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, W.; Zhang, R. Movable Antennas for Wireless Communication: Opportunities and Challenges. IEEE Commun. Mag. 2024, 62, 114–120. [Google Scholar] [CrossRef]
- Wong, K.K.; Shojaeifard, A.; Tong, K.F.; Zhang, Y. Performance Limits of Fluid Antenna Systems. IEEE Commun. Lett. 2020, 24, 2469–2472. [Google Scholar] [CrossRef]
- Ning, B.; Yang, S.; Wu, Y.; Wang, P.; Mei, W.; Yuen, C.; Bjornson, E. Movable Antenna-Enhanced Wireless Communications: General Architectures and Implementation Methods. IEEE Wirel. Commun. 2025, 1–9. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, W.; Zhang, R. Modeling and Performance Analysis for Movable Antenna Enabled Wireless Communications. IEEE Trans. Wirel. Commun. 2023, 23, 6234–6250. [Google Scholar] [CrossRef]
- Lai, X.; Wu, T.; Yao, J.; Pan, C.; Elkashlan, M.; Wong, K.K. On Performance of Fluid Antenna System Using Maximum Ratio Combining. IEEE Commun. Lett. 2024, 28, 402–406. [Google Scholar] [CrossRef]
- Wong, K.K.; Tong, K.F. Fluid Antenna Multiple Access. IEEE Trans. Wirel. Commun. 2022, 21, 4801–4815. [Google Scholar] [CrossRef]
- Zhu, L.; Ma, W.; Ning, B.; Zhang, R. Movable-Antenna Enhanced Multiuser Communication via Antenna Position Optimization. IEEE Trans. Wirel. Commun. 2023, 23, 7214–7229. [Google Scholar] [CrossRef]
- Qin, H.; Chen, W.; Li, Z.; Wu, Q.; Cheng, N.; Chen, F. Antenna Positioning and Beamforming Design for Fluid-Antenna Enabled Multi-user Downlink Communications. arXiv 2023, arXiv:2311.03046. [Google Scholar]
- Yang, S.; Lyu, W.; Ning, B.; Zhang, Z.; Yuen, C. Flexible Precoding for Multi-User Movable Antenna Communications. IEEE Wirel. Commun. Lett. 2024, 13, 1404–1408. [Google Scholar] [CrossRef]
- Pi, X.; Zhu, L.; Xiao, Z.; Zhang, R. Multiuser Communications with Movable-Antenna Base Station Via Antenna Position Optimization. arXiv 2023, arXiv:2308.05546. [Google Scholar] [CrossRef]
- Yang, S.; An, J.; Xiu, Y.; Lyu, W.; Ning, B.; Zhang, Z.; Debbah, M.; Yuen, C. Flexible Antenna Arrays for Wireless Communications: Modeling and Performance Evaluation. IEEE Trans. Wirel. Commun. 2025, 24, 4937–4951. [Google Scholar] [CrossRef]
- Lyu, W.; Yang, S.; Xiu, Y.; Zhang, Z.; Assi, C.; Yuen, C. Movable Antenna Enabled Integrated Sensing and Communication. IEEE Trans. Wirel. Commun. 2025, 24, 2862–2875. [Google Scholar] [CrossRef]
- Kuang, Z.; Liu, W.; Wang, C.; Jin, Z.; Ren, J.; Zhang, X.; Shen, Y. Movable-Antenna Array Empowered ISAC Systems for Low-Altitude Economy. In Proceedings of the 2024 IEEE/CIC International Conference on Communications in China (ICCC Workshops), Hangzhou, China, 7–9 August 2024; pp. 776–781. [Google Scholar]
- Sun, Y.; Xu, H.; Ning, B.; Cheng, Z.; Ouyang, C.; Yang, H. Sum-Rate Optimization for RIS-Aided Multiuser Communications With Movable Antennas. IEEE Wirel. Commun. Lett. 2025, 14, 450–454. [Google Scholar] [CrossRef]
- Zhang, B.; Xu, K.; Xia, X.; Hu, G.; Wei, C.; Li, C.; Cheng, K. Sum-Rate Enhancement for RIS-Assisted Movable Antenna Systems: Joint Transmit Beamforming, Reflecting Design, and Antenna Positioning. IEEE Trans. Veh. Technol. 2025, 74, 4376–4392. [Google Scholar] [CrossRef]
- Wei, X.; Mei, W.; Wu, Q.; Ning, B.; Chen, Z. Movable Antennas Meet Intelligent Reflecting Surface: When Do We Need Movable Antennas? In Proceedings of the 2025 IEEE Wireless Communications and Networking Conference (WCNC), Milan, Italy, 24–27 March 2025; pp. 1–6. [Google Scholar]
- Yang, S.; Wan, Z.; Ning, B.; Mei, W.; An, J.; Eldar, Y.C.; Yuen, C. Flexible Intelligent Metasurface-Aided Wireless Communications: Architecture and Performance. arXiv 2025, arXiv:2503.11112. [Google Scholar]
- Zhang, Y.; Dey, I.; Marchetti, N. RIS-aided Wireless Communication with Movable Elements Geometry Impact on Performance. arXiv 2024, arXiv:2405.00141. [Google Scholar] [CrossRef]
- Fletcher, R.; Leyffer, S.; Toint, P.L. On the Global Convergence of a Filter–SQP Algorithm. SIAM J. Optim. 2002, 13, 44–59. [Google Scholar] [CrossRef]


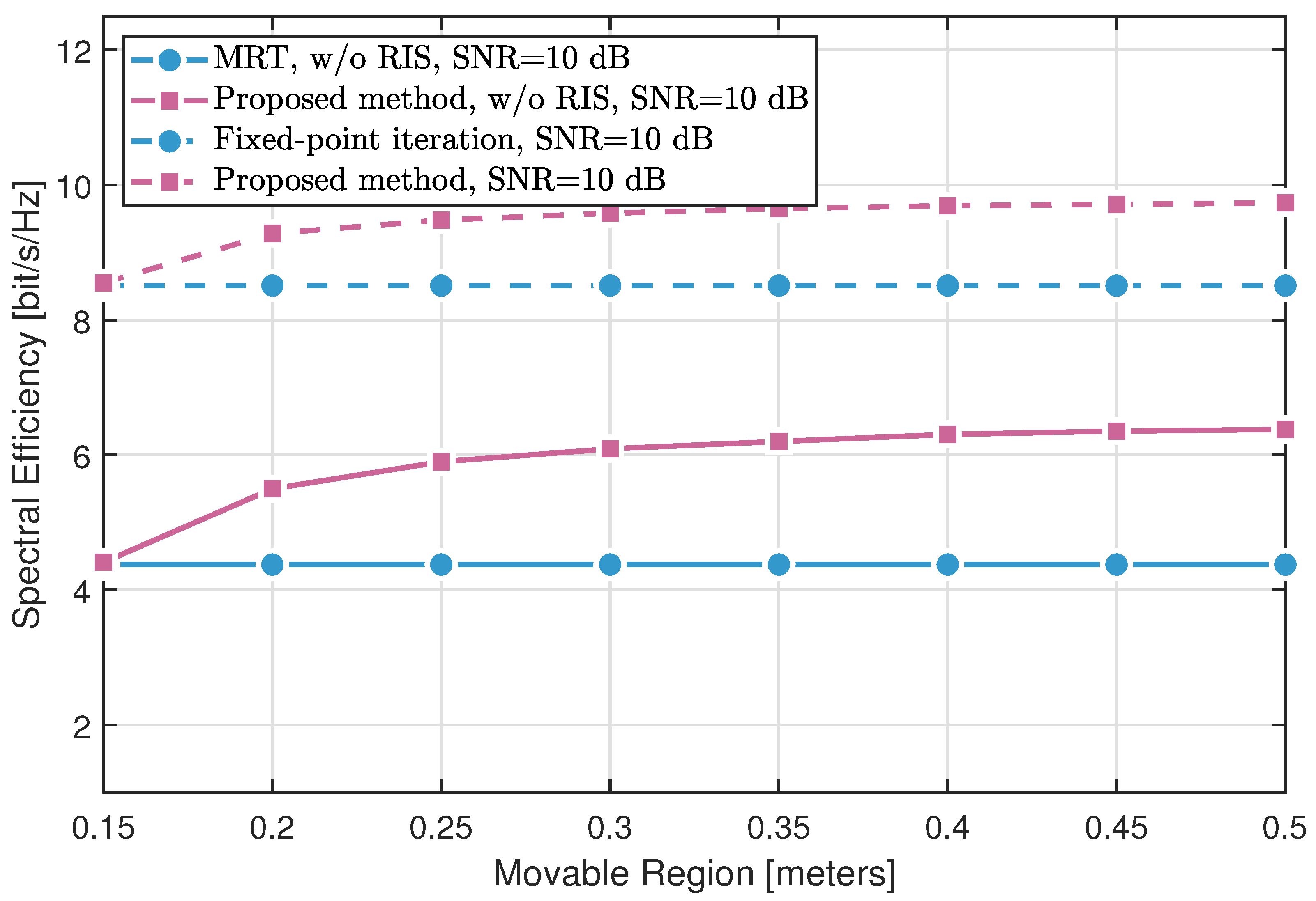

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, L.; Ren, Y. Achievable Rate Optimization for Reconfigurable Intelligent Surface-Aided Multi-User Movable Antenna Systems. Sensors 2025, 25, 4694. https://doi.org/10.3390/s25154694
Yu L, Ren Y. Achievable Rate Optimization for Reconfigurable Intelligent Surface-Aided Multi-User Movable Antenna Systems. Sensors. 2025; 25(15):4694. https://doi.org/10.3390/s25154694
Chicago/Turabian StyleYu, Liji, and Yuhui Ren. 2025. "Achievable Rate Optimization for Reconfigurable Intelligent Surface-Aided Multi-User Movable Antenna Systems" Sensors 25, no. 15: 4694. https://doi.org/10.3390/s25154694
APA StyleYu, L., & Ren, Y. (2025). Achievable Rate Optimization for Reconfigurable Intelligent Surface-Aided Multi-User Movable Antenna Systems. Sensors, 25(15), 4694. https://doi.org/10.3390/s25154694





