Adaptive Guided Filtering and Spectral-Entropy-Based Non-Uniformity Correction for High-Resolution Infrared Line-Scan Images
Abstract
1. Introduction
1.1. Background
1.2. Related Work
- (1)
- Filtering-based methods: These extract low-frequency bias components using spatial or frequency domain techniques such as mean [30], Gaussian [31], or guided filtering [32,33,34]. The estimated noise is subtracted from the original image. Although computationally efficient, these methods often lead to over-smoothing or texture loss in regions with varying stripe intensities or complex backgrounds [35,36,37,38].
- (2)
- (3)
- Model optimization methods: These construct priors and regularization terms using approaches like total variation [42,43], wavelet transforms [44], curvelet transforms [45], or low-rank decomposition [46]. Although capable of preserving details and separating structured noise, they often suffer from high computational costs and sensitivity to parameter tuning [47,48,49].
- (4)
- Neural-network-based methods: End-to-end learning models [50], including convolutional neural networks [51], residual networks [52], and autoencoders [53], have shown strong performance on labeled datasets. However, their reliance on extensive training data, poor generalization to unseen scenes, and limited interpretability constrain their practical deployment [54,55,56].
1.3. Our Contributions
- (1)
- Row-mean-based 1D modeling: Projects 2D images into 1D sequences through row averaging, which improves stripe directionality, simplifies modeling, and boosts sensitivity to directional noise.
- (2)
- MAD-driven adaptive guided filtering: A fusion framework combines global background trends with local structural features. Filter scales are adaptively chosen based on local median absolute deviation (MAD), allowing spatially adaptive smoothing while maintaining structural accuracy.
- (3)
- Spectral-entropy-based frequency masking: A frequency-domain suppression method is introduced that uses spectral entropy to build adaptive thresholds, enabling the isolation and suppression of both periodic and aperiodic interference without requiring iterative optimization or high-order reconstruction.
- (4)
- Lightweight and efficient implementation: The complete algorithm is streamlined for real-time applications. It requires only a single pass of guided filtering and two FFT operations, making it suitable for embedded and resource-constrained platforms.
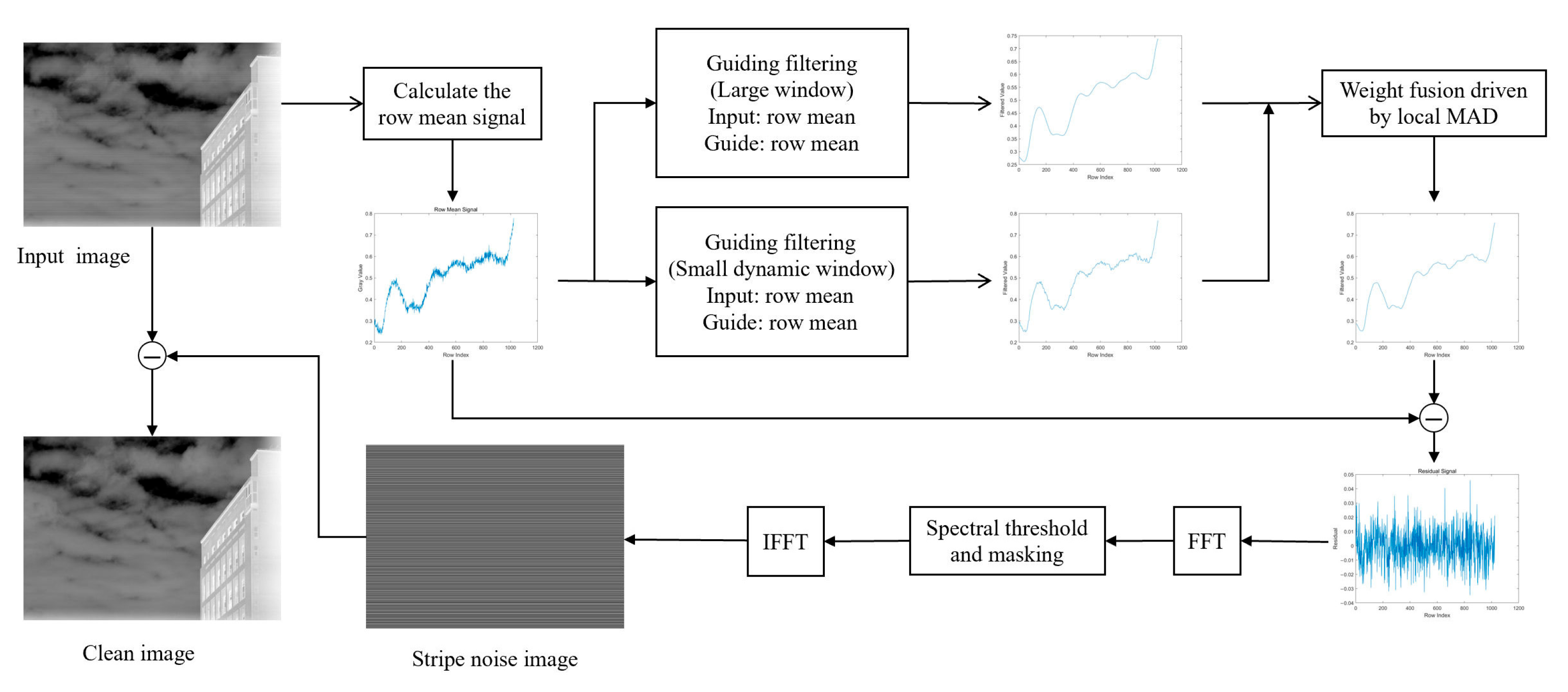
2. Materials and Methods
2.1. One-Dimensional Modeling and Orientation Feature Extraction
2.2. Multi-Scale Guided Filtering with MAD-Based Adaptation
2.2.1. Principle of Guided Filtering
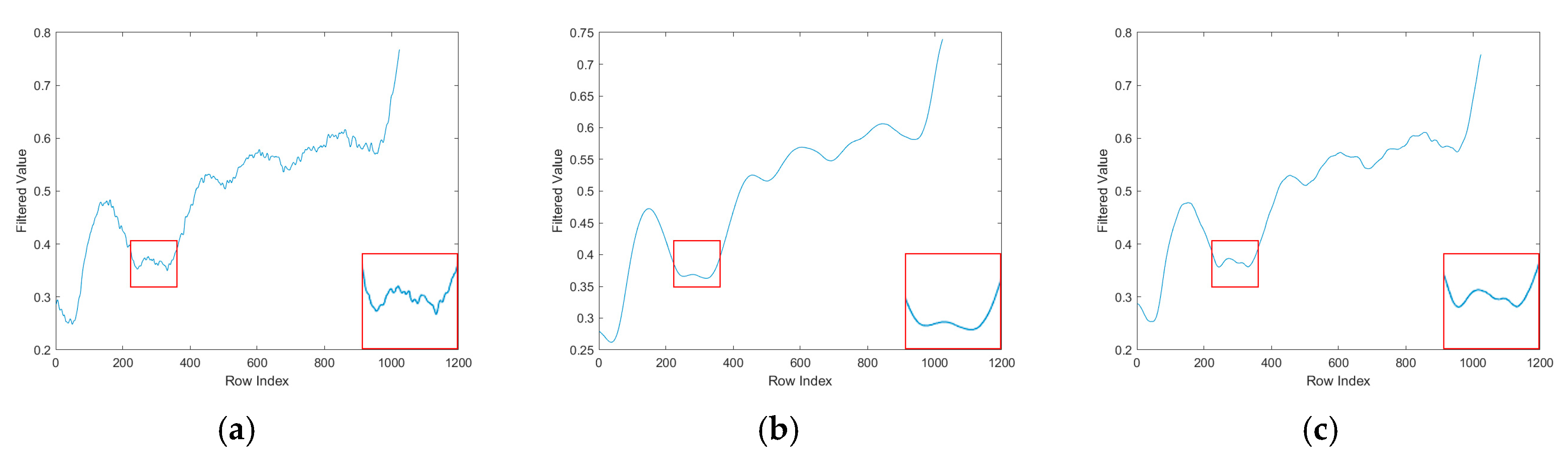
2.2.2. MAD-Driven Dynamic Fusion Strategy
2.3. Frequency-Domain Spectral Entropy Gating Mechanism
2.4. Stripe Expansion and Image Restoration
2.5. Experimental Setup
3. Results
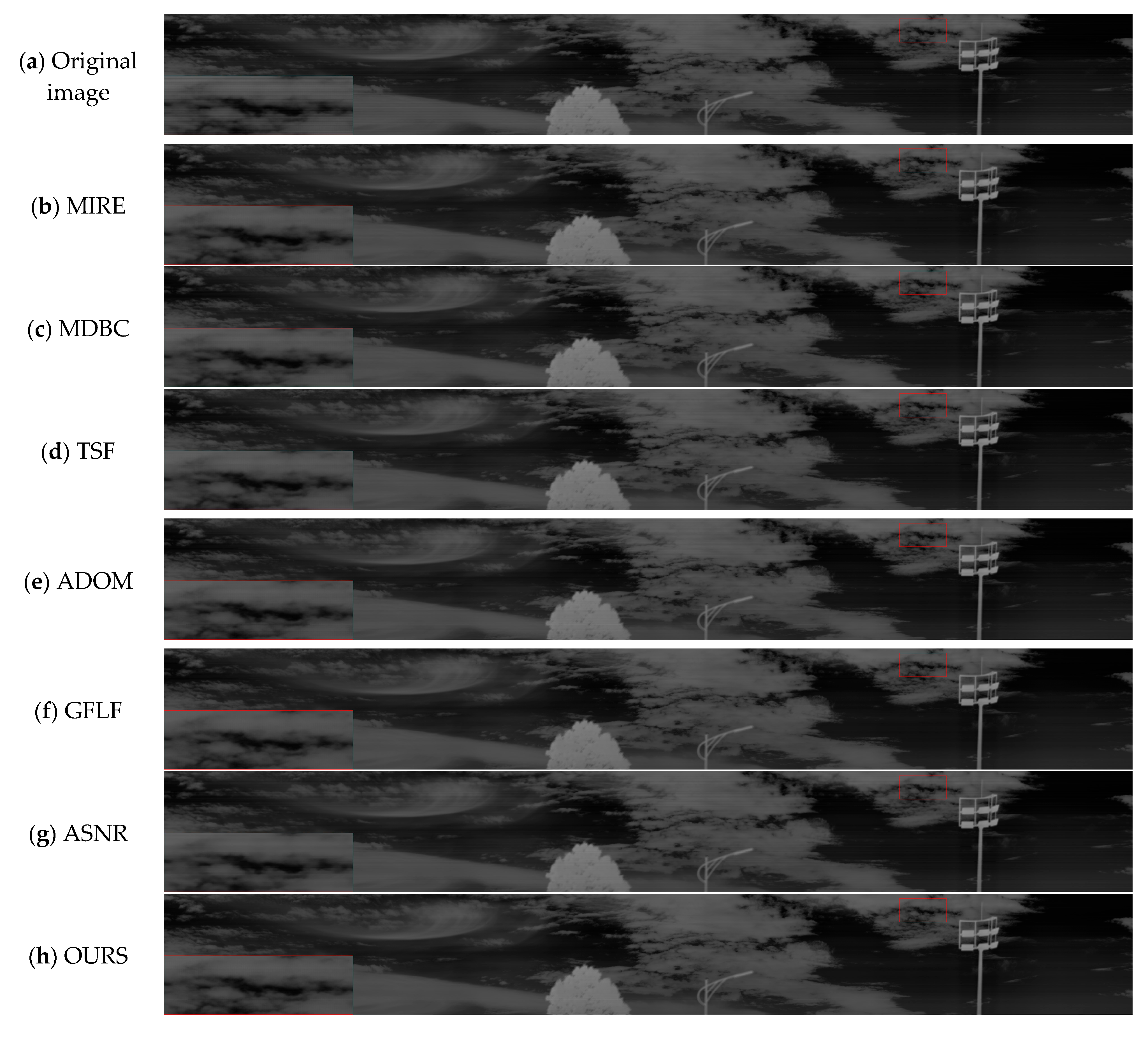
- (1)
- Frequency-domain filtering-based methods: the two-stage filtering (TSF) approach proposed by Zeng in 2018 [36] combines frequency-domain filtering with one-dimensional row-guided filtering, aiming to remove stripe artifacts while preserving image structures.
- (2)
- Spatial-domain guided filtering approaches: the guided filtering with linear fitting (GFLF) method proposed by Li in 2023 [32] performs non-uniformity correction via one-dimensional guided filtering and regression modeling. The ASNR method proposed by Hamadouche in 2024 [33] further integrates frequency mask extraction with guided filtering to enhance stripe suppression capability.
- (3)
- Optimization-based methods: the ADOM model [49] incorporates Weighted Paradigm Regularization and a Momentum Update Mechanism within an ADMM optimization framework to correct non-uniformity artifacts adaptively.
- (4)
- Traditional methods: the Median-Histogram-Equalization-based Non-uniformity Correction Algorithm (MIRE) proposed by Tendero in 2012 [40] and the Estimating Bias by Minimizing the Differences Between Neighboring Columns (MDBC) method introduced by Wang in 2016 [47] serve as classical baselines in non-uniformity correction, relying on histogram statistics and local column differences, respectively.
3.1. Noise Modeling and Analysis
3.2. Evaluation Indicators
3.3. Ablation Experiments
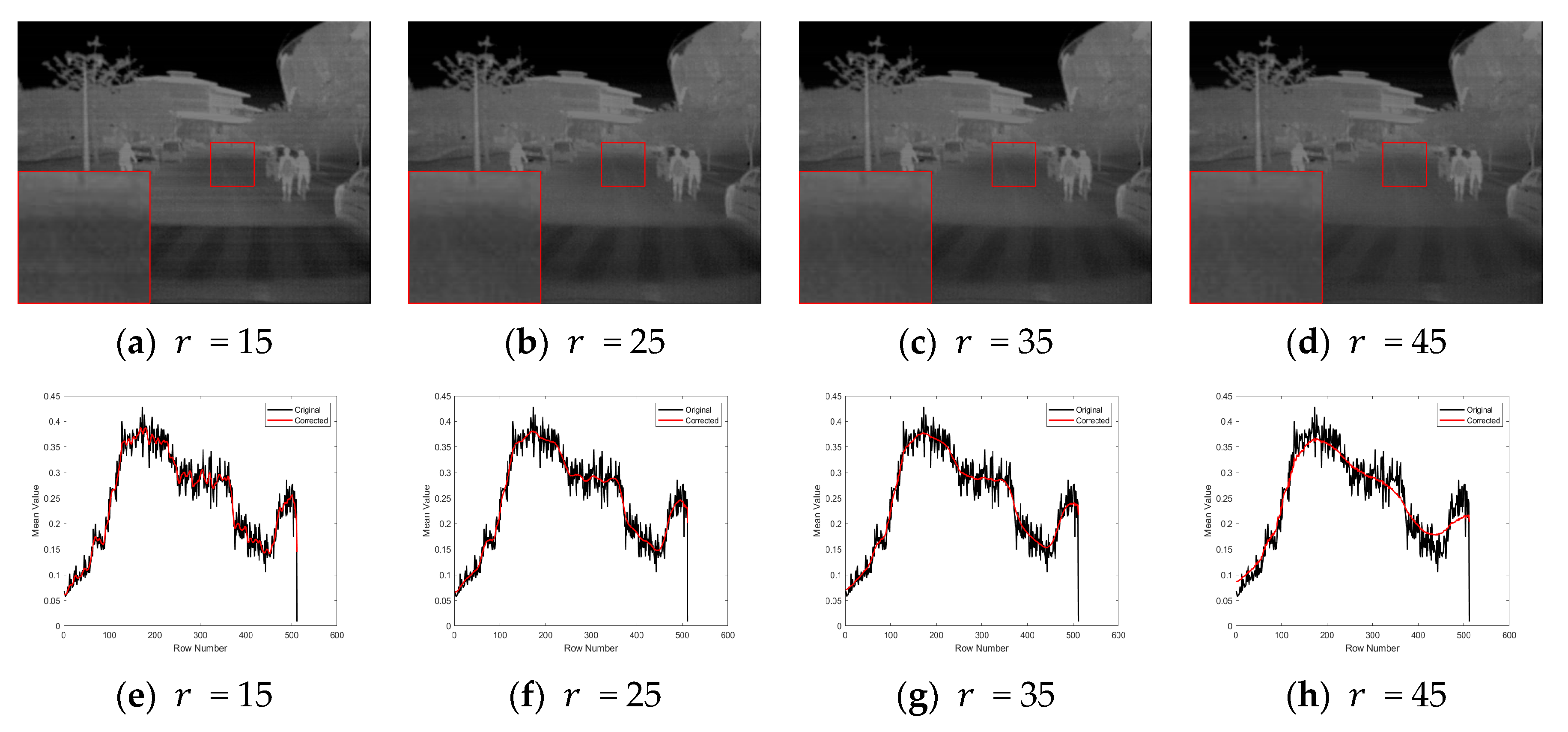
3.4. Parameter Sensitivity Analysis
3.5. Method Performance Comparison and Analysis
3.5.1. Comparison Algorithm and Experimental Setup
3.5.2. Quantitative Testing of Simulated Datasets
- (1)
- OSU Dataset [62]: Provided by Ohio State University, this dataset captures human activity scenes in natural outdoor environments. With a resolution of 240 × 320, it reflects low-resolution infrared imaging scenarios and is suitable for evaluating algorithm performance under small-scale conditions.
- (2)
- KAIST Dataset [63]: Released by the Korea Advanced Institute of Science and Technology, this dataset includes city streets, parking lots, and varying illumination conditions across day, dusk, and night. The image resolution is 512 × 640, which provides a moderately complex environment for evaluating detail preservation and mid-scale stripe correction.
- (3)
- LLVIP Dataset [64]: Developed by the University of Science and Technology of China, this dataset consists of indoor and outdoor scenes captured under low-light and nighttime conditions. The images include fine-grained thermal signatures from pedestrians, and the resolution is 1024 × 1280, making it ideal for high-resolution correction analysis.
3.5.3. Quantitative Testing on Real Datasets
3.5.4. Qualitative Visualization Comparison
3.6. Runtime Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Strickland, R.N. Infrared Techniques for Military Applications. In Infrared Methodology and Technology; CRC Press: Boca Raton, FL, USA, 2023; pp. 397–427. [Google Scholar]
- Kuenzer, C.; Dech, S. Thermal Infrared Remote Sensing. Remote Sens. Digit. Image Process. 2013, 10, 978–994. [Google Scholar]
- Huang, Z.; Zhang, Y.; Li, Q.; Zhang, T.; Sang, N.; Hong, H. Progressive Dual-Domain Filter for Enhancing and Denoising Optical Remote-Sensing Images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 759–763. [Google Scholar] [CrossRef]
- Raza, A.; Chelloug, S.A.; Alatiyyah, M.H.; Jalal, A.; Park, J. Multiple pedestrian detection and tracking in night vision surveillance systems. Comput. Mater. Contin. 2023, 75, 3275–3289. [Google Scholar] [CrossRef]
- Patel, H.; Upla, K.P. Night Vision Surveillance: Object Detection Using Thermal and Visible Images. In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020; pp. 1–6. [Google Scholar]
- Venegas, P.; Ivorra, E.; Ortega, M.; Sáez de Ocáriz, I. Towards the Automation of Infrared Thermography Inspections for Industrial Maintenance Applications. Sensors 2022, 22, 613. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Zhan, C.; Chen, L.; Wang, Y.; Li, G. Review of unmanned aerial vehicle infrared thermography (UAV-IRT) applications in building thermal performance: Towards the thermal performance evaluation of building envelope. Quant. InfraRed Thermogr. J. 2025, 22, 266–296. [Google Scholar] [CrossRef]
- Hua, W.; Zhao, J.; Cui, G.; Gong, X.; Ge, P.; Zhang, J.; Xu, Z. Stripe Nonuniformity Correction for Infrared Imaging System Based on Single Image Optimization. Infrared Phys. Technol. 2018, 91, 250–262. [Google Scholar] [CrossRef]
- Chen, W.; Li, B. Overcoming Periodic Stripe Noise in Infrared Linear Array Images: The Fourier-Assisted Correlative Denoising Method. Sensors 2023, 23, 8716. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Chen, W.; Zhu, Y.; Duan, Q.; Zhu, Y.; Zhang, Y. An Adaptive Weighted Residual-Guided Algorithm for Non-Uniformity Correction of High-Resolution Infrared Line-Scanning Images. Sensors 2025, 25, 1511. [Google Scholar] [CrossRef]
- Cao, Y.; Tisse, C.L. Solid state temperature-dependent NUC (non-uniformity correction) in uncooled LWIR (long-wave infrared) imaging system. In Proceedings of the Infrared Technology and Applications XXXIX, Bellingham, WA, USA, 18 June 2013; Volume 8704, pp. 838–845. [Google Scholar]
- Liu, S.; Cui, H.; Li, J.; Yao, M.; Wang, S.; Wei, K. Low-Contrast Scene Feature-Based Infrared Nonuniformity Correction Method for Airborne Target Detection. Infrared Phys. Technol. 2023, 133, 104799. [Google Scholar] [CrossRef]
- He, Y.; Zhang, C.; Tang, Q. Non-uniformity correction based on sparse directivity and low rankness for infrared maritime imaging. In Proceedings of the 6th International Conference on Information Communication and Signal Processing (ICICSP), Xi’an, China, 23–25 September 2023; pp. 154–158. [Google Scholar]
- Ding, S.; Wang, D.; Zhang, T. A median-ratio scene-based non-uniformity correction method for airborne infrared point target detection system. Sensors 2020, 20, 3273. [Google Scholar] [CrossRef]
- Boutemedjet, A.; Deng, C.; Zhao, B. Edge-aware unidirectional total variation model for stripe non-uniformity correction. Sensors 2018, 18, 1164. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Pezoa, J.E.; Figueroa, M. Modeling and compensating temperature-dependent non-uniformity noise in IR microbolometer cameras. Sensors 2016, 16, 1121. [Google Scholar] [CrossRef]
- Liu, C.; Sui, X.; Gu, G.; Chen, Q. Shutterless non-uniformity correction for the long-term stability of an uncooled long-wave infrared camera. Meas. Sci. Technol. 2018, 29, 025402. [Google Scholar] [CrossRef]
- Chang, S.; Li, Z. Single-reference-based solution for two-point nonuniformity correction of infrared focal plane arrays. Infrared Phys. Technol. 2019, 101, 96–104. [Google Scholar] [CrossRef]
- Averbuch, A.; Liron, G.; Bobrovsky, B.Z. Scene-based non-uniformity correction in thermal images using Kalman filter. Image Vis. Comput. 2007, 25, 833–851. [Google Scholar] [CrossRef]
- Liu, Y.; Qiu, B.; Tian, Y.; Cai, J.; Sui, X.; Chen, Q. Scene-based dual domain non-uniformity correction algorithm for stripe and optics-caused fixed pattern noise removal. Opt. Express 2024, 32, 16591–16610. [Google Scholar] [CrossRef] [PubMed]
- Lian, X.; Li, J.; Sun, D. Adaptive nonuniformity correction methods for push-broom hyperspectral cameras. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 7253–7263. [Google Scholar] [CrossRef]
- Song, S.; Zhai, X. Research on non-uniformity correction based on blackbody calibration. In Proceedings of the 2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, China, 12–14 June 2020; Volume 1, pp. 2146–2150. [Google Scholar]
- Wang, H.; Ma, C.; Cao, J.; Zhang, H. An adaptive two-point non-uniformity correction algorithm based on shutter and its implementation. In Proceedings of the 5th International Conference on Measuring Technology and Mechatronics Automation, Hong Kong, China, 16–17 January 2013; pp. 174–177. [Google Scholar]
- Kim, S. Two-point correction and minimum filter-based nonuniformity correction for scan-based aerial infrared cameras. Opt. Eng. 2012, 51, 106401. [Google Scholar] [CrossRef]
- Hu, J.; Xu, Z.; Wan, Q. Non-uniformity correction of infrared focal plane array in point target surveillance systems. Infrared Phys. Technol. 2014, 66, 56–69. [Google Scholar] [CrossRef]
- Wang, J.; Hong, W. Non-uniformity correction for infrared cameras with variable integration time based on two-point correction. In Proceedings of the AOPC 2021: Infrared Device and Infrared Technology 2021, Beijing, China, 23–25 July 2021; Volume 12061, pp. 258–263. [Google Scholar]
- Zhai, G.; Cheng, Y.; Han, Z.; Wang, D. The implementation of non-uniformity correction in multi-TDICCD imaging system. In Proceedings of the AOPC 2015: Image Processing and Analysis, Beijing, China, 5–7 May 2015; Volume 9675, pp. 66–70. [Google Scholar]
- Njuguna, J.C.; Alabay, E.; Çelebi, A.; Çelebi, A.T.; Güllü, M.K. Field programmable gate arrays implementation of two-point non-uniformity correction and bad pixel replacement algorithms. In Proceedings of the 2021 International Conference on Innovations in Intelligent Systems and Applications (INISTA), Kocaeli, Turkey, 25–27 August 2021; pp. 1–6. [Google Scholar]
- Ashiba, H.I.; Sadic, N.; Hassan, E.S.; El-Dolil, S.; Abd El-Samie, F.E. New proposed algorithms for infrared video sequences non-uniformity correction. Wirel. Pers. Commun. 2022, 126, 1051–1073. [Google Scholar] [CrossRef]
- Scribner, D.A.; Sarkady, K.A.; Kruer, M.R.; Caulfield, J.T. Adaptive nonuniformity correction for IR focal plane arrays using neural networks. In Proceedings of the SPIE, San Diego, CA, USA, 21 July 1991; Volume 1541, pp. 100–109. [Google Scholar]
- Sghaier, A.; Douik, A.; Machhout, M. FPGA implementation of filtered image using 2D Gaussian filter. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 7. [Google Scholar]
- Li, B.; Chen, W.; Zhang, Y. A nonuniformity correction method based on 1D guided filtering and linear fitting for high-resolution infrared scan images. Appl. Sci. 2023, 13, 3890. [Google Scholar] [CrossRef]
- Hamadouche, S.A.; Boutemedjet, A.; Bouaraba, A. Destriping model for adaptive removal of arbitrary oriented stripes in remote sensing images. Phys. Scr. 2024, 99, 095130. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zheng, X.; Wu, Q. Adaptive temporal high-pass infrared non-uniformity correction algorithm based on guided filter. In Proceedings of the 2021 7th International Conference on Computing and Artificial Intelligence, Tianjin, China, 23–26 April 2021; pp. 459–464. [Google Scholar]
- Li, M.; Wang, Y.; Sun, H. Single-frame infrared image non-uniformity correction based on wavelet domain noise separation. Sensors 2023, 23, 8424. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Qin, H.; Yan, X.; Yang, S.; Yang, T. Single infrared image-based stripe nonuniformity correction via a two-stage filtering method. Sensors 2018, 18, 4299. [Google Scholar] [CrossRef]
- Song, H.; Zhang, K.; Tan, W.; Guo, F.; Zhang, X.; Cao, W. A non-uniform correction algorithm based on scene nonlinear filtering residual estimation. Curr. Opt. Photonics 2023, 7, 408–418. [Google Scholar]
- Hamadouche, S.A. Effective three-step method for efficient correction of stripe noise and non-uniformity in infrared remote sensing images. Phys. Scr. 2024, 99, 065539. [Google Scholar] [CrossRef]
- Cao, B.; Du, Y.; Xu, D.; Li, H.; Liu, Q. An improved histogram matching algorithm for the removal of striping noise in optical remote sensing imagery. Optik 2015, 126, 4723–4730. [Google Scholar] [CrossRef]
- Tendero, Y.; Landeau, S.; Gilles, J. Non-uniformity correction of infrared images by midway equalization. Image Process. Line 2012, 2, 134–146. [Google Scholar] [CrossRef]
- Li, D.; Ding, X.; Chai, M.; Ma, C.; Sun, D. Nonuniformity correction method of infrared detector based on statistical properties. IEEE Photonics J. 2024, 16, 7800408. [Google Scholar]
- Liang, S.; Yan, J.; Chen, M.; Zhang, Y.; Sang, D.; Kang, Y. Non-uniformity correction method of remote sensing images based on improved total variation model. J. Electron. Imaging 2025, 34, 013006. [Google Scholar] [CrossRef]
- Boutemedjet, A.; Hamadouche, S.A.; Belghachem, N. Joint first and second order total variation decomposition for remote sensing images destriping. Imaging Sci. J. 2025, 73, 135–149. [Google Scholar] [CrossRef]
- Lv, X.G.; Song, Y.Z.; Li, F. An efficient nonconvex regularization for wavelet frame and total variation based image restoration. J. Comput. Appl. Math. 2015, 290, 553–566. [Google Scholar] [CrossRef]
- Dong, L.Q.; Jin, W.Q.; Zhou, X.X. Fast curvelet transform based non-uniformity correction for IRFPA. In Proceedings of the Infrared Materials, Devices, and Applications, Beijing, China, 11–15 November 2008; Volume 6835, pp. 331–338. [Google Scholar]
- Wu, X.; Zheng, L.; Liu, C.; Gao, T.; Zhang, Z.; Yang, B. Single-image simultaneous destriping and denoising: Double low-rank property. Remote Sens. 2023, 15, 5710. [Google Scholar] [CrossRef]
- Wang, S.P. Stripe noise removal for infrared image by minimizing difference between columns. Infrared Phys. Technol. 2016, 77, 58–64. [Google Scholar] [CrossRef]
- Chen, Y.; He, W.; Yokoya, N.; Huang, T.-Z. Hyperspectral image restoration using weighted group sparsity-regularized low-rank tensor decomposition. IEEE Trans. Cybern. 2020, 50, 3556–3570. [Google Scholar] [CrossRef]
- Kim, N.; Han, S.S.; Jeong, C.S. ADOM: ADMM-based optimization model for stripe noise removal in remote sensing image. IEEE Access 2023, 11, 106587–106606. [Google Scholar] [CrossRef]
- Silver, D.; Hasselt, H.; Hessel, M.; Schaul, T.; Guez, A.; Harley, T.; Dulac-Arnold, G.; Reichert, D.; Rabinowitz, N.; Barreto, A.; et al. The predictron: End-to-end learning and planning. In Proceedings of the International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017; pp. 3191–3199. [Google Scholar]
- Chen, S.; Deng, F.; Zhang, H.; Lyu, S.; Kou, Z.; Yang, J. Infrared non-uniformity correction model via deep convolutional neural network. In Proceedings of the IET Conference CP820, Beijing, China, 11–13 November 2022; pp. 178–184. [Google Scholar]
- Jiang, C.; Li, Z.; Wang, Y.; Chen, T. Non-uniformity correction of spatial object images using multi-scale residual cycle network (CycleMRSNet). Sensors 2025, 25, 1389. [Google Scholar] [CrossRef]
- Shi, M.; Wang, H. Infrared dim and small target detection based on denoising autoencoder network. Mob. Netw. Appl. 2020, 25, 1469–1483. [Google Scholar] [CrossRef]
- Li, T.; Zhao, Y.; Li, Y.; Zhou, G. Non-uniformity correction of infrared images based on improved CNN with long-short connections. IEEE Photonics J. 2021, 13, 7800213. [Google Scholar] [CrossRef]
- Ma, Z.; Zhang, S.; Wang, L.; Rao, Q. Global context-aware method for infrared image non-uniformity correction. In Proceedings of the 3rd International Conference on Artificial Intelligence and Computer Information Technology (AICIT), Yichang, China, 20–22 September 2024; pp. 1–5. [Google Scholar]
- Zhang, S.; Sui, X.; Yao, Z.; Gu, G.; Chen, Q. Research on nonuniformity correction based on deep learning. In Proceedings of the AOPC 2021: Infrared Device and Infrared Technology, Beijing, China, 23–25 July 2021; Volume 12061, pp. 97–102. [Google Scholar]
- Zhang, A.; Li, Y.; Wang, S. 2DDSRU-MobileNet: An end-to-end cloud-noise-robust lightweight convolution neural network. J. Appl. Remote Sens. 2024, 18, 024511. [Google Scholar] [CrossRef]
- Zhang, Y.; Gu, Z. DMANet: An image denoising network based on dual convolutional neural networks with multiple attention mechanisms. Circuits Syst. Signal Process. 2025; in press. [Google Scholar]
- Zhao, M.; Cao, G.; Huang, X.; Yang, L. Hybrid transformer-CNN for real image denoising. IEEE Signal Process. Lett. 2022, 29, 1252–1256. [Google Scholar] [CrossRef]
- Hsiao, T.Y.; Sfarra, S.; Liu, Y.; Yao, Y. Two-dimensional Hilbert–Huang transform-based thermographic data processing for non-destructive material defect detection. Quant. InfraRed Thermogr. J. 2024; in press. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.; Keck, M. A two-stage approach to person detection in thermal imagery. In Proceedings of the IEEE Workshop on Applications of Computer Vision (WACV), Breckenridge, CO, USA, 5–7 January 2005. [Google Scholar]
- Hwang, S.; Park, J.; Kim, N.; Choi, Y.; Kweon, I.S. Multispectral pedestrian detection: Benchmark dataset and baseline. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1037–1045. [Google Scholar]
- Jia, X.; Zhu, C.; Li, M.; Tang, W.; Zhou, W. LLVIP: A visible-infrared paired dataset for low-light vision. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]











| Combinatorial | DR | FM | ET | Clarification |
|---|---|---|---|---|
| B0 (Baseline) | × | × | × | Guided filtering using only large windows |
| B1 (B0 + DR) | √ | × | × | Validating the local adaptive role of DR |
| B2 (B0 + FM) | × | √ | × | Verification of periodic stripe suppression for FM |
| B3 (B0 + DR + FM) | √ | √ | × | Testing the complementarity of DR and FM |
| B4 (Full) | √ | √ | √ | Full model |
| Combinatorial | PSNR/(dB) | SSIM | Roughness | GC | NR |
|---|---|---|---|---|---|
| B0 (Baseline) | 38.59 | 0.9164 | 0.0218 | 0.5478 | 0.999 |
| B1 (B0 + DR) | 38.88 | 0.9168 | 0.022 | 0.5488 | 1 |
| B2 (B0 + FM) | 39.49 | 0.9341 | 0.027 | 0.4925 | 0.999 |
| B3 (B0 + DR + FM) | 42.2 | 0.9652 | 0.0319 | 0.3558 | 1 |
| B4 (Full) | 42.44 | 0.9669 | 0.0324 | 0.3447 | 1.001 |
| Noise Group | Characterization | ||||||
|---|---|---|---|---|---|---|---|
| OSU-1 | 0.01 | 0.01 | --- | --- | --- | --- | Mild column bias and gain error |
| OSU-2 | 0.015 | 0.035 | --- | --- | --- | --- | Offset dominant stripe structure enhancement |
| OSU-3 | 0.04 | 0.015 | --- | --- | --- | --- | The gain of the dominant response varies significantly |
| OSU-4 | --- | --- | --- | 0.05 | 0.08 | π/3 | Independent simulation of periodic disturbances |
| OSU-5 | 0.025 | 0.025 | 0.01 | 0.06 | 0.06 | π/2 | Stripe and periodic complex interference |
| KAIST-1 | 0.02 | 0.02 | --- | --- | --- | --- | Moderately equilibrated non-homogeneous structures |
| KAIST-2 | 0.04 | 0.015 | --- | --- | --- | --- | Gain dominance and texture perturbation |
| KAIST-3 | 0.025 | 0.045 | --- | --- | --- | --- | Bias enhancement with distinctive streaks |
| KAIST-4 | --- | --- | --- | 0.07 | 0.07 | π/4 | Simulation of purely periodic mains frequency interference |
| KAIST-5 | 0.03 | 0.03 | 0.01 | 0.08 | 0.05 | π/2 | Structural streaks and cyclic coupling |
| LLVIP-1 | 0.02 | 0.015 | --- | --- | --- | --- | Slightly non-uniform structure at high resolution |
| LLVIP-2 | 0.035 | 0.025 | --- | --- | --- | --- | Gain dominates band microstructure texture interference |
| LLVIP-3 | 0.03 | 0.04 | 0.02 | --- | --- | --- | Bias enhancement with a bit of white noise |
| LLVIP-4 | --- | --- | --- | 0.09 | 0.04 | π/2 | High-resolution periodic stripe jitter characteristics |
| LLVIP-5 | 0.04 | 0.04 | 0.01 | 0.12 | 0.03 | π | Multi-source joint extreme interference simulation |
| Simulated Image Data | Metric | Noise | MIRE | MDBC | TSF | ADOM | GFLF | ASNR | OURS |
|---|---|---|---|---|---|---|---|---|---|
| OSU-1 | PSNR | --- | 35.62 | 32.36 | 31.18 | 22.46 | 33.27 | 29.11 | 36.39 |
| SSIM | --- | 0.9641 | 0.9381 | 0.934 | 0.8782 | 0.9397 | 0.8895 | 0.9686 | |
| Roughness | 0.1275 | 0.1179 | 0.1179 | 0.1164 | 0.1059 | 0.1142 | 0.0782 | 0.1202 | |
| OSU-2 | PSNR | --- | 31.68 | 30.33 | 30.56 | 22.34 | 32.21 | 28.15 | 33.89 |
| SSIM | --- | 0.9211 | 0.9186 | 0.9208 | 0.8512 | 0.9274 | 0.8199 | 0.9361 | |
| Roughness | 0.1898 | 0.1229 | 0.1205 | 0.1175 | 0.1032 | 0.1184 | 0.0956 | 0.1273 | |
| OSU-3 | PSNR | --- | 33.06 | 31.73 | 30.77 | 22.34 | 32.57 | 28.59 | 34.83 |
| SSIM | --- | 0.9419 | 0.9243 | 0.9221 | 0.8551 | 0.9279 | 0.8567 | 0.9501 | |
| Roughness | 0.1531 | 0.1233 | 0.1222 | 0.1202 | 0.1087 | 0.1188 | 0.0864 | 0.1274 | |
| OSU-4 | PSNR | --- | 29.49 | 30.51 | 30.66 | 22.08 | 31.66 | 28.24 | 32.18 |
| SSIM | --- | 0.9047 | 0.9045 | 0.9239 | 0.8422 | 0.9272 | 0.8294 | 0.9305 | |
| Roughness | 0.1311 | 0.1237 | 0.1184 | 0.1156 | 0.1031 | 0.1135 | 0.091 | 0.1288 | |
| PSNR | --- | 28.3 | 29.23 | 29.35 | 22.42 | 31.18 | 26.51 | 31.82 | |
| OSU-5 | SSIM | --- | 0.8592 | 0.8648 | 0.8768 | 0.8142 | 0.8918 | 0.7661 | 0.9085 |
| Roughness | 0.1836 | 0.1428 | 0.1416 | 0.139 | 0.1164 | 0.1374 | 0.1135 | 0.1453 |
| Simulated Image Data | Metric | Noise | MIRE | MDBC | TSF | ADOM | GFLF | ASNR | OURS |
|---|---|---|---|---|---|---|---|---|---|
| KAIST-1 | PSNR | --- | 40.87 | 34.64 | 41.45 | 35.24 | 41.58 | 39.9 | 42.25 |
| SSIM | --- | 0.9271 | 0.9112 | 0.9299 | 0.8792 | 0.9274 | 0.9153 | 0.9302 | |
| Roughness | 0.2204 | 0.0631 | 0.0825 | 0.0705 | 0.0591 | 0.0676 | 0.0607 | 0.091 | |
| KAIST-2 | PSNR | --- | 41.73 | 34.8 | 42.27 | 39.26 | 42.28 | 41.02 | 42.64 |
| SSIM | --- | 0.9393 | 0.9194 | 0.9405 | 0.9178 | 0.9382 | 0.9327 | 0.9431 | |
| Roughness | 0.1875 | 0.0645 | 0.084 | 0.0727 | 0.0695 | 0.0695 | 0.0561 | 0.102 | |
| KAIST-3 | PSNR | --- | 36.84 | 33.1 | 36.27 | 32.54 | 36.9 | 34.81 | 37.27 |
| SSIM | --- | 0.8687 | 0.8321 | 0.8638 | 0.7998 | 0.8623 | 0.8243 | 0.8755 | |
| Roughness | 0.434 | 0.0704 | 0.1076 | 0.0866 | 0.0797 | 0.0877 | 0.0871 | 0.1119 | |
| KAIST-4 | PSNR | --- | 38.56 | 31.89 | 36.8 | 30.17 | 38.56 | 29.81 | 39.57 |
| SSIM | --- | 0.8757 | 0.7785 | 0.8488 | 0.7423 | 0.8753 | 0.6493 | 0.8938 | |
| Roughness | 0.1785 | 0.0518 | 0.0916 | 0.0686 | 0.0901 | 0.0563 | 0.1232 | 0.132 | |
| KAIST-5 | PSNR | --- | 34.51 | 27.88 | 30.47 | 32.25 | 34.26 | 27.18 | 36.6 |
| SSIM | --- | 0.7862 | 0.6646 | 0.7098 | 0.7447 | 0.7817 | 0.5774 | 0.8548 | |
| Roughness | 0.3886 | 0.192 | 0.2235 | 0.2097 | 0.2215 | 0.1985 | 0.2194 | 0.2406 |
| Simulated Image Data | Metric | Noise | MIRE | MDBC | TSF | ADOM | GFLF | ASNR | OURS |
|---|---|---|---|---|---|---|---|---|---|
| LLVIP-1 | PSNR | --- | 41.45 | 40.33 | 42.47 | 32.36 | 43.73 | 39.88 | 44.29 |
| SSIM | --- | 0.9804 | 0.9621 | 0.9726 | 0.8917 | 0.9798 | 0.9706 | 0.9827 | |
| Roughness | 0.0675 | 0.028 | 0.0356 | 0.033 | 0.0326 | 0.0307 | 0.0276 | 0.0378 | |
| LLVIP-2 | PSNR | --- | 39.32 | 36.45 | 39.22 | 32.07 | 41.04 | 37.42 | 41.76 |
| SSIM | --- | 0.9738 | 0.9302 | 0.9521 | 0.8807 | 0.9682 | 0.9474 | 0.9747 | |
| Roughness | 0.1004 | 0.0292 | 0.0424 | 0.038 | 0.0365 | 0.0344 | 0.0342 | 0.0478 | |
| LLVIP-3 | PSNR | --- | 33.53 | 32.54 | 33.9 | 31.13 | 34.5 | 33.8 | 35.71 |
| SSIM | --- | 0.8055 | 0.7891 | 0.8051 | 0.7909 | 0.8119 | 0.8254 | 0.847 | |
| Roughness | 0.1613 | 0.0785 | 0.0822 | 0.08 | 0.0702 | 0.079 | 0.0565 | 0.0827 | |
| LLVIP-4 | PSNR | --- | 36.1 | 27.91 | 28.17 | 26.24 | 34.74 | 25.17 | 37.05 |
| SSIM | --- | 0.9625 | 0.8207 | 0.0832 | 0.7776 | 0.9527 | 0.723 | 0.9712 | |
| Roughness | 0.0509 | 0.0272 | 0.0392 | 0.0381 | 0.0416 | 0.0278 | 0.0454 | 0.047 | |
| PSNR | --- | 28.3 | 29.23 | 29.35 | 22.42 | 31.18 | 26.51 | 31.82 | |
| LLVIP-5 | SSIM | --- | 0.8592 | 0.8648 | 0.8768 | 0.8142 | 0.8918 | 0.7661 | 0.9085 |
| Roughness | 0.1836 | 0.1428 | 0.1416 | 0.139 | 0.1164 | 0.1374 | 0.1135 | 0.1453 |
| Real Image Data | Metric | Noise | MIRE | MDBC | TSF | ADOM | GFLF | ASNR | OURS |
|---|---|---|---|---|---|---|---|---|---|
| Tendero’s data | PSNR | --- | 25.63 | 21.71 | 25.65 | 23.72 | 27.84 | 28.34 | 29.74 |
| SSIM | --- | 0.6043 | 0.6219 | 0.6048 | 0.5761 | 0.7811 | 0.745 | 0.8296 | |
| Roughness | 0.3357 | 0.1419 | 0.1515 | 0.1429 | 0.1298 | 0.2118 | 0.1105 | 0.2291 | |
| GC | --- | 0.5014 | 0.418 | 0.4287 | 0.4204 | 0.3663 | 0.4974 | 0.3322 | |
| NR | --- | 1.041 | 1.0318 | 1.042 | 1.058 | 1.0344 | 1.0428 | 1.0671 |
| Real Image Data | Metric | Noise | MIRE | MDBC | TSF | ADOM | GFLF | ASNR | OURS |
|---|---|---|---|---|---|---|---|---|---|
| Long-wave infrared weekly scanning dataset | PSNR | --- | 36.55 | 37.05 | 36.96 | 30.85 | 36.63 | 37.27 | 37.78 |
| SSIM | --- | 0.8372 | 0.8601 | 0.844 | 0.807 | 0.8415 | 0.8721 | 0.8784 | |
| Roughness | 0.0393 | 0.0305 | 0.0361 | 0.0337 | 0.0215 | 0.0315 | 0.0189 | 0.0372 | |
| GC | --- | 0.8638 | 0.7728 | 0.8245 | 0.8462 | 0.8286 | 0.8428 | 0.5748 | |
| NR | --- | 1.0097 | 1.0115 | 1.0089 | 1.0367 | 1.0125 | 1.0092 | 1.0417 |
| Algorithms | MIRE | MDBC | TFS | ADOM | GFLF | ASNR | OURS |
|---|---|---|---|---|---|---|---|
| Time/s | 492.1527 | 0.2744 | 5.9356 | 192.0058 | 1.5345 | 7.1714 | 0.1815 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Zhu, Y.; Duan, Q.; Zhu, Y.; Jiang, J.; Zhang, Y. Adaptive Guided Filtering and Spectral-Entropy-Based Non-Uniformity Correction for High-Resolution Infrared Line-Scan Images. Sensors 2025, 25, 4287. https://doi.org/10.3390/s25144287
Huang M, Zhu Y, Duan Q, Zhu Y, Jiang J, Zhang Y. Adaptive Guided Filtering and Spectral-Entropy-Based Non-Uniformity Correction for High-Resolution Infrared Line-Scan Images. Sensors. 2025; 25(14):4287. https://doi.org/10.3390/s25144287
Chicago/Turabian StyleHuang, Mingsheng, Yanghang Zhu, Qingwu Duan, Yaohua Zhu, Jingyu Jiang, and Yong Zhang. 2025. "Adaptive Guided Filtering and Spectral-Entropy-Based Non-Uniformity Correction for High-Resolution Infrared Line-Scan Images" Sensors 25, no. 14: 4287. https://doi.org/10.3390/s25144287
APA StyleHuang, M., Zhu, Y., Duan, Q., Zhu, Y., Jiang, J., & Zhang, Y. (2025). Adaptive Guided Filtering and Spectral-Entropy-Based Non-Uniformity Correction for High-Resolution Infrared Line-Scan Images. Sensors, 25(14), 4287. https://doi.org/10.3390/s25144287






