An Anti-Interrupted-Sampling Repeater Jamming Method Based on Simulated Annealing–2-Optimization Parallel Optimization of Waveforms and Fractional Domain Extraction
Abstract
1. Introduction
- 1.
- Optimizing the radar signal coding, which involves alternating positive and negative modulation rates of sub-pulses and joint coding of modulation rate and carrier frequency. The problem is abstracted into a two-dimensional Traveling Salesman Problem (TSP), and an SA-2opt parallel optimization algorithm is proposed to find an approximate solution, ensuring good detection capabilities of the radar even in the absence of jamming.
- 2.
- Using segmented FrFT filtering and combining it with the K-means algorithm to complete ISRJ detection, achieving effective suppression of ISRJ in high-signal-to-clutter-ratio environments.
2. Introduction of the Waveform Mathematical Model and Performance Analysis
2.1. Signal Model
2.2. Analysis of the Necessity of Sub-Pulse Orthogonality
2.3. Analysis of Signal Autocorrelation Sidelobes
3. Introduction of Optimization Algorithm
3.1. Signal Sidelobe Optimization Model
3.2. Analysis of the SA-2opt Parallel Optimization Algorithm
4. Anti-ISRJ Method
4.1. Echo Signal Model
4.2. Target Energy Extraction Based on the FrFT
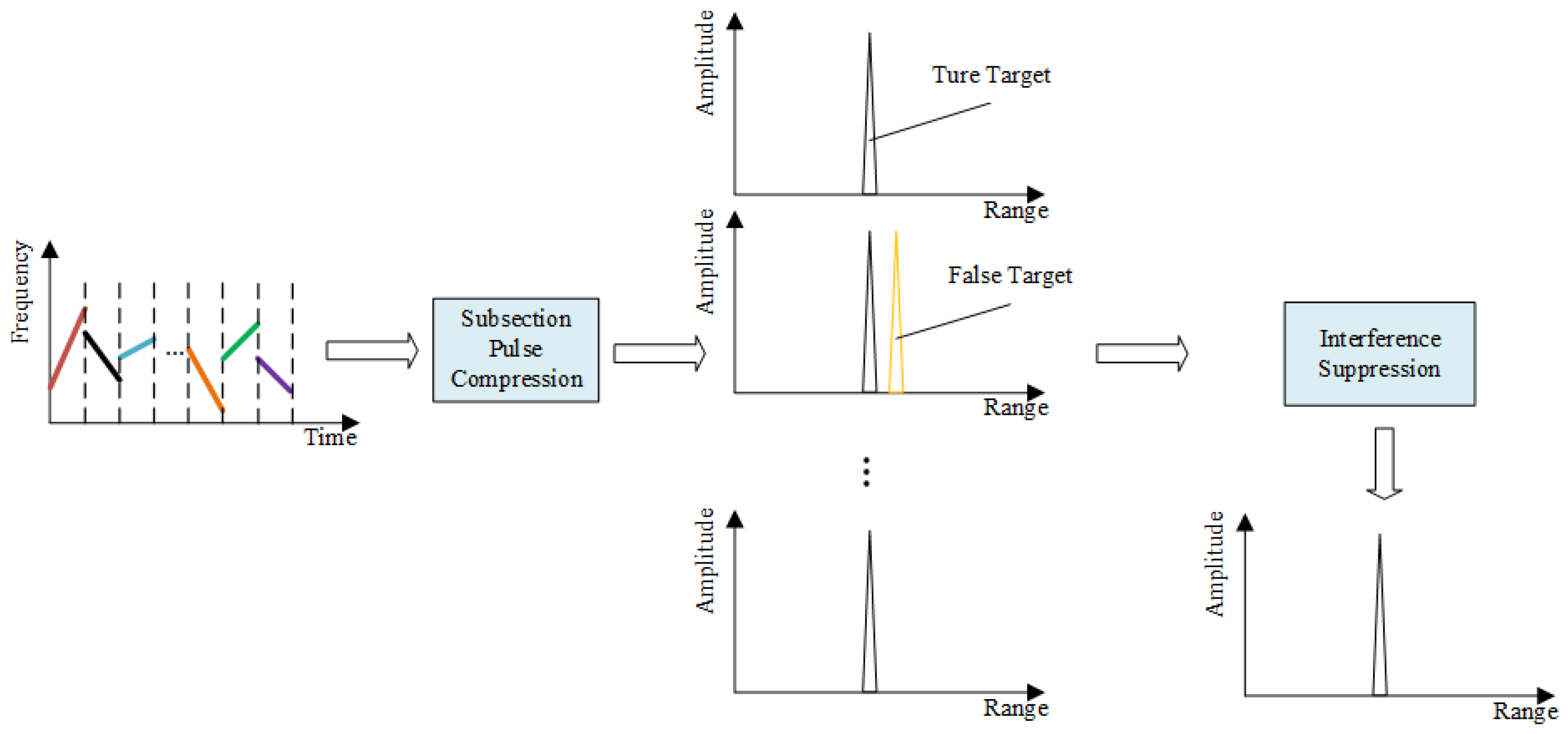
4.3. Segmented Pulse Compression and Jamming Suppression
- is given initial centroids and .
5. Simulation Experiments and Analysis
5.1. Comparison of Sidelobe Peak Levels Before and After Optimization
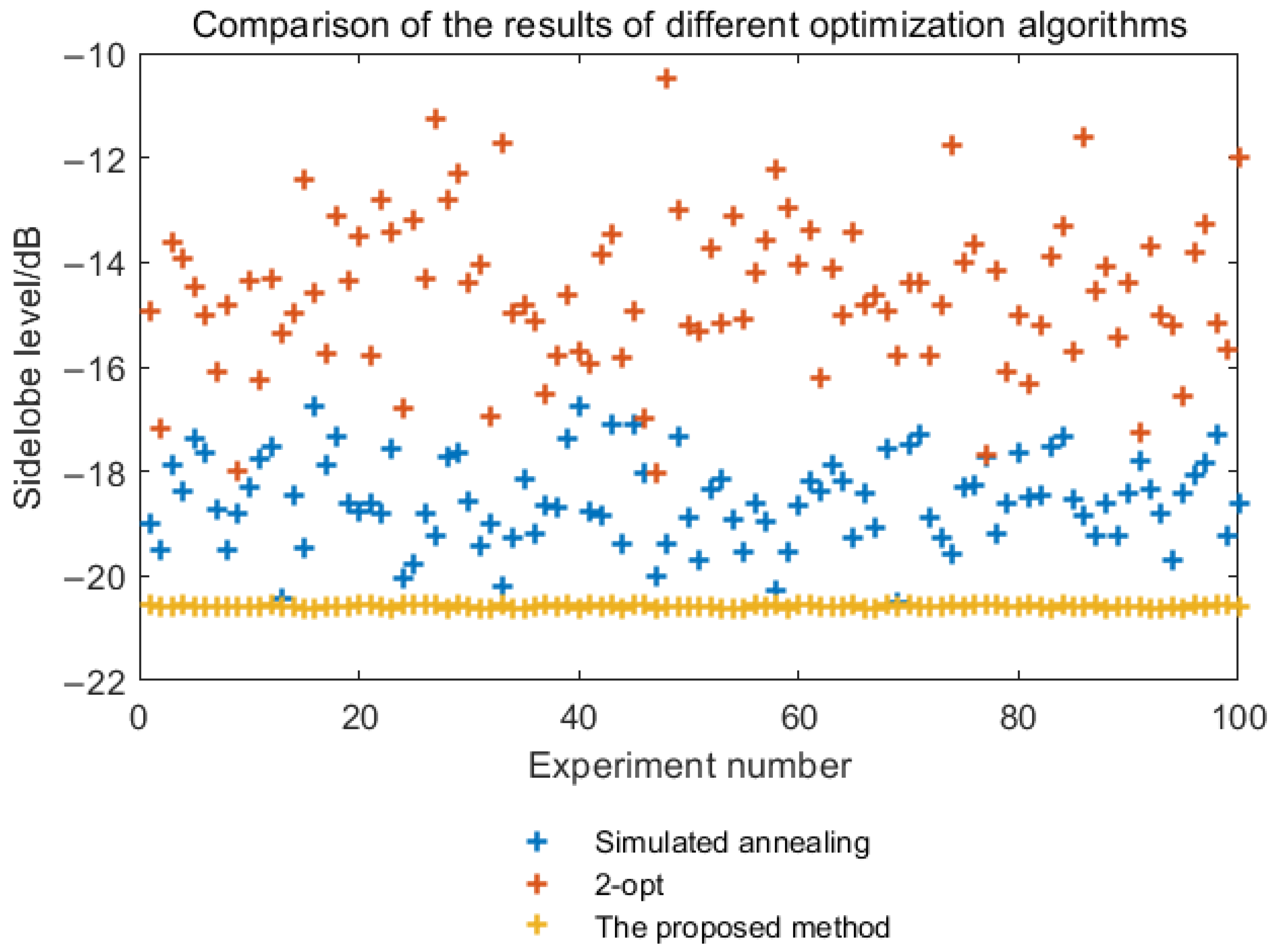
5.2. Comparison with Traditional Optimization Algorithms
5.3. Performance of the Optimized Waveform When the Target Has Radial Velocity
5.4. Analysis of the Impact of Various Parameters on Optimization Results and Computation Time
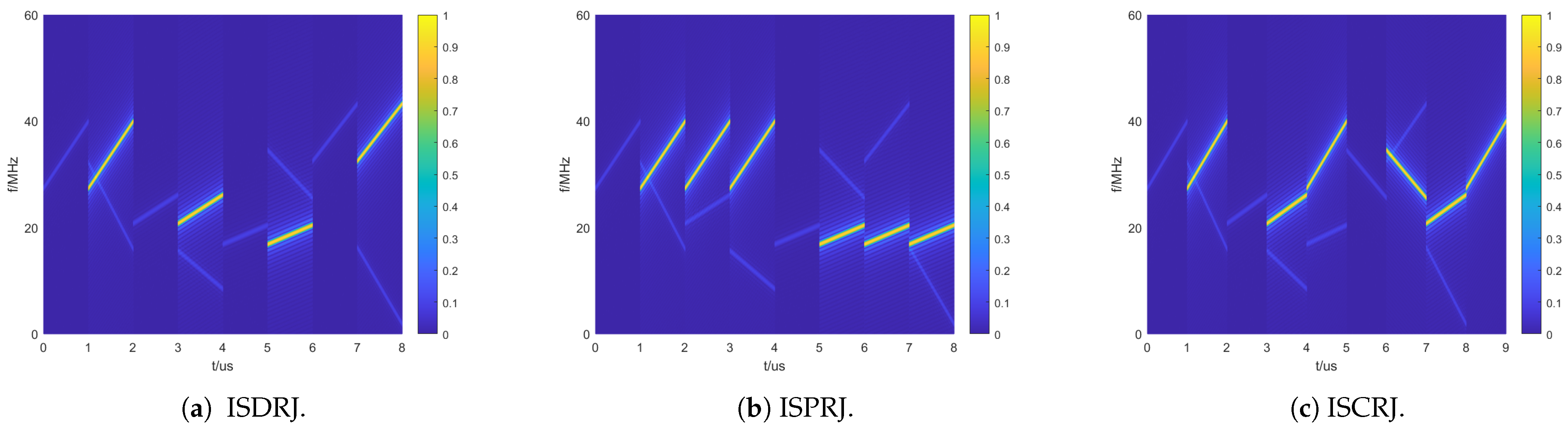
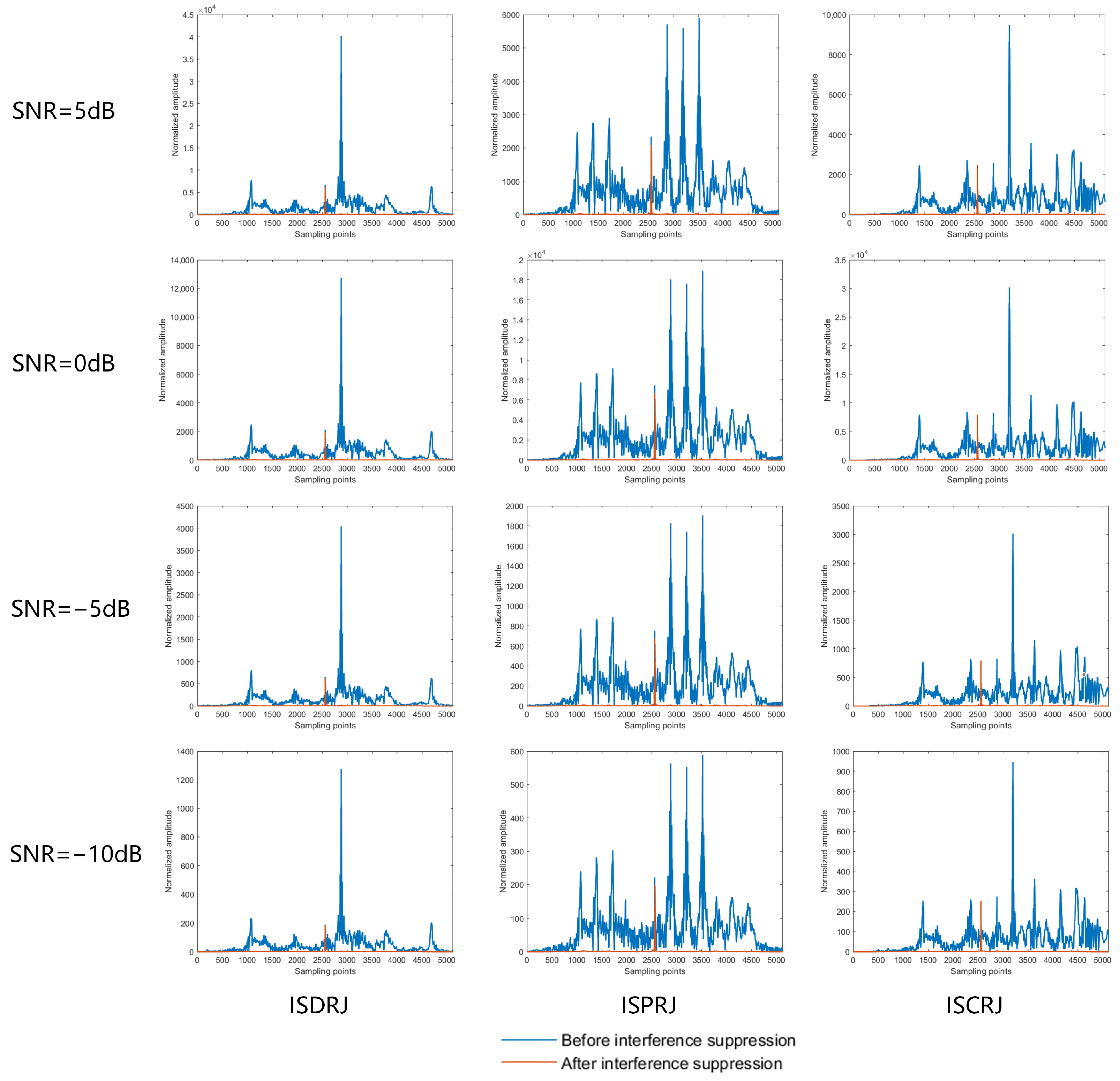
5.5. Waveform Anti-Jamming Performance
5.6. Effect of Delay on Jamming Suppression
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
DURC Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECM | Electronic counter measure |
| DRFM | Digital Radio Frequency Memory |
| ISRJ | Interrupted-sampling repeater jamming |
| ISDRJ | Interrupted-Sampling Direct Repeater Jamming |
| ISPRJ | Interrupted-Sampling Periodic Repeater Jamming |
| ISCRJ | Interrupted-Sampling Cyclic Repeater Jamming |
| SA | Simulated annealing |
| 2-opt | 2-optimization |
| FrFT | Fractional Fourier transform |
| LFM | Linear frequency modulation |
| JSR | Jamming-to-signal ratio |
| SNR | Signal-to-noise ratio |
References
- Joshi, S.K.; Baumgartner, S.V.; Krieger, G. Tracking and Track Management of Extended Targets in Range-Doppler Using Range-Compressed Airborne Radar Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–20. [Google Scholar] [CrossRef]
- Wu, S.; Zhao, C.; Chen, Z.; Wang, X.; Zhang, C.; Wei, Y. A New Doppler Model for Shipboard Coherent Microwave Ocean Radar. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–13. [Google Scholar] [CrossRef]
- Sørensen, K.A.; Kusk, A.; Heiselberg, P.; Heiselberg, H. Finding Ground-Based Radars in SAR Images: Localizing Radio Frequency Interference Using Unsupervised Deep Learning. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–15. [Google Scholar] [CrossRef]
- Liu, Y.X.; Zhang, Q.; Xiong, S.C.; Wang, H.B.; Yuan, H.; Luo, Y. A Multiple-False-Target ISAR Shape Deception Jamming Method Based on Improved Template Multiplication Modulated Time-Delay Algorithm and Sub-Nyquist Sampling. Remote Sens. 2023, 15, 5015. [Google Scholar] [CrossRef]
- Duan, J.; Zhang, L.; Wu, Y.; Li, Y. Interrupted-sampling repeater jamming suppression with one-dimensional semi-parametric signal decomposition. Digit. Signal Process. 2022, 127, 103546. [Google Scholar] [CrossRef]
- Zheng, H.; Jiu, B.; Liu, H. Waveform design based ECCM scheme against interrupted sampling repeater jamming for wideband MIMO radar in multiple targets scenario. IEEE Sensors J. 2021, 22, 1652–1669. [Google Scholar] [CrossRef]
- Fan, Y.; Jiu, B.; Pu, W.; Li, Z.; Li, K.; Liu, H. Sensing Jamming Strategy From Limited Observations: An Imitation Learning Perspective. IEEE Trans. Signal Process. 2024, 72, 4098–4114. [Google Scholar] [CrossRef]
- Zhou, C.; Liu, Q.; Chen, X. Parameter estimation and suppression for DRFM-based interrupted sampling repeater jammer. IET Radar, Sonar Navig. 2018, 12, 56–63. [Google Scholar] [CrossRef]
- Lan, L.; Zhang, Y.; Liao, R.; Liao, G.; Xu, J.; So, H.C. Mainlobe Deceptive Jammer Mitigation with Multipath in EPC-MIMO Radar Exploiting Matrix Decomposition. IEEE Trans. Veh. Technol. 2024, 73, 14674–14688. [Google Scholar] [CrossRef]
- Zhai, W.; Wang, R.; Wang, X.; Shi, F.; Pang, X.; Gao, Y.; Cui, W. Wideband Photonic Radar Target Simulator Based on All-Optical IQ Upconverter. IEEE Trans. Microw. Theory Tech. 2024, 73, 1203–1214. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.; Zhou, Z.; Yu, G.; Li, Y. An Attention-Guided Complex-Valued Transformer for Intra-Pulse Retransmission Interference Suppression. Remote Sens. 2024, 16, 1989. [Google Scholar] [CrossRef]
- Sun, Z.; Quan, Y.; Liu, Z. A non-uniform interrupted-sampling repeater jamming method for intra-pulse frequency agile radar. Remote Sens. 2023, 15, 1851. [Google Scholar] [CrossRef]
- Qi, J.; Li, S.; Chen, J.; Li, H. Optimization Method of Interrupted Sampling Frequency Shift Repeater Jamming Based on Group Teaching Optimization Algorithm. Electronics 2024, 13, 2622. [Google Scholar] [CrossRef]
- Xiao, J.; Wei, X.; Sun, J. Interrupted-sampling multi-strategy forwarding jamming with amplitude constraints based on simultaneous transmission and reception technology. Digit. Signal Process. 2024, 147, 104416. [Google Scholar] [CrossRef]
- Benvenuti, D.; Addabbo, P.; Giunta, G.; Foglia, G.; Orlando, D. ECCM Strategies for Radar Systems Against Smart Noise-Like Jammers. IEEE Trans. Signal Process. 2024, 72, 3912–3926. [Google Scholar] [CrossRef]
- Huang, T.; Shlezinger, N.; Xu, X.; Ma, D.; Liu, Y.; Eldar, Y.C. Multi-Carrier Agile Phased Array Radar. IEEE Trans. Signal Process. 2020, 68, 5706–5721. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Liu, Z.; Li, G.; Xiong, S.; Luo, Y. An anti-jamming method against interrupted sampling repeater jamming based on compressed sensing. Sensors 2022, 22, 2239. [Google Scholar] [CrossRef]
- Lv, Q.; Quan, Y.; Sha, M.; Feng, W.; Xing, M. Deep neural network-based interrupted sampling deceptive jamming countermeasure method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 9073–9085. [Google Scholar] [CrossRef]
- Wu, M.; Li, M.; Shi, H.; Cheng, X.; Rao, B.; Wang, W. Using range-Doppler spectrum-based deep learning method to detect radar target in interrupted sampling repeater jamming. IEEE Sensors J. 2023, 23, 29084–29096. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, L.; Duan, L.; Liu, Z.; Xing, M.; Quan, Y. Fine-grained Recognition and Suppression of ISRJ Based on UNet-A. IEEE Geosci. Remote Sens. Lett. 2024, 21, 3508805. [Google Scholar] [CrossRef]
- Huan, S.; Dai, G.; Luo, G.; Ai, S. Bayesian compress sensing based countermeasure scheme against the interrupted sampling repeater jamming. Sensors 2019, 19, 3279. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Li, W.; Cheng, X.; Wu, M.; Rao, B.; Wang, W. The transmit and receive optimization for polarimetric radars against interrupted sampling repeater jamming. IEEE Sens. J. 2023, 24, 3927–3943. [Google Scholar] [CrossRef]
- Zhan, H.; Wang, T.; Guo, T.; Su, X. An Anti-Intermittent Sampling Jamming Technique Utilizing the OTSU Algorithm of Random Orthogonal Sub-Pulses. Remote Sens. 2023, 15, 3080. [Google Scholar] [CrossRef]
- Wang, F.; Li, N.; Pang, C.; Li, C.; Li, Y.; Wang, X. Complementary sequences and receiving filters design for suppressing interrupted sampling repeater jamming. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, X.; Li, B.; Liu, W.; Chen, H.; Zhu, Y.; Ni, M. Anti-interrupted sampling repeater jamming based on intra-pulse frequency modulation slope agile radar waveform joint FrFT. Digit. Signal Process. 2024, 147, 104418. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Fan, T.; Cui, G. Design of Cognitive Radar Orthogonal Subpulse Width against Multiple Jamming. In Proceedings of the 2024 32nd European Signal Processing Conference (EUSIPCO), Lyon, France, 26–30 August 2024; pp. 2392–2396. [Google Scholar]
- Li, Y.; Wang, J.; Wang, Y.; Zhang, P.; Zuo, L. Random-frequency-Coded waveform optimization and signal coherent accumulation against compound deception jamming. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 4434–4449. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Zhang, H.; Zhang, K.; Liu, Q. Suppression method for main-lobe interrupted sampling repeater jamming in distributed radar. IEEE Access 2020, 8, 139255–139265. [Google Scholar] [CrossRef]
- Zhang, J.; Mu, H.; Wen, S.; Liao, S.; Sha, M. Anti-intermittent sampling jamming method based on intra-pulse LFM-Costas frequency stepping. Syst. Eng. Electron. 2019, 41, 2170. [Google Scholar] [CrossRef]
- Dong, S.; Quan, Y.; Sha, M.; Fang, W.; Xing, M.D. Frequency agile radar combined with intra-pulse frequency coding to resist intermittent sampling jamming. Syst. Eng. Electron. 2022, 44, 3371. [Google Scholar] [CrossRef]
- Lu, L.Y.; Li, M.; Chen, H.; Zuo, L.; Zhang, P. CFAR detection of DRFM deception jamming based on entropy feature. Syst. Eng. Electron. 2016, 38, 732. [Google Scholar]
















| Parameters | Values |
|---|---|
| Sub-pulse chirp rate | |
| Sub-pulse frequency hopping interval | 3 |
| Sampling rate | 160 |
| Sub-pulse width | 1 |
| Number of sub-pulses M | 8 |
| Target Radial Velocity | Pulse Pressure Loss |
|---|---|
| 0 | 0 |
| m/s | 8.69 dB |
| m/s | 4.00 dB |
| m/s | 0.37 dB |
| m/s | 1.04 dB |
| m/s | 4.55 dB |
| m/s | 12.62 dB |
| Maximum Number of Iterations | Number of Parallel Computing | Running Time | Sidelobe Peak |
|---|---|---|---|
| 5000 | 50 | 160 min | 0.09 |
| 5000 | 10 | 32 min | 0.10 |
| 2000 | 30 | 15 min | 0.09 |
| 1500 | 100 | 40 min | 0.09 |
| 1000 | 30 | 8 min | 0.11 |
| 1000 | 100 | 60 min | 0.10 |
| Parameters | Values |
|---|---|
| Sub-pulse width (us) | 1 |
| Frequency hopping interval | 3 |
| Maximum bandwidth of sub-pulses | 16.2 |
| Minimum bandwidth of sub-pulse | 3.6 |
| Jamming-to-signal ratio JSR | 20 |
| Signal-to-noise ratio SNR | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Z.; Guo, P.; Wei, Y.; Gao, S.; Wang, J.; Xue, A.; Wang, K. An Anti-Interrupted-Sampling Repeater Jamming Method Based on Simulated Annealing–2-Optimization Parallel Optimization of Waveforms and Fractional Domain Extraction. Sensors 2025, 25, 3000. https://doi.org/10.3390/s25103000
Yin Z, Guo P, Wei Y, Gao S, Wang J, Xue A, Wang K. An Anti-Interrupted-Sampling Repeater Jamming Method Based on Simulated Annealing–2-Optimization Parallel Optimization of Waveforms and Fractional Domain Extraction. Sensors. 2025; 25(10):3000. https://doi.org/10.3390/s25103000
Chicago/Turabian StyleYin, Ziming, Pengcheng Guo, Yunyu Wei, Sizhe Gao, Jingjing Wang, Anxiang Xue, and Kuo Wang. 2025. "An Anti-Interrupted-Sampling Repeater Jamming Method Based on Simulated Annealing–2-Optimization Parallel Optimization of Waveforms and Fractional Domain Extraction" Sensors 25, no. 10: 3000. https://doi.org/10.3390/s25103000
APA StyleYin, Z., Guo, P., Wei, Y., Gao, S., Wang, J., Xue, A., & Wang, K. (2025). An Anti-Interrupted-Sampling Repeater Jamming Method Based on Simulated Annealing–2-Optimization Parallel Optimization of Waveforms and Fractional Domain Extraction. Sensors, 25(10), 3000. https://doi.org/10.3390/s25103000






