Mobile Laser-Induced Breakdown Spectroscopy for Future Application in Precision Agriculture—A Case Study
Abstract
1. Introduction
2. Experimental Part and Data Analysis
2.1. Materials
2.2. Reference Analysis
2.3. LIBS Measurements
2.4. Data Analysis
3. Results
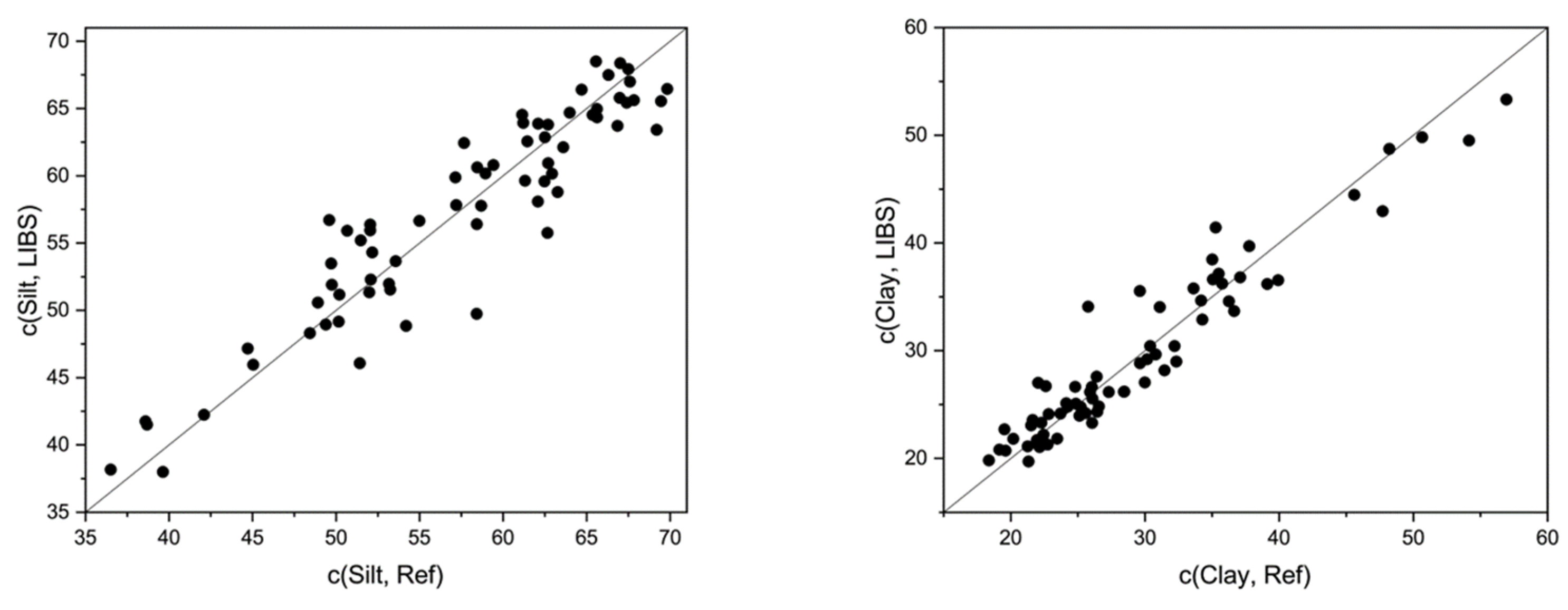
3.1. Determination of Soil Parameters
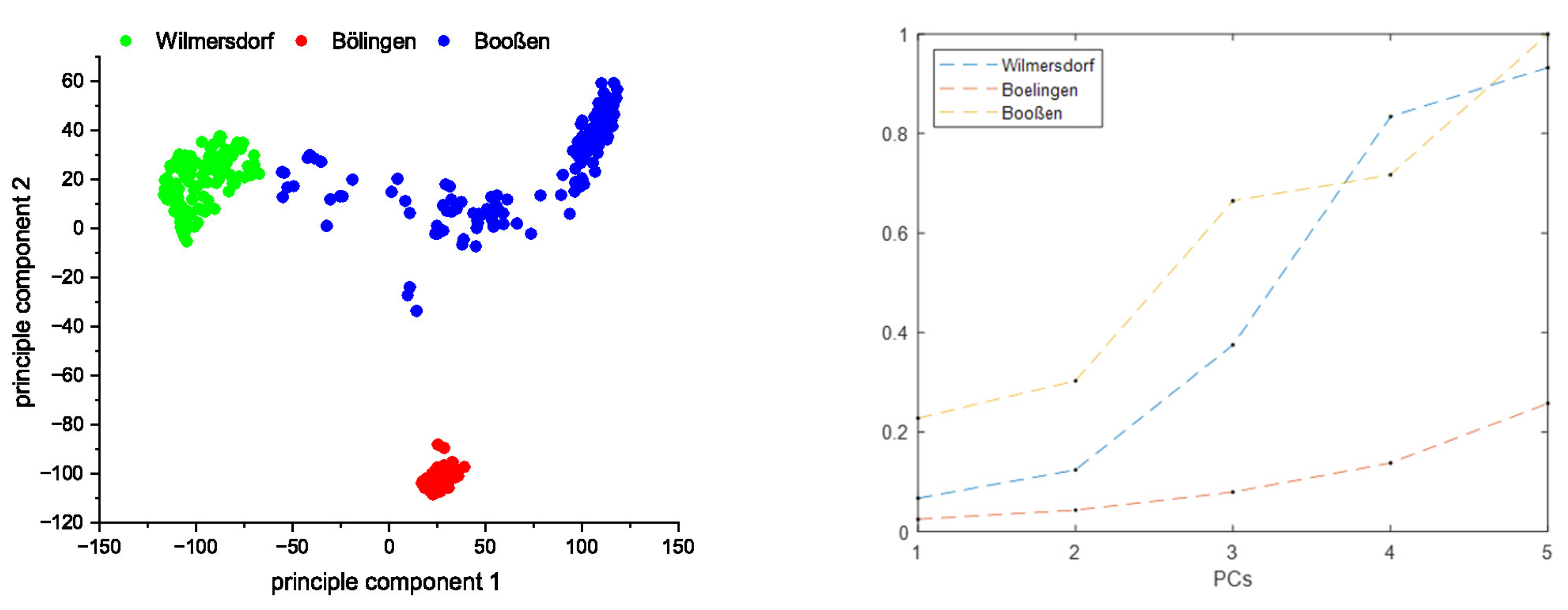
3.2. Matrix Influence
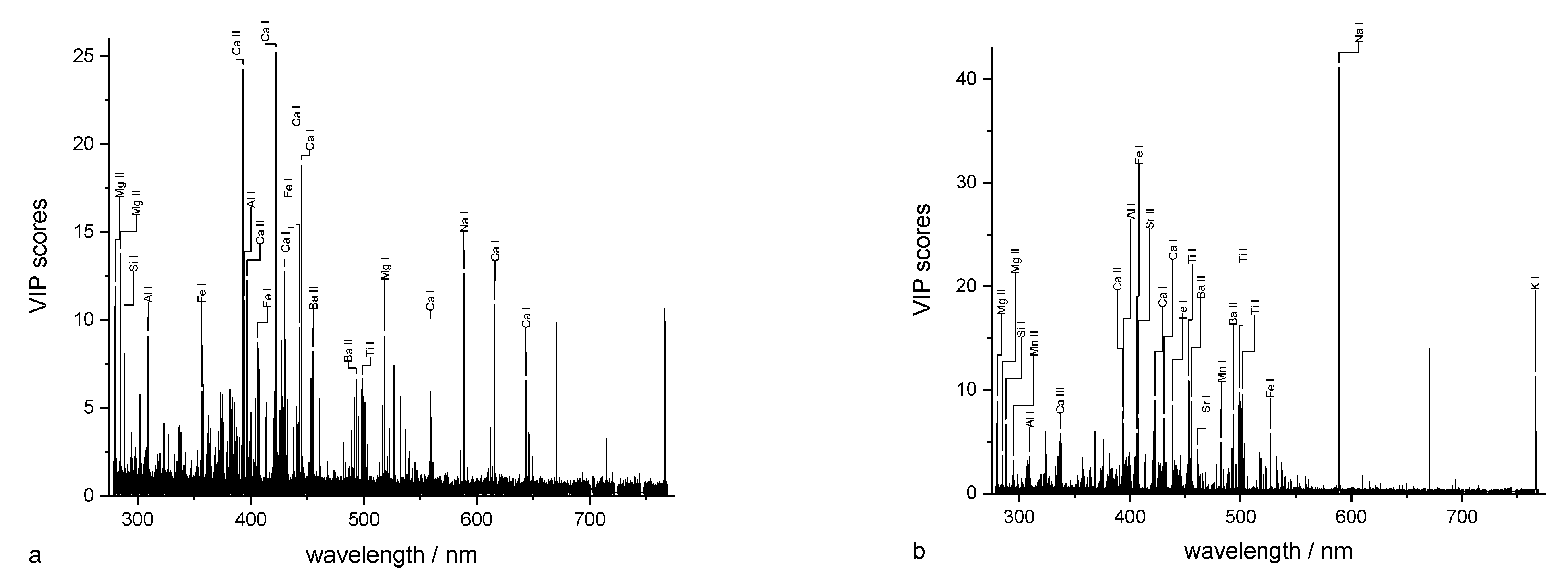
3.3. Different Aspects of Measurement and Data Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Villas-Boas, P.R.; Franco, M.A.; Martin-Neto, L.; Gollany, H.T.; Milori, D.M.B.P. Applications of laser-induced breakdown spectroscopy for soil analysis, part I: Review of fundamentals and chemical and physical properties. Eur. J. Soil. Sci. 2019, 71, 789–804. [Google Scholar] [CrossRef]
- Heggemann, T.; Welp, G.; Amelung, W.; Angst, G.; Franz, S.O.; Koszinski, S.; Schmidt, K.; Pätzold, S. Proximal gamma-ray spectrometry for site-independent in situ prediction of soil texture on ten heterogeneous fields in Germany using support vector machines. Soil Tillage Res. 2017, 168, 99–109. [Google Scholar] [CrossRef]
- Gebbers, R.; Lück, E.; Dabas, M.; Domsch, H. Comparison of instruments for geoelectrical soil mapping at the field scale. Near Surf. Geophys. 2009, 7, 179–190. [Google Scholar] [CrossRef]
- Adamchuk, V.I.; Morgan, M.T.; Ess, D.R. An Automated Sampling System for Measuring Soil pH. Trans. ASAE 1999, 42, 885–892. [Google Scholar] [CrossRef]
- Botto, A.; Campanella, B.; Legnaioli, S.; Lezzerini, M.; Lorenzetti, G.; Pagnotta, S.; Poggialini, F.; Palleschi, V. Applications of laser-induced breakdown spectroscopy in cultural heritage and archaeology: A critical review. J. Anal. At. Spectrom. 2019, 34, 81–103. [Google Scholar] [CrossRef]
- Cremers, D.A.; Chinni, R.C. Laser-Induced Breakdown Spectroscopy—Capabilities and Limitations. Appl. Spectrosc. Rev. 2009, 44, 457–506. [Google Scholar] [CrossRef]
- Hahn, D.W.; Omenetto, N. Laser-induced breakdown spectroscopy (LIBS), part II: Review of instrumental and methodological approaches to material analysis and applications to different fields. Appl. Spectrosc. 2012, 66, 347–419. [Google Scholar] [CrossRef]
- Zorov, N.B.; Popov, A.M.; Zaytsev, S.M.; Labutin, T.A. Qualitative and quantitative analysis of environmental samples by laser-induced breakdown spectrometry. Russ. Chem. Rev. 2015, 84, 1021–1050. [Google Scholar] [CrossRef]
- Erler, A.; Riebe, D.; Beitz, T.; Löhmannsröben, H.-G.; Gebbers, R. Soil Nutrient Detection for Precision Agriculture Using Handheld Laser-Induced Breakdown Spectroscopy (LIBS) and Multivariate Regression Methods (PLSR, Lasso and GPR). Sensors 2020, 20, 418. [Google Scholar] [CrossRef]
- Riebe, D.; Erler, A.; Brinkmann, P.; Beitz, T.; Löhmannsröben, H.-G.; Gebbers, R. Comparison of Calibration Approaches in Laser-Induced Breakdown Spectroscopy for Proximal Soil Sensing in Precision Agriculture. Sensors 2019, 19, 5244. [Google Scholar] [CrossRef]
- Rühlmann, M.; Büchele, D.; Ostermann, M.; Bald, I.; Schmid, T. Challenges in the quantification of nutrients in soils using laser-induced breakdown spectroscopy—A case study with calcium. Spectrochim. Acta Part B At. Spectrosc. 2018, 146, 115–121. [Google Scholar] [CrossRef]
- Villas-Boas, P.R.; Franco, M.A.; Martin-Neto, L.; Gollany, H.T.; Milori, D.M.B.P. Applications of laser-induced breakdown spectroscopy for soil characterization, part II: Review of elemental analysis and soil classification. Eur. J. Soil Sci. 2020, 71, 805–818. [Google Scholar] [CrossRef]
- Nicolodelli, G.; Cabral, J.; Menegatti, C.R.; Marangoni, B.; Senesi, G.S. Recent advances and future trends in LIBS applications to agricultural materials and their food derivatives: An overview of developments in the last decade (2010–2019). Part I. Soils and fertilizers. TrAC Trends Anal. Chem. 2019, 115, 70–82. [Google Scholar] [CrossRef]
- Díaz, D.; Hahn, D.W.; Molina, A. Evaluation of Laser-Induced Breakdown Spectroscopy (LIBS) as a Measurement Technique for Evaluation of Total Elemental Concentration in Soils. Appl. Spectrosc. 2012, 66, 99–106. [Google Scholar] [CrossRef]
- Nicolodelli, G.; Senesi, G.S.; de Oliveira Perazzoli, I.L.; Marangoni, B.S.; de Melo Benites, V.; Milori, D.M.B.P. Double pulse laser induced breakdown spectroscopy: A potential tool for the analysis of contaminants and macro/micronutrients in organic mineral fertilizers. Sci. Total Environ. 2016, 565, 1116–1123. [Google Scholar] [CrossRef]
- El Haddad, J.; Villot-Kadri, M.; Ismaël, A.; Gallou, G.; Michel, K.; Bruyère, D.; Laperche, V.; Canioni, L.; Bousquet, B. Artificial neural network for on-site quantitative analysis of soils using laser induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2013, 79–80, 51–57. [Google Scholar] [CrossRef]
- Guo, G.; Niu, G.; Shi, Q.; Lin, Q.; Di, T.; Duan, Y. Multi-element quantitative analysis of soils by laser induced breakdown spectroscopy (LIBS) coupled with univariate and multivariate regression methods. Anal. Methods 2019, 11, 3006–3013. [Google Scholar] [CrossRef]
- Ebinger, M.H.; Norfleet, M.L.; Breshears, D.D.; Cremers, D.A.; Ferris, M.J.; Unkefer, P.J.; Lamb, M.S.; Goddard, K.L.; Meyer, C.W. Extending the Applicability of Laser-Induced Breakdown Spectroscopy for Total Soil Carbon Measurement. Soil Sci. Soc. Am. J. 2003, 67, 1616–1619. [Google Scholar] [CrossRef]
- Martin, M.Z.; Mayes, M.A.; Heal, K.R.; Brice, D.J.; Wullschleger, S.D. Investigation of laser-induced breakdown spectroscopy and multivariate analysis for differentiating inorganic and organic C in a variety of soils. Spectrochim. Acta Part B At. Spectrosc. 2013, 87, 100–107. [Google Scholar] [CrossRef]
- Ferreira, E.C.; Gomes Neto, J.A.; Milori, D.M.; Ferreira, E.J.; Anzano, J.M. Laser-induced breakdown spectroscopy: Extending its application to soil pH measurements. Spectrochim. Acta Part B At. Spectrosc. 2015, 110, 96–99. [Google Scholar] [CrossRef]
- Villas-Boas, P.R.; Romano, R.A.; de Menezes Franco, M.A.; Ferreira, E.C.; Ferreira, E.J.; Crestana, S.; Milori, D.M.B.P. Laser-induced breakdown spectroscopy to determine soil texture: A fast analytical technique. Geoderma 2016, 263, 195–202. [Google Scholar] [CrossRef]
- Knadel, M.; Gislum, R.; Hermansen, C.; Peng, Y.; Moldrup, P.; de Jonge, L.W.; Greve, M.H. Comparing predictive ability of laser-induced breakdown spectroscopy to visible near-infrared spectroscopy for soil property determination. Biosyst. Eng. 2017, 156, 157–172. [Google Scholar] [CrossRef]
- Xu, X.; Du, C.; Ma, F.; Shen, Y.; Zhou, J. Fast and Simultaneous Determination of Soil Properties Using Laser-Induced Breakdown Spectroscopy (LIBS): A Case Study of Typical Farmland Soils in China. Soil Syst. 2019, 3, 66. [Google Scholar] [CrossRef]
- Dyar, M.D.; Carmosino, M.L.; Breves, E.A.; Ozanne, M.V.; Clegg, S.M.; Wiens, R.C. Comparison of partial least squares and lasso regression techniques as applied to laser-induced breakdown spectroscopy of geological samples. Spectrochim. Acta Part B At. Spectrosc. 2012, 70, 51–67. [Google Scholar] [CrossRef]
- Li, H.; Liang, Y.; Xu, Q.; Cao, D. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration. Anal. Chim. Acta 2009, 648, 77–84. [Google Scholar] [CrossRef]
- Hubert, M.; Rousseeuw, P.J.; Vanden Branden, K. ROBPCA: A New Approach to Robust Principal Component Analysis. Technometrics 2005, 47, 64–79. [Google Scholar] [CrossRef]
- Andersen, C.M.; Bro, R. Variable selection in regression-a tutorial. J. Chemom. 2010, 24, 728–737. [Google Scholar] [CrossRef]




| SP | Method | Median | IQR | Range (90%) | R2 (CV) | R2 (Val) | RMSECV | RMSEV |
|---|---|---|---|---|---|---|---|---|
| Ca | GP | 0.59 | 0.21 | 0.50 | 0.86 | 0.86 | 0.0645 | 0.0775 |
| Mg | GP | 0.65 | 0.16 | 0.41 | 0.80 | 0.79 | 0.0561 | 0.0602 |
| K | GP | 1.71 | 0.43 | 1.02 | 0.92 | 0.92 | 0.0901 | 0.0655 |
| P | GP | 0.09 | 0.04 | 0.10 | 0.77 | 0.82 | 0.0174 | 0.0184 |
| N | GP | 0.13 | 0.02 | 0.06 | 0.62 | 0.71 | 0.0118 | 0.011 |
| Fe | GP | 3.51 | 1.71 | 4.52 | 0.93 | 0.92 | 0.3489 | 0.431 |
| Mn | PLS | 0.10 | 0.04 | 0.10 | 0.79 | 0.77 | 0.0189 | 0.0203 |
| Zn | PLS | 0.01 | 0.01 | 0.02 | 0.87 | 0.84 | 0.0018 | 0.002 |
| Cu | PLS | 0.003 | 0.002 | 0.006 | 0.87 | 0.85 | 6.62 × 10−4 | 7.11 × 10−4 |
| SOM | GP | 2.39 | 0.57 | 1.43 | 0.67 | 0.71 | 0.2583 | 0.227 |
| pH | GP | 6.07 | 0.27 | 1.15 | 0.54 | 0.57 | 0.2203 | 0.2343 |
| Silt | GP | 58.57 | 12.34 | 28.43 | 0.83 | 0.89 | 3.4688 | 3.1757 |
| Clay | GP | 26.51 | 11.86 | 28.84 | 0.91 | 0.91 | 2.6018 | 3.0933 |
| Soil Parameter | HH | Lab/10 mJ | Lab/40 mJ | PF/25 mJ | PF/40 mJ |
|---|---|---|---|---|---|
| R2 (CV) | |||||
| Ca | 0.85 | 0.74 | 0.86 | 0.91 | 0.95 |
| K | 0.96 | 0.92 | 0.92 | 0.86 | 0.95 |
| Mg | 0.88 | 0.60 | 0.79 | 0.89 | 0.84 |
| P | 0.69 | 0.63 | 0.82 | 0.75 | 0.62 |
| N | 0.59 | 0.64 | 0.71 | 0.30 | 0.59 |
| Mn | 0.69 | 0.68 | 0.77 | 0.40 | 0.94 |
| Fe | 0.94 | 0.87 | 0.92 | 0.87 | 0.88 |
| SOM | 0.55 | 0.63 | 0.71 | 0.65 | 0.35 |
| soil pH | −0.06 | 0.10 | 0.57 | 0.31 | 0.55 |
| silt | 0.86 | 0.84 | 0.89 | 0.85 | 0.83 |
| clay | 0.83 | 0.86 | 0.91 | 0.93 | 0.94 |
| PLS | PCR | SVM | GP | |||||
|---|---|---|---|---|---|---|---|---|
| Soil Parameter | R2 (CV) | R2 (Val) | R2 (CV) | R2 (Val) | R2 (CV) | R2 (Val) | R2 (CV) | R2 (Val) |
| Ca | 0.86 | 0.84 | 0.82 | 0.82 | 0.82 | 0.82 | 0.86 | 0.86 |
| K | 0.92 | 0.91 | 0.92 | 0.93 | 0.91 | 0.93 | 0.92 | 0.92 |
| Mg | 0.77 | 0.74 | 0.74 | 0.76 | 0.74 | 0.76 | 0.8 | 0.79 |
| P | 0.72 | 0.69 | 0.71 | 0.71 | 0.73 | 0.73 | 0.77 | 0.82 |
| N | 0.49 | 0.48 | 0.55 | 0.68 | 0.64 | 0.7 | 0.67 | 0.75 |
| Cu | 0.87 | 0.87 | 0.87 | 0.86 | 0.65 | 0.56 | 0.81 | 0.76 |
| Mn | 0.81 | 0.85 | 0.72 | 0.78 | 0.72 | 0.85 | 0.72 | 0.76 |
| Zn | 0.85 | 0.76 | 0.82 | 0.69 | 0.58 | 0.59 | 0.82 | 0.66 |
| Fe | 0.93 | 0.98 | 0.93 | 0.92 | 0.93 | 0.92 | 0.93 | 0.92 |
| Humus | 0.64 | 0.62 | 0.63 | 0.69 | 0.62 | 0.74 | 0.67 | 0.71 |
| pH | 0.54 | 0.39 | 0.48 | 0.52 | 0.52 | 0.49 | 0.54 | 0.57 |
| Silt | 0.88 | 0.86 | 0.83 | 0.88 | 0.84 | 0.89 | 0.83 | 0.89 |
| Clay | 0.93 | 0.9 | 0.92 | 0.89 | 0.92 | 0.9 | 0.91 | 0.91 |
| Mean (K, Ca, Mg) | 0.85 | 0.83 | 0.83 | 0.84 | 0.82 | 0.84 | 0.86 | 0.86 |
| Mean (MN) | 0.75 | 0.73 | 0.75 | 0.78 | 0.77 | 0.79 | 0.80 | 0.83 |
| Mean (TN) | 0.87 | 0.87 | 0.84 | 0.81 | 0.72 | 0.73 | 0.82 | 0.78 |
| Mean (SP) | 0.75 | 0.69 | 0.72 | 0.75 | 0.73 | 0.76 | 0.74 | 0.77 |
| Mean | 0.79 | 0.76 | 0.76 | 0.78 | 0.74 | 0.76 | 0.79 | 0.79 |
| SP | Method | Features | R2 (CV) | R2 (Val) | SP | Method | Features | R2 (CV) | R2 (Val) |
|---|---|---|---|---|---|---|---|---|---|
| Ca | PLS | 37,633 | 0.86 | 0.84 | N | PLS | 37,633 | 0.49 | 0.48 |
| PCA | 242 | 0.87 | 0.85 | PCA | 242 | 0.58 | 0.56 | ||
| PCA | 17 | 0.86 | 0.84 | PCA | 17 | 0.57 | 0.56 | ||
| CARS | 1012/61 | 0.80 | 0.84 | CARS | 5/8 | 0.56 | 0.64 | ||
| Lasso | 14 | 0.65 | Lasso | 36 | 0.44 | ||||
| Mg | PLS | 37,633 | 0.77 | 0.74 | SOM | PLS | 37,633 | 0.64 | 0.62 |
| PCA | 242 | 0.80 | 0.78 | PCA | 242 | 0.65 | 0.65 | ||
| PCA | 17 | 0.79 | 0.76 | PCA | 17 | 0.65 | 0.65 | ||
| CARS | 22/61 | 0.90 | 0.80 | CARS | 12/7 | 0.64 | 0.69 | ||
| Lasso | 9 | 0.53 | Lasso | 12 | 0.46 | ||||
| K | PLS | 37,633 | 0.92 | 0.91 | Silt | PLS | 37,633 | 0.88 | 0.86 |
| PCA | 242 | 0.93 | 0.92 | PCA | 242 | 0.87 | 0.87 | ||
| PCA | 17 | 0.92 | 0.91 | PCA | 17 | 0.87 | 0.85 | ||
| CARS | 7/61 | 0.93 | 0.96 | CARS | 7/453 | 0.89 | 0.90 | ||
| Lasso | 21 | 0.83 | Lasso | 13 | 0.73 | ||||
| P | PLS | 37,633 | 0.72 | 0.69 | Clay | PLS | 37,633 | 0.93 | 0.90 |
| PCA | 242 | 0.72 | 0.68 | PCA | 242 | 0.93 | 0.91 | ||
| PCA | 17 | 0.72 | 0.61 | PCA | 17 | 0.92 | 0.90 | ||
| CARS | 6172/4130 | 0.75 | 0.75 | CARS | 7545/22 | 0.92 | 0.91 | ||
| Lasso | 11 | 0.40 | Lasso | 8 | 0.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erler, A.; Riebe, D.; Beitz, T.; Löhmannsröben, H.-G.; Leenen, M.; Pätzold, S.; Ostermann, M.; Wójcik, M. Mobile Laser-Induced Breakdown Spectroscopy for Future Application in Precision Agriculture—A Case Study. Sensors 2023, 23, 7178. https://doi.org/10.3390/s23167178
Erler A, Riebe D, Beitz T, Löhmannsröben H-G, Leenen M, Pätzold S, Ostermann M, Wójcik M. Mobile Laser-Induced Breakdown Spectroscopy for Future Application in Precision Agriculture—A Case Study. Sensors. 2023; 23(16):7178. https://doi.org/10.3390/s23167178
Chicago/Turabian StyleErler, Alexander, Daniel Riebe, Toralf Beitz, Hans-Gerd Löhmannsröben, Mathias Leenen, Stefan Pätzold, Markus Ostermann, and Michal Wójcik. 2023. "Mobile Laser-Induced Breakdown Spectroscopy for Future Application in Precision Agriculture—A Case Study" Sensors 23, no. 16: 7178. https://doi.org/10.3390/s23167178
APA StyleErler, A., Riebe, D., Beitz, T., Löhmannsröben, H.-G., Leenen, M., Pätzold, S., Ostermann, M., & Wójcik, M. (2023). Mobile Laser-Induced Breakdown Spectroscopy for Future Application in Precision Agriculture—A Case Study. Sensors, 23(16), 7178. https://doi.org/10.3390/s23167178






