Universal Path-Following of Wheeled Mobile Robots: A Closed-Form Bounded Velocity Solution †
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions and Organization
- This study solves the path-following problem for all WMRs categories in which their wheels roll without skidding. To the best knowledge of the authors, this is the first study that coherently solves the path-following problem with this level of generality.
- Unlike other path-followers, in this design, the control signals and the resultant vector field of closed-loop equations of motion are linearly proportional to the base speed (In this paper, speed exclusively refers to the magnitude of velocity vectors.). In fact, the controller acts as a feedback path-planner that minimizes the Lyapunov function of errors as its corresponding cost function.
- The kinematic constraints of all types of wheels are rigorously derived in their most general form. We derive and prove sufficient conditions for a path-following controller that simplify the kinematic and nonholonomic constraints into explicit relations between the speed of the base and that of the wheels.
- Based on this framework, we present a closed-form solution for the speed of the WMR’s base so that all the wheels’ steering and driving speeds remain within their respective bounds. We show that the solution is time-optimal, because it provides a bang-bang velocity profile in which, at each time step, at least one of the wheels runs at its maximum speed.
- This solution allows WMRs with active steering wheels to get close to, and even pass, their singular configurations by regulating the speed of the WMR and the steering velocities of the wheels. Hence, this method expands the allowable configuration space of such robots and allows them to exploit their whole maneuverability.
2. Problem Description
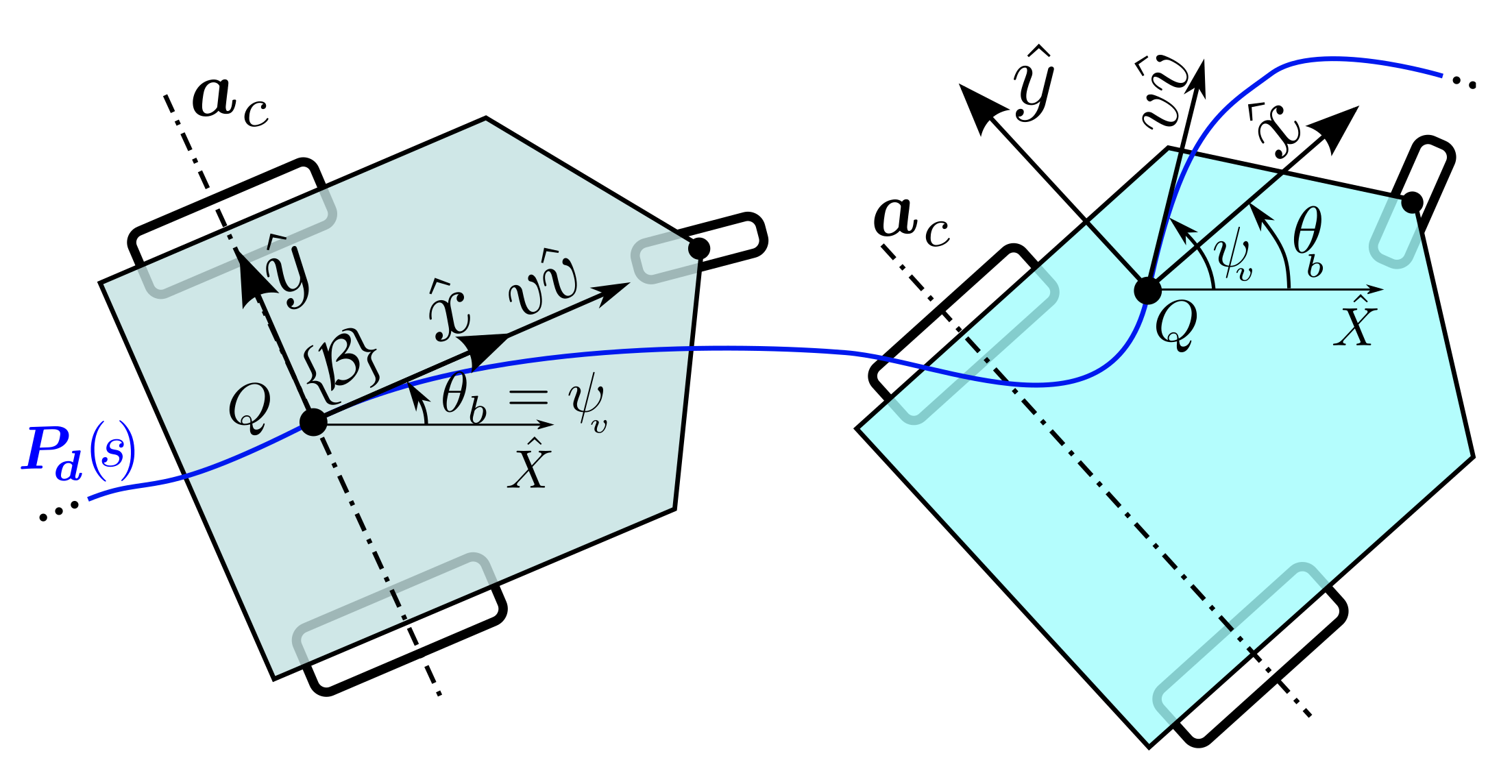
2.1. WMR Architecture and Definitions
2.2. Problem Formulation
- (I)
- Path-Following: The velocity frame converges and follows the tangent frame ; that is, error signals and , remain bounded and converge to zero (See Equation (4a)).
- (II)
- Heading Control: The body frame converges and follows ; that is, the heading error signal , remains bounded and converges to zero (See (4b)).
- (III)
- Bounded Velocity: and should not exceed their corresponding predefined limits.
3. WMR Path-Following: The Generic Form
3.1. Base Path-Following
3.2. Wheels’ Kinematic Constraints
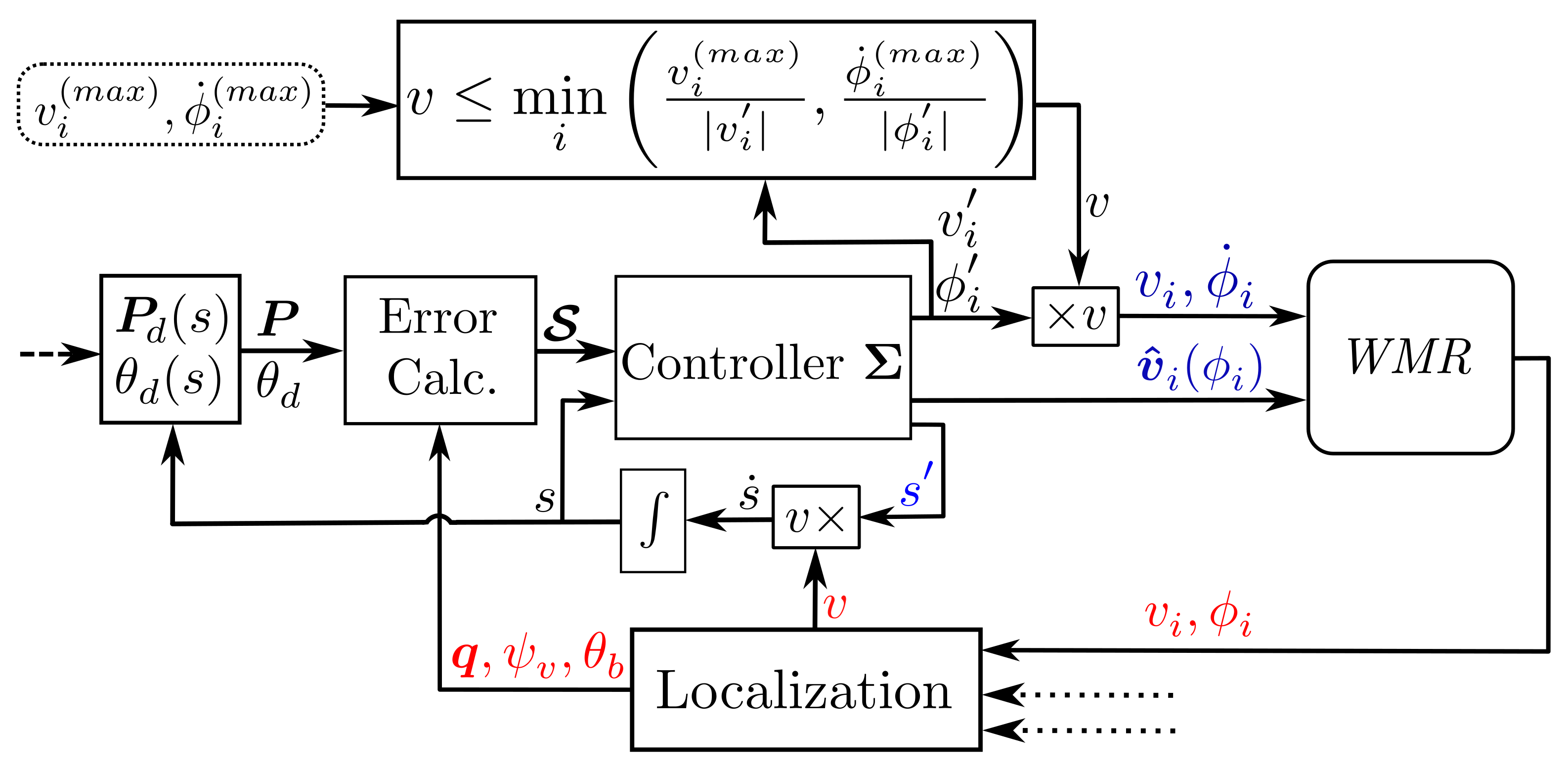
3.3. WMR Path-Following
| Algorithm 1: WMR Bounded Velocity Path-Following. |
Assume that the WMR possess driving actuators and steering actuators (). The maximum driving velocity of the ith driving actuator is denoted as , and the maximum steering velocity of the ith steering actuator is denoted as . At each time step, the control signals of wheels’ actuators is evaluated by |
4. WMR Path-Following: Detailed Illustration
4.1. Base Path-Following: The Controller
4.2. Customization of the Path-Following Algorithm
4.2.1. WMRs with
4.2.2. WMRs with
4.3. Analysis of Steering Wheels Singularities
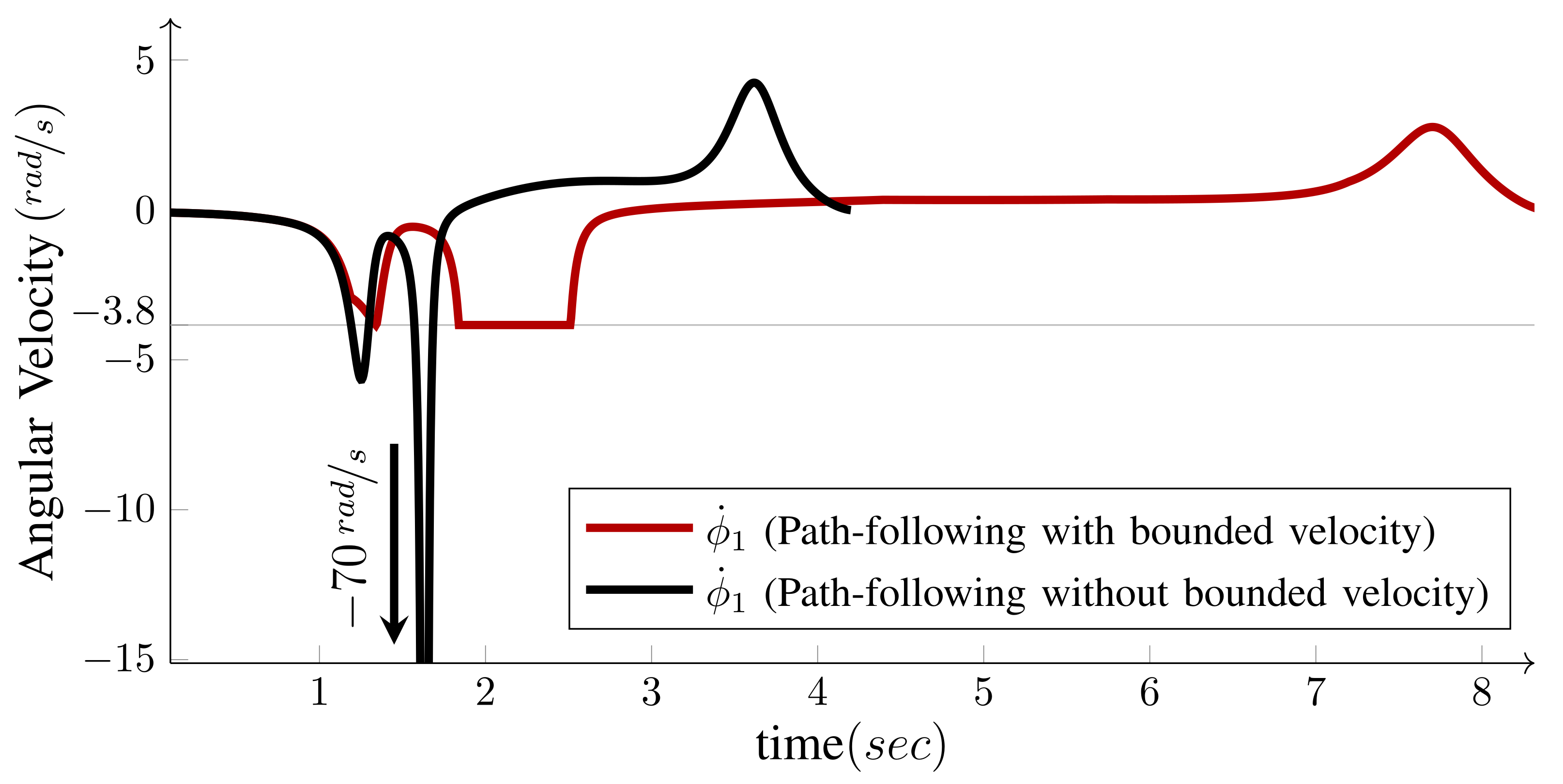
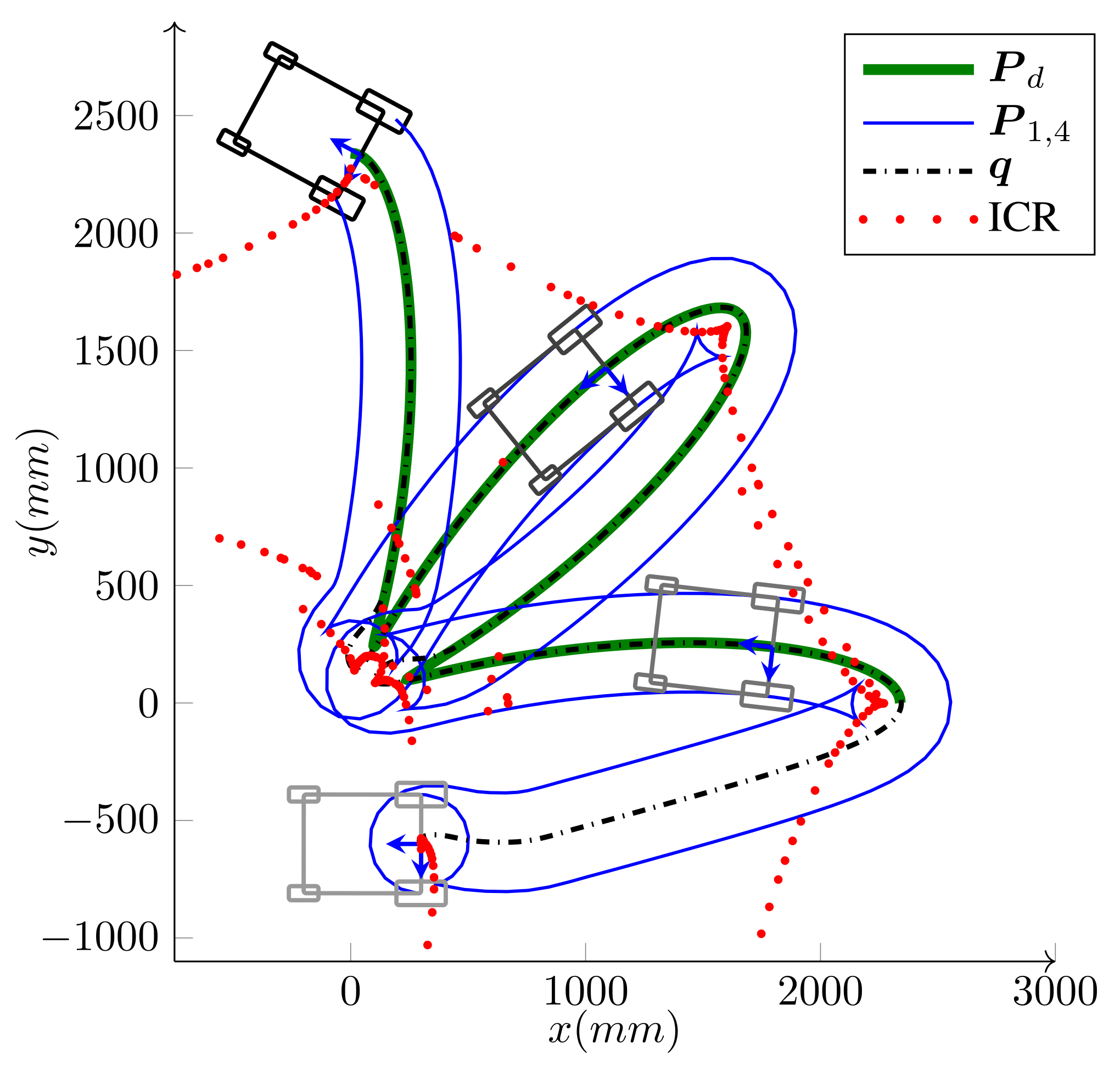
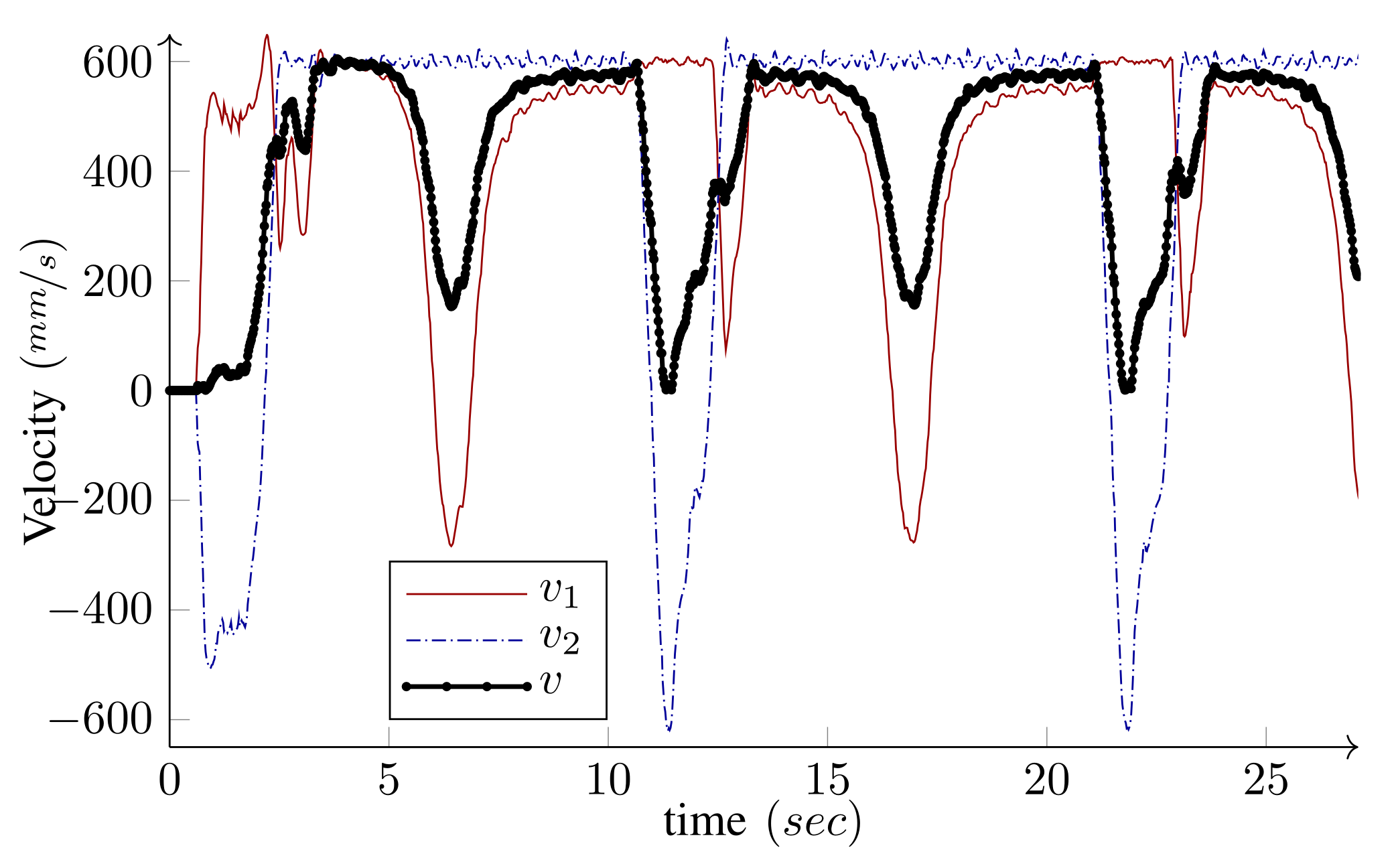
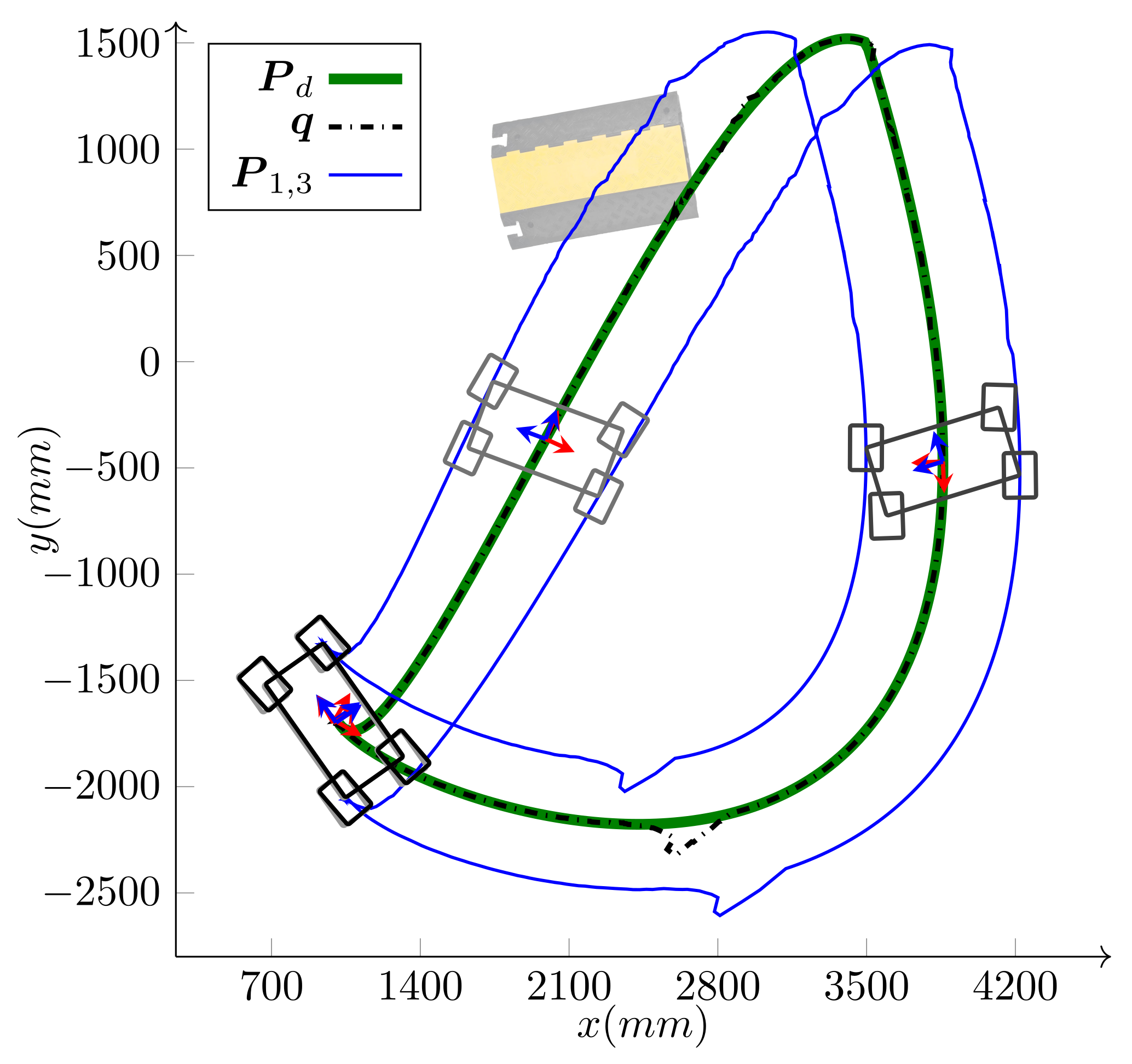
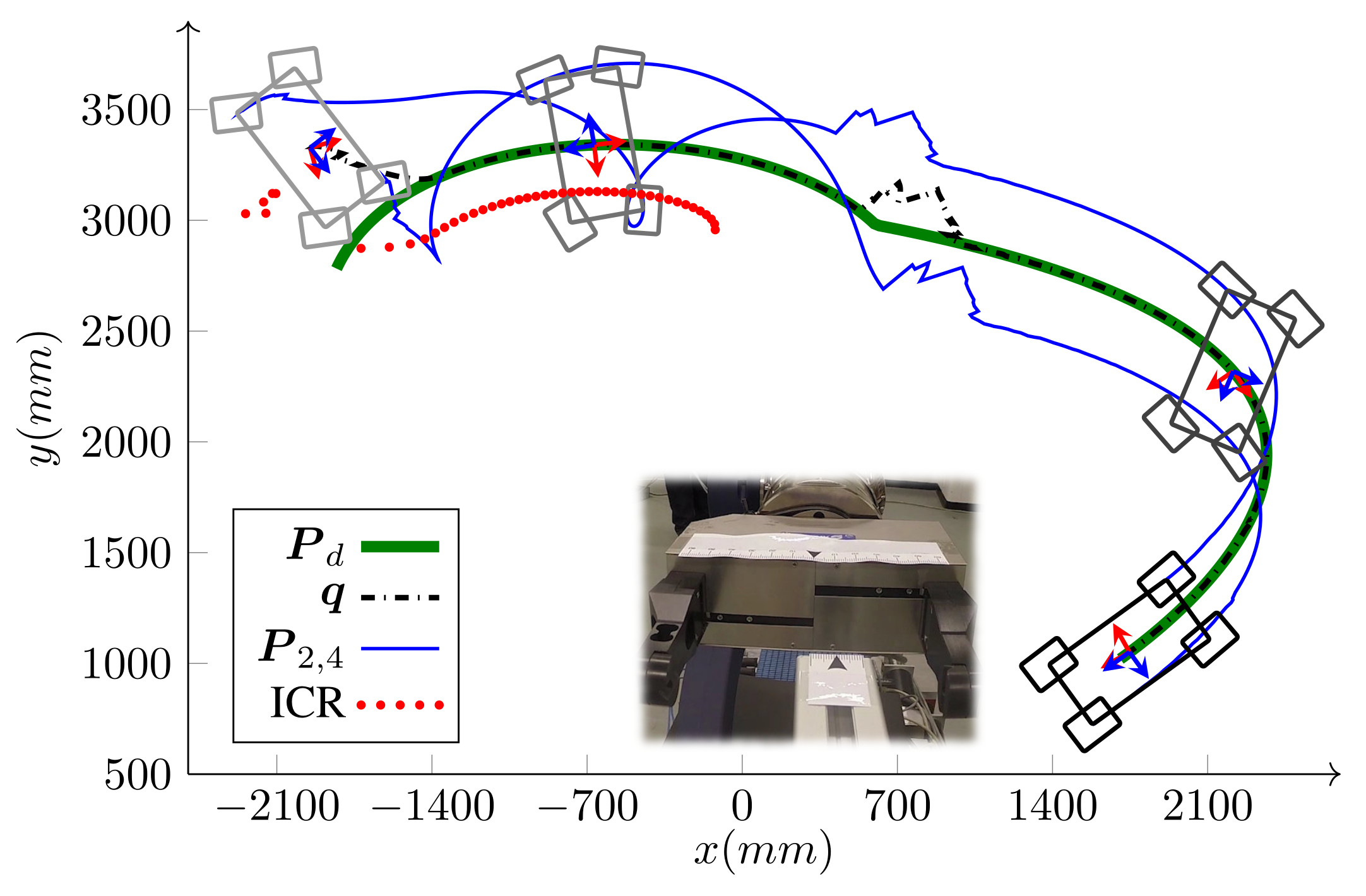
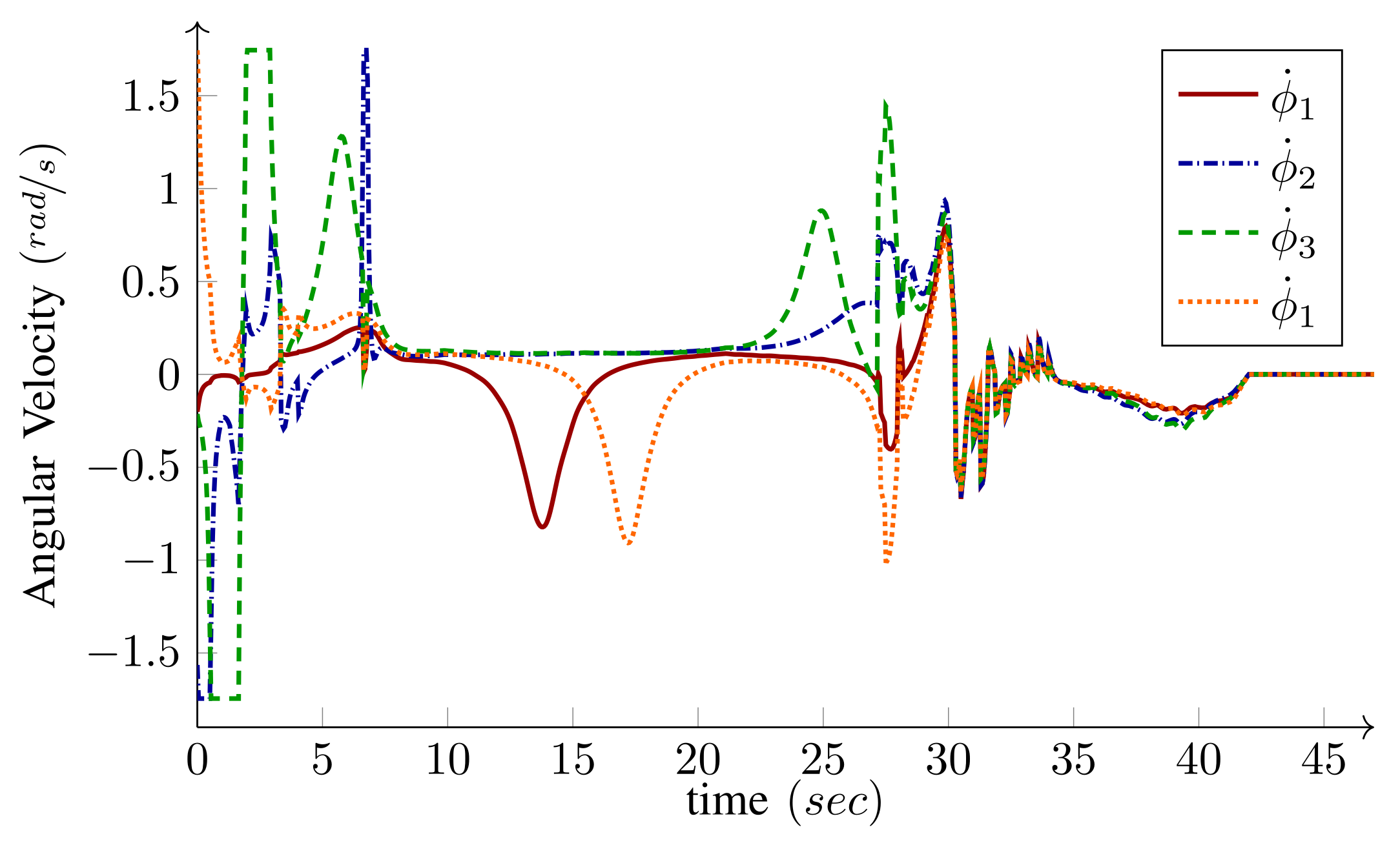
5. Experimental and Simulation Results
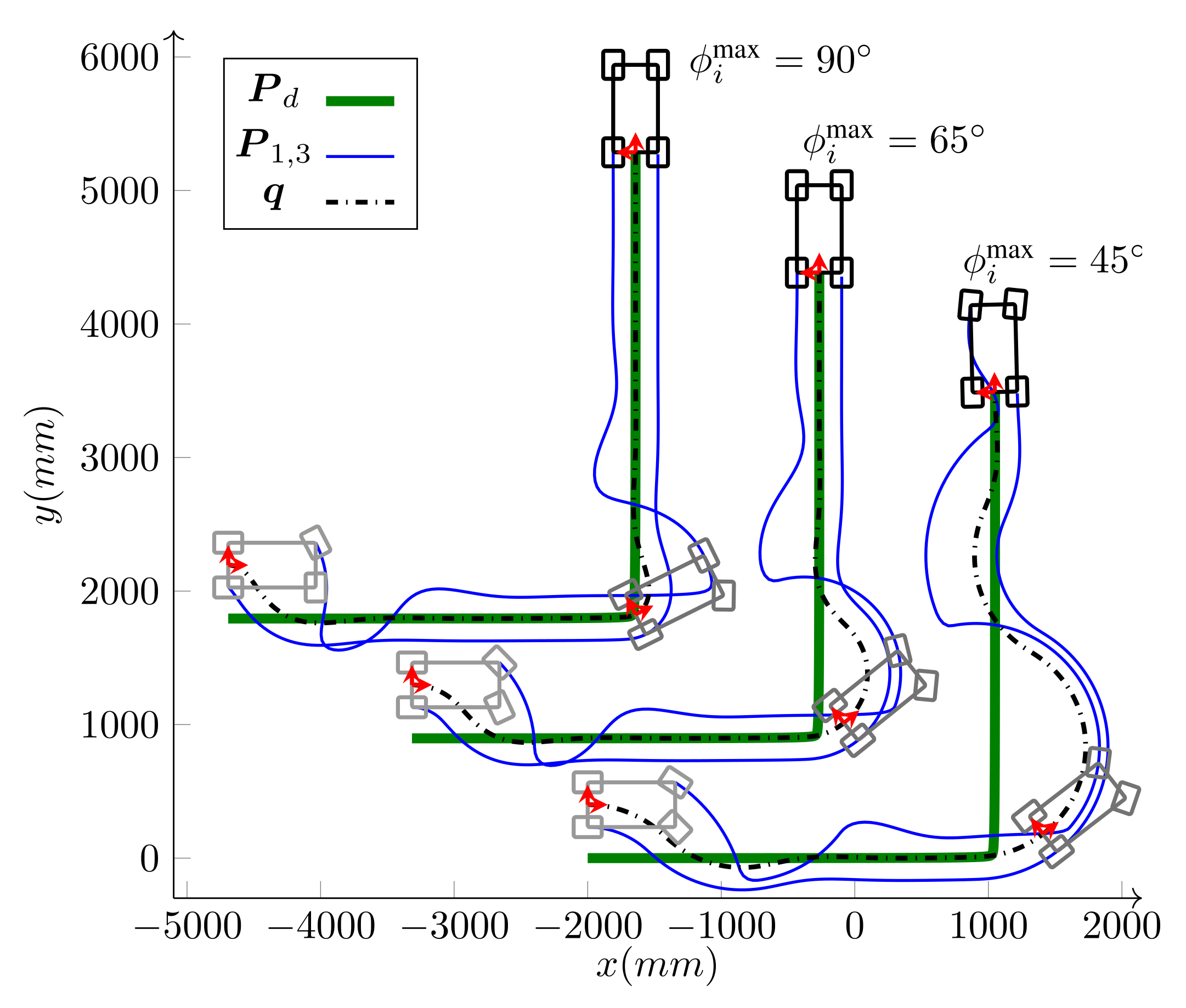
5.1. Case Study I: and
5.2. Case Study II:
5.3. Case Study III:
5.4. Restrictions
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morin, P.; Samson, C. Motion control of wheeled mobile robots. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 799–826. [Google Scholar]
- Park, K.; Chung, H.; Lee, J.G. Point stabilization of mobile robots via state-space exact feedback linearization. Robot. Comput.-Integr. Manuf. 2000, 16, 353–363. [Google Scholar] [CrossRef]
- Hwang, C.L.; Wu, H.M. Trajectory tracking of a mobile robot with frictions and uncertainties using hierarchical sliding-mode under-actuated control. IET Control Theory Appl. 2013, 7, 952–965. [Google Scholar] [CrossRef]
- Fossen, T.; Pettersen, K.Y.; Galeazzi, R. Line-of-sight path following for Dubins paths with adaptive sideslip compensation of drift forces. IEEE Trans. Control Syst. Technol. 2015, 23, 820–827. [Google Scholar] [CrossRef] [Green Version]
- Bullo, F.; Lynch, K.M. Kinematic controllability for decoupled trajectory planning in underactuated mechanical systems. IEEE Trans. Robot. Autom. 2001, 17, 402–412. [Google Scholar] [CrossRef]
- Van Loock, W.; Pipeleers, G.; Diehl, M.; De Schutter, J.; Swevers, J. Optimal Path Following for Differentially Flat Robotic Systems Through a Geometric Problem Formulation. IEEE Trans. Robot. 2014, 30, 980–985. [Google Scholar] [CrossRef] [Green Version]
- Debrouwere, F.; Van Loock, W.; Pipeleers, G.; Dinh, Q.T.; Diehl, M.; De Schutter, J.; Swevers, J. Time-optimal path following for robots with convex–concave constraints using sequential convex programming. IEEE Trans. Robot. 2013, 29, 1485–1495. [Google Scholar] [CrossRef]
- Akhtar, A.; Nielsen, C.; Waslander, S.L. Path following using dynamic transverse feedback linearization for car-like robots. IEEE Trans. Robot. 2015, 31, 269–279. [Google Scholar] [CrossRef]
- Ambrosino, G.; Ariola, M.; Ciniglio, U.; Corraro, F.; De Lellis, E.; Pironti, A. Path generation and tracking in 3-D for UAVs. IEEE Trans. Control Syst. Technol. 2009, 17, 980–988. [Google Scholar] [CrossRef]
- Yamasaki, T.; Balakrishnan, S. Sliding mode-based pure pursuit guidance for unmanned aerial vehicle rendezvous and chase with a cooperative aircraft. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 1057–1067. [Google Scholar] [CrossRef]
- Nelson, D.R.; Barber, D.B.; McLain, T.W.; Beard, R.W. Vector field path following for miniature air vehicles. IEEE Trans. Robot. 2007, 23, 519–529. [Google Scholar] [CrossRef] [Green Version]
- Sujit, P.; Saripalli, S.; Borges Sousa, J. Unmanned aerial vehicle path following: A survey and analysis of algorithms for fixed-wing unmanned aerial vehicless. IEEE Control Syst. 2014, 34, 42–59. [Google Scholar]
- Samson, C. Time-varying feedback stabilization of car-like wheeled mobile robots. Int. J. Robot. Res. 1993, 12, 55–64. [Google Scholar] [CrossRef]
- Aicardi, M.; Casalino, G.; Bicchi, A.; Balestrino, A. Closed loop steering of unicycle like vehicles via Lyapunov techniques. IEEE Robot. Autom. Mag. 1995, 2, 27–35. [Google Scholar] [CrossRef]
- Micaelli, A.; Samson, C. Trajectory Tracking for Unicycle-Type and Two-Steering-Wheels Mobile Robots; Technical Report 2097; INRIA: Rocquencourt, France, 1993. [Google Scholar]
- Soetanto, D.; Lapierre, L.; Pascoal, A. Adaptive, non-singular path-following control of dynamic wheeled robots. In Proceedings of the 42nd IEEE Conference on Decision and Control, Maui, HI, USA, 9–12 December 2003; Volume 2, pp. 1765–1770. [Google Scholar]
- Lapierre, L.; Soetanto, D.; Pascoal, A. Nonsingular path following control of a unicycle in the presence of parametric modelling uncertainties. Int. J. Robust Nonlinear Control 2006, 16, 485–503. [Google Scholar] [CrossRef]
- Lapierre, L.; Indiverri, G. Path-Following Control of a Wheeled Robot under actuation saturation constraints. In Proceedings of the IAV07 Conference, Toulouse, France, 3–5 September 2007. [Google Scholar]
- Lapierre, L.; Zapata, R.; Lepinay, P. Combined path-following and obstacle avoidance control of a wheeled robot. Int. J. Robot. Res. 2007, 26, 361–375. [Google Scholar] [CrossRef]
- Kaminer, I.; Pascoal, A.; Xargay, E.; Hovakimyan, N.; Cao, C.; Dobrokhodov, V. Path following for small unmanned aerial vehicles using L1 adaptive augmentation of commercial autopilots. J. Guid. Control. Dyn. 2010, 33, 550–564. [Google Scholar] [CrossRef] [Green Version]
- Encarnaçao, P.; Pascoal, A. 3D path following for autonomous underwater vehicle. In Proceedings of the 39 th IEEE Conference on Decision and Control, Sydney, NSW, Australia, 12–15 December 2000. [Google Scholar]
- Ghabcheloo, R.; Hyvonen, M. Modeling and motion control of an articulated-frame-steering hydraulic mobile machine. In Proceedings of the 17th Mediterranean Conference on Control and Automation (MED’09), Thessaloniki, Greece, 24–26 June 2009; pp. 92–97. [Google Scholar]
- Bibuli, M.; Bruzzone, G.; Caccia, M.; Lapierre, L. Path-following algorithms and experiments for an unmanned surface vehicle. J. Field Robot. 2009, 26, 669–688. [Google Scholar] [CrossRef] [Green Version]
- Kanjanawanishkul, K.; Zell, A. Path following for an omnidirectional mobile robot based on model predictive control. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA’09), Kobe, Japan, 12–17 May 2009; pp. 3341–3346. [Google Scholar]
- Thuilot, B.; d’Aandrea Novel, B.; Micaelli, A. Modeling and feedback control of mobile robots equipped with several steering wheels. IEEE Trans. Robot. Autom. 1996, 12, 375–390. [Google Scholar] [CrossRef]
- Connette, C.P.; Pott, A.; Hagele, M.; Verl, A. Control of an pseudo-omnidirectional, non-holonomic, mobile robot based on an ICM representation in spherical coordinates. In Proceedings of the 47th IEEE Conference on Decision and Control (CDC 2008), Cancun, Mexico, 9–11 December 2008; pp. 4976–4983. [Google Scholar]
- Song, J.B.; Byun, K.S. Steering control algorithm for efficient drive of a mobile robot with steerable omni-directional wheels. J. Mech. Sci. Technol. 2009, 23, 2747–2756. [Google Scholar] [CrossRef]
- Moore, K.L.; Davidson, M.; Bahl, V.; Rich, S.; Jirgal, S. Modelling and control of a six-wheeled autonomous robot. In Proceedings of the IEEE 2000 American Control Conference, Chicago, IL, USA, 28–30 June 2000; Volume 3, pp. 1483–1490. [Google Scholar]
- Connette, C.; Parlitz, C.; Hägele, M.; Verl, A. Singularity avoidance for over-actuated, pseudo-omnidirectional, wheeled mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 4124–4130. [Google Scholar]
- Schwesinger, U.; Pradalier, C.; Siegwart, R. A novel approach for steering wheel synchronization with velocity/acceleration limits and mechanical constraints. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 5360–5366. [Google Scholar]
- Cousins, S. Ros on the pr2 [ros topics]. IEEE Robot. Autom. Mag. 2010, 17, 23–25. [Google Scholar] [CrossRef]
- Graf, B.; Reiser, U.; Hagele, M.; Mauz, K.; Klein, P. Robotic home assistant Care-O-bot® 3-product vision and innovation platform. In Proceedings of the 2009 IEEE Workshop on Advanced Robotics and its Social Impacts (ARSO), Tokyo, Japan, 23–25 November 2009; pp. 139–144. [Google Scholar]
- Dietrich, A.; Wimbock, T.; Albu-Schaffer, A.; Hirzinger, G. Reactive Whole-Body Control: Dynamic Mobile Manipulation Using a Large Number of Actuated Degrees of Freedom. IEEE Robot. Autom. Mag. 2012, 19, 20–33. [Google Scholar] [CrossRef] [Green Version]
- Bak, T.; Jakobsen, H. Agricultural robotic platform with four wheel steering for weed detection. Biosyst. Eng. 2004, 87, 125–136. [Google Scholar] [CrossRef]
- Cariou, C.; Lenain, R.; Thuilot, B.; Berducat, M. Automatic guidance of a four-wheel-steering mobile robot for accurate field operations. J. Field Robot. 2009, 26, 504–518. [Google Scholar] [CrossRef]
- Frémy, J.; Ferland, F.; Lauria, M.; Michaud, F. Force-guidance of a compliant omnidirectional non-holonomic platform. Robot. Auton. Syst. 2014, 62, 579–590. [Google Scholar] [CrossRef]
- Connette, C.; Hagele, M.; Verl, A. Singularity-free state-space representation for non-holonomic, omnidirectional undercarriages by means of coordinate switching. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 4959–4965. [Google Scholar]
- Connette, C.; Pott, A.; Hägele, M.; Verl, A. Addressing input saturation and kinematic constraints of overactuated undercarriages by predictive potential fields. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 4775–4781. [Google Scholar]
- Oftadeh, R.; Aref, M.M.; Ghabcheloo, R.; Mattila, J. Bounded-velocity motion control of four wheel steered mobile robots. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Wollongong, NSW, Australia, 9–12 July 2013; pp. 255–260. [Google Scholar]
- Oftadeh, R.; Ghabcheloo, R.; Mattila, J. A novel time optimal path following controller with bounded velocities for mobile robots with independently steerable wheels. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–7 November 2013; pp. 4845–4851. [Google Scholar]
- Oftadeh, R.; Ghabcheloo, R.; Mattila, J. A time-optimal bounded velocity path-following controller for generic Wheeled Mobile Robots. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 676–683. [Google Scholar]
- Campion, G.; Bastin, G.; Dandrea-Novel, B. Structural properties and classification of kinematic and dynamic models of wheeled mobile robots. IEEE Trans. Robot. Autom. 1996, 12, 47–62. [Google Scholar] [CrossRef]
- Osmolovskii, N.; Maurer, H. Applications to Regular and Bang-Bang Control; Advances in Design and Control, Society for Industrial and Applied Mathematics; SIAM: Philadelphia, PA, USA, 2012. [Google Scholar]
- Oftadeh, R.; Aref, M.M.; Ghabcheloo, R.; Mattila, J. Unified framework for rapid prototyping of linux based real-time controllers with matlab and simulink. In Proceedings of the 2012 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Kaohsiung, Taiwan, 11–14 July 2012; pp. 274–279. [Google Scholar]
- Aref, M.M.; Oftadeh, R.; Ghabcheloo, R.; Mattila, J. Real-time vision-based navigation for nonholonomic mobile robots. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016; pp. 515–522. [Google Scholar]
- Oftadeh, R.; Ghabcheloo, R.; Mattila, J. Time Optimal Path Following with Bounded Velocities and Accelerations for Mobile Robots with Independently Steerable Wheels. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]









| Coordinate Frames and Their Basis | ||
|---|---|---|
| The inertial frame with its origin | ||
| The body frame attached to the WMR’s base | ||
| The base velocity coordinate frame at | ||
| The Frenet–Serret frame of the desired path, , at | ||
| The desired heading coordinate frame at | ||
| Paths’ Parameters and Variables | ||
| s | Natural parameter(arc length) of the desired path, | |
| The curvature of the desired path, () | ||
| Natural parameter(arc length) of the asymptotic path, | ||
| Position Vectors | ||
| ≜ | ; the position vector of the virtual target point, , with respect to | |
| ≜ | ; the position vector of the base, , with respect to | |
| The position of ith wheel attachment point, , to the base with respect to | ||
| Angles | ||
| The WMR’s heading angle that defines the body frame | ||
| The desired heading angle; defines the frame at | ||
| The angle of the base linear velocity direction, | ||
| The desired angle for the base linear velocity direction, | ||
| ≜ | ||
| The tangent angle; defines the desired path tangent vector | ||
| The ith wheel steering angle | ||
| The angle between the base linear velocity and the ith wheel position vector, | ||
| Others | ||
| The direction vector of the base linear velocity at | ||
| v | The speed of the base at | |
| The direction vector of the ith wheel linear velocity | ||
| The driving speed of the ith wheel | ||
| ≜ | ; the base angular velocity | |
| ≜ | ; the angular rate of | |
| ≜ | ||
| Type | Fixed Wheel | Centered Steering Wheel | Caster Wheel | Swedish Wheel | |
|---|---|---|---|---|---|
| Variable | |||||
| Fixed | Measurement or Equation (24) | Measurement | Fixed | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oftadeh, R.; Ghabcheloo, R.; Mattila, J. Universal Path-Following of Wheeled Mobile Robots: A Closed-Form Bounded Velocity Solution. Sensors 2021, 21, 7642. https://doi.org/10.3390/s21227642
Oftadeh R, Ghabcheloo R, Mattila J. Universal Path-Following of Wheeled Mobile Robots: A Closed-Form Bounded Velocity Solution. Sensors. 2021; 21(22):7642. https://doi.org/10.3390/s21227642
Chicago/Turabian StyleOftadeh, Reza, Reza Ghabcheloo, and Jouni Mattila. 2021. "Universal Path-Following of Wheeled Mobile Robots: A Closed-Form Bounded Velocity Solution" Sensors 21, no. 22: 7642. https://doi.org/10.3390/s21227642
APA StyleOftadeh, R., Ghabcheloo, R., & Mattila, J. (2021). Universal Path-Following of Wheeled Mobile Robots: A Closed-Form Bounded Velocity Solution. Sensors, 21(22), 7642. https://doi.org/10.3390/s21227642








