Enhancing the Sensor Node Localization Algorithm Based on Improved DV-Hop and DE Algorithms in Wireless Sensor Networks
Abstract
1. Introduction
- The equation formula for calculating the average distance per hop of anchor nodes is improved. The minimum mean square error criterion more excellent to calculate the average distance per hop, and the average distance per hop of anchor nodes is obtained by applying its average value.
- DE algorithm has the defects of search stagnation and premature convergence; this improves the mutation formula and introduces random variation. In the crossover operation, the social learning part of the particle swarm optimization algorithm is introduced, and the heuristic information carried by the group optimal value is used to permit the current individual to learn from the group optimal individual, which is then intersected with the mutation vector. With the improvement of mutation operation and crossover operation of the basic DE algorithm, the diversity of the population is enhanced as well as information of the optimal individual in the population is effectively used to raise the efficiency of the algorithm.
- To validate and show the effectiveness of the proposed algorithm, the proposed DEIDV-Hop algorithm is evaluated under four different network environments. In comparison with known algorithms, DV-Hop, PSODV-Hop [32], and GSODV-Hop [33], experimental results show that the proposed DEIDV-Hop algorithm has smaller localization errors and greater stability, yet more suitable for application scenarios with higher localization accuracy and stability requirements.
2. Related Work
3. Distance Vector-Hop (DV-Hop) and Differential Evolution (DE) Algorithms
3.1. DV-Hop Algorithm
3.2. Differential Evolution Algorithm
3.2.1. Initialization
3.2.2. Mutation
3.2.3. Crossover
3.2.4. Selection
4. Proposed DEIDV-Hop Algorithm
4.1. Goal
4.2. Process of Flooding
4.3. Process of Calculating the Average Distance per Hop
4.4. Improvement of Differential Evolution Algorithm
4.4.1. Crossover
4.4.2. Selection
4.5. Differential Evolution Algorithm Implementation
4.6. Complete DEIDV-Hop Algorithm
| Algorithm 1: The procedure of DEIDV-Hop |
| 1: Initialization: total number of nodes N, Percentage p of anchor nodes, communication radius R; |
| 2: Input: Parameter settings of DEIDV-Hop and the experimental area; |
| Parameter settings of DEIDV-Hop: see Table 1 |
| Experimental area is 100 × 100 m2 |
| 3: Network deployment nodes to generate simulated network topology; |
| 4: Calculate the hop-count value according to the shortest path algorithm |
| 5: for k = 1 to N |
| 6: for i = 1 to N |
| 7: for j =1 to N |
| 8: if short_path(i,k) + short_path(k,j) < short_path(i,j) |
| 9: short_path(i,j) = short_path(i,k) + short_path(k,j); |
| 10: end |
| 11: end |
| 12: end |
| 13: end |
| 14: Calculate the average distance per hop, according to Equation (16); |
| 15: Calculate the unknown distances; |
| 16: for k = 1 to |
| 17: Initialization: Generates individuals that contain 2 dimensions of variables according to Equation (9); |
| 18: Calculate and evaluate each individual ; |
| 19: = 1; |
| 20: While do |
| 21: for = 1 to //Mutation and Crossover |
| 22: According to Equation (18), mutation vector is generated; |
| 23: for j = 1 to |
| 24: Trial vector was obtained by crossover according to Equation (19); |
| 25: end |
| 26: Trial vector was selected; |
| 27: if then //Minimize optimization problems |
| 28: ; |
| 29: else |
| 30: ; |
| 31: end |
| 32: end |
| 33: ; |
| 34: end |
| 35: The best individual is the location of the unknown node; |
| 36: end |
5. Experimental Results and Analysis
5.1. Effect of Deployment Deviation Ratio in a Grid Topology
5.2. Effect of Communication Radius on Average Localization Error (ALE)
- PSODV-Hop reduces the average ALE by 7.61%, GSODV-Hop reduces by 26.35%, and DEIDV-Hop reduces by 34.88% when compared with DV-Hop in the square random topology,
- PSODV-Hop reduces the average ALE by 32.3%, GSODV-Hop reduces by 33.15% and DEIDV-Hop reduces by 40.36% when compared with DV-Hop in the square grid topology,
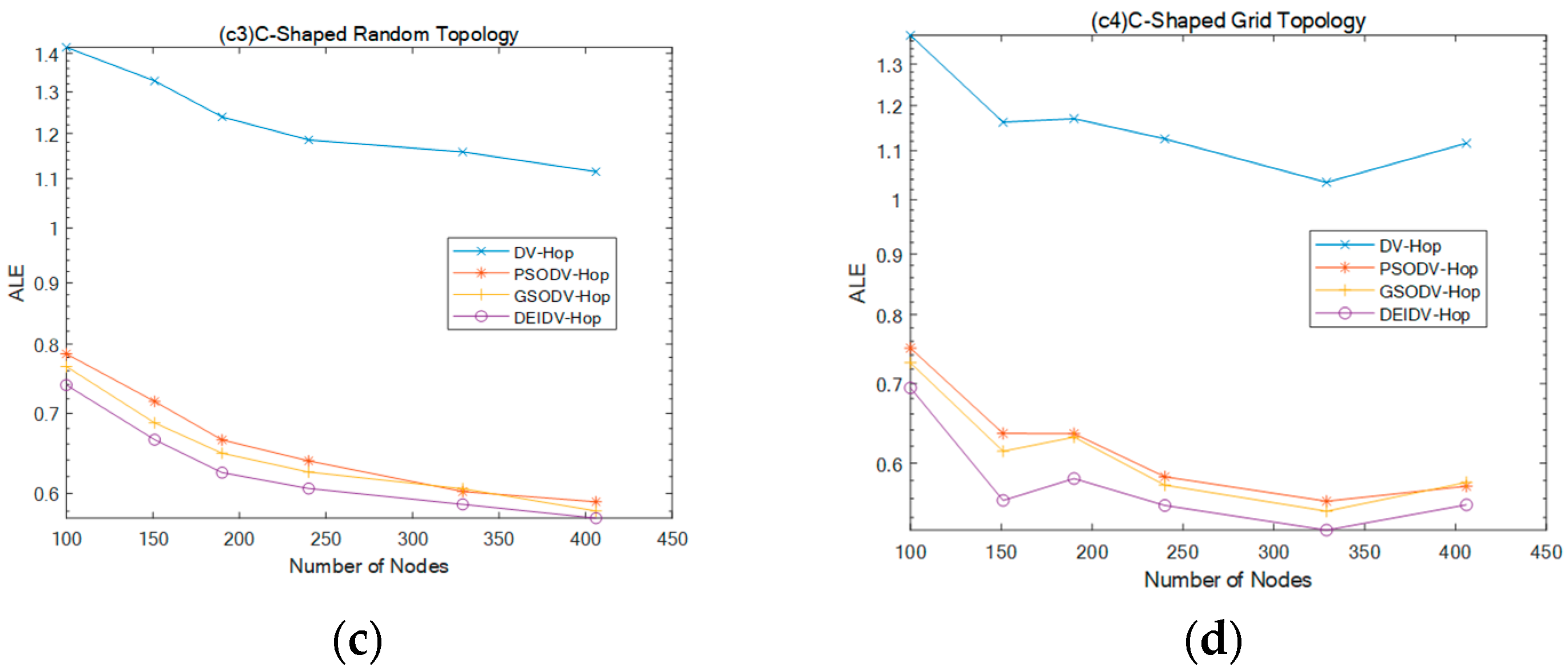
- Three meta-heuristic localization algorithms PSODV-Hop, GSODV-Hop, and DEIDV-Hop improve in average 40.71%, 41.05%, and 44.79%, respectively on localization accuracy when compared with DV-Hop in the C-Shaped random topology,
- Three meta-heuristic localization algorithms PSODV-Hop, GSODV-Hop, and DEIDV-Hop improve on average 41.49%, 42.85%, and 45.48%, respectively, on localization accuracy when compared with DV-Hop in C-Shaped grid topology.
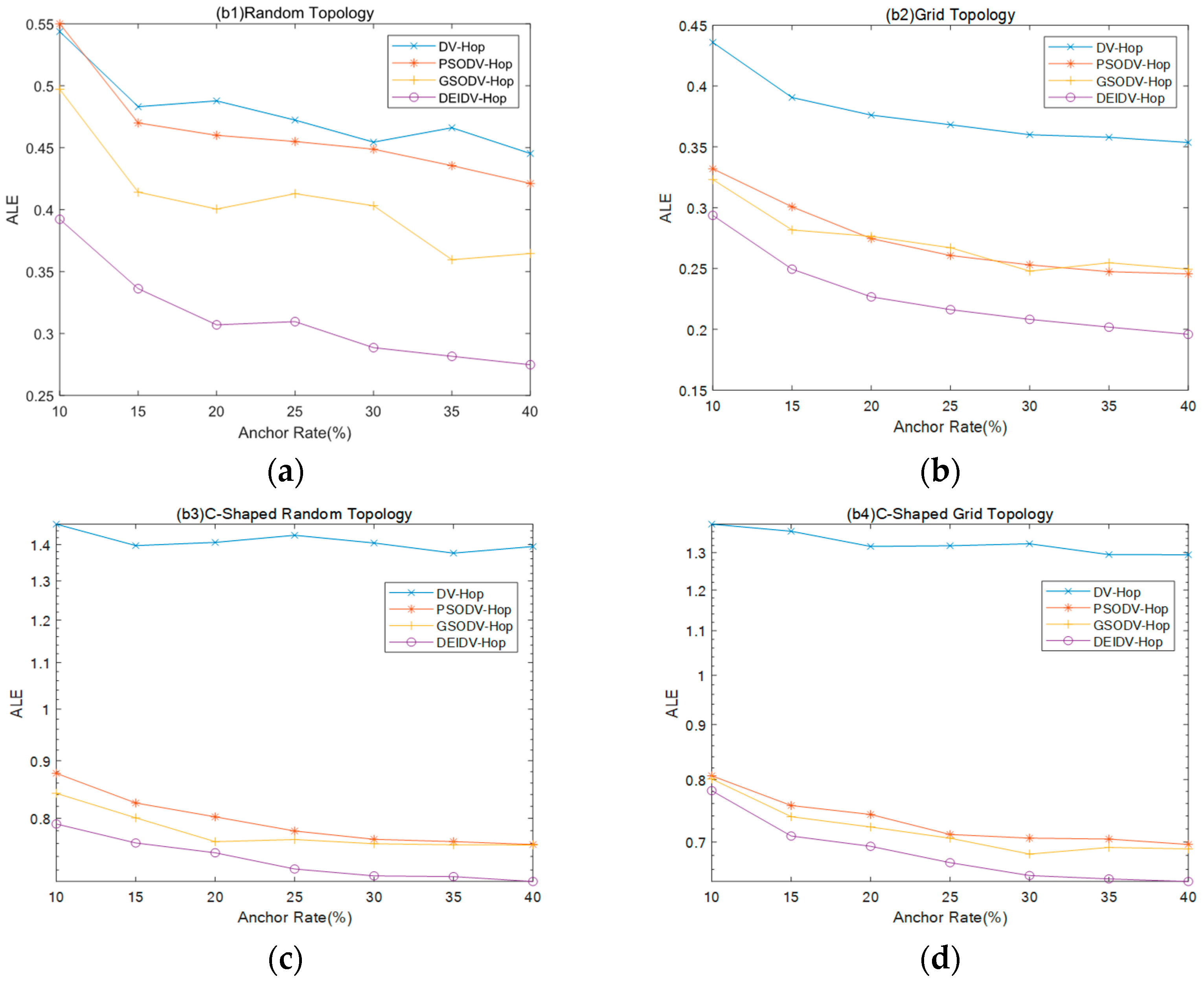
5.3. Effect of the Percentage of Anchor Nodes on ALE
- PSODV-Hop reduces the average of ALE by 3.36%, GSODV-Hop reduces by 14.95%, and DEIDV-Hop reduces by 34.68% in the square random topology,
- PSODV-Hop reduces the average of ALE by 27.58%, GSODV-Hop reduces by 27.89%, and DEIDV-Hop reduces by 39.76% in the square grid topology;
- Three meta-heuristic localization algorithms PSODV-Hop, GSODV-Hop, and DEIDV-Hop improve average 43.51%, 44.79%, and 47.86%, respectively, on localization accuracy in the C-shaped random topology;
- Three meta-heuristic localization algorithms PSODV-Hop, GSODV-Hop, and DEIDV-Hop improve average 44.87%, 45.85%, and 48.4%, respectively, on localization accuracy in the C-shaped grid topology.
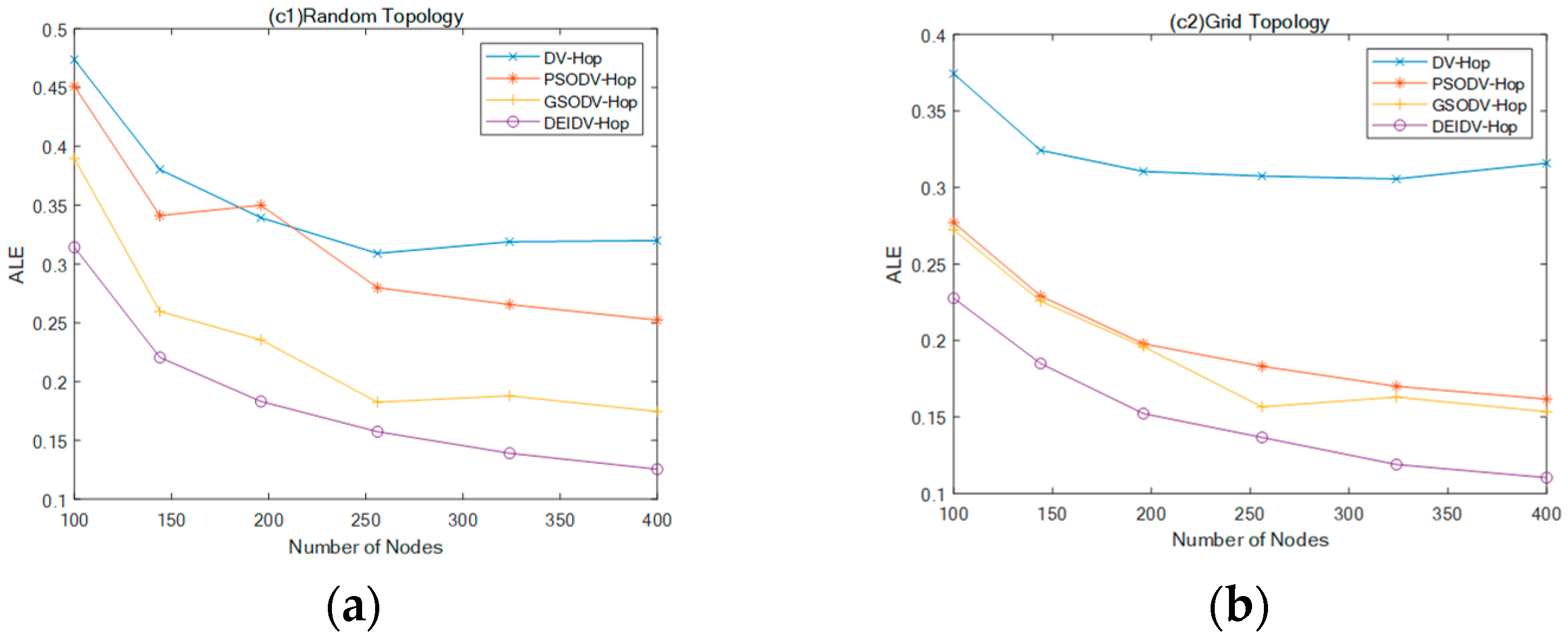
5.4. Effect of Node Density on ALE
- PSODV-Hop reduces the average of ALE by 9.41%, GSODV-Hop reduces by 33.23%, and DEIDV-Hop reduces by 46.76% in the square random topology;
- PSODV-Hop reduces the average of ALE by 37.09%, GSODV-Hop reduces by 39.78%, and DEIDV-Hop reduces by 51.95% in the square grid topology;
- Three meta-heuristic localization algorithms PSODV-Hop, GSODV-Hop, and DEIDV-Hop improve average 46.25%, 47.41%, and 49%, respectively, on localization accuracy in the C-shaped random topology;
- Three meta-heuristic localization algorithms PSODV-Hop, GSODV-Hop, and DEIDV-Hop improve average 46.49%, 47.39%, and 50.33%, respectively, on localization accuracy in the C-shaped grid topology.
6. Convergence Speed of the Algorithm and the Localization Error of Unknown Nodes
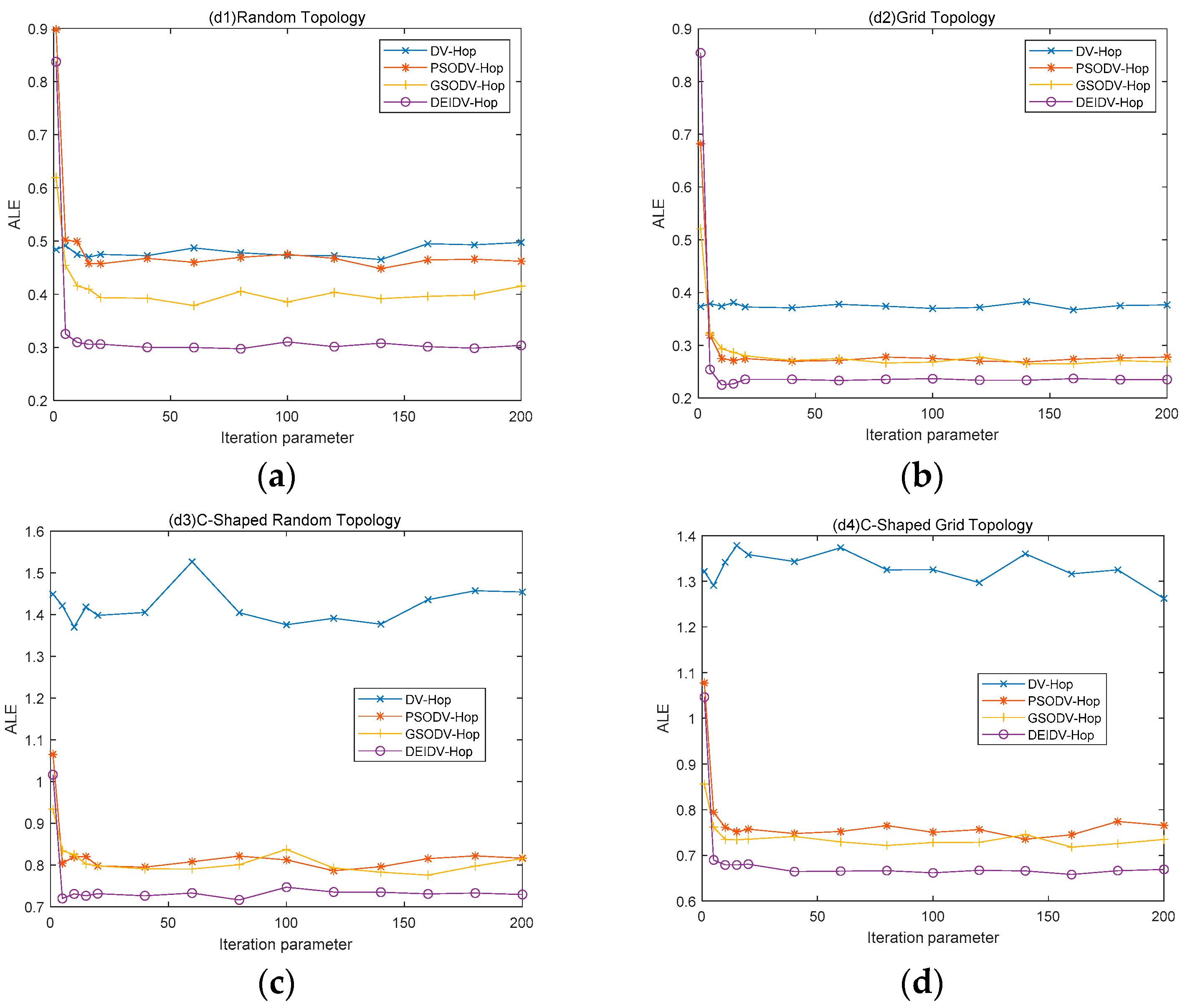
6.1. Convergence Speed of the Algorithm
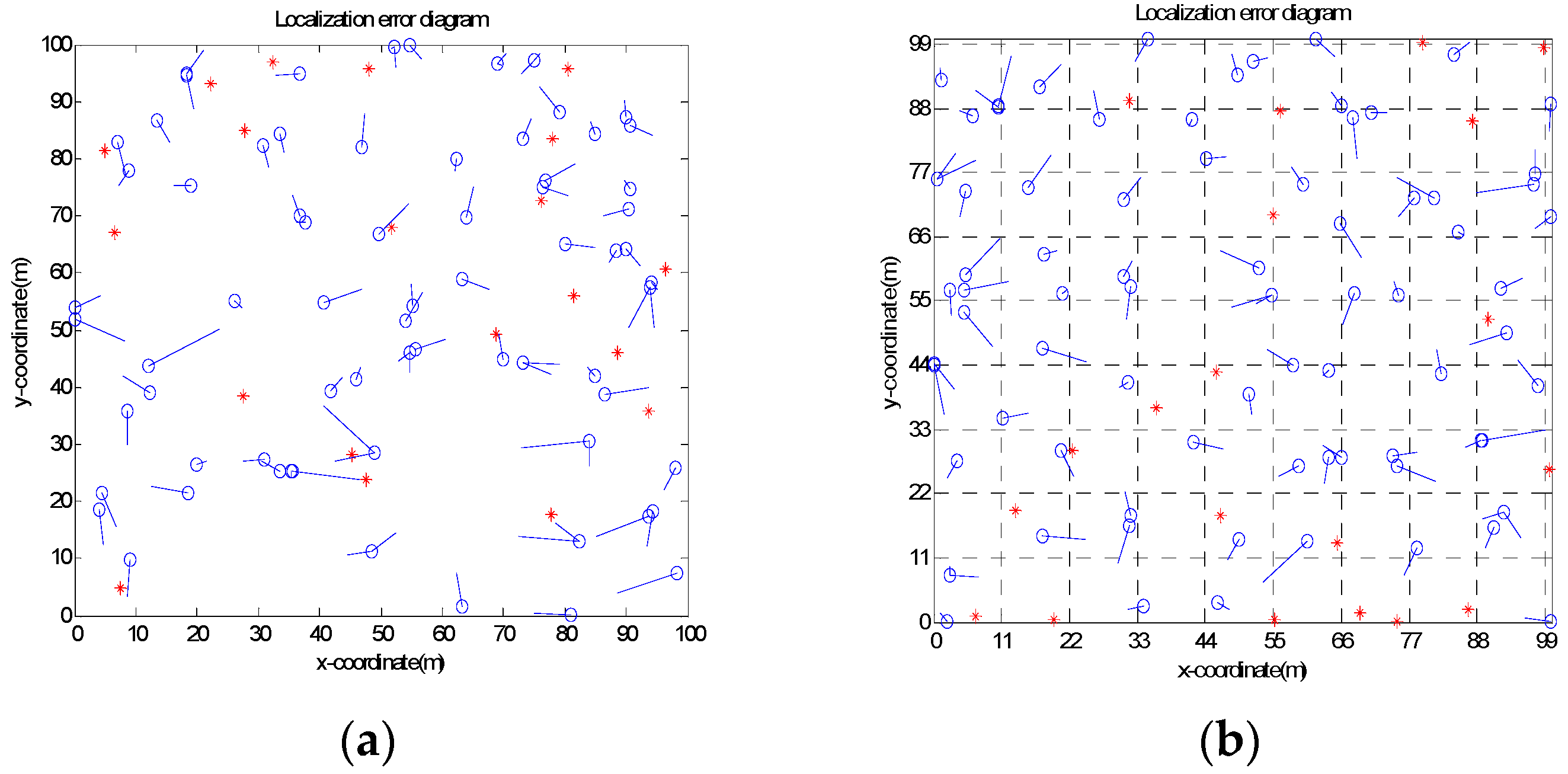
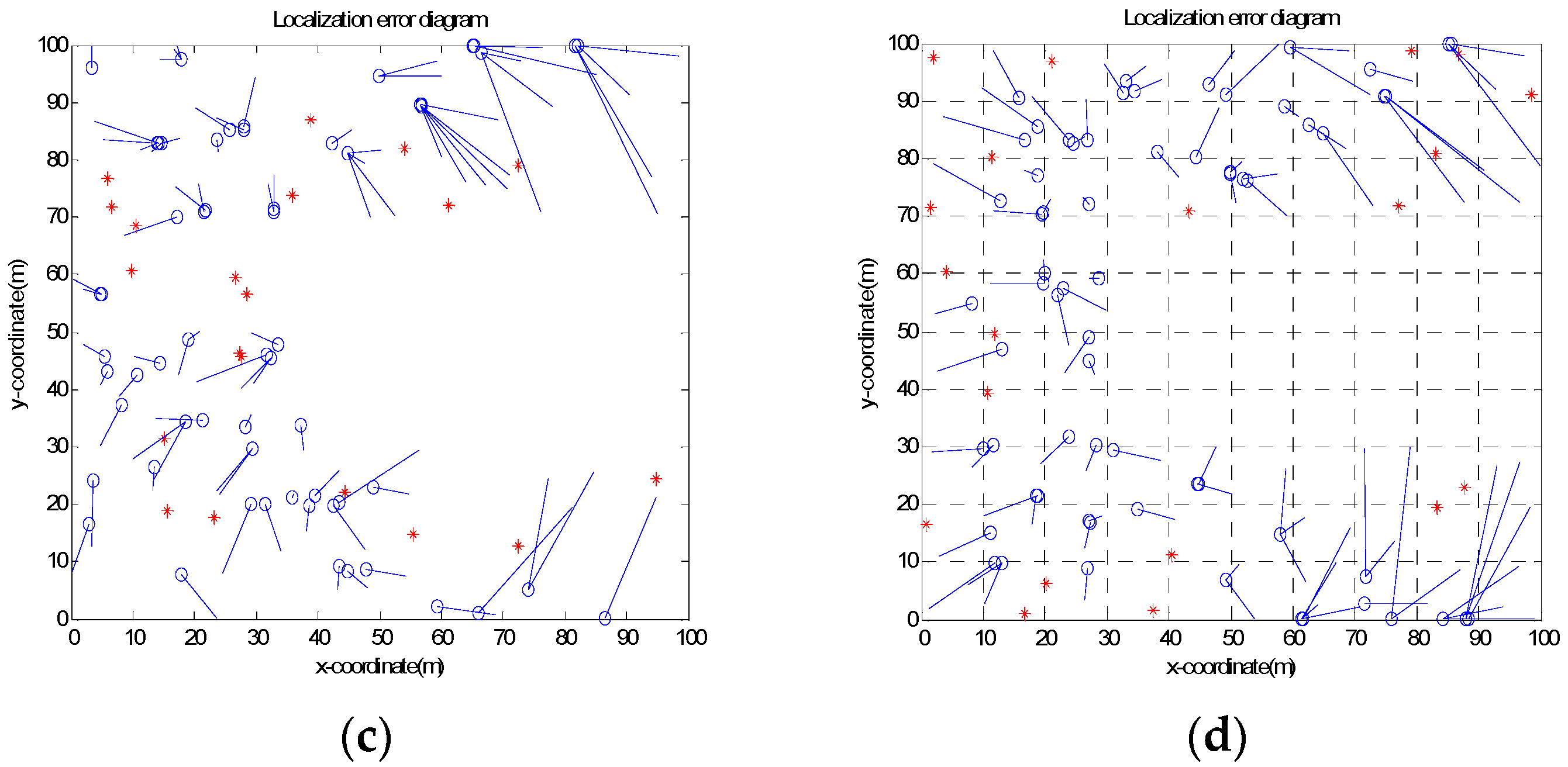
6.2. The Localization Error of Unknown Nodes
- In the square random topology, there are four nodes in the DV-Hop algorithm that cannot be located, and 33 nodes are higher than the average of the localization error. In the PSODV-Hop algorithm, one node cannot be located, and the localization error of 44 nodes is higher than the average. In the GSODV-Hop algorithm, two nodes cannot be located, and the localization error of 38 nodes is higher than the average. In the DEIDV-Hop algorithm, one node cannot be located, and 28 nodes are higher than the average.
- In the square grid topology, among the four algorithms, no unknown node cannot be located. In the DV-Hop algorithm, the localization error of 41 nodes is higher than the average of the localization errors. The localization error of 36 unknown nodes in the PSODV-Hop algorithm is higher than the average. In the GSODV-Hop algorithm, the localization error of 36 nodes is higher than the average. In the DEIDV-Hop algorithm, the localization error of 36 nodes is higher than the average.
- In the C-shaped random topology, there are 46 nodes in the DV-Hop algorithm that cannot be located, and the localization error of 37 nodes is higher than the mean of the localization error. In the PSODV-Hop algorithm, there are 25 nodes cannot be located, and the localization error of 29 nodes is higher than the average. In the GSODV-Hop algorithm, 25 nodes cannot be located, and the localization error of 26 nodes is higher than the average. In the DEIDV-Hop algorithm, 14 nodes cannot be located, and the localization error of 36 nodes is higher than the average.
- In the C-shaped grid topology, there are 38 nodes in the DV-Hop algorithm that cannot be located, and the localization error of 34 nodes is higher than the mean of the localization error, where 26 nodes cannot be located and the localization error of 31 nodes is higher than the average in the PSODV-Hop algorithm. In the GSODV-Hop algorithm, 20 nodes cannot be located, and the localization error of 31 nodes is higher than the average. In the DEIDV-Hop algorithm, 18 nodes cannot be located, and the localization error of 30 nodes is higher than the average.
7. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Z.; Wang, X.; Liu, L.; Huang, M.; Zhang, Y. Decentralized feedback control for wireless sensor and actuator networks with multiple controllers. Int. J. Mach. Learn. Cybern. 2017, 8, 1471–1483. [Google Scholar] [CrossRef]
- Bhatti, G. Machine Learning Based Localization in Large-Scale Wireless Sensor Networks. Sensors 2018, 18, 4179. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ghosh, R.K.; Das, S.K. A survey on sensor localization. J. Control Theory Appl. 2010, 8, 2–11. [Google Scholar] [CrossRef]
- Han, G.; Xu, H.; Duong, T.Q.; Jiang, J.; Hara, T. Localization algorithms of wireless sensor networks: A survey. Telecommun. Syst. 2013, 52, 2419–2436. [Google Scholar] [CrossRef]
- Liang, W.; Tang, M.; Long, J.; Peng, X.; Xu, J.; Li, K.-C. A Secure Fabric Blockchain-based Data Transmission Technique for Industrial Internet-of-Things. IEEE Trans. Ind. Inform. 2019, 15, 3582–3592. [Google Scholar] [CrossRef]
- Romer, K.; Mattern, F. The design space of wireless sensor networks. IEEE Wirel. Commun. 2004, 11, 54–61. [Google Scholar] [CrossRef]
- Liang, W.; Li, K.-C.; Long, J.; Kui, X.; Zomaya, A.Y. An Industrial Network Intrusion Detection Algorithm based on Multi-Feature Data Clustering Optimization Model. IEEE Trans. Ind. Inform. 2019. [Google Scholar] [CrossRef]
- Cui, M.; Han, D.; Wan, J. An Efficient and Safe Road Condition Monitoring Authentication Scheme Based on Fog Computing. IEEE Internet Things J. 2019, 6, 9076–9084. [Google Scholar] [CrossRef]
- Liang, W.; Long, J.; Weng, T.-H.; Chen, X.; Li, K.-C.; Zomaya, A.Y. TBRS: A trust based recommendation scheme for vehicular CPS network. Future Gener. Comput. Syst. 2019, 92, 383–398. [Google Scholar] [CrossRef]
- Zhao, W.; Su, S.; Shao, F. Improved DV-hop algorithm using locally weighted linear regression in anisotropic wireless sensor networks. Wirel. Pers. Commun. 2018, 98, 3335–3353. [Google Scholar] [CrossRef]
- Peng, B.; Li, L. An improved localization algorithm based on genetic algorithm in wireless sensor networks. Cogn. Neurodyn. 2015, 9, 249–256. [Google Scholar] [CrossRef] [PubMed]
- Harikrishnan, R.; Kumar, V.J.S.; Ponmalar, P.S. Differential Evolution Approach for Localization in Wireless Sensor Networks. In Proceedings of the IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 18–20 December 2014; pp. 1–4. [Google Scholar]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Sarker, R.A.; Elsayed, S.M.; Ray, T. Differential evolution with dynamic parameters selection for optimization problems. IEEE Trans. Evol. Comput. 2013, 18, 689–707. [Google Scholar] [CrossRef]
- Xie, P.; You, K.; Song, S.; Wu, C. Distributed Range-free Localization via Hierarchical Nonconvex Constrained Optimization. Signal Process. 2019, 164, 136–145. [Google Scholar] [CrossRef]
- Bachrach, J.; Nagpal, R.; Salib, M.; Shrobe, H. Experimental results for and theoretical analysis of a self-organizing global coordinate system for ad hoc sensor networks. Telecommun. Syst. 2004, 26, 213–233. [Google Scholar] [CrossRef]
- He, T.; Huang, C.; Blum, B.M.; Stankovic, J.A.; Abdelzaher, T. Range-Free Localization Schemes for Large Scale Sensor Networks. In Proceedings of the 9th Annual International Conference on Mobile Computing and Networking, San Diego, CA, USA, 14–19 September 2003; pp. 81–95. [Google Scholar]
- Zhang, S.; Liu, X.; Wang, J.; Cao, J.; Min, G. Accurate range-free localization for anisotropic wireless sensor networks. ACM Trans. Sens. Netw. 2015, 11, 51. [Google Scholar] [CrossRef]
- Manickam, M.; Selvaraj, S. Range-based localisation of a wireless sensor network using Jaya algorithm. IET Sci. Meas. Technol. 2019. [Google Scholar] [CrossRef]
- Wei, H.; Wan, Q.; Chen, Z.; Ye, S. A novel weighted multidimensional scaling analysis for time-of-arrival-based mobile location. IEEE Trans. Signal Process. 2008, 56, 3018–3022. [Google Scholar] [CrossRef]
- Xiao, J.; Ren, L.; Tan, J. Research of Tdoa Based Self-Localization Approach in Wireless Sensor Network. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 2035–2040. [Google Scholar]
- Niculescu, D.; Nath, B. Ad Hoc Positioning System (APS) Using AOA. In Proceedings of the IEEE INFOCOM 2003. Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies (IEEE Cat. No.03CH37428), San Francisco, CA, USA, 30 March–3 April 2003; pp. 1734–1743. [Google Scholar]
- Xie, H.; Li, W.; Li, S.; Xu, B. An Improved DV-Hop Localization Algorithm Based on RSSI Auxiliary Ranging. In Proceedings of the 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 8319–8324. [Google Scholar]
- Kulkarni, V.R.; Desai, V.; Kulkarni, R.V. A comparative investigation of deterministic and metaheuristic algorithms for node localization in wireless sensor networks. Wirel. Netw. 2019, 25, 2789–2803. [Google Scholar] [CrossRef]
- Čapkun, S.; Hamdi, M.; Hubaux, J. GPS-free positioning in mobile ad hoc networks. Clust. Comput. 2002, 5, 157–167. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. DV based positioning in ad hoc networks. Telecommun. Syst. 2003, 22, 267–280. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, W.; Han, D.; Chen, W.; Wang, J. Routing algorithm with uneven clustering for energy heterogeneous wireless sensor networks. J. Sens. 2016, 2016, 9. [Google Scholar] [CrossRef]
- Garimella, R.M.; Edla, D.R.; Kuppili, V. Energy Efficient Design of Wireless Sensor Network: Clustering; Centre for Communications International Institute of Information Technology Hyderabad-500 032: Hyderabad, India, 2018. [Google Scholar]
- Thiagarajan, R. Energy consumption and network connectivity based on Novel-LEACH-POS protocol networks. Comput. Commun. 2020, 149, 90–98. [Google Scholar]
- Ji, W.; Liu, Z. Study on the application of DV-Hop localization algorithms to random sensor networks. J. Electron. Inf. Technol. 2008, 30, 970–974. [Google Scholar] [CrossRef]
- Niculescu, D.; Nath, B. Ad Hoc Positioning System (APS). In Proceedings of the GLOBECOM’01. IEEE Global Telecommunications Conference (Cat. No.01CH37270), San Antonio, TX, USA, 25–29 November 2001; pp. 2926–2931. [Google Scholar]
- Shang, Y.; Ruml, W. Improved MDS-Based Localization. In Proceedings of the IEEE INFOCOM, Hong Kong, China, 7–11 March 2004; pp. 2640–2651. [Google Scholar]
- Nian-qiang, L.; Ping, L. A Range-Free Localization Scheme in Wireless Sensor Networks. In Proceedings of the IEEE International Symposium on Knowledge Acquisition and Modeling Workshop, Wuhan, China, 21–22 December 2008; pp. 525–528. [Google Scholar]
- Gumaida, B.F.; Luo, J. A hybrid particle swarm optimization with a variable neighborhood search for the localization enhancement in wireless sensor networks. Appl. Intell. 2019, 49, 3539–3557. [Google Scholar] [CrossRef]
- Girod, L.; Bychkovskiy, V.; Elson, J.; Estrin, D. Locating Tiny Sensors in Time and Space: A Case Study. In Proceedings of the IEEE International Conference on Computer Design: VLSI in Computers and Processors, Freiberg, Germany, 18 September 2002; pp. 214–219. [Google Scholar]
- Singh, S.P.; Sharma, S.C. Critical analysis of distributed localization algorithms in wireless sensor networks. Int. J. Wirel. Microw. Technol. 2016, 4, 72–83. [Google Scholar] [CrossRef][Green Version]
- Cui, L.; Xu, C.; Li, G.; Ming, Z.; Feng, Y.; Lu, N. A high accurate localization algorithm with DV-Hop and differential evolution for wireless sensor network. Appl. Soft Comput. 2018, 68, 39–52. [Google Scholar] [CrossRef]
- Wu, L.; Meng, M.Q.; Huang, J.; Liang, H.; Lin, Z. An Improvement of DV-Hop Algorithm Based on Collinearity. In Proceedings of the International Conference on Information and Automation, Zhuhai, Macau, China, 22–24 June 2009; pp. 90–95. [Google Scholar]
- Xu, S.; Wang, X.; Wang, Y.; Wang, J. Iterative Cooperation DV-Hop Localization Algorithm in Wireless Sensor Networks. In Proceedings of the IEEE 71st Vehicular Technology Conference, Taipei, Taiwan, 16–19 May 2010; pp. 1–5. [Google Scholar]
- Chen, K.; Wang, Z.; Lin, M.; Yu, M. An Improved DV-Hop Localization Algorithm for Wireless Sensor Networks. In Proceedings of the IET International Conference on Wireless Sensor Network 2010 (IET-WSN 2010), Beijing, China, 15–17 November 2010. [Google Scholar]
- Cheikhrouhou, O.; Bhatti, G.M.; Alroobaea, R. A hybrid DV-hop algorithm using RSSI for localization in large-scale wireless sensor networks. Sensors 2018, 18, 1469. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Han, D.; Wu, H.; Zhou, R. Fuzzy-logic based distributed energy-efficient clustering algorithm for wireless sensor networks. Sensors 2017, 17, 1554. [Google Scholar] [CrossRef]
- Singh, S.P.; Sharma, S.C. A PSO based improved localization algorithm for wireless sensor network. Wirel. Pers. Commun. 2018, 98, 487–503. [Google Scholar] [CrossRef]
- Song, L.; Zhao, L.; Ye, J. DV-Hop Node Location Algorithm Based on GSO in Wireless Sensor Networks. J. Sens. 2019, 2019, 9. [Google Scholar] [CrossRef]
- Li, H.; Han, D. EduRSS: Blockchain-Based Educational Records Secure Storage and Sharing Scheme. IEEE Access. 2019, 7, 179273–179289. [Google Scholar] [CrossRef]




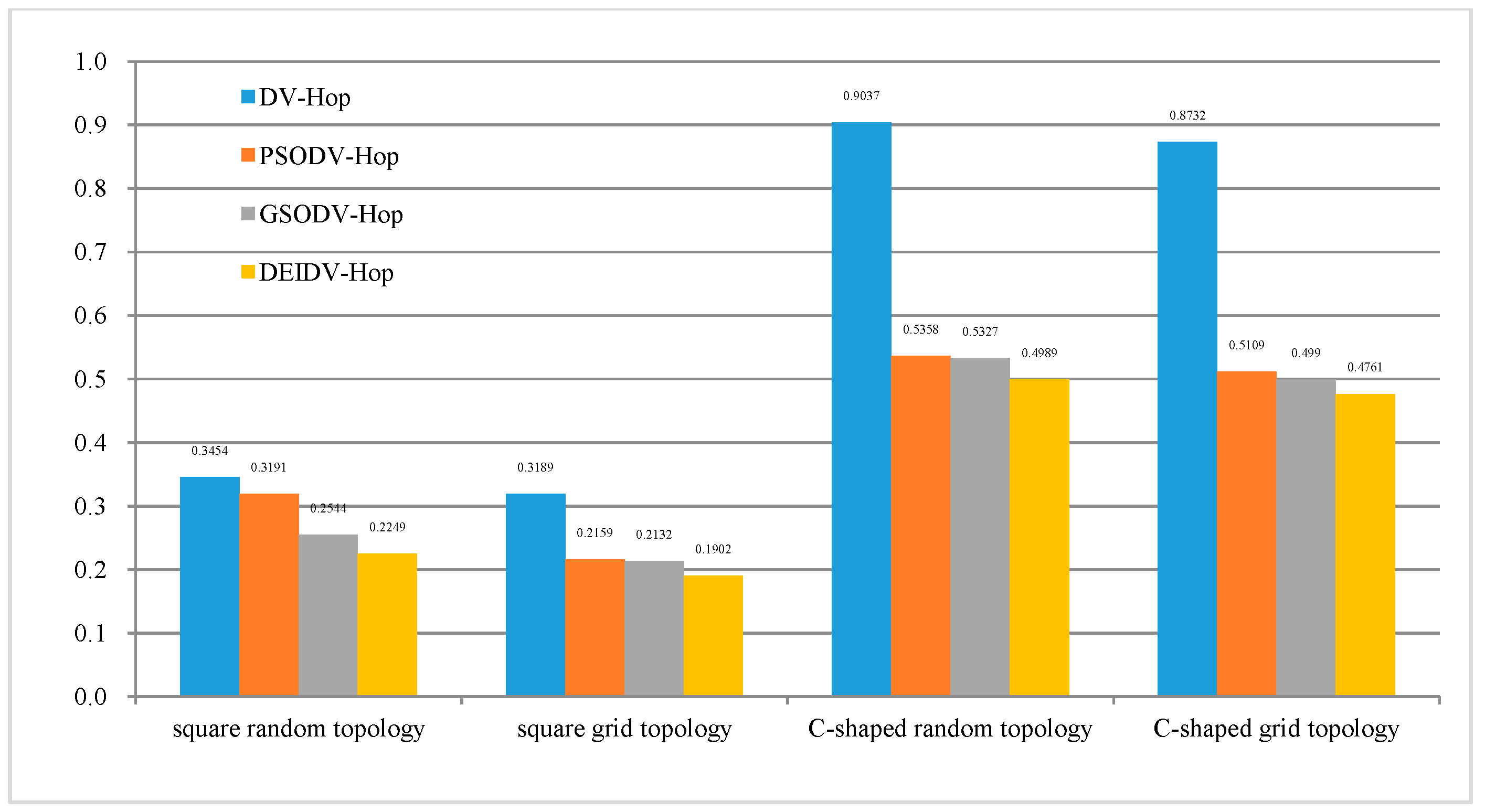



| Parameter | Value |
|---|---|
| Deployment area size | 100 m × 100 m |
| Percentage of the anchor node | 10–40% |
| Communication radius R | 20–40 m |
| 20 | |
| 0.9 | |
| 0.2 | |
| 20 | |
| 0.02 |
| Parameter | Value |
|---|---|
| 2.05 | |
| 2.05 | |
| No of particles | 20 |
| 10 | |
| No of iterations | 20 |
| Parameter | Value |
|---|---|
| 0.4 | |
| 0.6 | |
| 0.08 | |
| 5 | |
| 5 | |
| 100 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, D.; Yu, Y.; Li, K.-C.; de Mello, R.F. Enhancing the Sensor Node Localization Algorithm Based on Improved DV-Hop and DE Algorithms in Wireless Sensor Networks. Sensors 2020, 20, 343. https://doi.org/10.3390/s20020343
Han D, Yu Y, Li K-C, de Mello RF. Enhancing the Sensor Node Localization Algorithm Based on Improved DV-Hop and DE Algorithms in Wireless Sensor Networks. Sensors. 2020; 20(2):343. https://doi.org/10.3390/s20020343
Chicago/Turabian StyleHan, Dezhi, Yunping Yu, Kuan-Ching Li, and Rodrigo Fernandes de Mello. 2020. "Enhancing the Sensor Node Localization Algorithm Based on Improved DV-Hop and DE Algorithms in Wireless Sensor Networks" Sensors 20, no. 2: 343. https://doi.org/10.3390/s20020343
APA StyleHan, D., Yu, Y., Li, K.-C., & de Mello, R. F. (2020). Enhancing the Sensor Node Localization Algorithm Based on Improved DV-Hop and DE Algorithms in Wireless Sensor Networks. Sensors, 20(2), 343. https://doi.org/10.3390/s20020343






