Parameter Estimation for Two-Dimensional Incoherently Distributed Source with Double Cross Arrays
Abstract
1. Introduction
- Generally, the parameters of ID sources constitute an approximate conclusion under the condition of smaller sensor spacing. We propose a double cross array that satisfies both the small space between sensors and the aperture equalization in the elevation and azimuth dimensions.
- Based on the reconstructed received signal vectors and deduced rotating invariant relations, we propose an approach to a solution for nominal angles according to the ESPRIT framework, and we propose an angle matching as well as angular spreads solutions using the Capon estimation.
- The proposed method has an advantage in the DOA estimation with respect to the computational cost, shows advantages in terms of estimation accuracy with a similar number of sensors, and shows robustness in the case of a model mismatch.
2. 2D ID Source Model and Double Cross Arrays
3. Proposed Method
3.1. Rotating Invariant Relations
3.2. Estimation of Nominal Angles
3.3. Angle Matching
- Choose as the estimated nominal elevation from the set , traverse the set and solve the paired nominal angles according to Equation (56).
- Substitute into (58) to select the pair that makes the maximum value of and denote the pair as .
- Remove from the set and remove from the set .
- Repeat steps 1–3.
3.4. Estimation of Angular Spread
3.5. Algorithm Procedure and Complexity Analysis
- Calculate the sample covariance matrix and .
- Obtain and by decomposition of and . Calculate and according to (44) and (55).
- Conduct the decomposition of and to obtain the eigenvalues and , and then calculate the nominal elevations and nominal azimuths from (45) and (56).
- Determine the nominal angles according to the angle matching method.
- Substitute into according to Equation (61) or (63). Solve the angular spreads parameters and from (64).
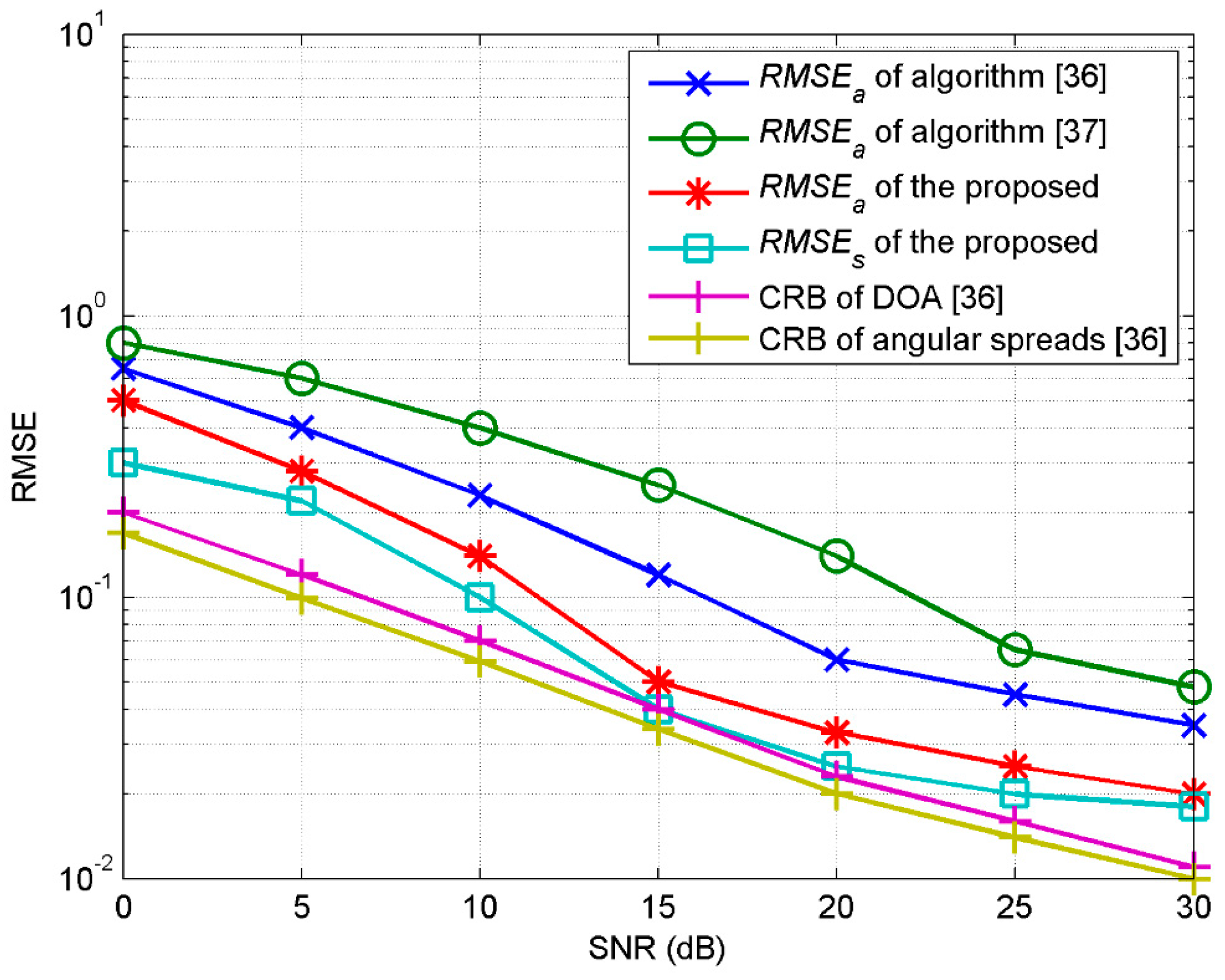
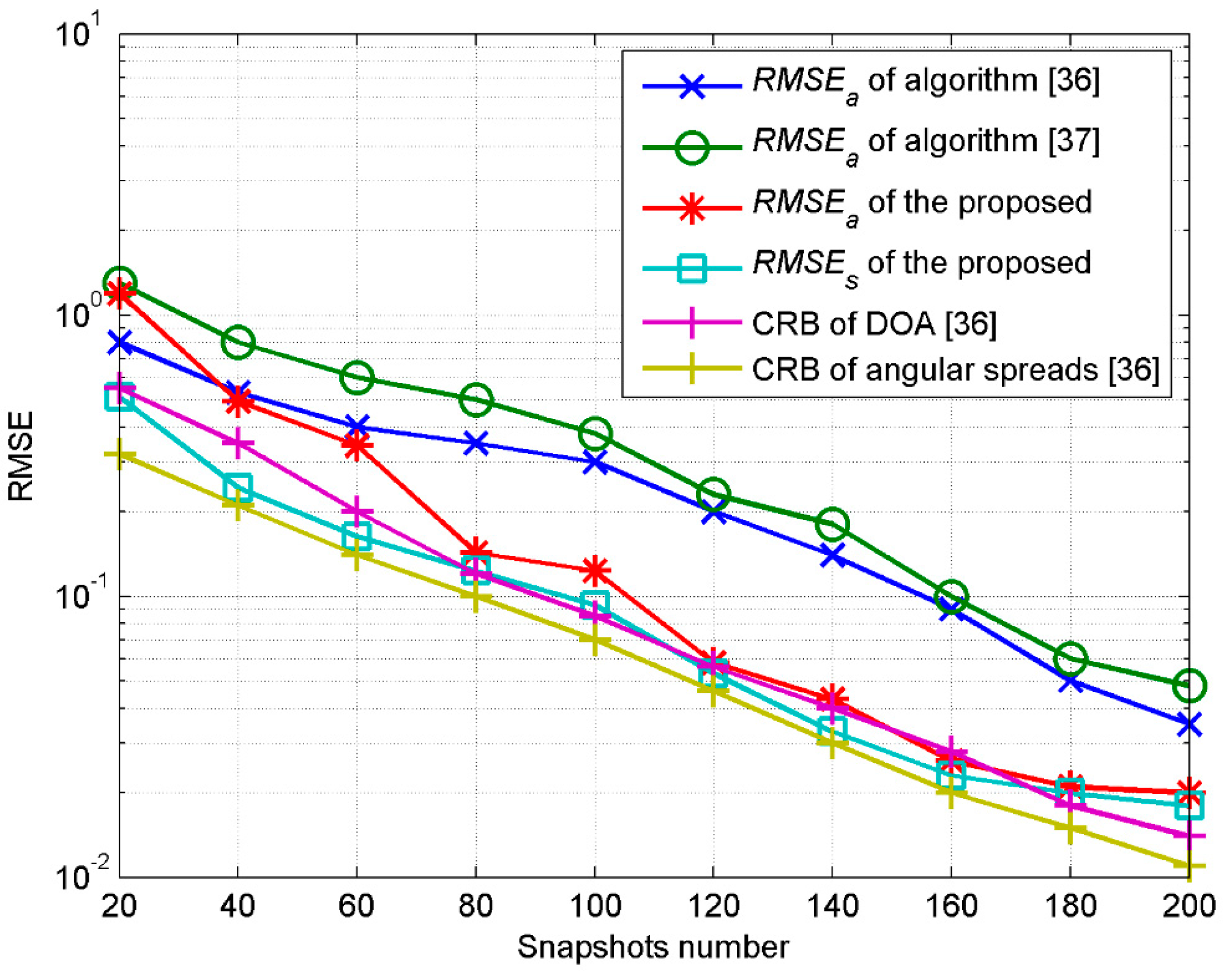
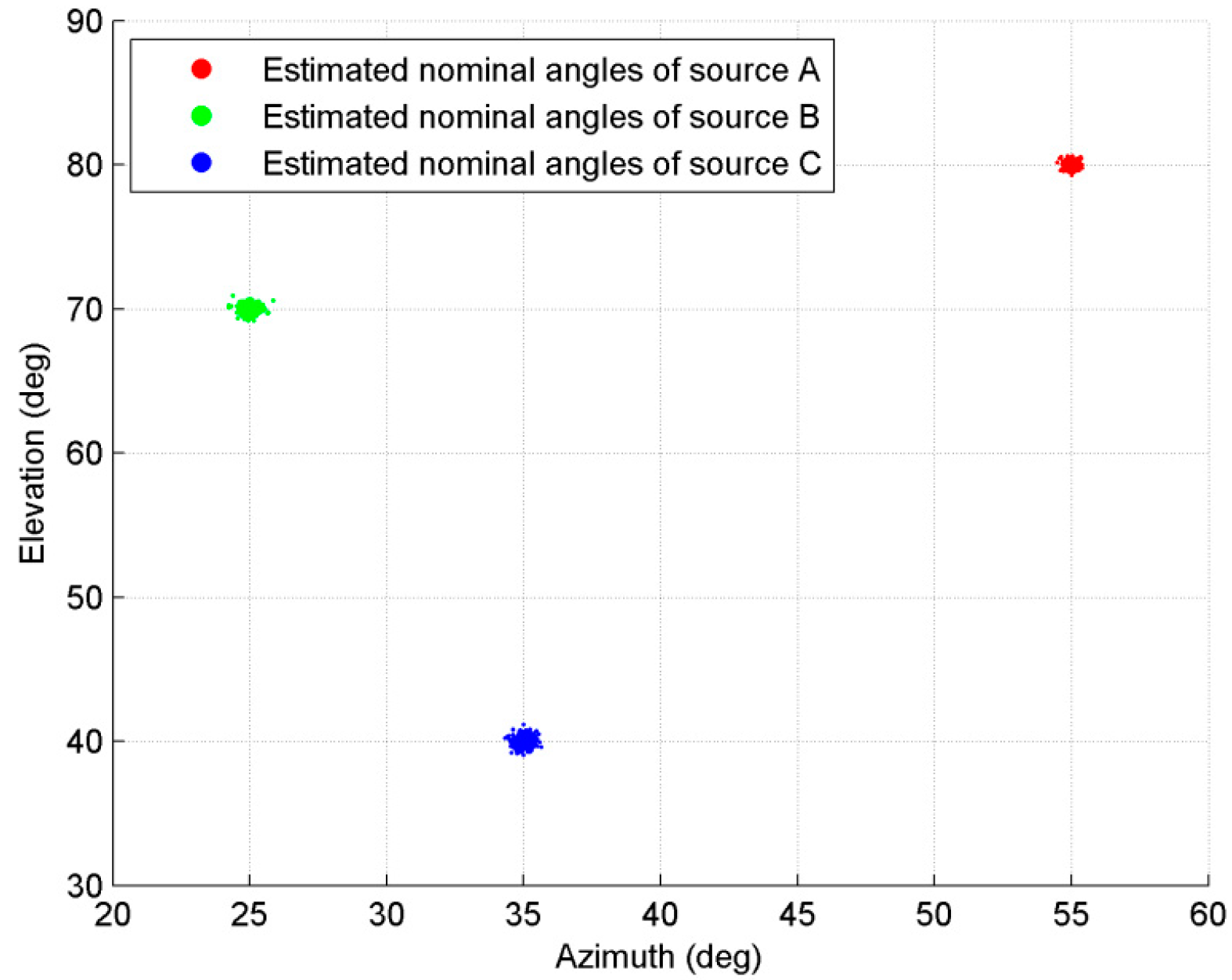
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiong, W.; José, P.; Sylvie, M. Performance analysis of distributed source parameter estimator (DSPE) in the presence of modeling errors due to the spatial distributions of sources. Signal Process. 2018, 143, 146–151. [Google Scholar] [CrossRef]
- Goldberg, J.M.; Fonollosa, J.R. Downlink beamforming for spatially distributed sources in cellular mobile communications. Signal Process. 1998, 65, 181–197. [Google Scholar] [CrossRef]
- Monakov, A.A. Observation of extended targets with antenna arrays. IEEE Trans. Aero. Elec. Sys. 2000, 36, 297–302. [Google Scholar] [CrossRef]
- Meng, Y.; Stoica, P.; Wong, K.M. Estimation of direction of arrival of spatially dispersed signals in array processing. IET Radar Sonar Navig. 1995, 143, 1–9. [Google Scholar] [CrossRef]
- Wu, T.; Deng, Z.H.; Li, Y.W. Estimation of Two-Dimensional Non-Symmetric Incoherently Distributed Source with L-Shape Arrays. Sensors 2019, 5, 1226. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Hou, C.P.; Zhu, W.P.; Liu, W.; Liu, W.; Dong, Y.-Y.; Peng, Z.; Wang, Q. ESPRIT-like two-dimensional direction finding for mixed circular and strictly noncircular sources based on joint diagonalization. Signal Proces. 2017, 141, 48–56. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; He, S.; Shi, Z. A robust and efficient algorithm for coprime array adaptive beamforming. IEEE Trans. Veh. Technol. 2018, 67, 1099–1112. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-arrival estimation for coprime array via virtual array interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, C.; Gu, Y.; Goodman, N.A.; Qu, F. Source estimation using coprime array: A sparse reconstruction perspective. IEEE Sens. J. 2016, 17, 755–765. [Google Scholar] [CrossRef]
- Zhou, C.W.; Zhou, J.F. Direction-of-arrival estimation with coarray ESPRIT for coprime array. Sensors 2017, 17, 1779. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Shi, Z.; Zhang, Y.D. Off-grid direction-of-arrival estimation using coprime array interpolation. IEEE Signal Process Lett. 2018, 25, 1710–1714. [Google Scholar] [CrossRef]
- Wen, F.Q.; Shi, J.P. Fast direction finding for bistatic EMVS-MIMO radar without pairing. Signal Process. 2020, 173, 107512. [Google Scholar] [CrossRef]
- Liu, T.; Wen, F.; Zhang, L.; Wang, K. Off-grid DOA estimation for colocated MIMO radar via reduced-complexity sparse Bayesian learning. IEEE Access 2019, 7, 99907–99916. [Google Scholar] [CrossRef]
- Wen, F.; Zhang, Z.; Wang, K.; Sheng, G.; Zhang, G. Angle estimation and mutual coupling self-calibration for ULA-based bistatic MIMO radar. Signal Process. 2018, 144, 61–67. [Google Scholar] [CrossRef]
- Dai, Z.; Cui, W.; Ba, B.; Wang, D.; Sun, Y. Two-Dimensional DOA Estimation for Coherently Distributed Sources with Symmetric Properties in Crossed Arrays. Sensors 2017, 17, 1300. [Google Scholar] [CrossRef]
- Wen, C.; Shi, G.; Xie, X. Estimation of directions of arrival of multiple distributed sources for nested array. Signal Process. 2017, 130, 315–322. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, Z.; Chi, C.K.; Zhong, L. Low-complexity 2D parameter estimation of coherently distributed noncircular signals using modified propagator. Multidimens. Syst. Signal Process. 2017, 28, 1–20. [Google Scholar] [CrossRef]
- Wan, L.; Han, G.; Jiang, J.; Zhu, C.; Shu, L. A DOA estimation approach for transmission performance guarantee in D2D Communication. Mob. Netw. Appl. 2017, 36, 1–12. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, G.J.; Teng, Y. 2D DOA Estimator for Multiple Coherently Distributed Sources Using Modified Propagator. Circ. Syst. Signal Process. 2012, 31, 255–270. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, G.J.; Teng, Y. Low-complexity 2D DOA estimator for multiple coherently distributed sources. Int. J. Comp. Math. Electr. Electron. Eng. 2012, 31, 443–459. [Google Scholar] [CrossRef]
- Zoubir, A.; Wang, Y. Performance analysis of the generalized beamforming estimators in the case of coherently distributed sources. Signal Process. 2008, 88, 428–435. [Google Scholar] [CrossRef]
- Han, K.; Nehorai, A. Nested Array Processing for Distributed Sources. IEEE Signal Process. Lett. 2014, 21, 1111–1114. [Google Scholar] [CrossRef]
- Yang, X.; Li, G.; Zheng, Z.; Zhong, L. 2D DOA Estimation of Coherently Distributed Noncircular Sources. Wirel. Pers. Commun. 2014, 78, 1095–1102. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, T.; Li, Y. Direction-of-arrival estimation for 2D coherently distributed sources with nested array based on matrix reconstruction. Math. Probl. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Xiong, W.; José, P.; Sylvie, M. Robustness of the coherently distributed MUSIC algorithm to the imperfect knowledge of the spatial distribution of the sources. Signal Image Video Process. 2017, 11, 721–728. [Google Scholar] [CrossRef]
- Besson, O.; Stoica, P. Decoupled estimation of DOA and angular spread for a spatially distributed source. IEEE Trans. Signal Process. 2000, 48, 1872–1882. [Google Scholar] [CrossRef]
- Shahbazpanahi, S.; Valaee, S.; Gershman, A.B. A covariance fitting approach to parametric localization of multiple incoherently distributed sources. IEEE Trans. Signal Process. 2004, 52, 592–600. [Google Scholar] [CrossRef]
- Zoubir, A.; Wang, Y.; Charge, P. On the ambiguity of COMET-EXIP algorithm for estimating a scattered source. In Proceedings of the IEEE International Conference on Acoustics, peech, and Signal Processing, Philadelphia, PA, USA, 23–23 March 2005. [Google Scholar]
- Raich, R.; Goldberg, J.; Messer, H. Bearing estimation for a distributed source: Modeling, inherent accuracy limitations and algorithms. IEEE Trans. Signal Process. 2000, 48, 429–441. [Google Scholar] [CrossRef]
- Besson, O.; Vincent, F.; Stoica, P.; Gershman, A.B. Approximate maximum likelihood estimators for array processing in multiplicative noise environments. IEEE Trans. Signal Process. 2000, 48, 2506–2518. [Google Scholar] [CrossRef]
- Trump, T.; Ottersten, B. Estimation of nominal direction of arrival and angular spread using an array of sensors. Signal Process. 1996, 50, 57–69. [Google Scholar] [CrossRef]
- Cao, R.; Gao, F.; Zhang, X.F. An angular parameter estimation method for incoherently distributed sources via generalized shift invariance. IEEE Trans. Signal Process. 2016, 64, 261–270. [Google Scholar] [CrossRef]
- Zoubir, A.; Wang, Y. Robust generalised Capon algorithm for estimating the angular parameters of multiple incoherently distributed sources. IET Signal Process. 2008, 2, 163–168. [Google Scholar] [CrossRef]
- Xu, X. Spatially-spread sources and the SMVDR estimator. In Proceedings of the IEEE Signal Processing Advances in Wireless Communications (SPAWC), Rome, Italy, 15–18 June 2003. [Google Scholar]
- Hassanien, A.; Shahbazpanahi, S.; Gershman, A.B. A generalized capon estimator for localization of multiple spread sources. IEEE Trans. Signal Process. 2004, 52, 280–283. [Google Scholar] [CrossRef]
- Boujemâa, H. Extension of COMET algorithm to multiple diffuse source localization in azimuth and elevation. Eur. Telecommun. 2012, 16, 557–566. [Google Scholar] [CrossRef]
- Zhou, J.; Li, G.J. Low-Complexity Estimation of the Nominal Azimuth and Elevation for Incoherently Distributed Sources. Wirel. Pers. Commun. 2013, 71, 1777–1793. [Google Scholar] [CrossRef]




| Method | Sample Covariance Matrix | Eigendecomposition/Alternating Projection Technique | Searching | Total |
|---|---|---|---|---|
| Proposed | O(NK2) | O(K3) + O(k3) | O(NK2) + O(K3) + O(k3) | |
| Reference [36] | O(NK2) | O(K4) | O(NK2) + O(K4) | |
| Reference [37] | O(NK2) | O(K3) | O(kLφK2) | O(NK2) + O(K3) + O(kLφK2) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, T.; Li, Y.; Deng, Z.; Feng, B.; Ma, X. Parameter Estimation for Two-Dimensional Incoherently Distributed Source with Double Cross Arrays. Sensors 2020, 20, 4562. https://doi.org/10.3390/s20164562
Wu T, Li Y, Deng Z, Feng B, Ma X. Parameter Estimation for Two-Dimensional Incoherently Distributed Source with Double Cross Arrays. Sensors. 2020; 20(16):4562. https://doi.org/10.3390/s20164562
Chicago/Turabian StyleWu, Tao, Yiwen Li, Zhenghong Deng, Bo Feng, and Xinping Ma. 2020. "Parameter Estimation for Two-Dimensional Incoherently Distributed Source with Double Cross Arrays" Sensors 20, no. 16: 4562. https://doi.org/10.3390/s20164562
APA StyleWu, T., Li, Y., Deng, Z., Feng, B., & Ma, X. (2020). Parameter Estimation for Two-Dimensional Incoherently Distributed Source with Double Cross Arrays. Sensors, 20(16), 4562. https://doi.org/10.3390/s20164562




