Classification of Alpine Skiing Styles Using GNSS and Inertial Measurement Units
Abstract
1. Introduction
2. Materials and Methods
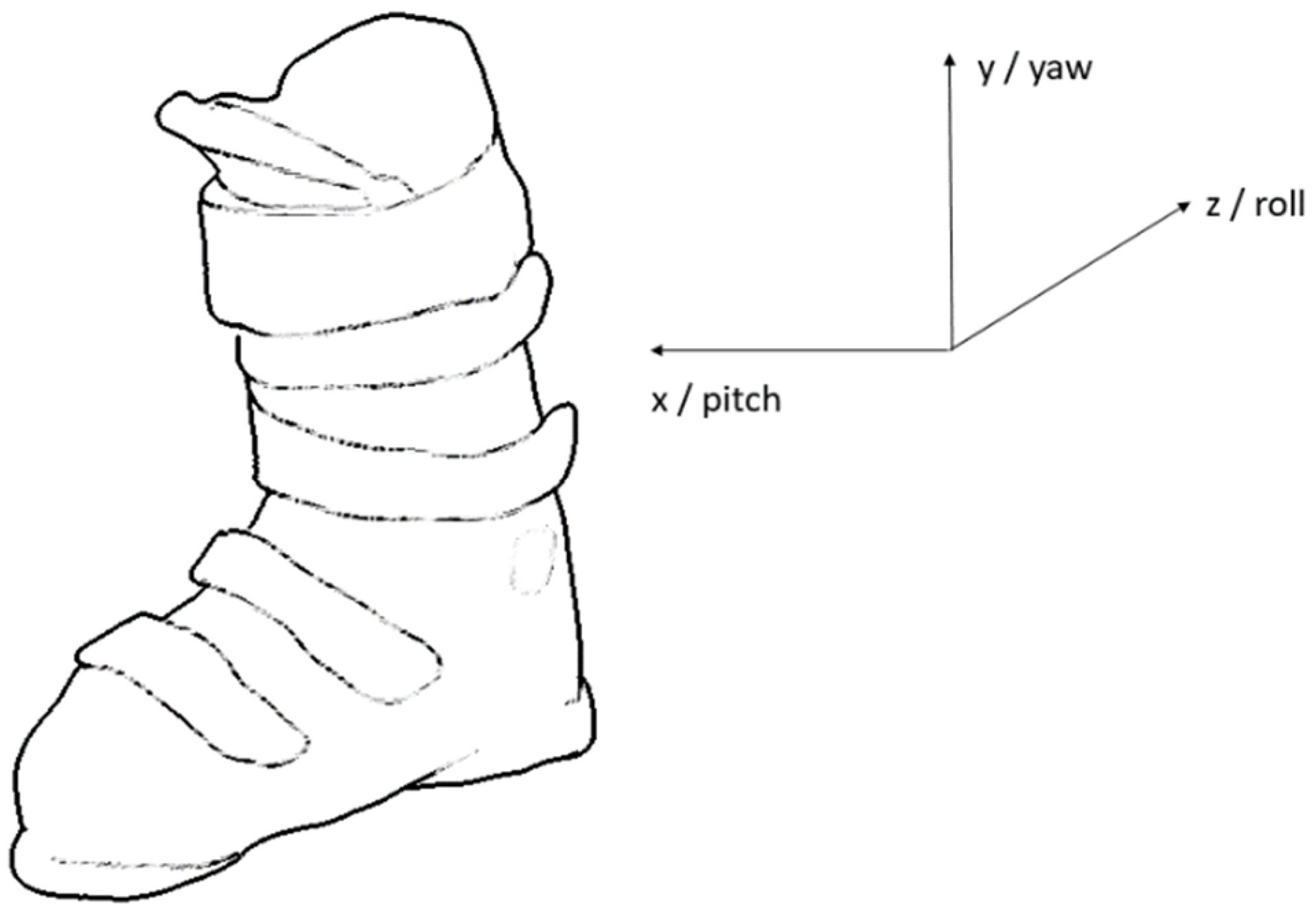
2.1. Sensors
2.2. Data
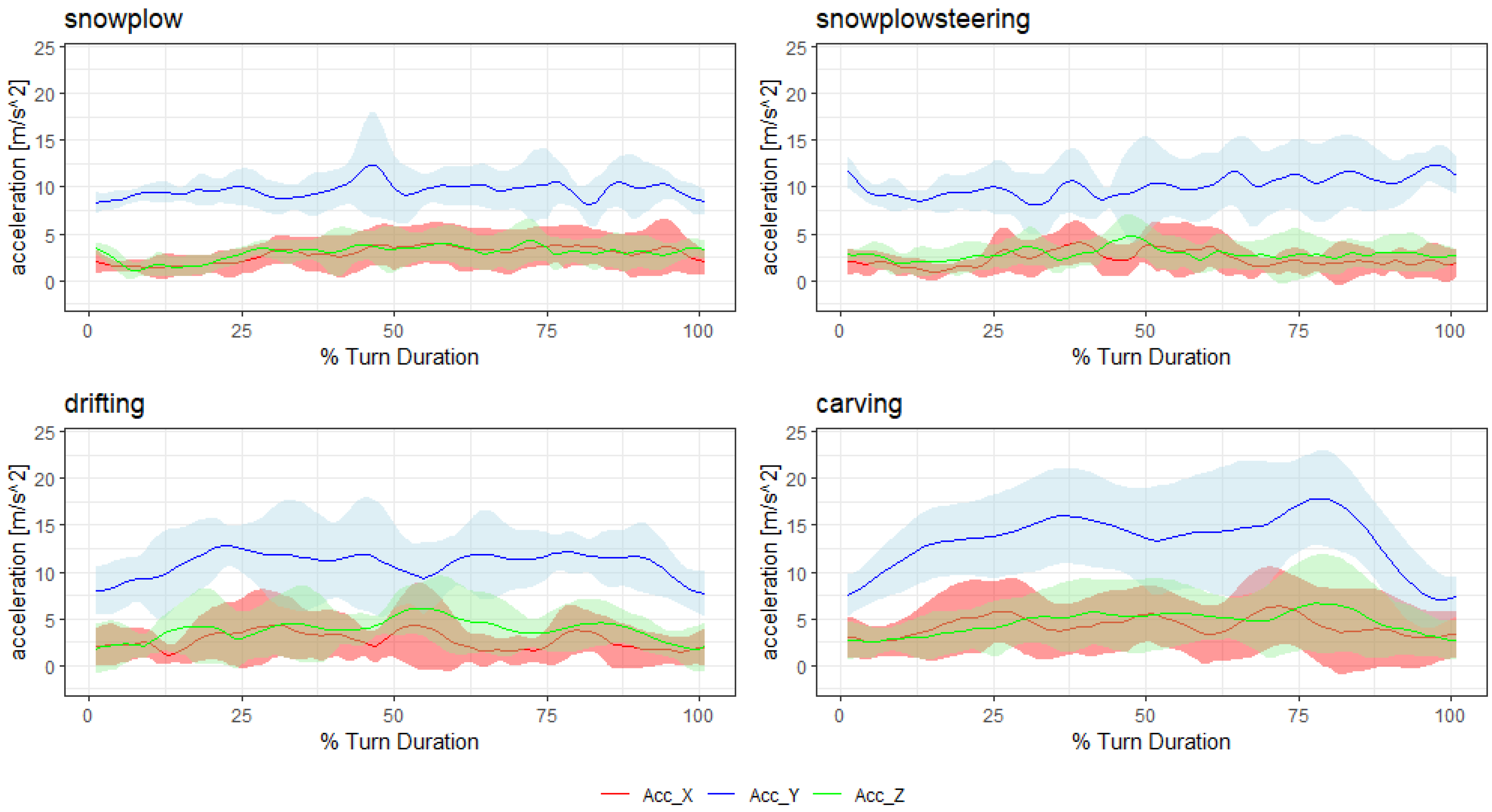
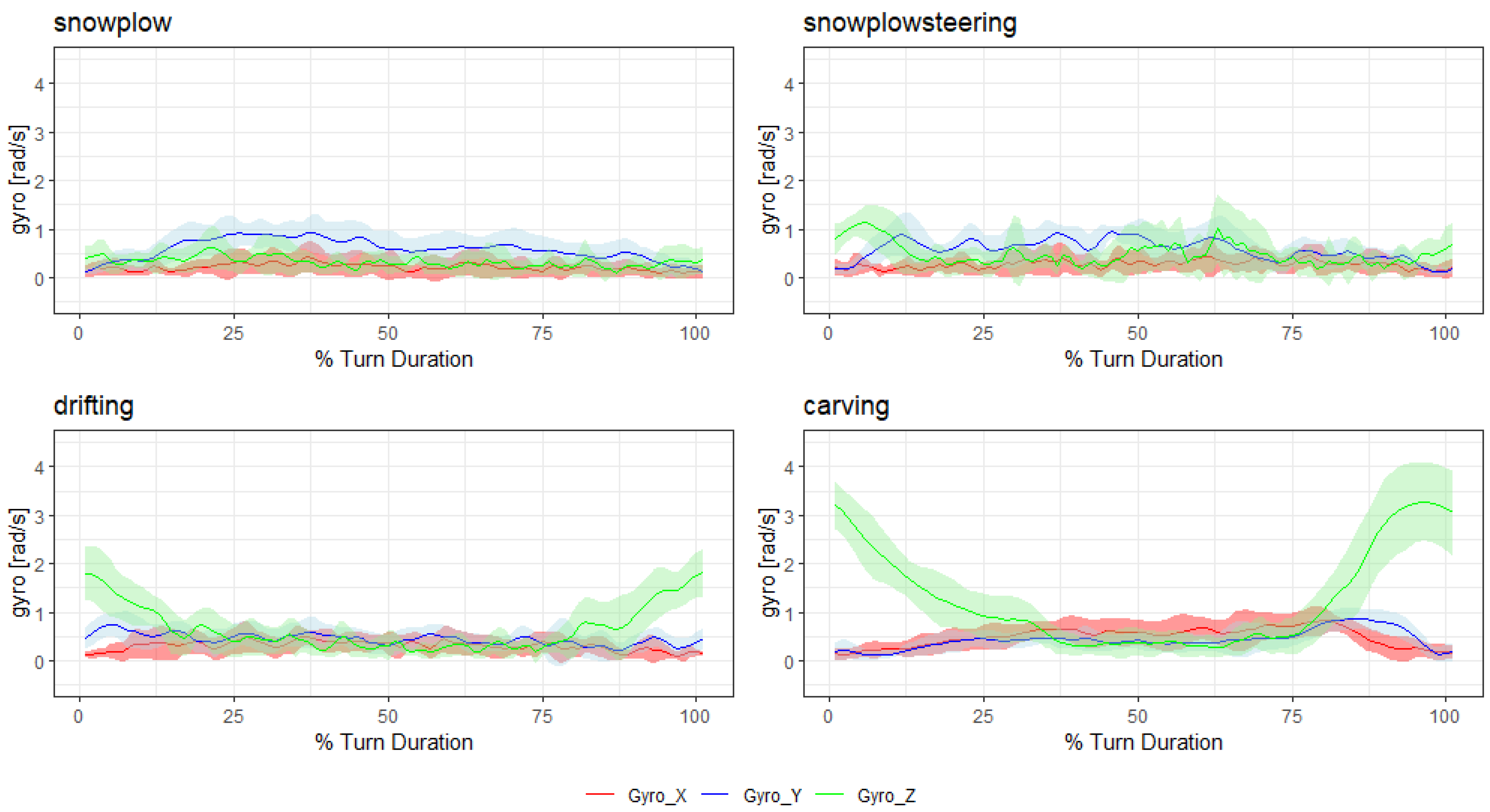
2.2.1. Data Generation
2.2.2. Data Pre-Processing
2.2.3. Training and Testing Data
2.3. Methods
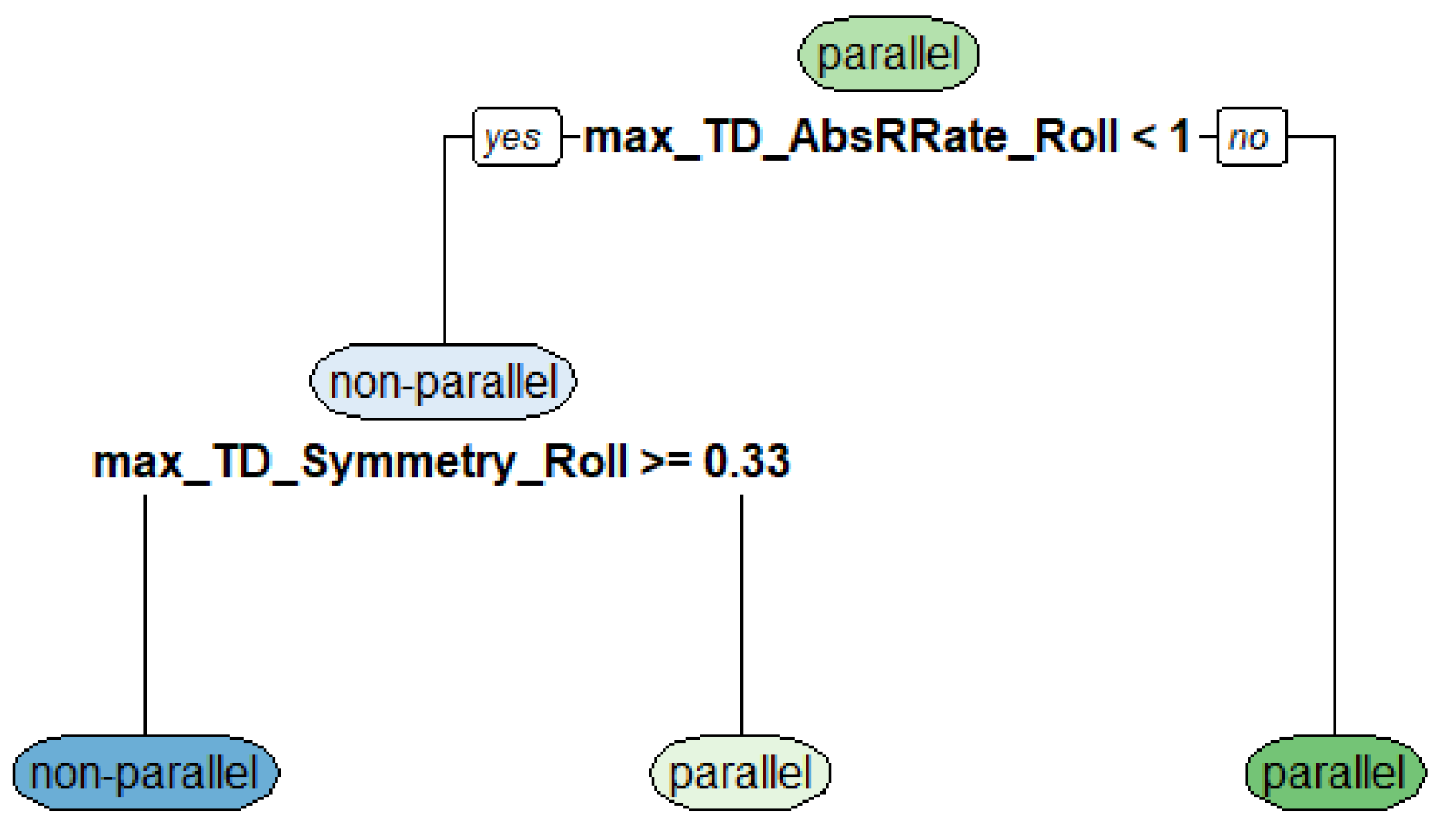
2.3.1. Pre-Classification into Parallel and Non-Parallel
2.3.2. Feature Extraction
2.3.3. Feature Selection
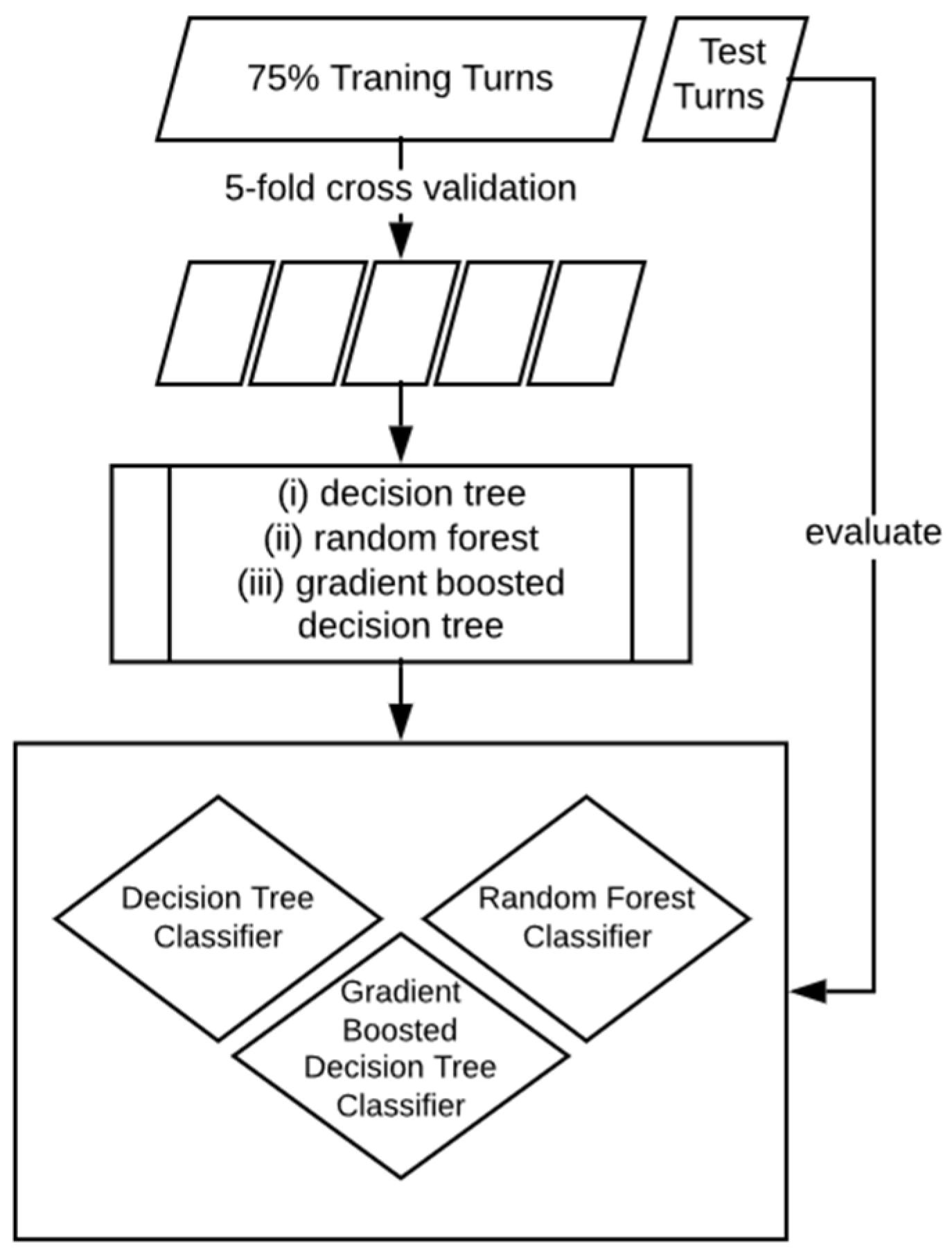
2.3.4. Classification Methods
2.3.5. Performance Measures
2.4. Software
3. Results
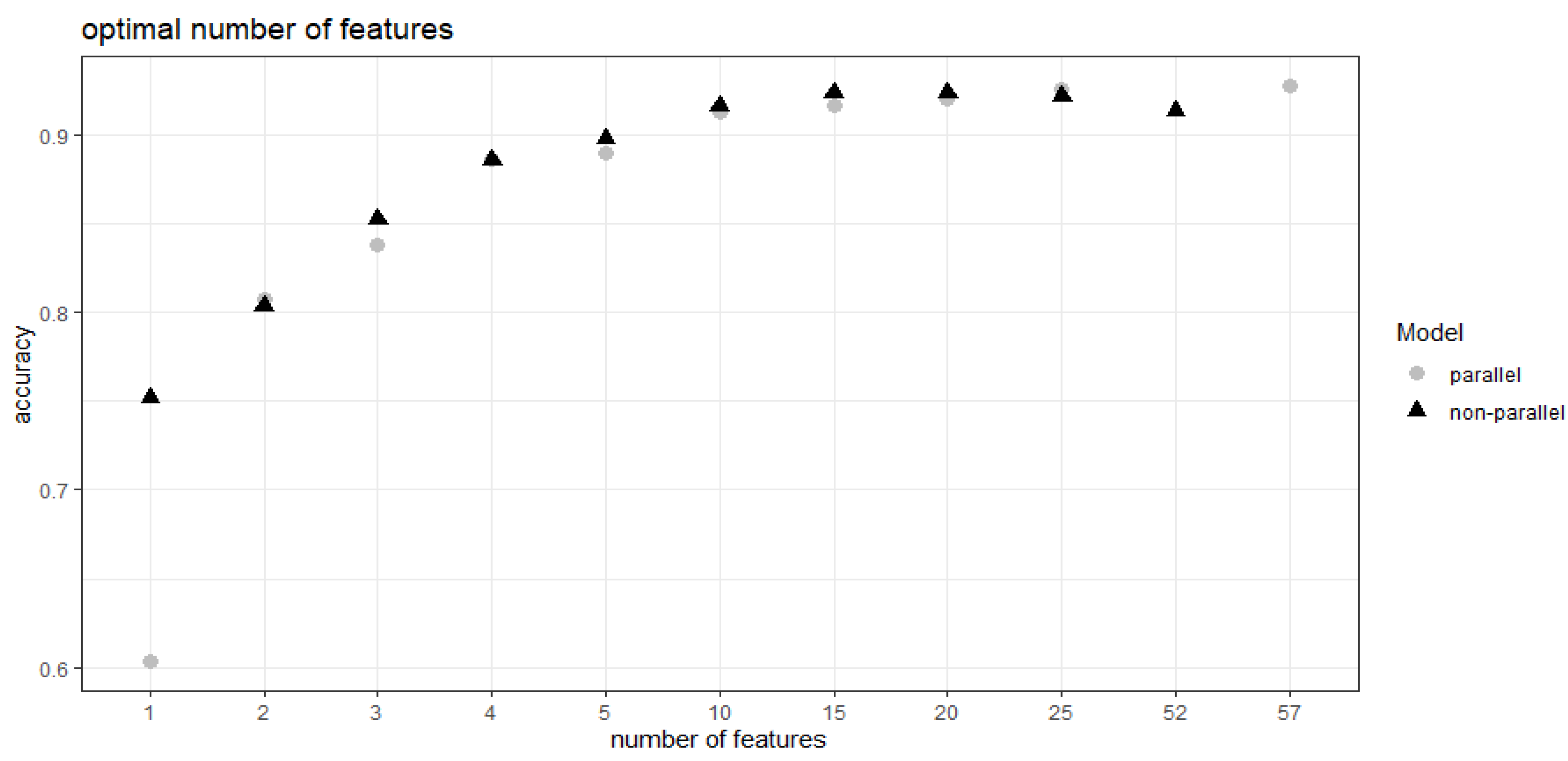
3.1. Feature Selection
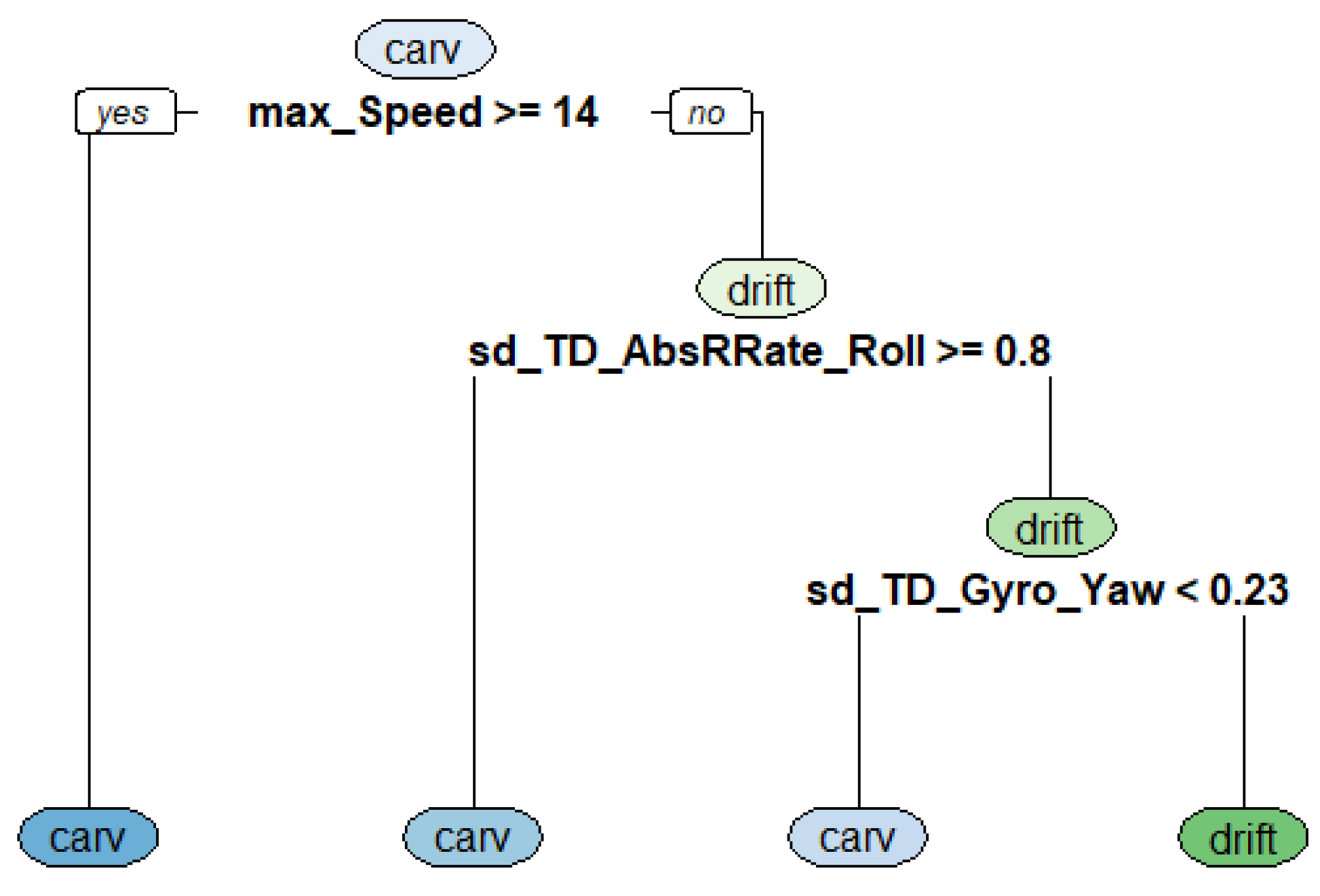
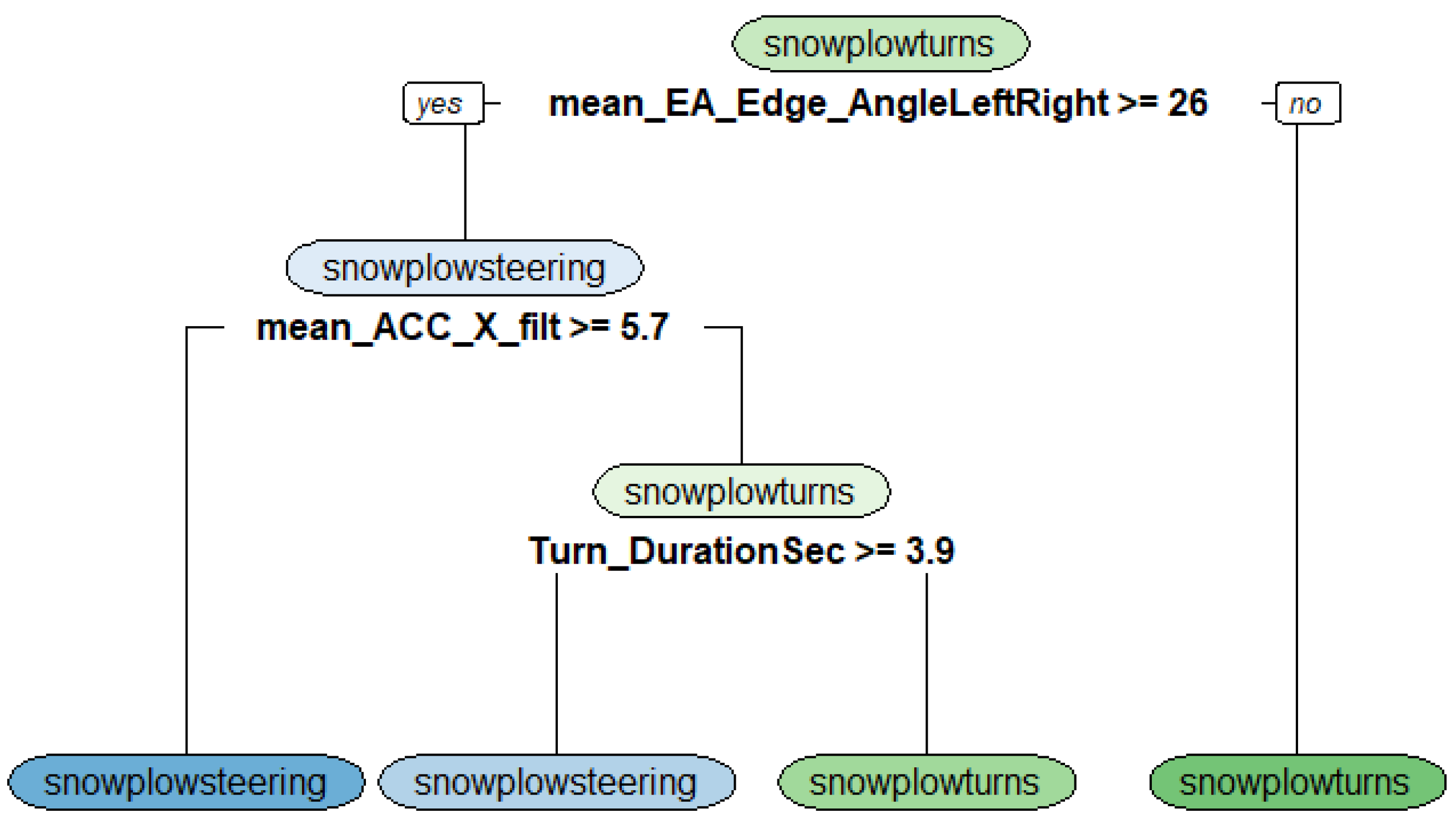
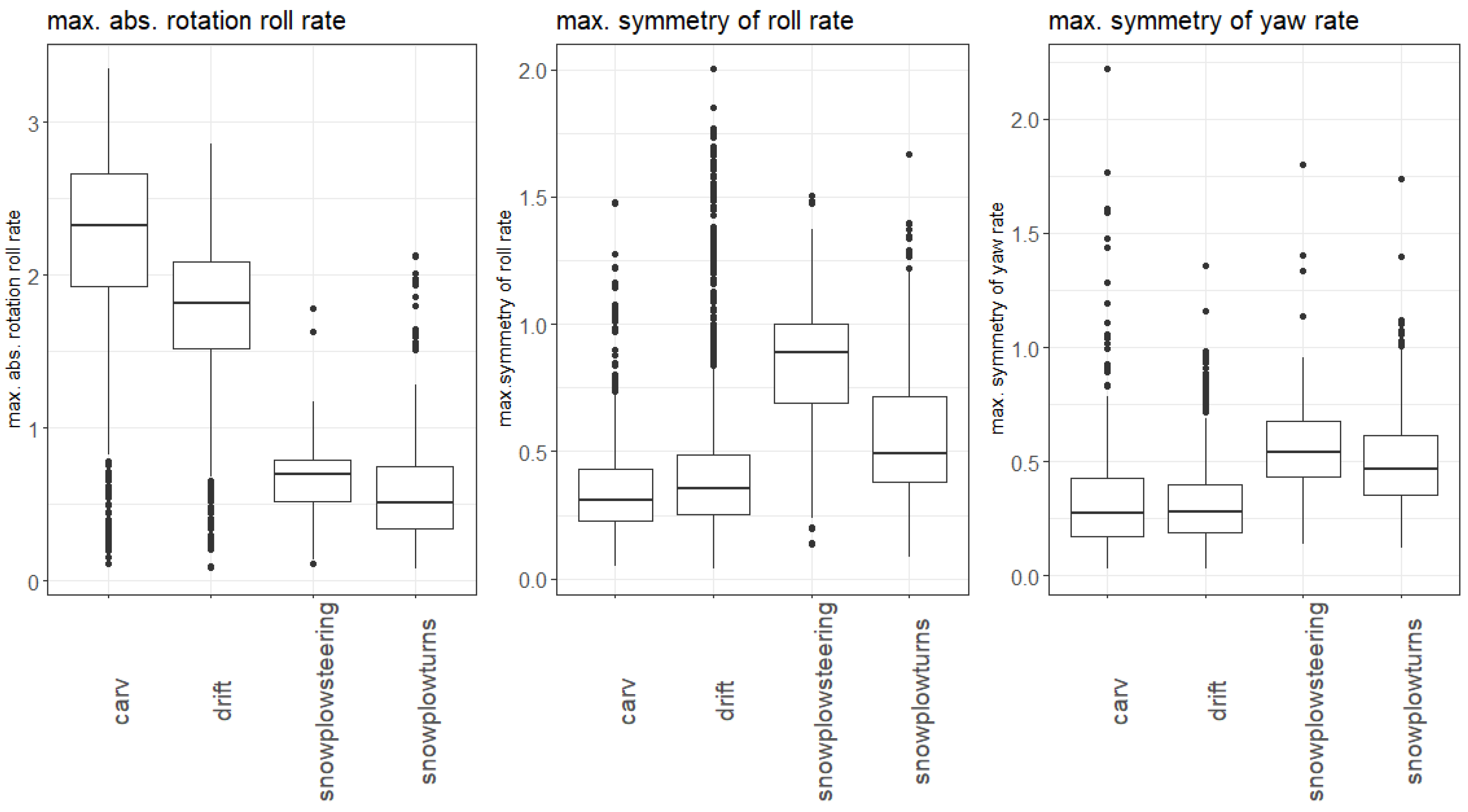
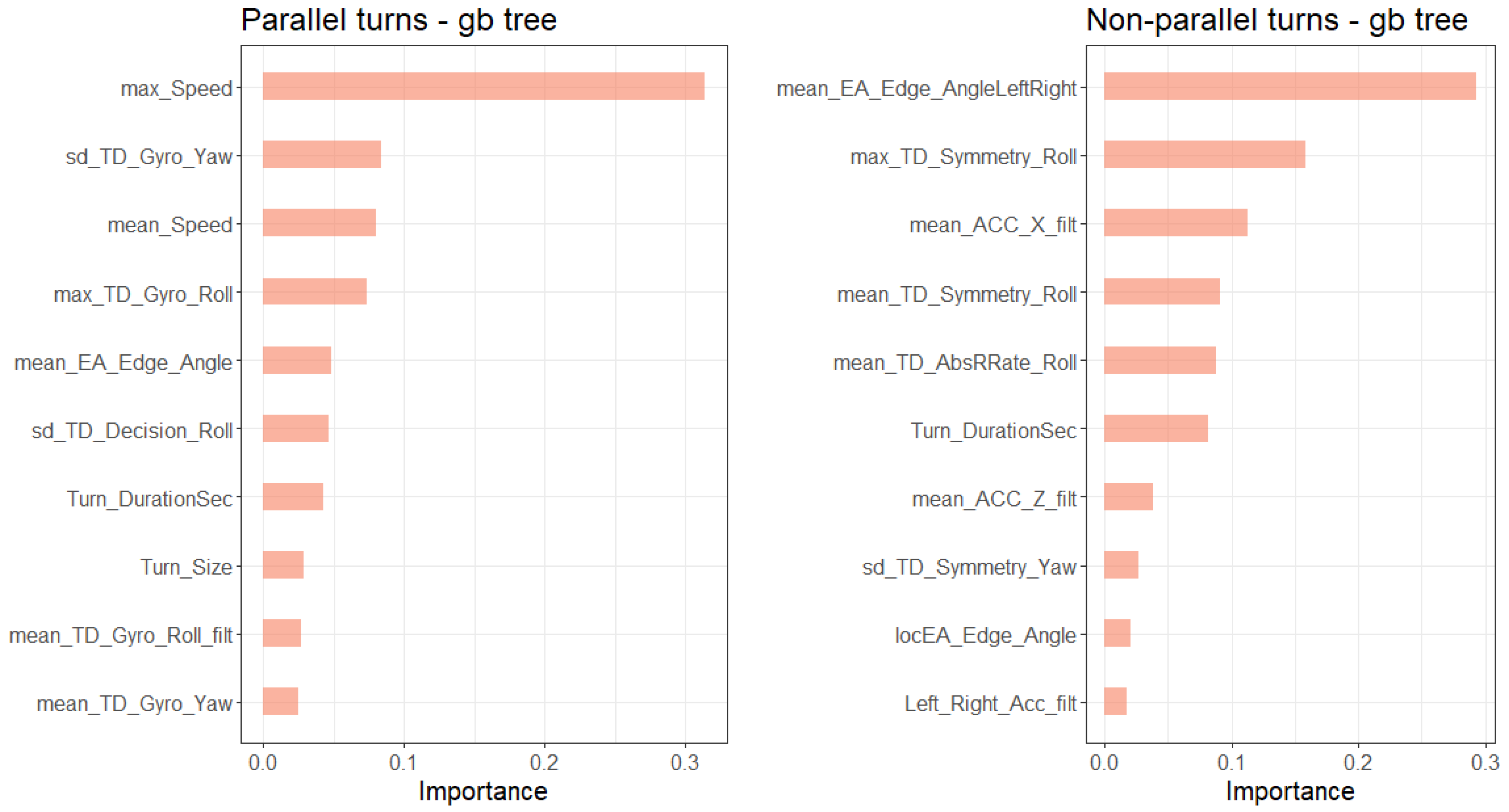
3.2. Important Features for Classifcation of the Alpine Skiing Styles
3.3. Comparison of Model Performance
4. Discussion
4.1. Classification Performance
4.2. Limitations
4.3. Application of the Classifier
4.4. Sensor Setup
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| R Package Name | Version |
|---|---|
| caret [48] | 6.0–84 |
| data.table [49] | 1.12.2 |
| tidyr [50] | 1.0.0 |
| dplyr [51] | 0.8.3 |
| packrat [52] | 0.5.0 |
| randomForest [45] | 4.6–14 |
| xgboost [39] | 0.90.0.2 |
| rpart [38] | 4.1–15 |
| rpart.plot [53] | 3.0.8 |
| ggplot2 [54] | 3.2.1 |
| Feature | Description |
|---|---|
| sd_TD_Gyro_Yaw | Standard deviation of gyroscope roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| max_Speed | Maximum speed of turn (m/s) |
| mean_Speed | Mean speed of turn (m/s) |
| max_TD_Gyro_Roll | Max gyroscope roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| min_Speed | Minimum speed of turn (m/s) |
| mean_EA_Edge_Angle | Mean estimated inclination angle of turn (mean of left and right boot) (rad/s) |
| Turn_DurationSec | Duration of turn (s) |
| sd_TD_Gyro_Roll | Standard deviation of gyroscope roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| sd_TD_Decision_Yaw | Standard deviation of filtered (using a fourth-order, zero-lag, low-pass Butterworth filter with cut-off frequency of 0.5 Hz) yaw axis angular velocity of turn (mean of left and right boot) (rad/s) |
| max_TD_Gyro_Yaw | Maximum yaw axis angular velocity of turn (mean of left and right boot) (rad/s) |
| mean_GYRO_Z_filt | Mean of the maximum of the gyroscope of the Z-axis of left and right foot of turn (rad/s) |
| max_TD_AbsRRate_Roll | Maximum absolute roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| max_TD_Decision_Roll | Maximum filtered (using a fourth-order, zero-lag, low-pass Butterworth filter with cut-off frequency of 0.5 Hz) roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| Turn_Size | Size of turn |
| sd_TD_AbsRRate_Roll | Standard deviation of absolute roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| sd_TD_Decision_Roll | Standard deviation of filtered (using a fourth-order, zero-lag, low-pass Butterworth filter with cut-off frequency of 0.5 Hz) roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| mean_TD_Gyro_Roll_filt | Mean gyroscope roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| max_TD_Decision_Yaw | Maximum filtered (using a fourth-order, zero-lag, low-pass Butterworth filter with cut-off frequency of 0.5 Hz) yaw axis angular velocity of turn (mean of left and right boot) (rad/s) |
| max_TD_Symmetry_Roll | Maximum symmetry of the roll axis angular velocity of turn between left and right boot (rad/s) |
| mean_GYRO_Y_filt | Mean of the maximum of the gyroscope Y-axis of left and right foot of turn (rad/s) |
| mean_TD_Gyro_Yaw | Mean gyroscope yaw axis angular velocity of turn (mean of left and right boot) (rad/s) |
| sd_TD_Symmetry_Roll | Standard deviation of the symmetry of the roll axis angular velocity of turn between left and right boot (rad/s) |
| mean_TD_Gyro_Roll | Mean gyroscope roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| max_EA_Edge_Angle | Maximum estimated inclination angle of turn (mean of left and right boot) (degree) |
| EADiff_Left_Right | Mean difference of the absolute estimated inclination angle of left and estimated inclination angle of right foot of turn (degree) |
| Feature | Description |
|---|---|
| Turn_DurationSec | Duration of Turn (s) |
| mean_TD_Gyro_Roll_filt | Mean gyroscope roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| max_TD_Symmetry_Roll | Maximum symmetry of the roll axis angular velocity of turn between left and right boot (rad/s) |
| max_EA_Edge_Angle | Maximum estimated inclination angle of turn (mean of left and right boot) (degree) |
| locEA_Edge_Angle | Position (1–100) of the max estimated inclination angle of the turn |
| mean_EA_Edge_Angle | Mean estimated inclination angle of turn (mean of left and right boot) (degree) |
| mean_EA_Edge_AngleLeftRight | Mean of the maximum estimated inclination angle of the left and right foot of turn (degree) |
| mean_ACC_Z_filt | Mean of the maximum of the acceleration of the Z-axis of left and right foot of turn (m/s2) |
| mean_ACC_Y_filt | Mean of the maximum of the acceleration of the Y-axis of left and right foot of turn (m/s2) |
| mean_ACC_X_filt | Mean of the maximum of the acceleration of the X-axis of left and right foot of turn (m/s2) |
| mean_GF_GForce_PitchYaw | Mean resultant frontal plane acceleration of turn (mean of left and right boot) (m/s2) |
| max_GF_GForce_PitchYaw | Maximum resultant frontal plane of turn (mean of left and right boot) (m/s2) |
| mean_GF_GForce_PitchYaw_LeftRight | Mean of the maximum resultant frontal plane acceleration of the left and right foot of turn (m/s2) |
| Left_Right_Acc_filt | Mean of the maximal acceleration of the left and right foot of each turn (m/s2) |
| mean_TD_AbsRRate_Roll | Mean absolute roll axis angular velocity (mean of left and right boot) (rad/s) |
| mean_TD_Decision_Roll | Filtered (using a fourth-order, zero-lag, low-pass Butterworth filter with cut-off frequency of 0.5 Hz) roll axis angular velocity (mean of left and right boot) (rad/s) |
| mean_TD_Gyro_Roll | Mean gyroscope roll axis angular velocity of turn (mean of left and right boot) (rad/s) |
| mean_TD_Symmetry_Roll | Mean symmetry roll axis angular velocity of turn between left and right boot (rad/s) |
| sd_TD_Symmetry_Roll | Standard deviation of symmetry of the roll axis angular velocity of turn between left and right boot (rad/s) |
| sd_TD_Symmetry_Yaw | Standard deviation of symmetry of the yaw axis angular velocity of turn between left and right boot (rad/s) |
| Model | Parameters | |
|---|---|---|
| Parallel Turns | Non-Parallel Turns | |
| Decision tree (package: rpart [38]) | cp = 0.05076923. | cp = 0 |
| Random Forest (package: randomForest [45]) | mtry= 2, ntree = 1000 | mtry= 13, ntree = 1000 |
| Gradient boosted decision tree (package: xgboost [39]) | max.depth = 3 eta = 0.4 nrounds = 150 gamma =0 colsample_bytree = 0.68 min_child_weight = 1 subsample = 1 | max.depth = 3 eta = 0.3 nrounds = 150 gamma =0 colsample_bytree = 0.6 min_child_weight = 1 subsample = 1 |
| ID | Snow Conditions |
|---|---|
| S01 | hard groomed |
| S03 | hard groomed |
| S04 | soft (5 cm new snow) |
| S05 | hardpack |
| S06 | hardpack |
| S07 | soft groomed |
| S08 | soft groomed |
| S09 | soft groomed |
| S10 | hard groomed |
| S11 | hard groomed |
| S12 | hard groomed |
| S14 | hardpack |
| S15 | hardpack |
| S16 | soft (6 cm new snow) |
| S17 | hardpack |
| S19 | hardpack |
| S20 | hardpack |
| S21 | hardpack groomed |
| S23 | ice |
| S24 | refrozen spring snow |
References
- Peake, J.M.; Kerr, G.; Sullivan, J.P. A Critical Review of Consumer Wearables, Mobile Applications, and Equipment for Providing Biofeedback, Monitoring Stress, and Sleep in Physically Active Populations. Front. Physiol. 2018, 9, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Aroganam, G.; Manivannan, N.; Harrison, D. Review on Wearable Technology Sensors Used in Consumer Sport Applications. Sensors 2019, 19, 1983. [Google Scholar] [CrossRef] [PubMed]
- Martínez, A.; Jahnel, R.; Buchecker, M.; Snyder, C.; Brunauer, R.; Stöggl, T. Development of an Automatic Alpine Skiing Turn Detection Algorithm Based on a Simple Sensor Setup. Sensors 2019, 19, 902. [Google Scholar] [CrossRef] [PubMed]
- King, K.; Perkins, N.C.; Churchill, H.; McGinnis, R.; Doss, R.; Hickland, R. Bowling ball dynamics revealed by miniature wireless MEMS inertial measurement unit. Sport. Eng. 2011, 13, 95–104. [Google Scholar] [CrossRef]
- Al-Amri, M.; Nicholas, K.; Button, K.; Sparkes, V.; Sheeran, L.; Davies, J.; Al-Amri, M.; Nicholas, K.; Button, K.; Sparkes, V.; et al. Inertial Measurement Units for Clinical Movement Analysis: Reliability and Concurrent Validity. Sensors 2018, 18, 719. [Google Scholar] [CrossRef]
- Aminian, K.; Najafi, B. Capturing human motion using body-fixed sensors: Outdoor measurement and clinical applications. Comput. Animat. Virtual Worlds 2004, 15, 79–94. [Google Scholar] [CrossRef]
- Hintermeister, R.A.; O’Connor, D.D.; Lange, G.W.; Dillman, C.J.; Steadman, J.R. Muscle activity in wedge, parallel, and giant slalom skiing. Med. Sci. Sports Exerc. 1997, 29, 548–553. [Google Scholar] [CrossRef]
- Mueller, E.; Schwameder, H. Biomechanical aspects of new techniques in alpine skiing and ski-jumping. J. Sports Sci. 2003, 21, 679–692. [Google Scholar] [CrossRef]
- Federolf, P.; Roos, M.; Lüthi, A.; Dual, J. Finite element simulation of the ski-snow interaction of an alpine ski in a carved turn. Sport. Eng. 2010, 12, 123–133. [Google Scholar] [CrossRef]
- Reid, R.C.; Haugen, P.; Gilgien, M.; Kipp, R.W.; Smith, G.A. Alpine Ski Motion Characteristics in Slalom. Front. Sport. Act. Living 2020, 2, 25. [Google Scholar] [CrossRef]
- Brunauer, R.; Kremser, W.; Stöggl, T. From Sensor Data to Coaching in Alpine Skiing—A Software Design to Facilitate Immediate Feedback in Sports. In Proceedings of the 12th International Symposium on Computer Science in Sport, Moscow, Russia, 8–10 July 2019. [Google Scholar]
- Snyder, C.; Martínez, A.; Brunauer, R.; Stöggl, T. Validation of a Wearable System for Edge Angle Estimation during Alpine Skiing; Karczewska-Lindinger, M., Hakkarainen, A., Linnamo, V., Lindinger, S., Eds.; University of Jyväskylä: Jyväskylä, Finland, 2020. [Google Scholar]
- Camomilla, V.; Bergamini, E.; Fantozzi, S.; Vannozzi, G. Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 2018, 18, 873. [Google Scholar] [CrossRef] [PubMed]
- Nemec, B.; Petric, T.; Babic, J.; Supej, M. Estimation of Alpine Skier Posture Using Machine Learning Techniques. Sensors 2014, 14, 18898–18914. [Google Scholar] [CrossRef] [PubMed]
- Spörri, J.; Kröll, J.; Haid, C.; Fasel, B.; Müller, E. Potential Mechanisms Leading to Overuse Injuries of the Back in Alpine Ski Racing: A Descriptive Biomechanical Study. Am. J. Sports Med. 2015, 8, 2042–2048. [Google Scholar] [CrossRef] [PubMed]
- Fasel, B.; Spörri, J.; Gilgien, M.; Boffi, G.; Chardonnens, J.; Müller, E.; Aminian, K. Three-Dimensional Body and Centre of Mass Kinematics in Alpine Ski Racing Using Differential GNSS and Inertial Sensors. Remote Sens. 2016, 8, 671. [Google Scholar] [CrossRef]
- Spörri, J.; Kröll, J.; Fasel, B.; Aminian, K.; Müller, E. The Use of Body Worn Sensors for Detecting the Vibrations Acting on the Lower Back in Alpine Ski Racing. Front. Physiol. 2017, 8, 522. [Google Scholar] [CrossRef]
- Martínez, A.; Brunauer, R.; Venek, V.; Snyder, C.; Jahnel, R.; Buchecker, M.; Thorwartl, C.; Stöggl, T. Development and Validation of a Gyroscope-Based Turn Detection Algorithm for Alpine Skiing in the Field. Front. Sport. Act. Living 2019, 1, 18. [Google Scholar] [CrossRef]
- Rindal, O.M.H.; Seeberg, T.M.; Tjønnås, J.; Haugnes, P.; Sandbakk, Ø. Automatic Classification of Sub-Techniques in Classical Cross-Country Skiing Using a Machine Learning Algorithm on Micro-Sensor Data. Sensors 2017, 18, 75. [Google Scholar] [CrossRef]
- Jang, J.; Ankit, A.; Kim, J.; Jang, Y.J.; Kim, H.Y.; Kim, J.H.; Xiong, S.; Jang, J.; Ankit, A.; Kim, J.; et al. A Unified Deep-Learning Model for Classifying the Cross-Country Skiing Techniques Using Wearable Gyroscope Sensors. Sensors 2018, 18, 3819. [Google Scholar] [CrossRef]
- Stöggl, T.; Holst, A.; Jonasson, A.; Andersson, E.; Wunsch, T.; Norström, C.; Holmberg, H.-C. Automatic Classification of the Sub-Techniques (Gears) Used in Cross-Country Ski Skating Employing a Mobile Phone. Sensors 2014, 14, 20589. [Google Scholar] [CrossRef]
- Groh, B.H.; Fleckenstein, M.; Eskofier, B.M. Wearable trick classification in freestyle snowboarding. In Proceedings of the 2016 IEEE 13th International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Francisco, CA, USA, 14–17 June 2016; pp. 89–93. [Google Scholar]
- Han, B.; Ryu, J.; Kim, S. Context-Aware Winter Sports Based on Multivariate Sequence Learning. Sensors 2019, 19, 3296. [Google Scholar] [CrossRef]
- Pawlyta, M.; Hermansa, M.; Szczesna, A.; Janiak, M.; Wojciechowski, K. Deep Recurrent Neural Networks for Human Activity Recognition During Skiing. In Proceedings of the Man-Machine Interactions 6—6th International conference on Man-Machine Interactions, ICMMI, Cracow, Poland, 2–3 October 2019; pp. 136–145. [Google Scholar]
- Movesense. Available online: https://www.movesense.com/wp-content/uploads/2017/11/Movesense-Sensor-Datasheet-_-20171109.pdf (accessed on 20 May 2020).
- Saeb, S.; Lonini, L.; Jayaraman, A.; Mohr, D.; Kording, K. The need to approximate the use-case in clinical machine learning. Gigascience 2017, 6, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Little, M.A.; Varoquaux, G.; Saeb, S.; Lonini, L.; Jayaraman, A.; Mohr, D.C.; Kording, K.P. Using and understanding cross-validation strategies. Perspectives on Saeb et al. Gigascience 2017, 6, 1–6. [Google Scholar] [CrossRef]
- Neto, E.C.; Pratap, A.; Perumal, T.M.; Tummalacherla, M. Detecting the impact of subject characteristics on machine learning-based diagnostic applications. NPJ Digit. Med. 2019, 2. [Google Scholar] [CrossRef]
- Granitto, P.M.; Furlanello, C.; Biasioli, F.; Gasperi, F. Recursive feature elimination with random forest for PTR-MS analysis of agroindustrial products. Chemom. Intell. Lab. Syst. 2006, 83, 83–90. [Google Scholar] [CrossRef]
- Rosenfeld, A.; Richardson, A. Explainability in human–agent systems. Auton. Agent. Multi. Agent. Syst. 2019, 33, 673–705. [Google Scholar] [CrossRef]
- Barredo Arrieta, A.; Díaz-Rodríguez, N.; Del Ser, J.; Bennetot, A.; Tabik, S.; Barbado, A.; Garcia, S.; Gil-Lopez, S.; Molina, D.; Benjamins, R.; et al. Explainable Artificial Intelligence (XAI): Concepts, Taxonomies, Opportunities and Challenges toward Responsible AI. Inf. Fusion 2020, 82–115. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Chapman and Hall/CRC: Boca Raton, FL, USA, 1984; ISBN 9781138469525. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Gupta, B.; Rawat, A.; Jain, A.; Arora, A.; Dhami, N. Analysis of Various Decision Tree Algorithms for Classification in Data Mining. Int. J. Comput. Appl. 2017, 163, 15–19. [Google Scholar] [CrossRef]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning: With Applications in R, 7th ed.; Springer: New York, NY, USA, 2013; ISBN 9781461471370. [Google Scholar]
- Therneau, T.; Atkinson, B. rpart: Recursive Partitioning and Regression Trees, R Package Version 4.1-15; 2019. Available online: https://cran.r-project.org/package=rpart (accessed on 20 May 2020).
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. xgboost: Extreme Gradient Boosting, R Package Version 0.90.0.2; 2019. Available online: https://cran.r-project.org/package=xgboost (accessed on 20 May 2020).
- Hossin, M.; Sulaiman, M.N. A Review on Evaluation Metrics for Data Classification Evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar]
- Stehman, S.V. Selecting and interpreting measures of thematic classification accuracy. Remote Sens. Environ. 1997, 62, 77–89. [Google Scholar] [CrossRef]
- Tharwat, A. Classification assessment methods. Appl. Comput. Informa. 2018, in press. [Google Scholar] [CrossRef]
- Cust, E.E.; Sweeting, A.J.; Ball, K.; Robertson, S. Machine and deep learning for sport-specific movement recognition: A systematic review of model development and performance. J. Sports Sci. 2019, 37, 568–600. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.r-project.org/ (accessed on 20 May 2020).
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kos, A.; Wei, Y.; Tomažič, S.; Umek, A. The role of science and technology in sport. Procedia Comput. Sci. 2018, 129, 489–495. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; the R Core Team; et al. Caret: Classification and Regression Training, R Package Version 6.0-84; 2019. Available online: https://cran.r-project.org/package=caret (accessed on 20 May 2020).
- Dowle, M.; Srinivasan, A. data.table: Extension of ‘data.frame’, R Package Version 1.12.2; 2019. Available online: https://cran.r-project.org/package=data.table (accessed on 20 May 2020).
- Wickham, H.; Henry, L. tidyr: Tidy Messy Data, R Package Version 1.0.0; 2019. Available online: https://cran.r-project.org/package=tidyr (accessed on 20 May 2020).
- Wickham, H.; François, R.; Henry, L.; Müller, K. dplyr: A Grammar of Data Manipulation, R Package Version 0.8.1; 2019. Available online: https://cran.r-project.org/package=dplyr (accessed on 20 May 2020).
- Ushey, K.; McPherson, J.; Cheng, J.; Atkins, A.; Allaire, J.J. Packrat: A Dependency Management System for Projects and Their R Package Dependencies, R Package Version 0.5.0; 2018. Available online: https://cran.r-project.org/package=packrat (accessed on 20 May 2020).
- Milborrow, S. rpart.plot: Plot “rpart” Models: An Enhanced Version of “plot.rpart”, R Package Version 3.0.8; 2019. Available online: https://cran.r-project.org/package=rpart.plot (accessed on 20 May 2020).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]


| Parallel Turns | Actual | ||
|---|---|---|---|
| Drifting | Carving | ||
| Predicted | Drifting | True drifting turns (tp) | False carving turns (fn) |
| Carving | False drifting turns (fp) | True carving turns (tn) | |
| Non-Parallel Turns | Actual | ||
|---|---|---|---|
| Snowplow | Snowplow-Steering | ||
| Predicted | Snowplow | True snowplow turns (tp) | False snowplow-steering turns (fn) |
| Snowplow-Steering | False snowplow turns (fp) | True snowplow-steering turns (tn) | |
| Metrics | Formula |
|---|---|
| Accuracy (acc) | |
| Sensitivity (sn) | |
| Specificity (sp) | |
| Geometric mean |
| Accuracy | Sensitivity | Specificity | Geometric Mean | |
|---|---|---|---|---|
| Decision Tree | 0.885 | 0.901 | 0.866 | 0.883 |
| Random Forest | 0.948 | 0.938 | 0.960 | 0.949 |
| Boosted Tree | 0.953 | 0.959 | 0.945 | 0.951 |
| Accuracy | Sensitivity | Specificity | Geometric Mean | |
|---|---|---|---|---|
| Decision Tree | 0.822 | 0.688 | 0.860 | 0.769 |
| Random Forest | 0.890 | 0.688 | 0.947 | 0.807 |
| Boosted Tree | 0.877 | 0.688 | 0.930 | 0.800 |
| Parallel Turns | Actual | ||
|---|---|---|---|
| Carving | Drifting | ||
| Predicted | Carving | 218 (90.1%) | 27 (13.4%) |
| Drifting | 24 (9.9%) | 174 (86.6%) | |
| Parallel Turns | Actual | ||
|---|---|---|---|
| Carving | Drifting | ||
| Predicted | Carving | 227 (93.8%) | 8 (4.0%) |
| Drifting | 15 (6.2%) | 193 (96.0%) | |
| Parallel Turns | Actual | ||
|---|---|---|---|
| Carving | Drifting | ||
| Predicted | Carving | 232 (95.6%) | 11 (5.5%) |
| Drifting | 10 (4.1%) | 190 (94.5%) | |
| Non-Parallel Turns | Actual | ||
|---|---|---|---|
| Snowplow-Steering | Snowplow | ||
| Predicted | Snowplow-Steering | 11 (68.8%) | 8 (14.0%) |
| Snowplow | 5 (31.2%) | 49 (86.0%) | |
| Non-Parallel Turns | Actual | ||
|---|---|---|---|
| Snowplow-Steering | Snowplow | ||
| Predicted | Snowplow-Steering | 11 (68.5%) | 3 (5.3%) |
| Snowplow | 5 (31.2%) | 54 (94.7%) | |
| Non-Parallel Turns | Actual | ||
|---|---|---|---|
| Snowplow-Steering | Snowplow | ||
| Predicted | Snowplow-Steering | 11 (68.5%) | 4 (7.0%) |
| Snowplow | 5 (31.2%) | 53 (93.0%) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neuwirth, C.; Snyder, C.; Kremser, W.; Brunauer, R.; Holzer, H.; Stöggl, T. Classification of Alpine Skiing Styles Using GNSS and Inertial Measurement Units. Sensors 2020, 20, 4232. https://doi.org/10.3390/s20154232
Neuwirth C, Snyder C, Kremser W, Brunauer R, Holzer H, Stöggl T. Classification of Alpine Skiing Styles Using GNSS and Inertial Measurement Units. Sensors. 2020; 20(15):4232. https://doi.org/10.3390/s20154232
Chicago/Turabian StyleNeuwirth, Christina, Cory Snyder, Wolfgang Kremser, Richard Brunauer, Helmut Holzer, and Thomas Stöggl. 2020. "Classification of Alpine Skiing Styles Using GNSS and Inertial Measurement Units" Sensors 20, no. 15: 4232. https://doi.org/10.3390/s20154232
APA StyleNeuwirth, C., Snyder, C., Kremser, W., Brunauer, R., Holzer, H., & Stöggl, T. (2020). Classification of Alpine Skiing Styles Using GNSS and Inertial Measurement Units. Sensors, 20(15), 4232. https://doi.org/10.3390/s20154232







