Multilayer Thickness Measurements below the Rayleigh Limit Using FMCW Millimeter and Terahertz Waves
Abstract
1. Introduction
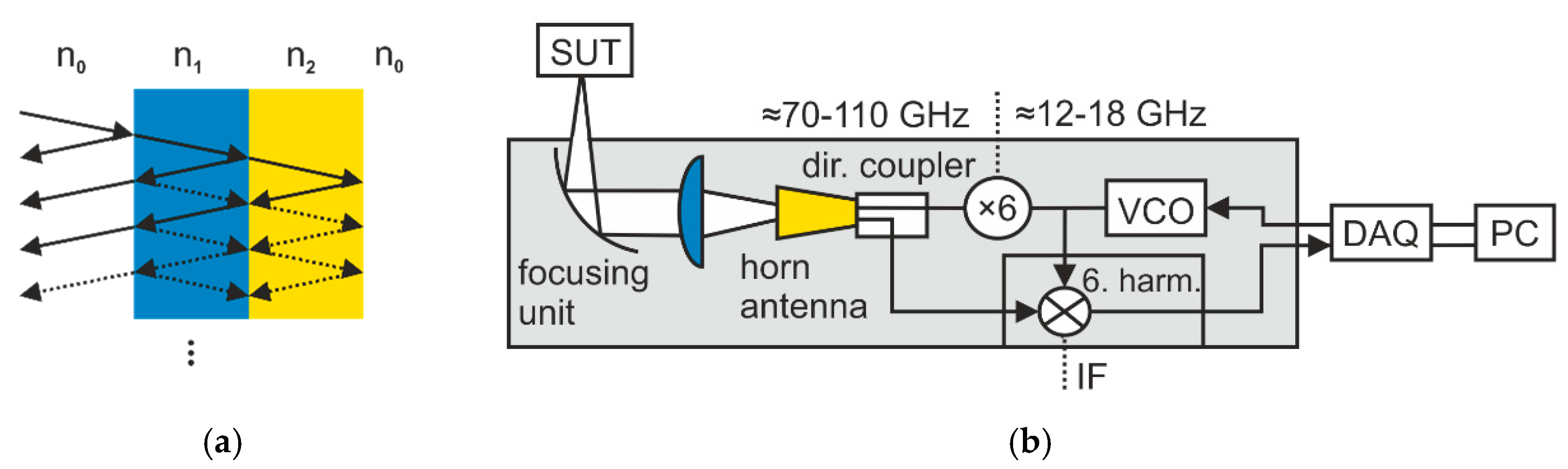
2. FMCW Thickness Measurements
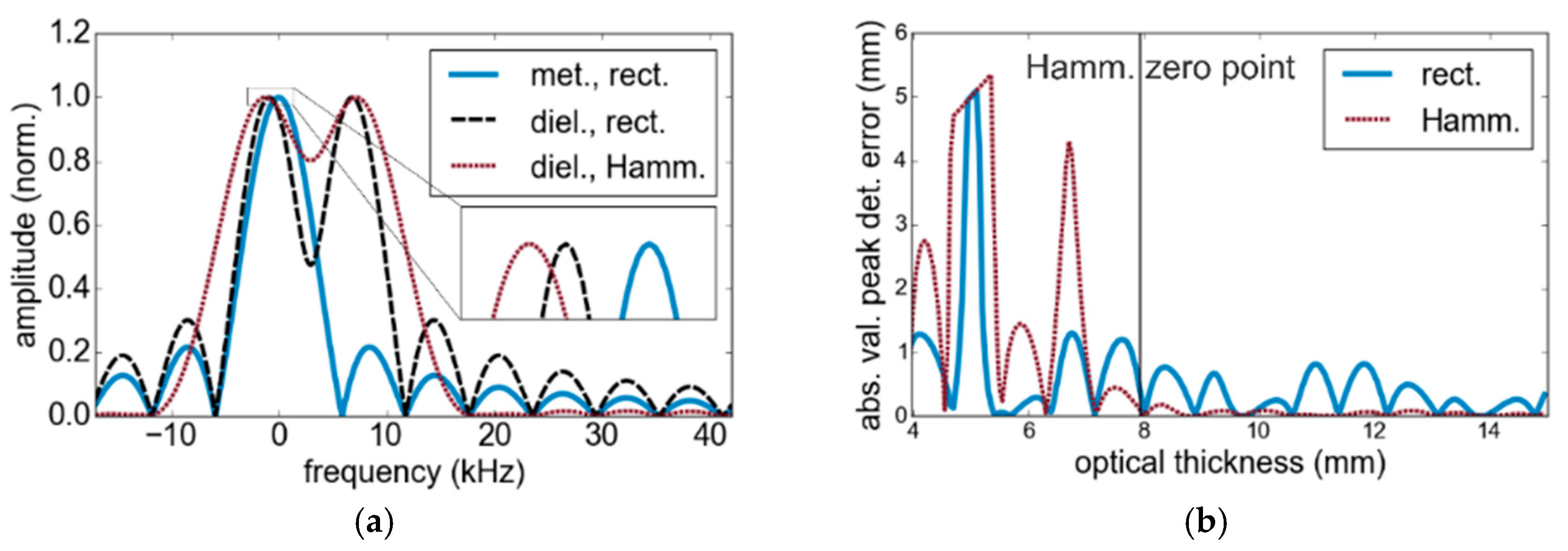
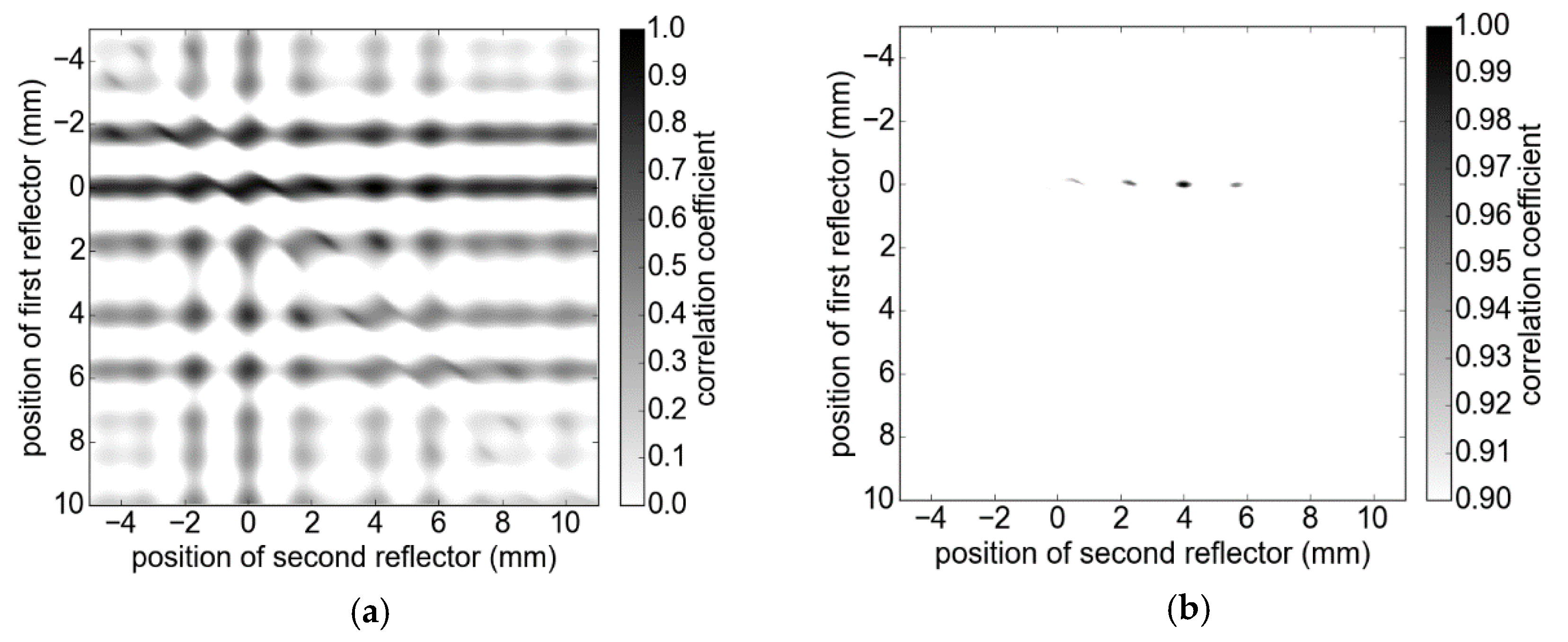
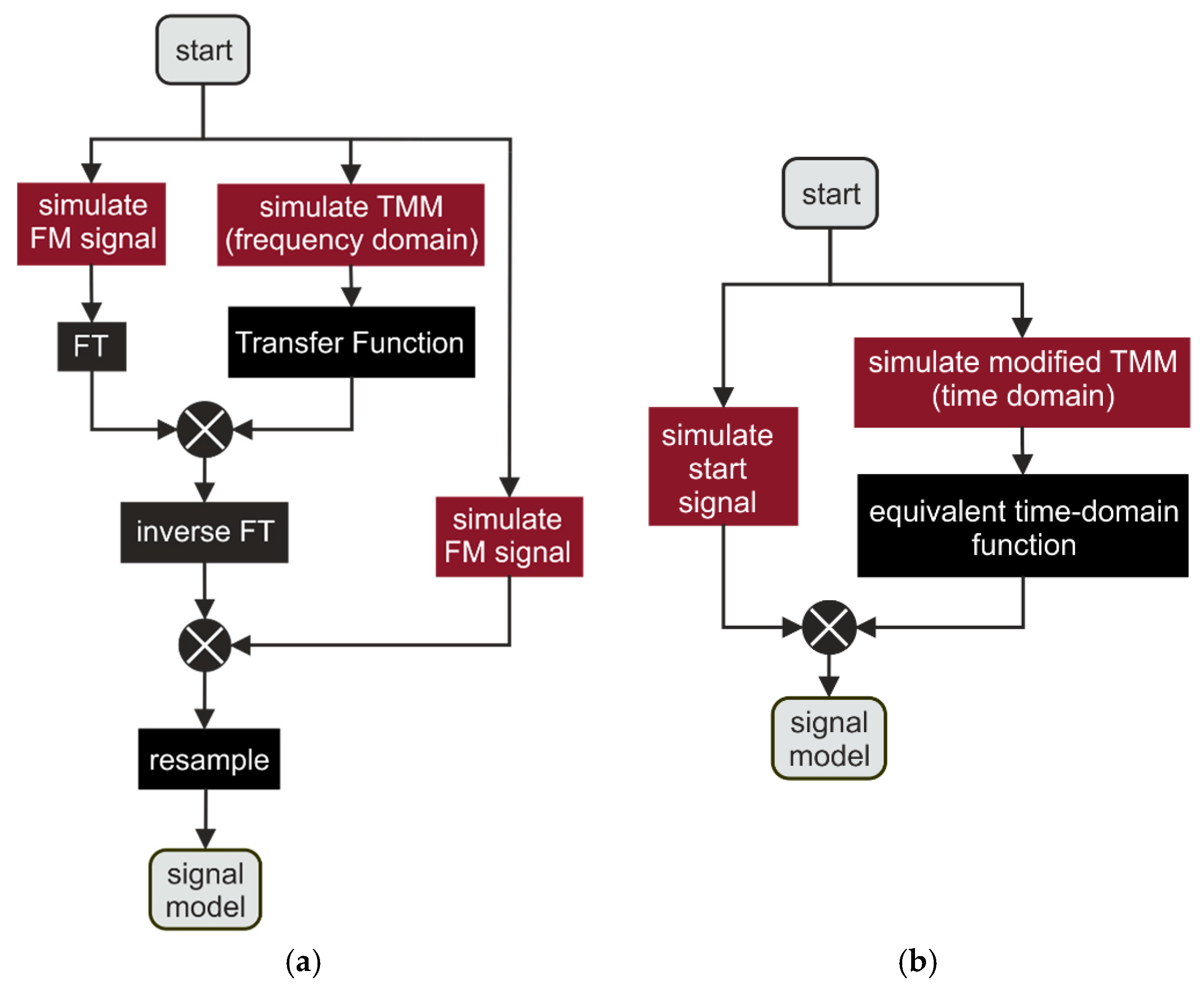
3. Model-Based Signal Processing Approach
4. Measurement Results
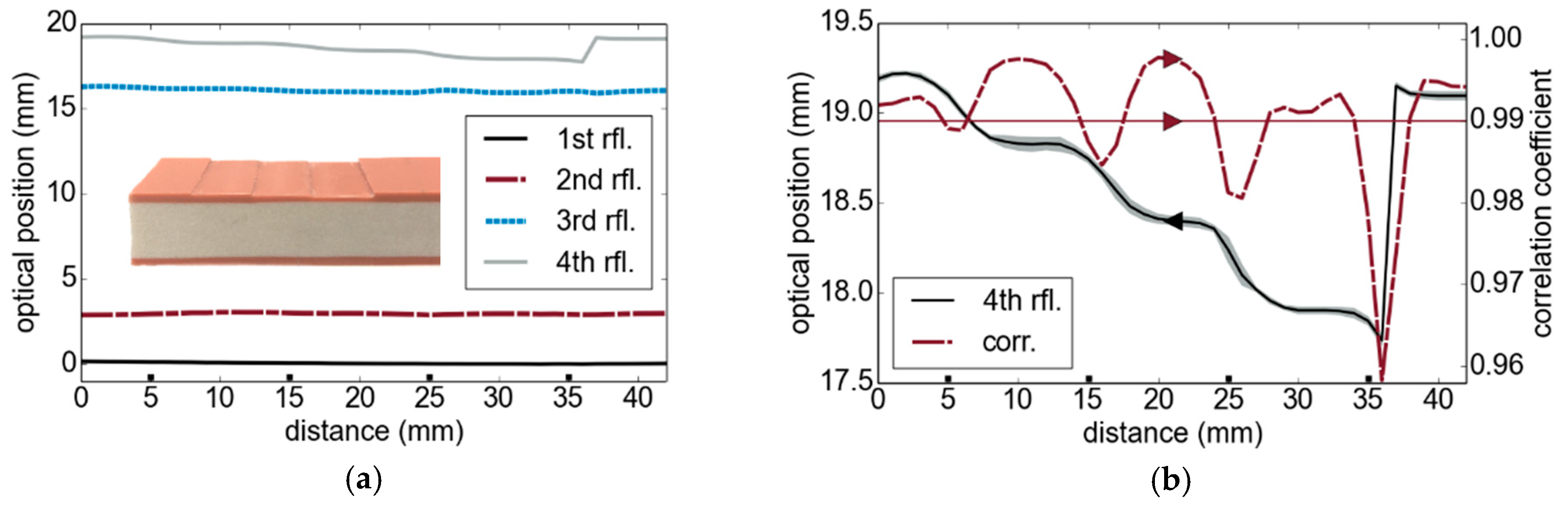
4.1. Calibration Plates
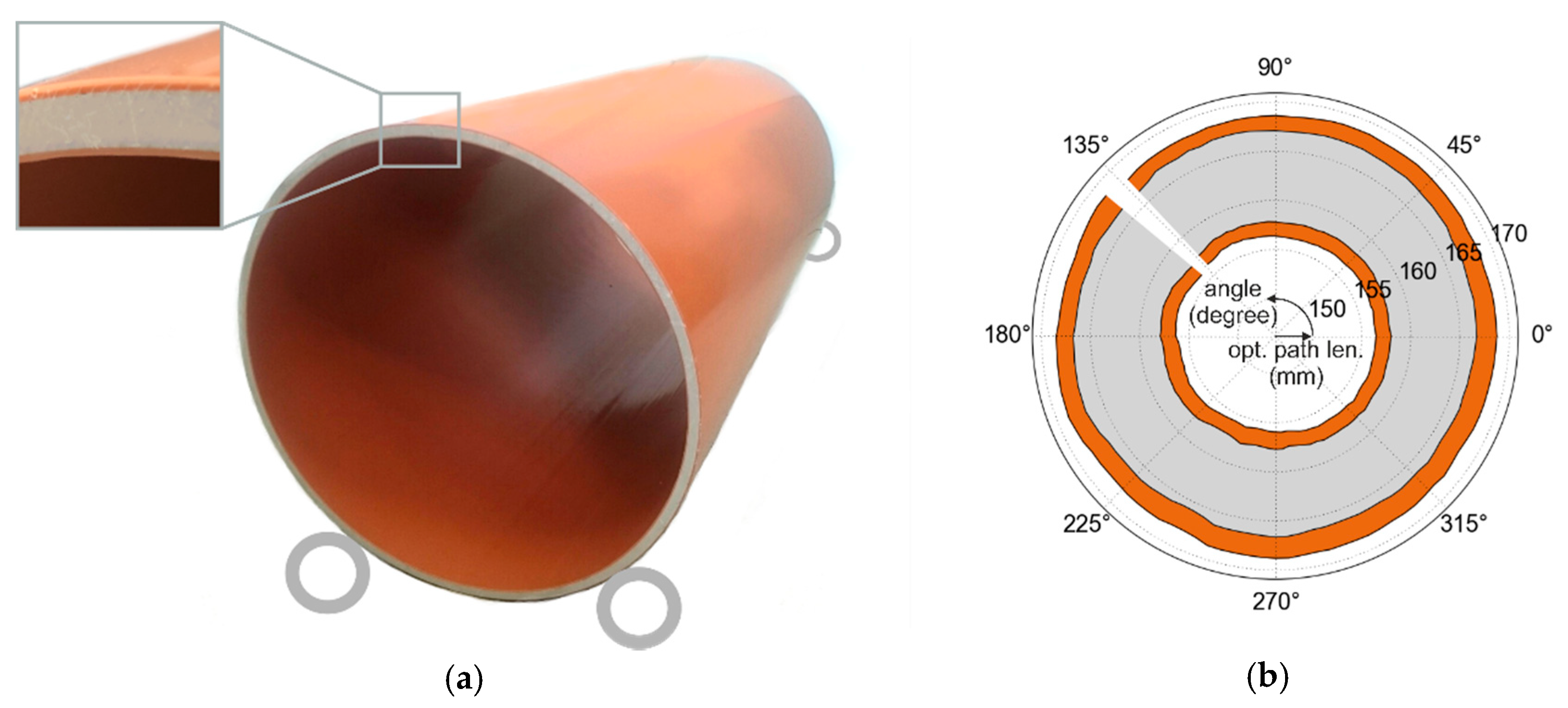
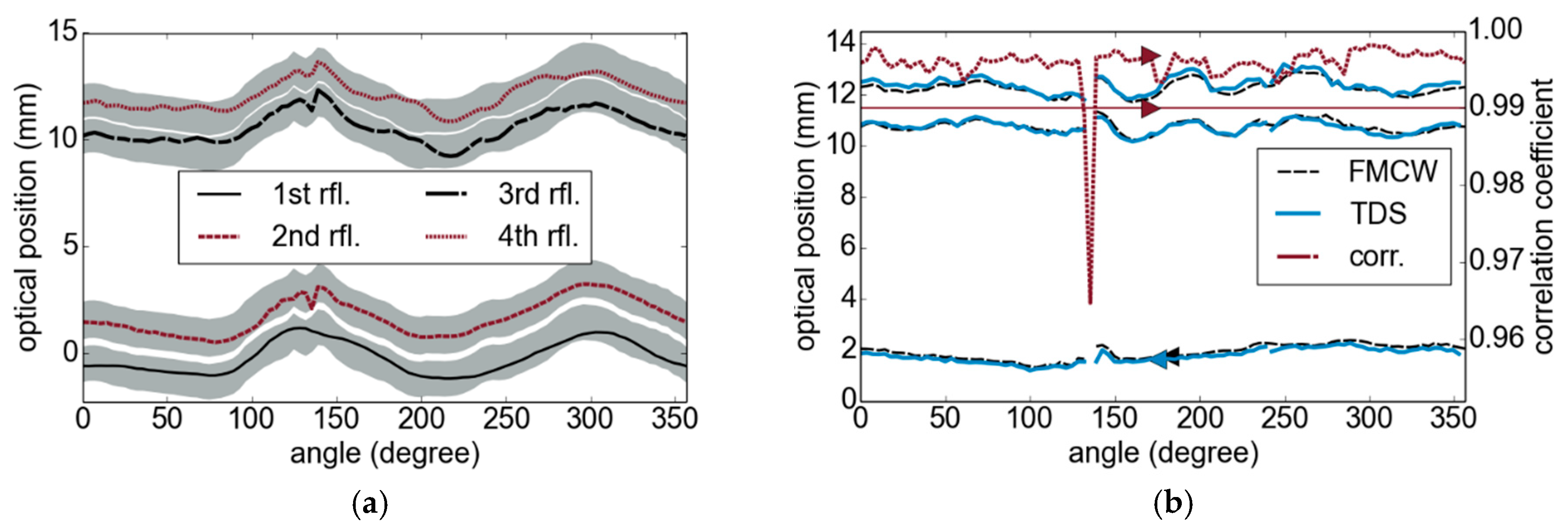
4.2. Industrial Multilayer Structures
4.3. Verification by Comparison with Terahertz Time-Domain Spectroscopy Measurements
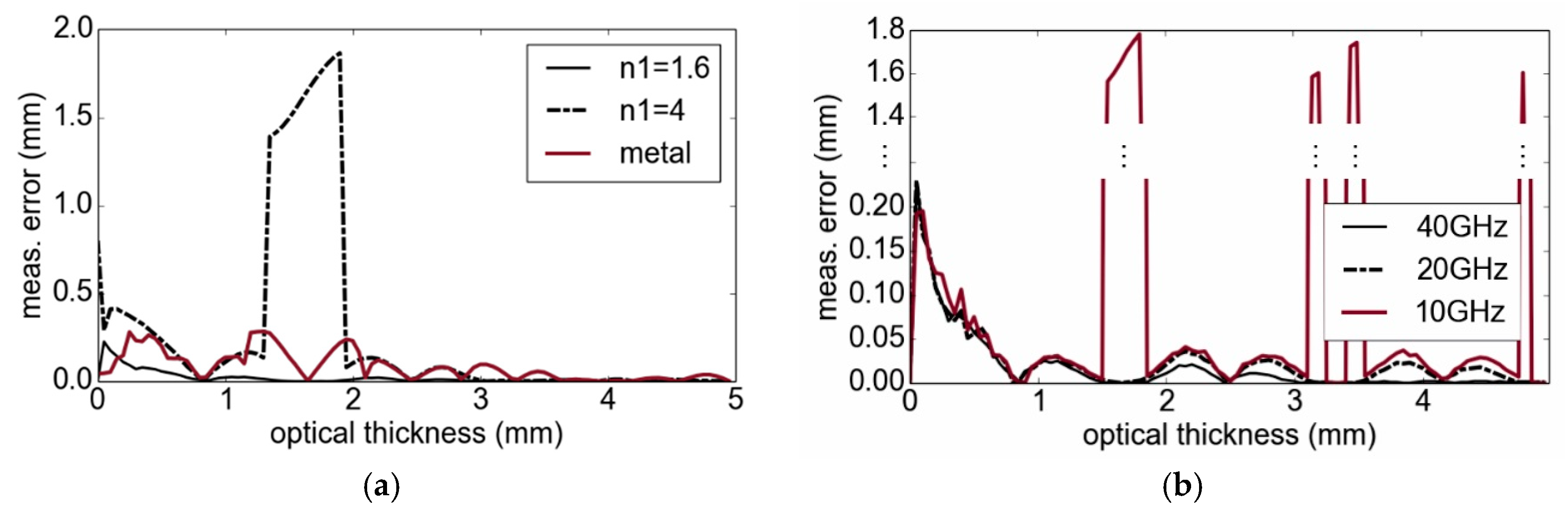
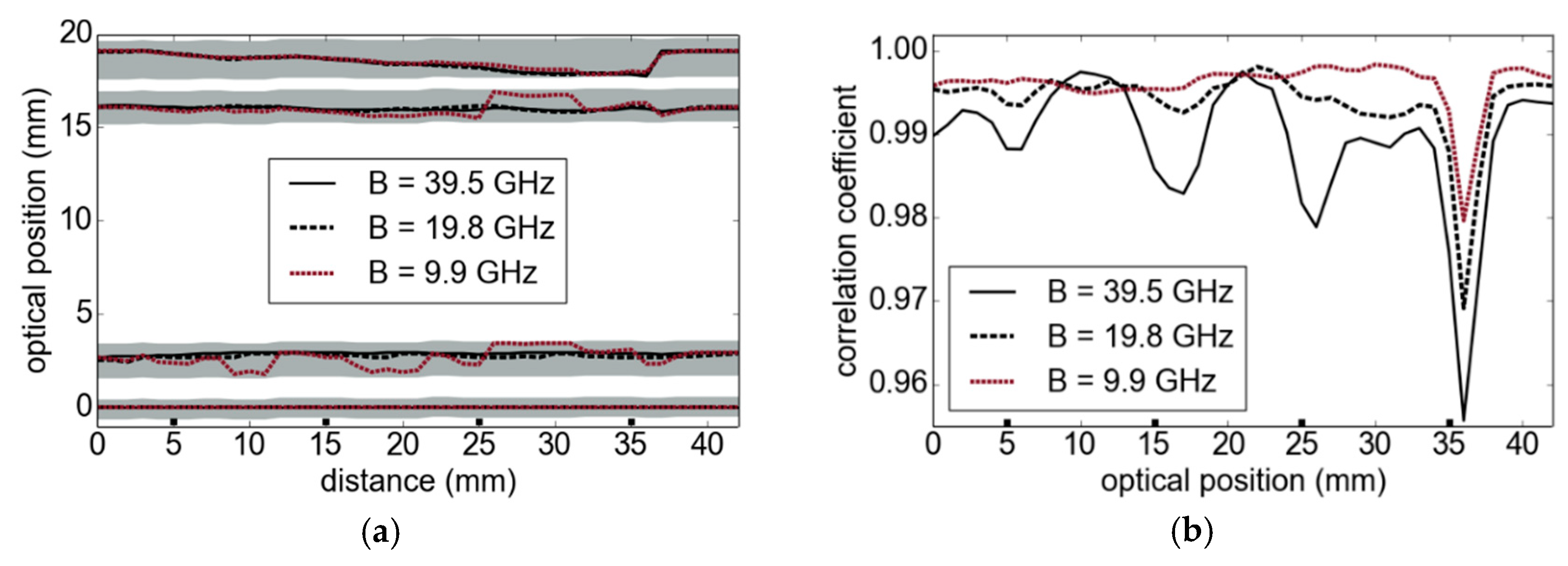
4.4. Toward Reduced Bandwidths and Highly Integrated Systems
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ultrasonic Paint Thickness Measurement on Plastic Substrates. Available online: https://www.defelsko.com/resources/ultrasonic-paint-thickness-measurement-on-plastic-substrates (accessed on 30 June 2019).
- Park, J.; Kim, J.-A.; Ahn, H.; Bae, J.; Jin, J. A Review of Thickness Measurements of Thick Transparent Layers Using Optical Interferometry. Int. J. Precis. Eng. Manuf. 2019, 20, 463–477. [Google Scholar] [CrossRef]
- Krimi, S.; Klier, J.; Jonuscheit, J.; von Freymann, G.; Urbansky, R.; Beigang, R. Highly accurate thickness measurement of multi-layered automotive paints using terahertz technology. Appl. Phys. Lett. 2016, 109, 021105. [Google Scholar] [CrossRef]
- Yasui, T.; Yasuda, T.; Sawanaka, K.I.; Araki, T. Terahertz paintmeter for noncontact monitoring of thickness and drying progress in paint film. App. Opt. 2005, 44, 6849–6856. [Google Scholar] [CrossRef] [PubMed]
- Su, K.; Shen, Y.C.; Zeitler, J.A. Terahertz sensor for non-contact thickness and quality measurement of automobile paints of varying complexity. Trans. Terahertz Sci. Technol. 2014, 4, 432–439. [Google Scholar] [CrossRef]
- Van Mechelen, J.L.M.; Kuzmenko, A.B.; Merbold, H. Stratified dispersive model for material characterization using terahertz time-domain spectroscopy. Opt. Lett. 2014, 39, 3853–3856. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Dong, Y.; Markl, D.; Williams, B.M.; Zheng, Y.; Shen, Y.; Zeitler, J.A. Measurement of the intertablet coating uniformity of a pharmaceutical pan coating process with combined terahertz and optical coherence tomography in-line sensing. J. Pharm Sci. 2017, 106, 1075–1084. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.-S.; Kim, G.-J.; Jeon, S.-G. Terahertz dielectric properties of polymers. J. Koran Phys. Soc. 2006, 49, 513–517. [Google Scholar]
- Wietzke, S.; Jansen, C.; Reuter, M.; Jung, T.; Kraft, D.; Chatterjee, S.; Fischer, B.M.; Koch, M. Terahertz spectroscopy on polymers: A review of morphological studies. J. Mol. Struct. 2011, 1006, 41–51. [Google Scholar] [CrossRef]
- Chen, L.F.; Ong, C.K.; Neo, C.P.; Varadan, V.V.; Varadan, V.K. Microwave Electronics: Measurement and Materials Characterization; John Wiley & Sons: Chichester, UK, 2004. [Google Scholar]
- Ghodgaonkar, D.K.; Varadan, V.V.; Varadan, V.K. Free-Space Measurement of Complex Permittivity and Complex Permeability of Magnetic Materials at Microwave Frequencies. IEEE Trans. Instrum. Meas. 1990, 39, 387–394. [Google Scholar] [CrossRef]
- Hollinger, R.D.; Jose, K.A.; Tellakula, A.; Varadan, V.V.; Varadan, V.K. Microwave characterization of dielectric materials from 8 to 110 GHz using a free-space setup. Microwave Opt. Technol. Lett. 2000, 26, 100–105. [Google Scholar] [CrossRef]
- Kumar, S.B.; Raveendranath, U.; Mohanan, P.; Mathew, K.T.; Hajian, M.; Ligthart, L.P. A simple free-space method for measuring the complex permittivity of single and compound dielectric materials. Microwave Opt. Technol. Lett. 2000, 26, 117–119. [Google Scholar] [CrossRef][Green Version]
- Elhawil, A.; Koers, G.; Zhang, L.; Stiens, J.; Vounckx, R. Comparison between two optimisation algorithms to compute the complex permittivity of dielectric multilayer structures using a free-space quasi-optical method in W-band. IET Sci. Meas. Technol. 2009, 3, 13–21. [Google Scholar] [CrossRef]
- Zwick, T.; Haala, J.; Wiesbeck, W. A genetic algorithm for the evaluation of material parameters of compound multilayer structures. IEEE Trans. Microw. Theory Tech. 2002, 20, 1180–1187. [Google Scholar] [CrossRef]
- Barowski, J.; Zimmermanns, M.; Rolfes, I. Millimeter-Wave Characterization of Dielectric Materials Using Calibrated FMCW Transceivers. IEEE Trans. Microw. Theory Tech. 2018, 66, 3683–3689. [Google Scholar] [CrossRef]
- Christofani, E.; Friederich, F.; Wohnsiedler, S.; Matheis, C.; Jonuscheit, J.; Vandewal, M.; Beigang, R. Nondestructive testing potential evaluation of a terahertz frequency-modulated continuous-wave imager for composite materials inspection. Opt. Eng. 2014, 51, 031211. [Google Scholar] [CrossRef]
- Schreiner, N.S.; Baccouche, B.; Sauer-Greff, W.; Urbansky, R.; Friederich, F. High-resolution FMCW millimeter-wave and terahertz thickness measurements. In Proceedings of the 2017 47th European Microwave Conference (EuMC), Nuremberg, Germany, 10–12 October 2017. [Google Scholar]
- Stelzer, A.; Pichler, M. Enhancement with Model-Based Frequency Estimation Algorithms in Radar Signal Processing. Subsurf. Sens. Technol. Appl. 2003, 4, 241–261. [Google Scholar] [CrossRef]
- Pohl, N.; Jaeschke, T.; Aufinger, K. An ultra-wideband 80 GHz FMCW radar system using a SiGe bipolar transceiver chip stabilized by a fractional-N PLL synthesizer. IEEE Trans. Microw. Theory Tech. 2012, 60, 757–765. [Google Scholar] [CrossRef]
- Scherr, S.; Göttel, B.; Ayhan, S.; Bhutani, A.; Pauli, M.; Winkler, W.; Scheytt, J.C.; Zwick, T. Miniaturized 122 GHz ISM band FMCW radar with micrometer accuracy. In Proceedings of the European Radar Conference (EuRAD), Paris, France, 9–11 September 2015. [Google Scholar]
- Grzyb, J.; Statnikov, K.; Sarmah, N.; Heinemann, B.; Pfeiffer, U.R. A 210–270-GHz circularly polarized FMCW radar with a single-lens-coupled SiGe HBT chip. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 771–783. [Google Scholar] [CrossRef]
- Stove, A.G. Linear FMCW radar techniques. IEE Proc. F Radar Signal Process. 1992, 139, 343–350. [Google Scholar] [CrossRef]
- Detlefsen, J.; Dallinger, A.; Schelkshorn, S.; Bertl, S. UWB millimeter-wave FMCW radar using Hilbert transform methods. In Proceedings of the IEEE 9th Symposium on Spread Spectrum Techniques and Applications, Manaus-Amazon, Brazil, 28–31 August 2006. [Google Scholar]
- Smith, F.C.; Chambers, B.; Bennett, J.C. Calibration techniques for free space reflection coefficient measurements. IEE Proc. A Sci. Meas. Technol. 1992, 139, 247–253. [Google Scholar] [CrossRef]
- Scherr, S.; Ayhan, S.; Fischbach, B.; Bhutani, A.; Pauli, M.; Zwick, T. An Efficient Frequency and Phase Estimation Algorithm with CRB Performance for FMCW Radar Applications. IEEE Trans. Instrum. Meas. 2015, 64, 1868–1875. [Google Scholar]
- Hecht, E. Optics, 4th ed.; Addison-Wesley Longman: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Balanis, C. Advanced Engineering Electromagnetics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Heavens, O.S. Optical properties of thin films. Rep. Progress Phys. 1960, 23, 1–65. [Google Scholar] [CrossRef]
- Katsidis, C.; I Siapkas, D. General Transfer-Matrix Method for Optical Multilayer Systems with Coherent, Partially Coherent, and Incoherent Interference. Appl. Opt. 2002, 41, 3978–3987. [Google Scholar] [CrossRef] [PubMed]
- Schreiner, N.S.; Baccouche, B.; Molter, D.; Sauer-Greff, W.; Urbansky, R.; Friederich, F. A transfer matrix modification for accurate terahertz FMCW thickness measurements. In Proceedings of the 10th UK-Europe-China Workshop on Millimetre Waves and Terahertz Technologies, Liverpool, UK, 11–13 September 2017. [Google Scholar]
- Sikora, H. Millimeter wave technology for precise measurement of diameter, ovality, wall thickness and sagging during tube making. Rubber World 2017, 256, 26–28. [Google Scholar]
- Schreiner, N.S.; Weber, S.; Keil, A.; Friederich, F. Mobile handheld FMCW terahertz multilayer inspection system. In Proceedings of the 44th International Conference on Infrared, Millimeter, and Terahertz Waves, Paris, France, 1–6 September 2019. [Google Scholar]
- Schreiner, N.; Sauer-Greff, W.; Urbansky, R.; Friederich, F. Analyzing the Precision of Frequency Modulated Continuous Wave Distance and Thickness Measurements. In Proceedings of the European Radar Conference (EURAD), Paris, France, 2–4 October 2019. [Google Scholar]
| Material | Step Size (µm) | Optical Correlation Interval (mm) | Refractive Index BC | Refractive Index TMM | Rayleigh Limit |
|---|---|---|---|---|---|
| Pertinax | 1 | 13.97–15.51 | 1.84 | 1.84 | 2.1 mm |
| Acrylic | 1 | 2.0–2.7 | 1.59 | 1.58 | 2.4 mm |
| Material | Thickness | Measured Thickness BC | Measured Thickness TMM | Optical Correlation Interval | Standard Deviation BC | Standard Deviation TMM |
|---|---|---|---|---|---|---|
| Pertinax | 8.04 mm ± 1% | 8.08 mm | 8.07 mm | (14.5–15.3) mm | 2.6 µm | 2.2 µm |
| Acrylic | 1.5166 mm ± 0.4% | 1.49 mm | 1.53 mm | (1.3–2.8) mm | 1.4 µm | 0 µm (*) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schreiner, N.S.; Sauer-Greff, W.; Urbansky, R.; von Freymann, G.; Friederich, F. Multilayer Thickness Measurements below the Rayleigh Limit Using FMCW Millimeter and Terahertz Waves. Sensors 2019, 19, 3910. https://doi.org/10.3390/s19183910
Schreiner NS, Sauer-Greff W, Urbansky R, von Freymann G, Friederich F. Multilayer Thickness Measurements below the Rayleigh Limit Using FMCW Millimeter and Terahertz Waves. Sensors. 2019; 19(18):3910. https://doi.org/10.3390/s19183910
Chicago/Turabian StyleSchreiner, Nina S., Wolfgang Sauer-Greff, Ralph Urbansky, Georg von Freymann, and Fabian Friederich. 2019. "Multilayer Thickness Measurements below the Rayleigh Limit Using FMCW Millimeter and Terahertz Waves" Sensors 19, no. 18: 3910. https://doi.org/10.3390/s19183910
APA StyleSchreiner, N. S., Sauer-Greff, W., Urbansky, R., von Freymann, G., & Friederich, F. (2019). Multilayer Thickness Measurements below the Rayleigh Limit Using FMCW Millimeter and Terahertz Waves. Sensors, 19(18), 3910. https://doi.org/10.3390/s19183910





