Circular Regression in a Dual-Phase Lock-In Amplifier for Coherent Detection of Weak Signal
Abstract
:1. Introduction
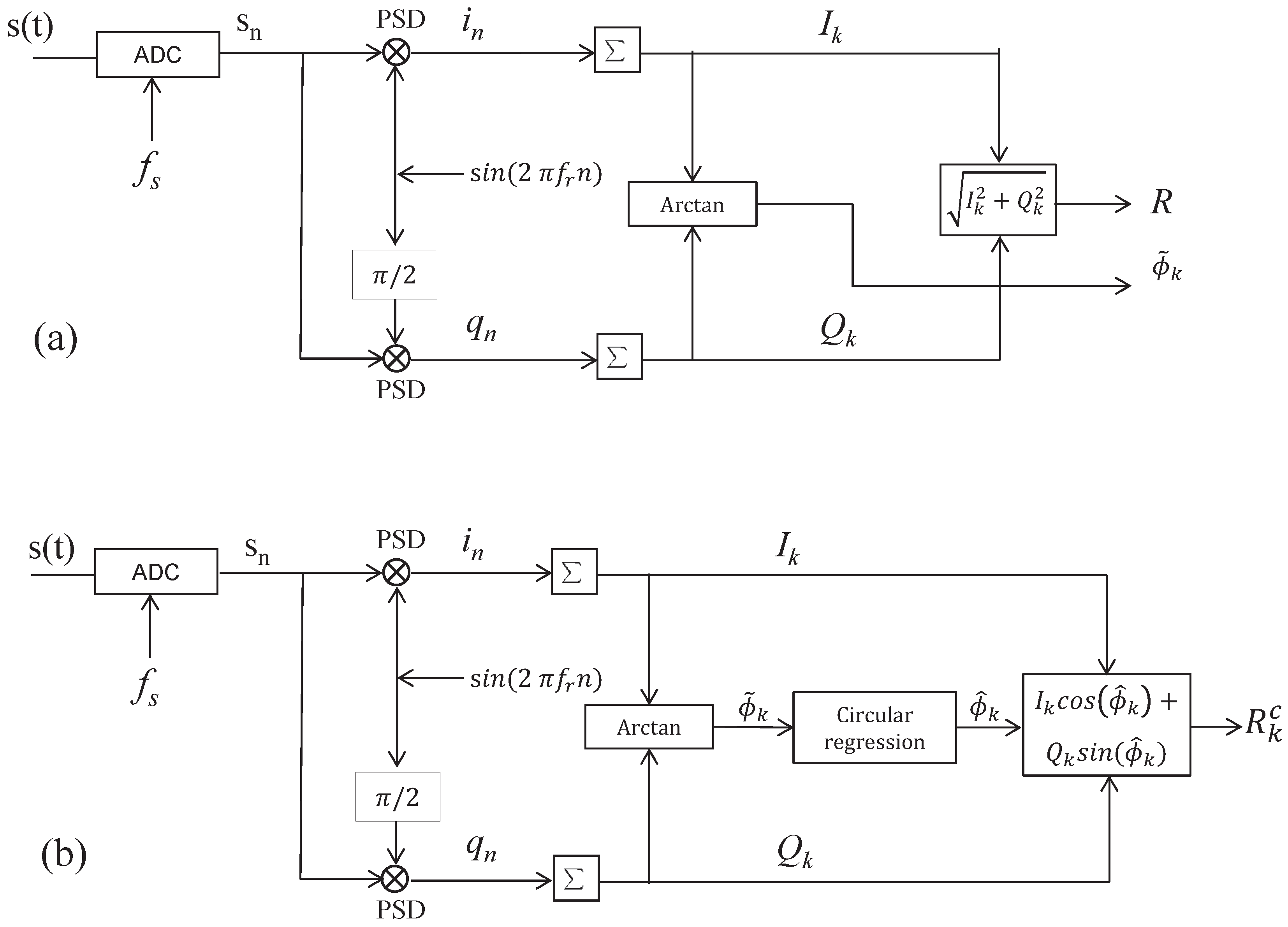
2. Digital Signal Detection
- Whenwhere is a Rician noise. In this case, and the proposed approach is equivalent to the classical dual-phase approach. The noise on the observed signal is distributed according to a Rician distribution. This approach is called incoherent detection (ID) in the rest of the article.
- WhenIn this case, is a Gaussian noise. This is the proposed approach. In this case the noise on the observed signal amplitude is distributed according to a Gaussian distribution. This approach is called coherent detection (CD).
3. Circular Regression
4. Experimental Assessments
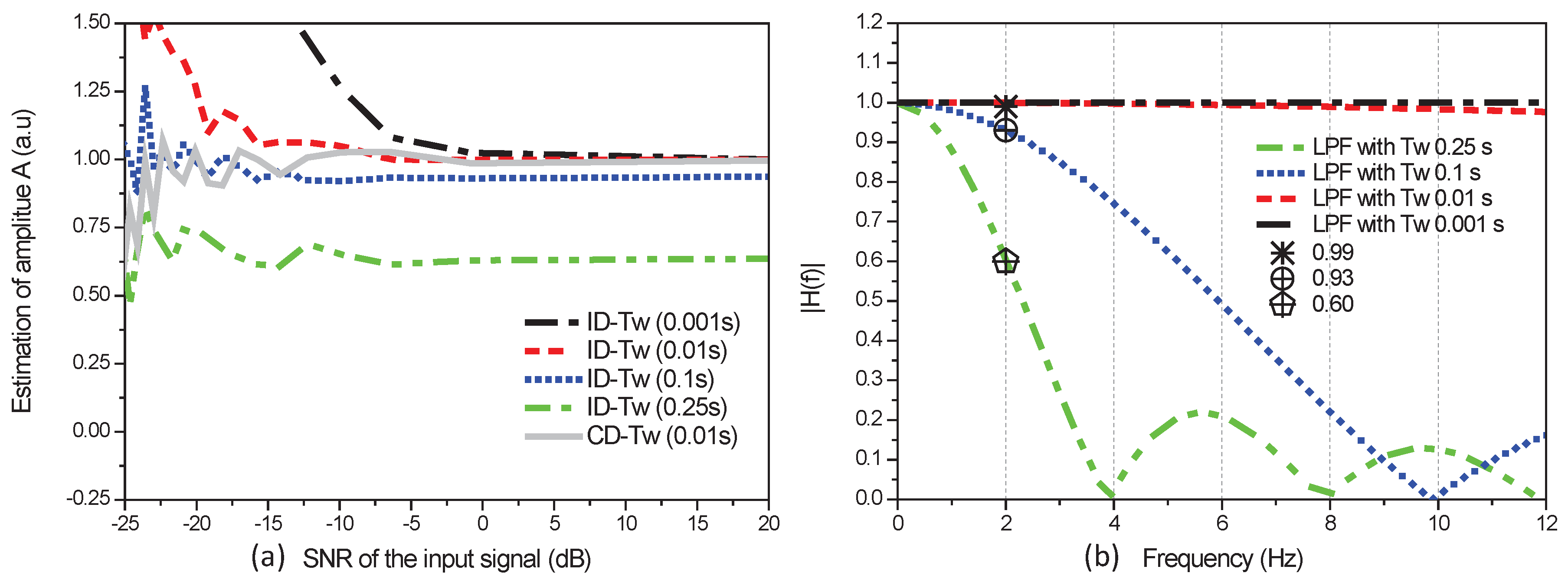
4.1. Simulation Assessment Using Synthetic Data
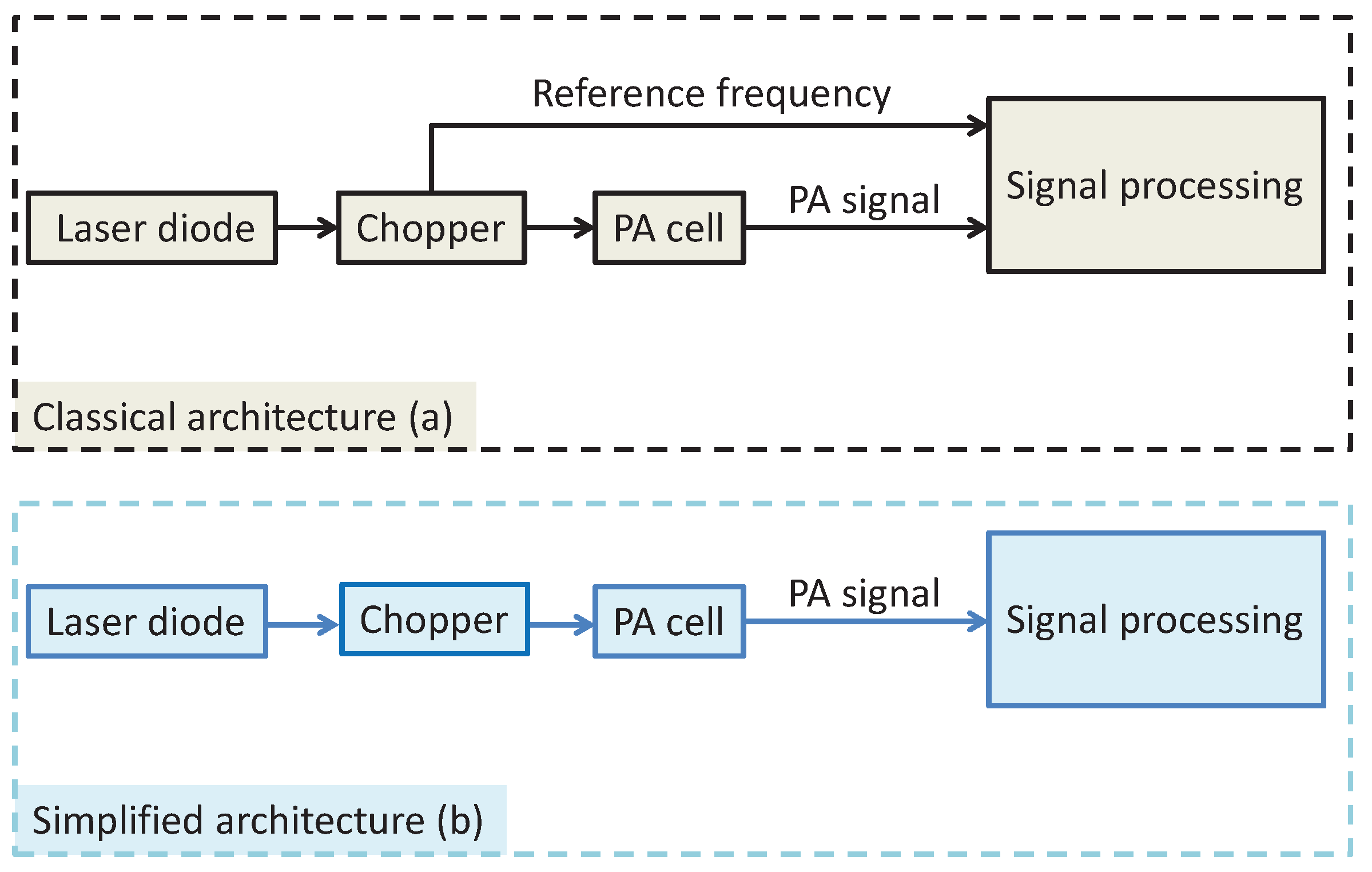
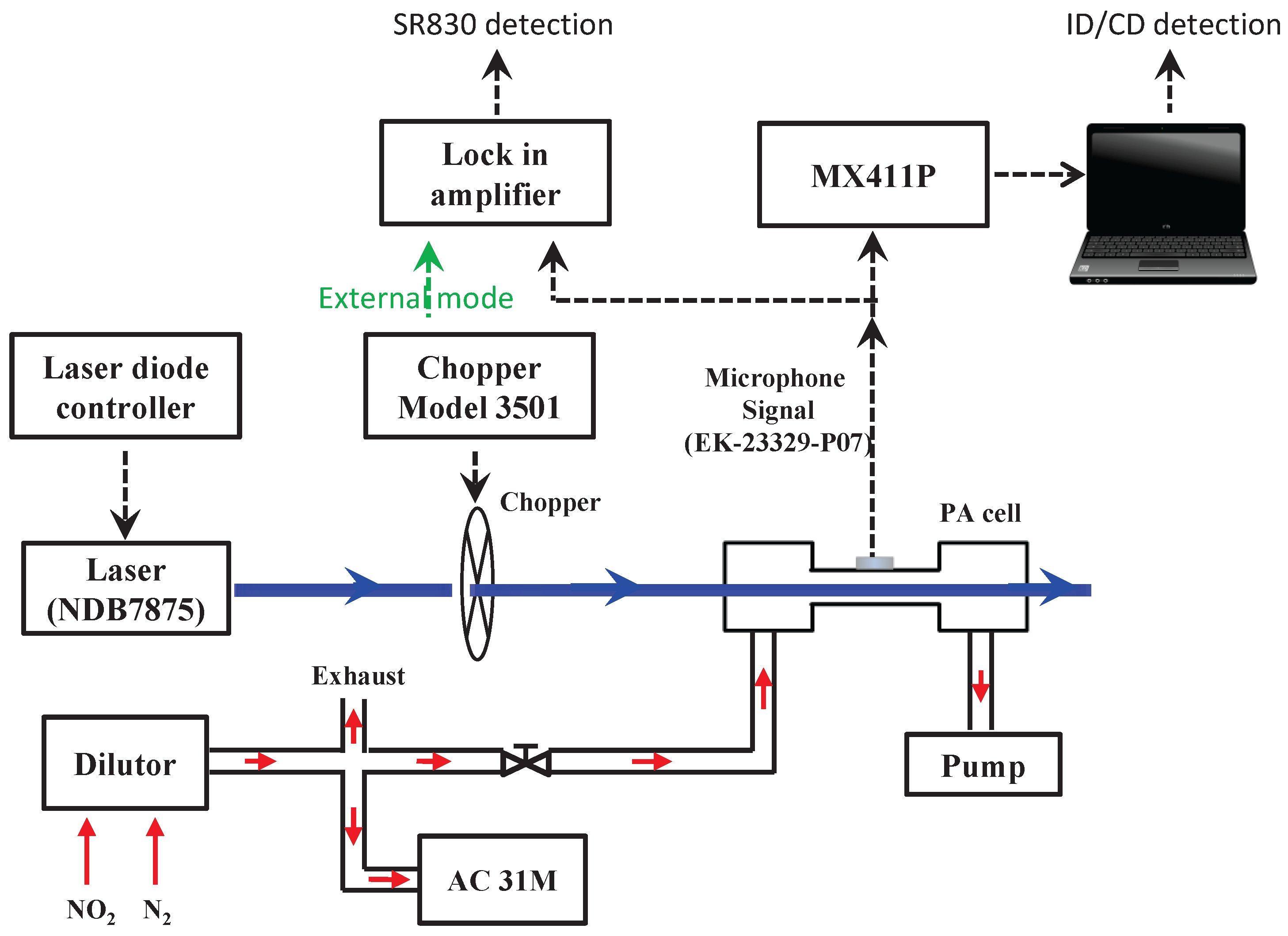
4.2. Application to High-Sensitivity and Accurate Measurements of NO at ppbv Concentration Level in the Environment
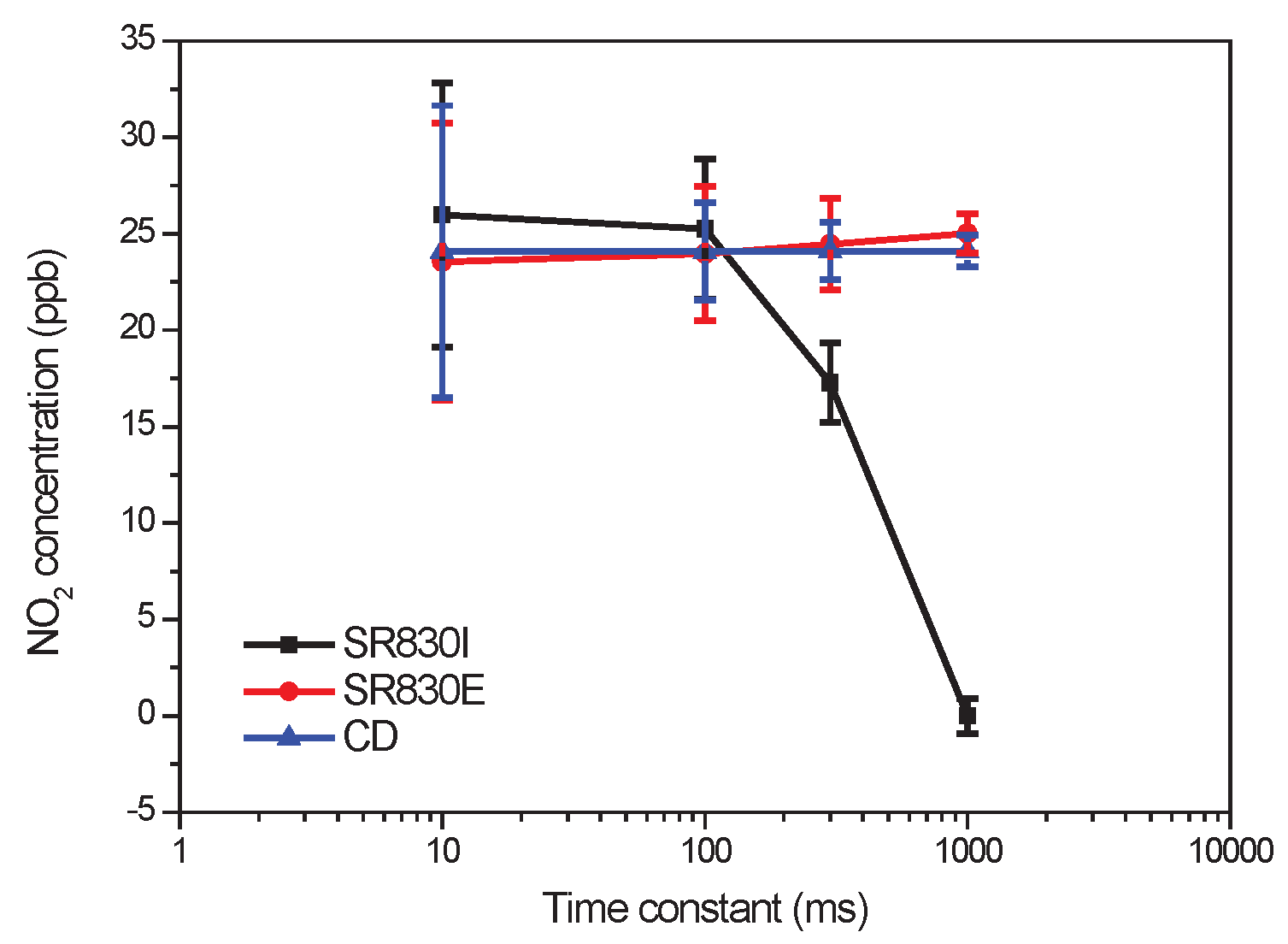
4.3. Comparison Measurements with Commercial LIA
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Masciotti, J.; Lasker, J.; Hielscher, A. Digital lock in detection for discrimi-nating multiple modulation frequency with high accuracy and computational efficiency. IEEE Trans. Instrum. Meas. 2008, 57, 182–189. [Google Scholar] [CrossRef]
- SRS. About Lock-In Amplifiers. Available online: http://www.thinksrs.com/downloads/PDFs/ApplicationNotes/AboutLIAs.pdf (accessed on 20 September 2017).
- Barragan, L.A.; Artigas, J.I.; Alonso, R.; Villuendas, F. A modular low cost digital signal processor-based lock-in card for measuring optical attenuation. Rev. Sci. Instrum. 2001, 72, 247–251. [Google Scholar] [CrossRef]
- Burdett, R. Handbook of Measuring System Design; John Wiley and Sons Inc.: Chichester, UK, 2005. [Google Scholar]
- Son, H.H.; Jung, I.I.; Hong, N.P.; Kim, D.G.; Choi, Y.W. Signal detection technique utilising ‘lock-in’ architecture using 2 ωc harmonic frequency for portable sensors. Electron. Lett. 2010, 46, 891–892. [Google Scholar] [CrossRef]
- Barone, F.; Calloni, E.; DiFiore, L.; Grado, A.; Milano, L.; Russo, G. High performance modular digital lock in amplifier. Rev. Sci. Instrum. 1995, 66. [Google Scholar] [CrossRef]
- Hu, A.; Chodavarapu, V. CMOS Optoelectronic Lock-In Amplifier With Integrated Phototransistor Array. IEEE Trans. Biomed. Circuits Syst. 2010, 5, 274–280. [Google Scholar] [CrossRef] [PubMed]
- De Marcellis, A.; Ferri, G.; D’Amico, A.; Di Natale, C.; Martinelli, E. A Fully-Analog Lock-In Amplifier with Automatic Phase Alignment for Accurate Measurements of ppb Gas Concentrations. IEEE Sens. J. 2012, 12, 1377–1383. [Google Scholar] [CrossRef]
- Macias-Bobadilla, G.; Rodríguez-Reséndiz, J.; Mota-Valtierra, G.; Soto-Zarazúa, G.; Méndez-Loyola, M.; Garduño-Aparicio, M. Dual-Phase Lock-In Amplifier Based on FPGA for Low-Frequencies Experiments. Sensors 2016, 16, 379. [Google Scholar] [CrossRef] [PubMed]
- Sijbers, J.; den Dekker, A.J.; Scheunders, P.; Dyck, D.V. Maximum-likelihood estimation of Rician distribution parameters. IEEE Trans. Med. Imaging 1998, 17, 357–361. [Google Scholar] [CrossRef] [PubMed]
- Alonso, R.; Villuendas, F.; Borja, J.; Barragán, L.; Salinas, I. Low-cost, digital lock-in module with external reference for coating glass transmission/reflection spectrophotometer. Meas. Sci. Technol. 2003, 14, 551–557. [Google Scholar] [CrossRef]
- Kempter, R.; Leibold, C.; Buzsáki, G.; Diba, K.; Schmidt, R. Quantifying circular associations: Hippocampal phase precession. J. Neurosci. Methods 2012, 207, 113–124. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, K.; Jammalamadaka, S.R.; Vasudaven, M. Change-point problems for the von Mises distribution. J. Appl. Stat. 1999, 26, 423–434. [Google Scholar] [CrossRef]
- Sengupta, A.; Laha, A.K. A Bayesian analysis of the change-point problem for directional data. J. Appl. Stat. 2008, 35, 693–700. [Google Scholar] [CrossRef]
- Routtenberg, T.; Tabrikian, J. Bayesian Parameter Estimation Using Periodic Cost Functions. IEEE Trans. Signal Process. 2012, 60, 1229–1240. [Google Scholar] [CrossRef]
- Jammalamadaka, S.R.; SenGupta, A. Topics in Circular Statistics; Series on Multivariate Analysis; World Scientific: Singapore, 2001; Volume 5, 336p. [Google Scholar]
- Mardia, K.; Jupp, P. Directional Statistics; Wiley Series in Probability and Statistics; John Wiley and Sons Inc.: Chichester, UK, 1999. [Google Scholar]
- Stienne, G.; Reboul, S.; Azmani, M.; Choquel, J.B.; Benjelloun, M. GNSS dataless signal tracking with a delay semi-open loop and a phase open loop. Signal Process. 2013, 93, 1192–1209. [Google Scholar] [CrossRef]
- Stienne, G.; Reboul, S.; Azmani, M.; Choquel, J.; Benjelloun, M. A multi-temporal multi sensor circular fusion filter. Inform. Fusion 2014, 18, 86–100. [Google Scholar] [CrossRef]
- Marković, I.; Ćesić, J.; Petrović, I. Von Mises Mixture PHD Filter. IEEE Signal Process. Lett. 2015, 22, 2229–2233. [Google Scholar] [CrossRef]
- Kurz, G.; Gilitschenski, I.; Julier, S.; Hanebeck, U. Recursive Bingham filter for directional estimation involving 180 degree symmetry. J. Adv. Inform. Fusion 2014, 9, 90–105. [Google Scholar]
- Kurz, G.; Gilitschenski, I.; Hanebeck, U.D. Recursive Bayesian filtering in circular state spaces. IEEE Aerosp. Electron. Syst. Mag. 2016, 31, 70–87. [Google Scholar] [CrossRef]
- Hussin, A.G. Hypothesis Testing of Parameters for Ordinary Linear Circular Regression. Pak. J. Stat. Oper. Res. 2006, 2, 79–86. [Google Scholar] [CrossRef]
- Jona-Lasinio, G.; Gelfand, A.; Jona-Lasinio, M. Spatial analysis of wave direction using wrapped Gaussian processes. Ann. Appl. Stat. 2012, 6, 1478–1498. [Google Scholar] [CrossRef]
- Kucwaj, J.C.; Reboul, S.; Stienne, G.; Choquel, J.B.; Benjelloun, M. Circular Regression Applied to GNSS-R Phase Altimetry. Remote Sens. 2017, 9, 651. [Google Scholar] [CrossRef]
- Gould, A.L. A Regression Technique for Angular Variates. Biometrics 1969, 25, 683–700. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.A.; Wehrly, T.E. Some Angular-Linear Distributions and Related Regression Models. J. Am. Stat. Assoc. 1978, 73, 602–606. [Google Scholar] [CrossRef]
- Fisher, N.I.; Lee, A.J. Regression models for an angular response. Biometrics 1992, 48, 665–677. [Google Scholar] [CrossRef]
- Esmaieeli Sikaroudi, A.; Park, C. A Mixture of Linear-Linear Regression Models for Linear-Circular Regression. arXiv, 2016; arXiv:stat.ME/1611.00030. [Google Scholar]
- Miklós, A.; Hess, P.; Bozóki, Z. Application of acoustic resonators in photoacoustic trace gas analysis and metrology. Rev. Sci. Instrum. 2001, 72, 1937–1955. [Google Scholar] [CrossRef]
- Wang, G.; Yi, H.; Hubert, P.; Deguine, A.; Petitprez, D.; Maamary, R.; Fertein, E.; Rey, J.M.; Sigrist, M.W.; Chen, W. Filter-Free Measurements of Black Carbon Absorption Using Photoacoustic Spectroscopy. In Proceedings of the SPIE Quantum Sensing and Nano Electronics and Photonics XIV, San Francisco, CA, USA, 28 January–2 February 2017. [Google Scholar]



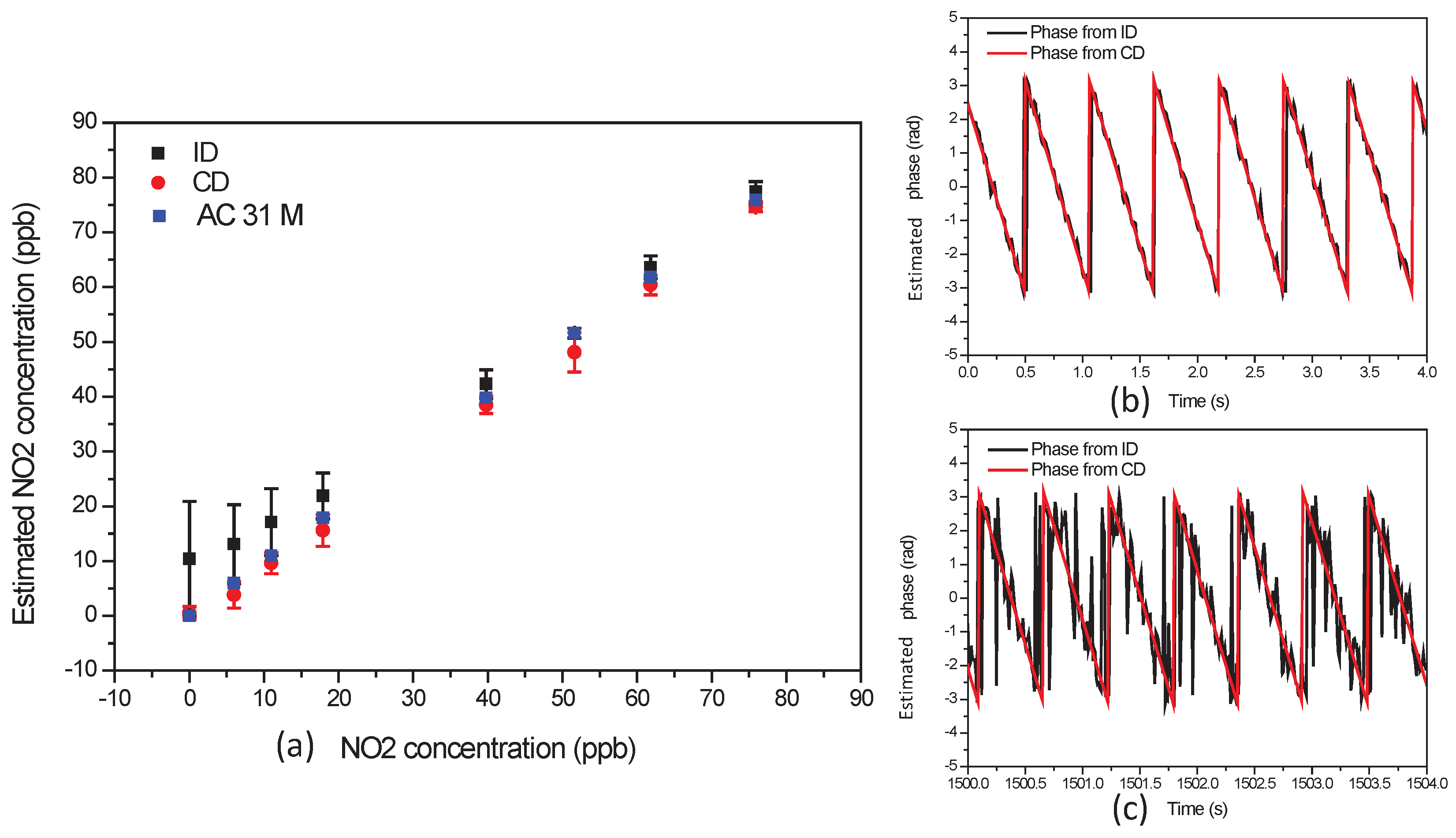

| (s) | 0.25 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 | 3.00 | 3.50 | 4.00 |
| SNR (dB) | −14 | −19 | −22 | −23 | −24 | −24 | −24 | −24 | −24 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Reboul, S.; Choquel, J.-B.; Fertein, E.; Chen, W. Circular Regression in a Dual-Phase Lock-In Amplifier for Coherent Detection of Weak Signal. Sensors 2017, 17, 2615. https://doi.org/10.3390/s17112615
Wang G, Reboul S, Choquel J-B, Fertein E, Chen W. Circular Regression in a Dual-Phase Lock-In Amplifier for Coherent Detection of Weak Signal. Sensors. 2017; 17(11):2615. https://doi.org/10.3390/s17112615
Chicago/Turabian StyleWang, Gaoxuan, Serge Reboul, Jean-Bernard Choquel, Eric Fertein, and Weidong Chen. 2017. "Circular Regression in a Dual-Phase Lock-In Amplifier for Coherent Detection of Weak Signal" Sensors 17, no. 11: 2615. https://doi.org/10.3390/s17112615
APA StyleWang, G., Reboul, S., Choquel, J.-B., Fertein, E., & Chen, W. (2017). Circular Regression in a Dual-Phase Lock-In Amplifier for Coherent Detection of Weak Signal. Sensors, 17(11), 2615. https://doi.org/10.3390/s17112615







