Theoretical Methods for Assessing the Density of Protein Nanodroplets
Abstract
1. Introduction
2. Results
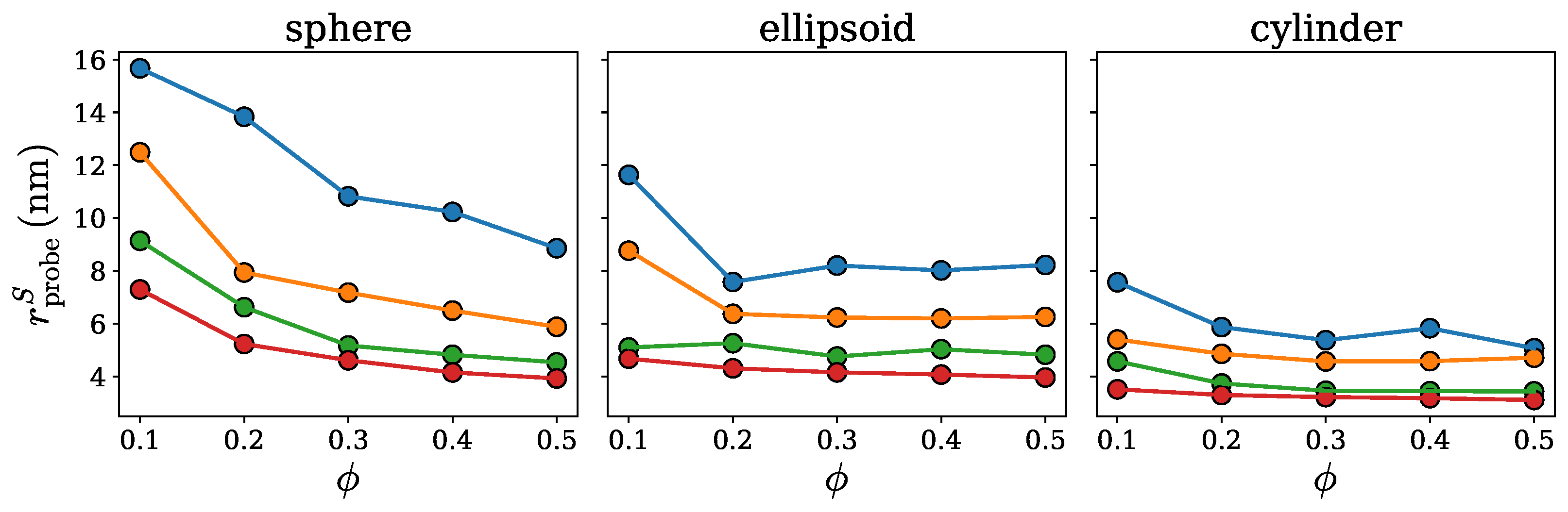
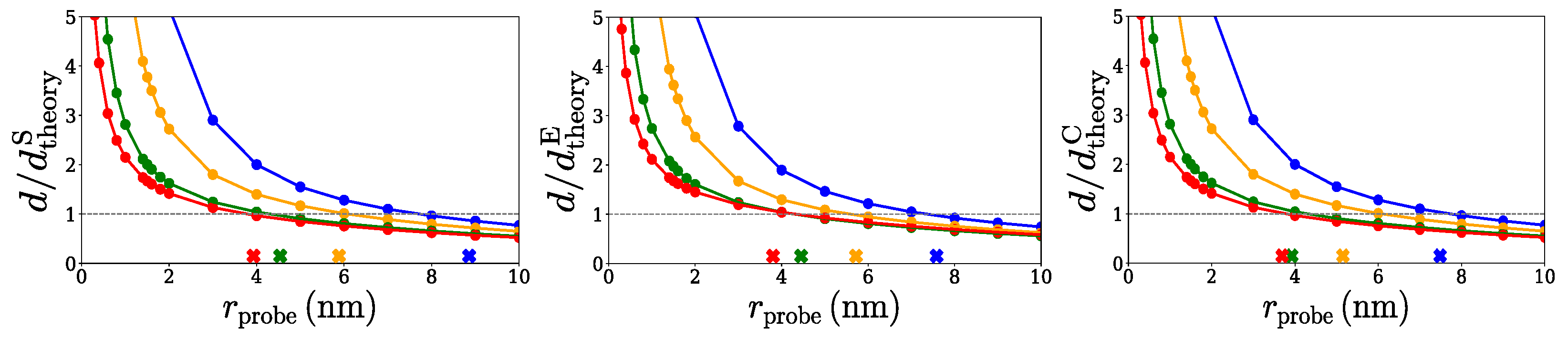
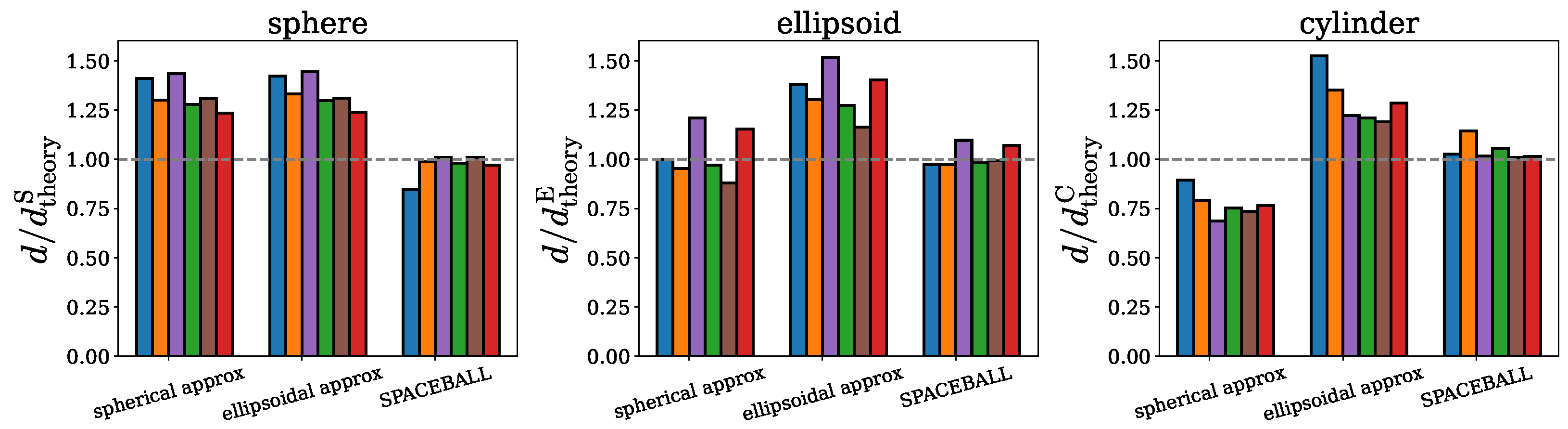
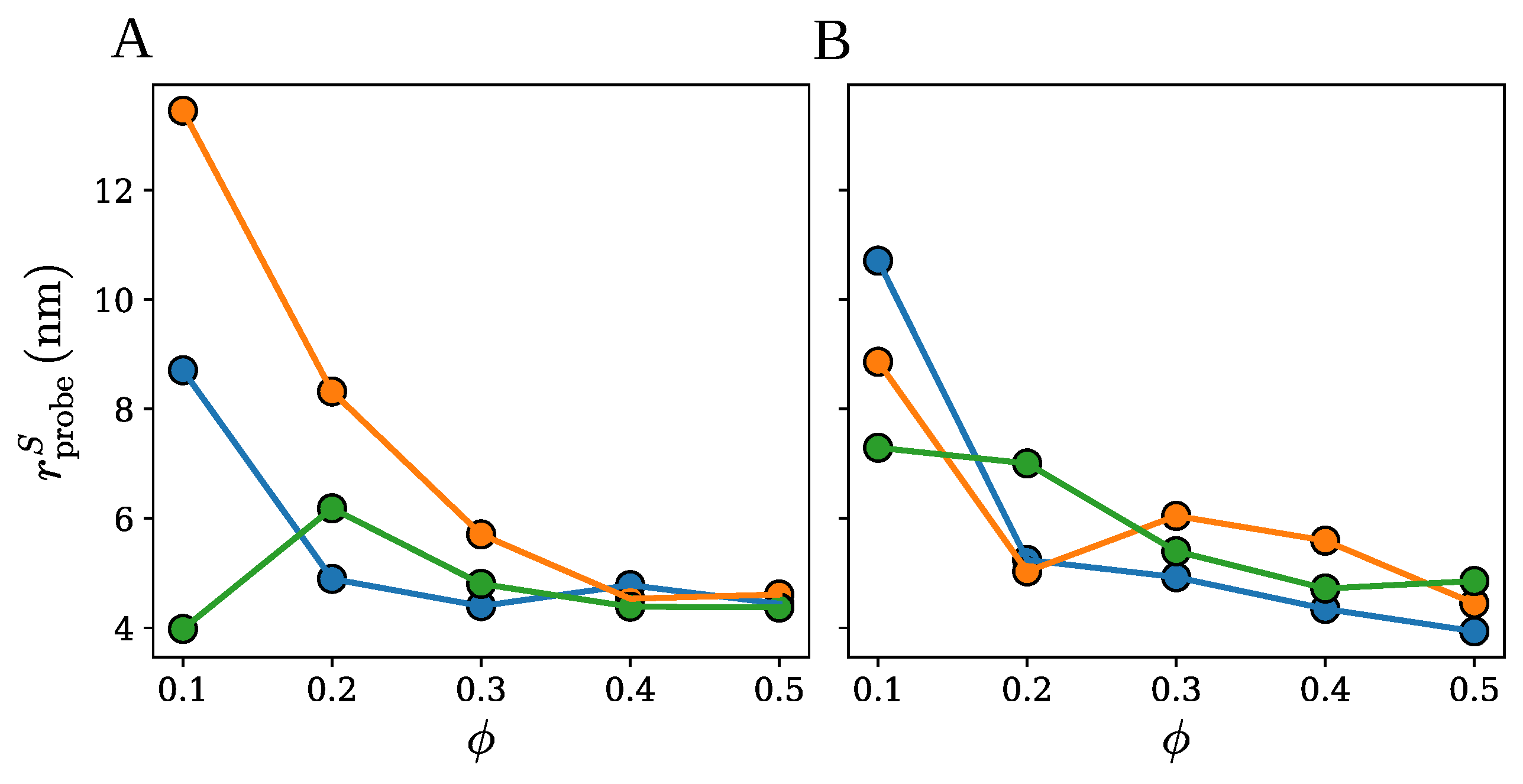
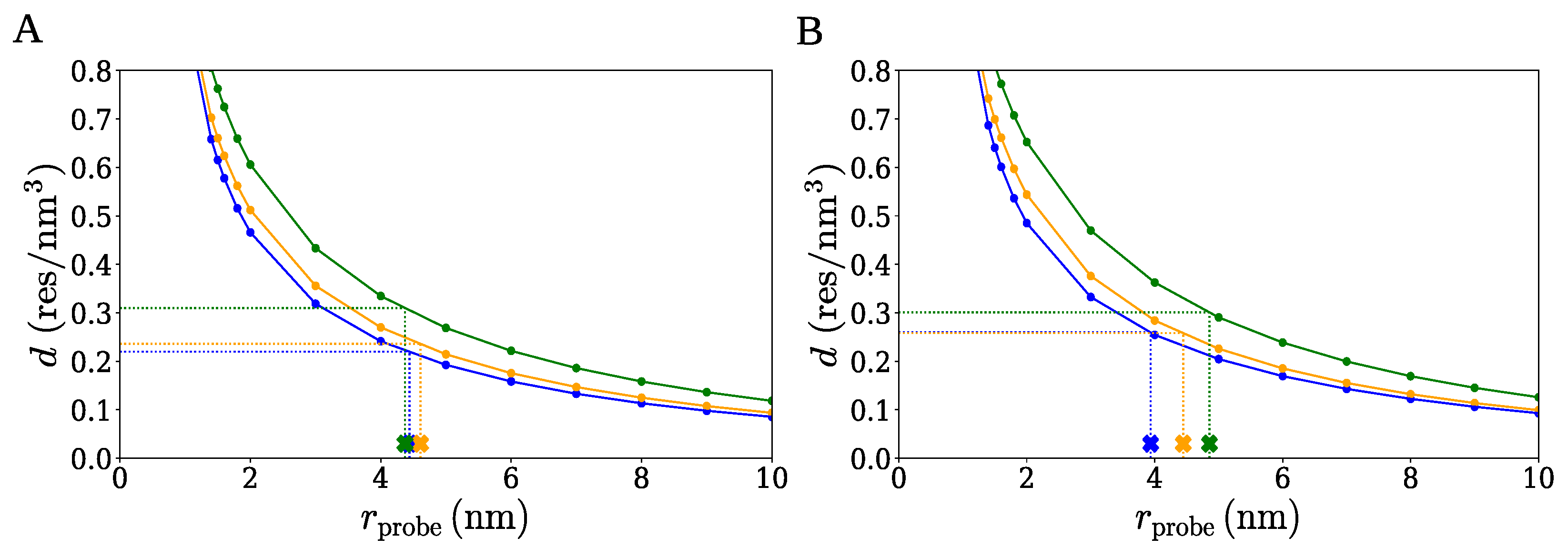
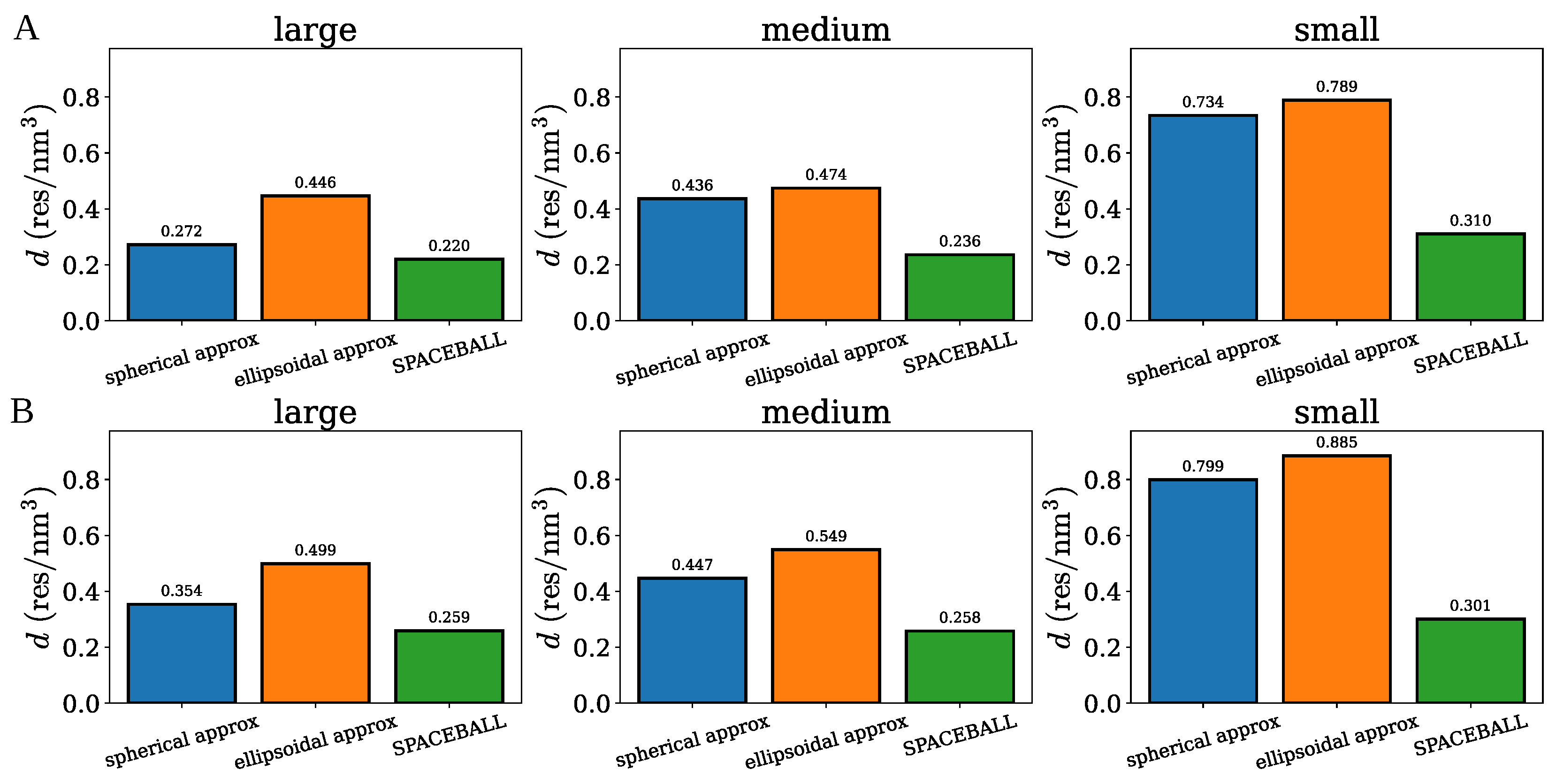
2.1. Spherical Approximation
2.2. Ellipsoidal Approximation
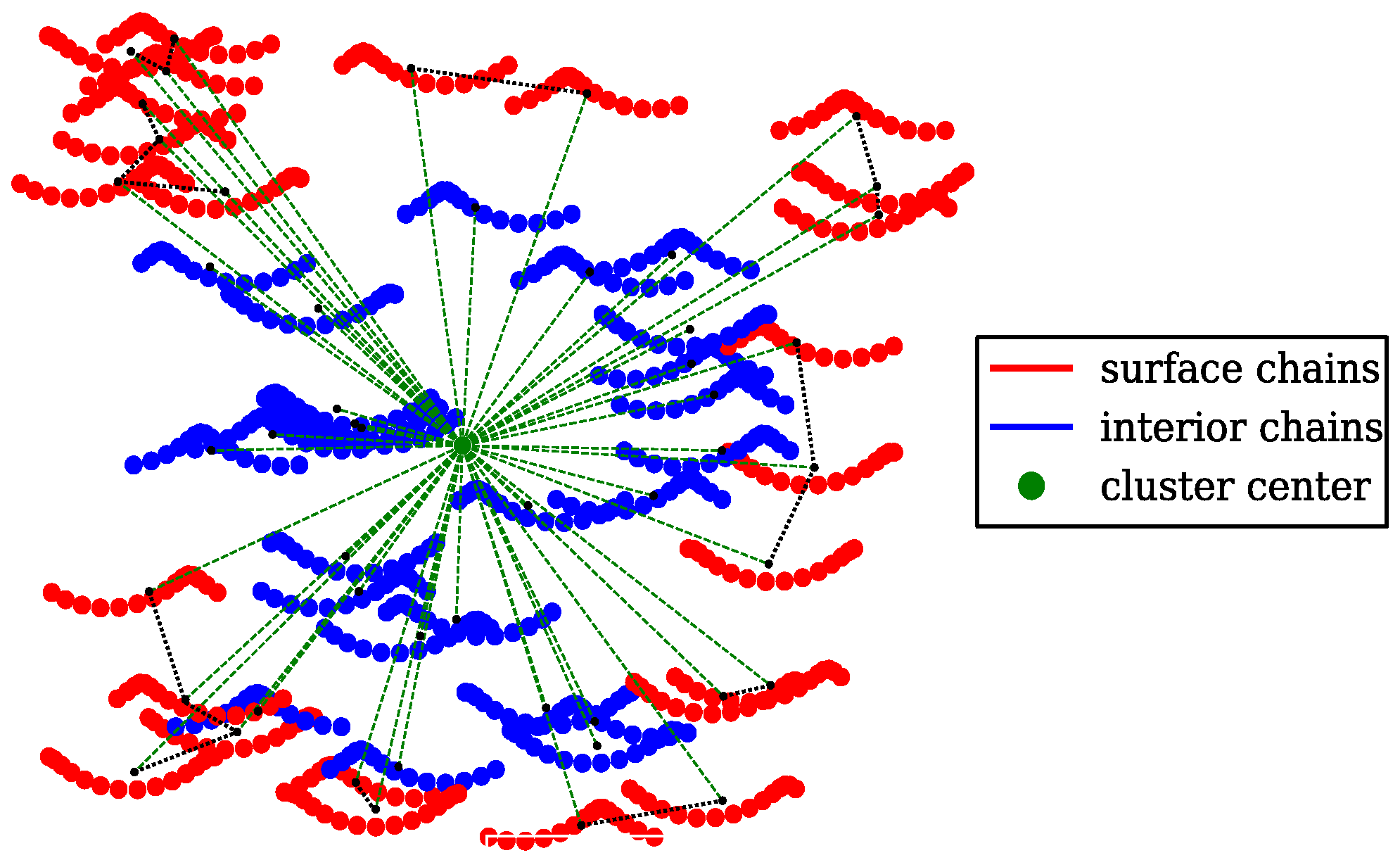
2.3. SPACEBALL
3. Discussion
4. Materials and Methods
4.1. MD Simulations
4.2. Cluster Analysis of the Coarse-Grained MD Trajectories
4.3. Generation of Spherical, Ellipsoidal, and Cylindrical Clusters
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Boeynaems, S.; Alberti, S.; Fawzi, N.L.; Mittag, T.; Polymenidou, M.; Rousseau, F.; Schymkowitz, J.; Shorter, J.; Wolozin, B.; Van Den Bosch, L.; et al. Protein phase separation: A new phase in cell biology. Trends Cell Biol. 2018, 28, 420–435. [Google Scholar] [CrossRef]
- Alberti, S.; Dormann, D. Liquid–liquid phase separation in disease. Annu. Rev. Genet. 2019, 53, 171–194. [Google Scholar] [CrossRef] [PubMed]
- Banani, S.F.; Lee, H.O.; Hyman, A.A.; Rosen, M.K. Biomolecular condensates: Organizers of cellular biochemistry. Nat. Rev. Mol. Cell Biol. 2017, 18, 285–298. [Google Scholar] [CrossRef] [PubMed]
- Weber, S.C. Evidence for and against liquid-liquid phase separation in the nucleus. Non-Coding RNA 2019, 5, 50. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Yoo, J.; Do, S.; Hwang, D.S.; Park, Y.; Shin, Y. RNA-mediated demixing transition of low-density condensates. Nat. Commun. 2023, 14, 2425. [Google Scholar] [CrossRef]
- Arter, W.E.; Qi, R.; Erkamp, N.A.; Krainer, G.; Didi, K.; Welsh, T.J.; Acker, J.; Nixon-Abell, J.; Qamar, S.; Guillén-Boixet, J.; et al. Biomolecular condensate phase diagrams with a combinatorial microdroplet platform. Nat. Commun. 2022, 13, 7845. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Mitchison, T.J.; Hyman, A.A. Active liquid-like behavior of nucleoli determines their size and shape in Xenopus laevis oocytes. Proc. Natl. Acad. Sci. USA 2011, 108, 4334–4339. [Google Scholar] [CrossRef]
- Brangwynne, C.P.; Eckmann, C.R.; Courson, D.S.; Rybarska, A.; Hoege, C.; Gharakhani, J.; Jülicher, F.; Hyman, A.A. Germline P granules are liquid droplets that localize by controlled dissolution/condensation. Science 2009, 324, 1729–1732. [Google Scholar] [CrossRef]
- Elbaum-Garfinkle, S. Matter over mind: Liquid phase separation and neurodegeneration. J. Biol. Chem. 2019, 294, 7160–7168. [Google Scholar] [CrossRef]
- Gebauer, D.; Kellermeier, M.; Gale, J.D.; Bergström, L.; Cölfen, H. Pre-nucleation clusters as solute precursors in crystallisation. Chem. Soc. Rev. 2014, 43, 2348–2371. [Google Scholar] [CrossRef]
- Alert, R.; Tierno, P.; Casademunt, J. Formation of metastable phases by spinodal decomposition. Nat. Commun. 2016, 7, 13067. [Google Scholar] [CrossRef] [PubMed]
- Yaragalla, S.; Mishra, R.K.; Thomas, S.; Kalarikkal, N.; Maria, H.J. Carbon-Based Nanofillers and Their Rubber Nanocomposites: Fundamentals and Applications; Elsevier: New York, NY, USA, 2019. [Google Scholar]
- Freire, E. Differential scanning calorimetry. Protein Stability And Folding: Theory and Practice; Humana: Totowa, NJ, USA, 1995; pp. 191–218. [Google Scholar]
- Guinier, A. X-Ray Crystallographic Technology; Hilger and Watts: London, UK, 1952. [Google Scholar]
- Stahlberg, H.; Walz, T. Molecular electron microscopy: State of the art and current challenges. ACS Chem. Biol. 2008, 3, 268–281. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A.P. CALPHAD (Calculation of Phase DIAGRAMS): A Comprehensive Guide; Elsevier: New York, NY, USA, 1998; Volume 1. [Google Scholar]
- Lukas, H.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Kattner, U.R. The CALPHAD method and its role in material and process development. Tecnol. Metal. Mater. Min. 2016, 13, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Schlick, T. Pursuing Laplace’s vision on modern computers. In Mathematical Approaches to Biomolecular Structure and Dynamics; Springer: New York, NY, USA, 1996; pp. 219–247. [Google Scholar]
- Van Mourik, T.; Gdanitz, R.J. A critical note on density functional theory studies on rare-gas dimers. J. Chem. Phys. 2002, 116, 9620–9623. [Google Scholar] [CrossRef]
- Ray, S.; Singh, N.; Kumar, R.; Patel, K.; Pandey, S.; Datta, D.; Mahato, J.; Panigrahi, R.; Navalkar, A.; Mehra, S.; et al. α-Synuclein aggregation nucleates through liquid–liquid phase separation. Nat. Chem. 2020, 12, 705–716. [Google Scholar] [CrossRef]
- Lashuel, H.A.; Overk, C.R.; Oueslati, A.; Masliah, E. The many faces of α-synuclein: From structure and toxicity to therapeutic target. Nat. Rev. Neurosci. 2013, 14, 38–48. [Google Scholar] [CrossRef]
- Pieri, L.; Madiona, K.; Bousset, L.; Melki, R. Fibrillar α-synuclein and huntingtin exon 1 assemblies are toxic to the cells. Biophys. J. 2012, 102, 2894–2905. [Google Scholar] [CrossRef]
- Ulmer, T.S.; Bax, A.; Cole, N.B.; Nussbaum, R.L. Structure and dynamics of micelle-bound human α-synuclein. J. Biol. Chem. 2005, 280, 9595–9603. [Google Scholar] [CrossRef]
- Ball, K.A.; Phillips, A.H.; Nerenberg, P.S.; Fawzi, N.L.; Wemmer, D.E.; Head-Gordon, T. Homogeneous and heterogeneous tertiary structure ensembles of amyloid-β peptides. Biochemistry 2011, 50, 7612–7628. [Google Scholar] [CrossRef]
- Cote, Y.; Delarue, P.; Scheraga, H.A.; Senet, P.; Maisuradze, G.G. From a highly disordered to a metastable state: Uncovering insights of α-synuclein. ACS Chem. Neurosci. 2018, 9, 1051–1065. [Google Scholar] [CrossRef]
- Ilie, I.M.; Nayar, D.; den Otter, W.K.; van der Vegt, N.F.; Briels, W.J. Intrinsic conformational preferences and interactions in α-synuclein fibrils: Insights from molecular dynamics simulations. J. Chem. Theory Comput. 2018, 14, 3298–3310. [Google Scholar] [CrossRef]
- Chwastyk, M.; Panek, E.A.; Malinowski, J.; Jaskólski, M.; Cieplak, M. Properties of cavities in biological structures—A survey of the Protein Data Bank. Front. Mol. Biosci. 2020, 7, 591381. [Google Scholar] [CrossRef]
- Mukherjee, S.; Sakunthala, A.; Gadhe, L.; Poudyal, M.; Sawner, A.S.; Kadu, P.; Maji, S.K. Liquid-liquid phase separation of α-synuclein: A new mechanistic insight for α-synuclein aggregation associated with Parkinson’s disease pathogenesis. J. Mol. Biol. 2023, 435, 167713. [Google Scholar] [CrossRef]
- Khare, S.D.; Chinchilla, P.; Baum, J. Multifaceted interactions mediated by intrinsically disordered regions play key roles in alpha synuclein aggregation. Curr. Opin. Struct. Biol. 2023, 80, 102579. [Google Scholar] [CrossRef]
- Sawner, A.S.; Ray, S.; Yadav, P.; Mukherjee, S.; Panigrahi, R.; Poudyal, M.; Patel, K.; Ghosh, D.; Kummerant, E.; Kumar, A.; et al. Modulating α-synuclein liquid–liquid phase separation: Published as part of the Biochemistry virtual special issue “Protein Condensates”. Biochemistry 2021, 60, 3676–3696. [Google Scholar] [CrossRef]
- Sternke-Hoffmann, R.; Sun, X.; Menzel, A.; Pinto, M.D.S.; Venclovaite, U.; Wördehoff, M.; Hoyer, W.; Zheng, W.; Luo, J. Phase Separation and Aggregation of Synuclein Diverge at Different Salt Conditions. Adv. Sci. 2024, 11, 2308279. [Google Scholar] [CrossRef]
- Ziaunys, M.; Sulskis, D.; Veiveris, D.; Kopustas, A.; Snieckute, R.; Mikalauskaite, K.; Sakalauskas, A.; Tutkus, M.; Smirnovas, V. Liquid–liquid phase separation of alpha-synuclein increases the structural variability of fibrils formed during amyloid aggregation. FEBS J. 2024, 291, 4522–4538. [Google Scholar] [CrossRef]
- Dada, S.T.; Hardenberg, M.C.; Toprakcioglu, Z.; Mrugalla, L.K.; Cali, M.P.; McKeon, M.O.; Klimont, E.; Michaels, T.C.; Knowles, T.P.; Vendruscolo, M. Spontaneous nucleation and fast aggregate-dependent proliferation of α-synuclein aggregates within liquid condensates at neutral pH. Proc. Natl. Acad. Sci. USA 2023, 120, e2208792120. [Google Scholar] [CrossRef]
- Siegert, A.; Rankovic, M.; Favretto, F.; Ukmar-Godec, T.; Strohäker, T.; Becker, S.; Zweckstetter, M. Interplay between tau and α-synuclein liquid–liquid phase separation. Protein Sci. 2021, 30, 1326–1336. [Google Scholar] [CrossRef]
- Chwastyk, M.; Jaskolski, M.; Cieplak, M. Structure-based analysis of thermodynamic and mechanical properties of cavity-containing proteins–case study of plant pathogenesis-related proteins of class 10. FEBS J. 2014, 281, 416–429. [Google Scholar] [CrossRef]
- Pham, D.Q.H.; Anila, M.M.; Chwastyk, M. Clustering-based Method for Constructing the Phase Diagram of the van der Waals Model Fluid. Curr. Protein Pept. Sci. 2025; online ahead of print. [Google Scholar] [CrossRef]
- Blas, F.J.; MacDowell, L.G.; de Miguel, E.; Jackson, G. Vapor-liquid interfacial properties of fully flexible Lennard-Jones chains. J. Chem. Phys. 2008, 129, 144703. [Google Scholar] [CrossRef]
- Dignon, G.L.; Zheng, W.; Best, R.B.; Kim, Y.C.; Mittal, J. Relation between single-molecule properties and phase behavior of intrinsically disordered proteins. Proc. Natl. Acad. Sci. USA 2018, 115, 9929–9934. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Wasim, A.; Menon, S.; Mondal, J. Modulation of α-synuclein aggregation amid diverse environmental perturbation. eLife 2024, 13, RP95180. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics; Elsevier: New York, NY, USA, 2013. [Google Scholar]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Hénin, J.; Jiang, W.; et al. Scalable molecular dynamics on CPU and GPU architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Tanner, D.E.; Chan, K.Y.; Phillips, J.C.; Schulten, K. Parallel generalized Born implicit solvent calculations with NAMD. J. Chem. Theory Comput. 2011, 7, 3635–3642. [Google Scholar] [CrossRef]
- Mioduszewski, Ł.; Rozycki, B.; Cieplak, M. Pseudo-improper-dihedral model for intrinsically disordered proteins. J. Chem. Theory Comput. 2020, 16, 4726–4733. [Google Scholar] [CrossRef]
- Kim, Y.C.; Hummer, G. Coarse-grained models for simulations of multiprotein complexes: Application to ubiquitin binding. J. Mol. Biol. 2008, 375, 1416–1433. [Google Scholar] [CrossRef]
- Dignon, G.L.; Zheng, W.; Kim, Y.C.; Best, R.B.; Mittal, J. Sequence determinants of protein phase behavior from a coarse-grained model. PLoS Comput. Biol. 2018, 14, e1005941. [Google Scholar] [CrossRef]
- Różycki, B.; Mioduszewski, Ł.; Cieplak, M. Unbinding and unfolding of adhesion protein complexes through stretching: Interplay between shear and tensile mechanical clamps. Proteins Struct. Funct. Bioinform. 2014, 82, 3144–3153. [Google Scholar] [CrossRef] [PubMed]
- Chiu, Y.P.; Sun, Y.C.; Qiu, D.C.; Lin, Y.H.; Chen, Y.Q.; Kuo, J.C.; Huang, J.-R. Liquid-liquid phase separation and extracellular multivalent interactions in the tale of galectin-3. Nat. Commun. 2020, 11, 1229. [Google Scholar] [CrossRef]
- Benayad, Z.; von Bulow, S.; Stelzl, L.S.; Hummer, G. Simulation of FUS protein condensates with an adapted coarse-grained model. J. Chem. Theory Comput. 2020, 17, 525–537. [Google Scholar] [CrossRef]
- Chen, C.R.; Makhatadze, G.I. ProteinVolume: Calculating molecular van der Waals and void volumes in proteins. BMC Bioinform. 2015, 16, 101. [Google Scholar] [CrossRef] [PubMed]
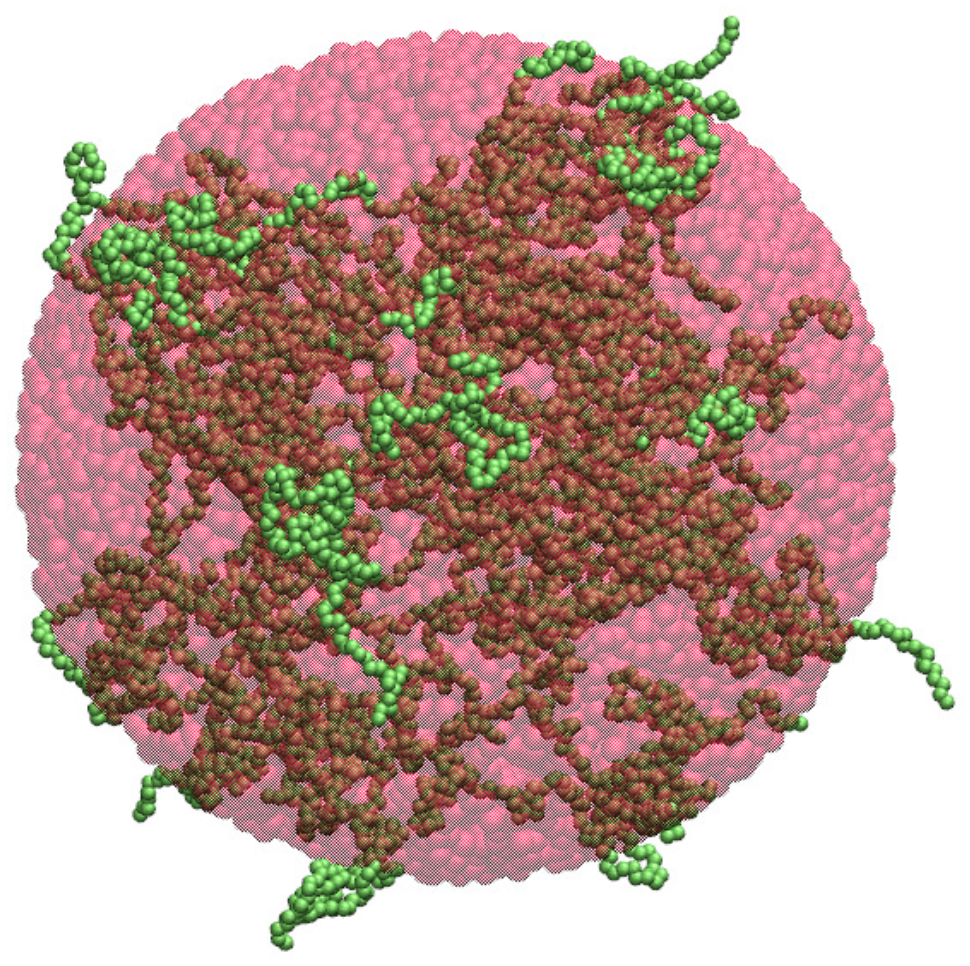
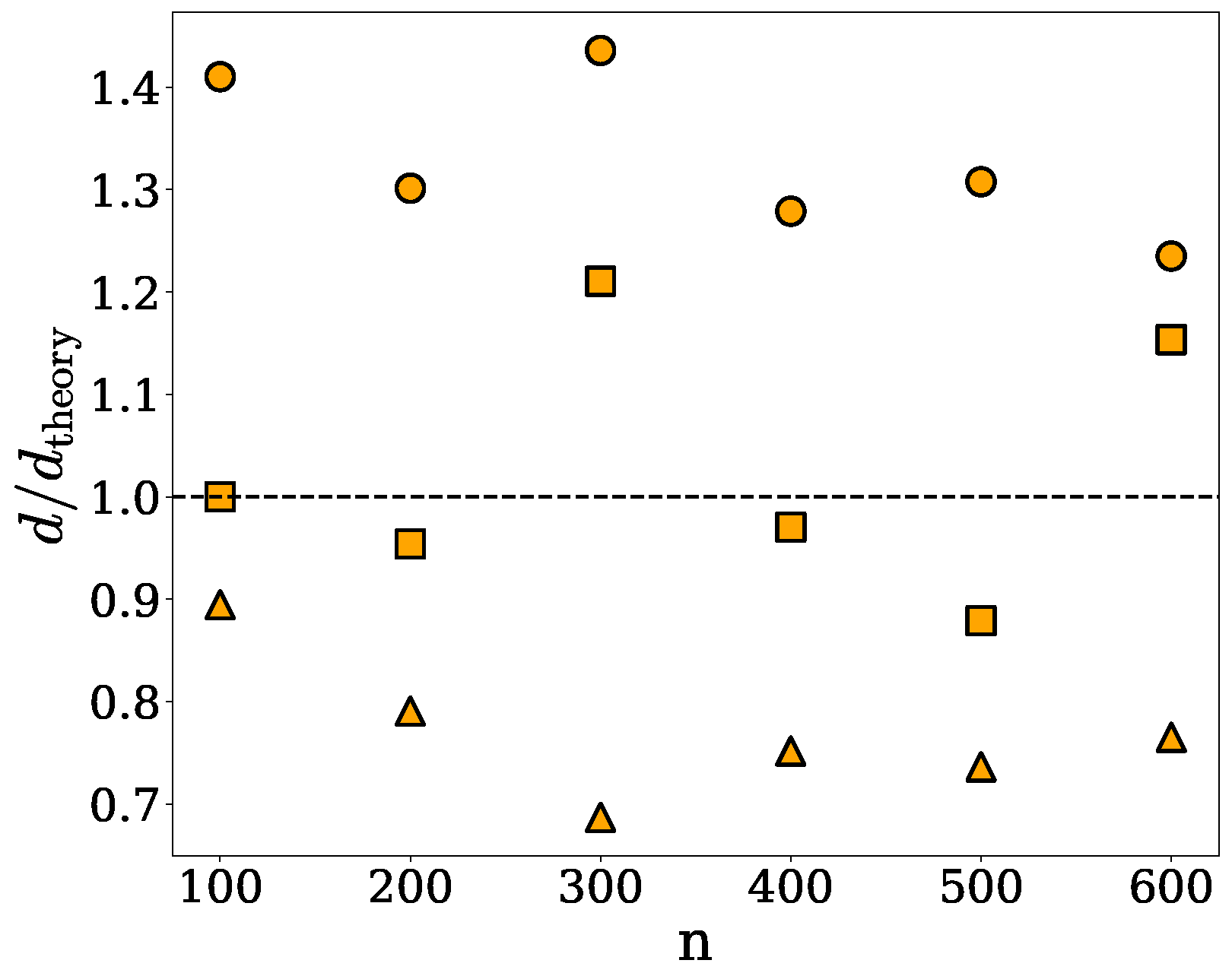
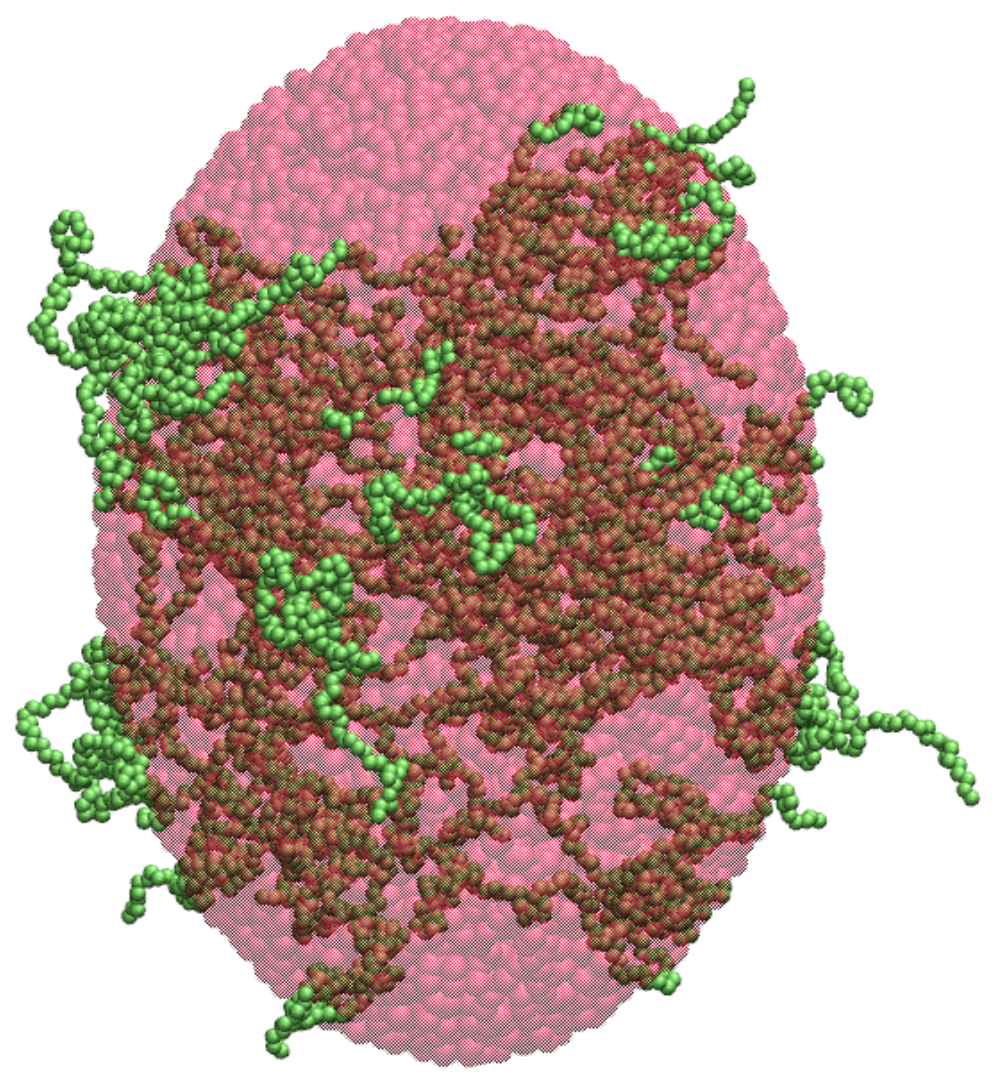
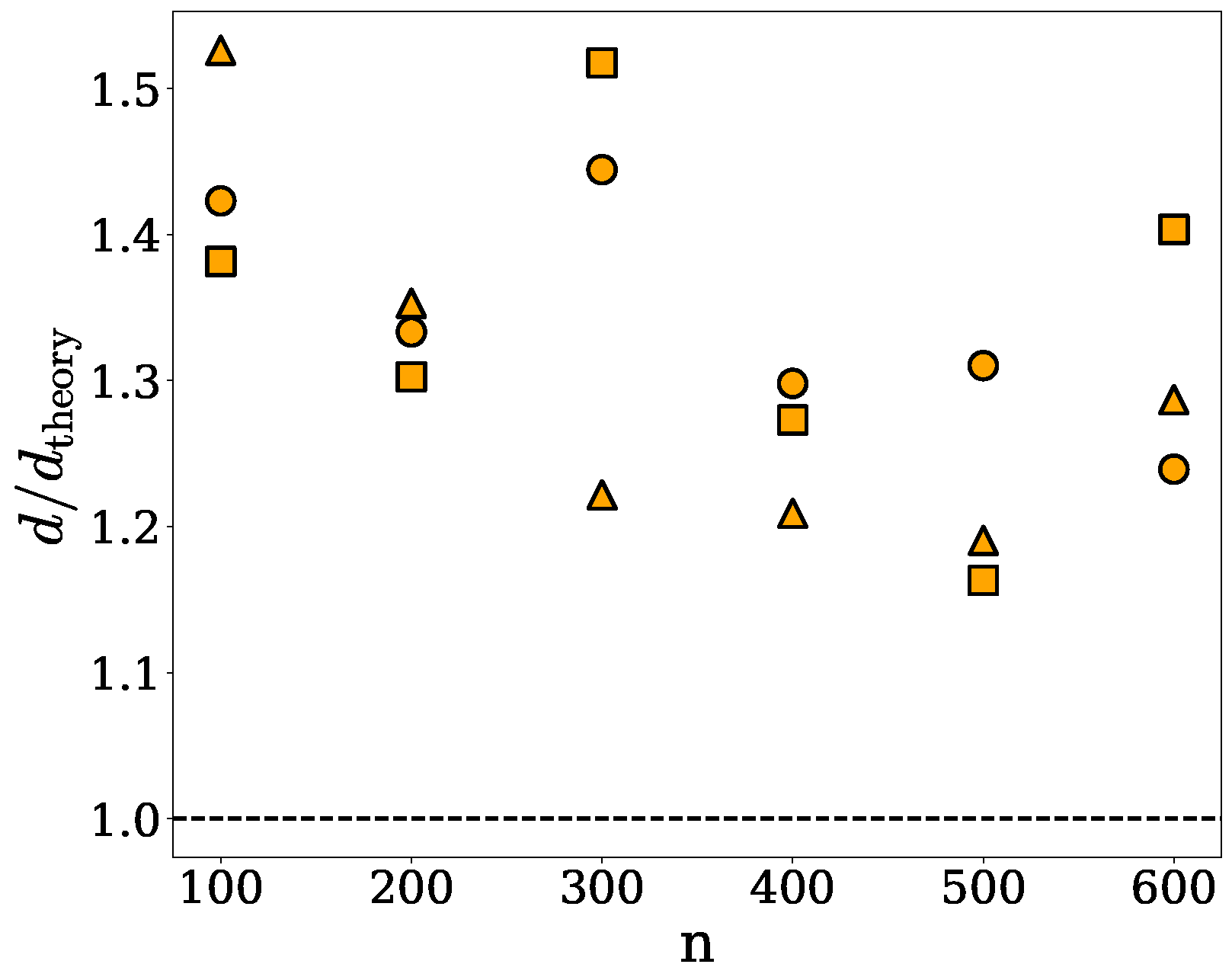
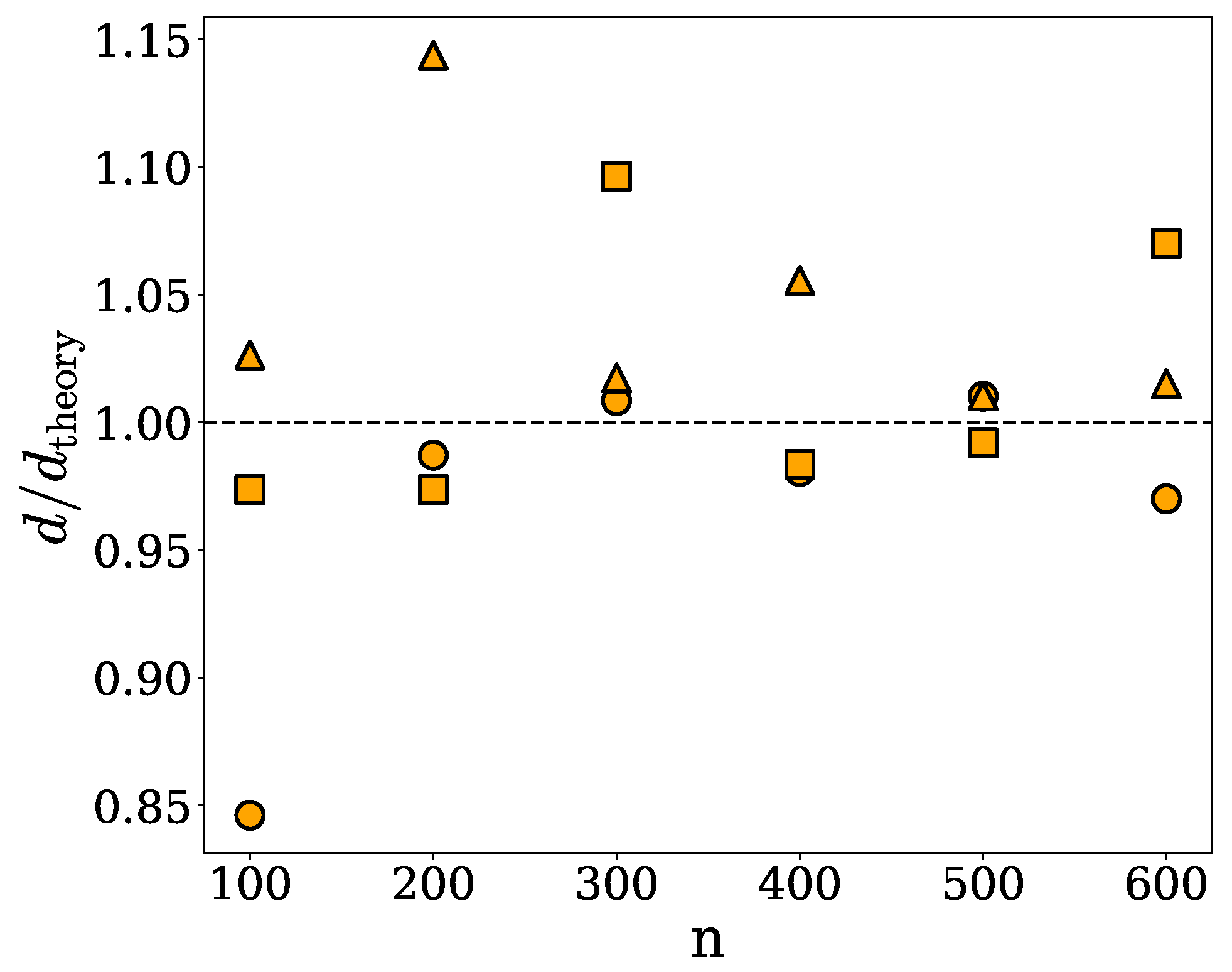


| n | (nm) | d (res/) | (res/) |
| 100 | 8.86 | 0.066 | 0.078 |
| 200 | 5.88 | 0.154 | 0.156 |
| 300 | 5.07 | 0.236 | 0.234 |
| 400 | 4.54 | 0.306 | 0.312 |
| 500 | 4.06 | 0.394 | 0.390 |
| 600 | 3.93 | 0.454 | 0.468 |
| n | (nm) | d (res/) | (res/) |
| 100 | 7.58 | 0.074 | 0.076 |
| 200 | 5.72 | 0.148 | 0.152 |
| 300 | 4.74 | 0.250 | 0.228 |
| 400 | 4.45 | 0.299 | 0.304 |
| 500 | 3.82 | 0.377 | 0.380 |
| 600 | 3.80 | 0.488 | 0.456 |
| n | (nm) | d (res/) | (res/) |
| 100 | 7.49 | 0.078 | 0.076 |
| 200 | 5.15 | 0.175 | 0.153 |
| 300 | 4.68 | 0.234 | 0.230 |
| 400 | 3.92 | 0.323 | 0.306 |
| 500 | 3.95 | 0.387 | 0.383 |
| 600 | 3.69 | 0.467 | 0.460 |
| Cluster Set | Cluster Extension | (nm) | d (res/) |
|---|---|---|---|
| A | large | 4.37 | 0.220 |
| medium | 4.61 | 0.236 | |
| small | 4.44 | 0.310 | |
| B | large | 4.86 | 0.259 |
| medium | 4.45 | 0.258 | |
| small | 3.94 | 0.301 |
| Temperature T () | Box Length L (nm) | Simulation Time (s) |
|---|---|---|
| 0.45 | 18.5 | 481 |
| 0.50 | 20.6 | 487 |
| 1.20 | 26.1 | 313 |
| Cluster Set | Cluster Extension | (nm) | (nm) | T () |
|---|---|---|---|---|
| A | large | 14.2 | 58.6 | 1.2 |
| medium | 12.1 | 44.3 | 0.5 | |
| small | 10.2 | 36.7 | 0.45 | |
| B | large | 13 | 52.3 | 1.2 |
| medium | 12 | 44.3 | 0.5 | |
| small | 9.9 | 38.7 | 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anila, M.M.; Wojciechowski, M.; Chwastyk, M.; Różycki, B. Theoretical Methods for Assessing the Density of Protein Nanodroplets. Int. J. Mol. Sci. 2025, 26, 8631. https://doi.org/10.3390/ijms26178631
Anila MM, Wojciechowski M, Chwastyk M, Różycki B. Theoretical Methods for Assessing the Density of Protein Nanodroplets. International Journal of Molecular Sciences. 2025; 26(17):8631. https://doi.org/10.3390/ijms26178631
Chicago/Turabian StyleAnila, Midhun Mohan, Michał Wojciechowski, Mateusz Chwastyk, and Bartosz Różycki. 2025. "Theoretical Methods for Assessing the Density of Protein Nanodroplets" International Journal of Molecular Sciences 26, no. 17: 8631. https://doi.org/10.3390/ijms26178631
APA StyleAnila, M. M., Wojciechowski, M., Chwastyk, M., & Różycki, B. (2025). Theoretical Methods for Assessing the Density of Protein Nanodroplets. International Journal of Molecular Sciences, 26(17), 8631. https://doi.org/10.3390/ijms26178631







