Next Article in Journal
Reactivity of Autologous Serum IgG to Gut Microbes in Pediatric Ulcerative Colitis
Previous Article in Journal
Systematic Analysis of Alternative Splicing in Transcriptomes of Multiple Sclerosis Patient Brain Samples
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 26
Issue 17
10.3390/ijms26178197
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Efficient pecG-n (n = 1, 2) Basis Sets for Ga, Ge, As, Se, and Br Specialized for the Geometry Optimization of Molecular Structures

by
Yuriy Yu. Rusakov
and
Irina L. Rusakova
*
A. E. Favorsky Irkutsk Institute of Chemistry, Siberian Branch of the Russian Academy of Sciences, Favorsky St. 1, 664033 Irkutsk, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2025, 26(17), 8197; https://doi.org/10.3390/ijms26178197
Submission received: 31 July 2025 / Revised: 19 August 2025 / Accepted: 20 August 2025 / Published: 23 August 2025
(This article belongs to the Section Physical Chemistry and Chemical Physics)
Browse Figures
Versions Notes

Abstract

In this paper, efficient pecG-n (n = 1, 2) basis sets for the 4th period p-elements, Ga, Ge, As, Se, and Br, specified for the optimization of molecular structures, are proposed. These basis sets were optimized via the property-energy consistent (PEC) algorithm directed to the minimization of molecular energy gradient relative to the bond lengths. The performance of the presented basis sets was tested against both theoretical and gas phase electron diffraction experimental reference data relative to the other popular basis sets that are usually employed for the geometry optimization of molecular structures. It was shown that the pecG-n (n = 1, 2) basis sets give equilibrium molecular structures of the quality that considerably surpasses the quality provided by the other commensurate basis sets.

1. Introduction

The quality of molecular equilibrium geometries is of crucial importance in quantum chemistry, as it usually represents a starting point for the calculation of any molecular property. At that, even a small alternation of the molecular equilibrium geometry, for example, a change in the bond lengths in thousandths of Å, can substantially affect different physicochemical properties calculated upon it [1,2]. Reducing the geometry factor error is very important for compounds containing 4th period p-elements, because these molecules have many areas of application in modern technology and an improper prediction of their properties, partially due to the geometry factor error, may substantially distort the knowledge about their usefulness in these areas. In particular, gallium, germanium, and arsenic are known to form efficient semiconductor materials [3,4,5,6,7,8,9,10], serving, for example, as quantum dots [11,12,13,14] with particular electronic and optical properties. Selenium and bromine compounds are of more interest in medicine and drug design [15,16,17,18,19,20,21], though, the use of selenium compounds gradually becomes more and more proliferated in many other areas, such as photoelectronics [22,23], solar cells technology [24], semiconductors industry [25,26], nanotechnology [27,28,29], synthesis of channelized porous materials [30,31], and some other.
At any level of electronic theory, the quality of the equilibrium geometry of a molecule can be substantially improved by increasing the basis set quality [32,33,34,35]. In common terms, this implies an increase in the cardinal number and extending the basis set functional space. In the case of 4th period atoms, such a basis set extension can be very significant as compared to the 1–3 period atoms, due to the fact that electrons of the 4th period elements occupy higher energy levels and have a greater spatial extent, requiring larger basis sets to accurately represent their behavior. Thus, the efficient basis sets for 4th period atoms that are capable of giving accurate results are of great interest in modern quantum chemical calculations.
There are many energy-optimized basis sets of different types and quality, including popular basis set series of Dunning [36], Jensen [37], People [38], Ahlrichs [39], that are used in the geometry optimization of molecules. The main criterion that was used in the optimization of such basis sets is the molecular or atomic energy minimum principle. Thus, these basis sets are naturally suitable for the energy calculations, and are surely applicable to the optimization of geometric parameters. However, the efficacy of the geometry optimization can substantially be increased by using specific exponents, optimized in such a way that a smaller number of them is required in order to obtain geometrical parameters of the same quality as those provided by large standard energy-optimized basis sets. Last year, we proposed a new approach to designing such exponents [1,2]. The idea consisted of using the property–energy consistent (PEC) algorithm [40] modified so as to minimize molecular energy gradient relative to the bond lengths consistent with the molecular energy minimization. Putting this idea into practice, we have already generated a series of the so-called geometry-oriented pecG-n (n = 1, 2) basis sets for hydrogen and p-elements of 2–3 period atoms [1,2]. These pecG-n basis sets turned out to be very effective in the calculation of equilibrium geometries of various compounds with atoms of 1–3 periods, giving geometrical parameters of a quality which is comparable with that provided by considerably larger energy-optimized basis sets.
Considering the utmost importance of the efficiency issue in predicting equilibrium geometries of compounds with 4th period p-elements and already proven usefulness of the pecG-n (n = 1, 2) basis sets for 1–3 period atoms, we propose herewith the application of our geometry-modified PEC approach to generating the geometry-oriented pecG-n (n = 1, 2) basis sets for Ga, Ge, As, Se, and Br. In the case of 4th period elements, the creation of basis sets by means of the PEC method is a much more demanding procedure than for the elements of previous periods, requiring, in particular, a more cautious approach to choosing fitting molecules and the usage of a modified algorithm adopted for dealing with large functional spaces. In this work, we have restricted the creation of the pecG-n basis set for 4th period atoms by considering particular five p-elements of the most active interest in many applications, while the development of the basis sets for d-elements of 4th period would require a considerably modified PEC approach due to their essentially different valence shell structure, therefore, this represents a separate demanding task worth accomplishing in the nearest future.

2. Results

The PEC approach is based on the property-energy consistent optimization of exponents for the chosen target property. In the case of geometry-oriented basis sets, the target property is the molecular energy gradient relative to the bond lengths of the selected bonds that involve a particular atom. In this respect, the PEC optimization represents finding a set of exponents that provide equilibrium bond lengths as close to the corresponding ideal equilibrium values as possible, under the condition that they give the lowest molecular energy. This can be expressed by Equations (1) and (2) as follows:
Δ ~ = 1 N b o n d ∑ i = 1 N b o n d L ~ i − L i i d e a l → m i n
E ~ t o t = 1 N b o n d ∑ i = 1 N m o l E ~ i → m i n
In Equation (1), the Δ ~ represents a varying target function that is the mean absolute deviation of the N b o n d varying bond lengths ( L ~ i ) in the N m o l fitting molecules relative to the corresponding ideal bond lengths ( L i i d e a l ). Equation (2) introduces the energy-minimization principle that guarantees that found exponents not only provide the bond lengths within a desired range but also give the lowest possible energy at that. In general, the PEC algorithm can be thought of as a nonlinear Monte-Carlo-based optimization problem with multiple solutions that can be pictured as random walking on the surface of multidimensional exponential space aimed at finding an isoline of “ideal” values of bond lengths. All points (basis sets) of this isoline give the same “ideal” values, but different total molecular energies. Among those energies, the PEC method selects the basis set that provides the lowest of them. For more details, please, see our main paper on the PEC method [40], and all other, including those pertaining geometry-oriented basis sets [1,2] and the basis sets developed for different NMR properties [41,42,43,44,45,46].
In generating the pecG-n basis sets for the 4th period elements, we have used several fitting molecules per atom: CH3GaH2, Ga2H2, and Ga2H4 for Ga; Ge2H6, Ge2H4, and GeH3CH3 for Ge; As2H4, As2H2 and H2AsCH3 for As; Se2H2 and HSeCH3 for Se; Br2 and CH3Br for Br. The uncontracted structures of the first- and second-level pecG-n basis sets were chosen so as to be exactly the same as structures of Dunning’s basis sets for the 4th period elements of double- and triple-zeta quality: [36] (14s,11p,6d) and (20s,13p,9d,1f), respectively. The PEC optimization of the exponents for each atom was carried out resorting to the optimization of geometric structures of corresponding fitting molecules performed within the DFT(B97-2) [47,48] method. During the basis sets optimization, previously obtained pecG-n (n = 1, 2) basis sets in contracted form were used on hydrogen and carbon atoms.
The “ideal” equilibrium bond lengths were obtained at the DFT(B97-2)/cc-pV5Z level of theory. The cc-pV5Z basis set represents the basis set of the highest cardinal number for the 4th period atoms in the cc-pVXZ (X = D, T, Q, 5) hierarchy [36]. This basis set is very large in size (specifically for the 4th period atoms, it contains 104 basis functions and bears the following structure: [8s,7p,5d,3f,2g,1h]), which makes it a good reference point in any equilibrium geometry calculation. In particular, it was shown recently that the mean absolute percentage error (MAPE), estimated for the equilibrium bond lengths calculated at the DFT(B97-2) level with the cc-pV5Z basis set in a wide variety of molecules containing 1-3 period atoms, relative to the corresponding values obtained with the cc-pV6Z basis set, equals only to 0.01 % [2]. This indicates a negligible difference between the cc-pV5Z and cc-pV6Z basis sets and allows us to consider the cc-pV5Z basis set as the one giving practically meaningful converged values of equilibrium geometry parameters within the cc-pVXZ hierarchy. In addition, in the mentioned paper, we also showed that the B97-2 functional provides the smallest deviations from highly accurate coupled clusters singles and doubles model (CCSD) geometries when the cc-pV5Z basis set is used.
The obtained uncontracted pecG-n basis sets were contracted using the PEC method and general contraction scheme [49]. The contraction coefficients were varied so as to minimize the function Δ ~ (see Equation (1)) relative to the target bond lengths calculated with the uncontracted (for particular shells) pecG-n basis sets, under the energetic constraint (see Equation (2)). For more details, please see the contraction of the pecG-n basis sets for atoms of previous periods [1,2]. The final contracted structures of the pecG-1 and pecG-2 basis sets are the same as those of the cc-pVDZ and cc-pVTZ basis sets, being as follows: [5s,4p,2d] and [6s,5p,3d,1f], respectively.
The exponents and contraction coefficients for the pecG-n (n = 1, 2) basis sets are presented in the Supplementary Materials in Gaussian format.

3. Discussion

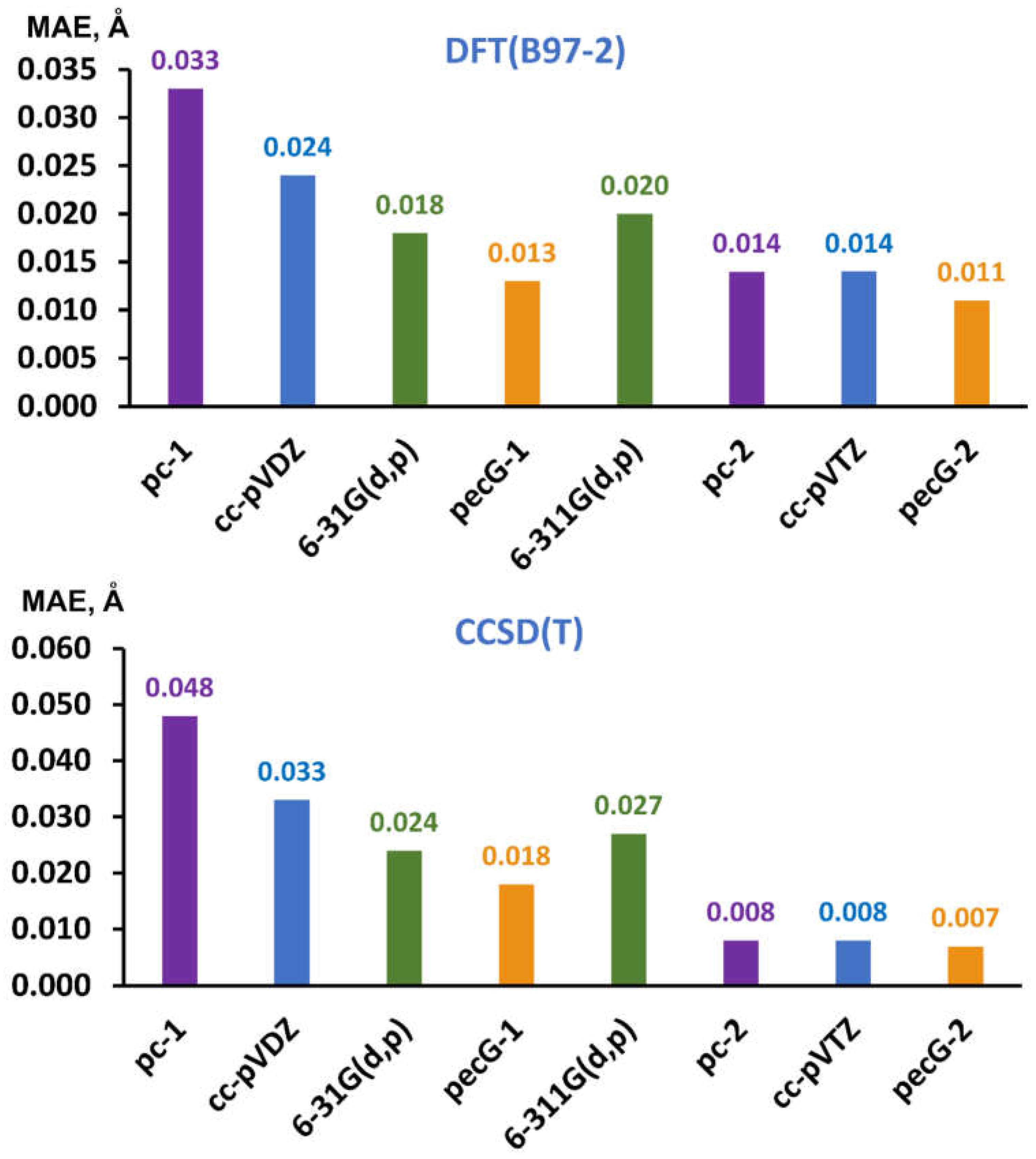
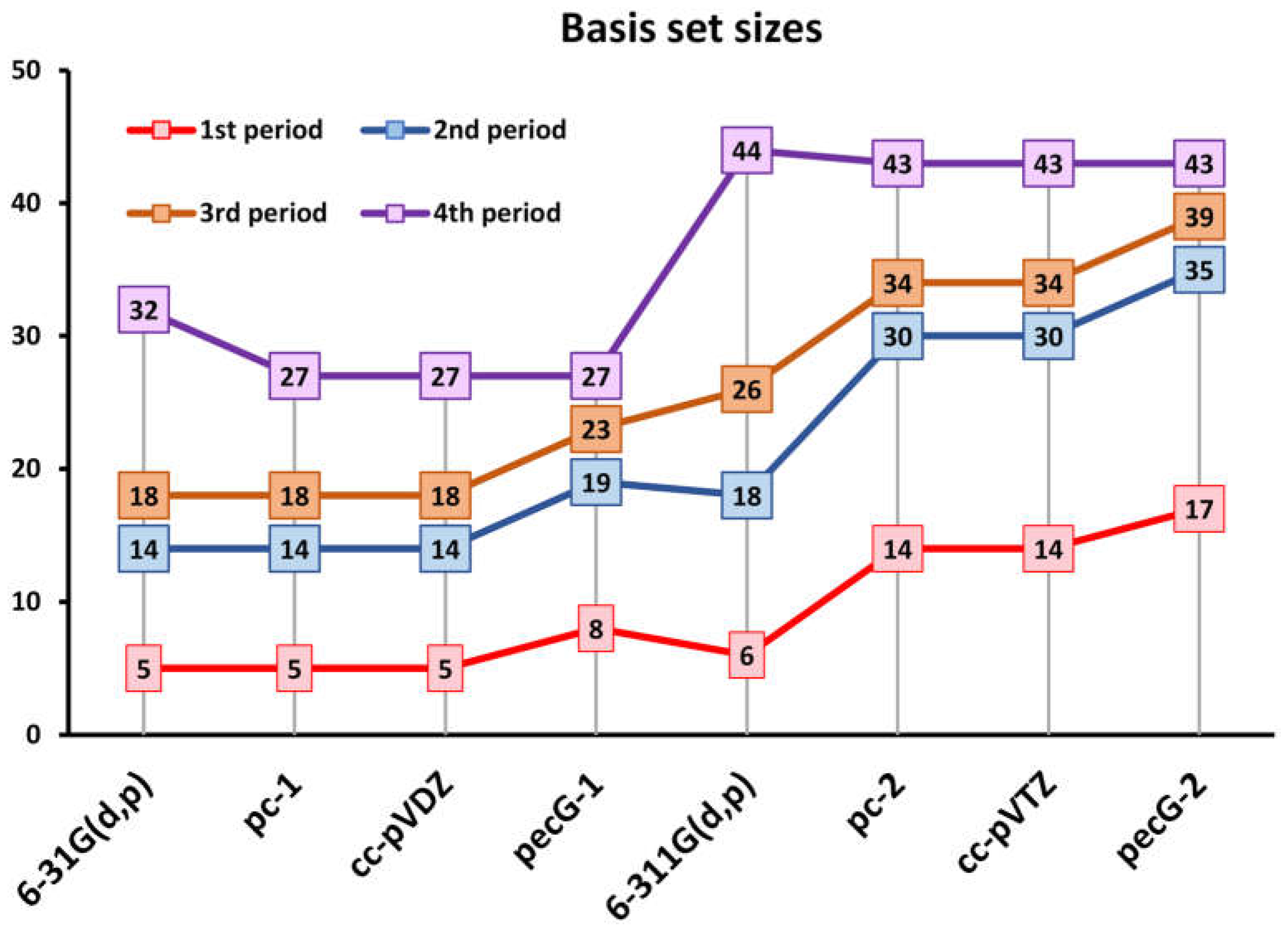
3.1. Theoretical Testing of the pecG-n (n = 1, 2) Basis Sets on the Equilibrium Bond Lengths

In this section, the performance of new pecG-n (n = 1, 2) basis sets was tested on the example of equilibrium bond lengths of 18 molecules via theoretical analysis. These molecules are as follows: As4 (1), AsBr3 (2), AsCl3 (3), AsF3 (4), CHBr3 (5), GaBr3 (6), GaCl3 (7), GeBr2 (8), O(GeH3)2 (9), PF2HSe (10), S(GeH3)2 (11), SeBr2 (12), SeCl2 (13), Se(SiH3)2 (14), Br2 (15), Me2GeF2 (16), AsP3 (17), HCBrClF (18).
Theoretical analysis has been performed within the DFT method with the B97-2 exchange-correlation functional that was used for generating the pecG-n basis sets, and within the second-order Møller–Plesset perturbation theory MP2 [50,51], which represents an ab initio method typically accounting for 80–90% of the correlation energy [52]. The performance of the pecG-n basis sets was compared to that of the Jensen’s pc-n (n = 1, 2) [37], Pople’s 6-31G(d,p) [53] and 6-311G(d,p) [38], and Dunning’s cc-pVXZ (X = D, T) basis sets [36], being of commensurate sizes with each other at both double- and triple-zeta levels of valence splitting. Please, note that whenever the calculations involved the pecG-n (n = 1, 2) basis sets, new pecG-n were assumed for the 4th period elements, while the rest of the atoms in the molecule were described with the previously proposed pecG-n (n = 1, 2) basis sets [1,2].
The reference theoretical values of equilibrium bond lengths have been calculated within each of the two methods of electronic theory using the cc-pV5Z basis, that is large enough ([8s,7p,5d,3f,2g,1h] for 4th period, 104 basis functions) to provide a nearly complete basis set limit (CBS). All values of equilibrium bond lengths calculated at the DFT(B97-2) and MP2 levels of theory with different basis sets are given in Tables S1 and S2.
In order to statistically estimate the measure of deviation of values of equilibrium bond lengths in molecules 1–18 calculated with different basis sets against the corresponding theoretical reference data, we have evaluated the mean absolute errors (MAEs, in Å) for the results obtained with each of the basis sets under consideration. The obtained MAEs are presented in Figure 1.
As can be seen from Figure 1, our new pecG-n (n = 1, 2) basis sets show the best accuracy for both cardinal numbers within all considered levels of electronic theory. Namely, for the compounds containing 4th period atoms, the pecG-n (n = 1, 2) basis sets provide equilibrium bond lengths, which are up to three and two times more accurate as compared to those obtained with the commensurate basis sets at the DFT and MP2 levels, respectively. At the same time, it is interesting to note that previously introduced pecG-n (n = 1, 2) basis sets for 1–3 periods [1,2] demonstrated a superior accuracy, which was characterized by six and two times less error for equilibrium bond lengths calculated at the DFT and CCSD levels.
It is also worth mentioning that the 6-31G(d,p) basis set demonstrates the second-best performance among the first-level basis sets, even outperforming the 6-311G(d,p) basis set at the DFT(B97-2) level and closely approaching it at the MP2 level.
We have also checked the valence angles in compounds 1–18 (see Tables S3 and S4) and found that the alternations in MAEs for bond angles in going from one basis set to another are insignificant. To be more precise, for the first-level basis sets (including pecG-1), the MAE for angles varies in the range of ca. 0.2–0.3° and 0.7–0.8° for the DFT(B97-2) and MP2 method, respectively. For the optimizations with the second-level basis sets (including pecG-2), these ranges diapasons are noticeably less, namely, around 0.05° and 0.5–0.7° for the DFT(B97-2) and MP2 method, respectively. It is also worth noting that the MAEs for the angles obtained in the optimizations with the 6-311G(d,p), performed within both considered methods, turned out to be among the MAEs for the first-level basis sets.

3.2. Testing the Performance of the pecG-n (n = 1, 2) Basis Sets by Comparison of the Calculated Bond Lengths with the Gas Phase Electron Diffraction Experiment

The other test that we have carried out for the pecG-n (n = 1, 2) basis sets is based on the comparison of theoretical values of bond lengths in molecules 1–18 with available gas phase electron diffraction (GED) experiment [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69]. Experimental GED data provides an effective internuclear distance bearing a degree of vibrational averaging with taking into account the effect of anharmonicity in the bond-stretching vibrations.
We have estimated the effective internuclear distances reff, which may be either rg or ra determined in the sense given by Bartell [70], depending on the available experimental data. The basic values were calculated as the equilibrium bond lengths re within the DFT(B97-2) or coupled clusters singles and doubles model with perturbative correction for triple excitations, the CCSD(T) [71,72,73,74,75], using all basis sets from the theoretical analysis given in the previous section, including pecG-n (n = 1, 2). Then, the vibrational and relativistic corrections were added to the basic values. The vibrational corrections were evaluated within the CCSD method [76,77,78,79,80] as the differences: Δrvib = reff − re, (where reff is either rg or ra), using the first-level basis sets of the corresponding type. The relativistic corrections Δrrel were evaluated at the 4-component DFT(PBE0 [81,82,83]) level as the differences between the relativistic and approximated nonrelativistic values: Δrrel = rrel − rnrel. For the estimation of Δrrel, the dyall.v3z basis set [84,85] was applied. For more information about the calculations of relativistic corrections, please, see the “Materials and Methods” section. All calculated equilibrium bond lengths of molecules 1–18, their vibrational and relativistic corrections, and corresponding experimental values are given in Tables S5–S12.
The MAE for each considered basis set was calculated analogously to that in the theoretical analysis, but with the reference data were taken from the GED experiment. The calculated MAEs are shown in Figure 2.
Figure 2 vividly demonstrates a superior performance of our new pecG-n (n = 1, 2) basis sets over the usual energy-optimized basis sets for both cardinal numbers within all considered levels of electronic theory. The 6-31G(d,p) basis set again demonstrates the second-best performance among the first-level basis sets, surpassing the 6-311G(d,p) basis set in the accuracy of the results for both the DFT(B97-2) and CCSD(T) methods. It is interesting to note that the values calculated within the CCSD(T)/pecG-2 scheme are characterized by the MAE of only 0.007 Å, which is very close to the average range of uncertainty of the experimental values, being 0.005 Å for the data under consideration.
Thus, in all tests, new pecG-n (n = 1, 2) basis sets demonstrated a superior accuracy over all considered standard energy-optimized basis sets. Moreover, it is worth mentioning that newly optimized pecG-n basis sets for the 4th period atoms are of the same sizes as the pc-n and cc-pVXZ basis sets for both double- and triple-zeta levels, numbering 27 and 43 basis functions, respectively. At the same time, the 6-31G(d,p) basis set is even five functions larger than the pecG-1, pc-1 and cc-pVDZ basis sets, and the 6-311G(d,p) is one function larger than the pecG-2, pc-2 and cc-pVTZ basis sets. For the sake of convenience, we have plotted the number of basis set functions for each considered basis set for atoms of 1–4 periods in Figure 3, so that one could estimate the size of the basis functional space for an arbitrary molecule.

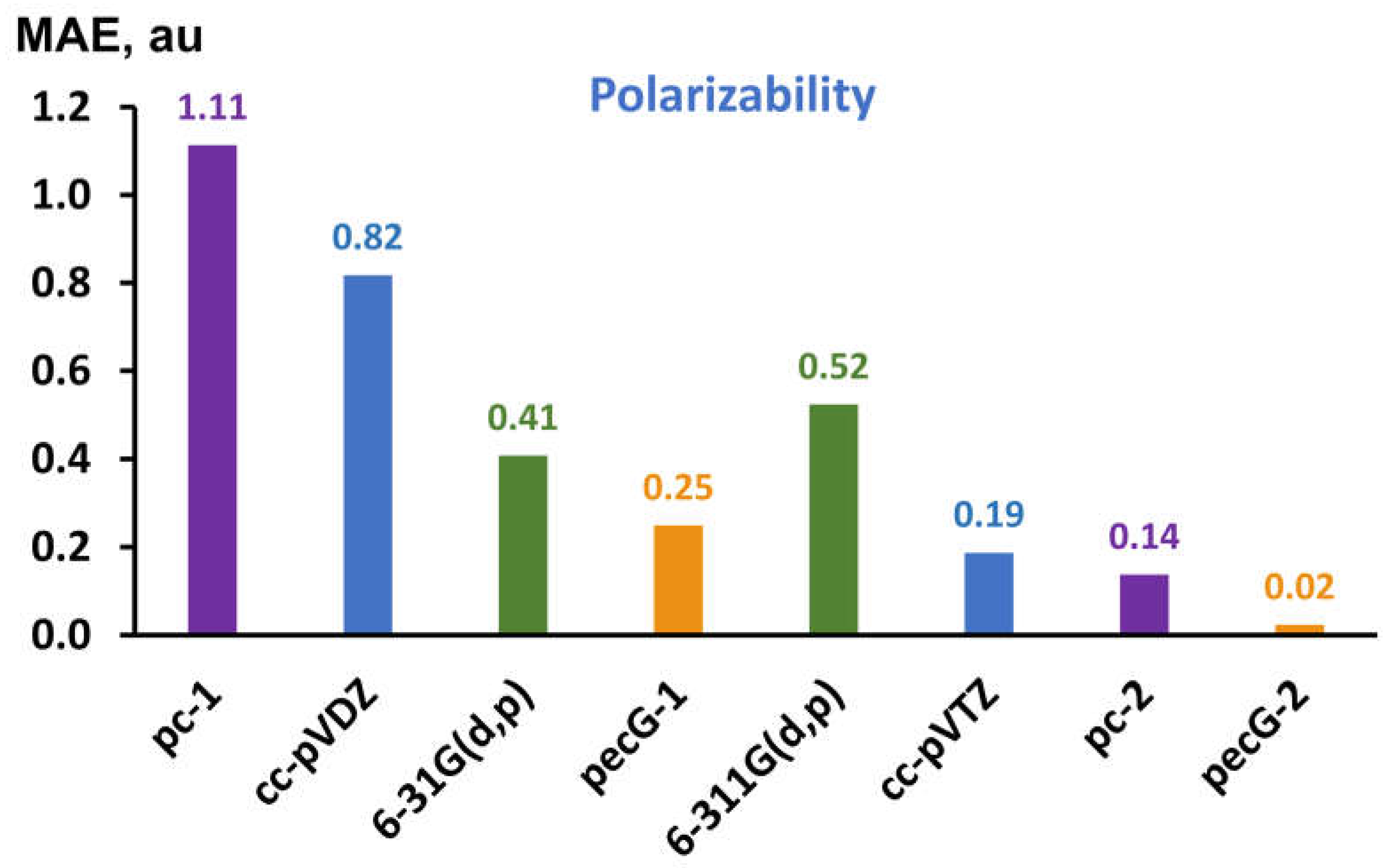
3.3. Testing the Performance of Equilibrium Geometries Obtained with the pecG-n (n = 1, 2) Basis Sets on Polarizability

Our previous tests were mostly concentrated on the equilibrium bond lengths, their results speak in favor of the pecG-n (n = 1, 2) basis sets as being the most accurate and efficient basis sets for these parameters, however, the quality of the whole equilibrium geometry provided by new basis sets can be unambiguously probed by the calculation of a molecular property that is drastically sensitive to the whole lot of geometry parameters of a molecule, including bond lengths, valence bond angles, and dihedral angles. Thus, we have chosen the static dipole polarizability to represent the property that defies our basis sets, because this property is known to be very sensitive to the whole geometry on which it is calculated [86,87,88,89]. Indeed, the problem of accurate prediction of linear optical properties is still sound, and static dipole polarizability is usually considered as a natural prerequisite property for elaborating computational methodologies for more complex static and dynamic optical properties. Static dipole polarizability is a second-order linear response electric property that is calculated through the sum-over-states expression over the singlet excited states of a molecule, which are essentially sensitive to all geometric parameters.
We have calculated static dipole polarizabilities of molecules 1−18 at the DFT(B97-2)/aug-cc-pVQZ level of theory on different equilibrium geometries obtained within the DFT(B97-2) method with various basis sets, including newly developed pecG-n (n = 1, 2) basis sets used on Ga−Br (and previously developed pecG-n (n = 1, 2) basis sets used for the rest atoms). In choosing the basis set for the calculation of dipole polarizabilities, we have relied upon the findings presented in the recent paper of Sauer et al. [90]. The reference theoretical data are calculated on the equilibrium geometries obtained with the cc-pV5Z basis set. All calculated polarizabilities are given in the Supplementary Materials in Table S13.
For polarizability values, we have calculated the MAEs against the theoretical reference data. The calculated MAEs are presented in Figure 4.
As can be seen from Figure 4, the least geometry factor error is provided by the pecG-1 basis set among the considered first-level basis sets, and by the pecG-2 basis set among the second-level basis sets. This unequivocally signifies that the equilibrium geometries obtained with our new pecG-n basis sets give the best values of polarizability calculated upon them, with the pecG-2 basis set providing the geometry factor error almost indistinguishable from that provided by the cc-pV5Z basis set (the MAE for polarizability is only 0.02). At the same time, Figure 4 testifies that the first-level pecG-1 basis set is not only the best one among the commensurate basis sets of double-zeta quality, but also surpasses the 6-311G(d,p) basis set of triple-zeta quality and gives the geometry factor error comparable to that provided by the triple-zeta cc-pVTZ basis set. In all this, it is pertinent to bear in mind that the pecG-n (n = 1, 2) basis sets for 4th period atoms are of the same sizes with the pc-n and cc-pVXZ basis sets of both doble- and triple-zeta levels, respectively, and the 6-31G(d,p) and 6-311G(d,p) basis sets are even larger.

4. Materials and Methods

The optimization of structures of molecules 1–18 was carried out within the DFT and MP2 methods using various basis sets in gas phase within the Gaussian 09 program (version C.01) [91]. The CCSD(T) and vibrationally averaged CCSD geometries for compounds 1–18 were obtained in the gas phase using the CFOUR program (version v2.1) [92]. Relativistic 4-component DFT geometry optimizations of molecules 1–18 were performed within the DIRAC code (release 14) [93]. The relativistic 4-component calculation of equilibrium geometry parameters was carried out using the full Dirac-Kohn-Sham Hamiltonian intrinsically covering both scalar and spin-orbit relativistic effects. In order to estimate nonrelativistic values of equilibrium bond lengths without leaving the 4-component representation, nonrelativistic 4-component Levy-Leblond approximation scheme [94] has been used. In all 4-component calculations, restricted kinetic balance (RKB) [95] has been applied. The static dipole polarizabilities were calculated using the Gaussian 09 program (version C.01). All calculations were carried out in A. E. Favorsky Irkutsk Institute of Chemistry on the facilities of the Baikal Analytical Centre (https://ckp-rf.ru/catalog/ckp/3050/, accessed on 20 July 2025).

5. Conclusions

In this paper, we have proposed new geometry-oriented pecG-n (n = 1, 2) basis sets for 4th-period p-elements, namely, Ga, Ge, As, Se, and Br. These basis sets were optimized via the property-energy consistent (PEC) algorithm directed to the minimization of the molecular energy gradient relative to the bond lengths. The presented basis sets demonstrated an outstanding performance in the geometry optimization of various molecules including Ga, Ge, As, Se, and Br elements as compared to the other popular commensurate basis sets of double- and triple-zeta quality that are frequently used for the calculation of equilibrium geometries.
The tests for new basis sets have been performed based not only on comparison of calculated equilibrium bond lengths with theoretical reference data, but also on the comparison with the values obtained in the gas phase electron diffraction experiment. The quality of equilibrium geometries obtained with the newly presented basis sets has also been tested against the other popular basis sets on the example of static dipole polarizability. The latter test, in particular, has unambiguously demonstrated that newly proposed pecG-n (n = 1, 2) basis sets provide the least geometry factor error relative to the data obtained with the reference geometry of the cc-pV5Z level. Even more so, the pecG-2 basis set used at the geometry optimization stage has provided the MAE for static dipole polarizability of only 0.02 au. This is a very encouraging result, as it speaks of the pecG-2 as the basis set that provides the equilibrium geometries of so high quality that the difference with the cc-pV5Z basis set is practically nought.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms26178197/s1.

Author Contributions

Conceptualization, Y.Y.R. and I.L.R.; methodology, Y.Y.R. and I.L.R.; software, Y.Y.R. and I.L.R.; validation, Y.Y.R. and I.L.R.; formal analysis, Y.Y.R. and I.L.R.; investigation, Y.Y.R. and I.L.R.; resources, Y.Y.R. and I.L.R.; data curation, Y.Y.R. and I.L.R.; writing—original draft preparation, I.L.R.; writing—review and editing, Y.Y.R. and I.L.R.; visualization, Y.Y.R. and I.L.R.; supervision, Y.Y.R. and I.L.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in this study are included in the article/Supplementary Materials. Further inquiries can be directed to the corresponding authors.

Acknowledgments

We are grateful to A. E. Favorsky Irkutsk Institute of Chemistry for the facilities of the Baikal Analytical Centre (https://ckp-rf.ru/catalog/ckp/3050/, accessed on 20 July 2025).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Rusakov, Y.Y.; Nikurashina, Y.A.; Rusakova, I.L. On the Utmost Importance of the Geometry Factor of Accuracy in the Quantum Chemical Calculations of 31P NMR Chemical Shifts: New Efficient pecG-n (n = 1, 2) Basis Sets for the Geometry Optimization Procedure. J. Chem. Phys. 2024, 160, 084109. [Google Scholar] [CrossRef]
  2. Rusakov, Y.Y.; Rusakova, I.L. Getaway from the Geometry Factor Error in the Molecular Property Calculations: Efficient pecG-n (n = 1, 2) Basis Sets for the Geometry Optimization of Molecules Containing Light p Elements. J. Chem. Theory Comput. 2024, 20, 6661–6673. [Google Scholar] [CrossRef] [PubMed]
  3. Rani, A.; Kumar, R. Structural and Electronic Properties of GaAs and GaP Semiconductors. AIP Conf. Proc. 2015, 1661, 050010. [Google Scholar] [CrossRef]
  4. Czelej, K.; Mansoor, M.; Sarsil, M.A.; Tas, M.; Sorkhe, Y.A.; Mansoor, M.; Mansoor, M.; Derin, B.; Ergen, O.; Timur, S.; et al. Atomistic Origins of Various Luminescent Centers and n-Type Conductivity in GaN: Exploring the Point Defects Induced by Cr, Mn, and O through an Ab Initio Thermodynamic Approach. Chem. Mater. 2024, 36, 6392–6409. [Google Scholar] [CrossRef]
  5. Singh, D.K.; Roul, B.K.; Nanda, K.K.; Krupanidhi, S.B. Group III-Nitrides and Their Hybrid Structures for Next-Generation Photodetectors. In Light-Emitting Diodes and Photodetectors—Advances and Future Directions; Casalino, M., Thirumalai, J., Eds.; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
  6. Roy, R.; Hill, V.G.; Osborn, E.F. Polymorphism of Ga2O3 and the System Ga2O3−H2O. J. Am. Chem. Soc. 1952, 74, 719–722. [Google Scholar] [CrossRef]
  7. Shi, F.; Qiao, H. Preparations, Properties and Applications of Gallium Oxide Nanomaterials—A Review. Nano Sel. 2022, 3, 348–373. [Google Scholar] [CrossRef]
  8. Zhang, S.; Yan, Z.; Li, Y.; Chen, Z.; Zeng, H. Atomically Thin Arsenene and Antimonene: Semimetal-Semiconductor and Indirect-Direct Band-Gap Transitions. Angew. Chem. Int. Ed. 2015, 54, 3112–3115. [Google Scholar] [CrossRef]
  9. Moss, S.J.; Ledwith, A. The Chemistry of the Semiconductor Industry, 1st ed.; Blackie & Son Ltd.: New York, NY, USA, 1987; ISBN 0-412-01321-5. [Google Scholar]
  10. Chen, Y.; Chen, C.; Kealhofer, R.; Liu, H.; Yuan, Z.; Jiang, L.; Suh, J.; Park, J.; Ko, C.; Choe, H.S.; et al. Black Arsenic: A Layered Semiconductor with Extreme In-Plane Anisotropy. Adv. Mater. 2018, 30, 1800754. [Google Scholar] [CrossRef] [PubMed]
  11. Luo, H.; Tuinenga, C.; Guidez, E.B.; Lewis, C.; Shipman, J.; Roy, S.; Aikens, C.M.; Chikan, V. Synthesis and Characterization of Gallium-Doped CdSe Quantum Dots. J. Phys. Chem. C 2015, 119, 10749–10757. [Google Scholar] [CrossRef]
  12. Sallen, G.; Kunz, S.; Amand, T.; Bouet, L.; Kuroda, T.; Mano, T.; Paget, D.; Krebs, O.; Marie, X.; Sakoda, K.; et al. Nuclear Magnetization in Gallium Arsenide Quantum Dots at Zero Magnetic Field. Nat. Commun. 2014, 5, 3268. [Google Scholar] [CrossRef]
  13. van Riggelen-Doelman, F.; Wang, C.-A.; de Snoo, S.L.; Lawrie, W.I.L.; Hendrickx, N.W.; Rimbach-Russ, M.; Sammak, A.; Scappucci, G.; Déprez, C.; Veldhorst, M. Coherent Spin Qubit Shuttling through Germanium Quantum Dots. Nat. Commun. 2024, 15, 5716. [Google Scholar] [CrossRef]
  14. Franke, D.; Harris, D.K.; Chen, O.; Bruns, O.T.; Carr, J.A.; Wilson, M.W.B.; Bawendi, M.G. Continuous Injection Synthesis of Indium Arsenide Quantum Dots Emissive in the Short-Wavelength Infrared. Nat. Commun. 2016, 7, 12749. [Google Scholar] [CrossRef]
  15. Eybl, V.; Kotyzová, D.; Sýkora, J.; Topolčan, O.; Pikner, R.; Mihaljevič, M.; Brtko, J.; Glattre, E. Effects of Selenium and Tellurium on the Activity of Selenoenzymes Glutathione Peroxidase and Type I Iodothyronine Deiodinase, Trace Element Thyroid Level, and Thyroid Hormone Status in Rats. Biol. Trace Elem. Res. 2007, 117, 105–114. [Google Scholar] [CrossRef]
  16. Johansson, L.; Gafvelin, G.; Arnér, E.S.J. Selenocysteine in Proteins − Properties and Biotechnological Use. Biochim. Biophys. Acta 2005, 1726, 1–13. [Google Scholar] [CrossRef]
  17. Schwarz, K.; Foltz, C.M. Selenium as an Integral Part of Factor 3 Against Dietary Necrotic Liver Degeneration. J. Am. Chem. Soc. 1957, 79, 3292–3293. [Google Scholar] [CrossRef]
  18. Behne, D.; Kyriakopoulos, A. Mammalian Selenium-Containing Proteins. Annu. Rev. Nutr. 2001, 21, 453–473. [Google Scholar] [CrossRef]
  19. Gribble, G.W. The Diversity of Naturally occurring Organobromine Compounds. Chem. Soc. Rev. 1999, 28, 335–346. [Google Scholar] [CrossRef]
  20. Slack, R.D.; Abramyan, A.M.; Tang, H.; Meena, S.; Davis, B.A.; Bonifazi, A.; Giancola, J.L.B.; Deschamps, J.R.; Naing, S.; Yano, H.; et al. A Novel Bromine-Containing Paroxetine Analogue Provides Mechanistic Clues for Binding Ambiguity at the Central Primary Binding Site of the Serotonin Transporter. ACS Chem. Neurosci. 2019, 10, 3946–3952. [Google Scholar] [CrossRef] [PubMed]
  21. Bouthenet, E.; Oh, K.-B.; Park, S.; Nagi, N.K.; Lee, H.-S.; Matthews, S.E. Synthesis and Antimicrobial Activity of Brominated Resorcinol Dimers. Bioorg. Med. Chem. Lett. 2011, 21, 7142–7145. [Google Scholar] [CrossRef] [PubMed]
  22. Garcia, R.I.; Lozano, R.D.; Martinez, E.A. A Transimpedance Circuit for Use with Selenium Photoelectric Cells. J. Phys. E Sci. Instrum. 1972, 5, 745. [Google Scholar] [CrossRef]
  23. Huang, W.; Zhang, Y.; You, Q.; Huang, P.; Wang, Y.; Huang, Z.N.; Ge, Y.; Wu, L.; Dong, Z.; Dai, X.; et al. Enhanced Photodetection Properties of Tellurium-Selenium Roll-to-Roll Nanotube Heterojunctions. Nano Micro Small 2019, 15, 1900902. [Google Scholar] [CrossRef] [PubMed]
  24. Hadar, I.; Song, T.-B.; Ke, W.; Kanatzidis, M.G. Modern Processing and Insights on Selenium Solar Cells: The World’s First Photovoltaic Device. Adv. Energy Mater. 2019, 9, 1802766. [Google Scholar] [CrossRef]
  25. Lin, J.-H.; Zhang, H.; Cheng, X.-L.; Miyamoto, Y. Two-Dimensional Wide-Band-Gap Nitride Semiconductors: Single-Layer 1T-XN2 (X= S, Se, and Te). Phys. Rev. B 2016, 94, 195404. [Google Scholar] [CrossRef]
  26. Malik, M.A.; Ramasamy, K.; O’Brien, P. Selenium and Tellurium Containing Precursors for Semiconducting Materials. In Selenium and Tellurium Chemistry From Small Molecules to Biomolecules and Materials, 1st ed.; Woollins, J.D., Laitinen, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
  27. Johnson, J.A.; Saboungi, M.-L.; Thiyagarajan, P.; Csencsits, R.; Meisel, D. Selenium Nanoparticles: A Small-Angle Neutron Scattering Study. J. Phys. Chem. B 1999, 103, 59–63. [Google Scholar] [CrossRef]
  28. Piacenza, E.; Presentato, A.; Zonaro, E.; Lampis, S.; Vallini, G.; Turner, R.J. Physical-Chemical Properties of Biogenic Selenium Nanostructures Produced by Stenotrophomonas maltophilia SeITE02 and Ochrobactrum sp. MPV1. Front. Microbiol. 2018, 9, 3178. [Google Scholar] [CrossRef]
  29. Mayers, B.; Jiang, X.; Sunderland, D.; Cattle, B.; Xia, Y. Hollow Nanostructures of Platinum with Controllable Dimensions Can Be Synthesized by Templating Against Selenium Nanowires and Colloids. J. Am. Chem. Soc. 2003, 125, 13364–13365. [Google Scholar] [CrossRef]
  30. Terasaki, O.; Yamazaki, K.; Thomas, J.M.; Ohsuna, T.; Watanabe, D.; Sanders, J.V.; Barry, J.C. Isolating Individual Chains of Selenium by Incorporation into the Channels of a Zeolite. Nature 1987, 330, 58–60. [Google Scholar] [CrossRef]
  31. Parise, J.B.; MacDougall, J.; Herron, N.; Farlee, R.; Sleight, A.W.; Wang, Y.; Bein, T.; Moller, K.; Moroney, L.M. Characterization of Selenium-Loaded Molecular Sieves A, X, Y, AIPO-5, and Mordenite. Inorg. Chem. 1988, 27, 221–228. [Google Scholar] [CrossRef]
  32. Helgaker, T.; Gauss, J.; Jørgensen, P.; Olsen, J. The Prediction of Molecular Equilibrium Structures by the Standard Electronic Wave Functions. J. Chem. Phys. 1997, 106, 6430–6440. [Google Scholar] [CrossRef]
  33. Faber, R.; Sauer, S.P.A. On the Discrepancy between Theory and Experiment for the F−F Spin−Spin Coupling Constant of Difluoroethyne. Phys. Chem. Chem. Phys. 2012, 14, 16440–16447. [Google Scholar] [CrossRef]
  34. Temelso, B.; Valeev, E.F.; Sherrill, C.D. A Comparison of One-Particle Basis Set Completeness, Higher-Order Electron Correlation, Relativistic Effects, and Adiabatic Corrections for Spectroscopic Constants of BH, CH+, and NH+. J. Phys. Chem. A 2004, 108, 3068–3075. [Google Scholar] [CrossRef]
  35. Heckert, M.; Kállay, M.; Tew, D.P.; Klopper, W.; Gauss, J. Basis-set Extrapolation Techniques for the Accurate Calculation of Molecular Equilibrium Geometries Using Coupled-Cluster Theory. J. Chem. Phys. 2006, 125, 044108. [Google Scholar] [CrossRef] [PubMed]
  36. Wilson, A.K.; Woon, D.E.; Peterson, K.A.; Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. IX. The Atoms Gallium through Krypton. J. Chem. Phys. 1999, 110, 7667–7676. [Google Scholar] [CrossRef]
  37. Jensen, F. Polarization Consistent Basis Sets. VII. The Elements K, Ca, Ga, Ge, As, Se, Br, and Kr. J. Chem. Phys. 2012, 136, 114107. [Google Scholar] [CrossRef]
  38. Curtiss, L.A.; McGrath, M.P.; Blaudeau, J.-P.; Davis, N.E.; Binning, R.C.; Radom, L. Extension of Gaussian-2 Theory to Molecules Containing Third-Row Atoms Ga-Kr. J. Chem. Phys. 1995, 103, 6104–6113. [Google Scholar] [CrossRef]
  39. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  40. Rusakov, Y.Y.; Rusakova, I.L. An Efficient Method for Generating Property-Energy Consistent Basis Sets. New pecJ-n (n = 1, 2) Basis Sets for High-Quality Calculations of Indirect Nuclear Spin–Spin Coupling Constants Involving 1H, 13C, 15N, and 19F Nuclei. Phys. Chem. Chem. Phys. 2021, 23, 14925–14939. [Google Scholar] [CrossRef]
  41. Rusakov, Y.Y.; Rusakova, I.L. New Efficient pecS-n (n = 1, 2) Basis Sets for Quantum Chemical Calculations of 31P NMR Chemical Shifts. Phys. Chem. Chem. Phys. 2023, 25, 18728–18741. [Google Scholar] [CrossRef]
  42. Rusakov, Y.Y.; Rusakova, I.L. New pecJ-n (n = 1, 2) Basis Sets for High Quality Calculations of Indirect Nuclear Spin–Spin Coupling Constants Involving 31P and 29Si: The Advanced PEC method. Molecules 2022, 27, 6145. [Google Scholar] [CrossRef]
  43. Rusakov, Y.Y.; Rusakova, I.L. New pecJ-n (n = 1, 2) Basis Sets for Selenium Atom Purposed for the Calculations of NMR Spin–Spin Coupling Constants Involving Selenium. Int. J. Mol. Sci. 2023, 24, 7841. [Google Scholar] [CrossRef]
  44. Rusakov, Y.Y.; Rusakova, I.L. New pecS-n (n = 1, 2) Basis Sets for Quantum Chemical Calculations of the NMR Chemical Shifts of H, C, N, and O Nuclei. J. Chem. Phys. 2022, 156, 244112. [Google Scholar] [CrossRef]
  45. Rusakov, Y.Y.; Rusakova, I.L. An Unusual Way of Augmenting One-Electron Basis Sets: New aug-pecS-n (n = 1, 2) Basis Sets for H, C, N, and O Atoms for NMR Shielding Constant Calculations that Require Extra Diffuse Functions. J. Chem. Phys. 2025, 162, 164111. [Google Scholar] [CrossRef] [PubMed]
  46. Rusakov, Y.Y.; Nikurashina, Y.A.; Rusakova, I.L. Going Beyond the Routine Consideration of Solvent Effects on 31P NMR Shielding Constants: A Meticulous Basis Set Study and New aug-pecS-n (n = 1 and 2) Basis Sets for Phosphorus Atoms. Phys. Chem. Chem. Phys. 2025, 27, 6730–6743. [Google Scholar] [CrossRef] [PubMed]
  47. Becke, A.D. Density-Functional Thermochemistry. V. Systematic Optimization of Exchange-Correlation Functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
  48. Wilson, P.J.; Bradley, T.J.; Tozer, D.J. Hybrid Exchange-Correlation Functional Determined from Thermochemical Data and Ab Initio Potentials. J. Chem. Phys. 2001, 115, 9233–9242. [Google Scholar] [CrossRef]
  49. Raffenetti, R.C. General Contraction of Gaussian Atomic Orbitals: Core, Valence, Polarization, and Diffuse Basis Sets; Molecular Integral Evaluation. J. Chem. Phys. 1973, 58, 4452–4458. [Google Scholar] [CrossRef]
  50. Cremer, D. Møller–Plesset Perturbation Theory: From Small Molecule Methods to Methods for Thousands of Atoms. WIREs Comput. Mol. Sci. 2011, 1, 509–530. [Google Scholar] [CrossRef]
  51. Gauss, J.; Stanton, J.F. Electron-correlated approaches for the calculation of NMR chemical shifts. In Advances in Chemical Physics, 1st ed.; Prigogine, I., Rice, S.A., Eds.; John Wiley & Sons, Inc.: New York, NY, USA, 2002; Volume 123, pp. 355–422. [Google Scholar]
  52. Jensen, F. Introduction to Computational Chemistry; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
  53. Rassolov, V.A.; Ratner, M.A.; Pople, J.A.; Redfern, P.C.; Curtiss, L.A. 6-31G* Basis Set for Third-Row Atoms. J. Comput. Chem. 2001, 22, 976–984. [Google Scholar] [CrossRef]
  54. Morino, Y.; Ukaji, T.; Ito, T. Molecular Structure Determination by Gas Electron Diffraction at High Temperatures. I. Arsenic. Bull. Chem. Soc. Jpn. 1966, 39, 64–71. [Google Scholar] [CrossRef]
  55. Samdal, S.; Barnhart, D.M.; Hedberg, K. An Electron-Diffraction Investigation of Gaseous AsBr3 I. Molecular Structure at 373 K and 466 K II. Quadratic Potential Constants from Amplitudes. J. Mol. Struct. 1976, 35, 67–80. [Google Scholar] [CrossRef]
  56. Konaka, S.; Kimura, M. Determination of the Molecular Structures of AsF3 and AsCl3 by Gas Electron Diffraction. Bull. Chem. Soc. Jpn. 1970, 43, 1693–1703. [Google Scholar] [CrossRef]
  57. Tamagawa, K.; Kimura, M. Molecular Structure of Bromoform as Determined by a Joint Analysis of Electron Diffraction and Microwave Data. Bull. Chem. Soc. Jpn. 1979, 52, 2747–2751. [Google Scholar] [CrossRef]
  58. Réffy, B.; Kolonits, M.; Hargittai, M. Gallium Tribromide: Molecular Geometry of Monomer and Dimer from Gas-Phase Electron Diffraction. J. Mol. Struct. 1998, 445, 139–148. [Google Scholar] [CrossRef]
  59. Haaland, A.; Hammel, A.; Martinsen, K.-G.; Tremmel, J.; Volden, H.V. Molecular Structures of Monomeric Gallium Trichloride, Indium Trichloride and Lead Tetrachloride by Gas Electron Diffraction. J. Chem. Soc. Dalton Trans. 1992, 14, 2209–2214. [Google Scholar] [CrossRef]
  60. Schultz, G.Y.; Tremmel, J.; Hargittai, I.; Kagramanov, N.D.; Maltsev, A.K.; Nefedov, O.M. Electron Diffraction Study of the Molecular Structure of Germanium Dibromide. J. Mol. Struct. 1982, 82, 107–113. [Google Scholar] [CrossRef]
  61. Glidewell, C.; Rankin, D.W.H.; Robiette, A.G.; Sheldrick, G.M.; Beagley, B.; Cradock, S. Molecular Structures of Digermyl Ether and Digermyl Sulphide in the Gas Phase, studied by Electron Diffraction. J. Chem. Soc. A. 1970, 315–317. [Google Scholar] [CrossRef]
  62. Boyd, A.S.F.; Laurenson, G.S.; Rankin, D.W.H. The Molecular Structure of Difluorophosphine Selenide, Determined Using a Combination of Gas Electron Diffraction and Liquid-Crystal NMR Data. J. Mol. Struct. 1981, 71, 217–226. [Google Scholar] [CrossRef]
  63. Shlykov, S.A.; Titov, A.V.; Oberhammer, H.; Giricheva, N.I.; Girichev, G.V. The Molecular Structure of Selenium Dibromide as Determined by Combined Gas-Phase Electron Diffraction–Mass Spectrometric Experiments and Quantum Chemical Calculations. Phys. Chem. Chem. Phys. 2008, 10, 6438–6445. [Google Scholar] [CrossRef]
  64. Fernholt, L.; Haaland, A.; Seip, R.; Kniep, R.; Korte, L. The Molecular Structure of Selenium Dichloride, SeCl2, Determined by Gas Electron Diffraction. Z. Naturforschung B 1983, 38, 1072–1073. [Google Scholar] [CrossRef]
  65. Almenningen, A.; Fernholt, L.; Seip, H.M. The Molecular Structure of Gaseous Disilyl Selenide, (SiH3)2Se. Acta Chem. Scand. 1968, 22, 51–58. [Google Scholar] [CrossRef]
  66. Kuchitsu, K. Effect of Molecular Vibrations on Gas Electron Diffraction. I. Probability Distribution Function and Molecular Intensity for Diatomic Molecules. Bull. Chem. Soc. Jpn. 1967, 40, 498–504. [Google Scholar] [CrossRef]
  67. Drake, J.E.; Hemmings, R.T.; Hencher, J.L.; Mustoe, F.M.; Shen, Q. Electron Diffraction Determination of the Molecular Structures of Difluoro(dimethyl)germane and Trifluoro(methyl)germane in the Vapour Phase. J. Chem. Soc. Dalton Trans. 1976, 5, 394–398. [Google Scholar] [CrossRef]
  68. Cossairt, B.M.; Cummins, C.C.; Head, A.R.; Lichtenberger, D.L.; Berger, R.J.F.; Hayes, S.A.; Mitzel, N.W.; Wu, G. On the Molecular and Electronic Structures of AsP3 and P4. J. Am. Chem. Soc. 2010, 132, 8459–8465. [Google Scholar] [CrossRef]
  69. Jacob, E.J. Structure of Bromochlorofluoromethane by Electron Diffraction. J. Mol. Struct. 1979, 52, 63–69. [Google Scholar] [CrossRef]
  70. Bartell, L.S. Effects of Anharmonicity of Vibration on the Diffraction of Electrons by Free Molecules. J. Chem. Phys. 1955, 23, 1219–1222. [Google Scholar] [CrossRef]
  71. Stanton, J.F. Why CCSD (T) Works: A Different Perspective. Chem. Phys. Lett. 1997, 281, 130–134. [Google Scholar] [CrossRef]
  72. Scuseria, G.E.; Lee, T.J. Comparison of Coupled‒Cluster Methods which Include the Effects of Connected Triple Excitations. J. Chem. Phys. 1990, 93, 5851–5855. [Google Scholar] [CrossRef]
  73. Valeev, E.F.; Crawford, T.D. Simple Coupled‒Cluster Singles and Doubles Method with Perturbative Inclusion of Triples and Explicitly Correlated Geminals: The CCSD(T)‒R12 Model. J. Chem. Phys. 2008, 128, 244113. [Google Scholar] [CrossRef]
  74. Purvis, G.D.; Bartlett, R.J., III. A Full Coupled‒Cluster Singles and Doubles Model: The Inclusion of Disconnected Triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
  75. Gauss, J.; Stanton, J.F. Analytic CCSD(T) Second Derivatives. Chem. Phys. Lett. 1997, 276, 70–77. [Google Scholar] [CrossRef]
  76. Scuseria, G.E.; Janssen, C.L.; Schaefer, H.F. An Efficient Reformulation of the Closed‒Shell Coupled Cluster Single and Double Excitation (CCSD) Equations. J. Chem. Phys. 1988, 89, 7382–7387. [Google Scholar] [CrossRef]
  77. Koch, H.; Sánchez de Merás, A.; Helgaker, T.; Christiansen, O. The integral-direct coupled cluster singles and doubles model. J. Chem. Phys. 1996, 104, 4157–4165. [Google Scholar] [CrossRef]
  78. Monkhorst, H.J. Calculation of Properties with the Coupled-Cluster Method. Int. J. Quantum Chem. Symp. 1977, 12, 421–432. [Google Scholar] [CrossRef]
  79. Christiansen, O. Coupled Cluster Theory with Emphasis on Selected New Developments. Theor. Chem. Acc. 2006, 116, 106–123. [Google Scholar] [CrossRef]
  80. Bartlett, R.J.; Musiał, M. Coupled-Cluster Theory in Quantum Chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [Google Scholar] [CrossRef]
  81. Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for Mixing Exact Exchange with Density Functional Approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
  82. Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
  83. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  84. Dyall, K.G. Relativistic and Nonrelativistic Finite Nucleus Optimized Triple-Zeta Basis Sets for the 4p, 5p and 6p Elements. Theor. Chem. Acc. 2002, 108, 335–340. [Google Scholar] [CrossRef]
  85. Dyall, K.G. Relativistic Quadruple-Zeta and Revised Triple-Zeta and Double-Zeta Basis Sets for the 4p, 5p, and 6p Elements. Theor. Chem. Acc. 2006, 115, 441–447. [Google Scholar] [CrossRef]
  86. Loboda, O.; Ingrosso, F.; Ruiz-Lopez, M.F.; Reis, H.; Millot, C. Dipole and quadrupole polarizabilities of the water molecule as a function of geometry. J. Comput. Chem. 2016, 37, 2125–2132. [Google Scholar] [CrossRef]
  87. Loboda, O.; Ingrosso, F.; Ruiz-López, M.F.; Szalewicz, K.; Millot, C. Geometry-dependent distributed polarizability models for the water molecule. J. Chem. Phys. 2016, 144, 034304. [Google Scholar] [CrossRef] [PubMed]
  88. Avila, G. Ab initio dipole polarizability surfaces of water molecule: Static and dynamic at 514.5 nm. J. Chem. Phys. 2005, 122, 144310. [Google Scholar] [CrossRef] [PubMed]
  89. Lao, K.U.; Jia, J.; Maitra, R.; DiStasio, R.A. On the geometric dependence of the molecular dipole polarizability in water: A benchmark study of higher-order electron correlation, basis set incompleteness error, core electron effects, and zero-point vibrational contributions. J. Chem. Phys. 2018, 149, 204303. [Google Scholar] [CrossRef]
  90. Jørgensen, M.W.; Faber, R.; Ligabue, A.; Sauer, S.P.A. Benchmarking correlated methods for frequency-dependent polarizabilities: Aromatic molecules with the CC3, CCSD, CC2, SOPPA, SOPPA(CC2), and SOPPA(CCSD) methods. J. Chem. Theory Comput. 2020, 16, 3006–3018. [Google Scholar] [CrossRef] [PubMed]
  91. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2016; Available online: https://gaussian.com/glossary/g09 (accessed on 20 July 2025).
  92. Stanton, J.F.; Gauss, J.; Cheng, L.; Harding, M.E.; Matthews, D.A.; Szalay, P.G.; Asthana, A.; Auer, A.A.; Bartlett, R.J.; Benedikt, U.; et al. CFOUR, a Quantum Chemical Program Package. Available online: http://www.cfour.de (accessed on 20 July 2025).
  93. DIRAC, a Relativistic ab Initio Electronic Structure Program, Release DIRAC14 (2014), Written by T. Saue, L. Visscher, H.J. Aa. Jensen, and R. Bast, with Contributions from V. Bakken, K.G. Dyall, S. Dubillard, U. Ekström, E. Eliav, T. Enevoldsen, E. Faßhauer, T. Fleig, O. Fossgaard, A.S.P. Gomes, T. Helgaker, J. Henriksson, M. Iliaš, Ch. R. Jacob, S. Knecht, S. Komorovský, O. Kullie, C.V. Larsen, J.K. Lærdahl, Y.S. Lee, H.S. Nataraj, P. Norman, G. Olejniczak, J. Olsen, Y.C. Park, J.K. Pedersen, M. Pernpointner, R. di Remigio, K. Ruud, P. Sałek, B. Schimmelpfennig, J. Sikkema, A.J. Thorvaldsen, J. Thyssen, J. van Stralen, S. Villaume, O. Visser, T. Winther, and S. Yamamoto. Available online: https://www.diracprogram.org (accessed on 20 July 2025).
  94. Lévy-Leblond, J.M. Nonrelativistic Particles and Wave Equations. Commun. Math. Phys. 1967, 6, 286–311. [Google Scholar] [CrossRef]
  95. Sun, Q.; Liu, W.; Kutzelnigg, W. Comparison of Restricted, Unrestricted, Inverse, and Dual Kinetic Balances for Four-Component Relativistic Calculations. Theor. Chem. Acc. 2011, 129, 423–436. [Google Scholar] [CrossRef]
Ijms 26 08197 g001
Figure 1. MAEs (in Å) for the equilibrium bond lengths in molecules 1–18 obtained in the optimization of their geometrical structures performed within the DFT(B97-2) (upper diagram) and MP2 (bottom diagram) levels of theory using different basis sets, evaluated against corresponding theoretical reference data. All calculated equilibrium bond lengths that were used to estimate the MAEs depicted in this Figure can be found in Tables S1 and S2 in Supplementary Materials.
Figure 1. MAEs (in Å) for the equilibrium bond lengths in molecules 1–18 obtained in the optimization of their geometrical structures performed within the DFT(B97-2) (upper diagram) and MP2 (bottom diagram) levels of theory using different basis sets, evaluated against corresponding theoretical reference data. All calculated equilibrium bond lengths that were used to estimate the MAEs depicted in this Figure can be found in Tables S1 and S2 in Supplementary Materials.
Ijms 26 08197 g001
Ijms 26 08197 g002
Figure 2. MAEs (in Å) for the equilibrium bond lengths in molecules 1–18 obtained in the optimization of their geometrical structures performed within the DFT(B97-2) (upper diagram) and CCSD(T) (bottom diagram) levels of theory using different basis sets, with taking into account relativistic and vibrational corrections, evaluated against corresponding experimental reference data.
Figure 2. MAEs (in Å) for the equilibrium bond lengths in molecules 1–18 obtained in the optimization of their geometrical structures performed within the DFT(B97-2) (upper diagram) and CCSD(T) (bottom diagram) levels of theory using different basis sets, with taking into account relativistic and vibrational corrections, evaluated against corresponding experimental reference data.
Ijms 26 08197 g002
Ijms 26 08197 g003
Figure 3. Number of basis set functions for the considered basis sets for 1–4 period atoms.
Figure 3. Number of basis set functions for the considered basis sets for 1–4 period atoms.
Ijms 26 08197 g003
Ijms 26 08197 g004
Figure 4. The MAEs (in au) for static dipole polarizabilities of molecules 1–18 that were calculated at the DFT(B97-2)/aug-cc-pVQZ level of theory on the equilibrium geometries obtained with different basis sets, evaluated against the corresponding theoretical reference data.
Figure 4. The MAEs (in au) for static dipole polarizabilities of molecules 1–18 that were calculated at the DFT(B97-2)/aug-cc-pVQZ level of theory on the equilibrium geometries obtained with different basis sets, evaluated against the corresponding theoretical reference data.
Ijms 26 08197 g004
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Rusakov, Y.Y.; Rusakova, I.L. Efficient pecG-n (n = 1, 2) Basis Sets for Ga, Ge, As, Se, and Br Specialized for the Geometry Optimization of Molecular Structures. Int. J. Mol. Sci. 2025, 26, 8197. https://doi.org/10.3390/ijms26178197

AMA Style

Rusakov YY, Rusakova IL. Efficient pecG-n (n = 1, 2) Basis Sets for Ga, Ge, As, Se, and Br Specialized for the Geometry Optimization of Molecular Structures. International Journal of Molecular Sciences. 2025; 26(17):8197. https://doi.org/10.3390/ijms26178197

Chicago/Turabian Style

Rusakov, Yuriy Yu., and Irina L. Rusakova. 2025. "Efficient pecG-n (n = 1, 2) Basis Sets for Ga, Ge, As, Se, and Br Specialized for the Geometry Optimization of Molecular Structures" International Journal of Molecular Sciences 26, no. 17: 8197. https://doi.org/10.3390/ijms26178197

APA Style

Rusakov, Y. Y., & Rusakova, I. L. (2025). Efficient pecG-n (n = 1, 2) Basis Sets for Ga, Ge, As, Se, and Br Specialized for the Geometry Optimization of Molecular Structures. International Journal of Molecular Sciences, 26(17), 8197. https://doi.org/10.3390/ijms26178197

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop