Development and Proof-of-Concept Application of Genome-Enabled Selection for Pea Grain Yield under Severe Terminal Drought
Abstract
1. Introduction
2. Results
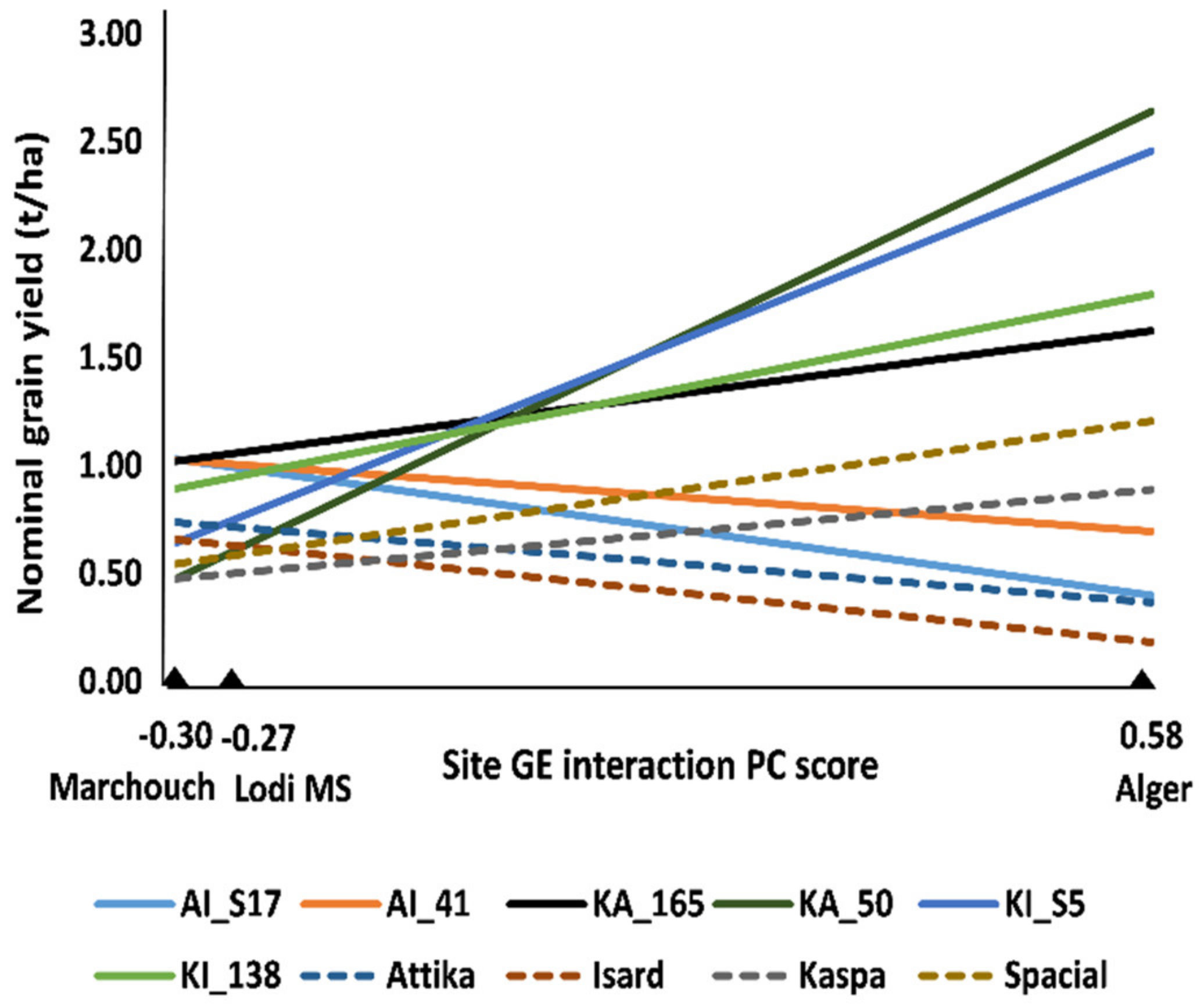
2.1. Multi-Environment Data Analysis of RIL Populations (Experiments 1, 2, and 3)
2.2. Predictive Ability of Genomic Selection Models (Experiments 1, 2, and 3)
2.3. Comparison of Genomic vs. Phenotypic Selection Based on Predicted Yield Gains (Experiments 1, 2, and 3)
2.4. Comparison of Genomic vs. Phenotypic Selection Based on Actual Yield Gains (Experiment 4)
2.5. Comparison of Material with Contrasting Genomic Predictions (Experiment 5)
2.6. Comparison of Genomic Selection vs. Marker-Assisted Selection for Intrinsic Drought Tolerance (Experiment 6)
3. Discussion
4. Materials and Methods
4.1. Multi-Environment Phenotyping and Data Analysis of RIL Populations (Experiments 1, 2, and 3)
4.2. Definition of GS and MAS Procedures
4.3. Comparison of Genomic vs. Phenotypic Selection Based on Predicted Yield Gains
4.4. Comparison of Genomic vs. Phenotypic Selection Based on Actual Yield Gains (Experiment 4)
4.5. Comparison of Material with Contrasting Genomic Predictions (Experiment 5)
4.6. Comparison of Genomic Selection vs. Marker-Assisted Selection for Intrinsic Drought Tolerance (Experiment 6)
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| rrBLUP | Ridge Regression BLUP (best linear unbiased prediction) |
| ANOVA | Analysis of variance |
| AMMI | Additive Main effects and Multiplicative Interaction |
| GBS | Genotyping-by-sequencing |
| MAS | Marker-assisted selection |
| RIL | Recombinant inbred line |
| SNP | Single nucleotide polymorphism |
| BL | Bayesian Lasso |
| GE | Genotype × environment |
| GS | Genomic selection |
| MS | Managed stress |
| PC | Principal component |
| PS | Phenotypic selection |
References
- Turral, H.; Burke, J.; Faurès, J.-M. Climate Change, Water and Food Security; FAO Water Reports No. 36; FAO: Rome, Italy, 2011. [Google Scholar]
- Gomiero, T. Soil degradation, land scarcity and food security: Reviewing a complex challenge. Sustainability 2016, 8, 281. [Google Scholar] [CrossRef]
- Lassaletta, L.; Billen, G.; Garnier, J.; Bouwman, L.; Velazquez, E.; Mueller, N.D. Nitrogen use in the global food system: Past trends and future trajectories of agronomic performance, pollution, trade, and dietary demand. Env. Res. Lett. 2016, 11, 095007. [Google Scholar] [CrossRef]
- Cellier, P.; Schneider, A.; Thiébeau, P.; Vertès, F. Impacts environnementaux de l’introduction de légumineuses dans les systèmes de production. In Les Légumineuses pour des Systèmes Agricoles et al. Imentaires Durables; Schneider, A., Huyghe, C., Eds.; Editions Quae: Versailles, France, 2015; pp. 297–338. [Google Scholar]
- Foyer, C.H.; Lam, H.-M.; Nguyen, H.T.; Siddique, K.H.M.; Varshney, R.K.; Colmer, T.D. Neglecting legumes has compromised human health and sustainable food production. Nat. Plants 2016, 2, 16112. [Google Scholar] [CrossRef] [PubMed]
- Zander, P.; Amjath-Babu, T.S.; Preissel, S.; Reckling, M.; Bues, A.; Schläfke, N. Grain legume decline and potential recovery in European agriculture: A review. Agron. Sustain. Dev. 2016, 36, 26. [Google Scholar] [CrossRef]
- FAO. The State of Food and Agriculture; Livestock in the balance; FAO: Rome, Italy, 2010. [Google Scholar]
- Pilorgé, E.; Muel, F. What vegetable oils and proteins for 2030? Would the protein fraction be the future of oil and protein crops? OCL 2016, 23, D402. [Google Scholar] [CrossRef]
- Schreuder, R.; De Visser, C. EIP-AGRI Focus Group on protein crops: Final Report; European Commission: Brussels, Belgium, 2014. [Google Scholar]
- Magrini, M.-B.; Anton, M.; Choleza, C.; Corre-Hellou, G.; Duc, G.; Jeuffroy, M.-H. Why are grain-legumes rarely present in cropping systems despite their environmental and nutritional benefits? Analyzing lock-in in the French agrifood system. Ecol. Econ. 2016, 126, 152–162. [Google Scholar] [CrossRef]
- Araújo, S.S.; Beebe, S.; Crespi, M.; Delbreil, B.; González, E.M.; Gruber, V. Abiotic stress responses in legumes: Strategies used to cope with environmental challenges. Crit. Rev. Plant Sci. 2015, 34, 237–280. [Google Scholar] [CrossRef]
- Alessandri, A.; De Felice, M.; Zeng, N.; Mariotti, A.; Pan, Y.; Cherchi, A. Robust assessment of the expansion and retreat of Mediterranean climate in the 21st century. Sci. Rep. 2014, 4, 7211. [Google Scholar] [CrossRef]
- Annicchiarico, P. Adaptation of cool-season grain legume species across climatically-contrasting environments of southern Europe. Agron. J. 2008, 100, 1647–1654. [Google Scholar] [CrossRef]
- Warkentin, T.; Smykal, P.; Coyne, C.J.; Weeden, N.; Domoney, C.; Bing, D. Pea (Pisum sativum L.). In Handbook of Plant Breeding: Grain Legumes; De Ron, A., Ed.; Springer Science and Business Media: New York, NY, USA, 2015; pp. 37–83. [Google Scholar]
- Annicchiarico, P. Feed legumes for truly sustainable crop-animal systems. It. J. Agron. 2017, 12, 880. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Thami-Alami, I.; Abbas, K.; Pecetti, L.; Melis, R.A.M.; Porqueddu, C. Performance of legume-based annual forage crops in three semi-arid Mediterranean environments. Crop Pasture Sci. 2017, 68, 932–941. [Google Scholar] [CrossRef]
- Carrouée, B.; Crépon, K.; Peyronnet, C. Les protéagineux: Intérêt dans les systèmes de production fourragers français et européens. Fourrages 2003, 174, 163–182. [Google Scholar]
- Meuwissen, T.H.E.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [CrossRef] [PubMed]
- Wiggans, G.R.; Cole, J.B.; Hubbard, S.M.; Sonstegard, T.S. Genomic selection in dairy cattle: The USDA experience. Ann. Rev. Anim. Biosci. 2017, 5, 309–327. [Google Scholar] [CrossRef]
- Elshire, R.J.; Glaubitz, J.C.; Sun, Q.; Poland, J.A.; Kawamoto, K.; Buckler, E.S. A robust, simple genotyping-by-sequencing (GBS) approach for high diversity species. PLoS ONE 2011, 6, 19379. [Google Scholar] [CrossRef]
- Elbasyoni, I.S.; Lorenz, A.J.; Guttieri, M.; Frels, K.; Baenziger, P.S.; Poland, J.; Akhunov, E. A comparison between genotyping-by-sequencing and array-based scoring of SNPs for genomic prediction accuracy in winter wheat. Plant Sci. 2018, 270, 123–130. [Google Scholar] [CrossRef]
- Varshney, R.K.; Kudapa, H.; Pazhamala, L.; Chitikineni, A.; Thudi, M.; Bohra, A. Translational genomics in agriculture: Some examples in grain legumes. Crit. Rev. Plant Sci. 2015, 34, 169–194. [Google Scholar] [CrossRef]
- Jarquín, D.; Kocak, K.; Posadas, L.; Hyma, K.; Jedlicka, J.; Graef, G. Genotyping by sequencing for genomic prediction in a soybean breeding population. BMC Genomics 2014, 15, 740. [Google Scholar] [CrossRef]
- Jarquín, D.; Specht, J.; Lorenz, A. Prospects of genomic prediction in the USDA soybean germplasm collection: Historical data creates robust models for enhancing selection of accessions. G3 (Bethesda) 2016, 6, 2329–2341. [Google Scholar] [CrossRef]
- Duhnen, A.; Gras, A.; Teyssèdre, S.; Romestant, M.; Claustres, B.; Daydé, J. Genomic selection for yield and seed protein content in soybean: A study of breeding program data and assessment of prediction accuracy. Crop Sci. 2017, 57, 1325–1337. [Google Scholar] [CrossRef]
- Ma, Y.; Reif, J.C.; Jiang, Y.; Wen, Z.; Wang, D.; Liu, Z. Potential of marker selection to increase prediction accuracy of genomic selection in soybean (Glycine max L.). Mol. Breed. 2016, 36, 113. [Google Scholar] [CrossRef] [PubMed]
- Annicchiarico, P.; Nazzicari, N.; Ferrari, B.; Harzic, N.; Carroni, A.M.; Romani, M.; Pecetti, L. Genomic prediction of grain yield in contrasting environments for white lupin genetic resources. Mol. Breed. 2019, 39, 142. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Nazzicari, N.; Pecetti, L.; Romani, M.; Russi, L. Pea genomic selection for Italian environments. BMC Genomics 2019, 20, 603. [Google Scholar] [CrossRef] [PubMed]
- Roorkiwal, M.; Rathore, A.; Das, R.R.; Singh, M.K.; Jain, A.; Srinivasan, S. Genome-enabled prediction models for yield related traits in chickpea. Front. Plant Sci. 2016, 7, 1666. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Nazzicari, N.; Pecetti, L.; Romani, M.; Ferrari, B.; Wei, Y. GBS-based genomic selection for pea grain yield under severe terminal drought. The Plant Genome 2017, 10. [Google Scholar] [CrossRef]
- Burstin, J.; Salloignon, P.; Chabert-Martinello, M.; Magnin-Robert, J.-B.; Siol, M.; Jacquin, F. Genetic diversity and trait genomic prediction in a pea diversity panel. BMC Genomics 2015, 16, 105. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Nazzicari, N.; Wei, Y.; Pecetti, L.; Brummer, E.C. Genotyping-by-sequencing and its exploitation for forage and cool-season grain legume breeding. Front. Plant Sci. 2017, 8, 679. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Iannucci, A. Winter survival of pea, faba bean and white lupin cultivars across contrasting Italian locations and sowing times, and implications for selection. J. Agric. Sci. 2007, 145, 611–622. [Google Scholar] [CrossRef]
- Cooper, M.; Stucker, R.E.; DeLacy, I.H.; Harch, B.D. Wheat breeding nurseries, target environments, and indirect selection for grain yield. Crop Sci. 1997, 37, 1168–1176. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Piano, E. Use of artificial environments to reproduce and exploit genotype × location interaction for lucerne in northern Italy. Theor. Appl. Genet. 2005, 110, 219–227. [Google Scholar] [CrossRef]
- Ceccarelli, S. Wide adaptation: How wide? Euphytica 1989, 40, 197–205. [Google Scholar] [CrossRef]
- Ceccarelli, S. Specific adaptation and breeding for marginal conditions. Euphytica 1994, 77, 205–219. [Google Scholar] [CrossRef]
- Sadras, V.O.; Lake, L.; Leonforte, A.; McMurray, L.S.; Paull, J.G. Screening field pea for adaptation to water and heat stress: Associations between yield, crop growth rate and seed abortion. Field Crops Res. 2013, 150, 63–73. [Google Scholar] [CrossRef]
- Annicchiarico, P.; Iannucci, A. Adaptation strategy, germplasm type and adaptive traits for field pea improvement in Italy based on variety responses across climatically contrasting environments. Field Crops Res. 2008, 108, 133–142. [Google Scholar] [CrossRef]
- Iglesias-García, R.; Prats, E.; Flores, F.; Amri, M.; Mikić, A.; Rubiales, D. Assessment of field pea (Pisum sativum L.) grain yield, aerial biomass and flowering date stability in Mediterranean environments. Crop Pasture Sci. 2017, 68, 915–923. [Google Scholar] [CrossRef]
- Pecetti, L.; Marcotrigiano, A.R.; Russi, L.; Romani, M.; Annicchiarico, P. Adaptation of field pea varieties to organic farming across different environments of Italy. Crop Pasture Sci. 2019, 70, 327–333. [Google Scholar] [CrossRef]
- Bocianowski, J.; Księżak, J.; Nowosad, K. Genotype by environment interaction for seeds yield in pea (Pisum sativum L.) using additive main effects and multiplicative interaction model. Euphytica 2019, 215, 191. [Google Scholar] [CrossRef]
- Rodríguez-Maribona, B.; Tenorio, J.L.; Conde, J.R.; Ayerbe, L. Correlation between yield and osmotic adjustment of peas (Pisum sativum L.) under drought stress. Field Crops Res. 1992, 29, 15–22. [Google Scholar] [CrossRef]
- Grzesiak, S.; Iijima, M.; Kono, Y.; Yamauchi, A. Differences in drought tolerance between cultivars of field bean and field pea. A comparison of drought-resistant and drought-sensitive cultivars. Acta Physiol. Plant. 1997, 19, 349–357. [Google Scholar] [CrossRef]
- Sánchez, F.J.; Manzanares, M.; de Andres, E.F.; Tenorio, J.L.; Ayerbe, L. Turgor maintenance, osmotic adjustment and soluble sugar and proline accumulation in 49 pea cultivars in response to water stress. Field Crops Res. 1998, 59, 225–235. [Google Scholar] [CrossRef]
- Blum, A. Effective use of water (EUW) and not water-use efficiency (WUE) is the target of crop yield improvement under drought stress. Field Crop Res. 2009, 112, 119–123. [Google Scholar] [CrossRef]
- Charmet, G.; Storlie, E.; Oury, F.X.; Laurent, V.; Beghin, D.; Chevarin, L. Genome-wide prediction of three important traits in bread wheat. Mol. Breed. 2014, 34, 1843–1852. [Google Scholar] [CrossRef] [PubMed]
- Brummer, E.C.; Li, X.; Wei, Y.; Hanson, J.L.; Viands, D.R. The imperative of improving yield of perennial forage crops: Will genomic selection help? Grassl. Sci. Eur. 2019, 24, 370–372. [Google Scholar]
- Lozada, D.N.; Mason, R.E.; Sarinelli, J.M.; Brown-Guedira, G. Accuracy of genomic selection for grain yield and agronomic traits in soft red winter wheat. BMC Genet. 2019, 20, 82. [Google Scholar] [CrossRef] [PubMed]
- Michel, S.; Ametz, C.; Gungor, H.; Akgöl, B.; Epure, D.; Grausgruber, H. Genomic assisted selection for enhancing line breeding: Merging genomic and phenotypic selection in winter wheat breeding programs with preliminary yield trials. Theor. Appl. Genet. 2017, 130, 363–376. [Google Scholar] [CrossRef]
- Beyene, Y.; Semagn, K.; Mugo, S.; Tarekegne, A.; Babu, R.; Meisel, B. Genetic gains in grain yield through genomic selection in eight bi-parental maize populations under drought stress. Crop Sci. 2015, 55, 154–163. [Google Scholar] [CrossRef]
- Beyene, Y.; Gowda, M.; Olsen, M.; Robbins, K.R.; Pérez-Rodríguez, P.; Alvarado, G. Empirical comparison of tropical maize hybrids selected through genomic and phenotypic selections. Front. Plant Sci. 2019, 10, 1502. [Google Scholar] [CrossRef]
- Môro, G.V.; Santos, M.F.; de Souza Jr, C.L. Comparison of genome-wide and phenotypic selection indices in maize. Euphytica 2019, 215, 76. [Google Scholar] [CrossRef]
- Sallam, A.; Smith, K.P. Genomic selection performs similarly to phenotypic selection in barley. Crop Sci. 2016, 56, 2871–2881. [Google Scholar] [CrossRef]
- Bernardo, R.; Yu, J. Prospects for genomewide selection for quantitative traits in maize. Crop Sci. 2007, 47, 1082–1090. [Google Scholar] [CrossRef]
- Massman, J.M.; Jung, H.J.G.; Bernardo, R. Genomewide selection versus marker-assisted recurrent selection to improve grain yield and stover-quality traits for cellulosic ethanol in maize. Crop Sci. 2013, 53, 1–9. [Google Scholar] [CrossRef]
- Annicchiarico, P. Scelta varietale in pisello e favino rispetto all’ambiente e all’utilizzo. Inf. Agr. 2005, 61, 47–52. [Google Scholar]
- Cochran, W.G.; Cox, G.M. Experimental Designs, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1957. [Google Scholar]
- Gauch, H.G.; Piepho, H.-P.; Annicchiarico, P. Statistical analysis of yield trials by AMMI and GGE: Further considerations. Crop Sci. 2008, 48, 866–889. [Google Scholar] [CrossRef]
- Piepho, H.-P. Robustness of statistical tests for multiplicative terms in the additive main effects and multiplicative interaction model for cultivar trials. Theor. Appl. Genet. 1995, 90, 438–443. [Google Scholar] [CrossRef]
- Robertson, A. The sampling variance of the genetic correlation coefficient. Biometrics 1959, 15, 469–485. [Google Scholar] [CrossRef]
- Falconer, D.S. Introduction to Quantitative Genetics, 3rd ed.; Longman: Harlow, UK, 1989. [Google Scholar]
- Cooper, M.; DeLacy, I.H.; Basford, K.E. Relationships among analytical methods used to analyse genotypic adaptation in multi-environment trials. In Plant Adaptation and Crop Improvement; Cooper, M., Hammer, G.L., Eds.; CABI: Wallingford, UK, 1996; pp. 193–224. [Google Scholar]
- DeLacy, I.H.; Basford, K.E.; Cooper, M.; Bull, I.K.; McLaren, C.G. Analysis of multi-environment trials – An historical perspective. In Plant Adaptation and Crop Improvement; Cooper, M., Hammer, G.L., Eds.; CABI: Wallingford, UK, 1996; pp. 39–124. [Google Scholar]
- SAS Institute. SAS/STAT® 9.3 User’s Guide; SAS Institute Inc.: Cary, NC, USA, 2011. [Google Scholar]
- IRRI. Cropstat Version 7.2; International Rice Research Institute: Manila, The Philippines, 2009. [Google Scholar]
- Schwender, H. Statistical Analysis of Genotype and Gene Expression Data. Available online: https://eldorado.tu-dortmund.de/handle/2003/23306 (accessed on 20 January 2020).
- Park, T.; Casella, G. The Bayesian Lasso. J. Am. Statist. Assoc. 2008, 103, 681–686. [Google Scholar] [CrossRef]
- Searle, S.R.; Casella, G.; McCulloch, C.E. Variance Components; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Wang, X.; Xu, Y.; Hu, Z.; Xu, C. Genomic selection methods for crop improvement: Current status and prospects. Crop J. 2018, 6, 330–340. [Google Scholar] [CrossRef]
- Lorenz, A.J.; Chao, S.; Asoro, F.G.; Heffner, E.L.; Hayashi, T.; Iwata, H.; Smith, K.P.; Sorrells, M.E.; Jannink, J.-L. Genomic selection in plant breeding: Knowledge and prospects. Adv. Agron. 2011, 110, 77–123. [Google Scholar] [CrossRef]
- Nazzicari, N.; Biscarini, F. GROAN: Genomic Regression Workbench (Version 1.0.0). Available online: https://cran.r-project.org/package=GROAN (accessed on 20 January 2020).
- Tayeh, N.; Aluome, C.; Falque, M.; Jacquin, F.; Klein, A.; Chauveau, A. Development of two major resources for pea genomics: The GenoPea 13.2K SNP Array and a high-density, high-resolution consensus genetic map. Plant J. 2015, 84, 1257–1273. [Google Scholar] [CrossRef]
- Kreplak, J.; Aubert, G. (INRA, Dijon, France). Personal communication, 2019. [Google Scholar]
- Kreplak, J.; Madoui, M.A.; Cápal, P.; Novák, P.; Labadie, K.; Aubert, G. A reference genome for pea provides insight into legume genome evolution. Nature Genet. 2019, 51, 1411–1422. [Google Scholar] [CrossRef]
- Li, H.; Durbin, R. Fast and accurate short read alignment with Burrows-Wheeler Transform. Bioinformatics 2009, 25, 1754–1760. [Google Scholar] [CrossRef] [PubMed]
- Heffner, E.L.; Lorenz, A.J.; Jannink, J.L.; Sorrells, M.E. Plant breeding with genomic selection: Gain per unit time and cost. Crop Sci. 2010, 50, 1681–1690. [Google Scholar] [CrossRef]
- Bassi, F.M.; Bentley, A.R.; Charmet, G.; Ortiz, R.; Crossa, J. Breeding schemes for the implementation of genomic selection in wheat (Triticum spp.). Plant Sci. 2016, 242, 23–36. [Google Scholar] [CrossRef] [PubMed]
| Exp. | Environment | Sowing Date 1 | Harvest Date 1 | Available Water (mm) 2 | Last Month’s Mean Temperature (°C) 3 | Mean Yield (t/ha) | Yield of Top-Yielding Line (t/ha) |
|---|---|---|---|---|---|---|---|
| Exp. 1 | MS Lodi | Feb. 25, 2015 | Jun. 3, 2015 | 120 | 19.3 | 0.32 | 0.75 |
| Exp. 2 | Marchouch | Nov. 28, 2015 | May 26, 2016 | 59 | 18.1 | 0.36 | 0.91 |
| Exp. 3 | Alger | Dec. 8, 2015 | May 18, 2016 | 327 | 20.3 | 1.38 | 3.33 |
| Exp. 4, 5, 6 | MS Lodi | Apr. 12, 2017 | Jun. 24, 2017 | 115 | 23.4 | 0.424 | - |
| Target Environment | Hj2 | Hj’2 | rg(j,j’) | Er, PS in MS a | rAbb | Er, GS c | ||
|---|---|---|---|---|---|---|---|---|
| A | B | A | B | |||||
| Marchouch | 0.475 | 0.870 | 0.408 | 0.550 | 0.240 | 0.260 | 0.633 | 0.685 |
| Alger | 0.522 | 0.870 | 0.015 | 0.021 | 0.184 | 0.031 | 0.441 | 0.074 |
| MS Lodi | 0.870 | − | − | − | 0.741 | 0.713 | 1.066 | 1.023 |
| Trait | Bayesian Lasso | Ridge Regression BLUP | ||
|---|---|---|---|---|
| All | Single | All | Single | |
| Yield, MS Lodi | 0.741 | 0.708 | 0.707 | 0.693 |
| Yield, Marchouch | 0.240 | 0.214 | 0.240 | 0.217 |
| Yield, Alger | 0.181 | 0.156 | 0.184 | 0.160 |
| Mean yield, MS Lodi and Marchouch 1 | 0.692 | 0.668 | 0.682 | 0.650 |
| Trait | Training Populations | |
|---|---|---|
| One | Two | |
| Yield, Alger | 0.099 | 0.151 |
| Mean yield, MS Lodi, and Marchouch 1 | 0.397 | 0.630 |
| Line Group | Total no. of Lines | Yield (t/ha Dry Weight) | Aerial Biomass (t/ha Dry Weight) | Onset of Flowering (dd from April 1) | |
|---|---|---|---|---|---|
| Value | Difference to Parent Line Group | ||||
| Experiment 4 1 | |||||
| PS in MS Lodi | 9 | 0.749 ** | 0.495 | 3.264 ** | 26.2 ** |
| GS, RIL population-specific model | 9 | 0.655 ** | 0.401 | 3.299 ** | 27.4 ** |
| PS across MS Lodi and Marchouch | 9 | 0.653 ** | 0.399 | 3.216 * | 27.4 ** |
| GS, model trained on all populations | 9 | 0.642 ** | 0.388 | 3.015 | 26.2 ** |
| PS in Marchouch | 9 | 0.540 ** | 0.286 | 3.094 | 28.5 ** |
| Parent lines | 3 | 0.254 | - | 2.819 | 30.8 |
| LSD (p < 0.05) | 0.104 | 0.195 | 0.5 | ||
| Experiment 5 2 | |||||
| GS, top-performing lines | 6 | 0.353 * | 0.128 | 2.786 | 31.2 |
| GS, mid-performing lines | 6 | 0.134 | −0.091 | 2.747 | 35.5 ** |
| GS, bottom-performing lines | 6 | 0.121 | −0.104 | 2.581 | 35.3 ** |
| Parent lines | 3 | 0.225 | - | 2.686 | 32.7 |
| LSD (p < 0.05) | 0.068 | 0.253 | 1.5 | ||
| Experiment 6 3 | |||||
| GS, top-performing lines | 9 | 0.638 ** | 0.286 | 3.375 ** | 28.8 |
| MAS, top-performing lines | 9 | 0.595 ** | 0.243 | 3.031 ** | 28.3 |
| GS/MAS mid-performing lines | 6 | 0.462 | 0.110 | 3.059 ** | 28.6 |
| GS, bottom-performing lines | 9 | 0.290 | −0.062 | 2.649 | 29.3 |
| MAS, bottom-performing lines | 9 | 0.208 | −0.144 | 2.597 | 30 |
| Parent lines | 2 | 0.352 | - | 2.506 | 28.6 |
| LSD (p < 0.05) | 0.114 | 0.297 | 1.0 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Annicchiarico, P.; Nazzicari, N.; Laouar, M.; Thami-Alami, I.; Romani, M.; Pecetti, L. Development and Proof-of-Concept Application of Genome-Enabled Selection for Pea Grain Yield under Severe Terminal Drought. Int. J. Mol. Sci. 2020, 21, 2414. https://doi.org/10.3390/ijms21072414
Annicchiarico P, Nazzicari N, Laouar M, Thami-Alami I, Romani M, Pecetti L. Development and Proof-of-Concept Application of Genome-Enabled Selection for Pea Grain Yield under Severe Terminal Drought. International Journal of Molecular Sciences. 2020; 21(7):2414. https://doi.org/10.3390/ijms21072414
Chicago/Turabian StyleAnnicchiarico, Paolo, Nelson Nazzicari, Meriem Laouar, Imane Thami-Alami, Massimo Romani, and Luciano Pecetti. 2020. "Development and Proof-of-Concept Application of Genome-Enabled Selection for Pea Grain Yield under Severe Terminal Drought" International Journal of Molecular Sciences 21, no. 7: 2414. https://doi.org/10.3390/ijms21072414
APA StyleAnnicchiarico, P., Nazzicari, N., Laouar, M., Thami-Alami, I., Romani, M., & Pecetti, L. (2020). Development and Proof-of-Concept Application of Genome-Enabled Selection for Pea Grain Yield under Severe Terminal Drought. International Journal of Molecular Sciences, 21(7), 2414. https://doi.org/10.3390/ijms21072414





