Modeling Anomalous Moisture Transport in Cement-Based Materials with Kinetic Permeability
Abstract
1. Introduction
2. Results
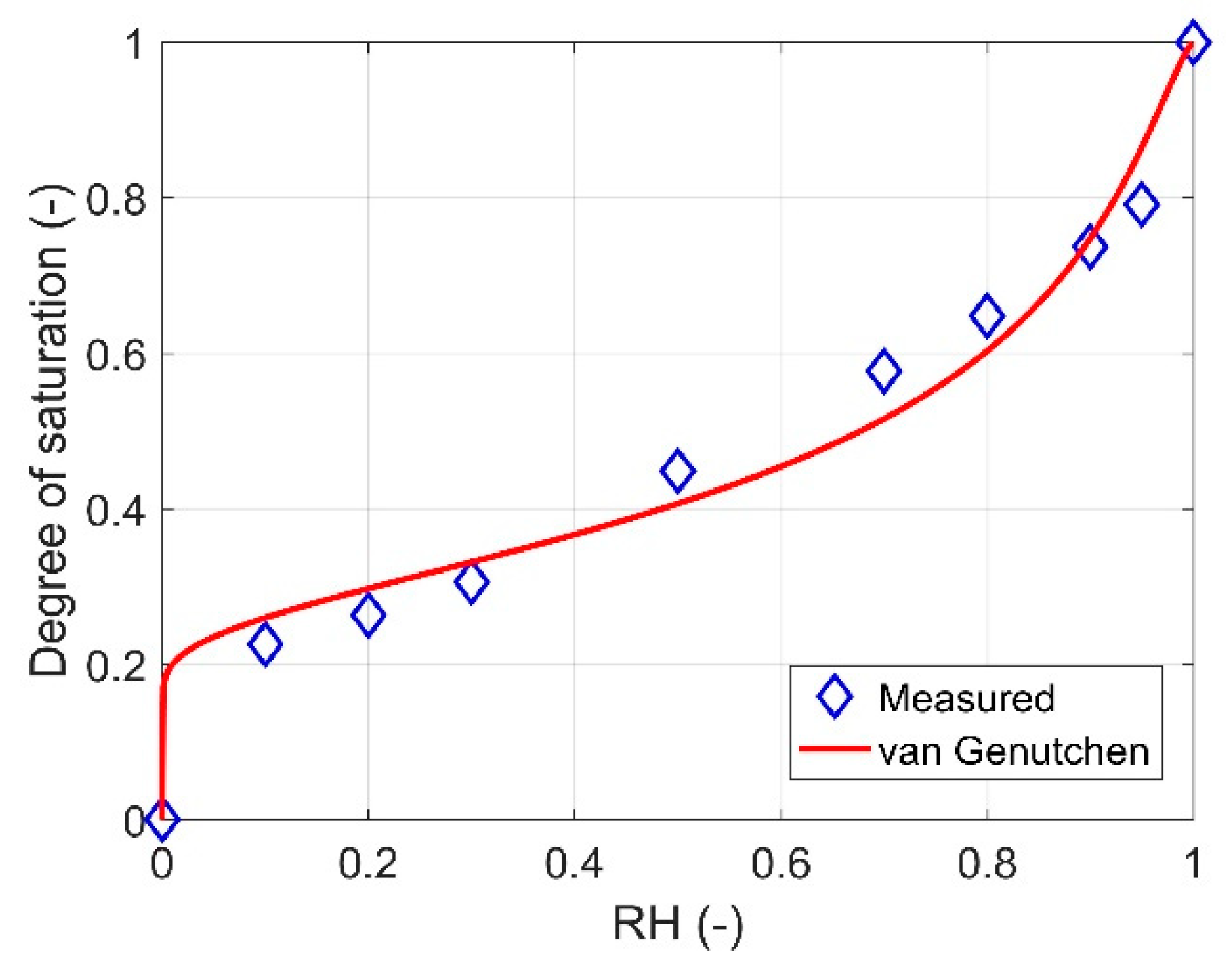
2.1. Fitted Sorption Isotherm
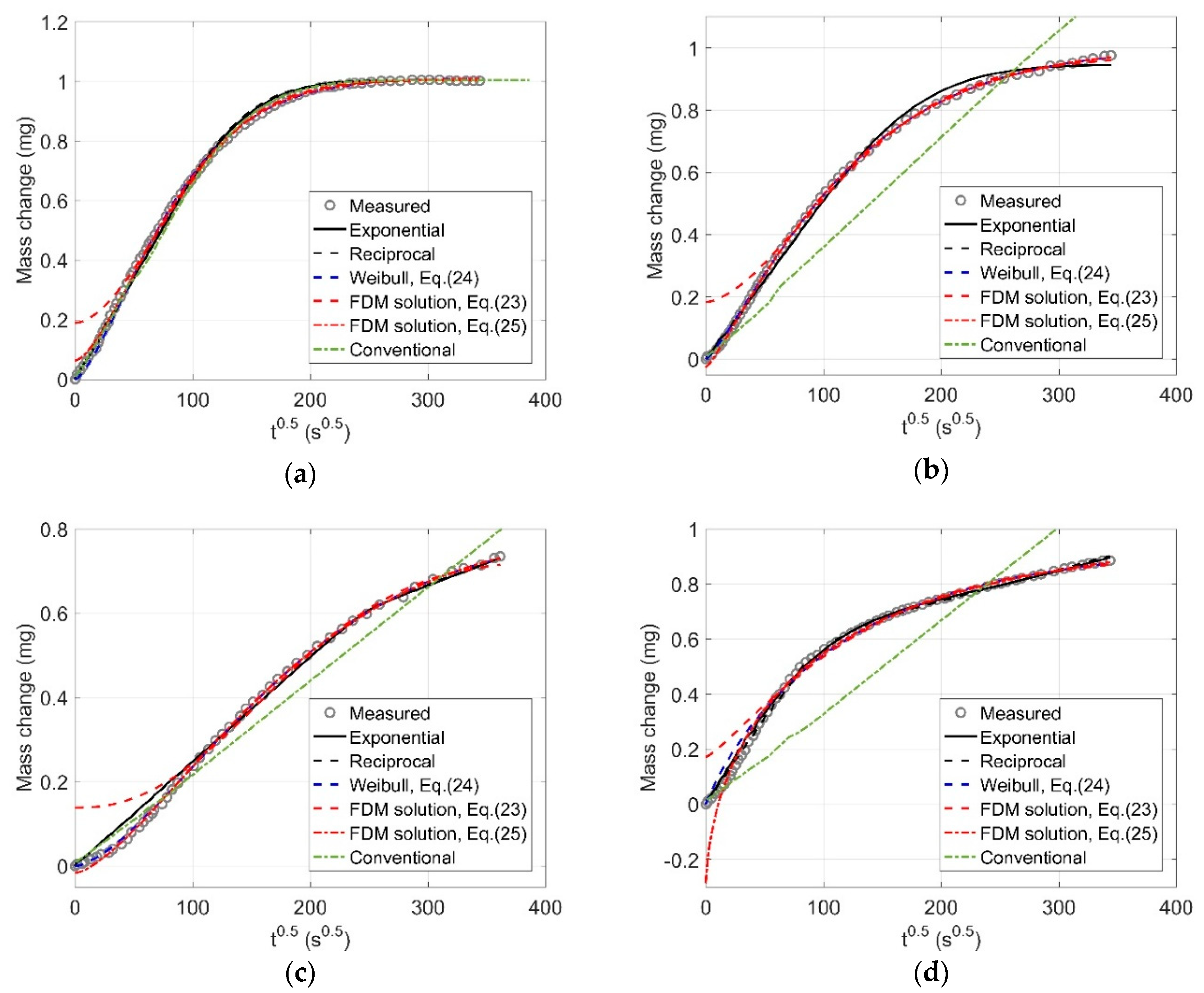
2.2. Fitted Mass Change Curves
3. Discussion
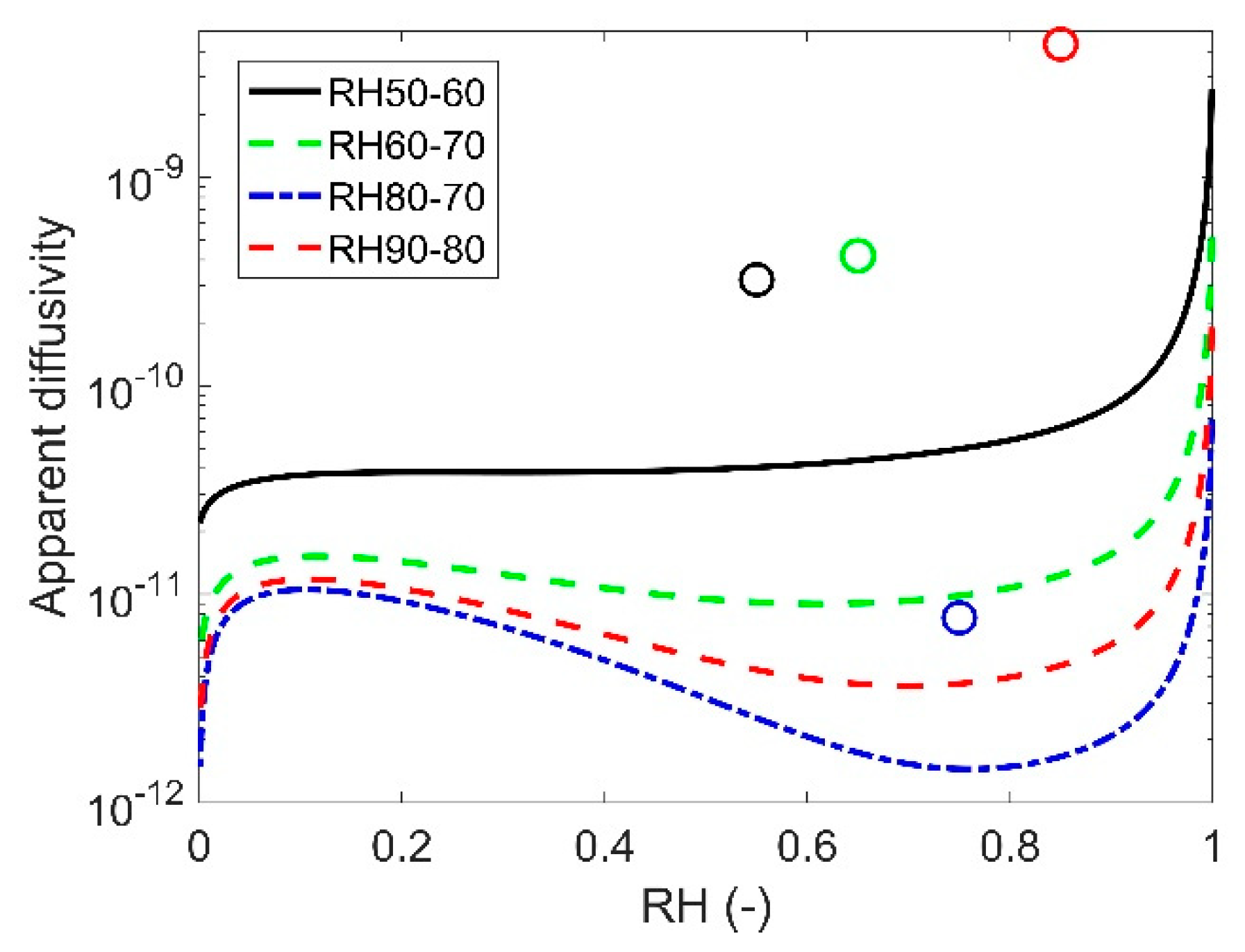
3.1. Apparent Diffusivity
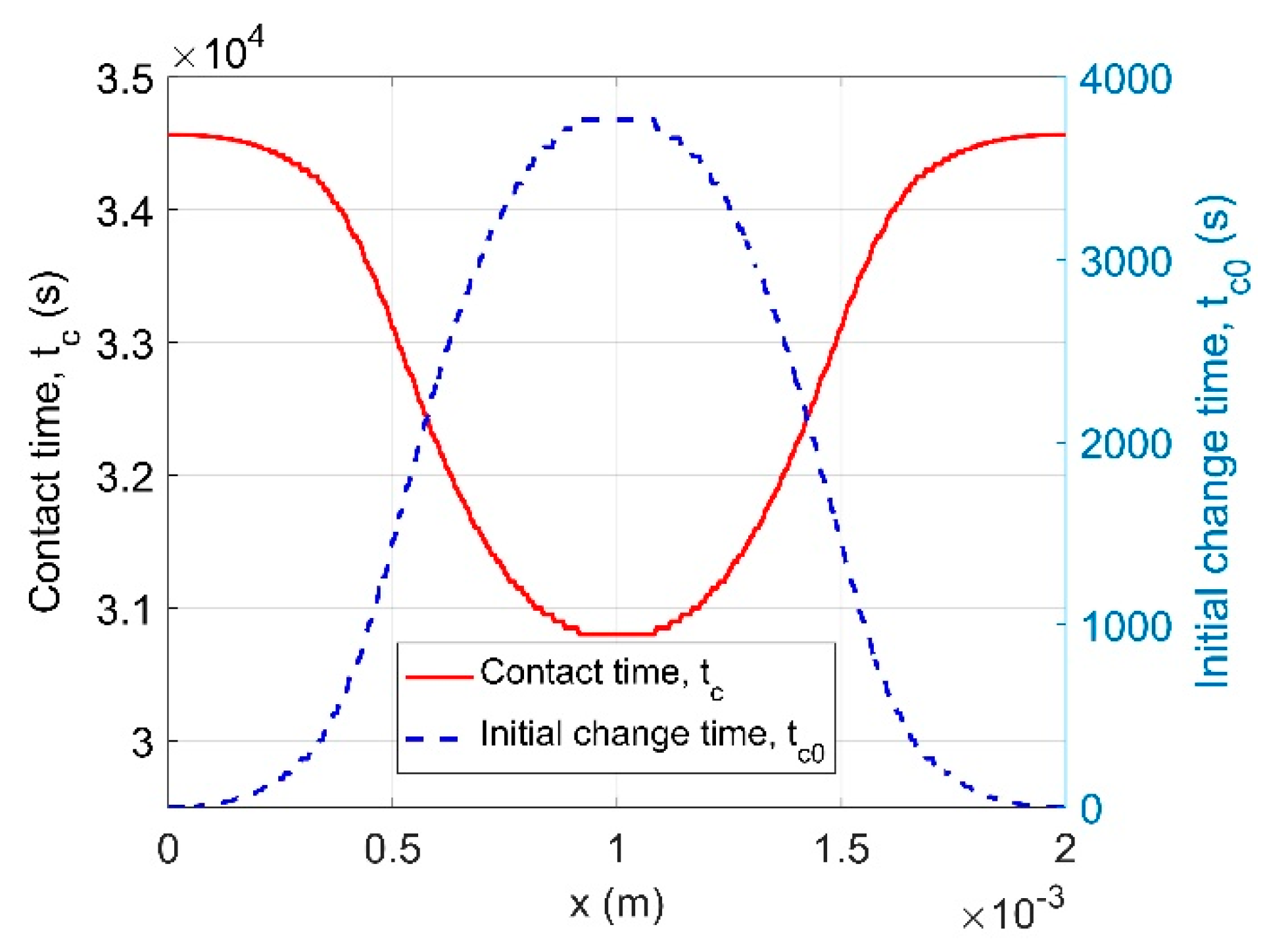
3.2. Validation Data
4. Materials and Methods
4.1. Proposed Moisture Transport with Kinetic Permeability
4.1.1. Conventional Moisture Transport Model
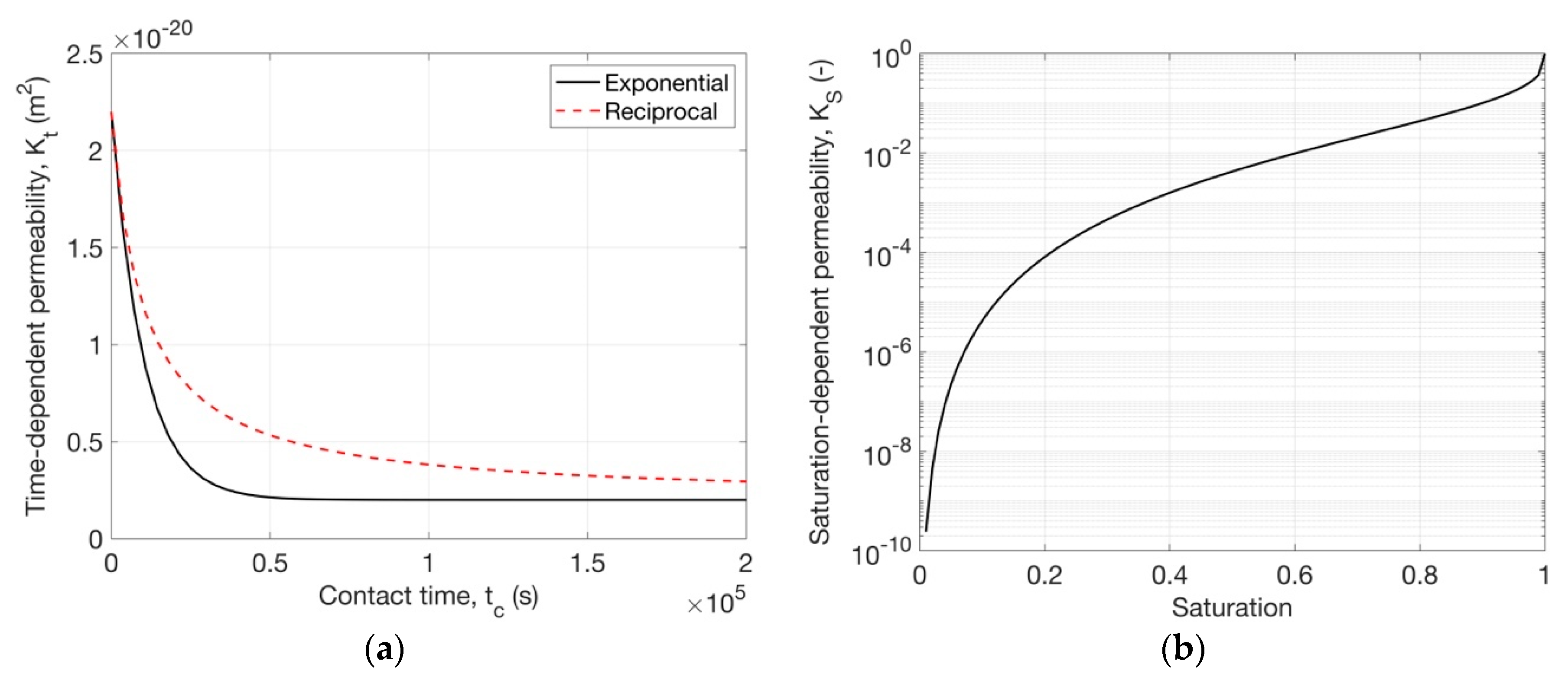
4.1.2. Time-Dependent Permeability
4.1.3. Saturation-Dependent Permeability
4.2. Fractional Derivative Model (FDM) of Diffusion Model
4.3. Experimental Data
4.4. Application Procedure
5. Conclusions
- The proposed model can improve the simulation results compared with the conventional model and the dual-permeability model. The main reason is that the time-dependent permeability is used in the model.
- The time-dependent permeability can be calculated either by an exponential function or by a reciprocal function. Both functions provided very similar results.
- The two simplified solutions to the fractional derivative model were not able to provide appropriate mass change curves because their curves do not pass through the origin.
- Weibull function can provide results as good as the proposed model, but the empirical equation lacks physical meanings. It may be useful for determining the final mass of a specimen when measuring the sorption isotherm.
Author Contributions
Funding
Conflicts of Interest
References
- USGS. Mineral Commodity Summaries 2019; U.S. Geological Survey: Reston, VA, USA, 2019. Available online: http://prd-wret.s3-us-west-2.amazonaws.com/assets/palladium/production/atoms/files/mcs2019_all.pdf (accessed on 8 January 2020).
- Angst, U.M. Challenges and Opportunities in Corrosion of Steel in Concrete. Mater. Struct. 2018, 51, 4. [Google Scholar] [CrossRef]
- Angst, U. Chloride Induced Reinforcement Corrosion in Concrete—Concept of Critical Chloride Content—Methods and Mechanisms. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2011. [Google Scholar]
- Nilsson, L.-O. Water and the Hygro-Thermal Characteristics of Hardened Concrete; Conseil International de la Langue Francaise: St-Remy-les-Chevreuse, France, 1985. [Google Scholar]
- Baroghel-Bouny, V.; Wang, X.; Thiery, M.; Saillio, M.; Barberon, F. Prediction of Chloride Binding Isotherms of Cementitious Materials by “Analytical” Model or “Numerical” Inverse Analysis. Cem. Concr. Res. 2012, 42, 1207–1224. [Google Scholar] [CrossRef]
- Mao, L.; Hu, Z.; Xia, J.; Feng, G.; Azim, I.; Yang, J.; Liu, Q. Multi-Phase Modelling of Electrochemical Rehabilitation for ASR and Chloride Affected Concrete Composites. Compos. Struct. 2019, 207, 176–189. [Google Scholar] [CrossRef]
- Hong, K.; Hooton, R.D. Effects of Cyclic Chloride Exposure on Penetration of Concrete Cover. Cem. Concr. Res. 1999, 29, 1379–1386. [Google Scholar] [CrossRef]
- Baroghel-Bouny, V.; Thiery, M.; Dierkens, M.; Wang, X. Aging and Durability of Concrete in Lab and in Field Conditions – Pore Structure and Moisture Content Gradients between Inner and Surface Zones in RC Structural Elements. J. Sustain. Cem. Mater. 2017, 6, 149–194. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Najjar, L.J. Nonlinear Water Diffusion in Nonsaturated Concrete. Matériaux Constr. 1972, 5, 3–20. [Google Scholar] [CrossRef]
- Coussy, O. Mechanics of Porous Continua; John Wiley and Sons Ltd.: Chichester, UK, 1995. [Google Scholar]
- Mainguy, M.; Coussy, O.; Baroghel-Bouny, V. Role of Air Pressure in Drying of Weakly Permeable Materials. J. Eng. Mech. 2001, 127, 582–592. [Google Scholar] [CrossRef]
- Philip, J.R.; De Vries, D.A.; Vries, D.A.D. Moisture Movement in Porous Materials under Temperature Gradients. Trans. Am. Geophys. Union 1957, 38, 222–232. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media. Soil Sci. 1975, 120, 162–163. [Google Scholar] [CrossRef]
- Hall, C.; Hoff, W.D.; Taylor, S.C.; Wilson, M.A.; Yoon, B.G.; Reinhardt, H.W.; Sosoro, M.; Meredith, P.; Donald, A.M. Water Anomaly in Capillary Liquid Absorption by Cement-Based Materials. J. Mater. Sci. Lett. 1993, 14, 1178–1181. [Google Scholar] [CrossRef]
- Taylor, S.C.; Hoff, W.D.; Wilson, M.A.; Green, K.M. Anomalous Water Transport Properties of Portland and Blended Cement-Based Materials. J. Mater. Sci. Lett. 1999, 18, 1925–1927. [Google Scholar] [CrossRef]
- Saeidpour, M.; Wadsö, L. Evidence for Anomalous Water Vapor Sorption Kinetics in Cement Based Materials. Cem. Concr. Res. 2015, 70, 60–66. [Google Scholar] [CrossRef]
- Wadsö, L. A Critical Review on Anomalous or Non-Fickian Vapor Sorption; Report No.: Intern 7000; Lund University: Lund, Sweden, 1992; Available online: https://lup.lub.lu.se/search/publication/75d4f4ad-3ff1-4ba2-a555-b724377710dd (accessed on 26 January 2020).
- Zhang, Z.; Angst, U. Modelling Anomalous Moisture Transport in Cement-Based Materials by the Dual- Permeability Concept. Transp. Porous Media 2020. under review. [Google Scholar]
- Zhang, Z.; Thiery, M.; Baroghel-Bouny, V. An Equation of Drying Kinetics for Cementitious Materials. Dry. Technol. 2018, 36, 1446–1459. [Google Scholar] [CrossRef]
- Lockington, D.; Parlange, J.-Y.; Dux, P. Sorptivity and the Estimation of Water Penetration into Unsaturated Concrete. Mater. Struct. 1999, 32, 342–347. [Google Scholar] [CrossRef]
- Mindess, S.; Young, J.F. Concrete; Prentice-Hall: Englewood Cliffs, NJ, USA, 1983. [Google Scholar]
- Zeng, Q.; Xu, S. A Two-Parameter Stretched Exponential Function for Dynamic Water Vapor Sorption of Cement-Based Porous Materials. Mater. Struct. 2017, 50, 128. [Google Scholar] [CrossRef]
- Scherer, G.W. Drying, Shrinkage, and Cracking of Cementitious Materials. Transp. Porous Media 2015, 110, 311–331. [Google Scholar] [CrossRef]
- Zhou, C.; Ren, F.; Wang, Z.; Chen, W.; Wang, W. Why Permeability to Water Is Anomalously Lower than That to Many Other Fluids for Cement-Based Material? Cem. Concr. Res. 2017, 100, 373–384. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.; Zhang, X.; Korošak, D. Anomalous Diffusion Modeling by Fractal and Fractional Derivatives. Comput. Math. Appl. 2010, 59, 1754–1758. [Google Scholar] [CrossRef]
- Gerolymatou, E.; Vardoulakis, I.; Hilfer, R. Modelling Infiltration by Means of a Nonlinear Fractional Diffusion Model. J. Phys. D. Appl. Phys. 2006, 39, 4104–4110. [Google Scholar] [CrossRef]
- Zhang, L.; Ren, Q.; Li, Z.; Zhang, G. Predicting the Drying of Concrete by an Anomalous Diffusion Model. J. Mater. Civ. Eng. 2019, 31. [Google Scholar] [CrossRef]
- Simpson, R.; Ramírez, C.; Nuñez, H.; Jaques, A.; Almonacid, S. Understanding the Success of Page’s Model and Related Empirical Equations in Fitting Experimental Data of Diffusion Phenomena in Food Matrices. Trends Food Sci. Technol. 2017, 62, 194–201. [Google Scholar] [CrossRef]
- Guerrini, I.A.; Swartzendruber, D. Soil Water Diffusivity as Explicitly Dependent on Both Time and Water Content. Soil Sci. Soc. Am. J. 1992, 56, 335–340. [Google Scholar] [CrossRef]
- Lockington, D.A.; Parlange, J.Y. Anomalous Water Absorption in Porous Materials. J. Phys. D. Appl. Phys. 2003, 36, 760–767. [Google Scholar] [CrossRef]
- Hall, C. Capillary Imbibition in Cement-Based Materials with Time-Dependent Permeability. Cem. Concr. Res. 2019, 124, 105835. [Google Scholar] [CrossRef]
- Baroghel-Bouny, V. Water Vapour Sorption Experiments on Hardened Cementitious Materials. Part I: Essential Tool for Analysis of Hygral Behaviour and Its Relation to Pore Structure. Cem. Concr. Res. 2007, 37, 414–437. [Google Scholar] [CrossRef]
- Pinson, M.B.; Zhao, T.; Jennings, H.M.; Bazant, M.Z. Inferring pore connectivity from sorption hysteresis in multiscale porous media. J. Colloid Interface Sci. 2018, 532, 118–127. [Google Scholar] [CrossRef]
- Maruyama, I.; Rymeš, J.; Vandamme, M.; Coasne, B. Cavitation of Water in Hardened Cement Paste under Short-Term Desorption Measurements. Mater. Struct. 2018, 51. [Google Scholar] [CrossRef]
- Sing, K.S.W. Reporting Physisorption Data for Gas/Solid Systems with Special Reference to the Determination of Surface Area and Porosity (Recommendations 1984). Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Zhang, Z. Modelling of Sorption Hysteresis and Its Effect on Moisture Transport Within Cementitious Materials, Universite Paris-Est. 2014. Available online: https://tel.archives-ouvertes.fr/tel-01127302 (accessed on 26 January 2020).
- Mualem, Y. Hysteretical Models for Prediction of the Hydraulic Conductivity of Unsaturated Porous Media. Water Resour. Res. 1976, 12, 1248–1254. [Google Scholar] [CrossRef]
- Zhang, Z.; Thiery, M.; Baroghel-Bouny, V. Investigation of Moisture Transport Properties of Cementitious Materials. Cem. Concr. Res. 2016, 89, 257–268. [Google Scholar] [CrossRef]
- Zhang, Z.; Scherer, G.W. Determination of Water Permeability for a Moisture Transport Model with Minimized Batch Effect. Constr. Build. Mater. 2018, 191, 193–205. [Google Scholar] [CrossRef]
- Carette, J.; Soleilhet, F.; Benboudjema, F.; Ma, X.; Nahas, G.; Abahri, K.; Darquennes, A.; Bennacer, R. Identifying the Mechanisms of Concrete Drying: An Experimental-Numerical Approach. Constr. Build. Mater. 2020, 230, 117001. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary Conduction of Liquids through Porous Mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Bear, J.; Verruijt, A. Modeling Groundwater Flow and Pollution; Reidel Book Co.: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Xi, Y.; Bažant, Z.P.; Molina, L.; Jennings, H.M. Moisture Diffusion in Cementitious Materials Moisture Capacity and Diffusivity. Adv. Cem. Based Mater. 1994, 1, 258–266. [Google Scholar] [CrossRef]
- Baroghel-Bouny, V. Water Vapour Sorption Experiments on Hardened Cementitious Materials. Part II: Essential Tool for Assessment of Transport Properties and for Durability Prediction. Cem. Concr. Res. 2007, 37, 438–454. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils1. Soil Sci. Soc. Am. J. 1980, 44, 892. [Google Scholar] [CrossRef]
- Savage, B.M.; Janssen, D.J. Soil Physics Principles Validated for Use in Predicting Unsaturated Moisture Movement in Portland Cement Concrete. ACI Mater. J. 1997, 94, 63–70. [Google Scholar] [CrossRef]
- Millington, R.J.; Quirk, J.P. Permeability of Porous Solids. Trans. Faraday Soc. 1961, 57, 1200–1207. [Google Scholar] [CrossRef]
- Thiery, M.; Baroghel-Bouny, V.; Bourneton, N.; vilain, G.; Stéfani, C. Modélisation Du Séchage Des Bétons. Analyse Des Différents Modes de Transfert Hydrique. Rev. Eur. Génie Civ. 2007, 11, 541–578. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Mualem, Y. A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media. Water Resour. Res. 1976, 12, 513. [Google Scholar] [CrossRef]
- Monlouis-Bonnaire, J.P.; Verdier, J.; Perrin, B. Prediction of the Relative Permeability to Gas Flow of Cement-Based Materials. Cem. Concr. Res. 2004, 34, 737–744. [Google Scholar] [CrossRef]
- Zhou, C. Predicting Water Permeability and Relative Gas Permeability of Unsaturated Cement-Based Material from Hydraulic Diffusivity. Cem. Concr. Res. 2014, 58, 143–151. [Google Scholar] [CrossRef]
- Leech, C.; Lockington, D.; Doug Hooton, R.; Galloway, G.; Cowin, G.; Dux, P. Validation of Mualem’s Conductivity Model and Prediction of Saturated Permeability from Sorptivity. ACI Mater. J. 2008, 105, 44–51. [Google Scholar] [CrossRef]
- Carlier, J.; Burlion, N. Experimental and Numerical Assessment of the Hydrodynamical Properties of Cementitious Materials. Transp. Porous Media 2011, 86, 87–102. [Google Scholar] [CrossRef]
- Küntz, M.; Lavallée, P. Experimental Evidence and Theoretical Analysis of Anomalous Diffusion during Water Infiltration in Porous Building Materials. J. Phys. D. Appl. Phys. 2001, 34, 2547–2554. [Google Scholar] [CrossRef]
- Li, Q.; Xu, S.; Zeng, Q. A Fractional Kinetic Model for Drying of Cement-Based Porous Materials. Dry. Technol. 2016, 34, 1231–1242. [Google Scholar] [CrossRef]
- Alderete, N.M.; Villagrán Zaccardi, Y.A.; De Belie, N. Physical Evidence of Swelling as the Cause of Anomalous Capillary Water Uptake by Cementitious Materials. Cem. Concr. Res. 2019, 120, 256–266. [Google Scholar] [CrossRef]
- Agrawal, O.P. Solution for a Fractional Diffusion-Wave Equation Defined in a Bounded Domain. Nonlinear Dyn. 2002, 29, 145–155. [Google Scholar] [CrossRef]
- Simpson, R.; Jaques, A.; Nuñez, H.; Ramirez, C.; Almonacid, A. Fractional Calculus as a Mathematical Tool to Improve the Modeling of Mass Transfer Phenomena in Food Processing. Food Eng. Rev. 2013, 5, 45–55. [Google Scholar] [CrossRef]
- Doymaz, I. Evaluation of Some Thin-Layer Drying Models of Persimmon Slices (Diospyros Kaki L.). Energy Convers. Manag. 2012, 56, 199–205. [Google Scholar] [CrossRef]
- Kucuk, H.; Midilli, A.; Kilic, A.; Dincer, I. A Review on Thin-Layer Drying-Curve Equations. Dry. Technol. 2014, 32, 757–773. [Google Scholar] [CrossRef]
- Zhang, Z.; Thiery, M.; Baroghel-Bouny, V. Numerical Modelling of Moisture Transfers with Hysteresis within Cementitious Materials: Verification and Investigation of the Effects of Repeated Wetting-Drying Boundary Conditions. Cem. Concr. Res. 2015, 68, 10–23. [Google Scholar] [CrossRef]
- Zhang, Z.; Thiéry, M.; Baroghel-Bouny, V. A Review and Statistical Study of Existing Hysteresis Models for Cementitious Materials. Cem. Concr. Res. 2014, 57, 44–60. [Google Scholar] [CrossRef]
- Carlier, J.P.; Rougelot, T.; Burlion, N. Performance Evaluation of Models Describing Sorption Isotherm in Cementitious Materials between Saturation and Oven Dryness. Constr. Build. Mater. 2012, 37, 58–66. [Google Scholar] [CrossRef]
| Models | Parameters | RH50-60 | RH60-70 | RH80-70 | RH90-80 |
|---|---|---|---|---|---|
| Proposed (Exponential , Equation (13)) | ( × 10−22) | 163.3 | 144.5 | 1.0 | 0.6 |
| ( × 10−22) | 9.4 | 5.7 | 3.5 | 11.4 | |
| 5.13 × 10−4 | 5.43 × 10−5 | 6.29 × 10−4 | 8.15 × 10−3 | ||
| 4.39 | 3.31 | 8.78 | 0.89 | ||
| 0.9983 | 0.9966 | 0.9963 | 0.9988 | ||
| Proposed (Reciprocal , Equation (14)) | ( × 10−22) | 171.3 | 144.8 | 0.8 | 0.6 |
| ( × 10−22) | 13.9 | 6.1 | 3.6 | 9.0 | |
| 6.33 × 10−4 | 8.65 × 10−5 | 6.00 × 10−4 | 7.68 × 10−3 | ||
| 3.10 | 2.57 | 7.96 | 2.24 | ||
| 0.9984 | 0.9966 | 0.9963 | 0.9988 | ||
| Weibull (Equation (24)) | 1.01 | 1.00 | 0.79 | 0.94 | |
| 8360 | 16134 | 38983 | 14129 | ||
| β | 0.71 | 0.61 | 0.77 | 0.45 | |
| 0.9988 | 0.9996 | 0.9996 | 0.9932 | ||
| Equation (23) (FDM) | 1.00 | 0.97 | 0.73 | 0.90 | |
| 11343 | 20532 | 41189 | 18405 | ||
| β | 0.91 | 0.83 | 1.15 | 0.60 | |
| 0.9965 | 0.9931 | 0.9897 | 0.9831 | ||
| 3.21 × 10−10 | 4.18 × 10−10 | 7.68 × 10−12 | 4.32 × 10−9 | ||
| Equation (25) (FDM) | 1.01 | 1.01 | 0.80 | 1.02 | |
| 9250 | 15589 | 39042 | 9489 | ||
| β | 0.76 | 0.59 | 0.74 | 0.32 | |
| 0.94 | 1.03 | 1.02 | 1.28 | ||
| 0.9983 | 0.9996 | 0.9997 | 0.9964 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Angst, U. Modeling Anomalous Moisture Transport in Cement-Based Materials with Kinetic Permeability. Int. J. Mol. Sci. 2020, 21, 837. https://doi.org/10.3390/ijms21030837
Zhang Z, Angst U. Modeling Anomalous Moisture Transport in Cement-Based Materials with Kinetic Permeability. International Journal of Molecular Sciences. 2020; 21(3):837. https://doi.org/10.3390/ijms21030837
Chicago/Turabian StyleZhang, Zhidong, and Ueli Angst. 2020. "Modeling Anomalous Moisture Transport in Cement-Based Materials with Kinetic Permeability" International Journal of Molecular Sciences 21, no. 3: 837. https://doi.org/10.3390/ijms21030837
APA StyleZhang, Z., & Angst, U. (2020). Modeling Anomalous Moisture Transport in Cement-Based Materials with Kinetic Permeability. International Journal of Molecular Sciences, 21(3), 837. https://doi.org/10.3390/ijms21030837






