Kinetic Analysis of the Thermal Decomposition of Iron(III) Phosphates: Fe(NH3)2PO4 and Fe(ND3)2PO4
Abstract
1. Introduction
2. Results
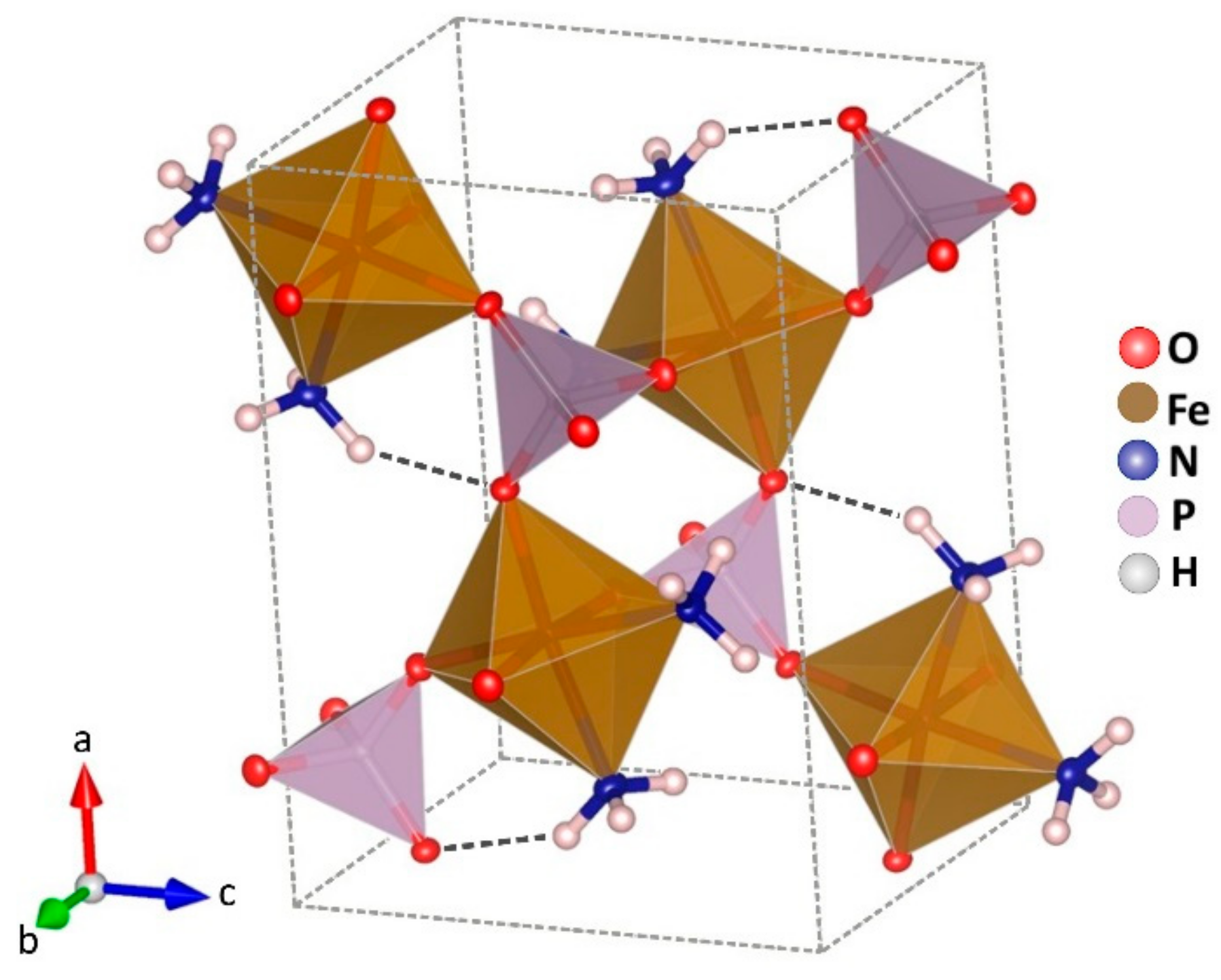
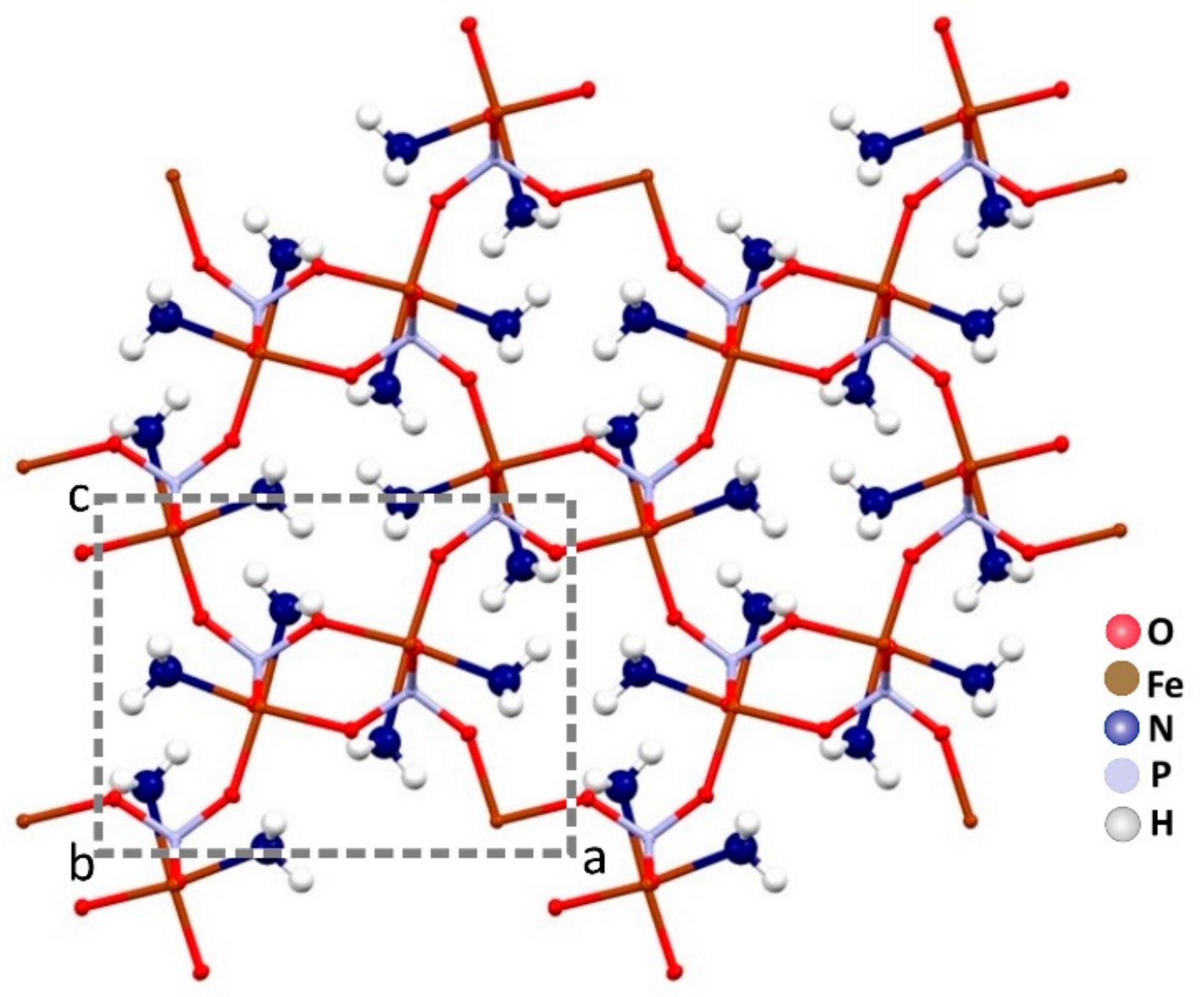
2.1. Morphological and Structural Results
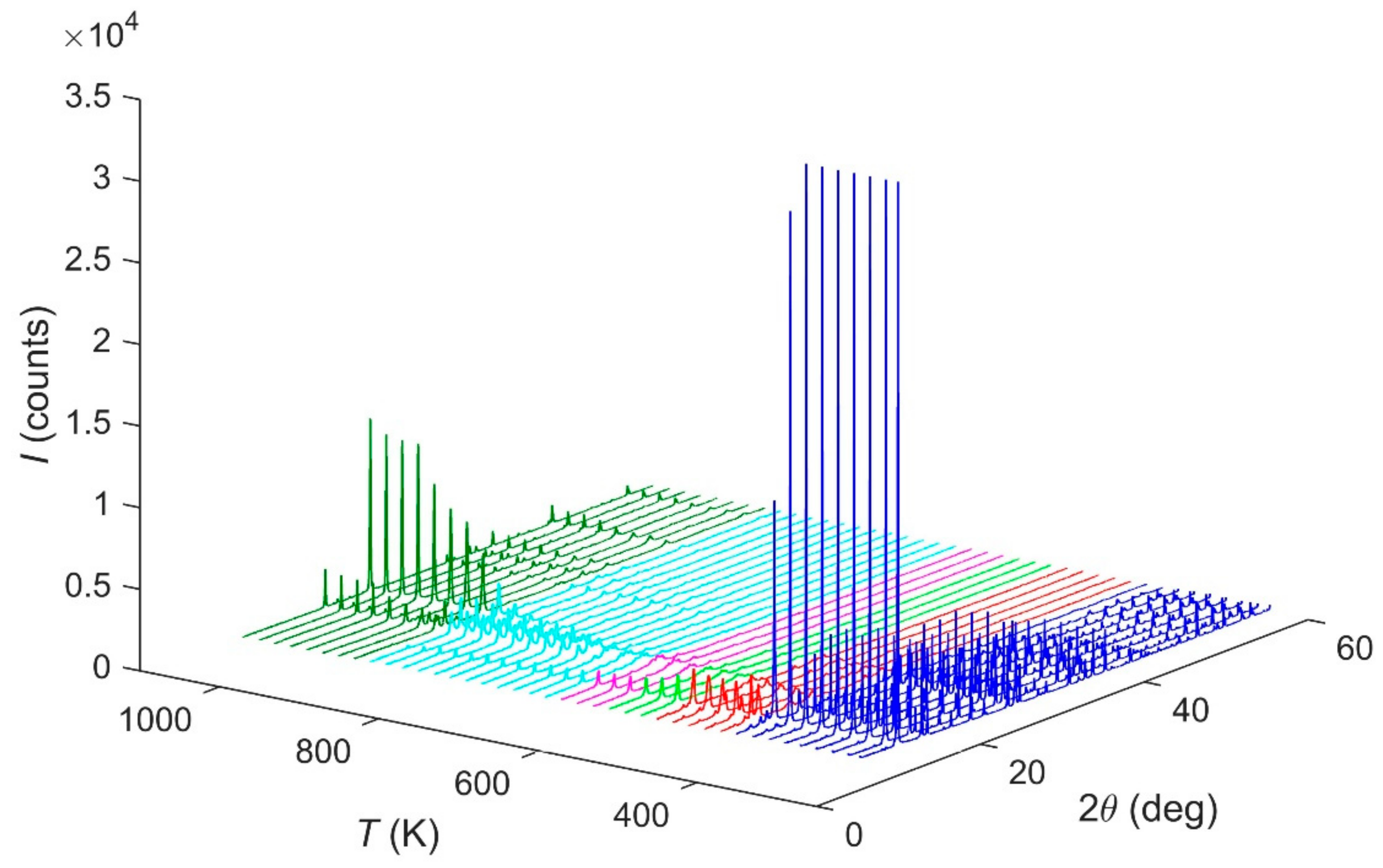
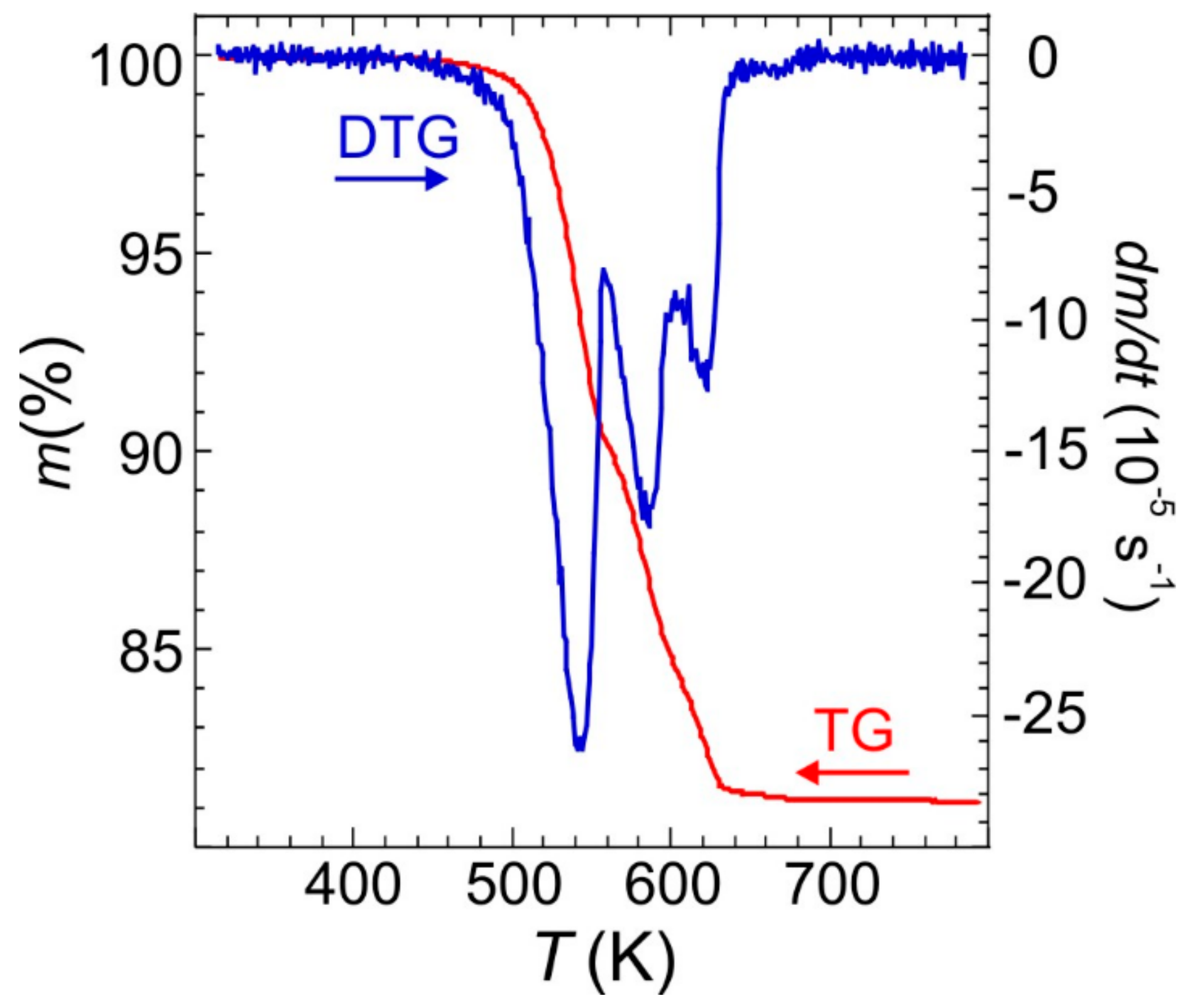
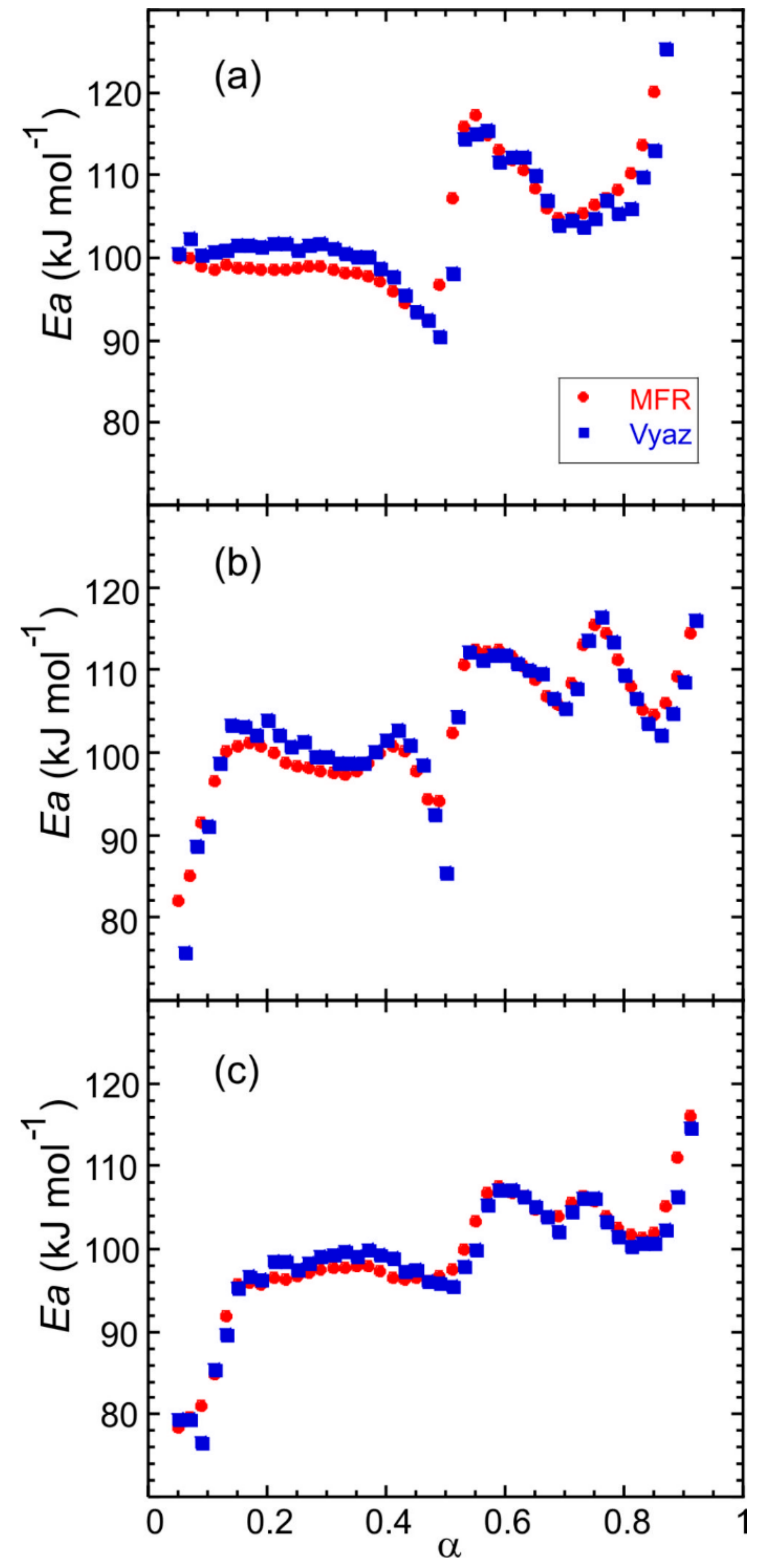
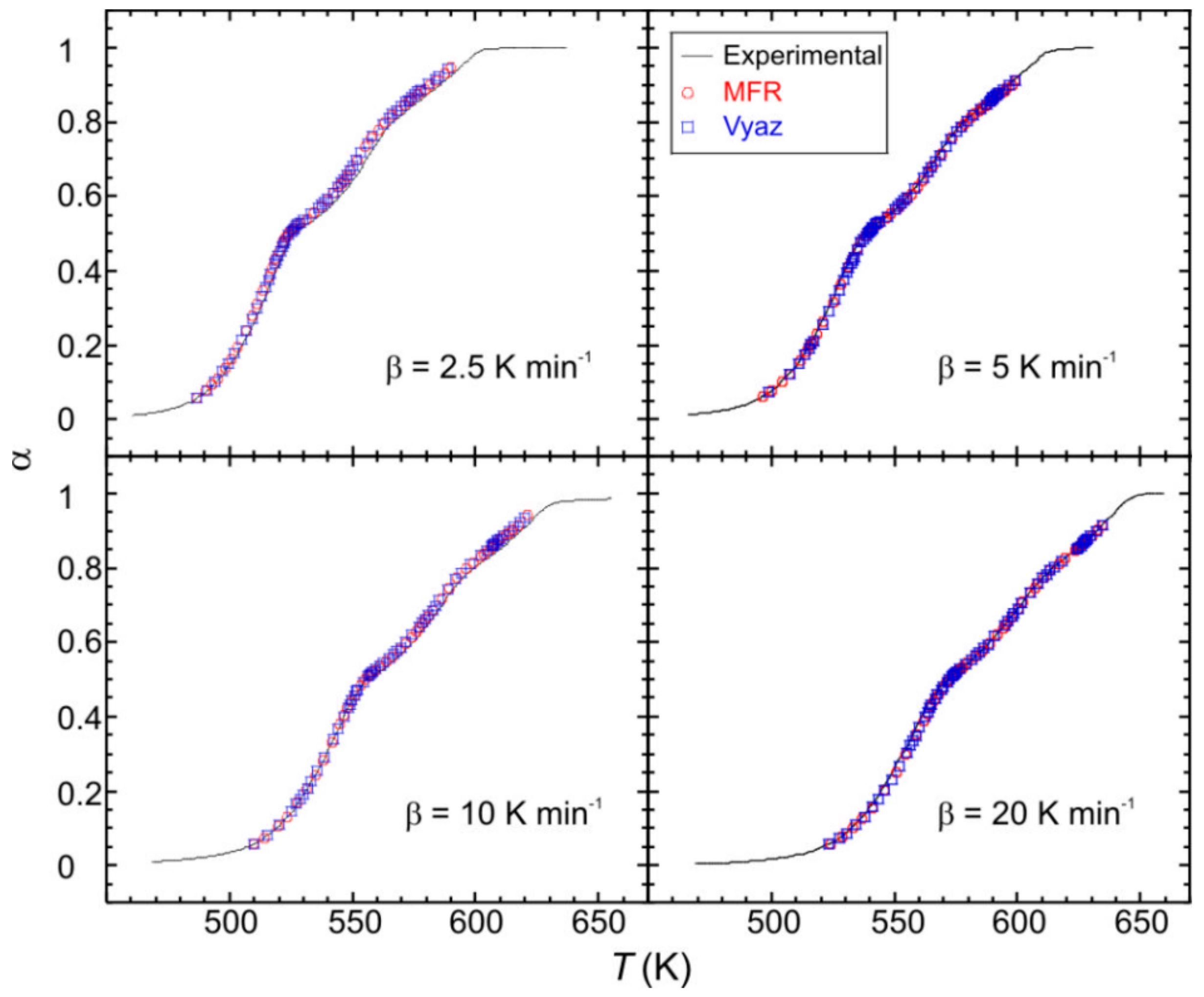
2.2. Thermogravimetric and Kinetic Analysis
3. Materials and Methods
3.1. Sample Preparation and Analytical Procedures
3.2. X-ray Diffraction Studies
3.3. Thermal Analysis and Kinetic Data
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| PND | Powder neutron diffraction data |
| PXRD | Powder X-ray diffraction |
| SEM | Scanning Electron Microscopy |
| HT-PXRD | High-Temperature X-ray Diffraction |
| TG | Thermogravimetry analysis |
| DTG | Derivative thermogravimetry analysis |
| MFR | Modified Friedman method |
| Vyaz | Vyazovkin method |
References
- Kang, S.A.; Li, W.; Lee, H.E.; Phillips, B.L.; Lee, Y.J. Phosphate uptake by TiO2: Batch studies and NMR spectroscopic evidence for multisite adsorption. J. Colloid. Interface. Sci. 2011, 364, 455–461. [Google Scholar] [CrossRef] [PubMed]
- Guesdon, A.; Adam, L.; Raveau, B. A new iron(II) hydroxyphosphate containing linear ammonium chloride chains: (NH4Cl)Fe14(OH)6(PO4)6(HPO4)2. Solid State Sci. 2011, 13, 1584–1588. [Google Scholar] [CrossRef]
- Padhi, A.K.; Nanjundaswamy, K.S.; Goodenough, J.B. Phospho-olivines as positive-electrode materials for rechargeable lithium batteries. J. Electrochem. Soc. 1997, 144, 1188–1194. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Park, K.S. The Li-Ion Rechargeable Battery: A Perspective. J Am Chem Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Whiteside, A.; Fisher, C.A.J.; Parker, S.C.; Islam, M.S. Particle shapes and surface structures of olivine NaFePO4 in comparison to LiFePO4. Phys. Chem. Chem. Phys. 2014, 16, 21788–21794. [Google Scholar] [CrossRef]
- Natarajan, S.; Mandal, S. Open-framework structures of transition-metal compounds. Angew. Chem. Int. Ed. 2008, 47, 4798–4828. [Google Scholar] [CrossRef]
- Maspoch, D.; Ruiz-Molina, D.; Veciana, J. Old materials with new tricks: Multifunctional open-framework materials. Chem. Soc. Rev. 2007, 36, 770–818. [Google Scholar] [CrossRef]
- Farzin, L.; Sheibani, S.; Moassesi, M.E.; Shamsipur, M. An overview of nanoscale radionuclides and radiolabeled nanomaterials commonly used for nuclear molecular imaging and therapeutic functions. J. Biomed. Mater. Res. A 2019, 107, 251–285. [Google Scholar] [CrossRef]
- Yoshimura, M.; Byrappa, K. Hydrothermal processing of materials: Past, present and future. J. Mater. Sci 2008, 43, 2085–2103. [Google Scholar] [CrossRef]
- Trobajo, C.; Espina, A.; Jaimez, E.; Khainakov, S.A.; García, J.R. Hydrothermal synthesis of iron(III) phosphates in the presence of urea. J. Chem. Soc. Dalton Trans. 2000, 5, 787–790. [Google Scholar] [CrossRef]
- Salvadó, M.A.; Pertierra, P.; García-Granda, S.; Espina, A.; Trobajo, C.; García, J.R. Hydrothermal synthesis and structure of Fe(NH3)2PO4: A novel monophosphate. Inorg. Chem. 1999, 38, 5944–5947. [Google Scholar] [CrossRef] [PubMed]
- Alfonso, B.F.; Trobajo, C.; Salvadó, M.A.; Pertierra, P.; García-Granda, S.; Rodríguez-Fernández, J.; Fernández-Díaz, M.T.; Blanco, J.A.; García, J.R. Structural and magnetic phases of Fe(ND3)2PO4. J. Phys. Condens. Matter. 2008, 20, 6–10. [Google Scholar] [CrossRef]
- Alfonso, B.F.; Trobajo, C.; Piqué, C.; Fernández-Díaz, M.T.; Fernández, J.R.; Salvadó, M.A.; Pertierra, P.; García-Granda, S.; García, J.R.; Blanco, J.A. Decoupled structural and non-collinear magnetic phase transitions in Fe(ND3)2PO4. ACTA Mater. 2010, 58, 1741–1749. [Google Scholar] [CrossRef]
- Reale, P.; Scrosati, B.; Delacourt, C.; Wurm, C.; Morcrette, M.; Masquelier, C. Synthesis of crystalline hydrated iron(III) phosphates. Chem. Mater. 2003, 15, 5051–5058. [Google Scholar] [CrossRef]
- Iglesias, I.; Alfonso, B.F.; Amghouz, Z.; Trobajo, C.; García, J.R.; Huidobro, J.A. Thorium(IV) phosphate-triphosphate: A valuable ceramic material obtained by thermal treatment of a layered ammonium-thorium(IV) phosphate. Kinetic analysis of the transformation. Ceram. Int. 2017, 43, 10776–10783. [Google Scholar] [CrossRef]
- Trobajo, C.; Espina, A.; Khainakov, S.A.; García, J.R. Direct synthesis of bis(n-alkylammonium) monohydrogen phosphates by solid-vapour reaction. Inorg. Chem. Commun. 2002, 5, 372–375. [Google Scholar] [CrossRef]
- Oxford Diffraction, CrysAlis CCD, CriysAlis RED and Scale3. Abingdon, UK, 2008.
- Altomare, A.; Cascarano, G.; Giacovazzo, G.; Guagliardi, A.; Burla, M.C.; Camalli, M. SIR92-a program for automatic solution of crystal structures by direct methods. J. Appl. Crystallogr. 1994, 27, 435. [Google Scholar] [CrossRef]
- Sheldrick, G.M. SHELXL-97, Program for the Refinement of Crystal Structure, University of Gottingen: Gottingen, Germany, 1997.
- Galwey, A.K.; Brown, M.E. A theoretical justification for the application of the Arrhenius equation to kinetics of solid-state reactions (mainly ionic-crystals). Proc. R. Soc. Math. Phys. Sci. 1995, 450, 501–512. [Google Scholar]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta. 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vyazovkin, S. Model-free kinetics. Staying free of multiplying entities without necessity. J. Therm. Anal. Calorim. 2006, 83, 45–51. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Huidobro, J.A.; Iglesias, I.; Alfonso, B.F.; Espina, A.; Trobajo, C.; García, J.R. Reducing the effects of noise in the calculation of activation energy by the Friedman method. Chemom. Intell. Lab. Syst. 2016, 151, 146–152. [Google Scholar] [CrossRef]
- Simon, P.; Thomas, P.; Dubaj, T.; Cibulkova, Z.; Peller, A.; Veverka, M. The mathematical incorrectness of the integral isoconversional methods in case of variable activation energy and the consequences. J. Therm. Anal. Calorim 2014, 115, 853–859. [Google Scholar] [CrossRef]
- Vyazovkin, S. Evaluation of activation energy of thermally stimulated solid-state reactions under arbitrary variation of temperature. J. Comput. Chem. 1997, 18, 393–402. [Google Scholar] [CrossRef]
- Vyazovkin, S. Modification of the integral isoconversional method to account for variation in the activation energy. J. Comput. Chem. 2001, 22, 178–188. [Google Scholar] [CrossRef]
- Huidobro, J.A.; Iglesias, I.; Alfonso, B.F.; Trobajo, C.; García, J.R. Modeling Chemical Kinetics in Solid State Reactions. Comput. Math. Numer. Anal. Appl. 2017, 229–233. [Google Scholar] [CrossRef]


| Molecular Formula | FeN2H6PO4 |
|---|---|
| Formula mass/g mol−1 | 184.89 |
| Color | Green |
| Wavelength/Å | 1.5418 |
| Crystal system | Orthorhombic |
| Space group | Pnma nº 62 |
| a/Å | 10.1116(2) |
| b/Å | 6.3652(1) |
| c/Å | 7.5691(1) |
| Z | 4 |
| Calculated density/g cm−3 | 2.521 |
| Volume/Å3 | 487.165(14) |
| Crystal size/mm3 | 0.08 × 0.02 × 0.01 |
| θ range/deg | 4° to 74° |
| Absorption coefficient/mm−1 | 27.462 |
| F(000) | 372 |
| Index ranges | −12<=h<=12 |
| −7<=k<=7 | |
| −9<=1<=9 | |
| Reflections colleted | 4187 |
| Independent reflections | 538 [R(int)=0.02] |
| Completeness θ = 70.00° | 100.0% |
| Refinememt method | Full-matrix least-squares on F2 |
| Data/restraints/parameters | 538/0/50 |
| Goodness-of-fit on F2 | 1.143 |
| Final R ind.[I > 2sigma(I)] | R1 = 0.0215 |
| wR2 = 0.0613 | |
| R índices (all data) | R1 = 0.0217 |
| wR2 = 0.0613 | |
| Largest diff. Peak and hole/e Å−3 | 0.289 and −0.816 |
| Atom | x | y | z | U(eq) |
|---|---|---|---|---|
| Fe | 0.8422(1) | 3/4 | 0.0896(1) | 10(1) |
| P | 0.8384(1) | 1/4 | −0.0412(1) | 10(1) |
| O(1) | 0.8348(1) | 0.4416(2) | 0.0819(1) | 16(1) |
| O(2) | 0.7826(1) | 3/4 | 0.3369(2) | 16(1) |
| O(3) | 1.0343(1) | 3/4 | 0.1536(2) | 16(1) |
| N(1) | 0.6428(2) | 3/4 | −0.0137(3) | 22(1) |
| Bond lengths (Å) | Bond Angles (deg) | ||
|---|---|---|---|
| Fe–O(1) | 1.9652(14) × 2) | O(1)–Fe(1)–O(1) | 174.45(6) |
| Fe–O(2) | 1.9663(16) | O(1)–Fe(1)–O(2) | 90.96(3) |
| Fe–O(3) | 2.0021(15) | O(2)–Fe(1)–O(3) | 92.53(3) |
| O(2)–Fe(1)–O(3) | 93.87(6) | ||
| Fe–N(1) | 2.1624(19) | O(1)–Fe(1)–N(1) | 87.34(3) |
| Fe–N(2) | 2.1661(18) | O(2)–Fe(1)–N(1) | 93.34(8) |
| P–O(1) | 1.5354(13) × 2 | O(3)–Fe(1)–N(1) | 172.79(8) |
| P–O(2) | 1.5318(15) × 2 | O(1)–Fe(1)–N(2) | 88.90(3) |
| P–O(3) | 1.5427(15) × 2 | O(2)–Fe(1)–N(2) | 176.68(7) |
| N(1)–H(11) | 0.9612 | O(3)–Fe(1)–N(2) | 89.45(6) |
| N(1)–H(12) | 0.9913 | N(1)–Fe(1)–N(2) | 83.34(8) |
| N(2)–H(21) | 0.9534 | O(2)–P(1)–O(1) | 110.29(5) |
| N(2)–H(22) | 0.9752 | O(1)–P(1)–O(1) | 105.20(10) |
| O(2)–P(1)–O(3) | 109.51(10) | ||
| O(1)–P(1)–O(3) | 110.74(5) | ||
| P(1)–O(1)–Fe(1) | 144.16(8) | ||
| P(1)–O(2)–Fe(1) | 144.90(10) | ||
| P(1)–O(3)–Fe(1) | 132.56(9) | ||
| Fe(1)N(1)H(11) | 109.3 | ||
| Fe(1)N(1)H(12) | 115.6 | ||
| H(11)N(1)H(12) | 105.1 | ||
| Fe(1)N(2)H(21) | 104.8 | ||
| Fe(1)N(2)H(22) | 124.6 | ||
| H(21)N(2)H(22) | 106.4 | ||
| Symmetry transformations used to generate equivalent atoms: #1 x, −y+3/2,z #2 −x+3/2, −y+1,z − 1/2 #3 x, −y + 1/2, z #4 – x + 2, −y + 1, −z #5 −x + 3/2, −y + 1,z + 1/2 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iglesias, I.; Huidobro, J.A.; Alfonso, B.F.; Trobajo, C.; Espina, A.; Mendoza, R.; García, J.R. Kinetic Analysis of the Thermal Decomposition of Iron(III) Phosphates: Fe(NH3)2PO4 and Fe(ND3)2PO4. Int. J. Mol. Sci. 2020, 21, 781. https://doi.org/10.3390/ijms21030781
Iglesias I, Huidobro JA, Alfonso BF, Trobajo C, Espina A, Mendoza R, García JR. Kinetic Analysis of the Thermal Decomposition of Iron(III) Phosphates: Fe(NH3)2PO4 and Fe(ND3)2PO4. International Journal of Molecular Sciences. 2020; 21(3):781. https://doi.org/10.3390/ijms21030781
Chicago/Turabian StyleIglesias, Isabel, José A. Huidobro, Belén F. Alfonso, Camino Trobajo, Aránzazu Espina, Rafael Mendoza, and José R. García. 2020. "Kinetic Analysis of the Thermal Decomposition of Iron(III) Phosphates: Fe(NH3)2PO4 and Fe(ND3)2PO4" International Journal of Molecular Sciences 21, no. 3: 781. https://doi.org/10.3390/ijms21030781
APA StyleIglesias, I., Huidobro, J. A., Alfonso, B. F., Trobajo, C., Espina, A., Mendoza, R., & García, J. R. (2020). Kinetic Analysis of the Thermal Decomposition of Iron(III) Phosphates: Fe(NH3)2PO4 and Fe(ND3)2PO4. International Journal of Molecular Sciences, 21(3), 781. https://doi.org/10.3390/ijms21030781





