Completing the Spectral Mosaic of Chloromethane by Adding the CHD2Cl Missing Piece Through the Interplay of Rotational/Vibrational Spectroscopy and Quantum Chemical Calculations
Abstract
1. Introduction
2. Results and Discussion
2.1. Rotational Analysis
2.2. Semi-Experimental Equilibrium Structure
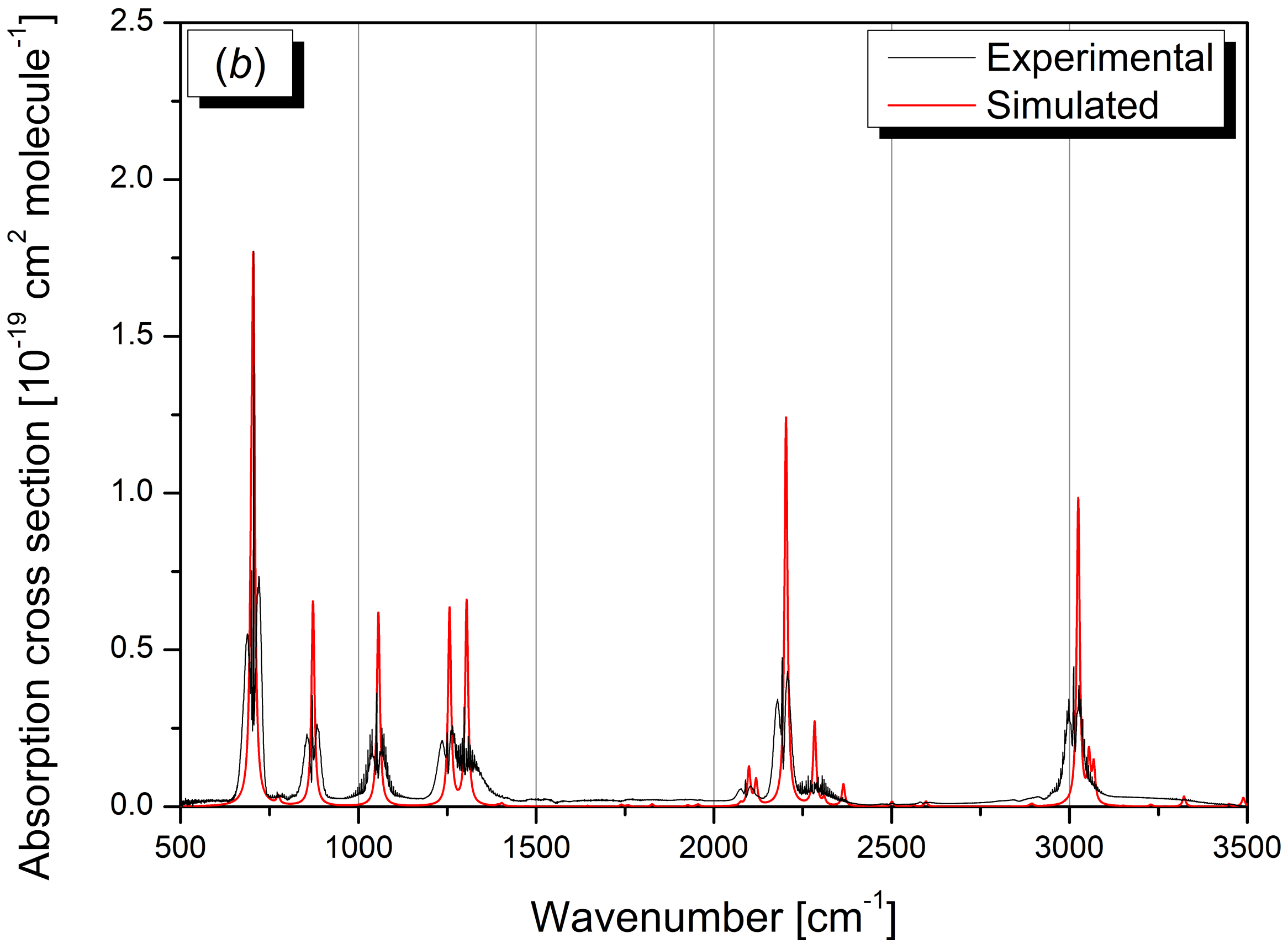
2.3. Vibrational Assignment of Gas-Phase Infrared Spectrum
2.3.1. Vibrational Analysis of the 500–1500 cm−1 Spectral Region
2.3.2. Vibrational Analysis of the 1500–3100 cm−1 Spectral Region
2.3.3. Vibrational Analysis of the 3100–6200 cm−1 Spectral Region
2.4. Radiative Efficiency
3. Materials and Methods
3.1. Computational Details
3.2. Experimental Details
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Forster, P.M.; Smith, C.; Walsh, T.; Lamb, W.F.; Lamboll, R.; Hall, B.; Hauser, M.; Ribes, A.; Rosen, D.; Gillett, N.P.; et al. Indicators of Global Climate Change 2023: Annual update of key indicators of the state of the climate system and human influence. Earth Syst. Sci. Data 2024, 16, 2625–2658. [Google Scholar] [CrossRef]
- Thornhill, G.D.; Smith, L.A.; Shine, K.P. Radiative Forcing From Halogen Reservoir and Halocarbon Breakdown Products. J. Geophys. Res. Atmos. 2024, 129, e2024JD040912. [Google Scholar] [CrossRef]
- Hodnebrog, Ø.; Aamaas, B.; Fuglestvedt, J.S.; Marston, G.; Myhre, G.; Nielsen, C.J.; Sandstad, M.; Shine, K.P.; Wallington, T.J. Updated Global Warming Potentials and Radiative Efficiencies of Halocarbons and Other Weak Atmospheric Absorbers. Rev. Geophys. 2020, 58, e2019RG000691. [Google Scholar] [CrossRef]
- Bruhwiler, L.; Basu, S.; Butler, J.H.; Chatterjee, A.; Dlugokencky, E.; Kenney, M.A.; McComiskey, A.; Montzka, S.A.; Stanitski, D. Observations of greenhouse gases as climate indicators. Clim. Change 2021, 165, 12. [Google Scholar] [CrossRef]
- Hughey, K.D.; Gallagher, N.B.; Zhao, Y.; Thakur, N.; Bradley, A.M.; Koster van Groos, P.G.; Johnson, T.J. PFAS remediation: Evaluating the infrared spectra of complex gaseous mixtures to determine the efficacy of thermal decomposition of PFAS. Chemosphere 2024, 362, 142631. [Google Scholar] [CrossRef]
- Thompson, C.J.; Gallagher, N.B.; Hughey, K.D.; Dunlap, M.K.; Myers, T.L.; Johnson, T.J. An Interactive Spectral Analysis Tool for Chemical Identification and Quantification of Gas-Phase Species in Complex Spectra. Appl. Spectrosc. 2023, 77, 557–568. [Google Scholar] [CrossRef] [PubMed]
- McNaughton, D.; Robertson, E.G.; Thompson, C.D.; Chimdi, T.; Bane, M.K.; Appadoo, D. Overview of High-Resolution Infrared Measurement and Analysis for Atmospheric Monitoring of Halocarbons. Anal. Chem. 2010, 82, 7958–7964. [Google Scholar] [CrossRef]
- Pietropolli Charmet, A.; Ceselin, G.; Stoppa, P.; Tasinato, N. The Spectroscopic Characterization of Halogenated Pollutants through the Interplay between Theory and Experiment: Application to R1122. Molecules 2022, 27, 748. [Google Scholar] [CrossRef]
- Pietropolli Charmet, A.; Stoppa, P.; Tasinato, N.; Giorgianni, S.; Gambi, A. Study of the Vibrational Spectra and Absorption Cross Sections of 1-Chloro-1-fluoroethene by a Joint Experimental and Ab Initio Approach. J. Phys. Chem. A 2016, 120, 8369–8386. [Google Scholar] [CrossRef]
- Alvarado-Jiménez, D.; Pietropolli Charmet, A.; Stoppa, P.; Tasinato, N. The Radiative Efficiency and Global Warming Potential of HCFC-132b. ChemPhysChem 2025, 26, e202400632. [Google Scholar] [CrossRef]
- Alvarado-Jiménez, D.; Tasinato, N. In silico modelling of radiative efficiencies of anthropogenic greenhouse gases. Atmos. Environ. 2024, 338, 120839. [Google Scholar] [CrossRef]
- Muthiah, B.; Li, S.C.; Li, Y.P. Developing machine learning models for accurate prediction of radiative efficiency of greenhouse gases. J. Taiwan Inst. Chem. Eng. 2023, 151, 105123. [Google Scholar] [CrossRef]
- WMO. Scientific Assessment of Ozone Depletion: 2022, GAW Report No. 278; WMO: Geneva, Switzerland, 2022. [Google Scholar]
- Laube, J.; Tegtmeier, S. Update of Ozone-Depleting Substances (ODSs) and other gases of interest in the Montreal Protocol. In Scientific Assessment of Ozone Depletion 2022; Scientific Assessment Panel (SAP); World Metereological Organization (WMO): Geneva, Switzerland, 2022; Volume 278, pp. 31–34. [Google Scholar]
- Hartmann, S.C.; Keppler, F.; Greule, M.; Lauer, R.; Horst, A. Triple-Element Stable Isotope Analysis of Chloromethane Emitted by Royal Fern and Degraded by Club Moss. J. Geophys. Res. Biogeosci. 2023, 128, e2022JG007256. [Google Scholar] [CrossRef]
- Bahlmann, E.; Keppler, F.; Wittmer, J.; Greule, M.; Schöler, H.F.; Seifert, R.; Zetzsch, C. Evidence for a major missing source in the global chloromethane budget from stable carbon isotopes. Atmos. Chem. Phys. 2019, 19, 1703–1719. [Google Scholar] [CrossRef]
- Yokouchi, Y.; Ikeda, M.; Inuzuka, Y.; Yukawa, T. Strong emission of methyl chloride from tropical plants. Nature 2002, 416, 163–165. [Google Scholar]
- Hu, L.; Yvon-Lewis, S.A.; Butler, J.H.; Lobert, J.M.; King, D.B. An improved oceanic budget for methyl chloride. J. Geophys. Res. Ocean. 2013, 118, 715–725. [Google Scholar] [CrossRef]
- Khalil, M.; Rasmussen, R. Atmospheric methyl chloride. Atmos. Environ. 1999, 33, 1305–1321. [Google Scholar] [CrossRef]
- Jiao, Y.; Zhang, W.; Kim, J.Y.R.; Deventer, M.J.; Vollering, J.; Rhew, R.C. Application of copper(II)-based chemicals induces CH3Br and CH3Cl emissions from soil and seawater. Nat. Commun. 2022, 13, 47. [Google Scholar] [CrossRef]
- Moore, R.; Gut, A.; Andreae, M. A pilot study of methyl chloride emissions from tropical woodrot fungi. Chemosphere 2005, 58, 221–225. [Google Scholar] [CrossRef]
- Keppler, F.; Röhling, A.N.; Jaeger, N.; Schroll, M.; Hartmann, S.C.; Greule, M. Sources and sinks of chloromethane in a salt marsh ecosystem: Constraints from concentration and stable isotope measurements of laboratory incubation experiments. Environ. Sci. Process. Impacts 2020, 22, 627–641. [Google Scholar] [CrossRef]
- Derendorp, L.; Holzinger, R.; Wishkerman, A.; Keppler, F.; Röckmann, T. Methyl chloride and C2–C5 hydrocarbon emissions from dry leaf litter and their dependence on temperature. Atmos. Environ. 2011, 45, 3112–3119. [Google Scholar] [CrossRef]
- Hu, X.; Chen, D.; Hu, L.; Li, B.; Li, X.; Fang, X. Global methyl halide emissions from biomass burning during 2003–2021. Environ. Sci. Ecotechnol. 2023, 14, 100228. [Google Scholar] [CrossRef] [PubMed]
- Andreae, M.; Atlas, E.; Harris, G.; Helas, G.; De Kock, A.; Koppmann, R.; Maenhaut, W.; Manø, S.; Pollock, W.; Rudolph, J.; et al. Methyl halide emissions from savanna fires in southern Africa. J. Geophys. Res. Atmos. 1996, 101, 23603–23613. [Google Scholar] [CrossRef]
- Thornton, B.F.; Horst, A.; Carrizo, D.; Holmstrand, H. Methyl chloride and methyl bromide emissions from baking: An unrecognized anthropogenic source. Sci. Total Environ. 2016, 551–552, 327–333. [Google Scholar] [CrossRef]
- Williams, J.; Wang, N.Y.; Cicerone, R.J.; Yagi, K.; Kurihara, M.; Terada, F. Atmospheric methyl halides and dimethyl sulfide from cattle. Glob. Biogeochem. Cycles 1999, 13, 485–491. [Google Scholar] [CrossRef]
- Keppler, F.; Fischer, J.; Sattler, T.; Polag, D.; Jaeger, N.; Schöler, H.F.; Greule, M. Chloromethane emissions in human breath. Sci. Total Environ. 2017, 605–606, 405–410. [Google Scholar] [CrossRef]
- Liu, Y.; Weng, W.; Zhang, Q.; Li, Q.; Xu, J.; Zheng, L.; Su, Y.; Wu, D.; Yan, W.; Zhang, J.; et al. Ozone-Depleting Substances Unintendedly Emitted From Iron and Steel Industry: CFCs, HCFCs, Halons and Halogenated Very Short-Lived Substances. J. Geophys. Res. Atmos. 2024, 129, e2024JD041035. [Google Scholar] [CrossRef]
- Schwieterman, E.W.; Leung, M. An Overview of Exoplanet Biosignatures. Rev. Mineral. Geochem. 2024, 90, 465–514. [Google Scholar] [CrossRef]
- Fujii, Y.; Angerhausen, D.; Deitrick, R.; Domagal-Goldman, S.; Grenfell, J.L.; Hori, Y.; Kane, S.R.; Pallé, E.; Rauer, H.; Siegler, N.; et al. Exoplanet Biosignatures: Observational Prospects. Astrobiology 2018, 18, 739–778. [Google Scholar] [CrossRef] [PubMed]
- Schwieterman, E.W.; Kiang, N.Y.; Parenteau, M.N.; Harman, C.E.; DasSarma, S.; Fisher, T.M.; Arney, G.N.; Hartnett, H.E.; Reinhard, C.T.; Olson, S.L.; et al. Exoplanet Biosignatures: A Review of Remotely Detectable Signs of Life. Astrobiology 2018, 18, 663–708. [Google Scholar] [CrossRef] [PubMed]
- Segura, A.; Kasting, J.F.; Meadows, V.; Cohen, M.; Scalo, J.; Crisp, D.; Butler, R.A.; Tinetti, G. Biosignatures from Earth-Like Planets Around M Dwarfs. Astrobiology 2005, 5, 706–725. [Google Scholar] [CrossRef] [PubMed]
- Madhusudhan, N.; Piette, A.A.A.; Constantinou, S. Habitability and Biosignatures of Hycean Worlds. Astrophys. J. 2021, 918, 1. [Google Scholar] [CrossRef]
- Wunderlich, F.; Scheucher, M.; Grenfell, J.L.; Schreier, F.; Sousa-Silva, C.; Godolt, M.; Rauer, H. Detectability of biosignatures on LHS 1140 b. Astron. Astrophys. 2021, 647, A48. [Google Scholar] [CrossRef]
- Gialluca, M.T.; Robinson, T.D.; Rugheimer, S.; Wunderlich, F. Characterizing Atmospheres of Transiting Earth-like Exoplanets Orbiting M Dwarfs with James Webb Space Telescope. Publ. Astron. Soc. Pac. 2021, 133, 054401. [Google Scholar] [CrossRef]
- Fayolle, E.C.; Öberg, K.I.; Jørgensen, J.K.; Altwegg, K.; Calcutt, H.; Müller, H.S.P.; Rubin, M.; van der Wiel, M.H.D.; Bjerkeli, P.; Bourke, T.L.; et al. Protostellar and cometary detections of organohalogens. Nat. Astron. 2017, 1, 703–708. [Google Scholar] [CrossRef]
- Calcutt, H.; Jørgensen, J.K.; Müller, H.S.P.; Kristensen, L.E.; Coutens, A.; Bourke, T.L.; Garrod, R.T.; Persson, M.V.; van der Wiel, M.H.D.; van Dishoeck, E.F.; et al. The ALMA-PILS survey: Complex nitriles towards IRAS 16293–2422. Astron. Astrophys. 2018, 616, A90. [Google Scholar] [CrossRef]
- Melosso, M.; Bizzocchi, L.; Sipilä, O.; Giuliano, B.M.; Dore, L.; Tamassia, F.; Martin-Drumel, M.-A.; Pirali, O.; Redaelli, E.; Caselli, P. First detection of NHD and ND2 in the interstellar medium—Amidogen deuteration in IRAS 16293–2422. Astron. Astrophys. 2020, 641, A153. [Google Scholar] [CrossRef]
- Bacmann, A.; Faure, A.; Hily-Blant, P.; Kobayashi, K.; Ozeki, H.; Yamamoto, S.; Pagani, L.; Lique, F. Deuterium fractionation of nitrogen hydrides: Detections of NHD and ND2. Mon. Not. R. Astron. Soc. 2020, 499, 1795–1804. [Google Scholar] [CrossRef]
- Coutens, A.; Vastel, C.; Caux, E.; Ceccarelli, C.; Bottinelli, S.; Wiesenfeld, L.; Faure, A.; Scribano, Y.; Kahane, C. A study of deuterated water in the low-mass protostar IRAS 16293–2422. Astron. Astrophys. 2012, 539, A132. [Google Scholar] [CrossRef]
- Wallström, S.H.J.; Muller, S.; Roueff, E.; Le Gal, R.; Black, J.H.; Gérin, M. Chlorine-bearing molecules in molecular absorbers at intermediate redshifts. Astron. Astrophys. 2019, 629, A128. [Google Scholar] [CrossRef]
- Ulenikov, O.; Bekhtereva, E.; Gromova, O.; Fomchenko, A.; Morzhikova, Y.; Sidko, S.; Sydow, C.; Bauerecker, S. Effective Dipole Moment Model for Axially Symmetric C3v Molecules: Application to the Precise Study of Absolute Line Strengths of the ν6 Fundamental of CH335Cl. Int. J. Mol. Sci. 2023, 24, 12122. [Google Scholar] [CrossRef] [PubMed]
- Hardy, P.; Richard, C.; Boudon, V.; Khan, M.V.; Manceron, L.; Dridi, N. High-resolution far-infrared spectroscopy and analysis of the ν3 and ν6 bands of chloromethane. J. Quant. Spectrosc. Radiat. Transf. 2023, 311, 108779. [Google Scholar] [CrossRef]
- Dridi, N.; Manceron, L.; Fathallah, O.B.; Rotger, M.; Aroui, H. O2- and N2-broadening parameters in the ν3 and 2ν3 − ν3 bands of methyl chloride. J. Quant. Spectrosc. Radiat. Transf. 2020, 253, 107180. [Google Scholar] [CrossRef]
- Dridi, N.; Manceron, L.; Hmida, F.; Rotger, M.; Aroui, H. Line intensity parameters in the ν3 and 2ν3 − ν3 bands of methyl chloride in the 13 μm region. J. Quant. Spectrosc. Radiat. Transf. 2020, 251, 107036. [Google Scholar] [CrossRef]
- Fathallah, O.; Manceron, L.; Dridi, N.; Rotger, M.; Aroui, H. Line intensities and self-broadening coefficients of methyl chloride in the 10 μm region. J. Quant. Spectrosc. Radiat. Transf. 2020, 242, 106777. [Google Scholar] [CrossRef]
- Leonis, S.; Lepère, M. N2-collisional broadening coefficients of lines in the ν2 band of chloromethane from low to room temperatures. J. Mol. Spectrosc. 2020, 369, 111269. [Google Scholar] [CrossRef]
- Dridi, N.; Maaroufi, N.; Manceron, L.; Rotger, M.; Aroui, H. Measurement and modeling of self-broadening coefficients of the ν3 and 2ν3 − ν3 bands of methyl chloride. J. Quant. Spectrosc. Radiat. Transf. 2019, 235, 108–119. [Google Scholar] [CrossRef]
- Owens, A.; Yachmenev, A.; Thiel, W.; Fateev, A.; Tennyson, J.; Yurchenko, S.N. ExoMol line lists—XXIX. The rotation-vibration spectrum of methyl chloride up to 1200 K. Mon. Not. R. Astron. Soc. 2018, 479, 3002–3010. [Google Scholar] [CrossRef]
- Nikitin, A.; Dmitrieva, T.; Gordon, I. Improved spectroscopic line list of methyl chloride in the 1900–2600 cm−1 spectral region. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 49–58. [Google Scholar] [CrossRef]
- Lucchesini, A.; Gozzini, S. Diode laser spectroscopy of methyl chloride overtones at 850–860 nm. J. Quant. Spectrosc. Radiat. Transf. 2016, 168, 170–175. [Google Scholar] [CrossRef]
- Bray, C.; Perrin, A.; Jacquemart, D.; Lacome, N. The ν1, ν4 and 3ν6 bands of methyl chloride in the 3.4-μm region: Line positions and intensities. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2446–2462. [Google Scholar] [CrossRef]
- Owens, A.; Yurchenko, S.N.; Yachmenev, A.; Tennyson, J.; Thiel, W. A global ab initio dipole moment surface for methyl chloride. J. Quant. Spectrosc. Radiat. Transf. 2016, 184, 100–110. [Google Scholar] [CrossRef]
- Owens, A.; Yurchenko, S.N.; Yachmenev, A.; Tennyson, J.; Thiel, W. Accurate ab initio vibrational energies of methyl chloride. J. Chem. Phys. 2015, 142, 244306. [Google Scholar] [CrossRef]
- Nová Stříteská, L.; Šimečková, M.; Kania, P.; Musil, P.; Kolesniková, L.; Koubek, J.; Štěpán Urban. Precise ground state molecular parameters of chloromethane. J. Mol. Struct. 2009, 919, 89–93. [Google Scholar] [CrossRef]
- Nikitin, A.; Champion, J. New ground state constants of 12CH335Cl and 12CH337Cl from global polyad analysis. J. Mol. Spectrosc. 2005, 230, 168–173. [Google Scholar] [CrossRef]
- Melosso, M.; Achilli, A.; Tamassia, F.; Canè, E.; Pietropolli Charmet, A.; Stoppa, P.; Dore, L. High-resolution millimeter-wave spectroscopy of CH2DCl: Paving the way for future astronomical observations of chloromethane isotopologues. J. Quant. Spectrosc. Radiat. Transf. 2020, 248, 106982. [Google Scholar] [CrossRef]
- Stoppa, P.; Pietropolli Charmet, A.; De Lorenzi, A.; Tamassia, F.; Melosso, M.; Cané, E.; Dore, L.; Puzzarini, C. High resolution FTIR study of the ν5, ν6, and ν9 fundamental bands of CH2D37Cl. J. Quant. Spectrosc. Radiat. Transf. 2021, 270, 107719. [Google Scholar] [CrossRef]
- Stoppa, P.; Pietropolli Charmet, A.; Tamassia, F.; Canè, E.; Melosso, M.; Achilli, A.; Dore, L.; Puzzarini, C. High resolution FTIR spectrum of CH2D37Cl: ν4 and ν8 fundamental bands. J. Quant. Spectrosc. Radiat. Transf. 2023, 309, 108703. [Google Scholar] [CrossRef]
- Pietropolli Charmet, A.; Stoppa, P.; De Lorenzi, A.; Melosso, M.; Achilli, A.; Dore, L.; Puzzarini, C.; Canè, E.; Tamassia, F. Computational, rotational and ro-vibrational experimental investigation of monodeuterated chloromethane. J. Quant. Spectrosc. Radiat. Transf. 2023, 305, 108624. [Google Scholar] [CrossRef]
- Pulay, P.; Meyer, W.; Boggs, J.E. Cubic force constants and equilibrium geometry of methane from Hartree–Fock and correlated wavefunctions. J. Chem. Phys. 1978, 68, 5077–5085. [Google Scholar] [CrossRef]
- Demaison, J.; Boggs, J.E.; Czázár, A.G. (Eds.) Equilibrium Molecular Structures: From Spectrocopy to Quantum Chemistry; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Matlack, G.; Glockler, G.; Bianco, D.; Roberts, A. The microwave spectra of isotopic methyl chloride. J. Chem. Phys. 1950, 18, 332–334. [Google Scholar] [CrossRef]
- Miller, S.; Kraitchman, J.; Dailey, B.; Townes, C. Microwave Spectrum of CHD235Cl and the Structure of Methyl Chloride. In Proceedings of the Physical Review. American Physical Soc One Physics Ellipse, College Park, MD, USA, 15 July 1951; Volume 82, pp. 327–328. [Google Scholar]
- Mallinson, P. The microwave spectrum of CHD2Cl. J. Mol. Spectrosc. 1977, 68, 68–76. [Google Scholar] [CrossRef]
- Constantin, F.; Demaison, J.; Féjard, L.; Litz, M.; Bürger, H.; Pracna, P. High-resolution infrared and subterahertz spectroscopy of the v2 = Y1, v5 = 1, and v3 = 2 levels of 13CH335Cl. J. Mol. Spectrosc. 2007, 243, 234–244. [Google Scholar] [CrossRef]
- Litz, M.; Bürger, H.; Féjard, L.; Constantin, F.; Margulès, L.; Demaison, J. Infrared and millimeter-wave studies of 13CH3Cl in the ground, 31, and 61 states. J. Mol. Spectrosc. 2003, 219, 238–247. [Google Scholar] [CrossRef]
- Misako, I.; Takehiko, T.; Eizi, H. Microwave Spectrum of Methyl Chloride in the Excited Vibrational States: Coriolis interaction between the ν2 and ν5 states. J. Mol. Spectrosc. 1976, 63, 265–280. [Google Scholar] [CrossRef]
- Sahoo, N.P.; Franke, P.R.; Stanton, J.F. On the performance of composite schemes in determining equilibrium molecular structures. J. Comput. Chem. 2024, 45, 1419–1427. [Google Scholar] [CrossRef]
- Duncan, J.; McKean, D.; Mallinson, P.; McCulloch, R. Infrared spectra of CHD2Cl and CHD2CCH and the geometries of methyl chloride and propyne. J. Mol. Spectrosc. 1973, 46, 232–239. [Google Scholar] [CrossRef]
- Pracht, P.; Grimme, S.; Bannwarth, C.; Bohle, F.; Ehlert, S.; Feldmann, G.; Gorges, J.; Müller, M.; Neudecker, T.; Plett, C.; et al. CREST-A program for the exploration of low-energy molecular chemical space. J. Chem. Phys. 2024, 160, 114110. [Google Scholar] [CrossRef]
- Pinnock, S.; Hurley, M.D.; Shine, K.P.; Wallington, T.J.; Smyth, T.J. Radiative forcing of climate by hydrochlorofluorocarbons and hydrofluorocarbons. J. Geophys. Res. Atmosph. 1995, 100, 23227–23238. [Google Scholar] [CrossRef]
- Shine, K.P.; Myhre, G. The Spectral Nature of Stratospheric Temperature Adjustment and its Application to Halocarbon Radiative Forcing. J. Adv. Model. Earth Syst. 2020, 12, e2019MS001951. [Google Scholar] [CrossRef]
- Wallington, T.J.; Pivesso, B.P.; Lira, A.M.; Anderson, J.E.; Nielsen, C.J.; Andersen, N.H.; Hodnebrog, Ø. CH3Cl, CH2Cl2, CHCl3, and CCl4: Infrared spectra, radiative efficiencies, and global warming potentials. J. Quant. Spectrosc. Radiat. Transfer. 2016, 174, 56–64. [Google Scholar] [CrossRef]
- Dunning, T.H.J. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Peterson, K.A.; Dunning, T.H.J. Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited. J. Chem. Phys. 2002, 117, 10548–10560. [Google Scholar] [CrossRef]
- Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Schwartz, C. Importance of Angular Correlations between Atomic Electrons. Phys. Rev. 1962, 126, 1015–1019. [Google Scholar] [CrossRef]
- Noga, J.; Bartlett, R.J. The full CCSDT model for molecular electronic structure. J. Chem. Phys. 1987, 86, 7041–7050. [Google Scholar] [CrossRef]
- Kucharski, S.A.; Bartlett, R.J. The coupled-cluster single, double, triple, and quadruple excitation method. J. Chem. Phys. 1992, 97, 4282–4288. [Google Scholar] [CrossRef]
- Gauss, J.; Tajti, A.; Kàllay, M.; Stanton, J.F.; Szalay, P. Analytic calculation of the diagonal Born-Oppenheimer correction within configuration-interaction and coupled-cluster theory. J. Chem. Phys. 2006, 125, 144111. [Google Scholar] [CrossRef]
- Dyall, K.G. An exact separation of the spin-free and spin-dependent terms of the Dirac–Coulomb–Breit Hamiltonian. J. Chem. Phys. 1994, 100, 2118–2127. [Google Scholar] [CrossRef]
- Cheng, L.; Gauss, J. Analytical evaluation of first-order electrical properties based on the spin-free Dirac-Coulomb Hamiltonian. J. Chem. Phys. 2011, 134, 244112. [Google Scholar] [CrossRef]
- Mendolicchio, M.; Penocchio, E.; Licari, D.; Tasinato, N.; Barone, V. Development and Implementation of Advanced Fitting Methods for the Calculation of Accurate Molecular Structures. J. Chem. Theory Comput. 2017, 13, 3060–3075. [Google Scholar] [CrossRef] [PubMed]
- Ceselin, G.; Salta, Z.; Bloino, J.; Tasinato, N.; Barone, V. Accurate Quantum Chemical Spectroscopic Characterization of Glycolic Acid: A Route Toward its Astrophysical Detection. J. Phys. Chem. A 2022, 126, 2373–2387. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Ceselin, G.; Lazzari, F.; Tasinato, N. Toward Spectroscopic Accuracy for the Structures of Large Molecules at DFT Cost: Refinement and Extension of the Nano-LEGO Approach. J. Phys. Chem. A 2023, 127, 5183–5192. [Google Scholar] [CrossRef] [PubMed]
- Santra, G.; Sylvetsky, N.; Martin, J.M.L. Minimally Empirical Double-Hybrid Functionals Trained against the GMTKN55 Database: RevDSD-PBEP86-D4, revDOD-PBE-D4, and DOD-SCAN-D4. J. Phys. Chem. A 2019, 123, 5129–5143. [Google Scholar] [CrossRef]
- Papajak, E.; Leverentz, H.R.; Zheng, J.; Truhlar, D.G. Efficient Diffuse Basis Sets: cc-pVxZ+ and maug-cc-pVxZ. J. Chem. Theory Comput. 2009, 5, 1197–1202. [Google Scholar] [CrossRef]
- Salta, Z.; Lupi, J.; Tasinato, N.; Barone, V.; Ventura, O.N. Unraveling the role of additional OH-radicals in the H-Abstraction from Dimethyl sulfide using quantum chemical computations. Chem. Phys. Lett. 2020, 739, 136963. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. Design of Density Functionals That Are Broadly Accurate for Thermochemistry, Thermochemical Kinetics, and Nonbonded Interactions. J. Phys. Chem. A 2005, 109, 5656–5667. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.J.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Grimme, S.; Anthony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
- Tasinato, N.; Pietropolli Charmet, A.; Ceselin, G.; Salta, Z.; Stoppa, P. In Vitro and In Silico Vibrational-Rotational Spectroscopic Characterization of the Next-Generation Refrigerant HFO-1123. J. Phys. Chem. 2022, 126, 5328–5342. [Google Scholar] [CrossRef] [PubMed]
- Boussessi, R.; Ceselin, G.; Tasinato, N.; Barone, V. DFT meets the segmented polarization consistent basis sets: Performances in the computation of molecular structures, rotational and vibrational spectroscopic properties. J. Mol. Struct. 2020, 1208, 127886. [Google Scholar] [CrossRef]
- Boussessi, R.; Tasinato, N.; Pietropolli Charmet, A.; Stoppa, P.; Barone, V. Sextic centrifugal distortion constants: Interplay of density functional and basis set for accurate yet feasible computations. Mol. Phys. 2020, 118, e1734678. [Google Scholar] [CrossRef]
- Puzzarini, C.; Tasinato, N.; Bloino, J.; Spada, L.; Barone, V. State-of-the-art computation of the rotational and IR spectra of the methyl-cyclopropyl cation: Hints on its detection in space. Phys. Chem. Chem. Phys. 2019, 21, 3431–3439. [Google Scholar] [CrossRef]
- Papoušek, D.; Aliev, M.R. Molecular Vibrational/Rotational Spectra; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Mills, I.M. Vibration-Rotation Structure in Asymmetric- and Symmetric-Top Molecules. In Molecular Spectroscopy: Modern Research; Rao, K.N., Mathews, C.W., Eds.; Academic Press: New York, NY, USA, 1972; pp. 115–140. [Google Scholar]
- Pietropolli Charmet, A.; Cornaton, Y. Benchmarking fully analytic DFT force fields for vibrational spectroscopy: A study on halogenated compounds. J. Mol. Struct. 2018, 1160, 455–462. [Google Scholar] [CrossRef]
- Gambi, A.; Pietropolli Charmet, A.; Stoppa, P.; Tasinato, N.; Ceselin, G.; Barone, V. Molecular synthons for accurate structural determinations: The equilibrium geometry of 1-chloro-1-fluoroethene. Phys. Chem. Chem. Phys. 2019, 21, 3615–3625. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef]
- Bloino, J.; Biczysko, M.; Barone, V. General Perturbative Approach for Spectroscopy, Thermodynamics, and Kinetics: Methodological Background and Benchmark Studies. J. Chem. Theory Comput. 2012, 8, 1015–1036. [Google Scholar] [CrossRef]
- Stanton, J.F.; Gauss, J.; Harding, M.E.; Szalay, P.G. CFOUR. A Quantum Chemical Program Package, 2016. with Contributions from A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, Y. J. Bomble, O. Christiansen, F. Engel, M. Heckert, O. Heun, C. Huber, T.-C. Jagau, D. Jonsson, J. Jusélius, K. Klein, W. J. Lauderdale, F. Lipparini, D. Matthews, T. Metzroth, L. A. Mück, D. P. O’Neill, D. R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, S. Stopkowicz, A. Tajti, J. Vázquez, F. Wang, J. D. Watts and the Integral Packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP Routines by A. V. Mitin and C. van Wüllen. For the Current Version. Available online: http://www.cfour.de (accessed on 27 February 2025).
- Baldacci, A.; Stoppa, P.; Charmet, A.P.; Giorgianni, S.; Nivellini, G. High resolution FTIR study of the ν5 and ν6 bands of CH2D35Cl: Analysis of resonances and determination of ground and upper state constants. Mol. Phys. 2005, 103, 2803–2811. [Google Scholar] [CrossRef]
- Melosso, M.; Conversazioni, B.; Degli Esposti, C.; Dore, L.; Cané, E.; Tamassia, F.; Bizzocchi, L. The Pure Rotational Spectrum of 15ND2 Observed by Millimetre and Submillimetre-Wave Spectroscopy. J. Quant. Spectrosc. Radiat. Transf. 2019, 222, 186–189. [Google Scholar]
- Melosso, M.; Bizzocchi, L.; Tamassia, F.; Degli Esposti, C.; Canè, E.; Dore, L. The Rotational Spectrum of 15ND. Isotopic-Independent Dunham-type Analysis of the Imidogen Radical. Phys. Chem. Chem. Phys. 2019, 21, 3564–3573. [Google Scholar]
- Umezawa, T.; Baker, A.K.; Brenninkmeijer, C.A.M.; Zahn, A.; Oram, D.E.; van Velthoven, P.F.J. Methyl chloride as a tracer of tropical tropospheric air in the lowermost stratosphere inferred from IAGOS-CARIBIC passenger aircraft measurements. J. Geophys. Res. Atmos. 2015, 120, 12313–12326. [Google Scholar] [CrossRef]
- Cristofanelli, P.; Arduini, J.; Calzolari, F.; Giostra, U.; Bonasoni, P.; Maione, M. First Evidences of Methyl Chloride (CH3Cl) Transport from the Northern Italy Boundary Layer during Summer 2017. Atmosphere 2020, 11, 238. [Google Scholar] [CrossRef]
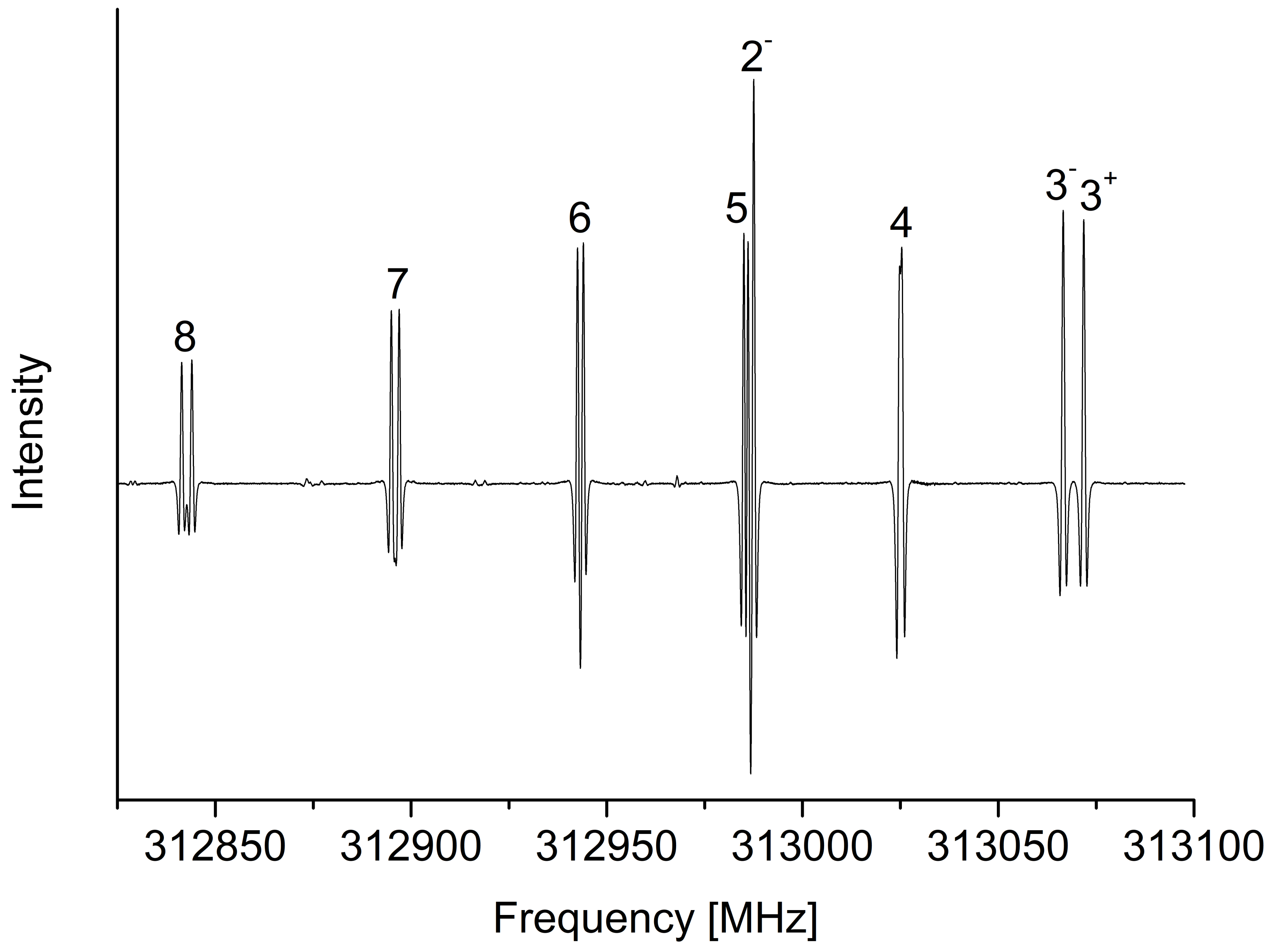

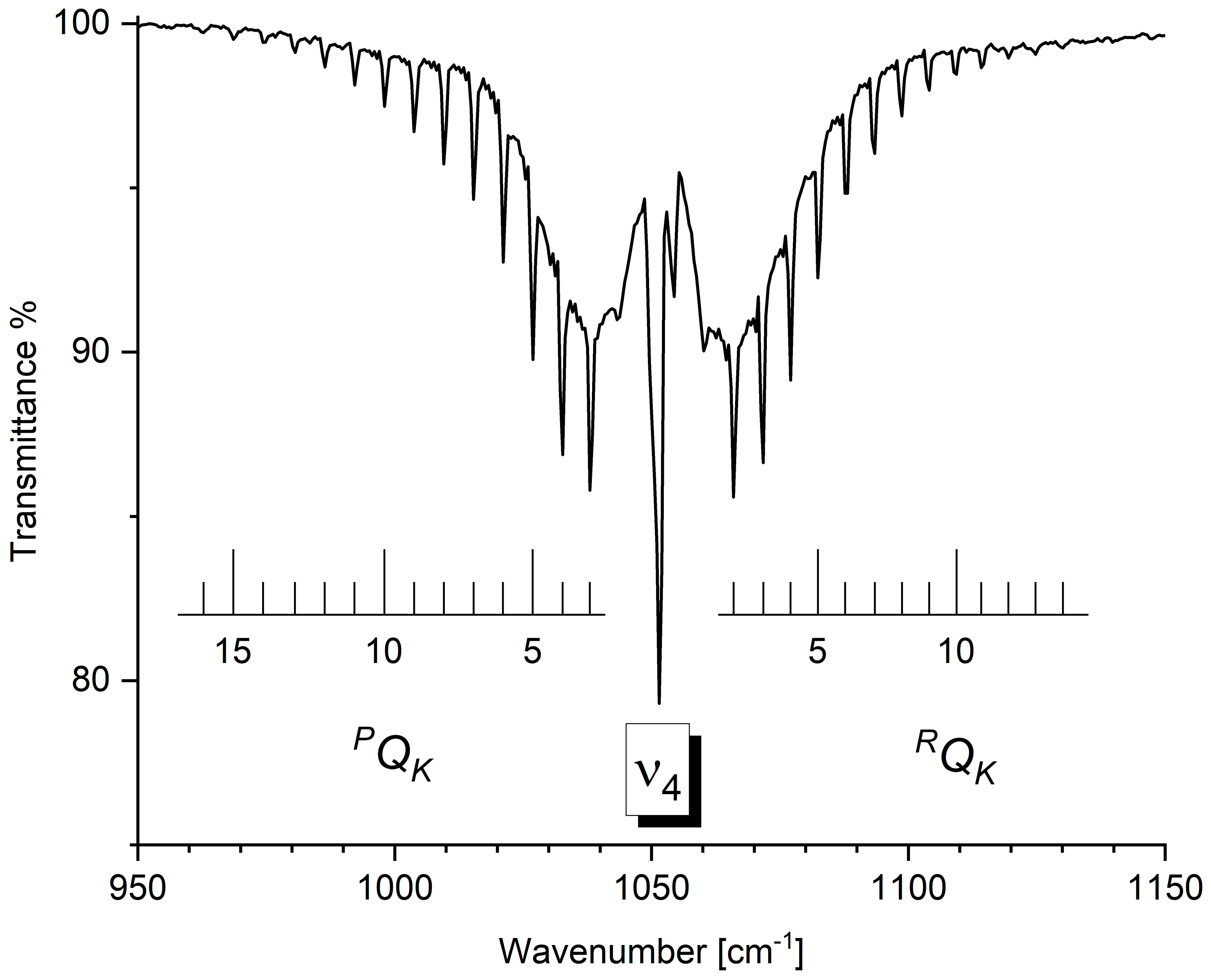

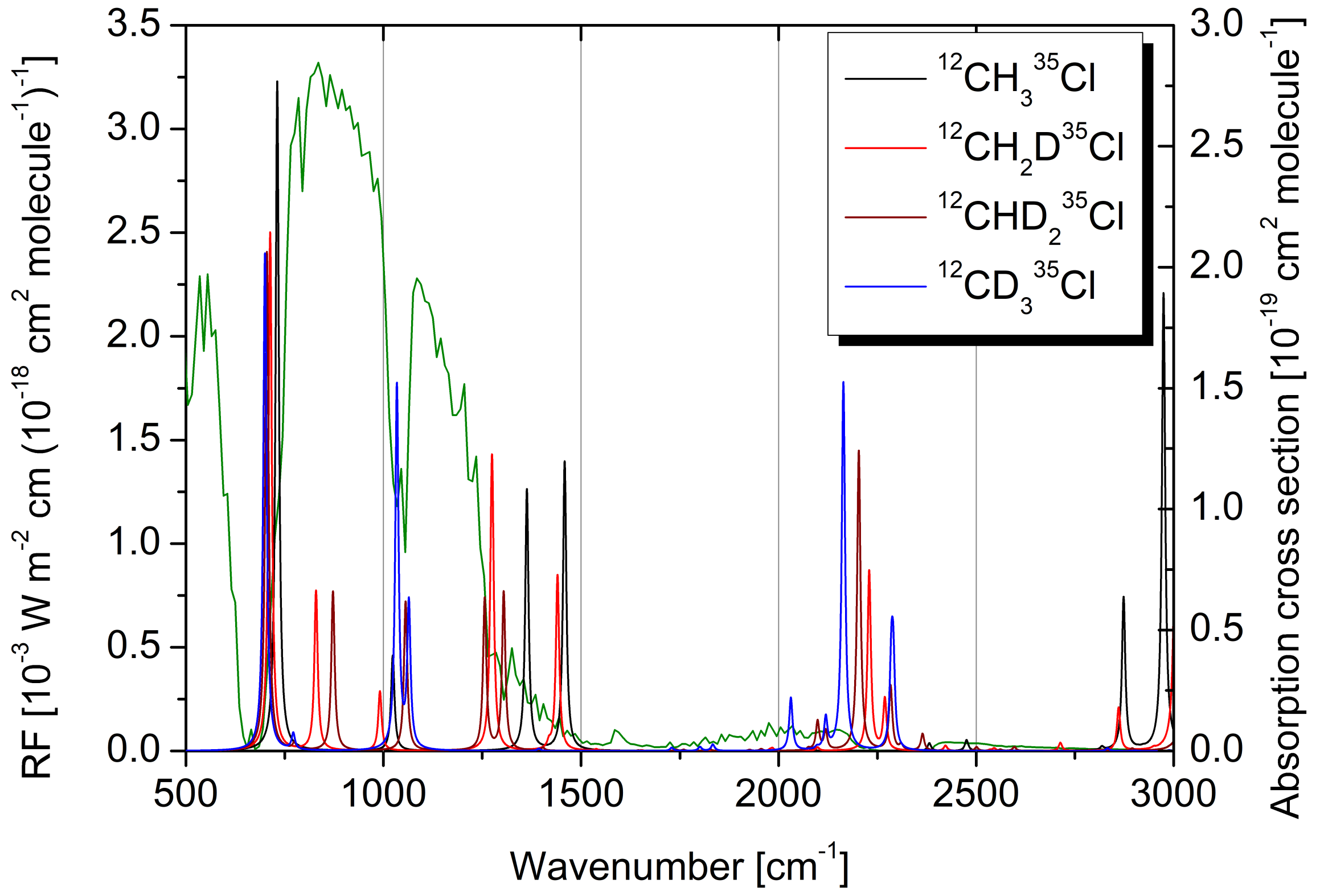
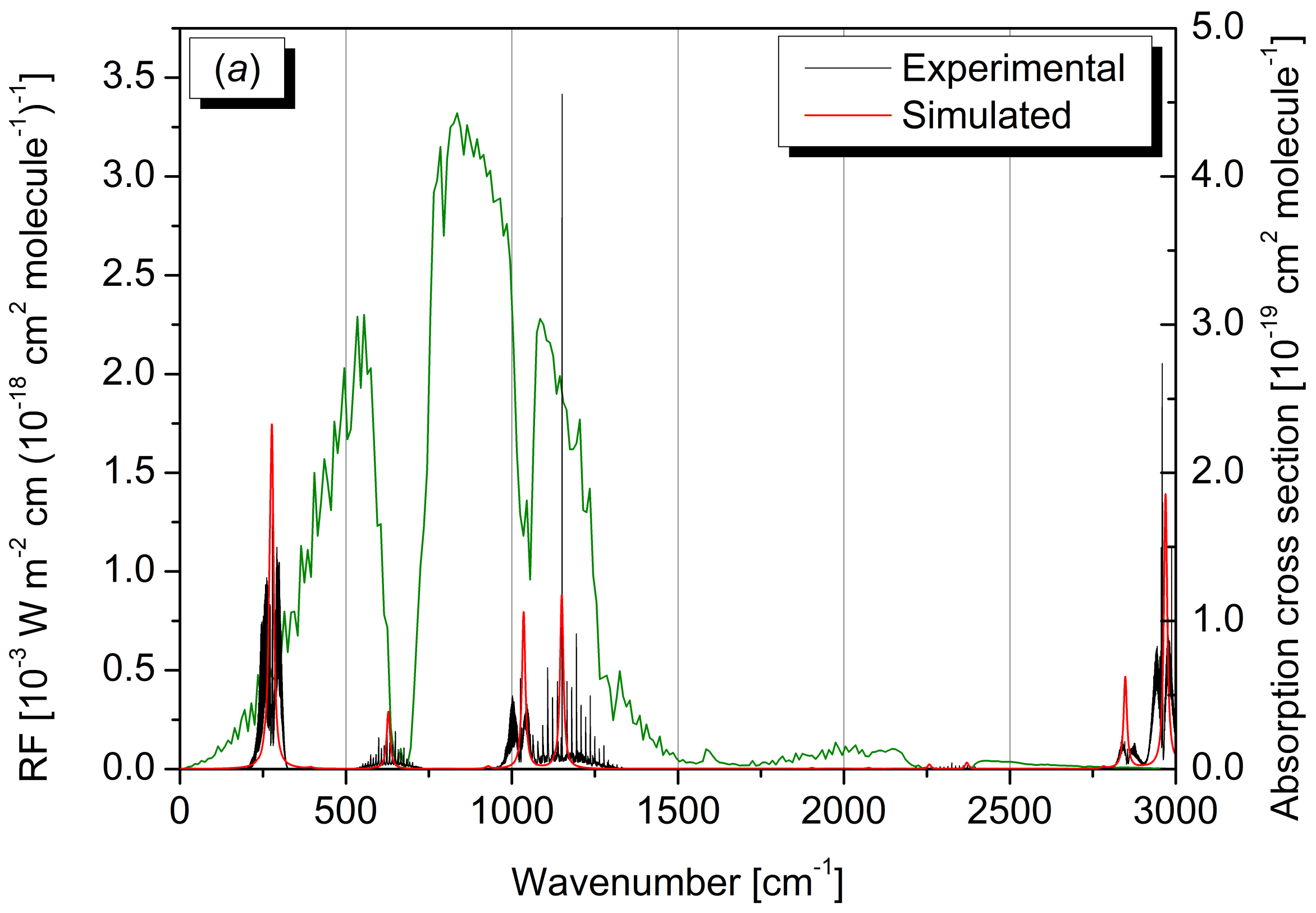
| Normal Mode | Symmetry | Appr. Description | 12CHD235Cl | 12CHD237Cl | 13CHD235Cl | 13CHD237Cl |
|---|---|---|---|---|---|---|
| CH stretch | 3152.9 | 3152.9 | 3143.3 | 3143.3 | ||
| CD2 sym. stretch | 2252.8 | 2252.8 | 2245.1 | 2245.1 | ||
| CD2 deform | 1279.4 | 1279.2 | 1275.4 | 1275.3 | ||
| CD2 wag | 1073.5 | 1073.5 | 1067.0 | 1067.0 | ||
| H/D-C-Cl deform | 883.8 | 883.3 | 873.3 | 872.8 | ||
| C-Cl stretch | 719.2 | 713.0 | 706.2 | 699.8 | ||
| CD2 asym. stretch | 2363.8 | 2363.8 | 2346.6 | 2346.6 | ||
| CD2 twist | 1332.6 | 1332.6 | 1329.1 | 1329.1 | ||
| CD2 rock | 782.1 | 781.6 | 777.9 | 777.3 |
| Constant | Unit | Experiment 1 | Theory 2 | Previous | Experiment 1 | Theory 2 | Previous |
|---|---|---|---|---|---|---|---|
| CHCl | CHCl | ||||||
| A | MHz | 95426.0588(23) | 95423.147 | 95426.077(61) | 95425.1307(67) | 95422.232 | 95425.23(11) |
| B | MHz | 11679.70196(17) | 11679.727 | 11679.7051(79) | 11485.12342(23) | 11485.022 | 11485.129(14) |
| C | MHz | 11370.06627(17) | 11370.068 | 11370.0711(80) | 11185.58835(23) | 11185.684 | 11185.596(14) |
| kHz | 12.66567(41) | 12.466 | 12.6698(92) | 12.27402(72) | 12.081 | 12.284(12) | |
| kHz | 127.1323(16) | 126.232 | 127.36(19) | 123.3620(20) | 122.474 | 123.90(21) | |
| kHz | 959.74(19) | 925.802 | 955.3(12) | 963.28(37) | 929.752 | 958.3(14) | |
| Hz | 310.662(40) | 299.671 | 310.2(4) | 296.208(41) | 285.950 | 295.9(3) | |
| kHz | 60.346(23) | 56.242 | 59.95(22) | 58.785(22) | 54.566 | 58.26(20) | |
| mHz | −2.428 | −2.428 | −2.322 | −2.322 | |||
| Hz | 0.333 | 0.333 | 0.50(2) | 0.346 | 0.346 | 0.64(10) | |
| Hz | 2.649 | 2.649 | 2.717 | 2.717 | |||
| Hz | 31.603 | 31.603 | 31.501 | 31.501 | |||
| mHz | 0.161 | 0.161 | 0.153 | 0.153 | |||
| Hz | 267.288 | 267.288 | 253.686 | 253.686 | |||
| Hz | 23.853 | 23.853 | 24.136 | 24.136 | |||
| MHz | −74.469(14) | −72.20 | −74.52 3 | −58.711(21) | −56.90 | −58.69 3 | |
| MHz | 37.325(23) | 36.01 | 37.260 3 | 29.52(19) | 28.38 | 29.345 3 | |
| Parameter | Unit | Experiment 1 | Theory 2 | Experiment 1 | Theory 2 |
|---|---|---|---|---|---|
| 13CHCl | 13CHCl | ||||
| A | MHz | 95358.5(50) | 95355.295 | 95359.1(56) | 95354.365 |
| B | MHz | 11330.5476(80) | 11330.523 | 11134.1477(85) | 11134.107 |
| C | MHz | 11039.9541(80) | 11039.920 | 10853.4201(85) | 10853.371 |
| kHz | 12.0282(34) | 11.835 | 11.6429(35) | 11.454 | |
| kHz | 122.738(19) | 121.916 | 118.943(20) | 118.162 | |
| kHz | 928.936 | 928.936 | 932.871 | 932.871 | |
| Hz | 282.7(27) | 274.503 | 272.2(30) | 261.408 | |
| kHz | 60.7(39) | 53.918 | 57.7(42) | 52.240 | |
| mHz | −2.656 | −2.656 | −2.532 | −2.532 | |
| Hz | 0.306 | 0.306 | 0.287 | 0.287 | |
| Hz | 2.655 | 2.655 | 2.544 | 2.544 | |
| Hz | 32.0 | 32.0 | 32.0 | 32.0 | |
| mHz | 0.128 | 0.128 | 0.122 | 0.122 | |
| Hz | 248. | 248. | 235. | 235. | |
| Hz | 23.0 | 23.0 | 22.0 | 22.0 | |
| MHz | −74.461(32) | −72.21 | −58.751(53) | −56.91 | |
| MHz | 37.307(63) | 36.02 | 29.71(19) | 28.39 | |
| Isotopologue | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 12CH335Cl | −2044.154 | −109.423 | - | −1974.703 | −106.636 | - | 21.628 | −0.139 | - |
| 12CH337Cl | −2044.542 | −107.197 | - | −1974.823 | −104.508 | - | 21.628 | −0.131 | - |
| 13CH335Cl | −2033.338 | −102.999 | - | −1964.000 | −100.400 | - | 21.628 | −0.132 | - |
| 13CH337Cl | −2033.459 | −100.845 | - | −1964.090 | −98.302 | - | 21.628 | −0.125 | - |
| 12CD335Cl | −1000.000 | −80.205 | - | −744.565 | −77.556 | - | 5.416 | −0.102 | - |
| 12CD337Cl | −1000.000 | −78.472 | - | −744.654 | −75.877 | - | 5.416 | −0.096 | - |
| 12CH2D35Cl | −1376.206 | −94.668 | −99.698 | −1328.560 | −92.306 | −97.133 | 12.686 | −0.123 | −0.124 |
| 12CH2D37Cl | −1376.326 | −92.744 | −97.642 | −1328.680 | −90.417 | −95.124 | 12.686 | −0.116 | −0.117 |
| 13CH2D35Cl | −1363.618 | −89.632 | −94.448 | −1316.359 | −87.390 | −92.036 | 12.658 | −0.118 | −0.119 |
| 13CH2D37Cl | −1363.738 | −87.726 | −92.410 | −1316.419 | −85.501 | −90.028 | 12.657 | −0.111 | −0.112 |
| 12CHD235Cl | −1000.610 | −85.817 | −89.513 | −966.231 | −83.792 | −87.180 | 8.032 | −0.112 | −0.112 |
| 12CHD237Cl | −1000.731 | −84.128 | −87.514 | −966.351 | −82.023 | −85.321 | 8.032 | −0.106 | −0.105 |
| 13CHD235Cl | −991.185 | −81.612 | −85.161 | −957.087 | −79.655 | −82.923 | 8.021 | −0.107 | −0.107 |
| 13CHD237Cl | −991.305 | −79.827 | −83.283 | −957.207 | −77.916 | −81.124 | 8.021 | −0.101 | −0.101 |
| 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|
| r(C-Cl) | 1.777716(10) | 1.777863(50) | 1.777725(11) | 1.77686 | 1.77792 | 1.7777 |
| r(C-H) | 1.083484(17) | 1.083699(65) | 1.083450(17) | 1.08338 | 1.08339 | 1.0834 |
| (Cl-C-H) | 108.3723(18) | 108.3739(81) | 108.3740(19) | 108.412 | 108.384 | 108.38 |
| 12CHD235Cl | 12CHD237Cl | 13CHD235Cl | 13CHD237Cl | |||||
|---|---|---|---|---|---|---|---|---|
| Wvn | I | Wvn | I | Wvn | I | Wvn | I | |
| 3010.4 | 9.56 | 3010.3 | 9.71 | 3001.2 | 10.40 | 3001.1 | 10.42 | |
| 2193.9 | 11.07 | 2193.8 | 11.08 | 2185.2 | 10.80 | 2185.2 | 10.80 | |
| 1251.4 | 5.57 | 1251.3 | 5.61 | 1247.9 | 4.86 | 1247.7 | 4.90 | |
| 1051.9 | 5.55 | 1051.9 | 5.56 | 1045.8 | 5.23 | 1045.8 | 5.25 | |
| 869.1 | 5.99 | 868.5 | 5.85 | 859.0 | 5.09 | 858.5 | 5.00 | |
| 706.0 | 18.13 | 700.0 | 17.89 | 693.2 | 18.40 | 687.0 | 18.11 | |
| 2274.5 | 2.15 | 2274.5 | 2.15 | 2259.9 | 2.30 | 2259.9 | 2.30. | |
| 1299.6 | 5.92 | 1299.4 | 5.92 | 1296.1 | 5.94 | 1296.0 | 5.94. | |
| 771.2 | 0.22 | 770.7 | 0.23 | 767.2 | 0.25 | 766.6 | 0.26. | |
| Band | Exp. | Wvn 1 | I 1 | Band | Exp. | Predicted 1 | I 1 |
|---|---|---|---|---|---|---|---|
| 705.9(5)/700.0(5) 2 | 706 | 18.13 | 2583.0(5) | 2588 | 0.15 | ||
| 771.6(5) | 771 | 0.22 | 3012.12(5) 3 | 3010 | 9.56 | ||
| 869.8(5) | 869 | 5.99 | 3315.15(11) 3 | 3308 | 0.30 | ||
| 1052.25(4) 3 | 1052 | 5.55 | 3442.0(5) | 3434 | 0.07 | ||
| 1250.3(5) | 1251 | 5.57 | 3462.0(5) | 3475 | 0.27 | ||
| 1300.50(6) 3 | 1300 | 5.92 | 3569.0(5) | 3562 | 0.21 | ||
| 1404.9(5) | 1405 | 0.13 | 3733.0(5) | 3719 | 0.05 | ||
| 1919.9(5) | 1919 | 0.04 | 3880.0(5) | 3877 | 0.30 | ||
| 1950.2(5) | 1952 | 0.06 | 4060.0(5) | 4061 | 0.07 | ||
| 2089.0(5) | 2091 | 0.80 | 4242.0(5) | 4244 | 0.57 | ||
| 2114.0(5) | 2112 | 0.61 | 4292.4(3) | 4288 | 0.05 | ||
| 2192.0(5) | 2194 | 11.07 | 4526.8(3) | 4510 | 0.20 | ||
| 2278.0(5) | 2275 | 2.15 | 5202.0(5) | 5192 | 0.04 | ||
| 2296.33(7) 3 | 2301 | 0.22 | 5290.0(5) | 5286 | 0.05 | ||
| 2491.0(5) | 2492 | 0.15 | 5897.0(5) | 5898 | 0.52 | ||
| 2553.0(5) | 2552 | 0.05 |
| Band | Std. Dev. 2 | |||||
|---|---|---|---|---|---|---|
| 1052.25(4) | 2.786(4) | 1.42(5) | 0.32(14) | 2.800(4) | 0.122 | |
| 1300.50(6) | 2.821(4) | −2.49(25) | – | 2.796(5) | 0.116 | |
| 2296.33(7) | 2.724(9) | 2.07(13) | 0.76(56) | 2.745(9) | 0.207 | |
| 3012.12(5) | 2.788(4) | 1.45(5) | 0.48(17) | 2.802(2) | 0.117 | |
| 3315.15(11) | 2.781(7) | 1.34(19) | – | 2.788(7) | 0.265 |
| 12CH335Cl | 12CH337Cl | 13CH335Cl | 13CH337Cl | 12CD335Cl | 12CH2D35Cl | 12CH2D37Cl | 12CHD235Cl | |
|---|---|---|---|---|---|---|---|---|
| IRE 2 | 6.92 | 6.24 | 4.89 | 4.26 | 6.54 | 8.01 | 5.67 | 7.50 |
| Weight. IRE 3 | 5.10 | 1.47 | 0.04 | 0.01 | 0.00 | 0.09 | 0.01 | 0.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melosso, M.; Stoppa, P.; Alvarado-Jiménez, D.; Tamassia, F.; Sapienza, C.; Bizzocchi, L.; Dore, L.; Puzzarini, C.; Pietropolli Charmet, A.; Tasinato, N. Completing the Spectral Mosaic of Chloromethane by Adding the CHD2Cl Missing Piece Through the Interplay of Rotational/Vibrational Spectroscopy and Quantum Chemical Calculations. Molecules 2025, 30, 1604. https://doi.org/10.3390/molecules30071604
Melosso M, Stoppa P, Alvarado-Jiménez D, Tamassia F, Sapienza C, Bizzocchi L, Dore L, Puzzarini C, Pietropolli Charmet A, Tasinato N. Completing the Spectral Mosaic of Chloromethane by Adding the CHD2Cl Missing Piece Through the Interplay of Rotational/Vibrational Spectroscopy and Quantum Chemical Calculations. Molecules. 2025; 30(7):1604. https://doi.org/10.3390/molecules30071604
Chicago/Turabian StyleMelosso, Mattia, Paolo Stoppa, Daniela Alvarado-Jiménez, Filippo Tamassia, Carlotta Sapienza, Luca Bizzocchi, Luca Dore, Cristina Puzzarini, Andrea Pietropolli Charmet, and Nicola Tasinato. 2025. "Completing the Spectral Mosaic of Chloromethane by Adding the CHD2Cl Missing Piece Through the Interplay of Rotational/Vibrational Spectroscopy and Quantum Chemical Calculations" Molecules 30, no. 7: 1604. https://doi.org/10.3390/molecules30071604
APA StyleMelosso, M., Stoppa, P., Alvarado-Jiménez, D., Tamassia, F., Sapienza, C., Bizzocchi, L., Dore, L., Puzzarini, C., Pietropolli Charmet, A., & Tasinato, N. (2025). Completing the Spectral Mosaic of Chloromethane by Adding the CHD2Cl Missing Piece Through the Interplay of Rotational/Vibrational Spectroscopy and Quantum Chemical Calculations. Molecules, 30(7), 1604. https://doi.org/10.3390/molecules30071604






