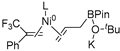
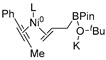
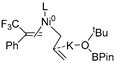
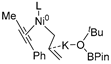
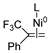
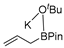
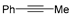Abstract
Density functional theory (DFT) characterizations were employed to resolve the structural and energetic aspects and product selectivities along the mechanistic reaction paths of the nickel-catalyzed three-component unsymmetrical bis-allylation of alkynes with alkenes. Our putative mechanism initiated with the in situ generation of the active catalytic species [Ni(0)L2] (L = NHC) from its precursors [Ni(COD)2, NHC·HCl] to activate the alkyne and alkene substrates to form the final skipped trienes. This proceeds via the following five sequential steps: oxidative addition (OA), β-F elimination, ring-opening complexation, C-B cleavage and reductive elimination (RE). Both the OA and RE steps (with respective free energy barriers of 24.2 and 24.8 kcal·mol−1) contribute to the observed reaction rates, with the former being the selectivity-controlling step of the entire chemical transformation. Electrophilic/nucleophilic properties of selected substrates were accurately predicted through dual descriptors (based on Hirshfeld charges), with the chemo- and regio-selectivities being reasonably predicted and explained. Further distortion/interaction and interaction region indicator (IRI) analyses for key stationary points along reaction profiles indicate that the participation of the third component olefin (allylboronate) and tBuOK additive played a crucial role in facilitating the reaction and regenerating the active catalyst, ensuring smooth formation of the skipped triene product under a favorably low dosage of the Ni(COD)2 catalyst (5 mol%).
1. Introduction
Multi-component reactions (MCRs) are an important strategy for the concise and efficient synthesis of complex molecules [1,2], including transition metal-catalyzed MCRs that remain established as a ‘hot topic’ [3,4,5,6]. In particular, nickel-catalyzed MCRs, due to the low cost, availability and special properties of nickel [7,8], continue to generate attention [9,10,11,12]. Yet, Ni-based MCRs still face many challenges such as (1) overcoming competitive and side reactions among multiple components and (2) effective control of chemo-, regio- and stereo-selectivities of the reaction [13,14]. Detailed computational characterizations provide atomistic details from which to raise awareness and understanding of MCRs towards helping overcome these challenges [15,16,17]. Yet, even for seasoned computational scientists, accurate determinations of structure and energetics along the reaction profiles of the putative mechanisms, towards predicting selectivities of MCRs, require significant computational resources, replete with technical difficulties and non-facile interpretation of the result trends. Hence, the provision of accurate reaction-selectivity predictions through relatively low-cost computations is of great significance to both computational and experimental developments in this and related areas [18,19].
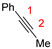
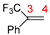
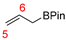
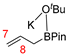
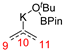
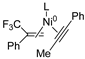
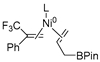
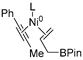
In 2014, Ichitsuka and co-workers prepared 2-fluoro-1,3-cyclopentadienes under mild conditions by using trifluoromethyl olefins and alkynes as substrates, assisted by Ni(0)/PCy3 species (Scheme 1a) [20]. This reaction can lead to cyclopentadiene frameworks directly and regioselectively, yet it requires 1.0 equiv of the nickel catalyst. Recently, Li and co-workers synthesized skip trienes (P1) by employing trifluoromethyl alkenes (R1), alkynes (R2) and allylboronate (R3) as substrates, realizing good yields (up to 83%) and high regio- and stereo-selectivities under mild conditions with the help of a Ni(0)/NHC catalytic system (Scheme 1b) [14]. It involved a third component (allylboronic acid pinacol ester) and potassium t-butoxide (tBuOK) additive, featuring a low dosage (5 mol%) of the nickel catalyst Ni(COD)2; it was favorable relative to Ichitsuka’s 1.0 equiv.
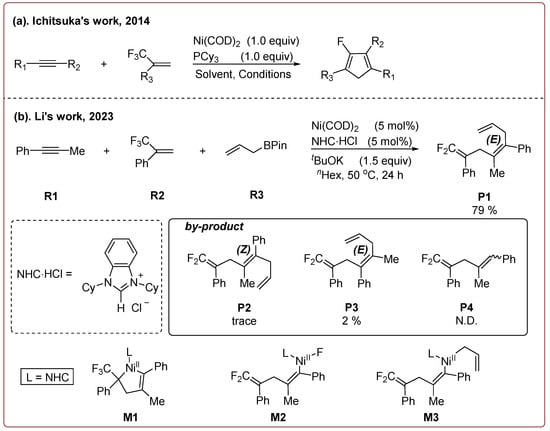
Scheme 1.
Overview of selected Ni-catalyzed two-component (a) [20] and three-component reactions (b) [14].
Li et al. speculated that the reaction may proceed by the following putative mechanism: substrates R1 and R2 undergo cyclization to form intermediate M1 under the help of catalysts (Scheme 1), then M1 experiences β-F elimination and is converted into intermediate M2, which coordinates with substrate R3, assisted by a base additive. Subsequently, intermediate M3 is generated through the removal of a -BPin group, after which the final product P1 is produced through reductive elimination of M3. However, this could be considered as being overly speculative due to the omission of the essential pre-catalysis process, while also failing to justify the high selectivities exhibited in the reaction. The participation of the third component R3 and tBuOK, as well as the significant changes in products and in the amount of catalysts, indicate that the mechanism of this reaction, especially the catalyst recycling mechanism, differs significantly with respect to the two-component reaction. However, the roles of the third component (allylboronic acid pinacol ester) and tBuOK additive, as well as the mechanistic bases for the pronounced reduction in catalyst dosage (from 1.0 equiv in Ichitsuka’s two-component reaction to 5 mol% in Li’s three-component reaction), are currently unclear, which hinders and limits the rapid development of MCRs.
Towards resolving the relevant atomistic aspects of MCRs (structure, energetics and specificity) and tackling the issues outlined above, we conducted computational studies on the reaction shown in Scheme 1b by employing the density functional theory (DFT) method, with the reaction mechanism (including pre-catalysis and recycling and regeneration of the catalyst) as well as selectivities explored and discussed in detail. Based on confirmation of the rate-determining step (RDS) and selectivity-controlling step (SCS), distortion/interaction analyses [21,22] and interaction region indicator (IRI) analyses [23] were employed to rationalize the high selectivities as well as the role of the base additive. In addition, relatively low-cost computational methods (e.g., dual descriptors [24]) were also used to reliably predict the selectivities of the reaction (Scheme 1b). The emerging good agreement of our theoretical predictions and the corresponding experimental trends makes this work meaningful in helping the organometallic and wider catalysis communities comprehend the mechanisms of such Ni-NHC catalyzed multi-component cyclizations at the molecular level. These trends emerging from relatively low-cost computations provide excellent guidance for experimental chemists in screening substrates and improving MCRs.
2. Results and Discussion
2.1. Reaction Mechanism
Characterizations of the reaction profile were initiated at the IDSCRF(nHex)-PBE0-D3(BJ)/6-311+G(d,p)-SDD(Ni)//IDSCRF(nHex)-PBE0-D3(BJ)/6-31+G(d)-SDD(Ni) level and showed that the reaction undergoes the following principal steps: pre-catalysis, oxidative addition (OA), ring-opening complexation and reductive elimination (RE). In addition, the third component R3 can easily interact with the tBuOK additive to form a new ‘substrate’ R3′, accompanied by a favorable release of 24.7 kcal·mol−1 of free energies (Figure 1). This signals that the majority of the unreacted substrate R3 should exist in the R3′ form. For reference, R1 + R2 + R3′ is set as the starting point of the catalyzed chemical transformation and assigned a relative free energy of zero (ΔG = 0), with all other energetics expressed relative to this.
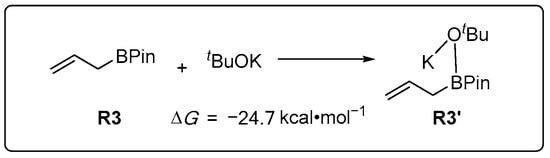
Figure 1.
Energetics (ΔG in kcal·mol−1) for the complexation of R3 with tBuOK.
2.1.1. Pre-Catalysis
The NHC ligand is shown to be cable of capturing protons from alcohols and generating NHC-H+ plus alkoxy anions (R-O−) [25], which would be the reverse process of the pre-catalysis. To understand the interaction mechanism of the catalyst precursors with the base additive well, we conducted DFT calculations on the pre-catalysis process of the reaction (Figure 2). The catalyst precursor NHC·HCl (CAT1) can initially interact with tBuOK to form the intermediate INT1-I, which then undergoes hydrogen migration through transition state TS1-I, transforming into intermediate INT2-I via a near barrier-free process (ΔΔE = 0.6 kcal·mol−1, with a negative ΔΔG). Afterwards, INT2-I removes the tBuOK·KCl fragments and forms the NHC ligand (L), which then undergoes ligand exchange with Ni(COD)2 to exothermically generate the active catalytic species Ni(0)L2 (L = NHC), releasing 30.2 kcal·mol−1 of free energies. On the contrary, the formation of Ni(0)L is endothermic and requires an absorption of 21.9 kcal·mol−1 of free energies, indicating that the formation of Ni(0)L is almost uncompetitive to the formation of Ni(0)L2. Namely, Ni(0)L2 is more stable than Ni(0)L, confirming the active catalytic species in this reaction is Ni(0)L2 rather than Ni(0)L.
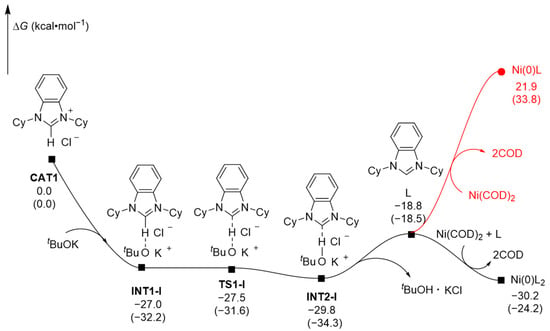
Figure 2.
Computed free energy profiles (ΔG in kcal·mol−1) for the activation of the pre-catalyst, with electronic energies (ΔE) noted in parentheses.
2.1.2. Oxidative Addition (OA)
After the generation of the active catalytic species Ni(0)L2, the oxidative addition (OA) between substrates R1 and R2 was evaluated at the IDSCRF(nHex)-PBE0-D3(BJ)/6-311+G(d,p)-SDD(Ni)//IDSCRF(nHex)-PBE0-D3(BJ)/6-31+G(d)-SDD(Ni) level (Figure 3). The active species Ni(0)L2 quickly coordinates with substrate R2 to form complex COM1-I, releasing 33.8 kcal·mol−1 of free energies. COM1-I then reacts with substrate R1 and removes one molecule of ligand L, transforming into complex COM2-I (Figure S1 in Supplementary Materials for other possible formation pathways of COM2-I), which subsequently undergoes oxidative addition (OA) through transition state TS2-I, surmounting a total free energy barrier of 24.2 kcal·mol−1 (COM1-I → COM2-I → TS2-I) to form a five-membered ring intermediate INT3-I (M1 in Scheme 1), which is feasible at the experimental temperature of 50 °C. Afterwards, intermediate INT3-I undergoes β-F elimination through transition state TS3-I and forms the intermediate INT4-I, overcoming a relatively low free energy barrier of 15.9 kcal·mol−1 (8.3 kcal·mol−1 lower than that of TS2-I), signaling that the oxidative addition step is the controlling process of the reaction rate at this stage. If the asymmetric alkene (R2) and alkyne (R1) coordinate with the nickel center in complex COM1-I in different orientations, complexes with different regioselectivities will be formed (see Section 2.2).
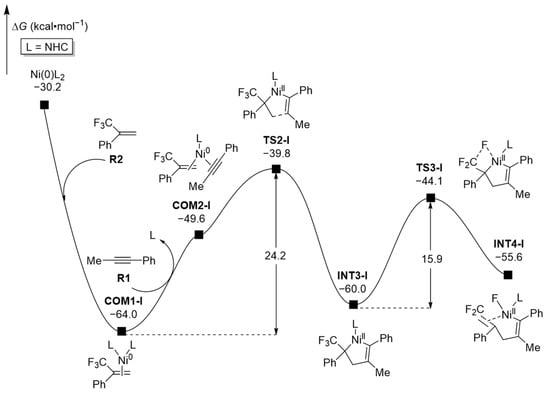
Figure 3.
Computed free energy profiles (ΔG in kcal·mol−1) for the oxidative addition of R1 with R2.
2.1.3. Ring-Opening Complexation
As shown in Figure 4, the five-membered ring intermediate INT4-I formed through the oxidative addition process can endothermically undergo C-C single bond rotation (ΔΔG = 2.6 kcal·mol−1) to convert into ring-opened intermediate INT5-I (M2 in Scheme 1), which is in a more favorable configuration for the subsequent formation of product P1. Intermediate INT5-I on Path I will then interact with R3′ (formed through interaction of the third component R3 with tBuOK, Figure 1) to form intermediate INT6-I, which then undergoes C-B cleavage through transition state TS4-I (ΔΔG = 7.1 kcal·mol−1) to form the more stable intermediate INT7-I. The whole process releases 27.6 kcal·mol−1 of free energies and should be easily achievable at an experimental temperature of 50 °C.
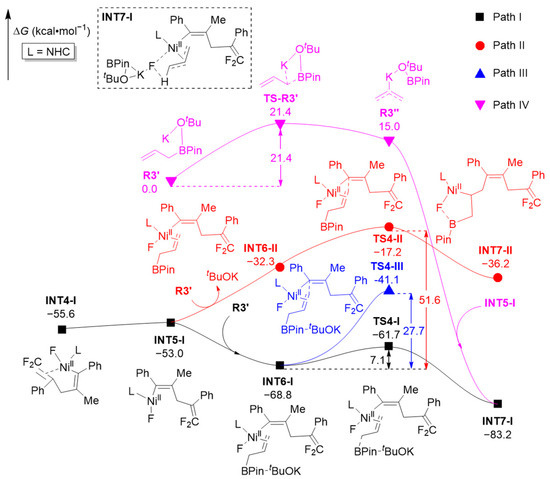
Figure 4.
Computed free energy profiles (ΔG in kcal·mol−1) for the ring-opening complexation process.
Alternatively, if intermediate INT5-I reacts with R3′ and removes tBuOK (i.e., tBuOK does not participate in the reaction), the reaction may undergo C-C coupling along Path II, transforming INT5-I into intermediate INT7-II through transition state TS4-II. However, the total free energy barrier of TS4-II (INT6-I → INT5-I → INT6-II → TS4-II, 51.6 kcal·mol−1) is 44.5 kcal·mol−1 higher than that of TS4-I (7.1 kcal·mol−1), which indicates null possibility for the reaction to occur along Path II (see Figure S2 for subsequent details of Path II). Similarly, if intermediate INT6-I does not undergo C-B cleavage but experiences C-C coupling and reductive elimination directly through transition state TS4-III, the reaction must surmount a free energy barrier of 27.7 kcal·mol−1, which is 20.6 kcal·mol−1 higher than TS4-I. This suggests that Path I is much more preferable than Path III in energy. In addition, the possibility of R3′ undergoing C-B cleavage through transition state TS-R3′ to transform into the intermediate R3″, and then reacting with intermediate INT5-I to transform into intermediate INT7-I (Path IV), was also investigated. It was found that the free energy barrier of TS-R3′ (21.4 kcal·mol−1) is 14.3 kcal·mol−1 higher than TS4-I, and all stationary points on Path IV are significantly less stable than those along Path I. Therefore, the reaction is most likely to proceed along Path I at this stage.
2.1.4. Reductive Elimination (RE)
As shown in Figure 5, the intermediate INT7-I formed will undergo C-C coupling and reductive elimination through transition state TS5-I, overcoming a free energy barrier of 24.8 kcal·mol−1 and transforming into intermediate INT8-I. Afterwards, INT8-I removes the tBuOB(Pin)·KF fragment and converts to intermediate INT9-I. Finally, INT9-I interacts with ligand L and forms the product P1, accompanied by the regeneration and recycling of the active catalytic species Ni(0)L2 (L = NHC). If intermediate INT7-I removes the tBuOB(Pin)·KF fragment and transforms to INT8-V (M3 in Scheme 1) first (Path V), the following C-C coupling and reductive elimination process must overcome a total free energy barrier as high as 35.4 kcal·mol−1 (INT7-I → INT8-V → TS5-V), which is ~10.6 kcal·mol−1 higher than that for Path I (24.8 kcal·mol−1). This indicates that the reaction would barely proceed along Path V at an experimental temperature of 50 °C, and Path I clearly dominates the formation of product P1.
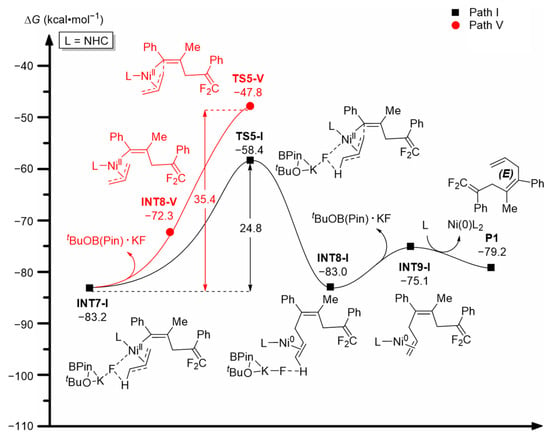
Figure 5.
Computed free energy profiles (ΔG in kcal·mol−1) for the reductive elimination process.
IRI analyses of transition states TS5-I and TS5-V show significant van der Waals interaction (Figure 6, in green) between the leaving fragment (tBuOB(Pin)·KF) and the remaining part of transition state TS5-I, translating to TS5-I being a more stable structure than TS5-V. Additionally, negligible steric hindrance (in red) can be seen in both molecular graphics, which suggests that the electronic effect is the key factor determining the reaction rate here.
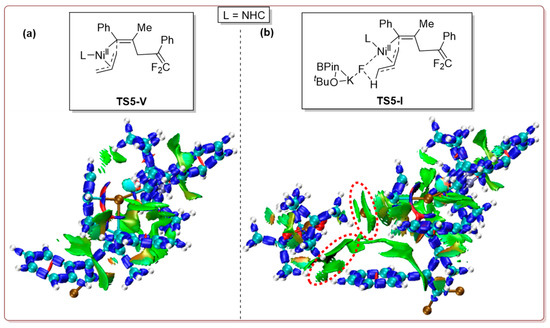
Figure 6.
Interaction region indicator (IRI) analyses for TS5-V (a) and TS5-I (b).
In summary, the final product P1 should be generated as follows: the catalyst precursors (Ni(COD)2 and NHC·HCl) initially interact with the tBuOK additive, which undergoes hydrogen migration and generates the active catalytic species Ni(0)L2 (L = NHC) in situ after removal of the tBuOH·KCl fragment (Figure 7). Then, Ni(0)L2 activates alkyne and olefin substrates (R2 and R1), undergoes oxidative addition to transform into the five-membered ring intermediate INT3-I, followed by β-F elimination and converts into intermediate INT4-I. Afterwards, INT4-I experiences ring-opening through C-C single bond rotation to complex with R3′, leading to intermediate INT7-I through C-B cleavage. Finally, INT7-I undergoes C-C coupling and reductive elimination, removes the tBuOB(Pin)·KF fragment and regenerates the active species Ni(0)L2, while forming product P1. The free energy barriers for the oxidative addition and reductive elimination processes are 24.2 (TS2-I) and 24.8 (TS5-I) kcal·mol−1, respectively, both higher than others and indicating their reaction rate-controlling characteristics. Half-lives transferred from the above two steps’ barriers are 0.66 h and 1.69 h, respectively, while the reaction times delivered from the energy span approximation formula proposed by Kozuch and Shaik [26] are 0.96 h and 2.44 h, respectively, with both being reasonably consistent with the experimental reaction time (~24 h) and illustrating that these kinetic predictions are reliable.
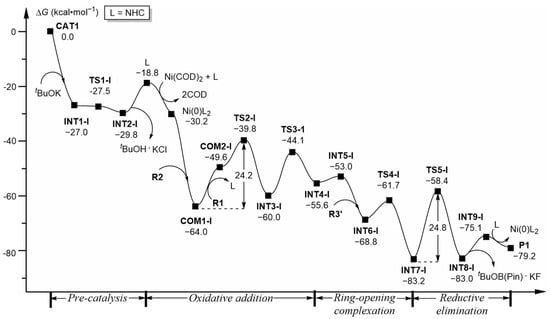
Figure 7.
Computed free energy profiles (ΔG in kcal·mol−1) for the whole reaction process.
2.2. Selectivities
2.2.1. Chemoselectivities
Based on Fu and Cao’s reports, the Hirshfeld charges and dual descriptors Δf can accurately predict the active sites of electrophilic and nucleophilic reagents [18,19]. Hence, the Hirshfeld charges [27] and dual descriptors Δf [24] (based on Hirshfeld charges) of various substrates were measured for evaluating their nucleophilic/electrophilic reaction activities, as well as for exploring the chemoselectivities of this reaction. Regardless, olefin R3 can interact with the tBuOK additive easily to form R3′ (Figure 1) and R3′ may transform into R3″ further (Figure 4); R3′ and R3″ were also taken into consideration (Table 1). For molecules with multiple reaction sites, the most nucleophilic/electrophilic sites are evaluated for their reaction activities.

Table 1.
Hirshfeld charge and dual descriptor (Δf, based on Hirshfeld charge) of key atoms in different substrates, with the nucleophilic sites in red and the electrophilic sites in green.
As shown in Table 1, the dual descriptors (Δf) of the C1 and C2 sites in substrate R1 are both negative, with that of the C1 site being lower. Contrarily, the Δf of the C3 and C4 sites in substrate R2 are both positive, with that of the C4 site being higher. This illustrates that R1 is a nucleophile while R2 is an electrophile. Similar to substrate R1, the dual descriptors of all sites in R3, R3′ and R3″ are negative, with that of the C5, C7 and C9 sites being lower in each of them and indicating that R3, R3′ and R3″ are also nucleophiles. Furthermore, the dual descriptors (Δf) of C5, C7 and C9 in R3, R3′ and R3″ are smaller than C1 in R1, which suggests that R1 is the weakest nucleophilic reagent (Lewis base). With the exception of R2, the nucleophilic/electrophilic reactivity predictions based on Hirshfeld charges are basically consistent with that delivered from the dual descriptors (Table 1). According to the calculated dual descriptors, the reaction between substrate R2 and R1 is most favorable, as R2 is a weak Lewis acid while R1 is a weak Lewis base. Further natural population analysis (NPA) results show that there are −0.05189 and 0.03468 charges populated on the C1 and C2 atoms in substrate R1, respectively (Table S1), while the NPA charges distributed on the C3 and C4 atoms in substrate R2 are −0.13534 and −0.31486, respectively. Thus, when R1 reacts with R2, the C2 atom in R1 is more likely to interact with the C4 atom in R2, leading to the experimentally detected main product P1.
The energetics for different substrates complexing with the nickel catalyst were further evaluated at the IDSCRF(nHex)-PBE0-D3(BJ)/6-311+G(d,p)-SDD(Ni)//IDSCRF (nHex)-PBE0-D3(BJ)/6-31+G(d)-SDD (Ni) level, with the most stable conformations presented in Table 2 (see Figure S3 for other conformations arising from varying orientations of functional groups). The relative stabilities of different complexes are consistent with the predictions derived from the dual descriptors (Δf) as a whole: substrate R2 is an electrophilic reagent, while other substrates are nucleophilic reagents. Therefore, the complexes involving substrate R2 are relatively more stable than others, with the one formed between substrate R2, R1 and the nickel catalyst being most stable (Entry 1 in Table 2). Clearly, the dual descriptors (Δf, Table 1) provide substantially accurate predictions for relative free energies of each complex, although it considers only the electronic structure of the substrates [18] while ignoring steric hindrance effects and other factors such as interactions in the forming complex, evidencing that electronic effects are the principal controlling factor for the reaction selectivities observed.

Table 2.
Energetics (in kcal·mol−1) for the complexation of different substrates with the nickel catalyst (L = NHC).
Trends in the free energy barrier can also validate the above predicted chemoselectivities quite well. As shown in Figure 3, the energy barrier for the oxidative addition of complex COM2-I formed by the complexation of substrate R2 with R1 and the nickel catalyst is 9.8 kcal·mol−1 (TS2-I), which is lower than that of the complex formed by the complexation of substrate R2 with R3/R3′ and the nickel catalyst (19.9/27.7 kcal·mol−1, Figure S3), also lower than that of the complex formed by the complexation of substrate R1 with R3 and the nickel catalyst (20.6 kcal·mol−1). For the complex formed by the complexation of substrate R1 with R3′ and the nickel catalyst (Entry 5 in Table 2), multiple attempts failed in locating any corresponding transition states, perhaps due to the fact that both R1 and R3′ are nucleophiles and it is electronically difficult for them to react with each other. In short, the complex COM2-I formed between substrate R2, R1 and the nickel catalyst is the most prone one in the oxidative addition step; this is consistent with previous predictions based on the dual descriptors (Δf, Table 1) and with the experimentally detected chemoselectivities.
2.2.2. Regioselectivities
As mentioned in Section 2.1.2, the oxidative addition step (COM2-I → TS2-I, Figure 3) has a regioselectivity-determining role in this reaction. When the asymmetric alkyne (R1) complexes with the nickel center in complex COM1-I in different orientations, another complex COM2-VI may be formed (Figure 8), which is of comparable stability to COM2-I. Nevertheless, the oxidative addition of COM2-VI requires overcoming a total free energy barrier of 28.8 kcal·mol−1 (COM1-I → COM2-VI → TS2-VI), which is 4.6 kcal·mol−1 higher than that of TS2-I on Path I (24.2 kcal·mol−1), justifying the dominant formation of product P1 along Path I. The regioselectivity predictions based on energetic results are in complete agreement with corresponding experimental results (79% of P1 detected at an experimental temperature of 50 °C, while only 2% of the regioisomer P3 could be detected), and they are also consistent with the predictions based on dual descriptors (the C1 site in R1 is more susceptible to the attack of the electrophilic nickel center).
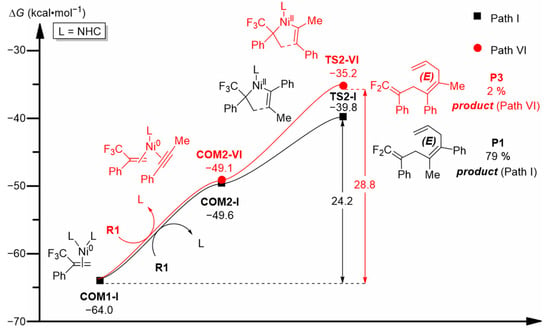
Figure 8.
Computed free energy profiles (ΔG in kcal·mol−1) for Path VI, with that of Path I noted (in black) for comparison.
2.3. Recycling and Regeneration of Catalyst
Experiments [14,20] showed that the participation of the third component R3 and the tBuOK additive significantly reduced the catalyst dosage (from 1.0 equiv to 5 mol%) compared to its two-component alternative. Towards resolving the bases of this reduction in catalyst loading, as well as the recycling and regeneration mechanism of the catalyst, we conducted computations on the corresponding two-component reaction (Path VII in Figure 9) at the same level to ensure comparability. In absence of the third component R3 and the tBuOK additive, intermediate INT4-I will undergo C-C coupling (through TS4-VII) along path VII to generate the five-membered ring intermediate INT5-VII, by surmounting a free energy barrier of 27.4 kcal·mol−1. Subsequently, intermediate INT5-VII accomplishes β-F elimination through transition state TS5-VII and converts into intermediate INT6-VII, which may remove a Ni(II)F2L fragment to generate the final product P5. However, in light of the fact that the energy barrier of TS4-VII (27.4 kcal·mol−1) is 2.6 kcal·mol−1 higher than that of the local maximum TS5-I on Path I (24.8 kcal·mol−1), this two-component reaction should be more difficult with respect to the three-component one, albeit it can also still proceed under the corresponding experimental conditions [20].
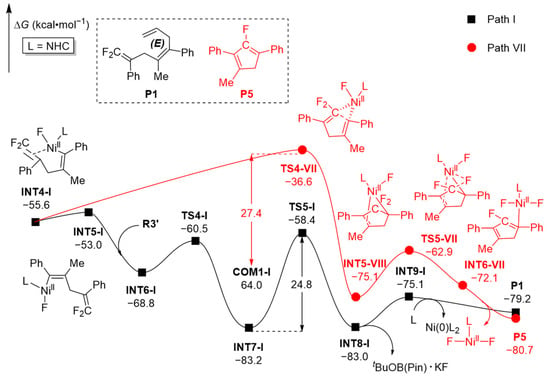
Figure 9.
Computed free energy profiles (ΔG in kcal·mol−1) for Path VII, with that of Path I noted (in black) for comparison.
Distortion/interaction analyses results on transition states TS5-I and TS4-VII are shown in Table 3. The distortion energies of each fragment as well as the total distortion energies of TS5-I (ΔEdist) are all higher than that of TS4-VII. Meanwhile, the interaction energies (ΔEint) of TS5-I are significantly lower than that of TS4-VII. This means that transition state TS5-I displays more pronounced distortions yet stronger interactions compared to TS4-VII, and the dual effects make it more stable than TS4-VII. The IRI analyses results of transition states TS5-I and TS4-VII (Figure 10) reveal pronounced van der Waals interactions (in red box) between the third component R3 and the tBuOK fragment with other parts of TS5-I, rationalizing TS5-I’s raised stability relative to TS4-VII. Both the results of energy decomposition and IRI analyses represent well the corresponding experimental result that the three-component reaction involving the tBuOK additive is easier than its two-component alternative without a base additive.

Table 3.
Distortion/interaction analysis results (single-point corrections [E(sp)] in kcal·mol−1) for TS5-I and TS4-VII (L = NHC), with ΔEdist and ΔEint indicating distortion and interaction energies, respectively; ΔΔE = ΔEdist + ΔEint.
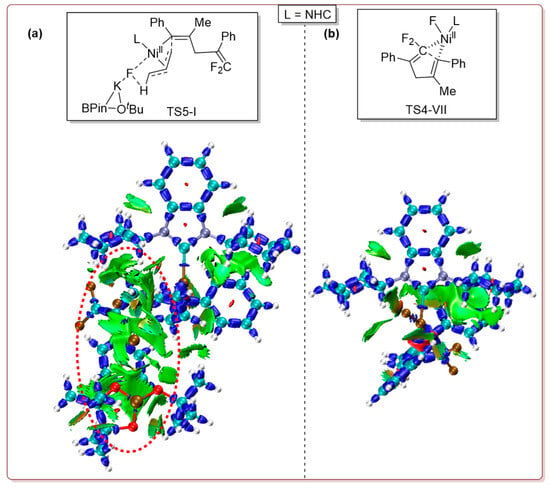
Figure 10.
Interaction region indicator (IRI) analyses for TS5-I (a) and TS4-VII (b).
It can also be seen in Figure 9 that the final product P5 in the two-component reaction without the tBuOK additive (Path VII) could be generated accompanied by the removal of the Ni(II)F2L fragment; however, it is near impossible for Ni(II)F2L to be converted into the active species Ni(0)L2 which can catalyze the reaction in the cycle (Figure S4). As a result, the two-component reaction developed by Ichitsuka requires 1.0 equiv of Ni(COD)2 to ensure that the reaction proceeds [20]. In contrast, the final product P1 in the three-component reaction involving the tBuOK additive (Path I) is formed accompanied by the removal of the active Ni(0)L2 species, and Ni(0)L2 can participate in subsequent catalytic cycles directly until the end of the reaction. Hence, the three-component reaction developed by Li only requires a catalytic amount of Ni(COD)2 catalyst (5 mol%), generating a 79% yield of P1 under mild conditions [14]. These results are of significance to raise understanding of the catalytic cycle and recycling mechanism of catalysts in transition metal-catalyzed multi-component reactions.
3. Computational Methods
Extensive literature on benchmark calculations for density functional theory (DFT) methods show that the PBE0 method combined with D3(BJ) dispersion correction, and the 6-31+G(d) and 6-311+G(d,p) basis sets, perform well and are sufficient for the correct description of geometries and energies in reaction systems involving transition metals, sufficient to reproduce related experimental trends with reasonable accuracy [28,29,30,31]. Thus, all computations in this work were performed using the Gaussian 16 software package [32] by employing the PBE0 method [33] and D3(BJ) [34] dispersion correction. All geometry optimizations and vibrational frequency analyses were conducted by using the 6-31+G(d) [35,36,37] (for C, H, O, N, F, B, and K) and SDD basis sets [38] (for Ni), with corresponding single-point corrections performed employing the 6-311+G(d,p) [35,39,40,41] (C, H, O, N, F, B, and K) and SDD basis sets (for Ni). All stationary points were confirmed as stable points or first-order saddle points (for TSs) on their respective potential energy hypersurfaces. Intrinsic reaction coordinate (IRC) [42,43] analyses were performed on key transition states to ensure their correct connections to correspondent reactants and products. The effect of the nHex solvent was taken into account in all computations by using the IDSCRF atomic radii [44], denoted as IDSCRF(nHex). All free energies reported have been corrected to experimental temperature (323.15 K) by using the THERMO program [45], to include the translational entropy contributions in solution (Strans(l)); the latter is in contrast to the default use of the gas-phase one (Strans(g)). Interaction region indicator (IRI) analyses, Hirshfeld charge and dual descriptor (based on Hirshfeld charge) calculations were performed by using the Multiwfn program [46]. Natural population analyses (NPA) were conducted on selected stationary points using the NBO 5.0 program [47].
4. Conclusions
Density functional theory (DFT) at the IDSCRF(nHex)-PBE0-D3(BJ)/6-311+G(d,p)- SDD(Ni)//IDSCRF(nHex)-PBE0-D3(BJ)/6-31+G(d)-SDD(Ni) level was employed to explore the reaction mechanism and selectivities of the nickel-catalyzed three-component asymmetrical bis-allylation of alkynes with alkenes. The following conclusions can be drawn based on present explorations: (1) The reaction proceeds via pre-catalysis, oxidative addition (OA), β-F elimination, ring opening complexation and reduction elimination (RE) in sequence, among which OA and RE are both essential in controlling the reaction rates, with free energy barriers being 24.2 and 24.8 kcal·mol−1, respectively. (2) The oxidative addition step (COM2-I → TS2-I) acts as the selectivity-controlling step, with the chemo- and regioselectivity predictions based on the dual descriptors (Δf, based on Hirshfeld charge) and energy barrier calculations being in good accordance with product selectivities observed in experiments. This evidences the dual descriptor and energy barrier calculations as excellent low-cost tools for predicting the selectivities of MCRs and even more complicated reactions. (3) The active Ni(0)L2 (L = NHC) species in the three-component reaction involving the tBuOK additive can be regenerated accompanied by the formation of the final skipped trienes (P1), allowing for a catalytic amount of Ni(COD)2 catalyst (5 mol%) to generate a 79% yield of P1 under mild conditions. Further energy decomposition and IRI analyses reveal that the van der Waals interactions between the third component (R3) and tBuOK fragment with other parts in the key stationary point (TS5-I) are essential in stabilizing it and thus facilitate the reaction under mild conditions. A reasonable explanation for the improvement in catalyst dosage (from 1.0 equiv to 5 mol%) further makes this work valuable to raise understanding of the catalytic cycle and recycling mechanism of catalysts in transition metal-catalyzed multi-component reactions.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/molecules29071475/s1, Figure S1: Computed free energy profiles for the generation of COM2-I, Figure S2: Computed free energy profiles for Path II, Figure S3: Computed free energies for the complexation of different substrates with the nickel catalyst, Figure S4: Energetics for the transformation of Ni(II)F2L to Ni(0)L2, Table S1: NPA charges on key atoms in reactants R1 and R2, Table S2: Calculated energy results; Optimized Cartesian coordinates for all stationary points (PDF and XYZ).
Author Contributions
Data curation, T.Y. and J.Z.; Funding acquisition, W.M.; Conceptualization and supervision, W.M.; Project administration, W.M. and G.L.; Visualization, T.Y.; Writing—original draft, T.Y. and W.M.; Writing—review and editing, W.M., G.L., L.D., K.V.T. and G.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (grant number 22363012, 21763033) and Top Young Talents of Yunnan Ten Thousand People Plan.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data underlying this study are available in the published article and its Supplementary Materials.
Acknowledgments
The authors acknowledge Xue Tan and Lin Zhu (Faculty of Chemistry and Chemical Engineering, Yunnan Normal University) for helpful discussion during the organization and writing of this manuscript. K. V. Tian and G. A. Chass acknowledge their support from CET Partnership (GA N101069750, project BUCKSSS).
Conflicts of Interest
Authors KVT and GAC have worked on some aspects of this manuscript and other related works together with Mesoscale Engineering Halcyon Srl (Rome, Italy), yet with no conflict of interest, commercial value or profit associated with this or any other related works. The remaining authors declare that the research and all work on this and any related manuscripts were conducted in the absence of any commercial or financial gain or relations that could be construed in any manner as a potential conflict of interest.
References
- Alegre-Requena, J.; Marqués-López, E.; Herrera, R. IntroductIon: Multicomponent Strategies. In Multicomponent Reactions: Concepts and Applications for Design and Synthesis; Herrera, R., Marqués-López, E., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 1–15. [Google Scholar]
- Cioc, R.; Ruijter, E.; Orru, R.V.A. Multicomponent Reactions: Advanced Tools for Sustainable Organic Synthesis. Green Chem. 2014, 16, 2958–2975. [Google Scholar] [CrossRef]
- Sharma, U.; Sharma, N.; Vachhani, D.; Van der Eycken, E.V. Metal-mediated Post-Ugi Transformations for the Construction of Diverse Heterocyclic Scaffolds. Chem. Soc. Rev. 2015, 44, 1836–1860. [Google Scholar] [CrossRef]
- Zhang, J.S.; Liu, L.; Chen, T.Q.; Han, L.B. Recent Advances in Transition Metal-Catalyzed Three-Component Difunctionalization of Alkenes. Chem. Asian J. 2018, 13, 2277–2291. [Google Scholar] [CrossRef] [PubMed]
- Sharma, U.; Ranjan, P.; Van der Eycken, E.V.; You, S.L. Sequential and Direct Multicomponent Reaction (MCR)-Based Dearomatization Strategies. Chem. Soc. Rev. 2020, 49, 8721–8748. [Google Scholar] [CrossRef] [PubMed]
- John, S.; Gulati, S.; Shankaraiah, N. Recent Advances in Multi-Component Reactions and Their Mechanistic Insights: A Triennium Review. Org. Chem. Front. 2021, 8, 4237–4287. [Google Scholar] [CrossRef]
- Tobisu, M.; Chatani, N. Cross-Couplings Using Aryl Ethers via C−O Bond Activation Enabled by Nickel Catalysts. Acc. Chem. Res. 2015, 48, 1717–1726. [Google Scholar] [CrossRef] [PubMed]
- Bhakta, S.; Ghosh, T. Nickel-Catalyzed Cascade Reactions. Eur. J. Org. Chem. 2021, 29, 4201–4215. [Google Scholar] [CrossRef]
- Ichitsuka, T.; Fujita, T.; Ichikawa, J. Nickel-Catalyzed Allylic C(sp3)−F Bond Activation of Trifluoromethyl Groups via β-Fluorine Elimination: Synthesis of Difluoro-1,4-Dienes. ACS Catal. 2015, 5, 5947–5950. [Google Scholar] [CrossRef]
- Pellissier, H. Enantioselective Nickel-Catalyzed Domino and Tandem Processes. Curr. Org. Chem. 2016, 20, 234–265. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, S.L. Nickel-Catalyzed Multicomponent Coupling: Synthesis of α-Chiral Ketones by Reductive Hydrocarbonylation of Alkenes. J. Am. Chem. Soc. 2021, 143, 14089–14096. [Google Scholar] [CrossRef]
- Ding, C.; Ren, Y.Y.; Yu, Y.; Yin, G.Y. Ligand-Modulated Nickel-Catalyzed Regioselective Silylalkylation of Alkenes. Nat. Commun. 2023, 14, 7670–7678. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Wang, H.; Mao, Y.J.; Shi, S.L. Ni-Catalyzed Three-Component Coupling Reaction of Butadiene, Aldimines and Alkenylboronic Acids. Chin. J. Org. Chem. 2022, 42, 1198–1209. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, W.S.; Yang, S.N.; Wang, X.Y.; Liu, Y.; Ji, D.W.; Chen, Q.A. Nickel-Catalyzed Unsymmetrical Bis-Allylation of Alkynes. Angew. Chem. Int. Ed. 2023, 62, e202300036. [Google Scholar] [CrossRef]
- Wang, X.G.; Li, Y.; Liu, H.C.; Zhang, B.S.; Gou, X.Y.; Wang, Q.; Ma, J.W.; Liang, Y.M. Three-Component Ruthenium-Catalyzed Direct Meta-Selective C–H Activation of Arenes: A New Approach to The Alkylarylation of Alkenes. J. Am. Chem. Soc. 2019, 141, 13914–13922. [Google Scholar] [CrossRef]
- Zhang, Z.; Sabat, N.; Frison, G.; Marinetti, A.; Guinchard, X. Enantioselective Au(I)-Catalyzed Multicomponent Annulation via Tethered Counterion-Directed Catalysis. ACS Catal. 2022, 12, 4046–4053. [Google Scholar] [CrossRef]
- Pannilawithana, N.; Son, M.; Hwang, D.; Baik, M.H.; Yi, C. Scope and Mechanistic Studies on the Ruthenium-Catalyzed Multicomponent Deaminative C–H Coupling Reaction of Phenols with Aldehydes and Enamines for the Formation of Xanthene and Dioxacyclic Derivatives. ACS Catal. 2023, 13, 9051–9063. [Google Scholar] [CrossRef]
- Fu, R.; Lu, T.; Chen, F.L. Comparing Methods for Predicting the Reactive Site of Electrophilic Substitution. Acta Phys. Chim. Sin. 2014, 30, 628–639. [Google Scholar]
- Cao, J.J.; Ren, Q.; Chen, F.L.; Lu, T. Comparative Study on the Methods for Predicting the Reactive Site of Nucleophilic Reaction. Sci. China-Chem. 2015, 45, 1281–1290. [Google Scholar] [CrossRef]
- Ichitsuka, T.; Fujita, T.; Arita, T.; Ichikawa, J. Double C-F Bond Activation through β-Fluorine Elimination: Nickel-Mediated [3+2] Cycloaddition of 2-Trifluoromethyl-1-Alkenes with Alkynes. Angew. Chem. Int. Ed. 2014, 53, 7564–7568. [Google Scholar] [CrossRef]
- Bickelhaupt, F.; Houk, K. Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model. Angew. Chem. Int. Ed. 2017, 56, 10070–10086. [Google Scholar] [CrossRef]
- Wolters, L.; Bickelhaupt, F. The Activation Strain Model and Molecular Orbital Theory. WIREs. Comput. Mol. Sci. 2015, 5, 324–343. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F.W. Interaction Region Indicator: A Simple Real Space Function Clearly Revealing Both Chemical Bonds and Weak Interactions. Chem.-Methods 2021, 1, 231–239. [Google Scholar] [CrossRef]
- Morell, C.; Grand, A.; Toro-Labbé, A. New Dual Descriptor for Chemical Reactivity. J. Phys. Chem. A 2004, 109, 205–212. [Google Scholar] [CrossRef]
- Lessa, M.; Fajardo, J.; Delarmelina, M.; Carneiro, J. A DFT Study on the Mechanism for Polymerization of δ-Valerolactone Initiated by N-heterocyclic Carbene (NHC) Catalysts. Mol. Catal. 2021, 515, 111896–111916. [Google Scholar] [CrossRef]
- Kozuch, S.; Shaik, S. How to Conceptualize Catalytic Cycles? The Energetic Span Model. Acc. Chem. Res. 2011, 44, 101–110. [Google Scholar] [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chem. Acc. 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Michael, B.; Reimann, C.; Pantazis, D.; Bredow, T.; Neese, F. Geometries of Third-Row Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2008, 4, 1449–1459. [Google Scholar]
- Steinmetz, M.; Grimme, S. Benchmark Study of the Performance of Density Functional Theory for Bond Activations with (Ni,Pd)-Based Transition-Metal Catalysts. ChemistryOpen 2013, 2, 115–124. [Google Scholar] [CrossRef]
- Dohm, S.; Hansen, A.; Steinmetz, M.; Grimme, S.; Checinski, M. Comprehensive Thermochemical Benchmark Set of Realistic Closed-Shell Metal Organic Reactions. J. Chem. Theory Comput. 2018, 14, 2596–2608. [Google Scholar] [CrossRef]
- Basiuk, V.; Escobar, A.; Molina, H. Basis Set Effects on B3LYP Geometries and Energies: Case Study of Interstellar Reaction HN=CH2 + •C≡N → H2N–C(•)H–C≡N. Int. J. Quantum Chem. 2002, 87, 101–109. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comp. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P. Efficient Diffuse Function-Augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-Row Elements, Li-F. J. Comp. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.; Al-Laham, M.A.; Shirley, W.; Mantzaris, J. A Complete Basis Set Model Chemistry. I. The Total Energies of Closed-Shell Atoms and Hydrides of the First-Row Elements. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Petersson, G.A.; Al-Laham, M.A. A Complete Basis Set Model Chemistry. II. Open-Shell Systems and the Total Energies of the First-Eow Atoms. J. Chem. Phys. 1991, 94, 6081–6090. [Google Scholar] [CrossRef]
- Dolg, M.; Wedig, U.; Stoll, H.; Preuss, H. Energyadjusted Ab Initio Pseudopotentials for the First Row Transition Elements. J. Chem. Phys. 1987, 86, 866–872. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian Basis Sets for Molecular Calculations. I. Second Row Atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Selfconsistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Frisch, M.J.; Pople, J.A. Selfconsistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets. J. Chem. Phys. 1984, 80, 3265–3269. [Google Scholar] [CrossRef]
- Fukui, K. Formulation of the Reaction Coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
- Fukui, K. The Path of Chemical Reactions—The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Tao, J.Y.; Mu, W.H.; Chass, G.A.; Tang, T.H.; Fang, D.C. Balancing the Atomic Waistline: Isodensity-Based SCRF Radii for Main-Group Elements and Transition Metals. Int. J. Quantum Chem. 2013, 113, 975–984. [Google Scholar] [CrossRef]
- Fang, D.-C. THERMO Program; Beijing Normal University: Beijing, China, 2013. [Google Scholar]
- Lu, T.; Chen, F.W. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Glendening, E.D.; Badenhoop, J.K.; Reed, A.E.; Carpenter, J.E.; Bohmann, J.A.; Morales, C.M.; Weinhold, F. NBO 5.0; Theoretical Chemistry Institute, University of Wisconsin: Madison, WI, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).