Theoretical Design of Tellurium-Based Two-Dimensional Perovskite Photovoltaic Materials
Abstract
1. Introduction
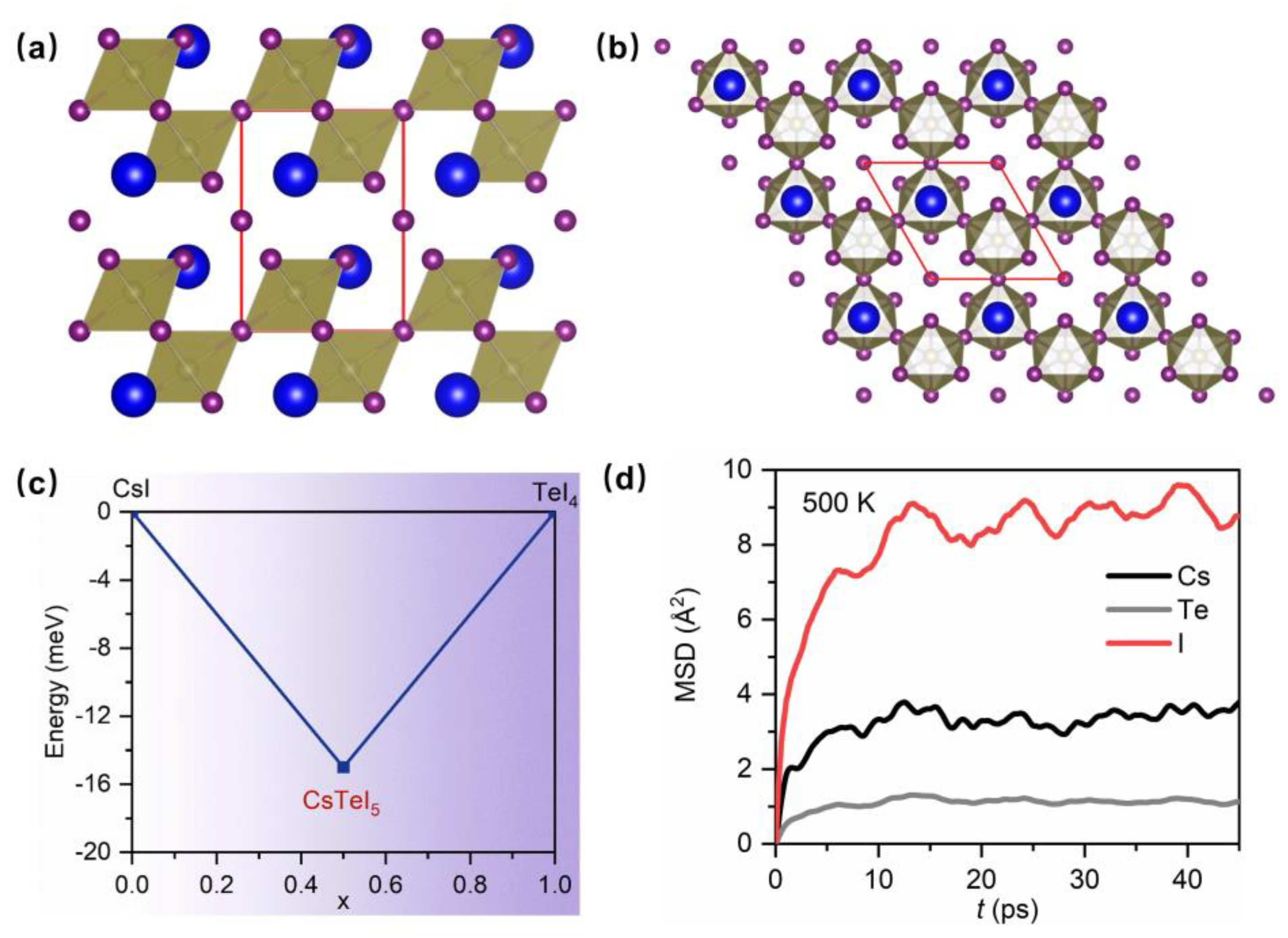
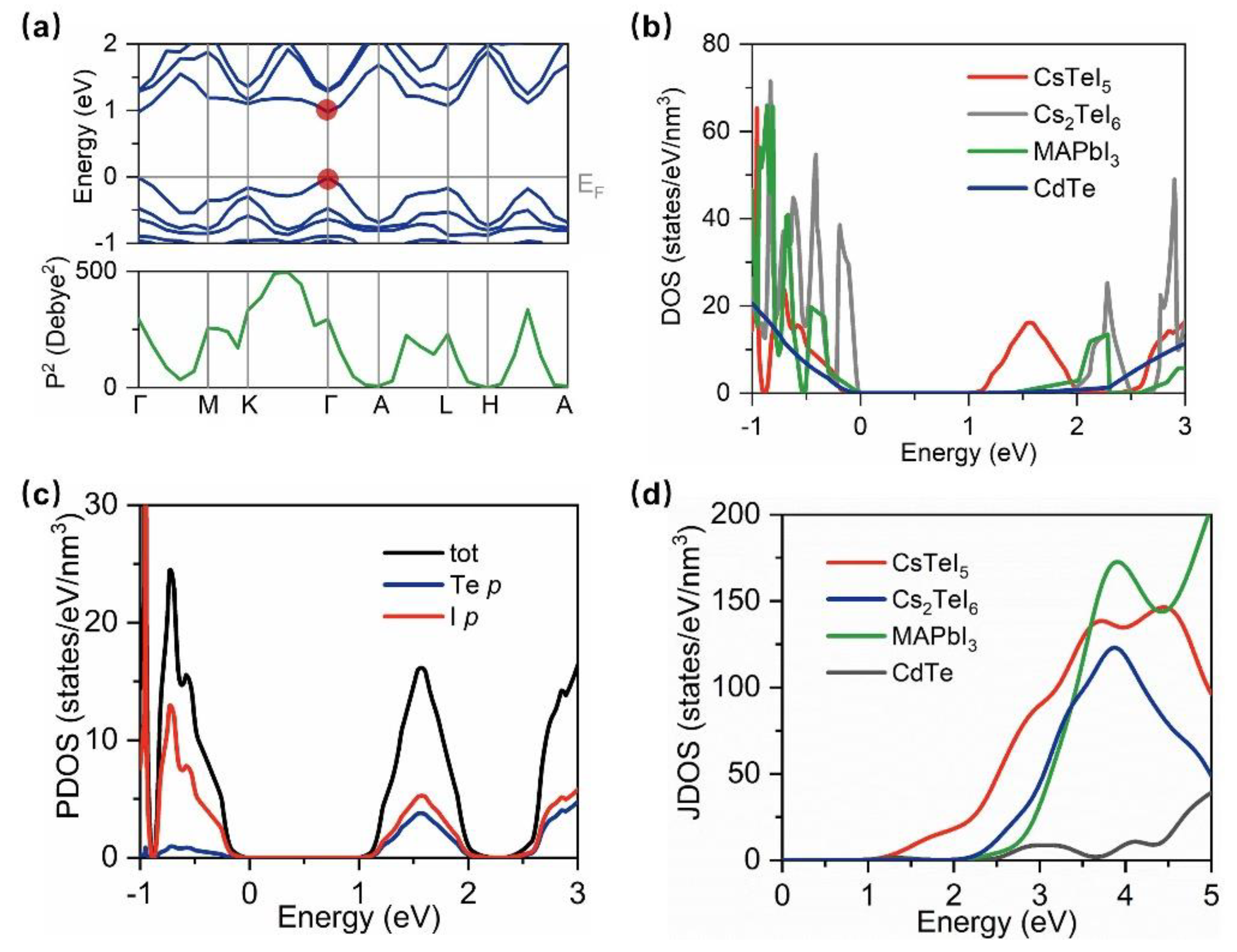
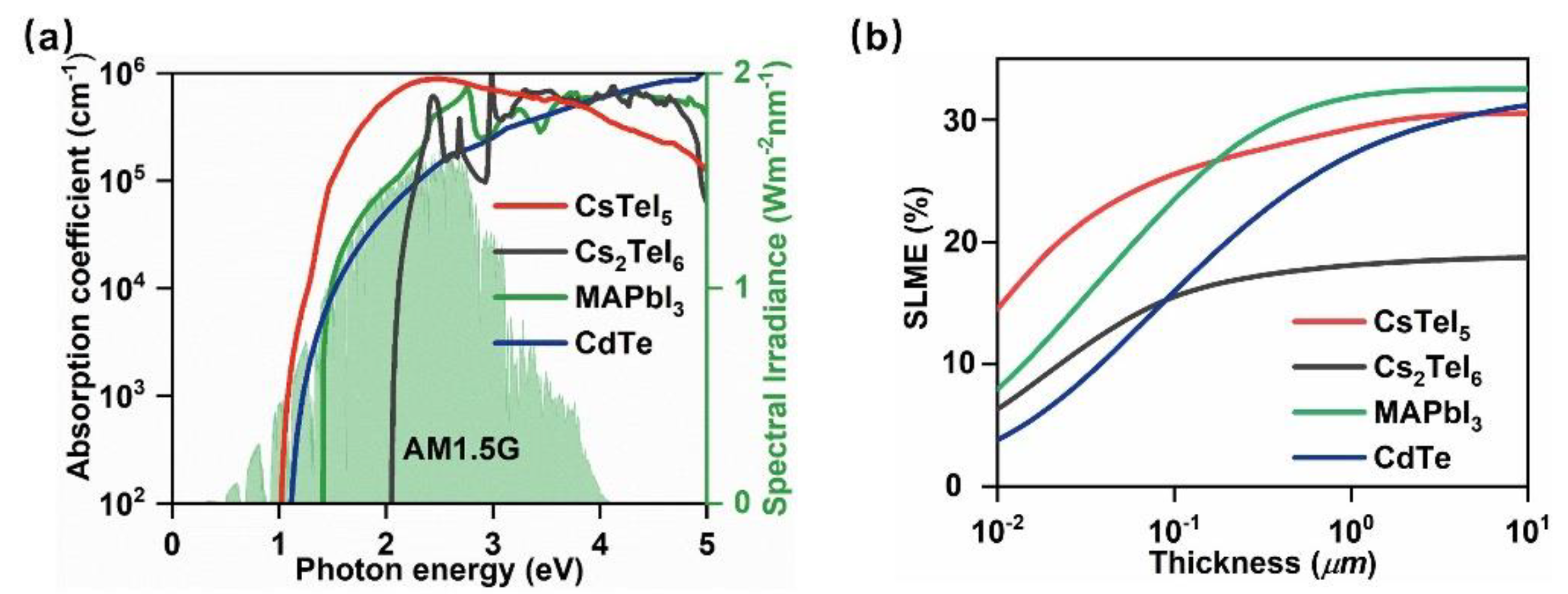
2. Results and Discussion
3. Methods
3.1. Crystal Structure Prediction and Electronic Properties Calculation
3.2. Photovoltaic Property Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Green, M.A.; Dunlop, E.D.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Siefer, G.; Hao, X. Solar cell efficiency tables (version 62). Prog. Photovolt. Res. Appl. 2023, 31, 651–663. [Google Scholar] [CrossRef]
- Jeong, M.; Choi, I.W.; Go, E.M.; Cho, Y.; Kim, M.; Lee, B.; Jeong, S.; Jo, Y.; Choi, H.W.; Lee, J.J.S. Stable perovskite solar cells with efficiency exceeding 24.8% and 0.3-V voltage loss. Science 2020, 369, 1615–1620. [Google Scholar] [CrossRef] [PubMed]
- He, T.; Li, S.; Jiang, Y.; Qin, C.; Cui, M.; Qiao, L.; Xu, H.; Yang, J.; Long, R.; Wang, H.; et al. Reduced-dimensional perovskite photovoltaics with homogeneous energy landscape. Nat. Commun. 2020, 11, 1672. [Google Scholar] [CrossRef]
- Sun, S.; Lu, M.; Gao, X.; Shi, Z.; Bai, X.; Yu, W.W.; Zhang, Y. 0D Perovskites: Unique Properties, Synthesis, and Their Applications. Adv. Sci. 2021, 8, 2102689. [Google Scholar] [CrossRef] [PubMed]
- Tsai, H.; Nie, W.; Blancon, J.-C.; Stoumpos, C.C.; Asadpour, R.; Harutyunyan, B.; Neukirch, A.J.; Verduzco, R.; Crochet, J.J.; Tretiak, S.J.N. High-efficiency two-dimensional Ruddlesden–Popper perovskite solar cells. Nature 2016, 536, 312–316. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, T.; Loo, Y.L. Advancing 2D perovskites for efficient and stable solar cells: Challenges and opportunities. Adv. Mater. 2022, 34, 2105849. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Lu, H.; Tong, J.; Berry, J.J.; Beard, M.C.; Zhu, K. Advances in two-dimensional organic–inorganic hybrid perovskites. Energy Environ. Sci. 2020, 13, 1154–1186. [Google Scholar] [CrossRef]
- Yao, H.; Li, Z.; Shi, C.; Xu, Y.; Wang, Q.; Li, Z.; Peng, G.; Lei, Y.; Wang, H.; Ci, Z.; et al. A novel multiple-ring aromatic spacer based 2d ruddlesden–popper CsPbI3 solar cell with record efficiency beyond 16%. Adv. Funct. Mater. 2022, 32, 2205029. [Google Scholar] [CrossRef]
- Adonin, S.A.; Frolova, L.A.; Sokolov, M.N.; Shilov, G.V.; Korchagin, D.V.; Fedin, V.P.; Aldoshin, S.M.; Stevenson, K.J.; Troshin, P.A. Antimony (V) complex halides: Lead-free perovskite-like materials for hybrid solar cells. Adv. Energy Mater. 2018, 8, 1701140. [Google Scholar] [CrossRef]
- Huang, P.; Yang, J.; Han, D.; Lu, S. Printable high-efficiency organic ionic photovoltaic materials discovered by high-throughput first-principle calculations. iScience 2022, 25, 105639. [Google Scholar] [CrossRef] [PubMed]
- Vázquez-Fernández, I.; Mariotti, S.; Hutter, O.S.; Birkett, M.; Veal, T.D.; Hobson, T.D.C.; Phillips, L.J.; Danos, L.; Nayak, P.K.; Snaith, H.J.; et al. Vacancy-ordered double perovskite Cs2TeI6 thin films for optoelectronics. Chem. Mater. 2020, 32, 6676–6684. [Google Scholar] [CrossRef] [PubMed]
- Maughan, A.E.; Ganose, A.M.; Bordelon, M.M.; Miller, E.M.; Scanlon, D.O.; Neilson, J.R. Defect tolerance to intolerance in the vacancy-ordered double perovskite semiconductors Cs2SnI6 and Cs2TeI6. J. Am. Chem. Soc. 2016, 138, 8453–8464. [Google Scholar] [CrossRef] [PubMed]
- Grandhi, G.K.; Hardy, D.; Krishnaiah, M.; Vargas, B.; Al-Anesi, B.; Suryawanshi, M.P.; Solis-Ibarra, D.; Gao, F.; Hoye, R.L.Z.; Vivo, P. Wide-bandgap perovskite-inspired materials: Defect-driven challenges for high-performance optoelectronics. Adv. Funct. Mater. 2023, 2307441. [Google Scholar] [CrossRef]
- Yin, W.-J.; Shi, T.; Yan, Y. Unique properties of halide perovskites as possible origins of the superior solar cell performance. Adv. Mater. 2014, 26, 4653–4658. [Google Scholar] [CrossRef] [PubMed]
- Jeon, N.J.; Noh, J.H.; Yang, W.S.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. Compositional engineering of perovskite materials for high-performance solar cells. Nature 2015, 517, 476–480. [Google Scholar] [CrossRef] [PubMed]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Giorgi, G.; Fujisawa, J.-I.; Segawa, H.; Yamashita, K. Small photocarrier effective masses featuring ambipolar transport in methylammonium lead iodide perovskite: A density functional analysis. J. Phys. Chem. Lett. 2013, 4, 4213–4216. [Google Scholar] [CrossRef] [PubMed]
- Lin, Q.; Armin, A.; Nagiri, R.C.R.; Burn, P.L.; Meredith, P. Electro-optics of perovskite solar cells. Nat. Photonics 2015, 9, 106–112. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063–2070. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 82, 094116. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
| Compounds | Bandgap (eV) | Effective Mass (m0) | Dielectric Constant | Exciton Binding Energy (meV) | Direct/Indirect Band Gap | SLME (0.5 μm/L μm) | ||
|---|---|---|---|---|---|---|---|---|
| PBE | HSE + SOC | |||||||
| CsTeI5 | 0.89 | 0.97 | 0.16 | 0.18 | 200.69 | 0.03 | Direct | 28.3/29.3 |
| Cs2TeI6 | 1.43 | 1.83 | 18.39 | 0.33 | 10.82 | 37 | Indirect | 17.7/18.1 |
| MAPbI3 | 1.77 | 1.35 | 0.29 | 0.22 | 88.05 | 0.2 | Direct | 30.7/31.8 |
| CdTe | 0.50 | 1.05 | 0.58 | 0.05 | 15.39 | 26 | Direct | 24.6/27.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, C.; Huang, P. Theoretical Design of Tellurium-Based Two-Dimensional Perovskite Photovoltaic Materials. Molecules 2024, 29, 3155. https://doi.org/10.3390/molecules29133155
Long C, Huang P. Theoretical Design of Tellurium-Based Two-Dimensional Perovskite Photovoltaic Materials. Molecules. 2024; 29(13):3155. https://doi.org/10.3390/molecules29133155
Chicago/Turabian StyleLong, Chunhong, and Peihao Huang. 2024. "Theoretical Design of Tellurium-Based Two-Dimensional Perovskite Photovoltaic Materials" Molecules 29, no. 13: 3155. https://doi.org/10.3390/molecules29133155
APA StyleLong, C., & Huang, P. (2024). Theoretical Design of Tellurium-Based Two-Dimensional Perovskite Photovoltaic Materials. Molecules, 29(13), 3155. https://doi.org/10.3390/molecules29133155






