Model Approach to Thermal Conductivity in Hybrid Graphene–Polymer Nanocomposites
Abstract
:1. Introduction
2. Results and Discussion
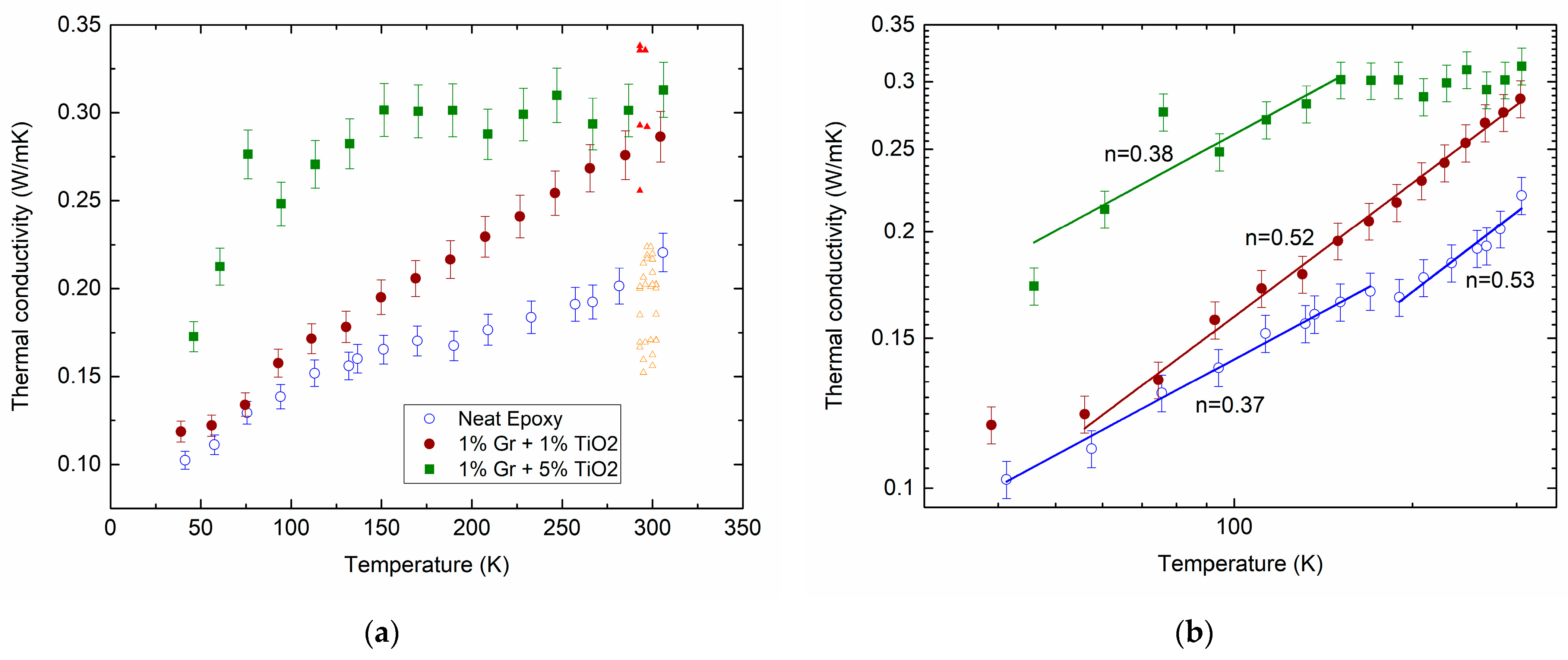
2.1. Temperature Dependence of the Thermal Conductivity
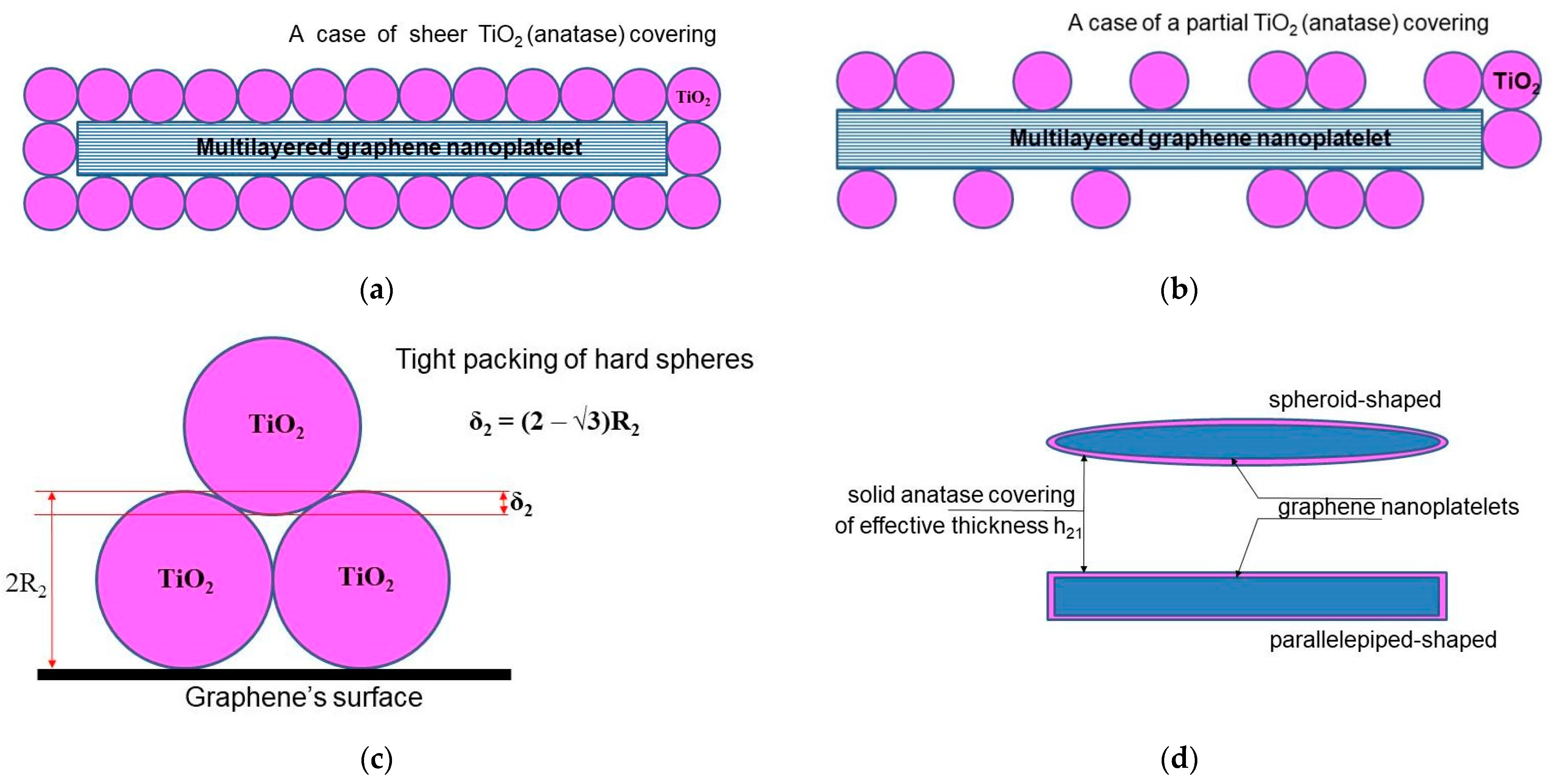
2.2. Development of the Model Formalism
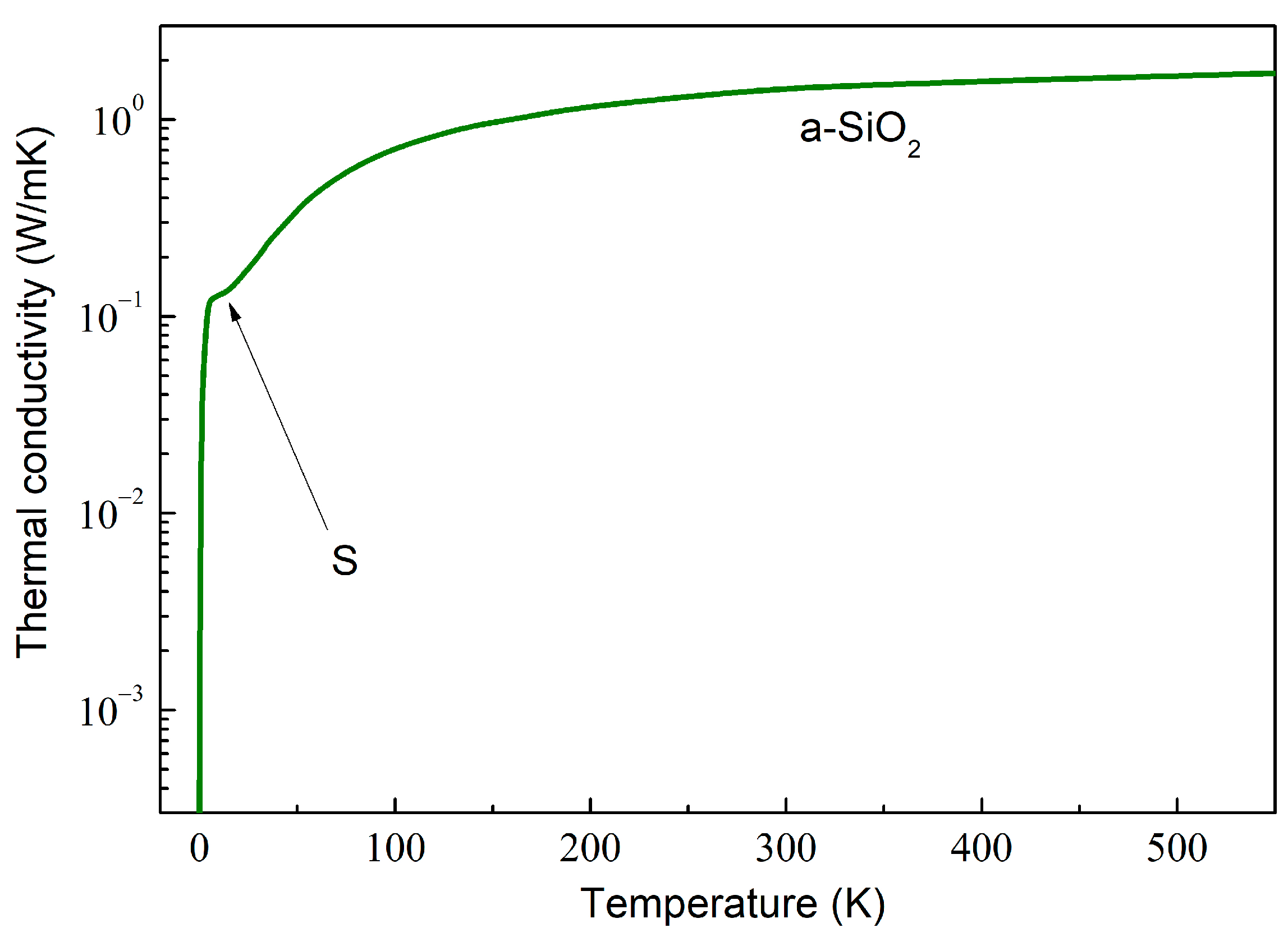
2.3. Discussing the Temperature Dependence of the Thermal Conductivity in Nanocomposites
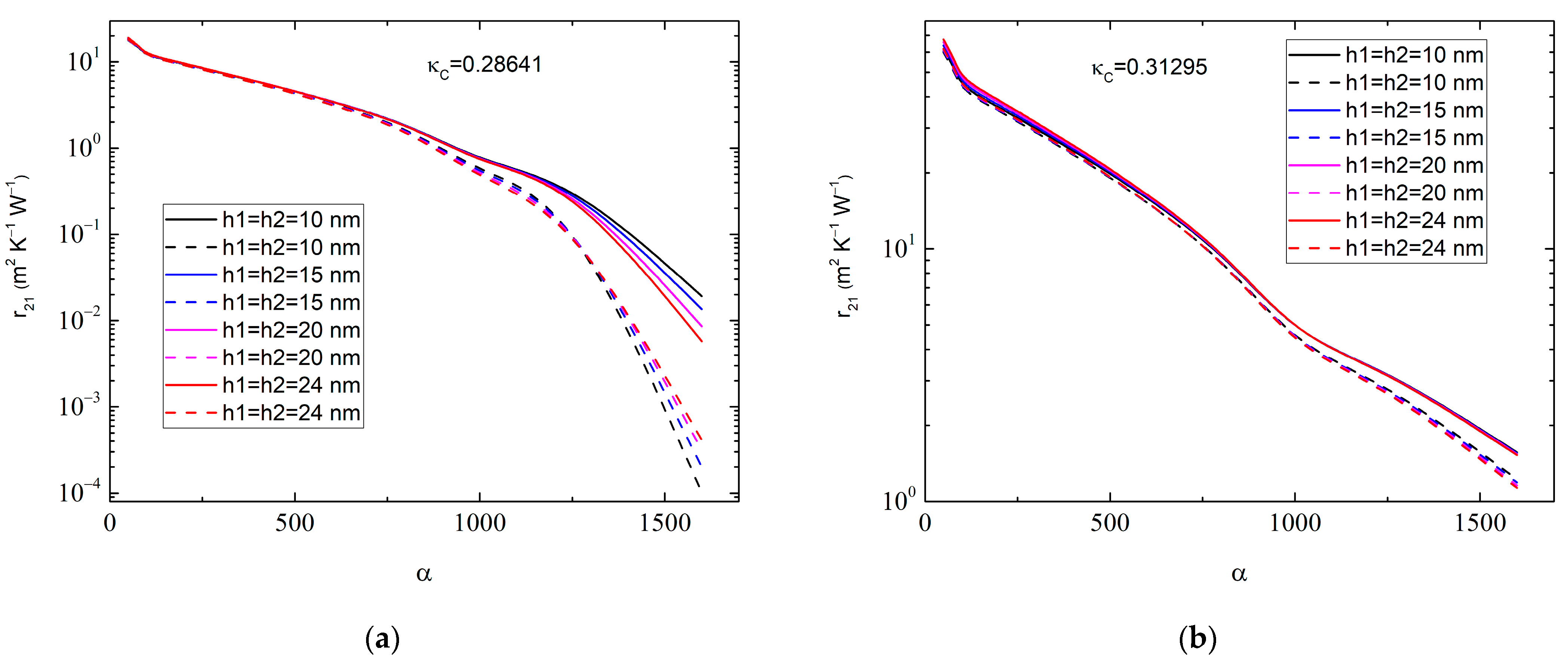
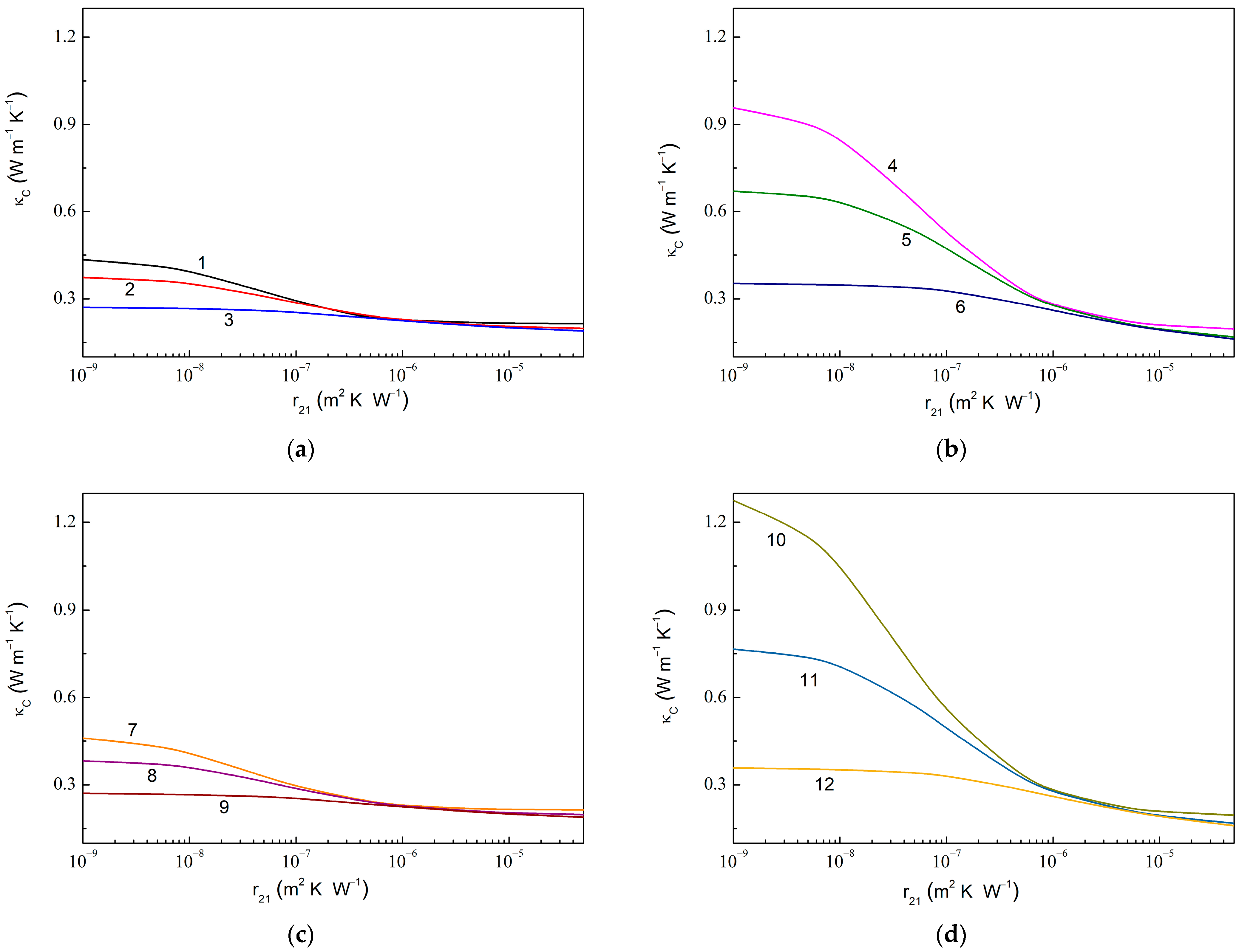
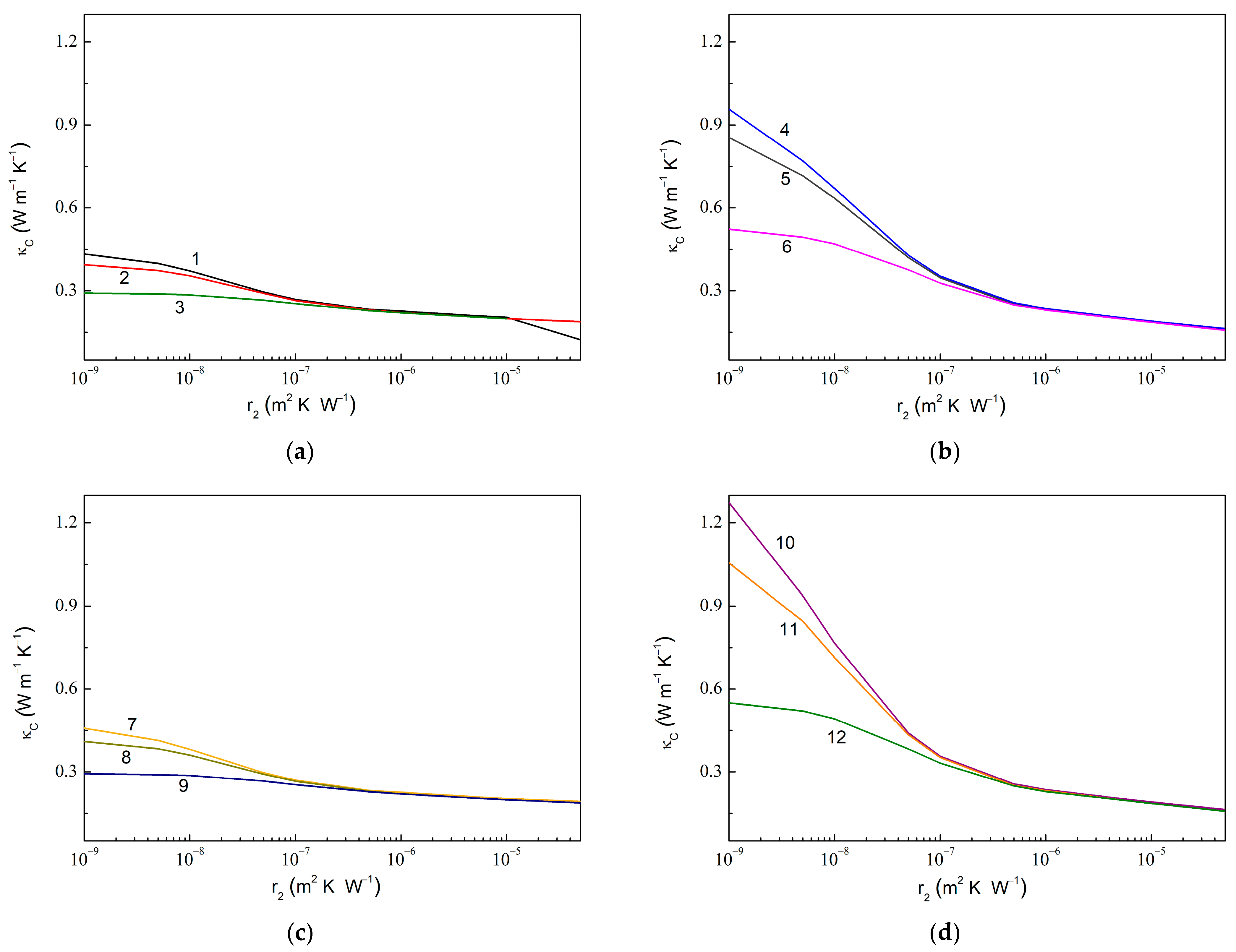
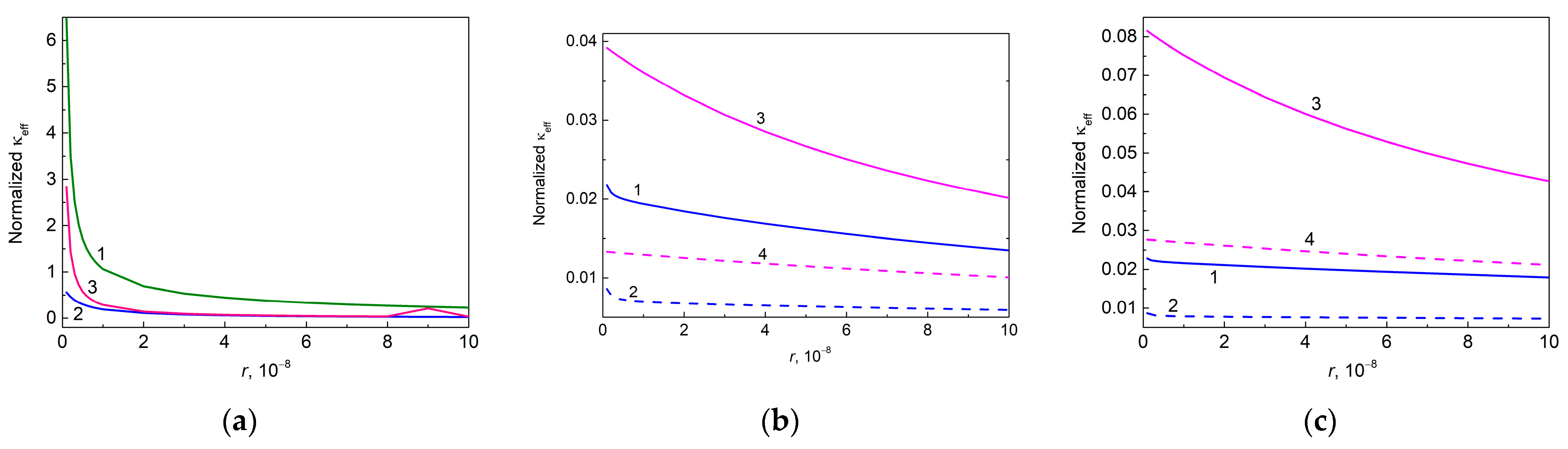
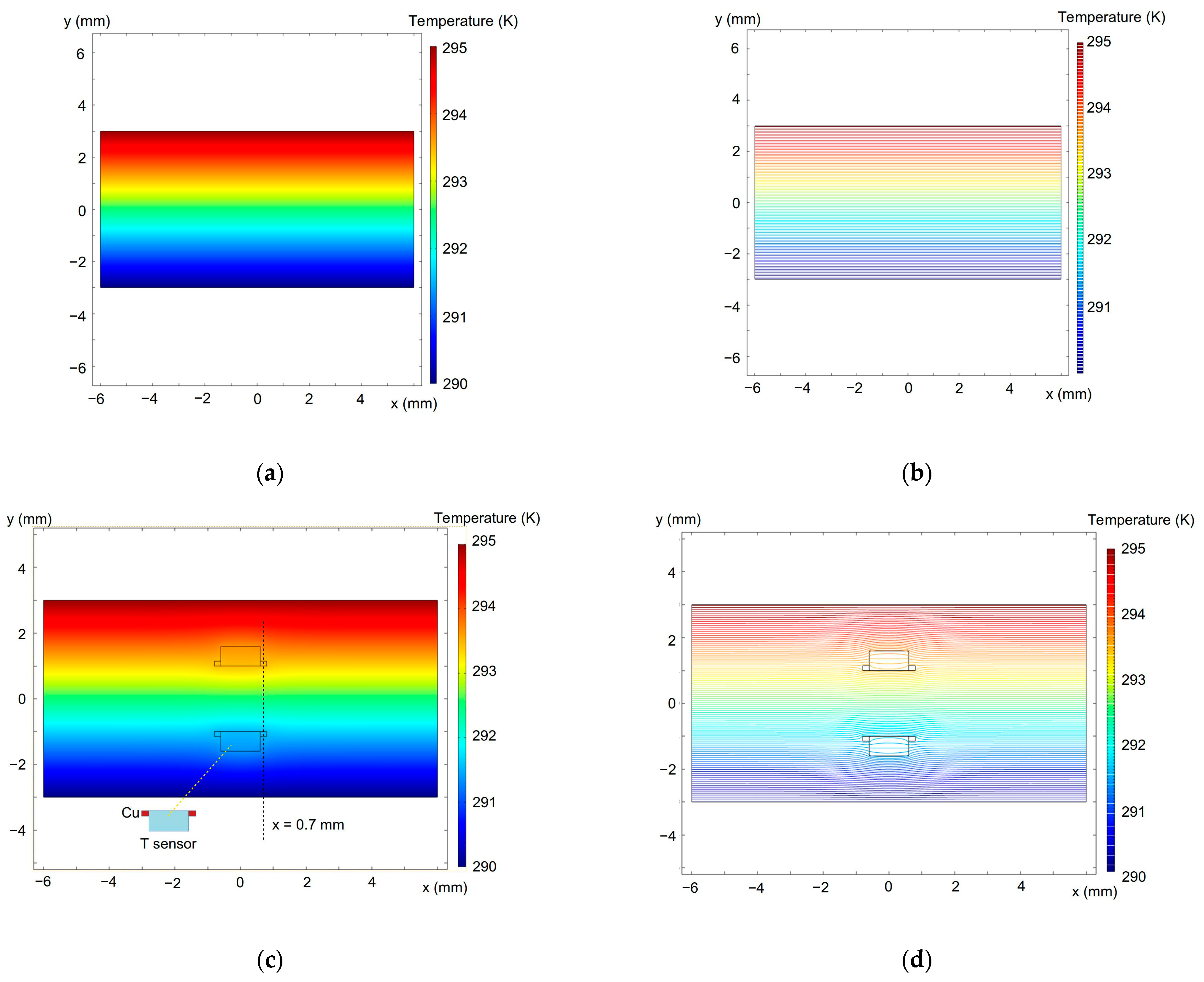
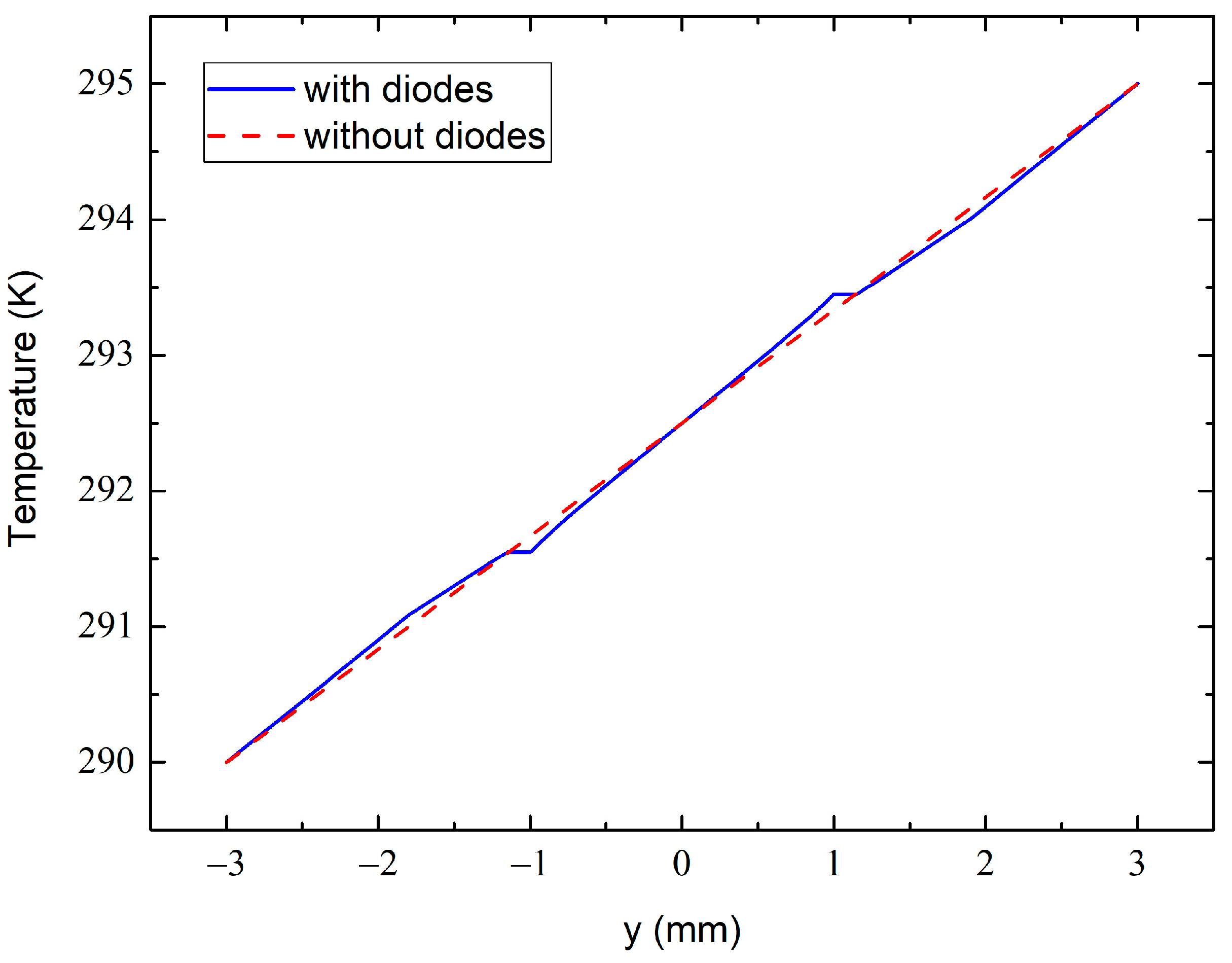
2.4. Theoretical Simulation and Numerical Calculations
2.5. Discussing the Loading Dependencies
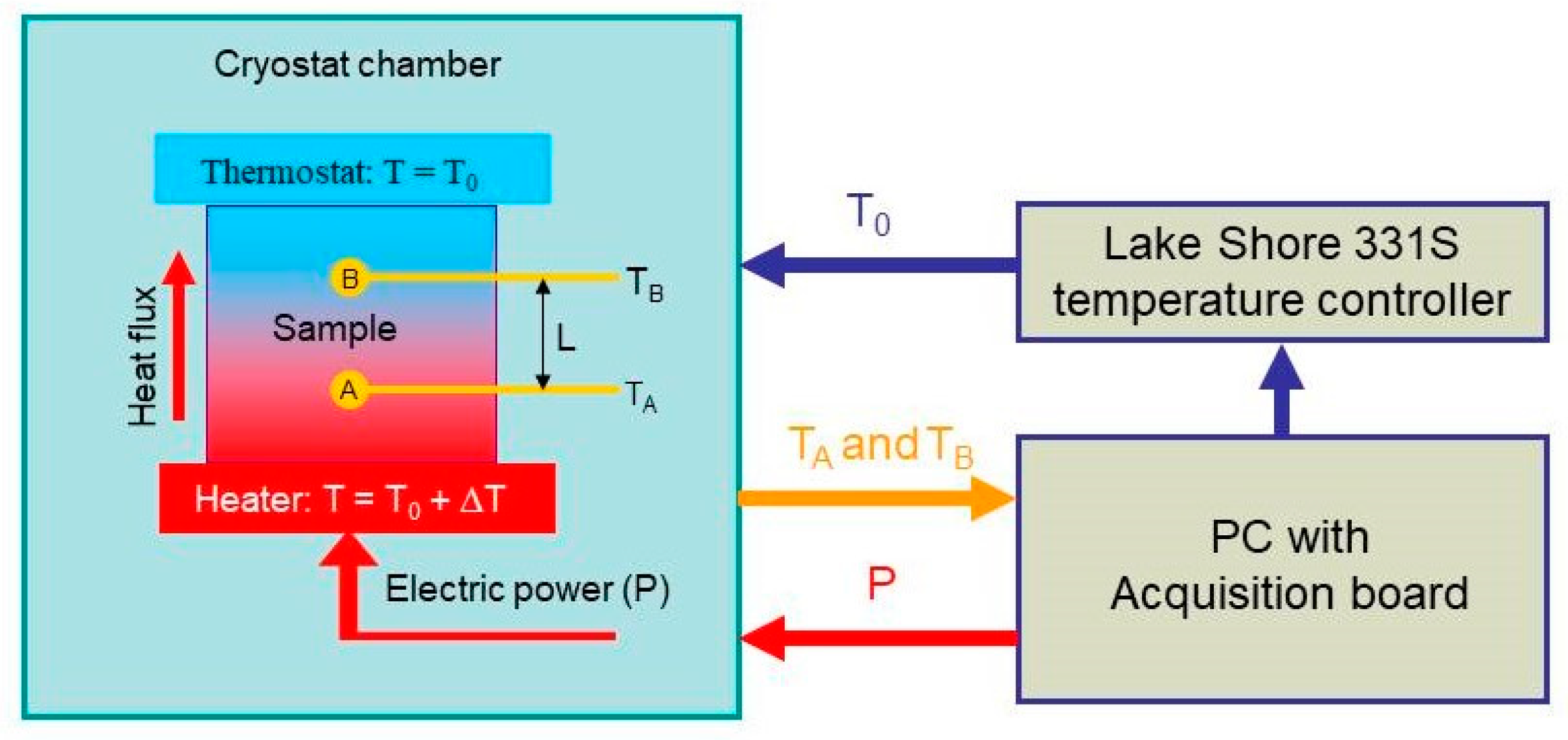
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature of the Model Parameters
| linear dimensions of graphene nanoplatelets, nm | |
| filler particle size, nm | |
| thickness-to-length aspect ratio of graphene nanoplatelets | |
| average radius of anatase nanoparticles, nm | |
| interphase layer thickness, nm | |
| thickness of the graphene–epoxy interphase layer, nm | |
| thickness of the anatase–epoxy interphase layer, nm | |
| effective thickness of an anatase covering graphene nanoplatelets in the “soft-spheres” approximation, nm | |
| thermal conductivity of the composite | |
| intrinsic thermal conductivity of an epoxy matrix, W∙m−1∙K−1 | |
| () | intrinsic thermal conductivity of anatase nanoparticles (fillers), W∙m−1∙K−1 |
| , | intrinsic in-plane (subscripts g11 and g22) and cross-plane (subscript g33) thermal conductivities of graphene nanoplatelets, W∙m−1∙K−1 |
| effective thermal conductivity of the hybrid nanoparticle | |
| () | effective thermal conductivity of anatase nanoparticles (fillers) embedded into epoxy (), W∙m−1∙K−1 |
| , | effective in-plane and cross-plane thermal conductivities of graphene nanoplatelets embedded into epoxy, W∙m−1∙K−1 |
| thermal conductivity of interphase regions (), W∙m−1∙K−1 | |
| thermal conductivity of the graphene–epoxy interphase layer, W∙m−1∙K−1 | |
| thermal conductivity of the anatase–epoxy interphase layer, W∙m−1∙K−1 | |
| effective thermal conductivity of the anatase layer covering the graphene nanoplatelet, W∙m−1∙K−1 | |
| ( and ) | Kapitza resistance (at MLG-TiO2 and TiO2-epoxy interfaces), W−1∙m2∙K |
| effective Kapitza thermal boundary resistance of the graphene–epoxy interface, W−1∙m2∙K | |
| in-plane Kapitza thermal boundary resistance of the graphene–epoxy interface, W−1∙m2∙K | |
| cross-plane Kapitza thermal boundary resistance of the graphene–epoxy interface, W−1∙m2∙K | |
| averaged Kapitza thermal boundary resistance of the graphene–epoxy interface, W−1∙m2∙K | |
| Kapitza thermal boundary resistance of the anatase–epoxy interface, W−1∙m2∙K | |
| Kapitza thermal boundary resistance of the graphene–anatase interface, W−1∙m2∙K | |
| Kapitza length (subscript matrix, filler), nm | |
| mass concentration of graphene nanoplatelets in the composite | |
| mass concentration of anatase nanoparticles in the composite | |
| volume concentration of constituent phases (subscripts 0, 1, 2, and 3 correspond to the polymer matrix, free MLG nanoplatelets, free anatase nanoparticles, and hybrid MLG@anatase nanoparticles, respectively); see Equations (S39)–(S45) (Supplementary Note S2) | |
| volume portion of the graphene–epoxy interphase layer | |
| volume portion of the anatase–epoxy interphase layer | |
| volume portion of the interphase layer surrounding graphene@anatase hybrid nanoparticles | |
| volume portion of an anatase in graphene@anatase hybrid nanoparticles | |
| functions defined by Equations (S1)–(S4) (Supplementary Note S1) | |
| volume factors, which determine the ratio of the interphase layer’s volume to the particle’s volume | |
| mass portions of free (unassembled) fillers, graphene (subscript 1), and anatase (subscript 2) | |
| mass densities of the polymer matrix (), graphene nanoplatelets (), and anatase nanoparticles (), kg∙m−3 | |
| mass densities of the graphene–epoxy (subscript 1) and anatase–epoxy (subscript 2) interphase layers | |
| , , | masses (in kg), volumes (in m3), and surface areas (in m2) of graphene nanoplatelets () and anatase nanoparticles () |
| two-rank Eshelby tensor | |
| total number of anatase nanoparticles per single graphene nanoplatelet | |
| maximum number of anatase nanoparticles that can be packed tightly over the surface of a single graphene nanoplatelet | |
| hypothetical number of layers of anatase particles covering graphene nanoplatelets | |
| effective thickness of an anatase covering graphene nanoplatelets in the “hard-spheres” approximation, nm | |
| radius of gyration of the polymer matrix | |
| grafting density |
References
- Wang, M.C.; Lai, Z.B.; Galpaya, D.; Yan, C.; Hu, N.; Zhou, L.M. Atomistic simulation of surface functionalization on the interfacial properties of graphene-polymer nanocomposites. J. Appl. Phys. 2014, 115, 123520. [Google Scholar] [CrossRef]
- Monteserín, C.; Blanco, M.; Aranzabe, E.; Aranzabe, A.; Vilas, J.L. Effects of graphene oxide and chemically reduced graphene oxide on the curing kinetics of epoxy amine composites. J. Appl. Polym. 2017, 134, 44803. [Google Scholar] [CrossRef]
- Vryonis, O.; Virtanen, S.T.H.; Andritsch, T.; Vaughan, A.S.; Lewin, P.L. Understanding the cross-linking reactions in highly oxidized graphene/epoxy nanocomposite systems. J. Mater. Sci. 2018, 54, 3035–3051. [Google Scholar] [CrossRef]
- Nadtochiy, A.; Gorelov, B.; Polovina, O.; Shulga, S.; Korotchenkov, O. Probing matrix/filler interphase with ultrasonic waves. J. Mater. Sci. 2021, 56, 14047–14069. [Google Scholar] [CrossRef]
- Katti, P.; Kundan, K.V.; Kumar, S.; Bose, S. Improved mechanical properties through engineering the interface by poly (ether ether ketone) grafted graphene oxide in epoxy based nanocomposites. Polymer 2017, 122, 184–193. [Google Scholar] [CrossRef]
- Li, M.; Zhou, H.; Zhang, Y.; Liao, Y.; Zhou, H. The effect of defects on the interfacial mechanical properties of graphene/epoxy composites. RSC Adv. 2017, 7, 46101–46108. [Google Scholar] [CrossRef]
- Rafiee, R.; Eskandariyun, A. Estimating Young’s modulus of graphene/polymer composites using stochastic multi-scale modeling. Compos. B Eng. 2019, 173, 106842. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H.; Feng, H.; Yan, J.; Liu, P.; Peng, Z. Relaxation processes and conduction mechanism of epoxy resin filled with graphene oxide. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 519–527. [Google Scholar] [CrossRef]
- Ravindran, A.; Feng, C.; Huang, S.; Wang, Y.; Zhao, Z.; Yang, J. Effects of graphene nanoplatelet size and surface area on the ac electrical conductivity and dielectric constant of epoxy nanocomposites. Polymers 2018, 10, 477. [Google Scholar] [CrossRef] [PubMed]
- Gorelov, B.M.; Mischanchuk, O.V.; Sigareva, N.V.; Shulga, S.V.; Gorb, A.M.; Polovina, O.I.; Yukhymchuk, V.O. Structural and dipole-relaxation processes in epoxy-multilayer graphene composites with low filler content. Polymers 2021, 13, 3360. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Wang, Z.; Wu, Y.; Liu, X.; He, Y.-B.; Kim, J.-K. Multilayer graphene enables higher efficiency in improving thermal conductivities of graphene/epoxy composites. Nano Lett. 2016, 16, 3585–3593. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.J.; Weng, G.J. Theory of thermal conductivity of graphene-polymer nanocomposites with interfacial Kapitza resistance and graphene-graphene contact resistance. Carbon 2018, 137, 222–233. [Google Scholar] [CrossRef]
- Xiao, W.; Zhai, X.; Ma, P.; Fan, T.; Li, X. Numerical study on the thermal behavior of graphene nanoplatelets/epoxy composites. Results Phys. 2018, 9, 673–679. [Google Scholar] [CrossRef]
- Gorelov, B.M.; Gorb, A.M.; Nadtochiy, A.; Starokadomskiy, D.L.; Kuryliuk, V.V.; Sigareva, N.V.; Shulga, S.V.; Ogenko, V.M.; Korotchenkov, O.O.; Polovina, O.I. Epoxy filled with bare and oxidized multi-layered graphene nanoplatelets: A comparative study of filler loading impact on thermal properties. J. Mater. Sci. 2019, 54, 9247–9266. [Google Scholar] [CrossRef]
- Zhang, P.; Zeng, J.; Zhai, S.; Xian, Y.; Yang, D.; Li, Q. Thermal properties of graphene filled polymer composite thermal interface materials. Macromol. Mater. Eng. 2017, 302, 1700068. [Google Scholar] [CrossRef]
- Lewis, J.S.; Perrier, T.; Barani, Z.; Kargar, F.; Balandin, A.A. Thermal interface materials with graphene fillers: Review of the state of the art and outlook for future applications. Nanotechnology 2021, 32, 142003. [Google Scholar] [CrossRef]
- Ma, H.; Gao, B.; Wang, M.; Yuan, Z.; Shen, J.; Zhao, J. Strategies for enhancing thermal conductivity of polymer-based thermal interface materials: A review. J. Mater. Sci. 2021, 56, 1064–1086. [Google Scholar] [CrossRef]
- El-Kady, M.F.; Shao, Y.; Kaner, R.B. Graphene for batteries, supercapacitors and beyond. Nat. Rev. Mater. 2016, 1, 16033. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, G.; Liu, K.; Cui, Y. Design of complex nanomaterials for energy storage: Past success and future opportunity. Acc. Chem. Res. 2017, 50, 2895–2905. [Google Scholar] [CrossRef] [PubMed]
- Al-Saleh, M. Carbon-based polymer nanocomposites as dielectric energy storage materials. Nanotechnology 2018, 30, 062001. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; El-Kady, M.F.; Wang, L.J.; Zhang, Q.; Li, Y.; Wang, H.; Mousavi, M.F.; Kaner, R.B. Graphene-based materials for flexible supercapacitors. Chem. Soc. Rev. 2015, 44, 3639–3665. [Google Scholar] [CrossRef]
- Azman, N.H.N.; Nazir, S.M.M.; Ngee, L.H.; Sulaiman, Y. Graphene-based ternary composites for supercapacitors. Int. J. Energy Res. 2018, 42, 2104–2116. [Google Scholar] [CrossRef]
- Ishaq, S.; Moussa, M.; Kanwal, F.; Ehsan, M.; Saleem, M.; Van, T.N.; Losic, D. Facile synthesis of ternary graphene nanocomposites with doped metal oxide and conductive polymers as electrode materials for high performance supercapacitors. Sci. Rep. 2019, 9, 5974. [Google Scholar] [CrossRef]
- Movil, O.; Frank, L.; Staser, J.A. Graphene oxide–polymer nanocomposite anion-exchange membranes. J. Electrochem. Soc. 2015, 162, F419–F426. [Google Scholar] [CrossRef]
- Luo, Z.; Gong, Y.; Liao, X.; Pan, Y.; Zhang, H. Nanocomposite membranes modified by graphene-based materials for anion exchange membrane fuel cells. RSC Adv. 2016, 6, 13618–13625. [Google Scholar] [CrossRef]
- Pandey, R.P.; Shukla, G.; Manohar, M.; Shahi, V.K. Graphene oxide based nanohybrid proton exchange membranes for fuel cell applications: An overview. Adv. Colloid Interface Sci. 2017, 240, 15–30. [Google Scholar] [CrossRef]
- Alabi, A.; Cseri, L.; Al Hajaj, A.; Szekely, G.; Budd, P.; Zou, L. Electrostatically-coupled graphene oxide nanocomposite cation exchange membrane. J. Membr. Sci. 2019, 594, 117457. [Google Scholar] [CrossRef]
- Yadav, R.; Subhash, A.; Chemmenchery, N.; Kandasubramanian, B. Graphene and graphene oxide for fuel cell technology. Ind. Eng. Chem. Res. 2018, 57, 9333–9350. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Yang, Z.; Hu, N. Review of recent progress on graphene-based composite gas sensors. Ceram. Int. 2021, 47, 16367–16384. [Google Scholar] [CrossRef]
- Chakraborthy, A.; Nuthalapati, S.; Nag, A.; Afsarimanesh, N.; Alahi, M.E.E.; Altinsoy, M.E. A critical review of the use of graphene-based gas sensors. Chemosensors 2022, 10, 355. [Google Scholar] [CrossRef]
- Anderson, L.; Govindaraj, P.; Ang, A.; Mirabedini, A.; Hameed, N. Modelling, fabrication and characterization of graphene/polymer nanocomposites for electromagnetic interference shielding applications. Carbon Trends 2021, 4, 100047. [Google Scholar] [CrossRef]
- Tan, X.; Yuan, Q.; Qiu, M.; Yu, J.; Jiang, N.; Lin, C.-T.; Dai, W. Rational design of graphene/polymer composites with excellent electromagnetic interference shielding effectiveness and high thermal conductivity: A mini review. J. Mater. Sci. Technol. 2022, 117, 238–250. [Google Scholar] [CrossRef]
- Panahi-Sarmad, M.; Noroozi, M.; Xiao, X.; Park, C.B. Recent advances in graphene-based polymer nanocomposites and foams for electromagnetic interference shielding applications. Ind. Eng. Chem. Res. 2022, 61, 1545–1568. [Google Scholar] [CrossRef]
- Rohini, R.; Katti, P.; Bose, S. Tailoring the interface in graphene/thermoset polymer composites: A critical review. Polymer 2015, 70, A17–A34. [Google Scholar] [CrossRef]
- Atif, R.; Shyha, I.; Inam, F. Mechanical, thermal, and electrical properties of graphene-epoxy nanocomposites—A review. Polymers 2016, 8, 281. [Google Scholar] [CrossRef] [PubMed]
- Atif, R.; Inam, F. Modeling and simulation of graphene based polymer nanocomposites: Advances in the last decade. Graphene 2016, 5, 96–142. [Google Scholar] [CrossRef]
- Mohan, V.B.; Lau, K.T.; Hui, D.; Bhattacharyya, D. Graphene-based materials and their composites: A review on production, applications and product limitations. Compos. B. Eng. 2018, 142, 200–220. [Google Scholar] [CrossRef]
- Szeluga, U.; Pusz, S.; Kumanek, B.; Olszowska, K.; Kobyliukh, A.; Trzebicka, B. Effect of graphene filler structure on electrical, thermal, mechanical, and fire retardant properties of epoxy-graphene nanocomposites—A review. Crit. Rev. Solid State Mater. Sci. 2021, 46, 152–187. [Google Scholar] [CrossRef]
- Siwal, S.S.; Zhang, Q.; Devi, N.; Thakur, V.K. Review: Carbon-based polymer nanocomposite for high-performance energy storage applications. Polymers 2020, 12, 505. [Google Scholar] [CrossRef]
- Dubey, R.; Guruviah, V. Review of carbon-based electrode materials for supercapacitor energy storage. Ionics 2019, 25, 1419–1445. [Google Scholar] [CrossRef]
- Luo, H.; Zhou, X.; Ellingford, C.; Zhang, Y.; Chen, S.; Zhou, K.; Zhang, D.; Bowen, C.R.; Wan, C. Interface design for high energy density polymer nanocomposites. Chem. Soc. Rev. 2019, 48, 4424–4465. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.-S.; Zhou, G.; Yin, L.-C.; Ren, W.; Li, F.; Cheng, H.-M. Graphene/metal oxide composite electrode materials for energy storage. Nano Energy 2012, 1, 107–131. [Google Scholar] [CrossRef]
- Farooq, U.; Ahmed, F.; Pervez, S.A.; Rehman, S.; Pope, M.A.; Fichtner, M.; Roberts, E.P.L. A stable TiO2–graphene nanocomposite anode with high rate capability for lithium-ion batteries. RSC Adv. 2020, 10, 29975–29982. [Google Scholar] [CrossRef]
- Tang, B.; Chen, H.; Peng, H.; Wang, Z.; Huang, W. Graphene modified TiO2 composite photocatalysts: Mechanism, progress and perspective. Nanomaterials 2018, 8, 105. [Google Scholar] [CrossRef] [PubMed]
- Martins, P.M.; Ferreira, C.G.; Silva, A.R.; Magalhães, B.; Alves, M.M.; Pereira, L.; Marques, P.A.A.P.; Melle-Franco, M.; Lanceros-Méndez, S. TiO2/graphene and TiO2/graphene oxide nanocomposites for photocatalytic applications: A computer modeling and experimental study. Compos. B Eng. 2018, 145, 39–46. [Google Scholar] [CrossRef]
- Sagadevan, S.; Lett, J.A.; Weldegebrieal, G.K.; Biswas, M.R.D.; Oh, W.C.; Alshahateet, S.F.; Fatimah, I.; Mohammad, F.; Al-Lohedan, H.A.; Paiman, S.; et al. Enhanced gas sensing and photocatalytic activity of reduced graphene oxide loaded TiO2 nanoparticles. Chem. Phys. Lett. 2021, 780, 138897. [Google Scholar] [CrossRef]
- Siwachi, B.; Mohan, D.; Sharma, S.; Jyoti, D. Process optimization of dye-sensitized solar cells using TiO2–graphene nanocomposites. Bull. Mater. Sci. 2017, 40, 1371–1377. [Google Scholar] [CrossRef]
- Kusiak-Nejman, E.; Morawski, A.W. TiO2/graphene-based nanocomposites for water treatment: A brief overview of charge carrier transfer, antimicrobial and photocatalytic performance. Appl. Catal. B Environ. 2019, 253, 179–186. [Google Scholar] [CrossRef]
- Simari, C.; Lufrano, E.; Godbert, N.; Gournis, D.; Coppola, L.; Nicotera, I. Titanium dioxide grafted on graphene oxide: Hybrid nanofiller for effective and low-cost proton exchange membranes. Nanomaterials 2020, 10, 1572. [Google Scholar] [CrossRef]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Thompson, T.L.; Yates, J.T. Surface science studies of the photoactivation of TiO2—New photochemical processes. Chem. Rev. 2006, 106, 4428–4453. [Google Scholar] [CrossRef]
- Chen, X.; Mao, S.S. Titanium dioxide nanomaterials: Synthesis, properties, modifications, and applications. Chem. Rev. 2007, 107, 2891–2959. [Google Scholar] [CrossRef] [PubMed]
- Nowotny, M.K.; Sheppard, L.R.; Bak, T.; Nowotny, J. Defect chemistry of titanium dioxide. Application of defect engineering in processing of TiO2-based photocatalysts. J. Phys. Chem. C 2008, 112, 5275–5300. [Google Scholar] [CrossRef]
- Angelis, F.D.; Valentin, C.D.; Fantacci, S.; Vittadini, A.; Selloni, A. Theoretical studies on anatase and less common TiO2 phases: Bulk, surfaces, and nanomaterials. Chem. Rev. 2014, 114, 9708–9753. [Google Scholar] [CrossRef] [PubMed]
- Kusiak-Nejman, E.; Wanag, A.; Kowalczyk, Ł.; Kapica-Kozar, J.; Colbeau-Justin, C.; Mendez Medrano, M.G.; Morawski, A.W. Graphene-oxide TiO2 and reduced graphene oxide-TiO2 nanocomposites: Insight in charge-carrier lifetime measurements. Catal. Today 2017, 287, 189–195. [Google Scholar] [CrossRef]
- Yadav, A.; Yadav, M.; Gupta, S.; Popat, Y.; Gangan, A.; Chakraborty, B.; Ramaniah, L.M.; Fernandes, R.; Miotello, A.; Press, M.R.; et al. Effect of graphene oxide loading on TiO2: Morphological, optical, interfacial charge dynamics—A combined experimental and theoretical study. Carbon 2019, 143, 51–62. [Google Scholar] [CrossRef]
- Heo, U.S.; Kim, D.-W.; Kim, K.-S.; Park, D.-W. A facile synthesis of anatase TiO2-Graphene nanocomposites using plasma and heat treatment. Appl. Surf. Sci. 2019, 474, 118–126. [Google Scholar] [CrossRef]
- Cui, W.; Du, F.; Zhao, J.; Zhang, W.; Yang, Y.; Xie, X.; Mai, Y.-W. Improving thermal conductivity while retaining high electrical resistivity of epoxy composites by incorporating silica-coated multi-walled carbon nanotubes. Carbon 2010, 49, 495–500. [Google Scholar] [CrossRef]
- Im, H.; Hwang, Y.; Moon, J.H.; Lee, S.H.; Kim, J. The thermal conductivity of Al(OH)3 covered MWCNT/epoxy terminated dimethyl polysiloxane composite based on analytical Al(OH)3 covered MWCNT. Compos. A Appl. Sci. Manuf. 2013, 54, 159–165. [Google Scholar] [CrossRef]
- Peierls, R.E. Quantum Theory of Solids; Oxford University Press: London, UK, 1955. [Google Scholar]
- Pierson, H.O. Handbook of Carbon, Graphite, Diamonds and Fullerenes: Processing, Properties and Applications; Noyes Publications: Norwich, NJ, USA, 2010. [Google Scholar]
- Balandin, A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef]
- Burger, N.; Laachachi, A.; Ferriol, M.; Lutz, M.; Toniazzo, V.; Ruch, D. Review of thermal conductivity in composites: Mechanisms, parameters and theory. Prog. Polym. Sci. 2016, 61, 1–28. [Google Scholar] [CrossRef]
- Kuryliuk, V.; Nadtochiy, A.; Korotchenkov, O.; Wang, C.C.; Li, P.W. A model for predicting the thermal conductivity of SiO2–Ge nanoparticle composites. Phys. Chem. Chem. Phys. 2015, 17, 13429–13441. [Google Scholar] [CrossRef]
- Goodson, K.E.; Su, L.T.; Antoniadis, D.A.; Flik, M.I. Prediction and measurement of the thermal conductivity of amorphous dielectric layers. J. Heat Transfer 1994, 116, 317–324. [Google Scholar] [CrossRef]
- Zeller, R.C.; Pohl, R.O. Thermal conductivity and specific heat of noncrystalline solids. Phys. Rev. B 1971, 4, 2029–2041. [Google Scholar] [CrossRef]
- Anderson, P.W.; Halperin, B.I.; Varma, M.M. Anomalous low-temperature thermal properties of glasses and spin glasses. Philos. Mag. 1972, 25, 1–9. [Google Scholar] [CrossRef]
- Phillips, W.A. Tunneling states in amorphous solids. J. Low Temp. Phys. 1972, 7, 351–360. [Google Scholar] [CrossRef]
- Galperin, Y.M.; Karpov, V.G.; Kozub, V.I. Localized states in glasses. Adv. Phys. 1989, 38, 669–737. [Google Scholar] [CrossRef]
- Parshin, D.A. Interactions of soft atomic potentials and universality of low-temperature properties of glasses. Phys. Rev. B 1994, 49, 9400–9418. [Google Scholar] [CrossRef] [PubMed]
- Grayson, M.; Eckroth, D. Encyclopedia of Chemical Technology, 3rd ed.; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar]
- Available online: https://rruff.info/doclib/hom/anatase.pdf (accessed on 24 October 2023).
- Gresil, M.; Wang, Z.; Poutrel, Q.-A.; Soutis, C. Thermal diffusivity mapping of graphene based polymer nanocomposites. Sci. Rep. 2017, 7, 5536. [Google Scholar] [CrossRef]
- Available online: http://webmineral.com/data/Anatase.shtml#.ZDwjK3ZByUk (accessed on 24 October 2023).
- Cabaleiro, D.; Nimo, J.; Pastoriza-Gallego, M.J.; Piceiro, M.M.; Legido, J.L.; Lugo, L. Thermal conductivity of dry anatase and rutile nano-powders and ethylene and propylene glycol-based TiO2 nanofluids. J. Chem. Thermodyn. 2015, 83, 67–76. [Google Scholar] [CrossRef]
- Shahil, K.M.F.; Balandin, A.A. Graphene−multilayer graphene nanocomposites as highly efficient thermal interface materials. Nano Lett. 2012, 12, 861–867. [Google Scholar] [CrossRef] [PubMed]
- Evans, W.; Prasher, R.; Fish, J.; Meakin, P.; Phelan, P.; Keblinski, P. Effect of aggregation and interfacial thermal resistance on thermal conductivity of nanocomposites and colloidal nanofluids. Int. J. Heat Mass Transf. 2008, 51, 1431–1438. [Google Scholar] [CrossRef]
- Bolis, V.; Busco, C.; Ciarletta, M.; Distasi, C.; Erriquez, J.; Fenoglio, I.; Livraghi, S.; Morel, S. Hydrophilic/hydrophobic features of TiO2 nanoparticles as a function of crystal phase, surface area and coating, in relation to their potential toxicity in peripheral nervous system. J. Colloid Interface Sci. 2012, 369, 28–39. [Google Scholar] [CrossRef]
- ter Haar, D. (Ed.) Collected Papers of P. L. Kapitza; Pergamon: Oxford, UK, 1965; Volume 2, p. 581. [Google Scholar]
- Roy, A.K.; Farmer, B.L.; Varshney, V.; Sihn, S.; Lee, J.; Ganguli, S. Importance of interfaces in governing thermal transport in composite materials: Modeling and experimental perspectives. ACS Appl. Mater. Interfaces 2012, 4, 545–563. [Google Scholar] [CrossRef] [PubMed]
- Kelham, S.; Rosenberg, H. Phonon scattering and the linear specific heat term in epoxy-resins at low temperatures. J. Phys. Colloq. 1978, 39, 982–983. [Google Scholar] [CrossRef]
- Garrett, K.W.; Rosenberg, H.M. The thermal conductivity of epoxy-resin / powder composite materials. J. Phys. D Appl. Phys. 1974, 7, 1247–1258. [Google Scholar] [CrossRef]
- Muñoz, E.; Lu, J.; Yakobson, B.I. Ballistic thermal conductance of graphene ribbons. Nano Lett. 2010, 10, 1652–1656. [Google Scholar] [CrossRef]
- Mingo, N.; Broido, D. Carbon nanotube ballistic thermal conductance and its limits. Phys. Rev. Lett. 2005, 95, 096105. [Google Scholar] [CrossRef]
- Cahill, D.G.; Ford, W.K.; Goodson, K.E.; Mahan, G.D.; Majumdar, A.; Maris, H.J.; Merlin, R.; Phillpot, R.S.R. Nanoscale thermal transport. J. Appl. Phys. 2003, 93, 793818. [Google Scholar] [CrossRef]
- Torres, P.; Rurali, R. Thermal conductivity of rutile and anatase TiO2 from first principles. J. Phys. Chem. C 2019, 123, 30851–30855. [Google Scholar] [CrossRef]
- Mettan, X.; Jaćimović, J.; Barišić, O.S.; Pisoni, A.; Batistić, I.; Horváth, E.; Brown, S.; Rossi, L.; Szirmai, P.; Farkas, B.; et al. Tailoring thermal conduction in anatase TiO2. Commun. Phys. 2019, 2, 123. [Google Scholar] [CrossRef]
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Chen, G. Thermal conductivity and ballistic-phonon transport in the cross-plane direction of superlattices. Phys. Rev. B 1998, 57, 14958–14973. [Google Scholar] [CrossRef]
- Prasher, R.S.; Phelan, P.E. Microscopic and macroscopic thermal contact resistances of pressed mechanical contacts. J. Appl. Phys. 2006, 100, 063538. [Google Scholar] [CrossRef]
- Yang, S.B.; Feng, X.L.; Müllen, K. Sandwich-Like, graphene-based titania nanosheets with high surface area for fast lithium storage. Adv. Mater. 2011, 23, 3575–3579. [Google Scholar] [CrossRef]
- Zheng, Q.; Braun, P.V.; Cahill, D.G. Thermal conductivity of graphite thin films grown by low temperature chemical vapor deposition on Ni (111). Adv. Mater. Interfaces 2016, 3, 1600234. [Google Scholar] [CrossRef]
- Wu, W.; Yang, H.; Liu, Y.; Yang, S.; Yang, P. Effect of defects on heat transfer at the graphene/epoxy interface. Int. Commun. Heat Mass Transf. 2022, 131, 105846. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, C.; Pei, Q.-X.; Zhang, Y. Some aspects of thermal transport across the interface between graphene and epoxy in nanocomposites. ACS Appl. Mater. Interfaces 2016, 8, 8272–8279. [Google Scholar] [CrossRef]
- Ndoro, T.V.M.; Böhm, M.C.; Müller-Plathe, F. Interface and interphase dynamics of polystyrene chains near grafted and ungrafted silica nanoparticles. Macromolecules 2011, 45, 171–179. [Google Scholar] [CrossRef]
- Eslami, H.; Rahimi, M.; Müller-Plathe, F. Molecular dynamics simulation of a silica nanoparticle in oligomeric poly(methyl methacrylate): A model system for studying the interphase thickness in a polymer−nanocomposite via different properties. Macromolecules 2013, 46, 8680–8692. [Google Scholar] [CrossRef]
- Park, H.; Chung, I.; Cho, M. Effect of molecular structure of curing agents on cyclic creep in highly cross-linked epoxy polymers. J. Polym. Sci. 2020, 58, 1617–1631. [Google Scholar] [CrossRef]
- Odegard, G.M.; Clancy, T.C.; Gates, T.S. Modeling of the mechanical properties of nanoparticle/polymer composites. Polymer 2005, 46, 553–562. [Google Scholar] [CrossRef]
- Pitsa, D.; Danikas, M.G. Interfaces features in polymer nanocomposites: A review of proposed models. Nano 2011, 6, 497–508. [Google Scholar] [CrossRef]
- Wang, Y.; Shan, J.W.; Weng, G.J. Percolation threshold and electrical conductivity of graphene-based nanocomposites with filler agglomeration and interfacial tunneling. J. Appl. Phys. 2015, 118, 06161. [Google Scholar] [CrossRef]
- Nan, C.-W.; Birringer, R.; Clarke, D.R.; Gleiter, H. Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 1997, 81, 6692–6699. [Google Scholar] [CrossRef]
- Kuilla, T.; Bhadra, S.; Yao, D.; Kim, N.H.; Bose, S.; Lee, J.H. Recent advances in graphene based polymer composites. Prog. Polym. Sci. 2010, 35, 1350–1375. [Google Scholar] [CrossRef]
- Punetha, V.D.; Rana, S.; Yoo, H.J.; Chaurasia, A.; McLeskey, J.T.; Ramasamy, M.S.; Sahoo, N.G.; Cho, J.W. Functionalization of carbon nanomaterials for advanced polymer nanocomposites: A comparison study between CNT and graphene. Prog. Polym. Sci. 2017, 67, 1–47. [Google Scholar] [CrossRef]
- Dreyer, D.R.; Park, S.; Bielawski, C.W.; Ruoff, R.S. The chemistry of graphene oxide. Chem. Soc. Rev. 2009, 39, 228–240. [Google Scholar] [CrossRef]
- Choi, E.-Y.; Han, T.H.; Hong, J.; Kim, J.E.; Lee, S.H.; Kim, H.W.; Kim, S.O. Noncovalent functionalization of graphene with end-functional polymers. J. Mater. Chem. 2010, 20, 1907–1912. [Google Scholar] [CrossRef]
- Tarannum, F.; Muthaiah, R.; Danayat, S.; Foley, K.; Annam, R.S.; Walters, K.B.; Garg, J. Chemically edge-carboxylated graphene enhances the thermal conductivity of polyetherimide–graphene nanocomposites. ACS Appl. Mater. Interfaces 2022, 14, 14753–14763. [Google Scholar] [CrossRef]
- Gao, Y.; Müller-Plathe, F. Increasing the thermal conductivity of graphene-polyamide-6,6 nanocomposites by surface-grafted polymer chains: Calculation with molecular dynamics and effective-medium approximation. J. Phys. Chem. B 2016, 120, 1336–1346. [Google Scholar] [CrossRef] [PubMed]
- Wong, C.H.A.; Sofer, Z.; Kubešová, M.; Kučera, J.; Matějková, S.; Pumera, M. Synthetic routes contaminate graphene materials with a whole spectrum of unanticipated metallic elements. Proc. Natl. Acad. Sci. USA 2014, 111, 13774–13779. [Google Scholar] [CrossRef] [PubMed]
- Barbolina, I.; Woods, C.R.; Lozano, N.; Kostarelos, K.; Novoselov, K.S.; Roberts, I.S. Purity of graphene oxide determines its antibacterial activity. 2D Mater. 2016, 3, 025025. [Google Scholar] [CrossRef]
- Kozbial, A.; Zhou, F.; Li, Z.; Liu, H.; Li, L. Are graphitic surfaces hydrophobic? Acc. Chem. Res. 2016, 49, 2765–2773. [Google Scholar] [CrossRef]
- Jalili, R.; Esrafilzadeh, D.; Aboutalebi, S.H.; Sabri, Y.M.; Kandjani, A.E.; Bhargava, S.K.; Della Gaspera, E.; Gengenbach, T.R.; Walker, A.; Chao, Y.; et al. Silicon as a ubiquitous contaminant in graphene derivatives with significant impact on device performance. Nat. Commun. 2018, 9, 5070. [Google Scholar] [CrossRef]
- Pumera, M.; Ambrosi, A.; Chng, E.L.K. Impurities in graphenes and carbon nanotubes and their influence on the redox properties. Chem. Sci. 2012, 3, 3347–3355. [Google Scholar] [CrossRef]
- Xia, Z.Y.; Pezzini, S.; Treossi, E.; Giambastiani, G.; Corticelli, F.; Morandi, V.; Zanelli, A.; Bellani, V.; Palermo, V. The exfoliation of graphene in liquids by electrochemical, chemical, and sonication-assisted techniques: A nanoscale study. Adv. Funct. Mater. 2013, 23, 4684–4693. [Google Scholar] [CrossRef]
- Gregg, S.J.; Sing, K.S.W. Adsorption, Surface Area and Porosity; Academic Press: London, UK; New York, NY, USA, 1982. [Google Scholar]
- Eller, K.; Henkes, E.; Rossbacher, R.; Höke, H. Amines, Aliphatic. Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2015. [Google Scholar]
- Kanzow, J.; Zaporojtchenko, V.; Nabika, H.; Mizuhata, M.; Deki, S.; Faupel, F. In situ investigations on the cross-linking process of the epoxy resin system DGEBA-DETA by means of positron annihilation lifetime spectroscopy in comparison with infrared spectroscopy. In Proceedings of the 13th International Conference on Positron Annihilation, Kyoto, Japan, 7–12 September 2003; Nalwa, H.S., Ed.; Materials Science Forum. Trans Tech Publications: Zurich, Switzerland, 2004; Volumes 445–446, pp. 313–331. [Google Scholar] [CrossRef]
- Moongraksathum, B.B.; Shang, J.-Y.; Chen, Y.-W. Photocatalytic antibacterial effectiveness of Cu-doped TiO2 thin film prepared via the peroxo sol-gel method. Catalysts 2018, 8, 352. [Google Scholar] [CrossRef]
- ASTM C177-19; Standard Test Method for Steady-State Heat Flux Measurements and Thermal Transmission Properties by Means of the Guarded-Hot-Plate Apparatus. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- ASTM C1045-07; Standard Practice for Calculating Thermal Transmission Properties Under Steady-State Conditions. ASTM International: West Conshohocken, PA, USA, 2013. [CrossRef]
- Rondeaux, F.; Bredy, P.; Rey, J.M. Thermal conductivity measurements of epoxy systems at low temperature. AIP Conf. Proc. 2002, 614, 197–203. [Google Scholar] [CrossRef]
- Physical Constants of IC Package Materials, Intel 2000 Packaging Databook. Available online: https://www.intel.com/content/dam/www/public/us/en/documents/packaging-databooks/packaging-chapter-05-databook.pdf (accessed on 24 October 2023).
- Soltani, A. Equations of Spheroid and Ellipsoid Surface Area by Analytical Method. Cambridge Open Engage. 2022. Available online: https://www.cambridge.org/engage/coe/article-details/61f7a44963acba4ce3201236 (accessed on 24 October 2023).
- Chang, S.-W.; Nair, A.K.; Buehler, M.J. Geometry and temperature effects of the interfacial thermal conductance in copper– and nickel–graphene nanocomposites. J. Phys. Cond. Matter 2012, 24, 245301. [Google Scholar] [CrossRef]


| Material | Density, ρ (kg m−3) | (W m−1 K−1) | (W−1 m2 K) |
|---|---|---|---|
| epoxy | 1.200 × 103 [71] | 0.22 (our data) | – |
| graphene | 2.267 × 103 [72] | in-plane 600–1200 cross-plane = 6 [73] | – |
| anatase TiO2 | 3.88 × 103 [74] | 0.455 [75] | – |
| graphene–epoxy interphase | – | – | 3.5 × 10−9 [76] |
| anatase–epoxy interphase | – | – | (0.1−1.0) × 10−8 [77,78] |
| graphene–anatase interphase | – | – | * |
| Interface | (W m−1 K−1) | (m2·K·W−1) | (W m−1 K−1) | (nm) | (nm) | , , (W−1 m2 K) |
|---|---|---|---|---|---|---|
| Anatase–epoxy | 0.455 | 1.0 × 10−8 (1.0 × 10−9) | 1.2 (12.0) | 50 | 4.55 (4.55 × 10−1) | 0.9166 (0.9910) |
| Graphene (in-plane)–epoxy | 600.0 (1200) | 3.5 × 10−9 | 3.43 (3.43) | 5 × 103 | 2.1 × 103 (4.2 × 103) | 0.7042 (0.5435) |
| Graphene (cross-plane)–epoxy | 6.0 | 3.5 × 10−9 | 3.43 | 50 | 2.1 × 101 | 0.7042 |
| The sandwich-like MLG@TiO2 structure | ||||||
| Graphene (in-plane)–anatase–epoxy | 600.0@0.455 | 1.0 × 10−6 (1.0 × 10−7) | 6.0 × 105 (6.0 × 104) | 0.00746/0.00752 * (0.0369/0.0384) * | ||
| Graphene (cross-plane)–anatase–epoxy | 6.0@0.455 | 1.0 × 10−6 (1.0 × 10−7) | 6.0 × 103 ** (6.0 × 102) ** | 0.01477/0.01489 * (0.0730/0.0760) * | ||
| Graphene-wrapped anatase | ||||||
| Graphene-wrapped anatase–epoxy | 606.0@0.455 | 1.0 × 10−6 (1.0 × 10−7) | 6.0 × 103 ** (6.0 × 102) ** | 0.00022 (0.00116) | ||
(W m−1 K−1) | (W m−1 K−1) | ·109 (m2·K−1·W−1) | ·109 (m2·K−1·W−1) | ·107 (m2·K−1·W−1) |
|---|---|---|---|---|
| the case of = (0.2864 ± 5%) W m−1 K−1 | ||||
| 600.0 | 3.5 | 1.0 * (10.0) ** | 0.923 * (0.699) ** | |
| 600.0 | 3.5 | 1.0 (10.0) | 0.653 (0.429) | |
| 600.0 | 3.5 | 1.0 (10.0) | 0.468 (0.247) | |
| 1200.0 | 3.5 | 1.0 (10.0) | 0.971 (0.749) | |
| 1200.0 | 3.5 | 1.0 (10.0) | 0.703 (0.481) | |
| 1200.0 | 3.5 | 1.0 (10.0) | 0.519 (0.297) | |
| the case of = (0.31295 ± 5%) W m−1 K−1 | ||||
| 600.0 | 3.5 | 1.0 (10.0) | 5.447 (4.927) | |
| 600.0 | 3.5 | 1.0 (10.0) | 4.476 (3.976) | |
| 600.0 | 3.5 | 1.0 (10.0) | 3.745 (3.265) | |
| 1200.0 | 3.5 | 1.0 (10.0) | 5.618 (5.131) | |
| 1200.0 | 3.5 | 1.0 (10.0) | 4.644 (4.185) | |
| 1200.0 | 3.5 | 1.0 (10.0) | 3.917 (3.472) | |
| 0 | 0 | 0 | 0 | 8.4889 × 10−3 | 8.4889 × 10−3 | 0 | 1.1266 × 10−3 | 1.1266 × 10−3 |
| 0 | 0 | 8.4898 × 10−2 | 8.4898 × 10−2 | 0 | 1.1268 × 10−3 | 1.1268 × 10−3 | ||
| 0.05 | 0.05 | 2.6799 × 10−4 | 1.5644 × 10−4 | 8.0643 × 10−3 | 8.4877 × 10−3 | 1.1020 × 10−4 | 1.3431 × 10−3 | 1.4533 × 10−3 |
| 2.6803 × 10−4 | 1.5647 × 10−4 | 8.0655 × 10−2 | 8.1092 × 10−2 | 1.1022 × 10−4 | 1.3433 × 10−3 | 1.4537 × 10−3 | ||
| 0.50 | 0.50 | 2.6795 × 10−3 | 1.5642 × 10−3 | 4.2437 × 10−3 | 8.4874 × 10−3 | 1.1019 × 10−3 | 3.2912 × 10−3 | 4.3931 × 10−3 |
| 2.6807 × 10−3 | 1.5690 × 10−3 | 4.2456 × 10−2 | 4.6706 × 10−2 | 1.1024 × 10−3 | 3.2927 × 10−3 | 4.3951 × 10−3 | ||
| 1.00 | 1.00 | 5.3581 × 10−3 | 3.1279 × 10−3 | 0 | 8.4860 × 10−3 | 2.2034 × 10−3 | 5.4250 × 10−2 | 5.6453 × 10−2 |
| 5.3602 × 10−3 | 3.1303 × 10−3 | 0 | 8.4905 × 10−3 | 2.2051 × 10−3 | 5.4592 × 10−2 | 5.6797 × 10−2 | ||
| 0 | 0 | 0 | 0 | 2.1608 × 10−2 | 2.1608 × 10−2 | 0 | 2.0947 × 10−3 | 2.0947 × 10−3 |
| 0 | 0 | 2.1612 × 10−2 | 2.1612 × 10−2 | 0 | 2.0952 × 10−3 | 2.0952 × 10−3 | ||
| 0.05 | 0.05 | 2.7567 × 10−4 | 8.0463 × 10−4 | 2.0526 × 10−2 | 2.1606 × 10−2 | 1.1336 × 10−4 | 3.3931 × 10−3 | 3.5065 × 10−3 |
| 2.7577 × 10−4 | 8.0543 × 10−4 | 2.0533 × 10−2 | 2.1614 × 10−2 | 1.1338 × 10−4 | 3.3943 × 10−3 | 3.5077 × 10−3 | ||
| 0.50 | 0.50 | 2.7550 × 10−3 | 8.0412 × 10−3 | 1.0796 × 10−2 | 2.1592 × 10−2 | 1.1329 × 10−3 | 1.5071 × 10−2 | 1.6204 × 10−2 |
| 2.7594 × 10−3 | 8.0543 × 10−3 | 1.0814 × 10−2 | 2.1628 × 10−2 | 1.1347 × 10−3 | 1.5095 × 10−2 | 1.6230 × 10−2 | ||
| 1.00 | 1.00 | 5.5060 × 10−3 | 1.6071 × 10−2 | 0 | 2.1577 × 10−2 | 2.2642 × 10−3 | 2.8028 × 10−2 | 3.0292 × 10−2 |
| 5.5227 × 10−3 | 1.6120 × 10−2 | 0 | 2.1643 × 10−2 | 2.2711 × 10−3 | 2.8113 × 10−2 | 3.0384 × 10−2 | ||
| Configuration | (nm) | ||||
|---|---|---|---|---|---|
| p-shaped | 0.01 | 4.585 | 0.0118 | 0.03121 | 0.02006 |
| p-shaped | 0.05 | 24.54 | 0.0196 | 0.02916 | 0.03248 |
| s-shaped | 0.01 | 4.571 | 0.0118 | 0.03119 | 0.02005 |
| s-shaped | 0.05 | 24,30 | 0.0195 | 0.02890 | 0.03233 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nadtochiy, A.B.; Gorb, A.M.; Gorelov, B.M.; Polovina, O.I.; Korotchenkov, O.; Schlosser, V. Model Approach to Thermal Conductivity in Hybrid Graphene–Polymer Nanocomposites. Molecules 2023, 28, 7343. https://doi.org/10.3390/molecules28217343
Nadtochiy AB, Gorb AM, Gorelov BM, Polovina OI, Korotchenkov O, Schlosser V. Model Approach to Thermal Conductivity in Hybrid Graphene–Polymer Nanocomposites. Molecules. 2023; 28(21):7343. https://doi.org/10.3390/molecules28217343
Chicago/Turabian StyleNadtochiy, Andriy B., Alla M. Gorb, Borys M. Gorelov, Oleksiy I. Polovina, Oleg Korotchenkov, and Viktor Schlosser. 2023. "Model Approach to Thermal Conductivity in Hybrid Graphene–Polymer Nanocomposites" Molecules 28, no. 21: 7343. https://doi.org/10.3390/molecules28217343
APA StyleNadtochiy, A. B., Gorb, A. M., Gorelov, B. M., Polovina, O. I., Korotchenkov, O., & Schlosser, V. (2023). Model Approach to Thermal Conductivity in Hybrid Graphene–Polymer Nanocomposites. Molecules, 28(21), 7343. https://doi.org/10.3390/molecules28217343







