Ab Initio Study of the Structures, Bonding Interactions, and Thermal Stability of the Li-Decorated 2D Biphenylene Sheet
Abstract
:1. Introduction
2. Materials and Methods
3. Results
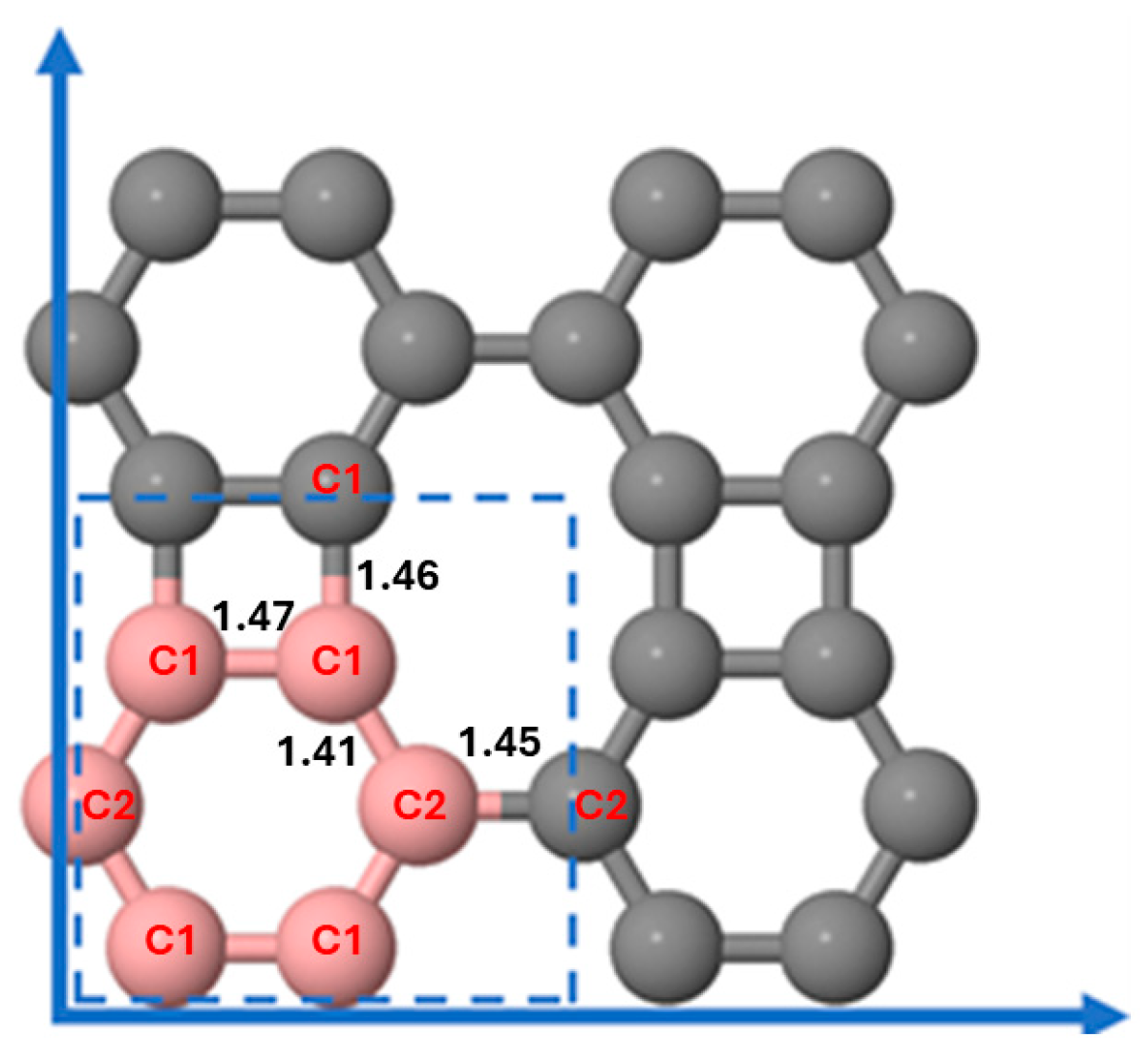
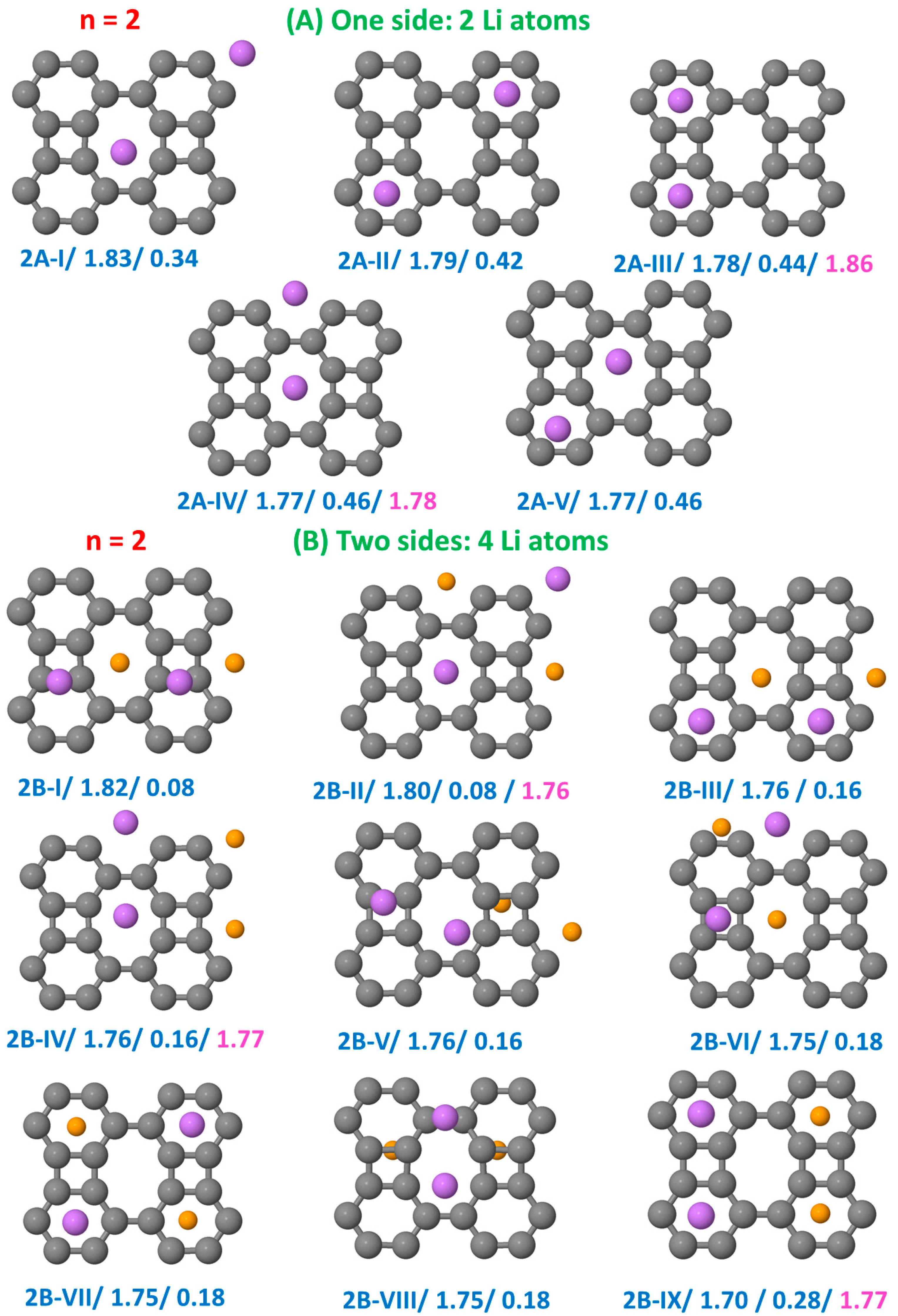
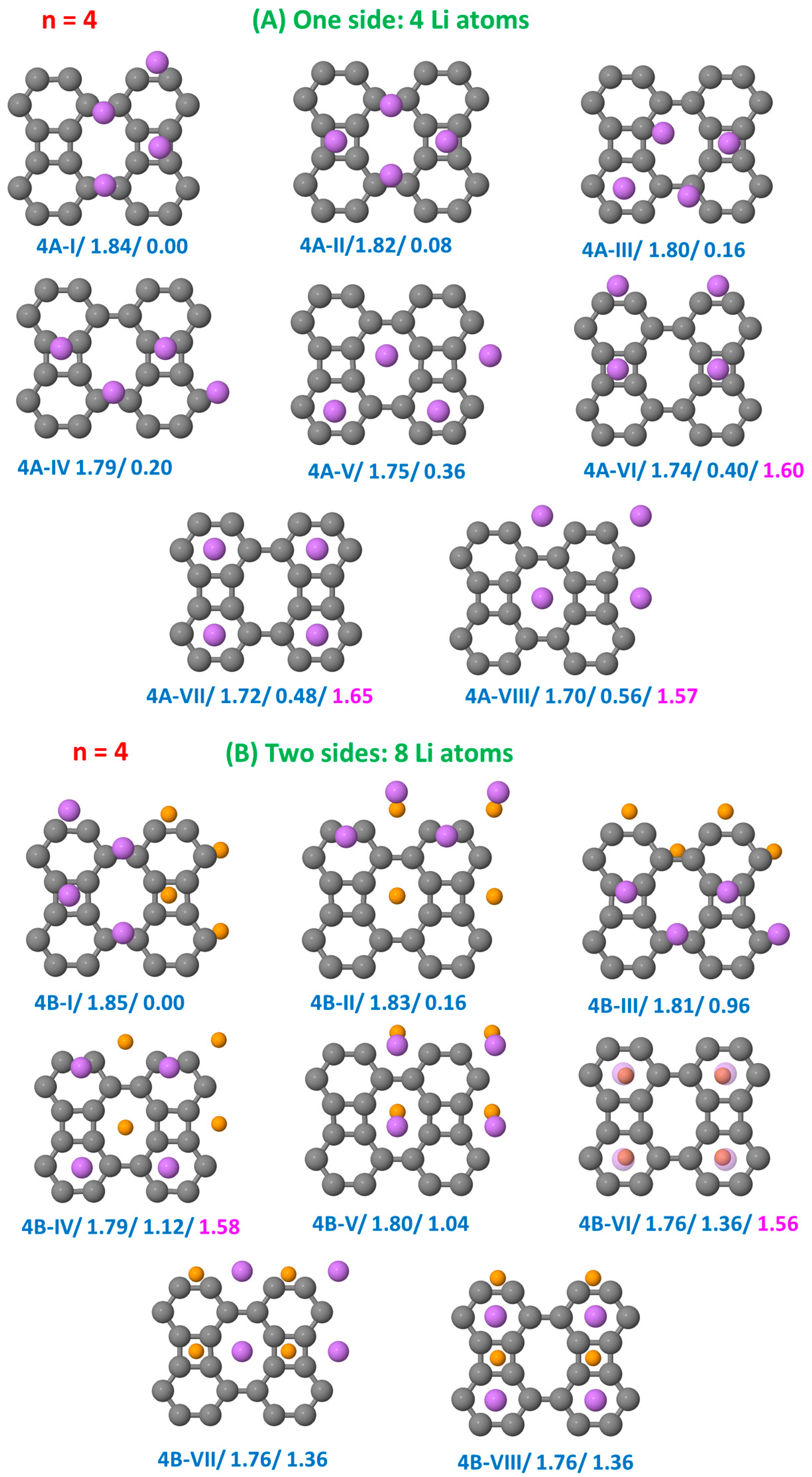
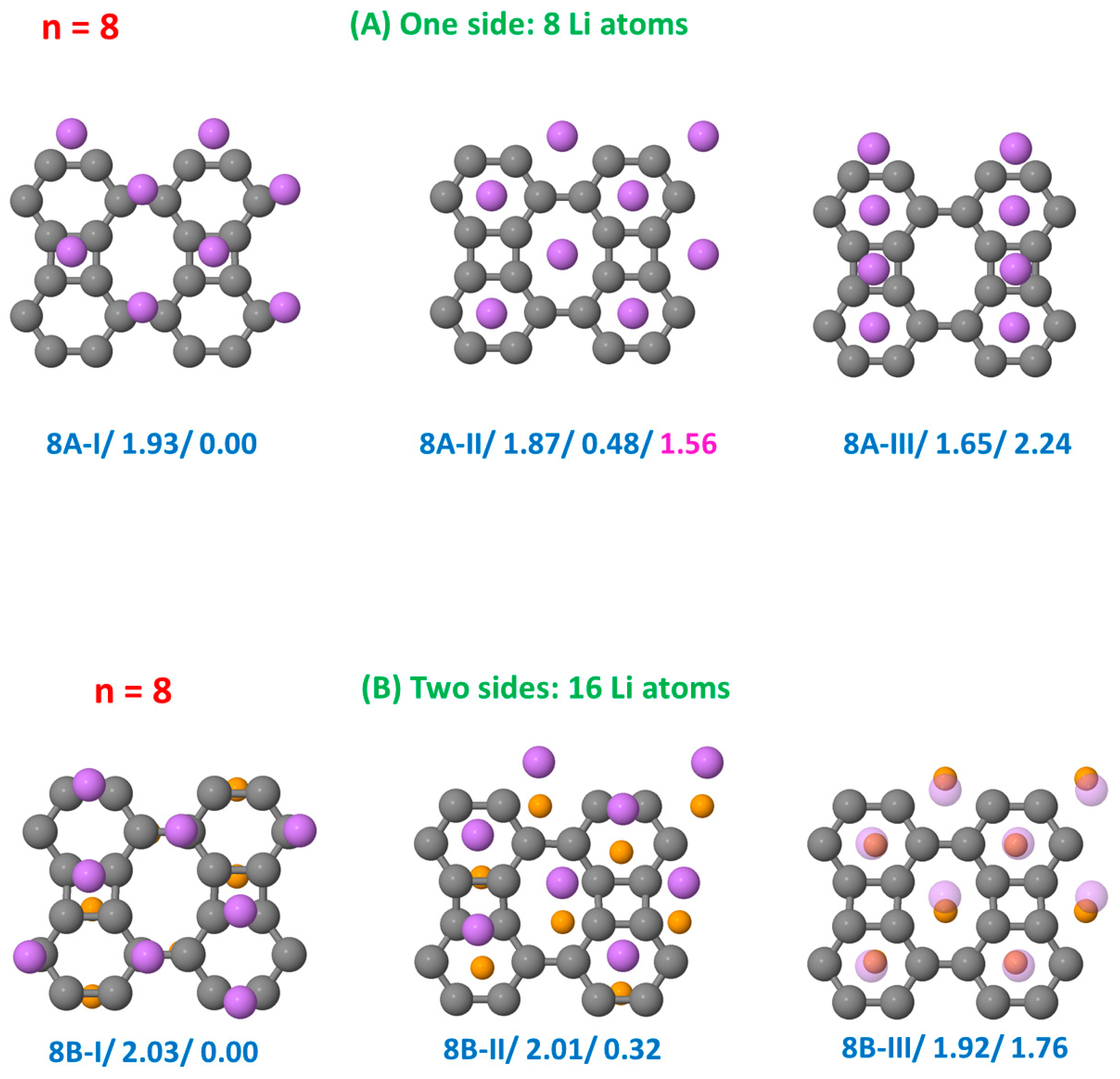
3.1. Structural Configurations of Li Atoms Adsorbed on Biphenylene
3.2. Quantum Chemical Topology Analysis
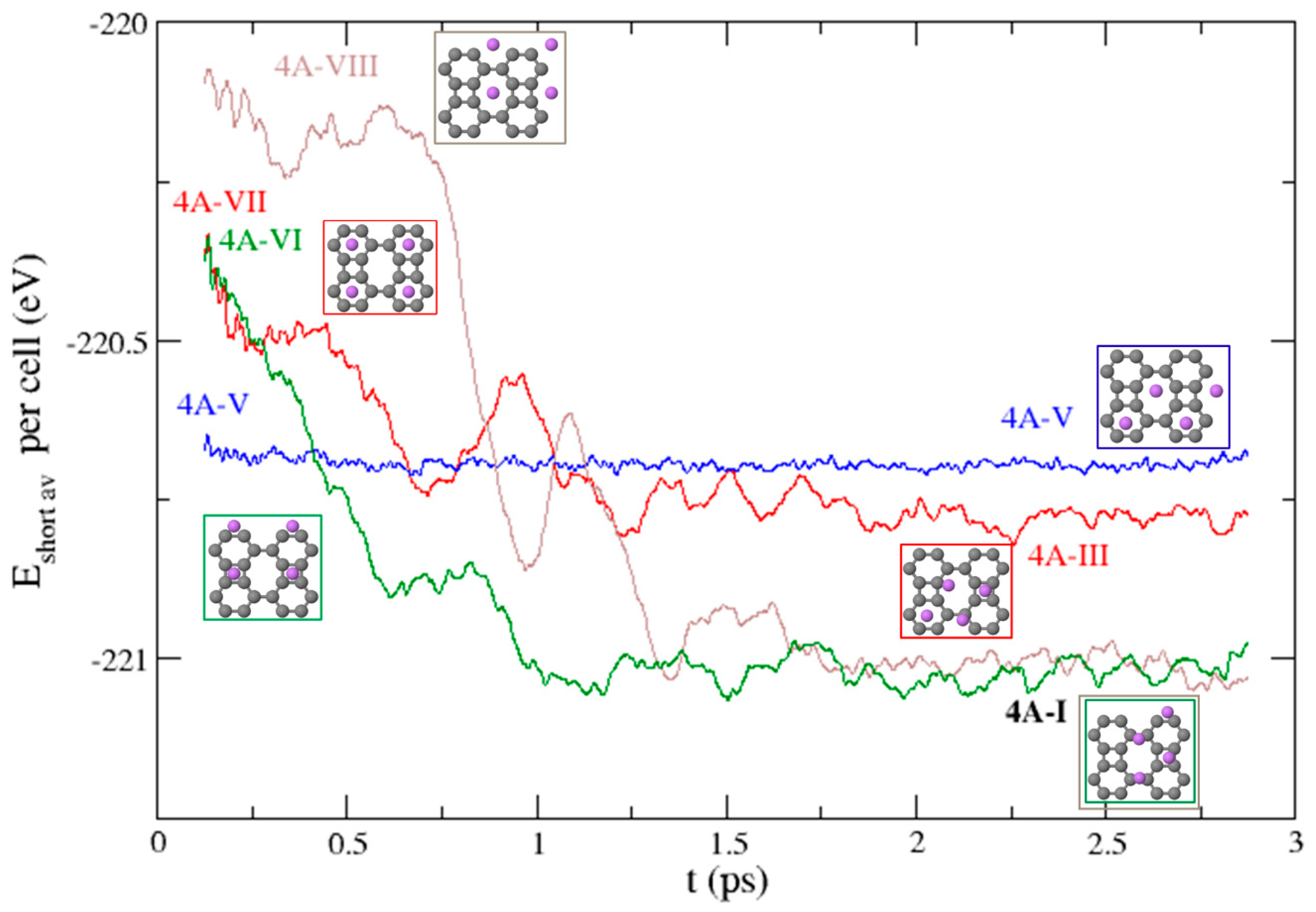
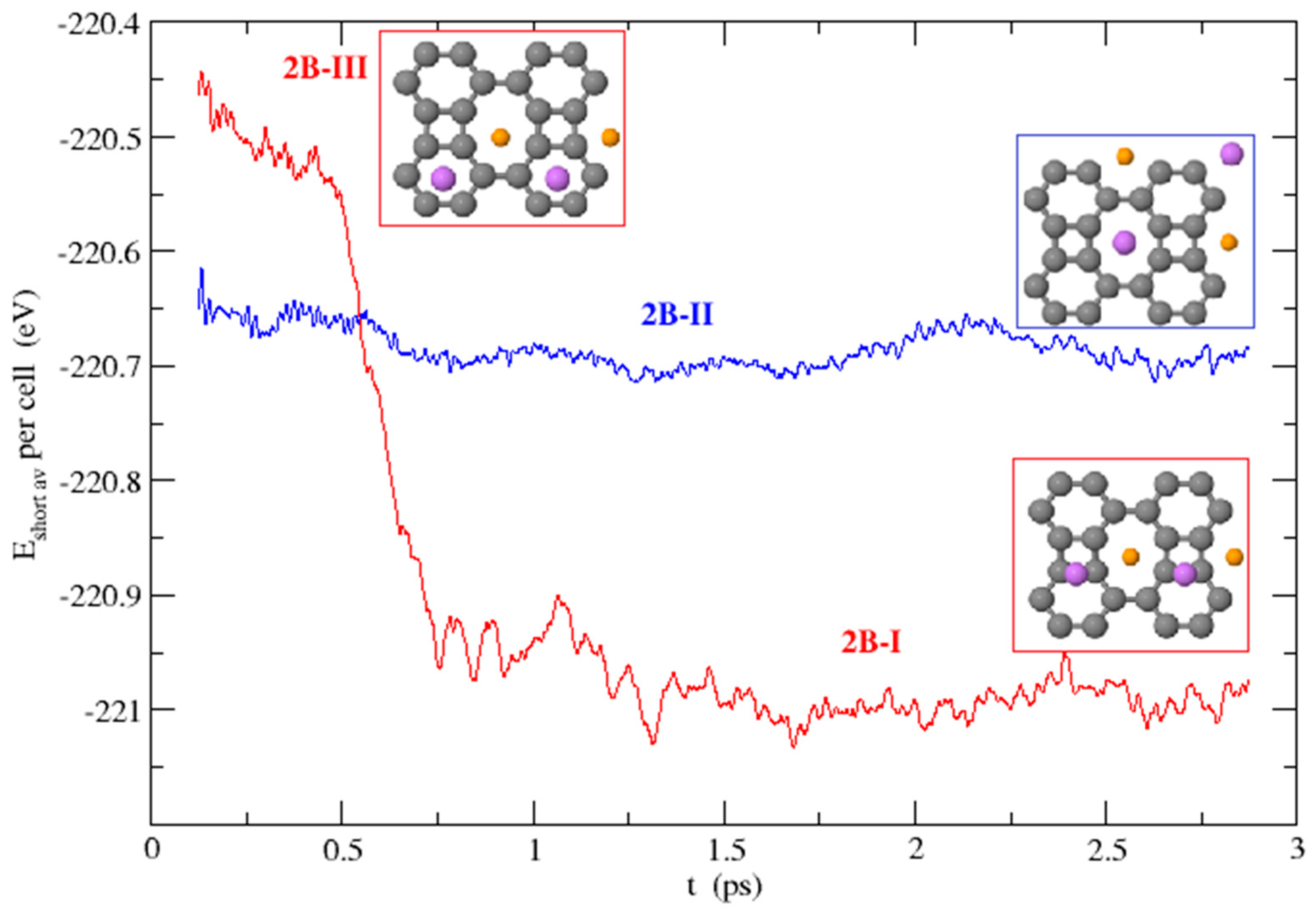
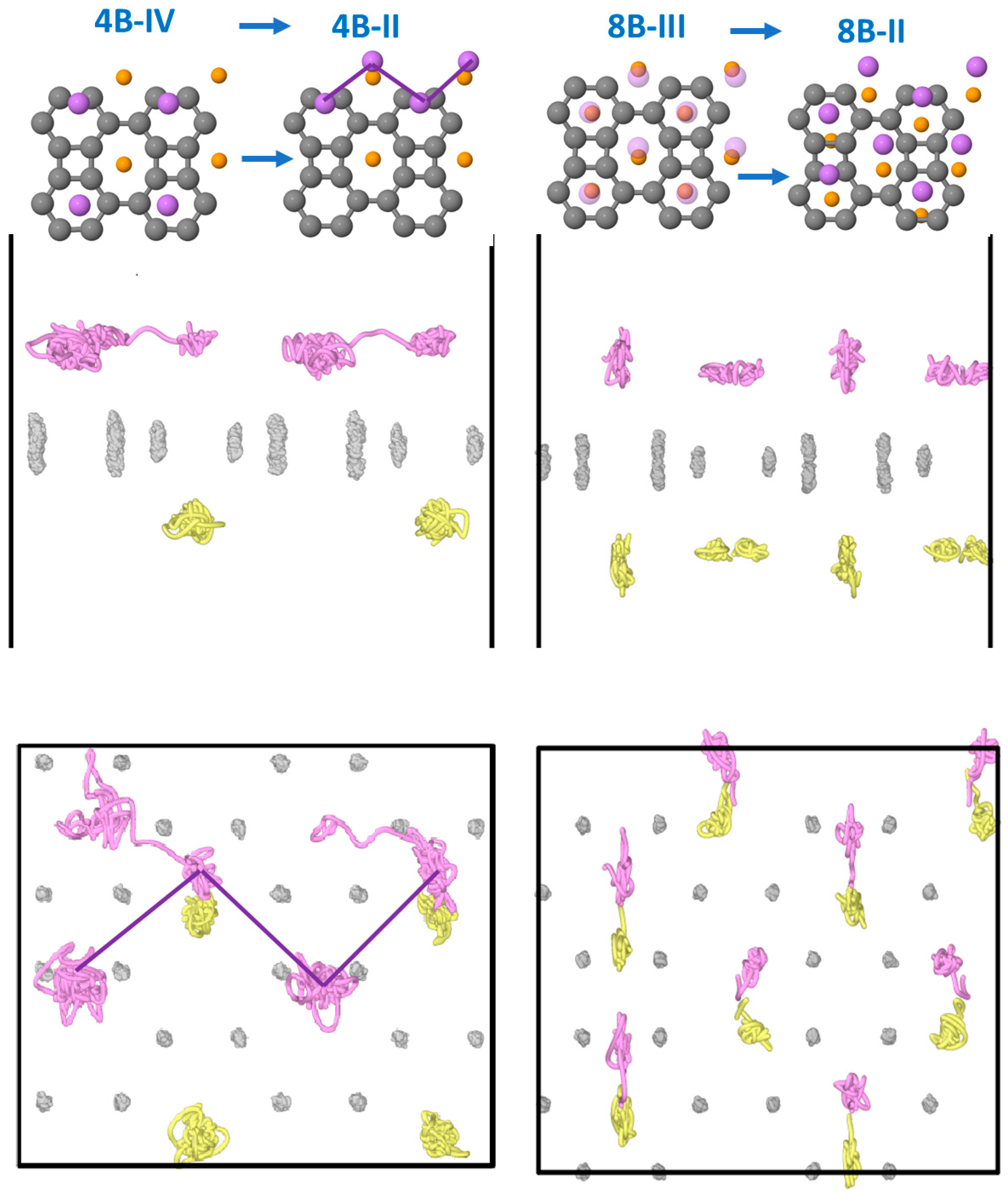
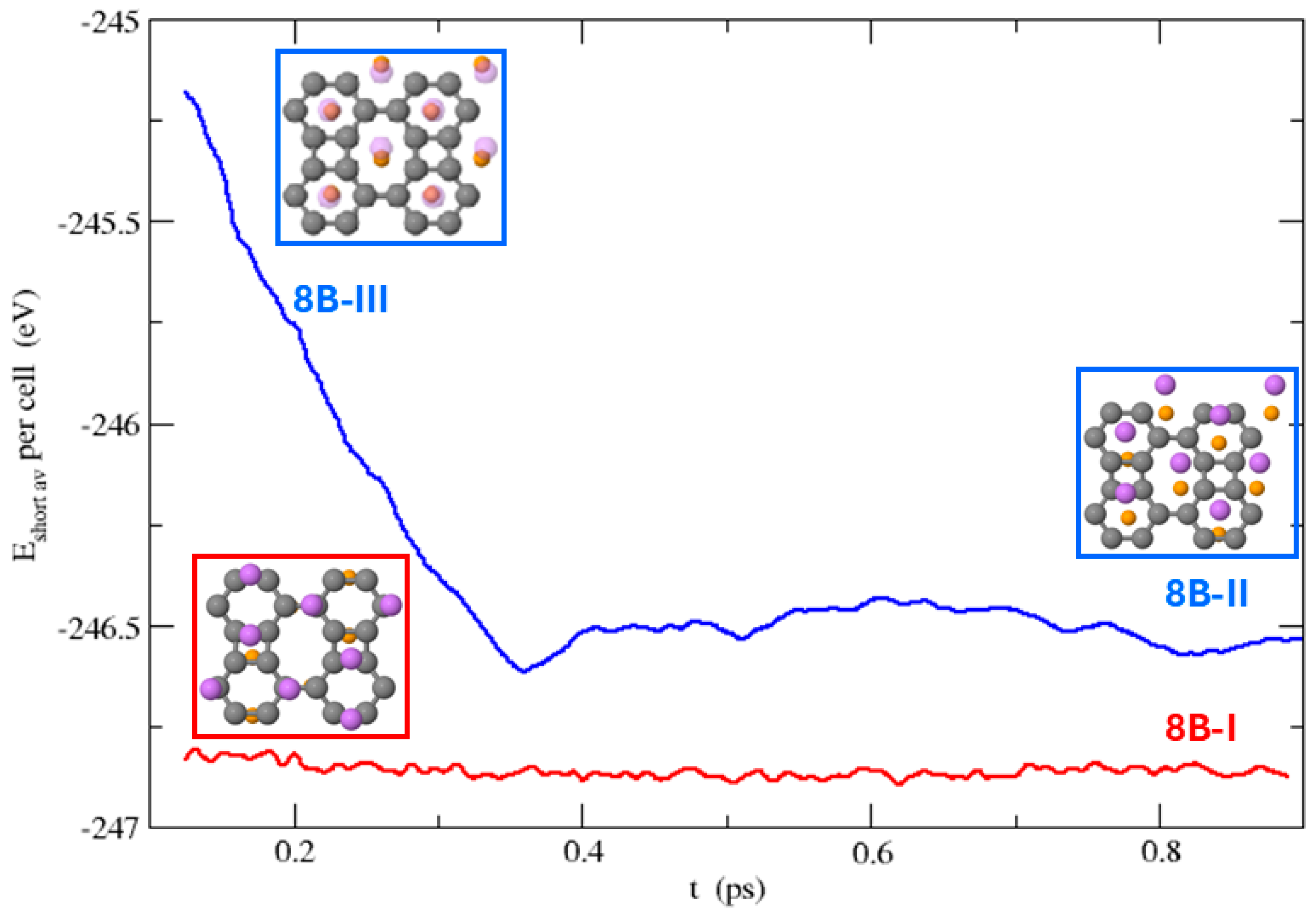
3.3. Dynamical Stability of the Structures
3.3.1. Li on One Side
3.3.2. Li on Both Sides
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Enyashin, A.N.; Ivanovskii, A.L. Graphene allotropes. Phys. Stat. Solidi B 2011, 248, 1879–1883. [Google Scholar] [CrossRef]
- Xu, L.-C.; Wang, R.-Z.; Miao, M.-S.; Wei, X.-L.; Chen, Y.-P.; Yan, H.; Lau, W.-M.; Liu, L.-M.; Ma, Y.-M. Two dimensional Dirac carbon allotropes from graphene. Nanoscale 2014, 6, 1113. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-graphene: A new carbon allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhou, X.-F.; Zhang, X.; Zhu, Q.; Dong, H.; Zhao, M.; Oganov, A.R. Phagraphene: A Low-Energy Graphene Allotrope Composed of 5–6–7 Carbon Rings with Distorted Dirac Cones. Nano Lett. 2015, 15, 6182–6186. [Google Scholar] [CrossRef]
- Li, X.; Wang, Q.; Jena, P. ψ-Graphene: A New Metallic Allotrope of Planar Carbon with Potential Applications as Anode Materials for Lithium-Ion Batteries. J. Phys. Chem. Lett. 2017, 8, 3234–3241. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Yang, B.; Chen, H.; Ruckenstein, E. Popgraphene: A new 2D planar carbon allotrope composed of 5-8-5 carbon rings for high-performance lithium-ion battery anodes from bottom-up programming. J. Mater. Chem. A 2018, 6, 6815–6821. [Google Scholar] [CrossRef]
- Zhuo, Z.; Wu, X.; Yang, J. Me-graphene: A graphene allotrope with near zero Poisson’s ratio, sizeable band gap, and high carrier mobility. Nanoscale 2020, 12, 19359. [Google Scholar] [CrossRef]
- Balaban, A.; Rentia, C.C.; Ciupitu, E. Chemical graphs. VI. Estimation of relative stability of several planar and tridimensional lattices for elementary carbon. Rev. Roum. De Chim. 1968, 13, 231. [Google Scholar]
- Hudspeth, M.A.; Whitman, B.W.; Barone, V.; Peralta, J.E. Electronic properties of the biphenylene sheet and its one-dimensional derivatives. ACS Nano 2010, 4, 4565–4570. [Google Scholar] [CrossRef]
- Wang, X.Q.; Li, H.D.; Wang, J.T. Prediction of a new two dimensional metallic carbon allotrope. Phys. Chem. Chem. Phys. 2013, 15, 2024–2030. [Google Scholar] [CrossRef]
- Denis, P.A. Stability and Electronic Properties of Biphenylene Based Functionalized Nanoribbons and Sheets. J. Phys. Chem. C 2014, 118, 24976–24982. [Google Scholar] [CrossRef]
- Rahaman, O.; Mortazavi, B.; Dianat, A.; Cuniberti, G.; Rabczuk, T. Metamorphosis in carbon network: From penta-graphene to biphenylene under uniaxial tension. FlatChem 2017, 1, 65–73. [Google Scholar] [CrossRef]
- Shahrokhi, M.; Mortazavi, B.; Berdiyorov, G.R. New two dimensional boron nitride allotropes with attractive electronic and optical properties. Solid State Commun. 2017, 253, 51–56. [Google Scholar] [CrossRef]
- He, C.; Wang, W. 2D Octagon-Structure Carbon and Its Polarization Resolved Raman Spectra. Nanomaterials 2020, 10, 2252. [Google Scholar] [CrossRef]
- Fan, Q.; Yan, L.; Tripp, M.W.; Krejcí, O.; Dimosthenous, S.; Kachel1, S.R.; Chen, M.; Foster, A.S.; Koert, U.; Liljeroth, P.; et al. Biphenylene network: A nonbenzenoid carbon allotrope. Science 2021, 372, 852–856. [Google Scholar] [CrossRef] [PubMed]
- Schlütter, F.; Nishiuchi, T.; Enkelmann, V.; Müllen, K. Octafunctionalized Biphenylenes: Molecular Precursors for Isomeric Graphene Nanostructures. Angew. Chem. Int. Ed. 2014, 53, 1538–1542. [Google Scholar] [CrossRef]
- Luo, Y.; Ren, C.; Xu, Y.; Yu, J.; Wang, S.; Sun, M. A first principles investigation on the structural, mechanical, electronic, and catalytic properties of biphenylene. Sci. Rep. 2021, 11, 19008. [Google Scholar] [CrossRef] [PubMed]
- Veeravenkata, H.P.; Jain, A. Density functional theory driven phononic thermal conductivity prediction of biphenylene: A comparison with graphene. Carbon 2021, 183, 893–898. [Google Scholar] [CrossRef]
- Liu, P.F.; Li, J.; Zhang, C.; Tu, X.-H.; Zhang, J.; Zhang, P.; Wang, B.-T.; Singh, D.J. Type-II Dirac cones and electron-phonon interaction in monolayer biphenylene from first-principles calculations. Phys. Rev. B 2021, 104, 235422. [Google Scholar] [CrossRef]
- Zhang, P.; Ouyang, T.; Tang, C.; He, C.; Li, J.; Zhang, C.; Hu, M.; Zhong, J. The intrinsic thermal transport properties of the biphenylene network and the influence of hydrogenation: A first-principles study. J. Mater. Chem. C 2021, 9, 16945–16951. [Google Scholar] [CrossRef]
- Son, Y.W.; Jin, H.; Kim, S. Magnetic Ordering, Anomalous Lifshitz Transition, and Topological Grain Boundaries in Two-Dimensional Biphenylene Network. Nano Lett. 2022, 22, 3112–3117. [Google Scholar] [CrossRef]
- Rublev, P.; Tkachenko, N.V.; Boldyrev, A.I. Overlapping electron density and the global delocalization of π-aromatic fragments as the reason of conductivity of the biphenylene network. J. Comput. Chem. 2022, 1, 26854. [Google Scholar] [CrossRef]
- Pereira Junior, M.L.; da Cunha, W.F.; de Sousa Junior, R.T.; Amvame Nze, G.D.; Galvão, D.S.; Ribeiro Junior, L.A. On the mechanical properties and fracture patterns of the nonbenzenoid carbon allotrope (biphenylene network): A reactive molecular dynamics study. Nanoscale 2022, 14, 3200–3211. [Google Scholar] [CrossRef] [PubMed]
- Mortazavi, B.; Shapeev, A.V. Anisotropic mechanical response, high negative thermal expansion, and outstanding dynamical stability of biphenylene monolayer revealed by machine-learning interatomic potentials. FlatChem 2022, 32, 100347. [Google Scholar] [CrossRef]
- Yinga, P.; Liang, T.; Dua, Y.; Zhanga, J.; Zeng, X.; Zhonga, Z. Thermal transport in planar sp2-hybridized carbon allotropes: A comparative study of biphenylene network, pentaheptite and graphene. Int. J. Heat Mass Transf. 2022, 183, 122060. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, J.; Liu, G.; Wan, X.G. Extraordinary negative thermal expansion of monolayer biphenylene. Carbon 2022, 187, 349–353. [Google Scholar] [CrossRef]
- Wang, K.; Ren, K.; Zhang, D.B.; Cheng, Y.; Zhang, G. Phonon properties of biphenylene monolayer by first-principles calculations. Appl. Phys. Lett. 2022, 121, 042203. [Google Scholar] [CrossRef]
- Mashhadzadeh, A.H.; Dehaghani, M.Z.; Molaie, F.; Fooladapanjeh, S.; Farzadian, O.; Spitas, C. A theoretical insight into the mechanical properties and phonon thermal conductivity of biphenylene network structure. Comput. Mater. Sci. 2022, 214, 111761. [Google Scholar] [CrossRef]
- Demirci, S.; Çallıoğlu, Ş.; Gorkan, T.; Aktürk, E.; Ciraci, S. Stability and electronic properties of monolayer and multilayer structures of group-IV elements and compounds of complementary groups in biphenylene network. Phys. Rev. B 2022, 105, 035408. [Google Scholar] [CrossRef]
- Obeid, M.M.; Sun, Q. Assembling biphenylene into 3D porous metallic carbon allotrope for promising anode of lithium-ion batteries. Carbon 2022, 188, 95–103. [Google Scholar] [CrossRef]
- Cabria, I.; López, M.J.; Alonso, J.A. Enhancement of hydrogen physisorption on graphene and carbon nanotubes by Li doping. J. Chem. Phys. 2005, 123, 204721. [Google Scholar] [CrossRef] [PubMed]
- Dimitrakakis, G.K.; Tylianakis, E.; Froudakis, G.E. Pillared graphene: A new3-D network nanostructure for enhanced hydrogen storage. Nano Lett. 2008, 8, 3166–3170. [Google Scholar] [CrossRef]
- Ozturk, Z.; Baykasoglu, C.; Kirca, M. Sandwiched graphene-fullerene composite: A novel 3-D nanostructured material for hydrogen storage. Int. J. Hydrogen Energy 2016, 41, 6403–6411. [Google Scholar] [CrossRef]
- Álvarez-Zapatero, P.; Herrero, A.; Lebon, A.; Gallego, L.J.; Vega, A. Ab initio study of lithium decoration of popgraphene and hydrogen storage capacity of the hybrid nanostructure. Int. J. Hydrogen Energy 2021, 46, 15724–15737. [Google Scholar] [CrossRef]
- Chen, H.J.; Autès, G.; Alem, N.; Gargiulo, F.; Gautam, A.; Linck, M.; Kisielowski, C.; Yazyev, O.V.; Louie, S.G.; Zettl, A. Controlled growth of a line defect in graphene and implications for gate-tunable valley filtering. Phys. Rev. B 2014, 89, 121407. [Google Scholar] [CrossRef]
- Filho, M.A.M.; Farmer, W.; Hsiao, C.-L.; Batista dos Santos, R.; Hultman, L.; Birch, J.; Ankit, K.; Gueorguiev, G.K. Density Functional Theory-Fed Phase Field Model for Semiconductor Nanostructures: The Case of Self-Induced Core–Shell InAlN Nanorods. Cryst. Growth Des. 2024, 24, 4717–4727. [Google Scholar] [CrossRef]
- Chen, H.-T.; Dhanthala, D.K.D. A new carbon allotrope: Biphenylene as promising anode material for Li-ion and Li-O2 batteries. Solid State Ion. 2023, 395, 116214. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigt, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456. [Google Scholar] [CrossRef]
- Shepard, R.; Shepard, S.; Smeu, M. Ab initio investigation into the physisorption of noble gases on graphene. Surf. Sci. 2019, 682, 38. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved adorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhop functionals. Phys. Rev. B 1999, 59, 7413. [Google Scholar] [CrossRef]
- Ullah, S.; Denis, P.A.; Sato, F. Hexagonal boron phosphide as a potential anode nominee for alkali-based batteries: A multi-flavor DFT study. Appl. Surf. Sci. 2019, 471, 134. [Google Scholar] [CrossRef]
- Thinus, S.; Islam, M.M.; Heitjans, P.; Bredow, T. Theoretical Study of Li Migration in Lithium-Graphite Intercalation Compounds with Dispersion-Corrected DFT Methods. J. Phys. Chem. C 2014, 118, 2273. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef]
- Popelier, P.L.A. Atoms in Molecules: An Introduction; Prentice Hall: London, UK, 2000. [Google Scholar]
- Matta, C.F. Hydrogen-Hydrogen Bonding: The Non-Electrostatic Limit of Closed-Shell Interaction Between two Hydrogen Atoms; A Critical Review; Springer: Dordrecht, The Netherlands, 2006; p. 337. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Rega, G.A.; Petersson, H.; Nakatsuji, M.; et al. Gaussian 16 Revision C.01, Gaussian Inc.: Wallingford, CT, USA, 2016.
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular-systems. J. Chem. Phys. 1990, 92, 5397. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683. [Google Scholar] [CrossRef]
- Lebon, A.; Orain, P.-Y.; Memboeuf, A. Understanding the CO dissociation in [Fe(CN)2(CO)2(dithiolate)]2− Complexes with Quantum Chemical Topology Tools. J. Phys. Chem. A 2017, 127, 7031. [Google Scholar] [CrossRef]
- Kohout, M. DGrid, Version 5.1; Gaussian, Inc.: Dresden, Germany, 2019.
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597. [Google Scholar] [CrossRef]
- Liu, T.; Jing, Y.; Li, Y. Two-dimensional Biphenylene: A graphene allotrope with superior activity toward electrochemical oxygen reduction reaction. J. Phys. Chem. Lett. 2021, 12, 12230–12234. [Google Scholar] [CrossRef] [PubMed]
- Averill, F.W. Calculation of the cohesive energies and bulk properties of the alkali metals. Phys. Rev. B 1972, 6, 3637–3642. [Google Scholar] [CrossRef]
- Chan, K.T.; Neaton, J.B.; Cohen, M.L. First-principles study of metal adatom adsorption on graphene. Phys. Rev. B 2008, 77, 235430. [Google Scholar] [CrossRef]
- Henkelman, G.; Jonsson, H. Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points. J. Chem. Phys. 2000, 113, 9978–9985. [Google Scholar] [CrossRef]

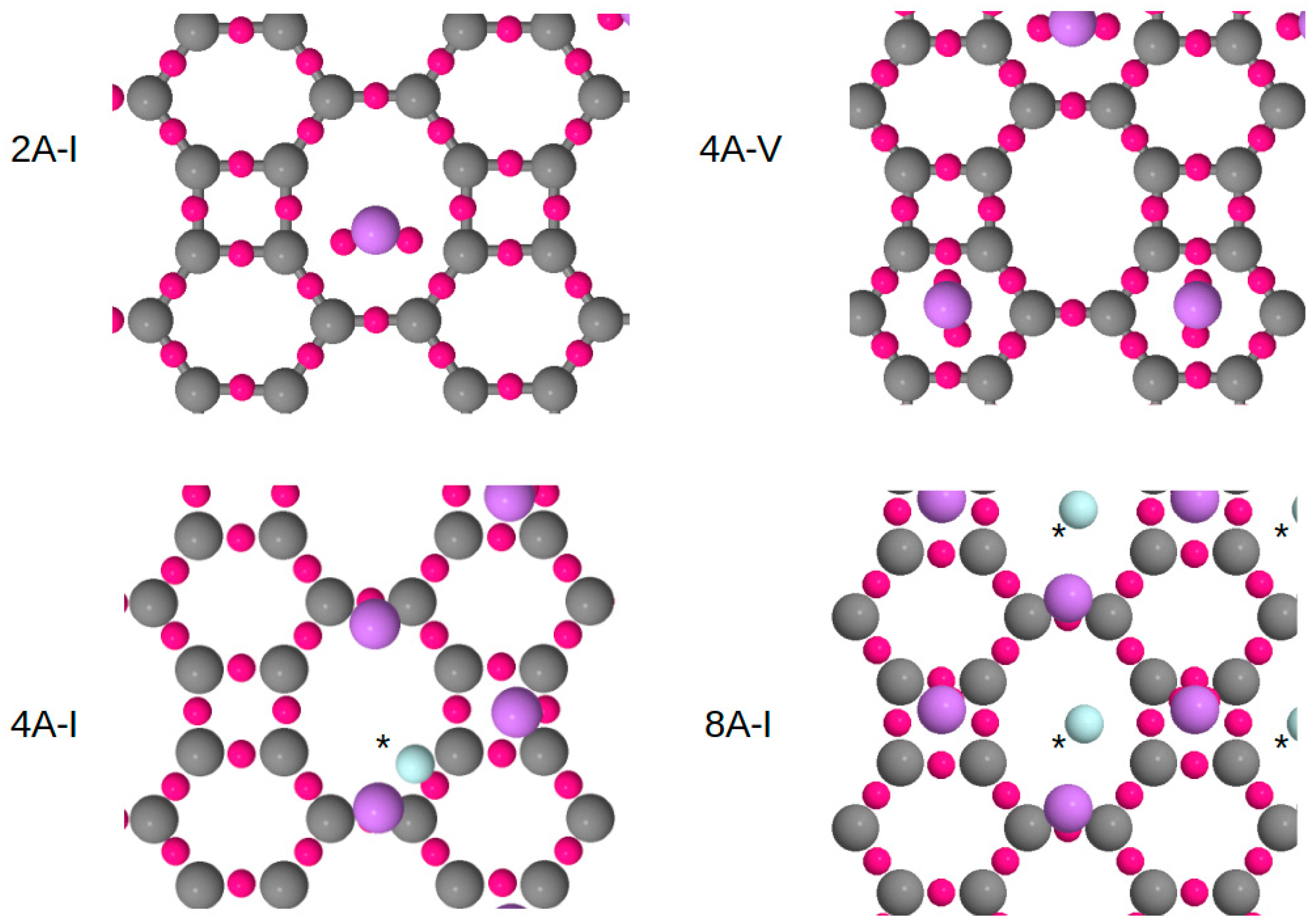
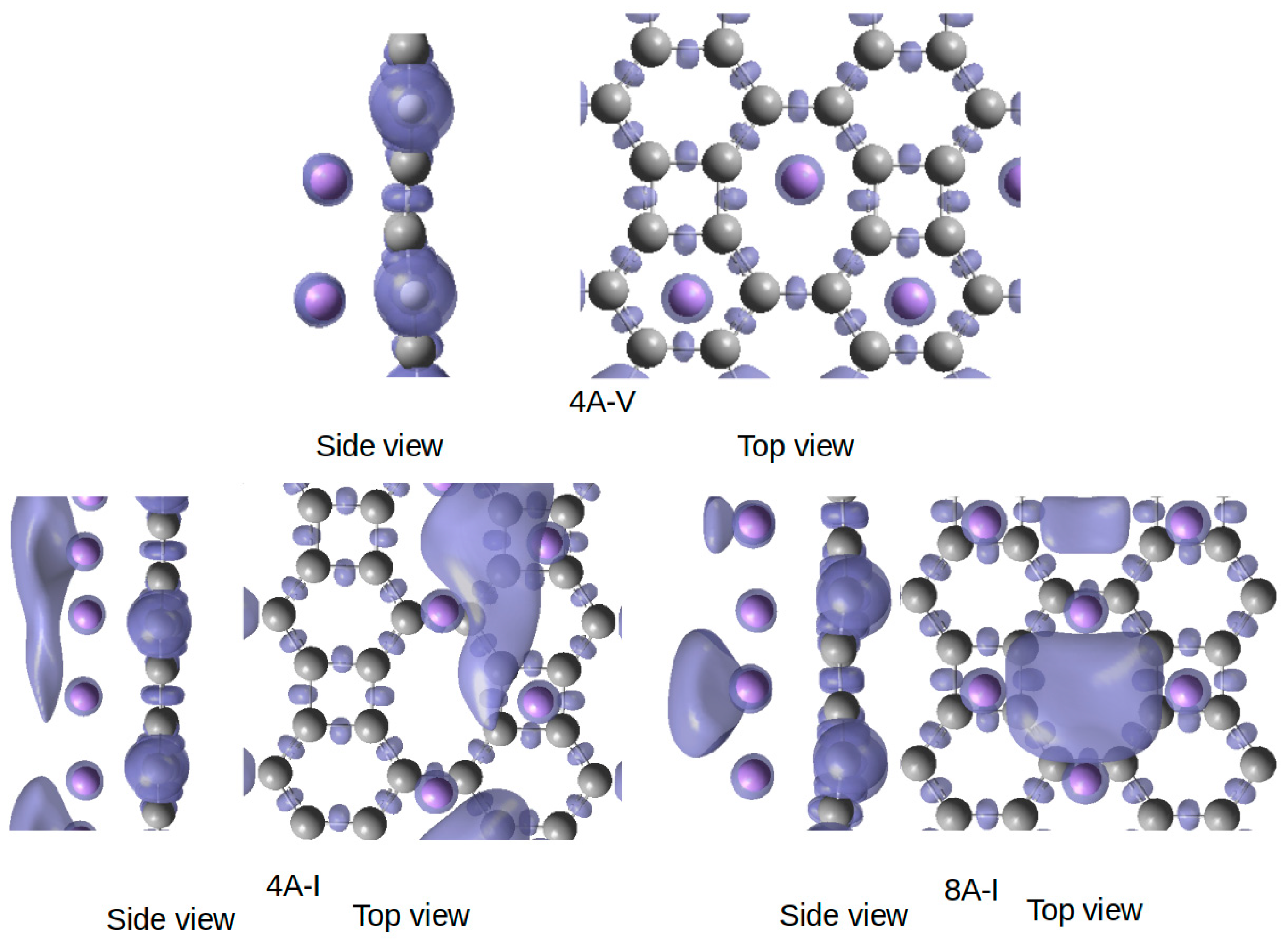

| Li-C | Li-Li | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Square | Hexagon | Octagon | ||||||||||
| 2A-I | -- | -- | 19.7 | 4.7 | 111.0 | |||||||
| (0.97) | ||||||||||||
| 4A-V | -- | 19.7 | 3.7 | 98.0 | 16.8 | 4.7 | 85.0 | -- | ||||
| (1.17) | (1.07) | |||||||||||
| 4A-I | 21.0 | 5.0 | 135.0 | -- | 19.5 | 5.5 | 135.0 | 8.0 | −0.8 | 4.3 | ||
| (1.21) | (1.23) | (2.03) | ||||||||||
| 8A-I | 19.4 | 4.0 | 107.5 | -- | 21.3 | 5.3 | 121.0 | 7.2 | −0.8 | 0.0 | ||
| (1.23) | (1.22) | (2.20) | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres, M.B.; Lebon, A.; González, L.E.; Gallego, L.J.; Vega, A. Ab Initio Study of the Structures, Bonding Interactions, and Thermal Stability of the Li-Decorated 2D Biphenylene Sheet. Nanomaterials 2025, 15, 700. https://doi.org/10.3390/nano15090700
Torres MB, Lebon A, González LE, Gallego LJ, Vega A. Ab Initio Study of the Structures, Bonding Interactions, and Thermal Stability of the Li-Decorated 2D Biphenylene Sheet. Nanomaterials. 2025; 15(9):700. https://doi.org/10.3390/nano15090700
Chicago/Turabian StyleTorres, María Begoña, Alexandre Lebon, Luis Enrique González, Luis Javier Gallego, and Andrés Vega. 2025. "Ab Initio Study of the Structures, Bonding Interactions, and Thermal Stability of the Li-Decorated 2D Biphenylene Sheet" Nanomaterials 15, no. 9: 700. https://doi.org/10.3390/nano15090700
APA StyleTorres, M. B., Lebon, A., González, L. E., Gallego, L. J., & Vega, A. (2025). Ab Initio Study of the Structures, Bonding Interactions, and Thermal Stability of the Li-Decorated 2D Biphenylene Sheet. Nanomaterials, 15(9), 700. https://doi.org/10.3390/nano15090700







