Entropy Best Poster Awards at the 39th Workshop on Bayesian Methods and Maximum Entropy Methods in Science and Engineering (MaxEnt 2019)
We are pleased to announce the winners of the two poster awards sponsored by Entropy at the 39th Workshop on Bayesian Methods and Maximum Entropy Methods in Science and Engineering (MaxEnt 2019) held in Garching/Munich (Germany) on 30 June to 5 July 2019.
1st prize (300 CHF, certificate)
"Nested Sampling for Atomic Physics Data: The Nested_Fit Program" by Martino Trassinelli
Nested_fit is a general-purpose data analysis code [1] written in Fortran and Python. It is based on the nested sampling algorithm with the implementation of the lawn mower robot method for finding new live points. The program has been especially designed for the analysis of atomic spectra where different numbers of peaks and line shapes have to be determined. For a given dataset and chosen model, the program provides the Bayesian evidence method for the comparison of different hypotheses/models and the different parameter probability distributions. To give a concrete illustration of applications, we consider a spectrum of examples: i) determination of the potential presence of non-resolved satellite peaks in a high-resolution X-ray spectrum of pionic atoms [2] and in a photoemission spectrum of gold nanodots [3], ii) the analysis of very low-statistics spectra in a high-resolution X-ray spectrum of He-like uranium (see figure) [1] and in a photoemission spectrum of carbon nanodots [4]. In cases where the number of components cannot be clearly identified, as for the He-like U case, we show how the main component position can nevertheless be determined from the probability distributions relative to the single models.
[1] M. Trassinelli. Nucl. Instrum. Methods B 2017, 408, 301.
[2] M. Trassinelli et al. Phys. Lett. B 2016, 759, 583–588.
[3] A. Lévy et al. submitted to Langmuir.
[4] I. Papagiannouli et al. J. Phys. Chem. C 2018, 122, 14889.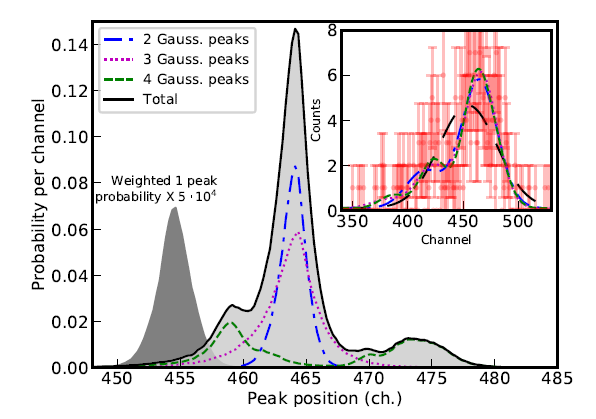

2nd prize (200 CHF, certificate)
“A Sequential Marginal Likelihood Approximation Using Stochastic Gradients” by Scott Cameron
Existing algorithms such as nested sampling and annealed importance sampling are able to produce accurate estimates of the marginal likelihood of a model, but tend to scale poorly to large datasets. This is because these algorithms need to recalculate the log-likelihood for each iteration by summing over the whole dataset. Efficient scaling to large datasets requires that algorithms only visit small subsets (mini-batches) of data on each iteration. To this end, we estimated the marginal likelihood via a sequential decomposition into a product of predictive distributions $p(y_n|y_{<n})$. Predictive distributions could be approximated efficiently through Bayesian updating using stochastic gradient Hamiltonian Monte Carlo, which approximates likelihood gradients using mini-batches. Since each datapoint typically contains little information compared to the whole dataset, the convergence to each successive posterior only requires a short burn-in phase. This approach can be viewed as a special case of sequential Monte Carlo (SMC) with a single particle, but it differs from typical SMC methods in that it uses stochastic gradients. We illustrate how this approach scales favorably to large datasets using some simple models.
