A Bayesian Model to Forecast the Time Series Kinetic Energy Data for a Power System
Abstract
:1. Introduction
- (a)
- A Bayesian model used to forecast the univariate time series data of kinetic energy is presented. One year of data for the kinetic energy of the INPS are used to forecast for the next 30 min of data. The results of the presented model are evaluated with other performance metrics and are found to within acceptable limits. Further, the results are cross-checked with the results of the ARIMA model.
- (b)
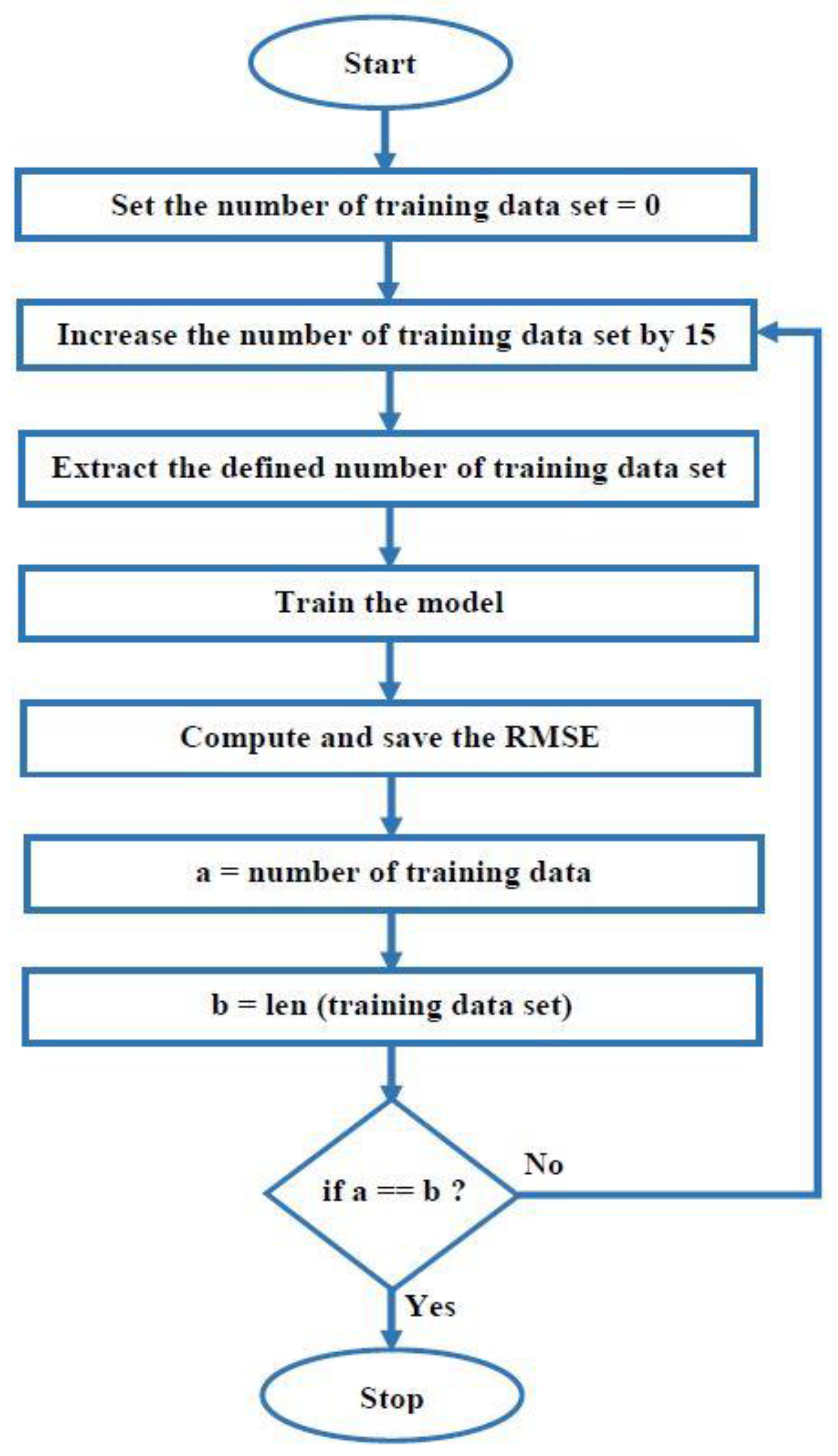
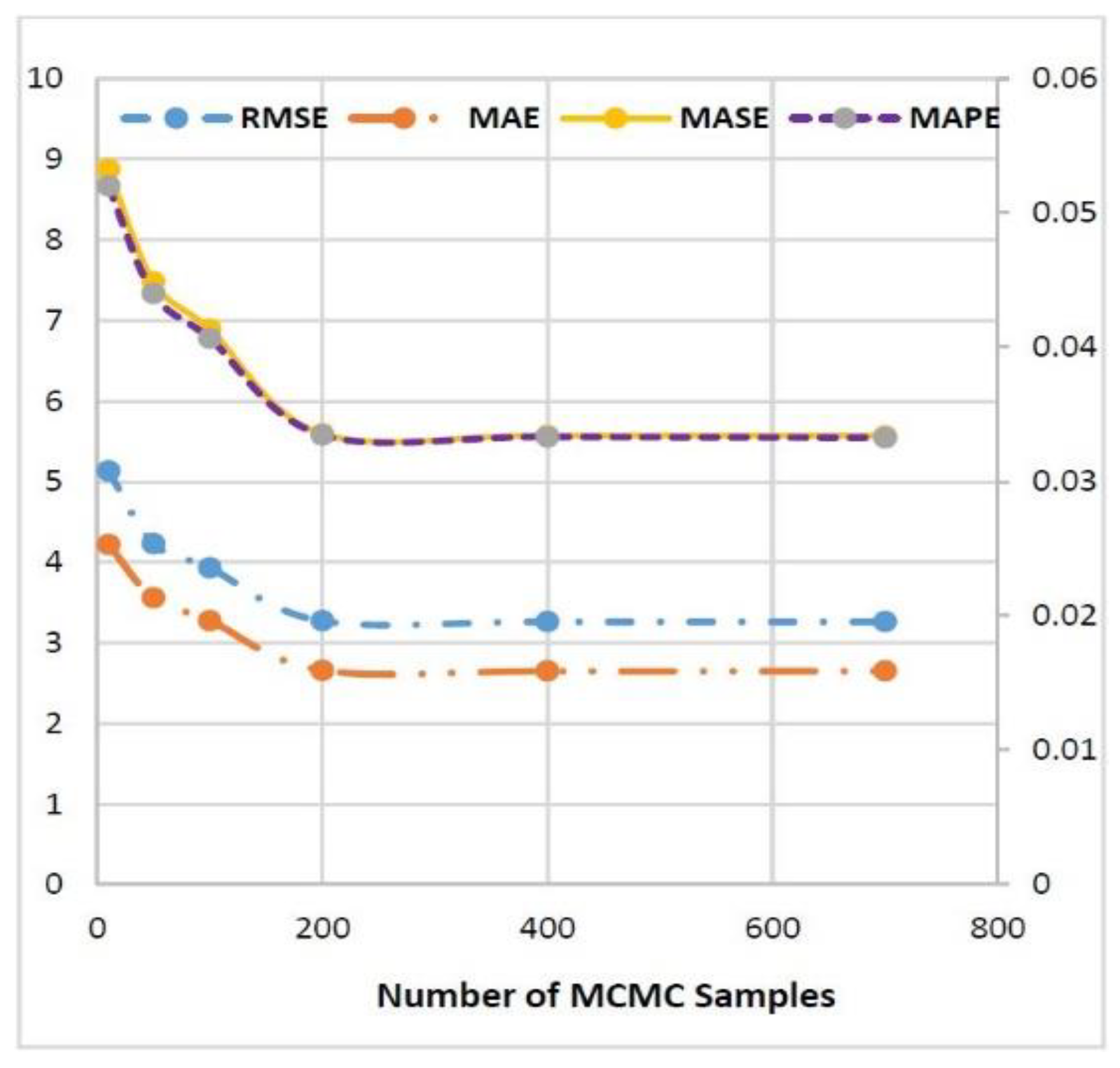
- The optimum training dataset size required to forecast 30-min values of the kinetic energy via an optimization technique is identified. There may be a considerable number of historical data, and this will result in a greater computational time if all of the data are used in the forecasting process. It is also very important to obtain results as quickly as possible, since decisions (i.e., control actions) must be made at the right time. Hence, determining the optimal training dataset size could be significant in terms of optimizing the required computational time and memory.
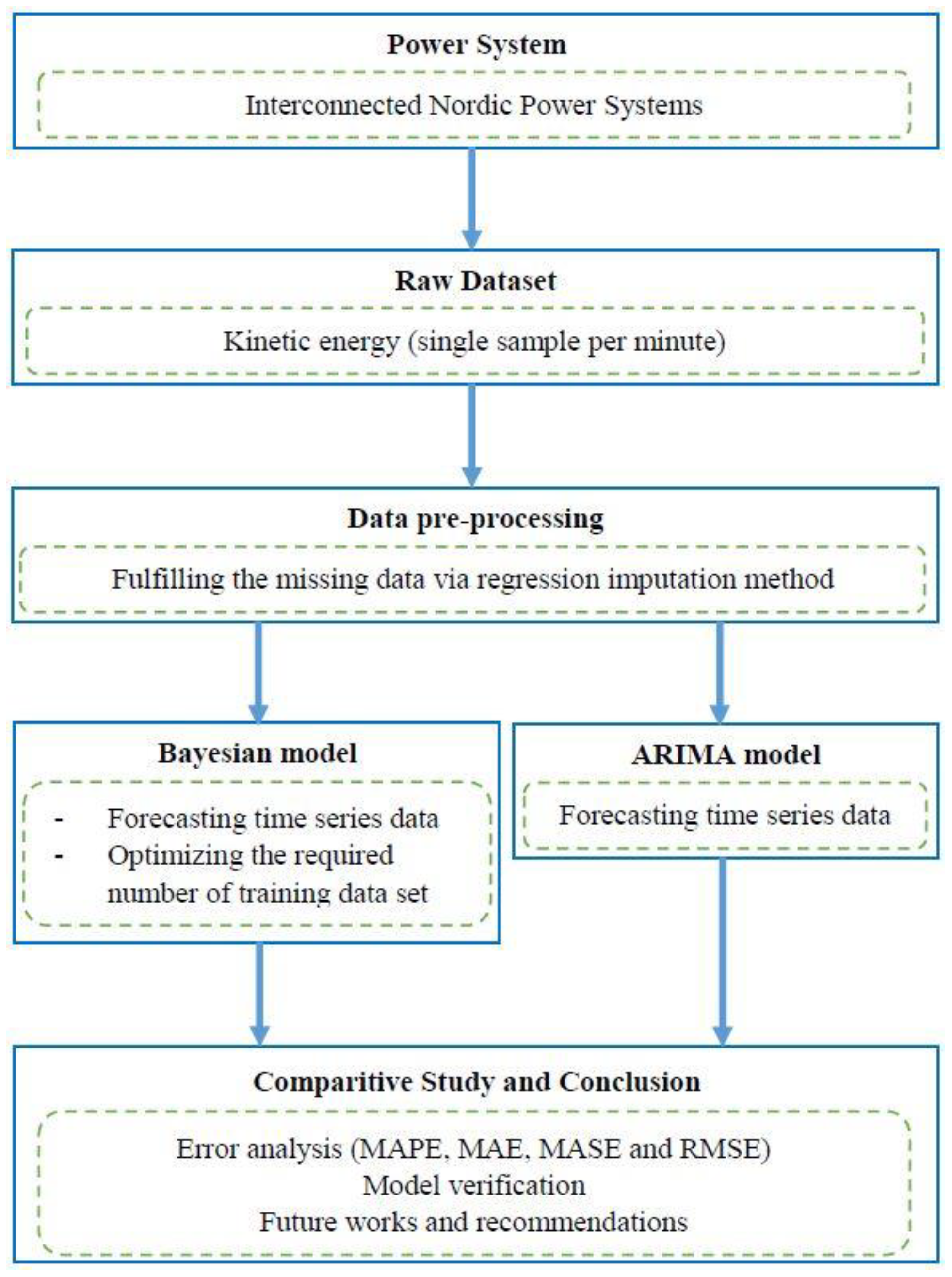
2. Methodology
2.1. Data Types and Preparation
2.2. Model Selection
2.2.1. Bayesian Approach
2.2.2. ARIMA Approach
2.2.3. Optimization
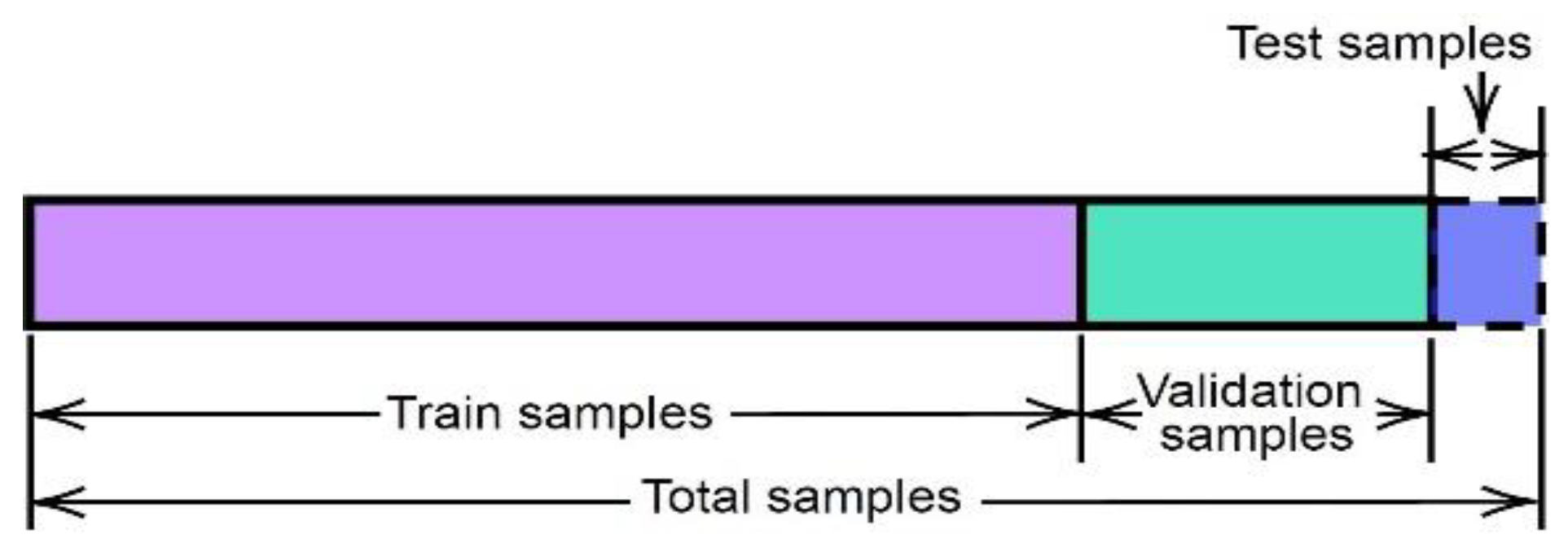
2.3. Performance Evaluation and Validation
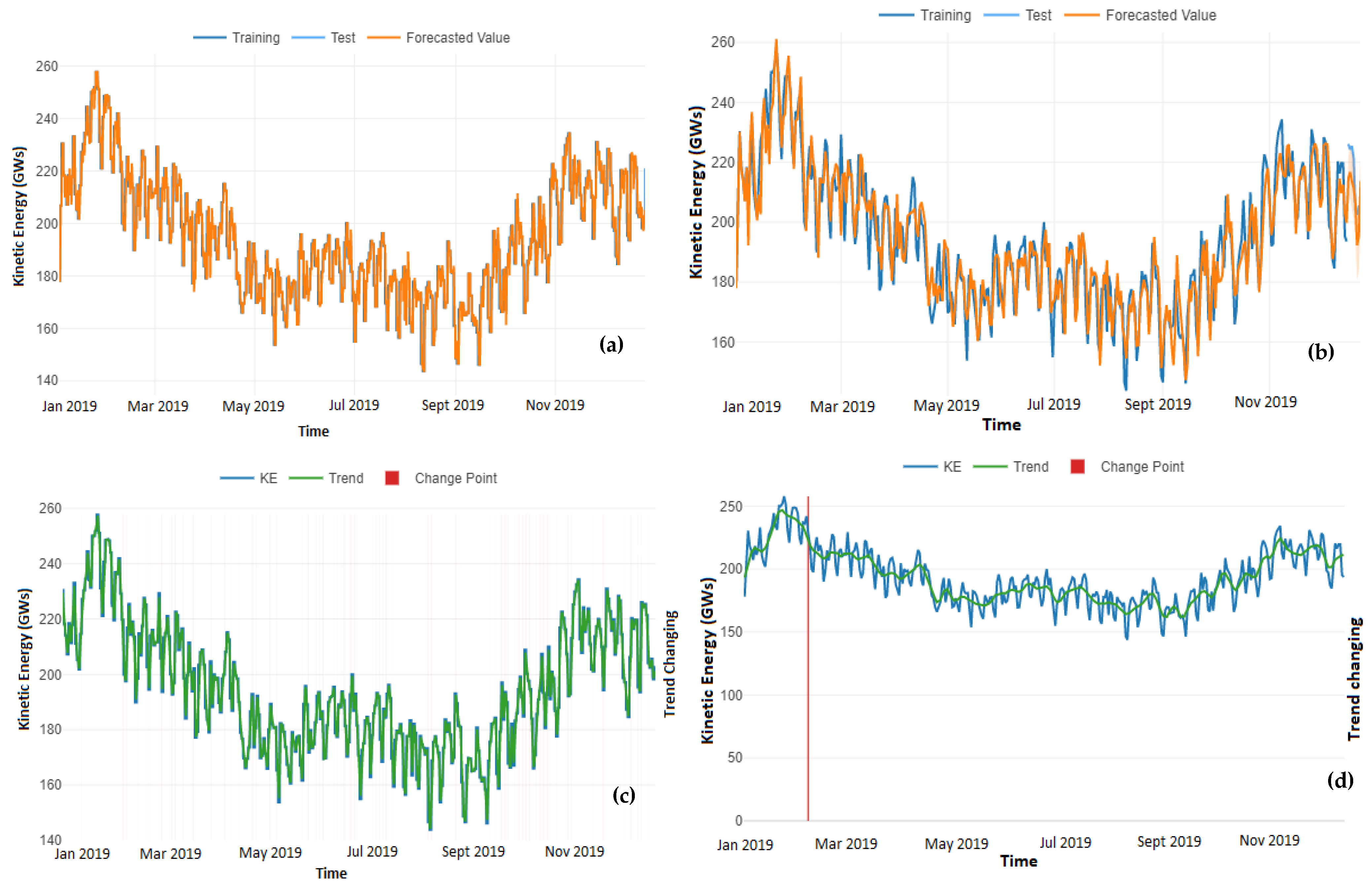
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kerdphol, T.; Rahman, F.S.; Mitani, Y. Virtual inertia control application to enhance frequency stability of interconnected power systems with high renewable energy penetration. Energies 2018, 11, 981. [Google Scholar] [CrossRef] [Green Version]
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.-M.; Hannegan, B. Achieving a 100% renewable grid: Operating electric power systems with extremely high levels of variable renewable energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Perez-Arriaga, I.J. Managing large scale penetration of intermittent renewables. In Proceedings of the MITEI Symposium on Managing Large-Scale Penetration of Intermittent Renewables, Cambridge, MA, USA, 20 April 2011; p. 2011. [Google Scholar]
- Khadka, N.; Paudel, R.; Adhikary, B.; Bista, A.; Sharma, S.; Shrestha, A. Transient Stability in Renewable Energy Penetrated Power Systems: A Review. In Proceedings of the RESSD 2020 International Conference on Role of Energy for Sustainable Social Development in ‘New Normal’ Era, Kathmandu, Nepal, 28–29 December 2020. [Google Scholar]
- Tuttelberg, K.; Kilter, J.; Wilson, D.; Uhlen, K. Estimation of power system inertia from ambient wide area measurements. IEEE Trans. Power Syst. 2018, 33, 7249–7257. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Bank, J.; Wan, Y.-H.; Muljadi, E.; Corbus, D. Synchrophasor measurement-based wind plant inertia estimation. In Proceedings of the 2013 IEEE Green Technologies Conference (GreenTech), Denver, CO, USA, 4–5 April 2013; pp. 494–499. [Google Scholar]
- Fereidouni, A.; Susanto, J.; Mancarella, P.; Hong, N.; Smit, T.; Sharafi, D. Online Security Assessment of Low-Inertia Power Systems: A Real-Time Frequency Stability Tool for the Australian South-West Interconnected System. arXiv 2020, arXiv:2010.14016. [Google Scholar]
- Schiffer, J.; Aristidou, P.; Ortega, R. Online estimation of power system inertia using dynamic regressor extension and mixing. IEEE Trans. Power Syst. 2019, 34, 4993–5001. [Google Scholar] [CrossRef] [Green Version]
- Beltran, O.; Peña, R.; Segundo, J.; Esparza, A.; Muljadi, E.; Wenzhong, D. Inertia estimation of wind power plants based on the swing equation and phasor measurement units. Appl. Sci. 2018, 8, 2413. [Google Scholar] [CrossRef] [Green Version]
- Zografos, D.; Ghandhari, M.; Eriksson, R. Power system inertia estimation: Utilization of frequency and voltage response after a disturbance. Electr. Power Syst. Res. 2018, 161, 52–60. [Google Scholar] [CrossRef]
- Zografos, D. Power System Inertia Estimation and Frequency Response Assessment; KTH Royal Institute of Technology: Stockholm, Sweden, 2019. [Google Scholar]
- Heylen, E.; Strbac, G.; Teng, F. Challenges and opportunities of inertia estimation and forecasting in low-inertia power systems. arXiv 2020, arXiv:2008.12692. [Google Scholar]
- Allella, F.; Chiodo, E.; Giannuzzi, G.M.; Lauria, D.; Mottola, F. On-line estimation assessment of power systems inertia with high penetration of renewable generation. IEEE Access 2020, 8, 62689–62697. [Google Scholar] [CrossRef]
- Cancelo, J.R.; Espasa, A.; Grafe, R. Forecasting the electricity load from one day to one week ahead for the Spanish system operator. Int. J. Forecast. 2008, 24, 588–602. [Google Scholar] [CrossRef] [Green Version]
- Amaral, L.F.; Souza, R.C.; Stevenson, M. A smooth transition periodic autoregressive (STPAR) model for short-term load forecasting. Int. J. Forecast. 2008, 24, 603–615. [Google Scholar] [CrossRef]
- Taylor, J.W. An evaluation of methods for very short-term load forecasting using minute-by-minute British data. Int. J. Forecast. 2008, 24, 645–658. [Google Scholar] [CrossRef]
- Gonzalez-Longatt, F.; Acosta, M.; Chamorro, H.; Topic, D. Short-Term Kinetic Energy Forecast using a Structural Time Series Model: Study Case of Nordic Power System. In Proceedings of the 2020 International Conference on Smart Systems and Technologies (SST), Osijek, Croatia, 14–16 October 2020; pp. 173–178. [Google Scholar]
- Harvey, A.C.; Peters, S. Estimation procedures for structural time series models. J. Forecast. 1990, 9, 89–108. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Novak, J.; McGarvie, S.; Garcia, B.E. A Bayesian model for forecasting hierarchically structured time series. arXiv 2017, arXiv:1711.04738. [Google Scholar]
- Vosseler, A.; Weber, E. Forecasting seasonal time series data: A Bayesian model averaging approach. Comput. Stat. 2018, 33, 1733–1765. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, M. Bayesian median autoregression for robust time series forecasting. Int. J. Forecast. 2021, 37, 1000–1010. [Google Scholar] [CrossRef]
- Xiao, Q.; Chaoqin, C.; Li, Z. Time series prediction using dynamic Bayesian network. Optik 2017, 135, 98–103. [Google Scholar] [CrossRef]
- Rodriguez, A.; Puggioni, G. Mixed frequency models: Bayesian approaches to estimation and prediction. Int. J. Forecast. 2010, 26, 293–311. [Google Scholar] [CrossRef]
- Steel, M.F. Bayesian time series analysis. In Macroeconometrics and Time Series Analysis; Springer: Berlin, Germany, 2010; pp. 35–45. [Google Scholar]
- Ganics, G.; Odendahl, F. Bayesian VAR forecasts, survey information, and structural change in the euro area. Int. J. Forecast. 2021, 37, 971–999. [Google Scholar] [CrossRef]
- Thompson, P.A.; Miller, R.B. Sampling the future: A Bayesian approach to forecasting from univariate time series models. J. Bus. Econ. Stat. 1986, 4, 427–436. [Google Scholar]
- Zhang, A.Y.; Lu, M.; Kong, D.; Yang, J. Bayesian Time Series Forecasting with Change Point and Anomaly Detection. In Proceedings of the Sixth International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Van der Heijden, M.; Velikova, M.; Lucas, P.J. Learning Bayesian networks for clinical time series analysis. J. Biomed. Inform. 2014, 48, 94–105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panagiotelis, A.; Smith, M. Bayesian density forecasting of intraday electricity prices using multivariate skew t distributions. Int. J. Forecast. 2008, 24, 710–727. [Google Scholar] [CrossRef]
- Carpenter, B.; Gelman, A.; Hoffman, M.D.; Lee, D.; Goodrich, B.; Betancourt, M.; Brubaker, M.A.; Guo, J.; Li, P.; Riddell, A. Stan: A probabilistic programming language. Grantee Submiss. 2017, 76, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Science & Business Media: Berlin, Germany, 2006. [Google Scholar]
- Neal, R.M. Slice sampling. Ann. Stat. 2003, 31, 705–741. [Google Scholar] [CrossRef]
- Nishio, M.; Arakawa, A. Performance of Hamiltonian Monte Carlo and No-U-Turn Sampler for estimating genetic parameters and breeding values. Genet. Sel. Evol. 2019, 51, 73. [Google Scholar] [CrossRef] [Green Version]
- Nishida, K. Introduction to Exploratory v6.0. Available online: https://exploratory.io/note/kanaugust/Online-Seminar-28-Introduction-to-Exploratory-v6-0-EdY3YOC2HC (accessed on 11 June 2020).





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shrestha, A.; Ghimire, B.; Gonzalez-Longatt, F. A Bayesian Model to Forecast the Time Series Kinetic Energy Data for a Power System. Energies 2021, 14, 3299. https://doi.org/10.3390/en14113299
Shrestha A, Ghimire B, Gonzalez-Longatt F. A Bayesian Model to Forecast the Time Series Kinetic Energy Data for a Power System. Energies. 2021; 14(11):3299. https://doi.org/10.3390/en14113299
Chicago/Turabian StyleShrestha, Ashish, Bishal Ghimire, and Francisco Gonzalez-Longatt. 2021. "A Bayesian Model to Forecast the Time Series Kinetic Energy Data for a Power System" Energies 14, no. 11: 3299. https://doi.org/10.3390/en14113299







