Analytical Solutions of (2+Time Fractional Order) Dimensional Physical Models, Using Modified Decomposition Method
Abstract
1. Introduction
2. Preliminaries Concepts
3. Implementation of Shehu Transform
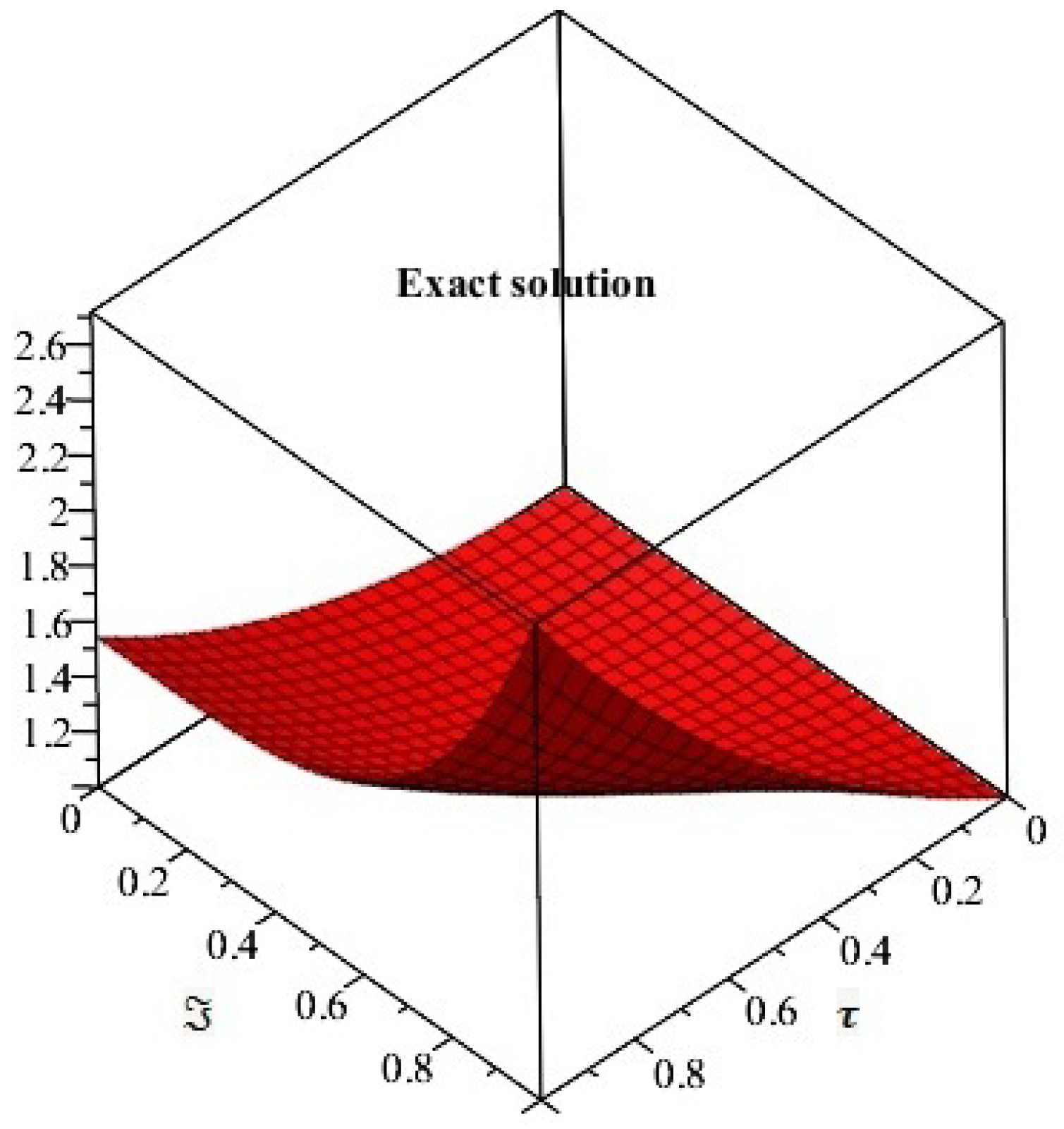
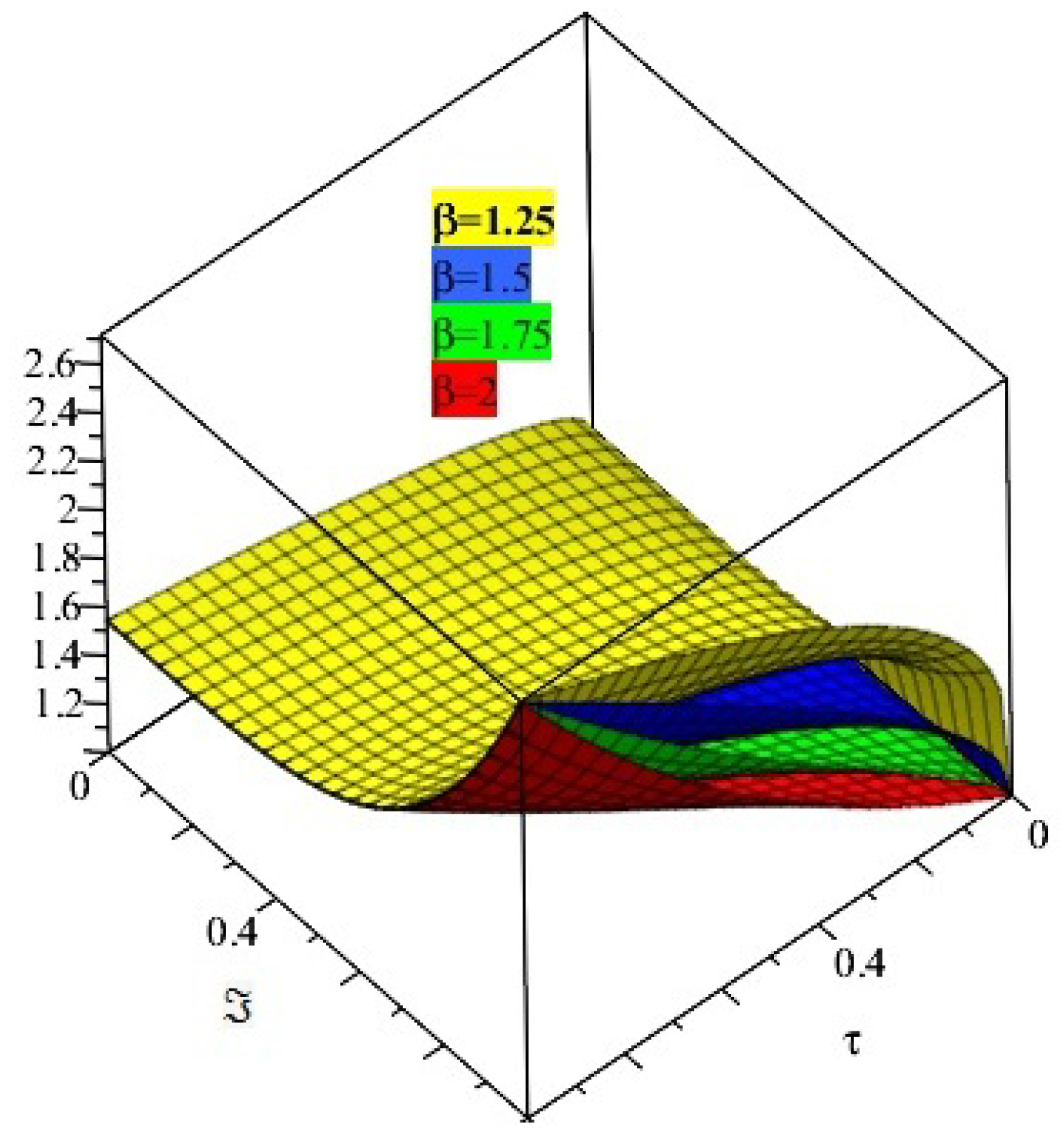
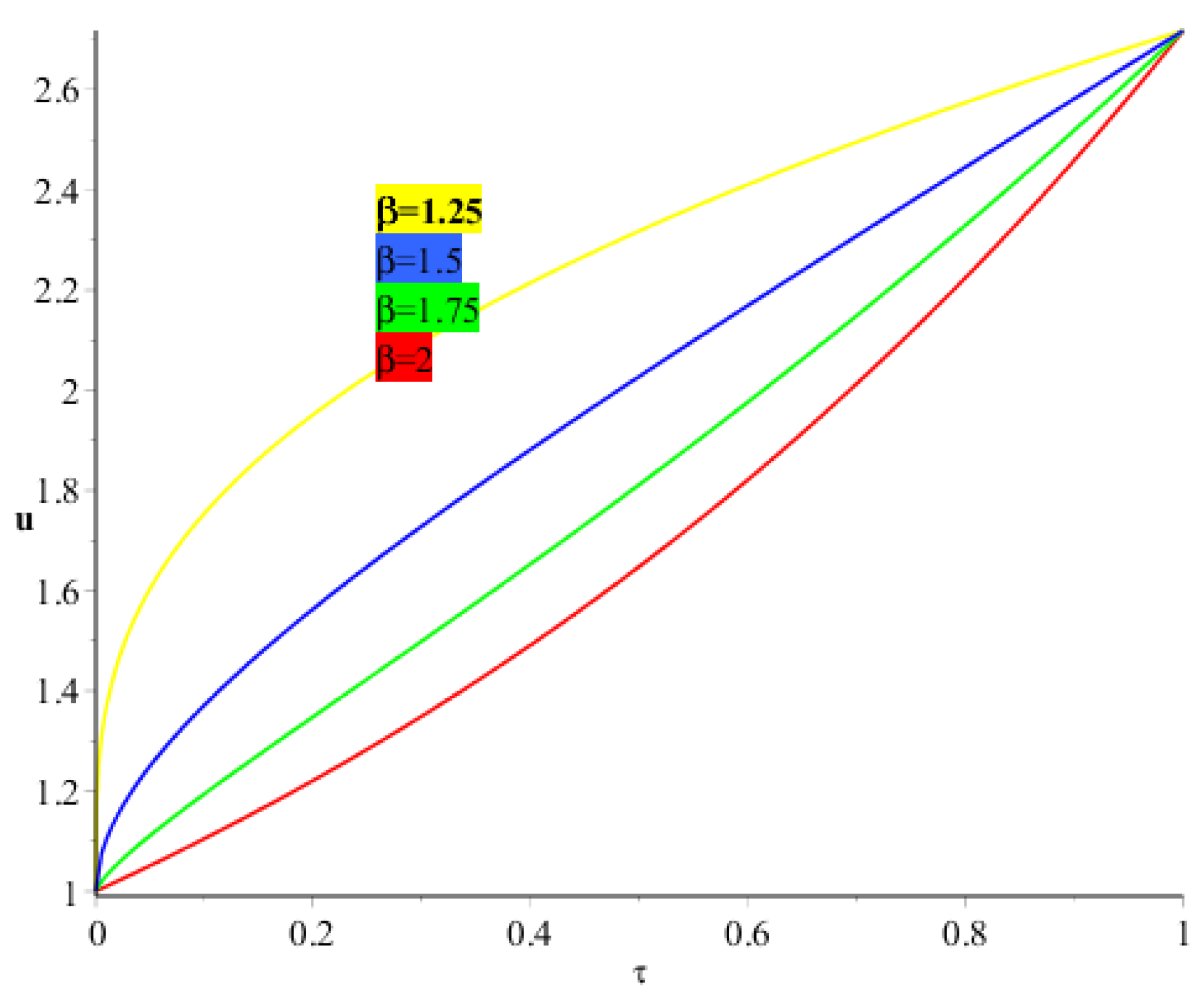
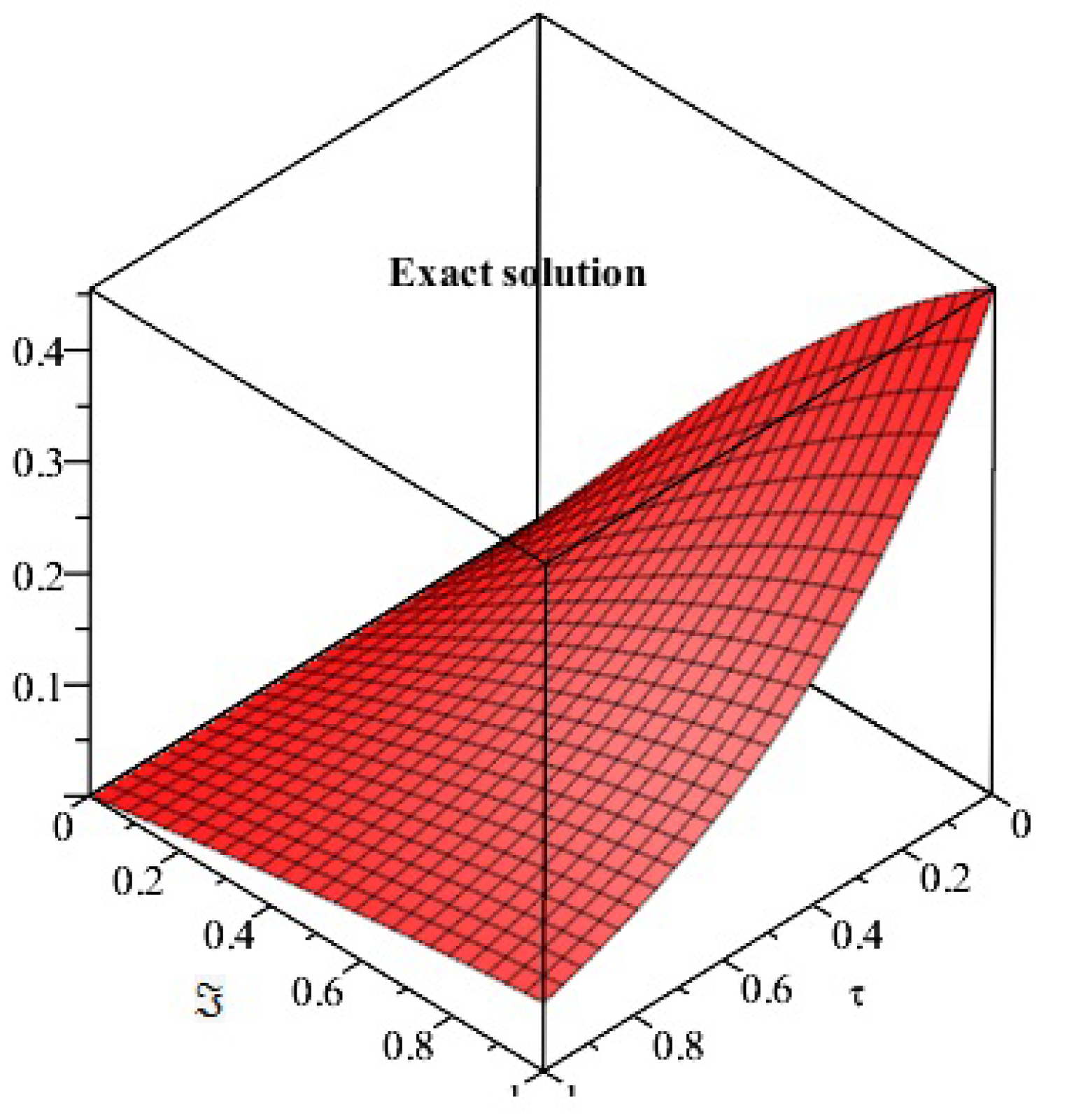
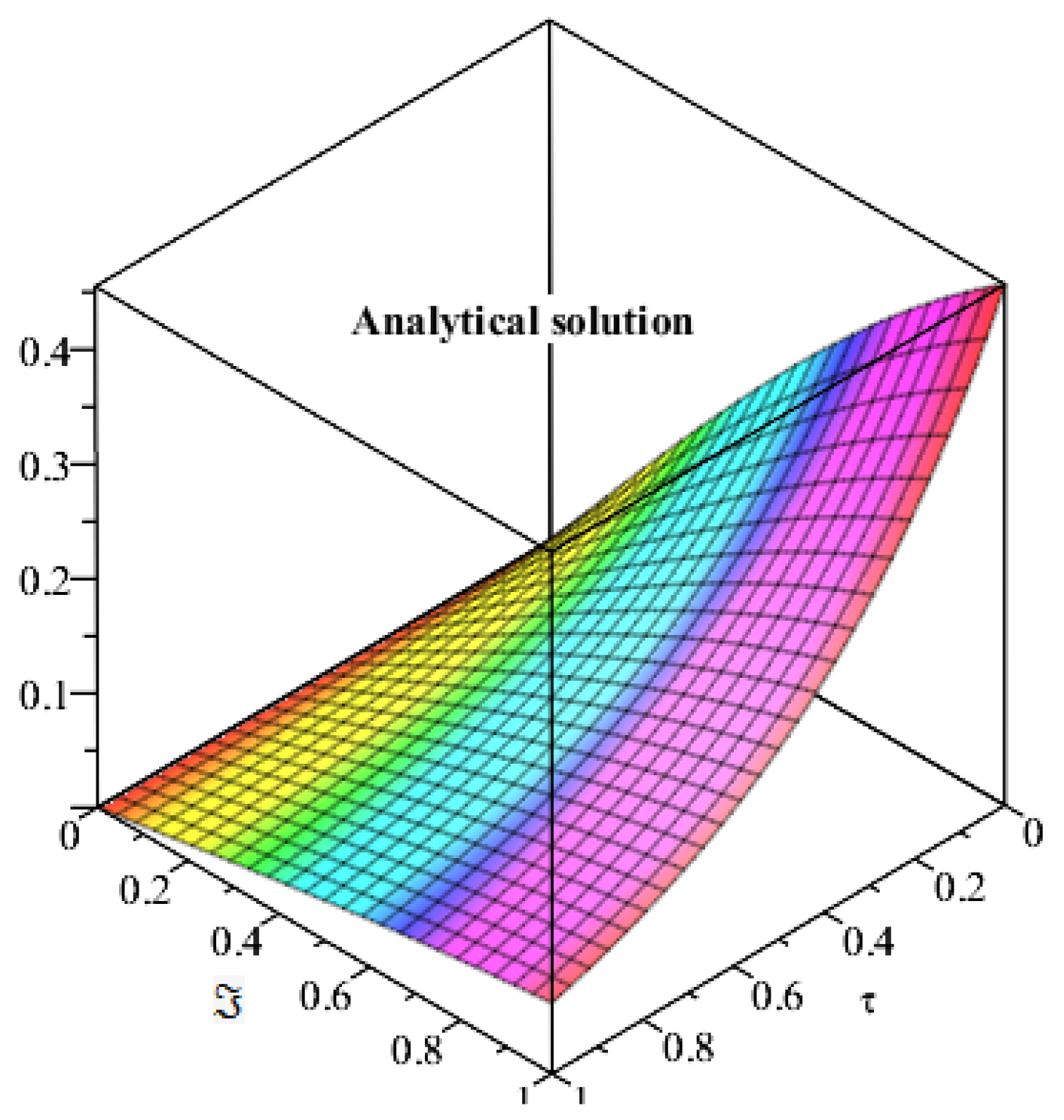
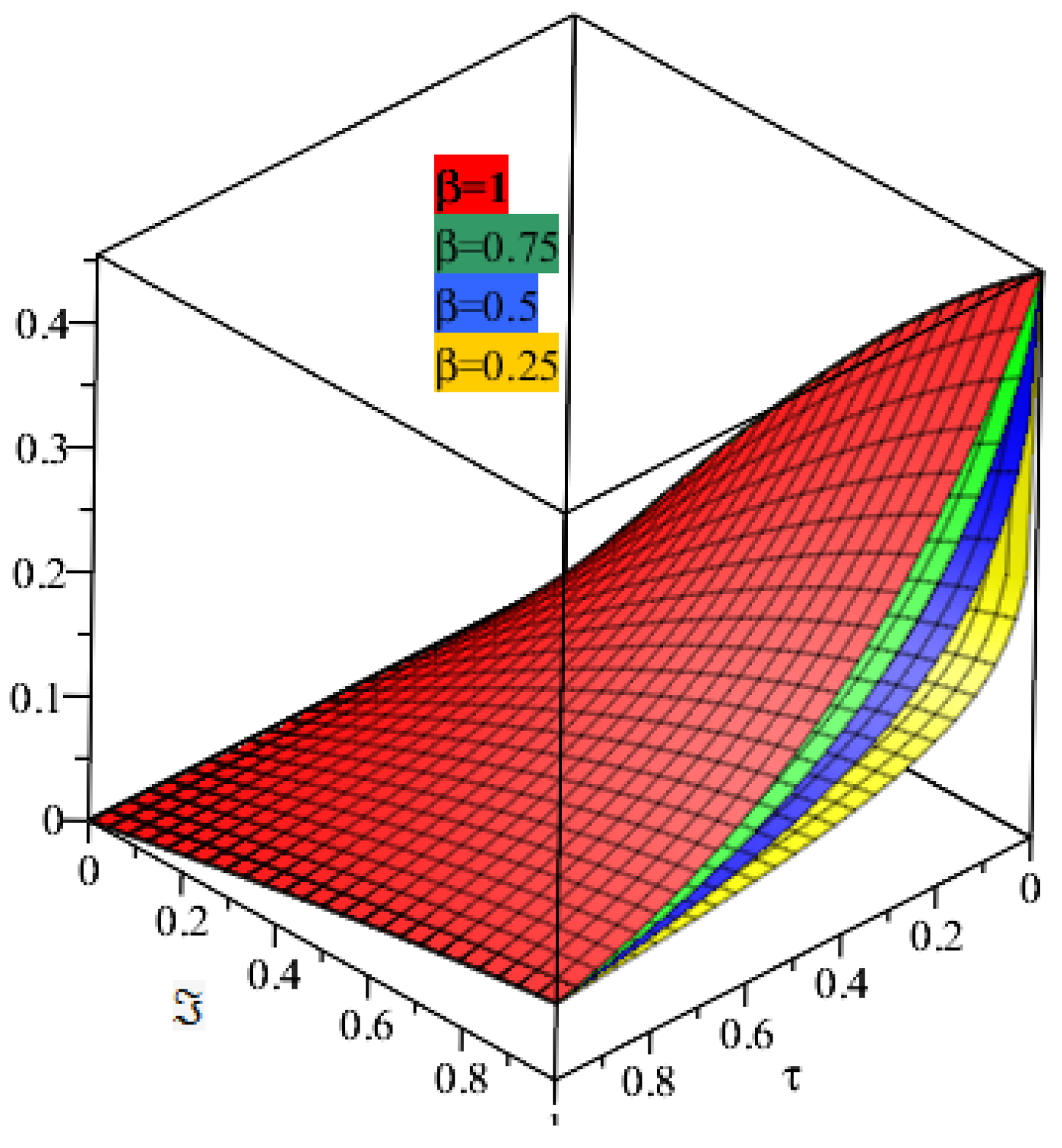
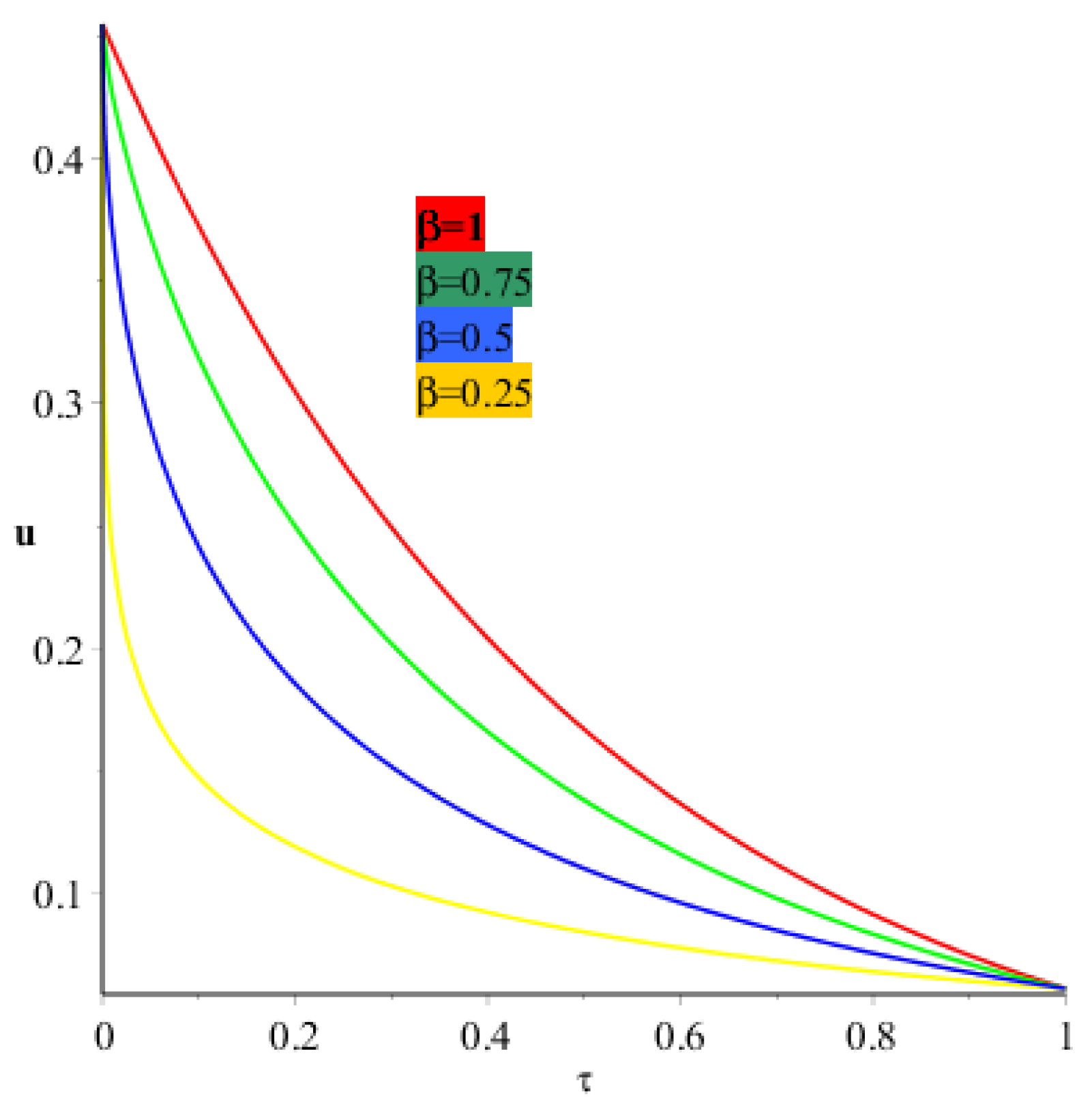
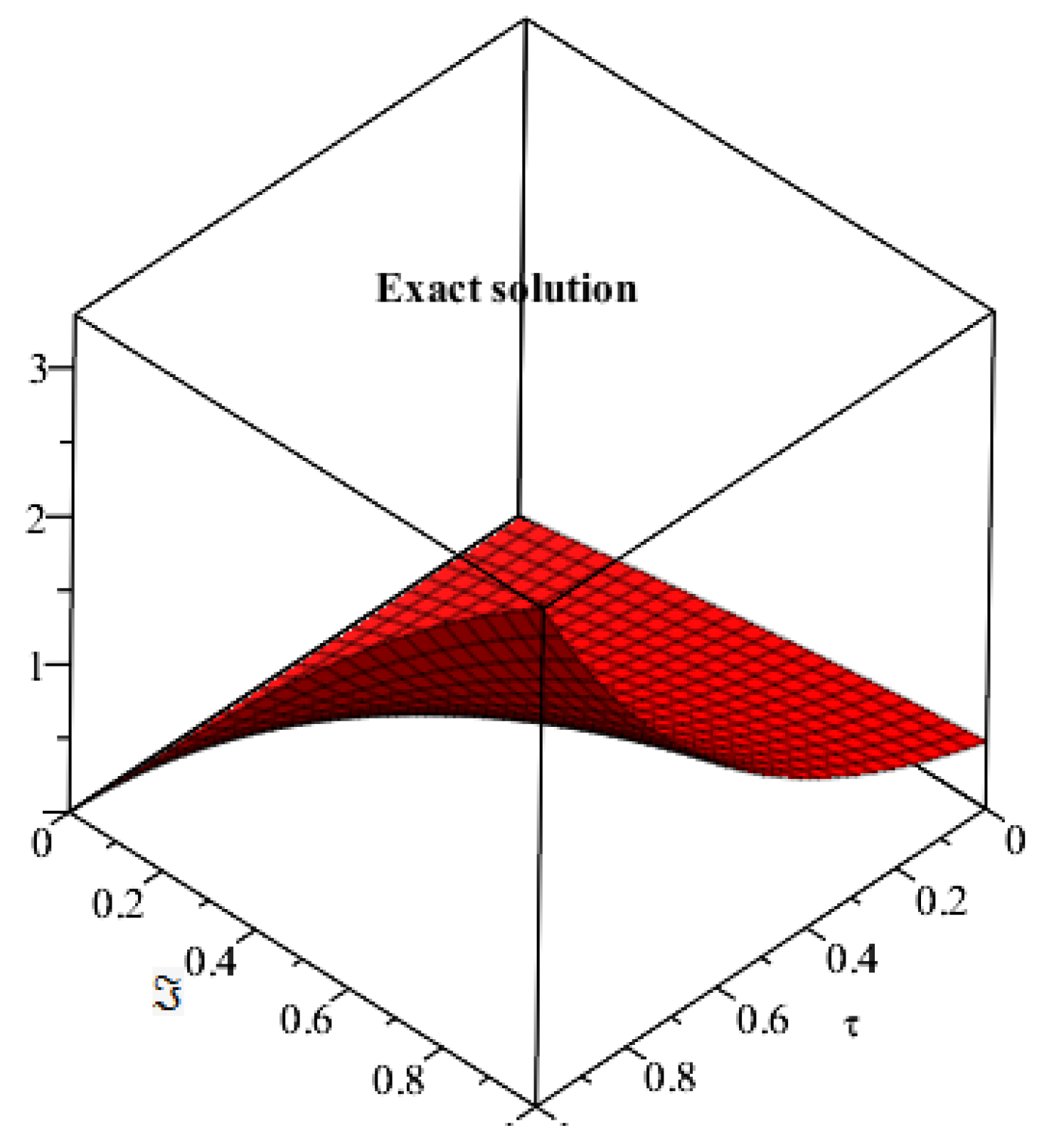
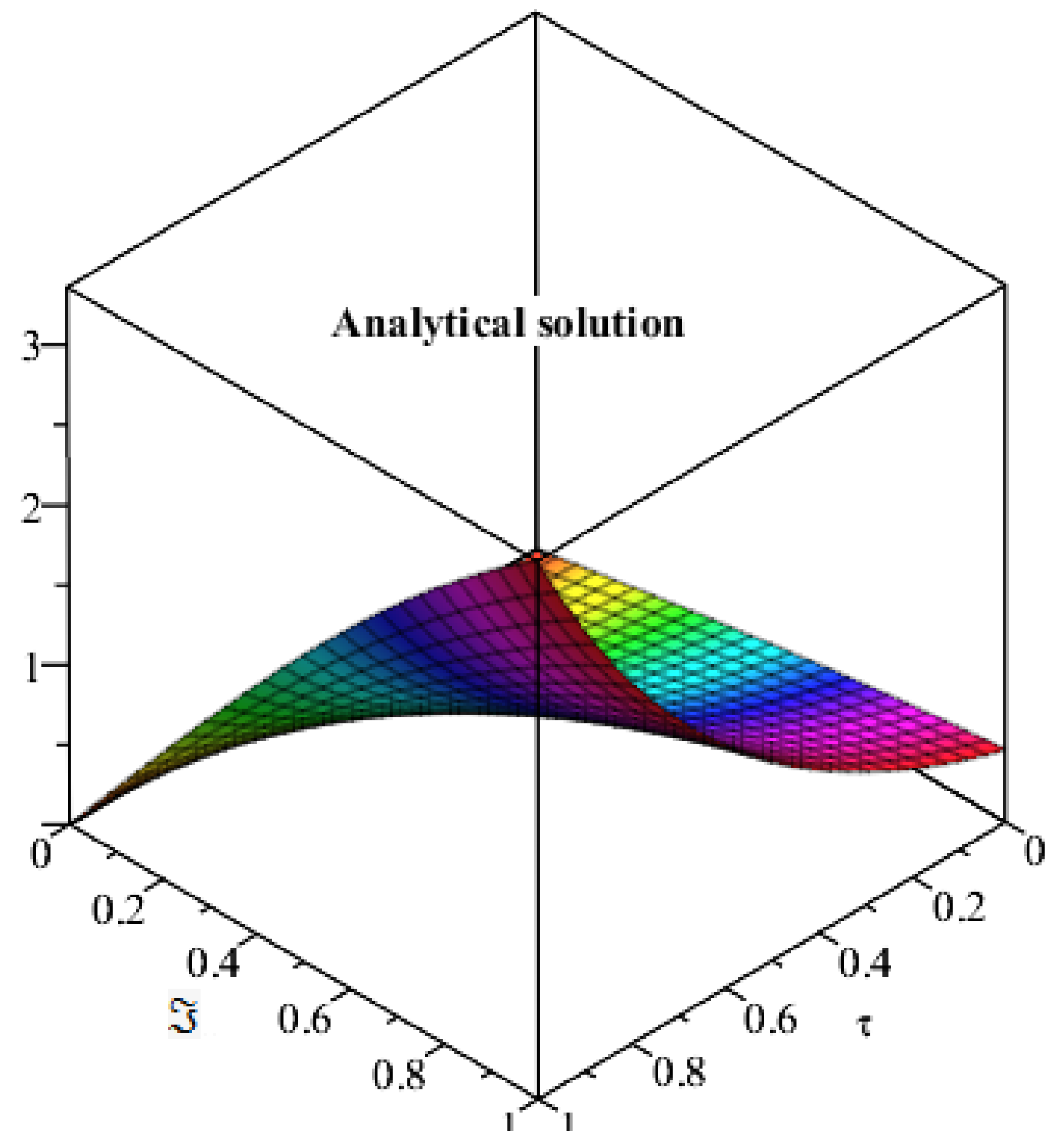
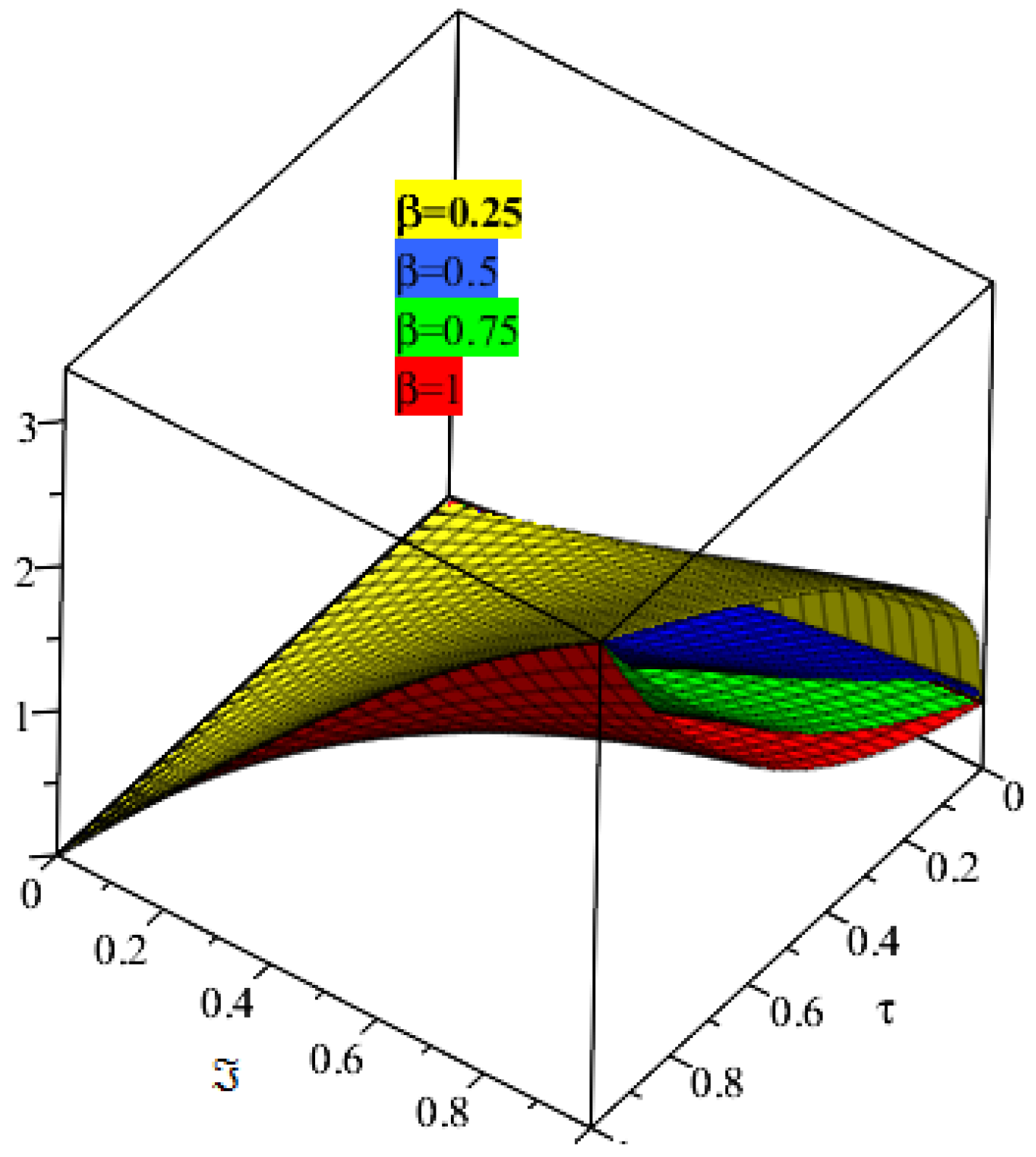
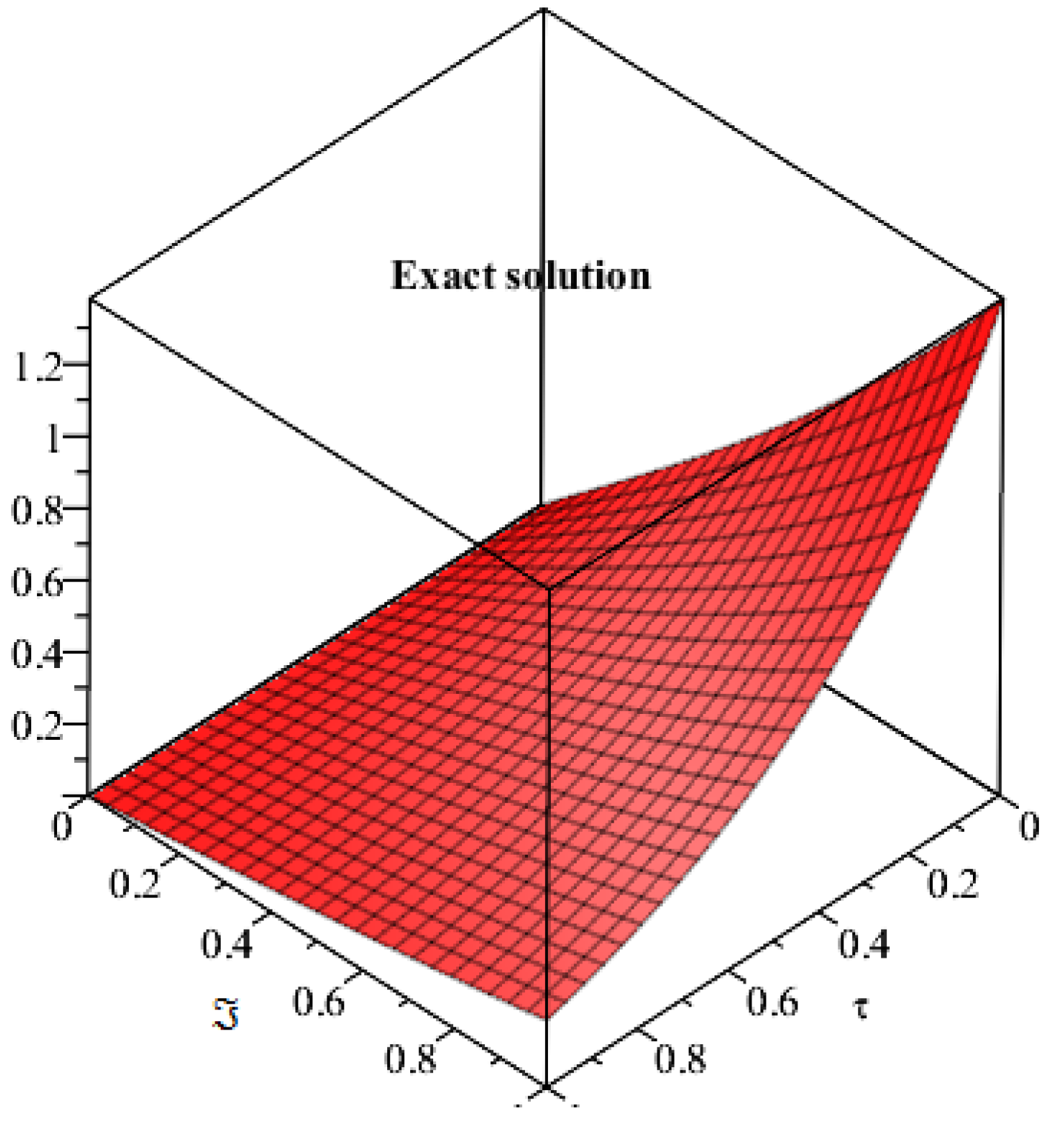
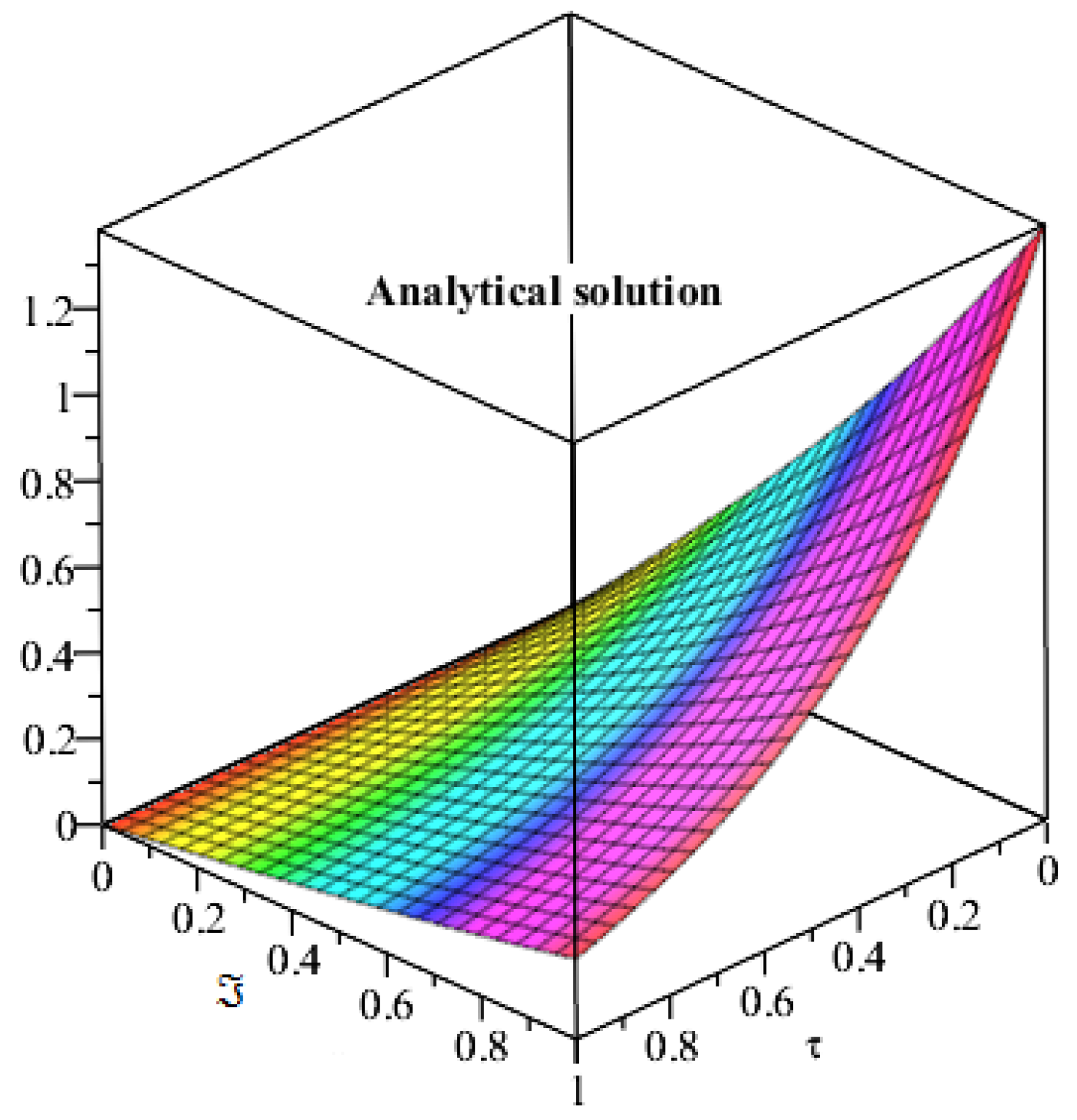
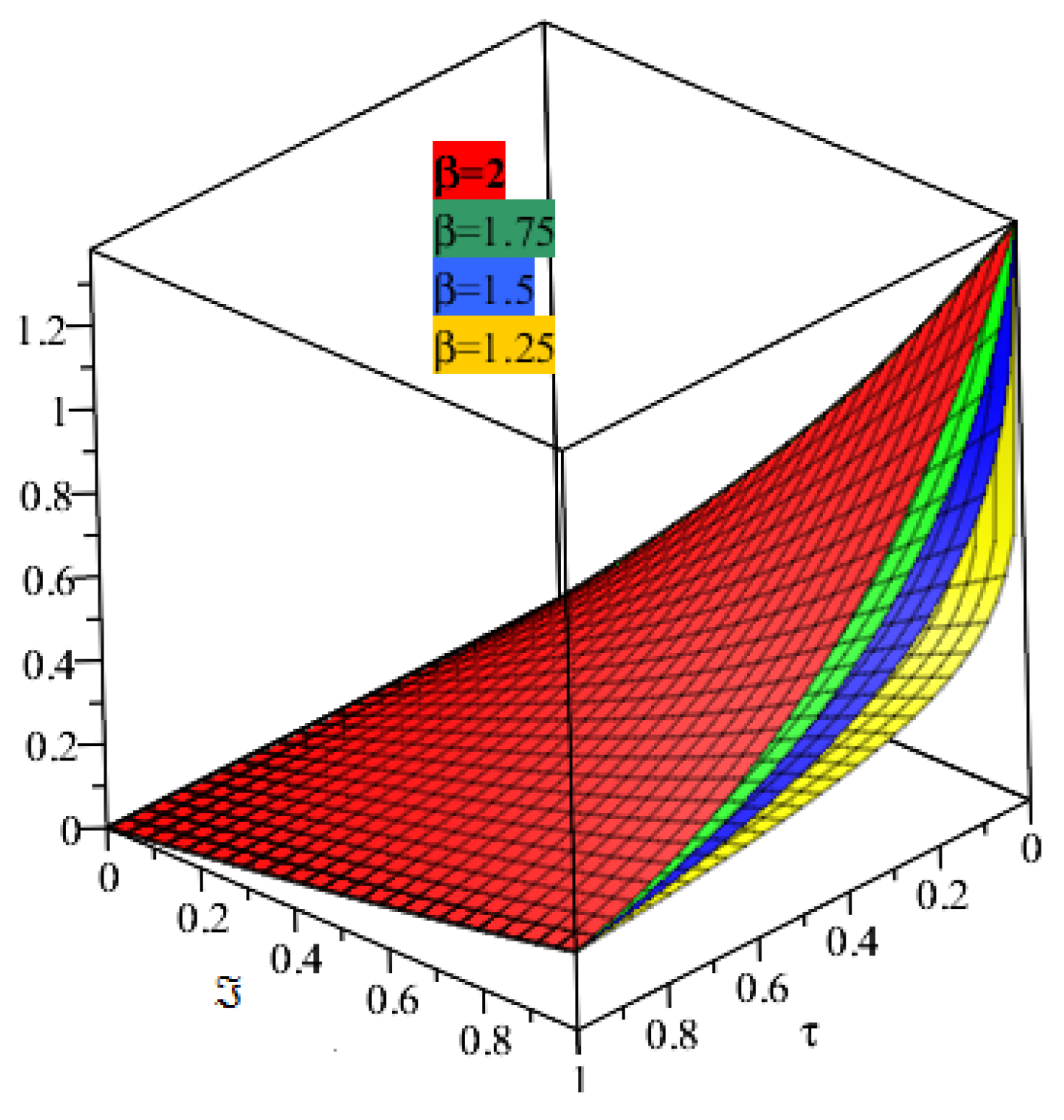
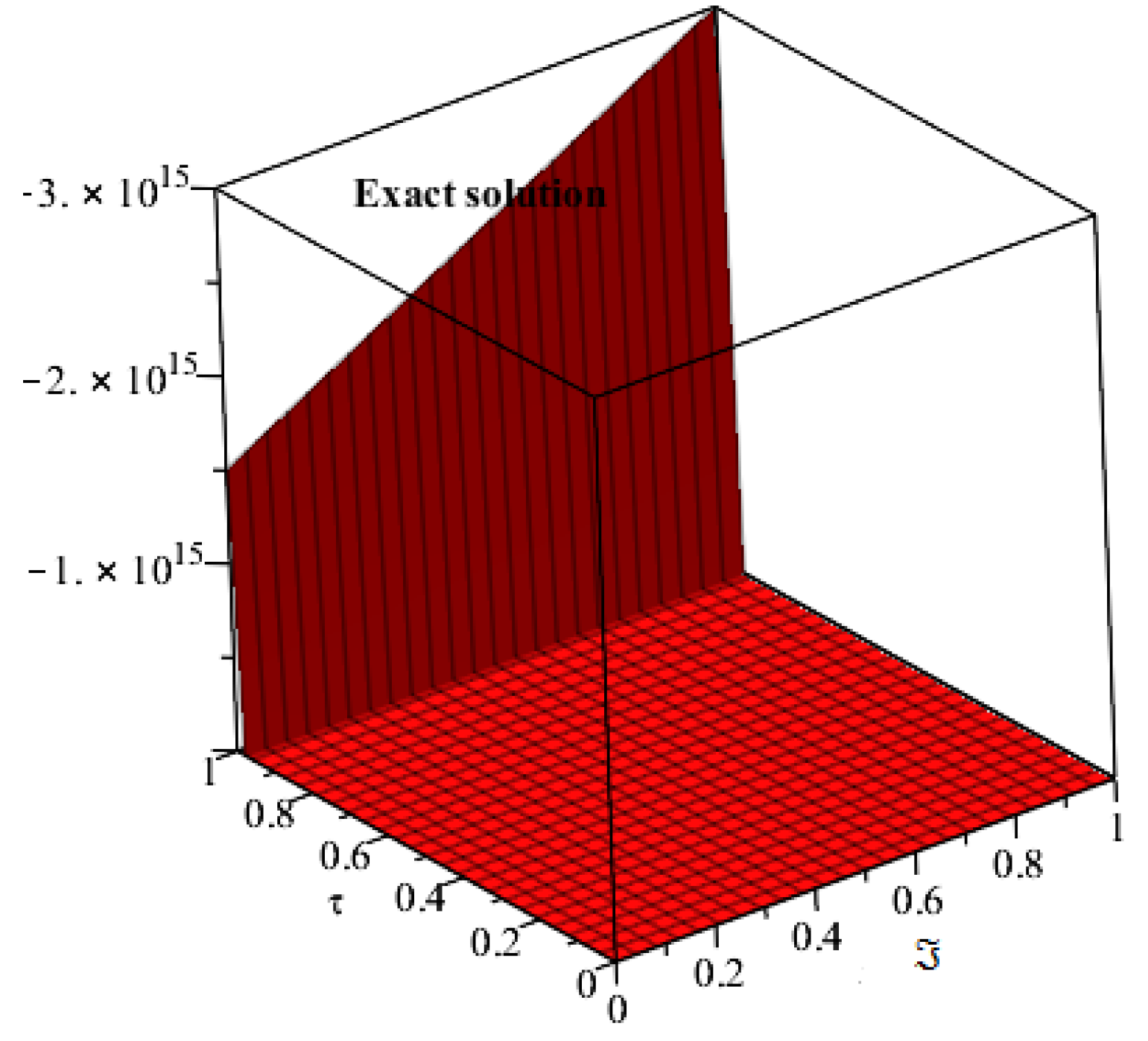
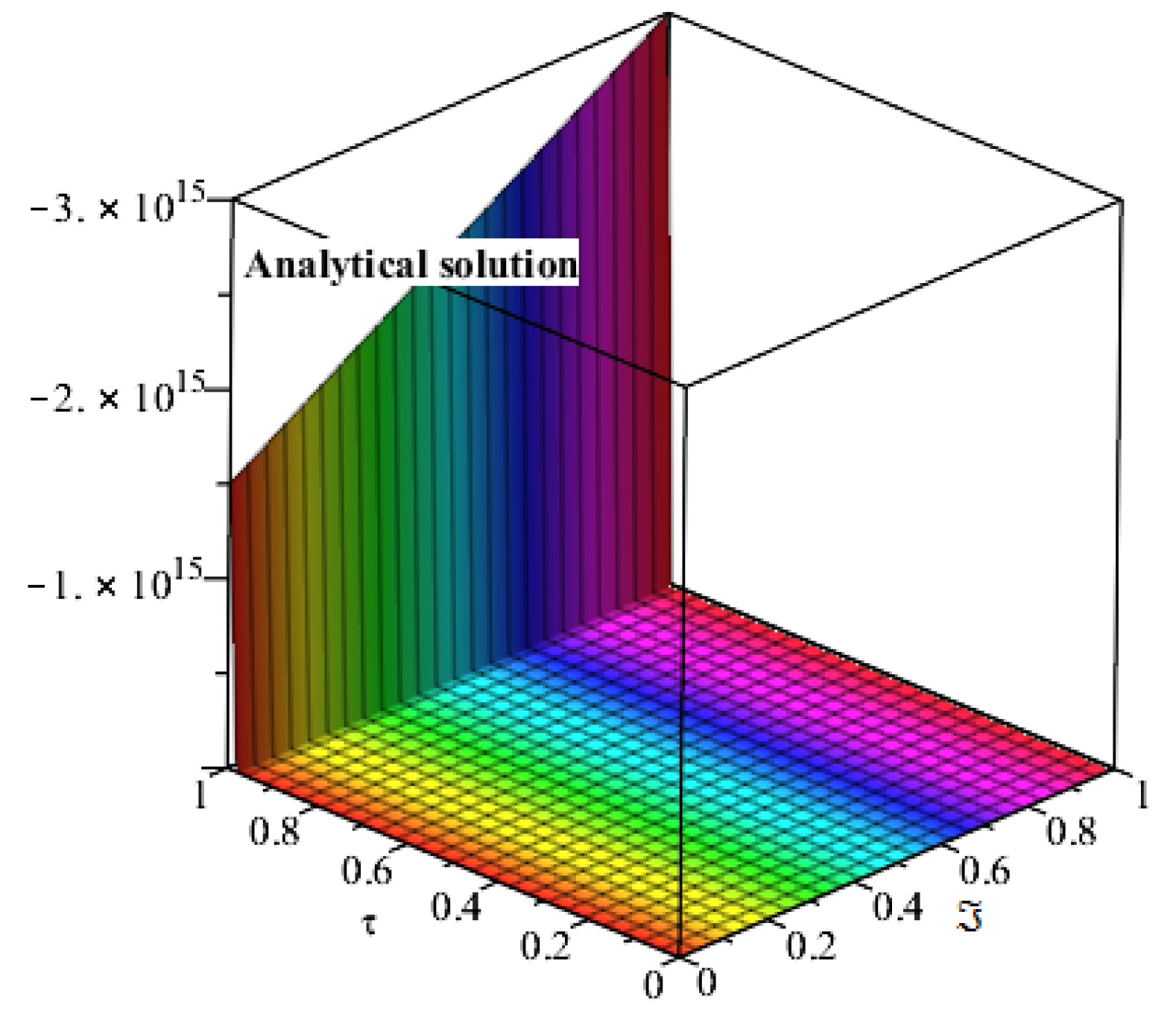
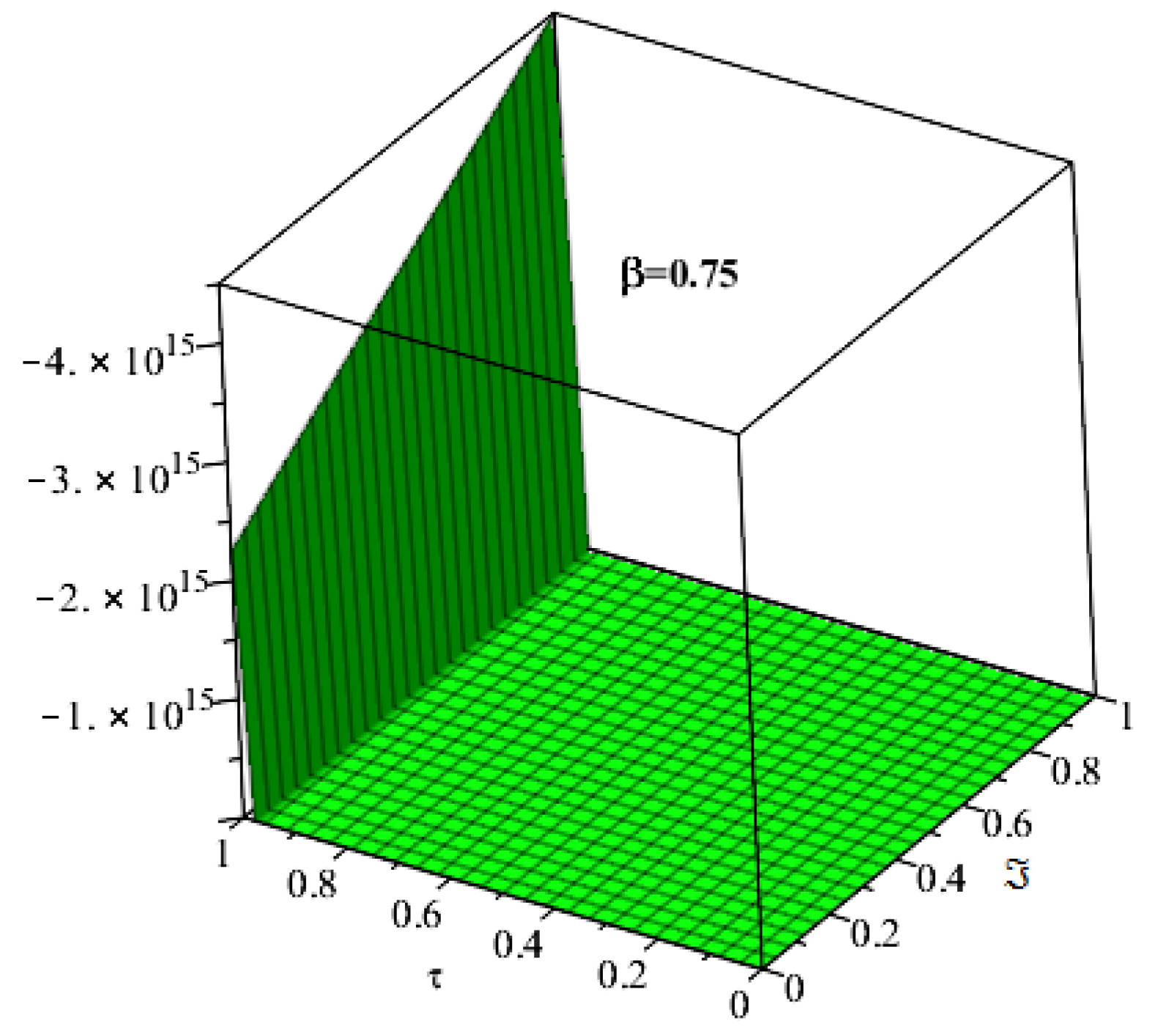
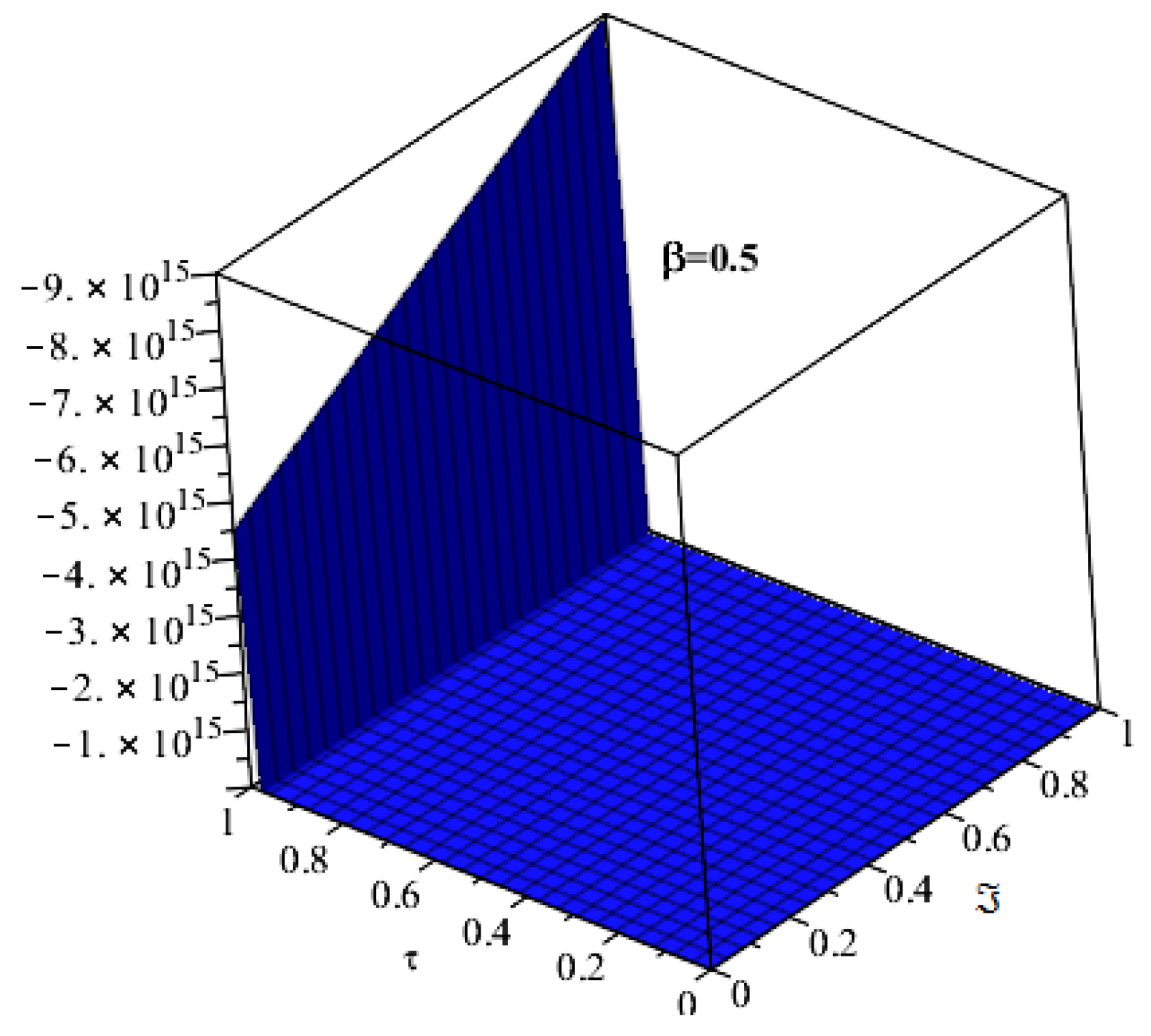
4. Applications and Discussion
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Abd-Elhameed, W.M.; Youssri, Y.H. Fifth-kind orthonormal Chebyshev polynomial solutions for fractional differential equations. Comput. Appl. Math. 2018, 37, 2897–2921. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Farooq, U.; Baleanu, D.; Kumam, P.; Arif, M. A New Analytical Technique to Solve System of Fractional-Order Partial Differential Equations. IEEE Access 2019, 7, 150037–150050. [Google Scholar] [CrossRef]
- Jain, S. Numerical analysis for the fractional diffusion and fractional Buckmaster equation by the two-step Laplace Adam-Bashforth method. Eur Phys. J. Plus 2018, 133, 19. [Google Scholar] [CrossRef]
- Prakash, A. Analytical method for space-fractional telegraph equation by homotopy perturbation transform method. Nonlinear Eng. 2016, 5, 123–128. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical Solution of Fractional-Order Hyperbolic Telegraph Equation, Using Natural Transform Decomposition Method. Electronics 2019, 8, 1015. [Google Scholar] [CrossRef]
- Safari, M.; Ganji, D.D.; Moslemi, M. Application of He’s variational iteration method and Adomian’s decomposition method to the fractional KdV–Burgers–Kuramoto equation. Comput. Math. Appl. 2009, 58, 2091–2097. [Google Scholar] [CrossRef]
- Kumar, D.; Tchier, F.; Singh, J.; Baleanu, D. An efficient computational technique for fractal vehicular traffic flow. Entropy 2018, 20, 259. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D.; Rathore, S. An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl. Math. Comput. 2018, 335, 12–24. [Google Scholar] [CrossRef]
- Shivanian, E.; Jafarabadi, A. Time fractional modified anomalous sub-diffusion equation with a nonlinear source term through locally applied meshless radial point interpolation. Mod. Phys. Lett. B 2018, 32, 1850251. [Google Scholar] [CrossRef]
- Ullah, S.; Khan, M.A.; Farooq, M. A new fractional model for the dynamics of the hepatitis B virus using the Caputo-Fabrizio derivative. Eur. Phys. J. Plus 2018, 133, 237. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Modeling chickenpox disease with fractional derivatives: From caputo to atangana-baleanu. Chaos Solitons Fractals 2019, 122, 111–118. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M.; Baleanu, D. Fractional modeling of blood ethanol concentration system with real data application. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013143. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Ullah, S.; Farooq, M. A new fractional model for tuberculosis with relapse via Atangana–Baleanu derivative. Chaos Solitons Fractals 2018, 116, 227–238. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S. Residual Power Series Method for Solving Time-fractional Model of Vibration Equation of Large Membranes. J. Appl. Comput. Mech. 2019, 5, 603–615. [Google Scholar]
- Jena, R.M.; Chakraverty, S. A new iterative method based solution for fractional Black–Scholes option pricing equations (BSOPE). SN Appl. Sci. 2019, 1, 95. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Jena, S.K. Dynamic response analysis of fractionally damped beams subjected to external loads using homotopy analysis method. J. Appl. Comput. Mech. 2019, 5, 355–366. [Google Scholar]
- Abd-Elhameed, W.M.; Youssri, Y.H. Spectral tau algorithm for certain coupled system of fractional differential equations via generalized Fibonacci polynomial sequence. Iran. J. Sci. Technol. Trans. A Sci. 2019, 43, 543–554. [Google Scholar] [CrossRef]
- Khan, H.; Shah, R.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Heat and Wave Equations by the Natural Transform Decomposition Method. Entropy 2019, 21, 597. [Google Scholar] [CrossRef]
- Shah, R.; Khan, H.; Mustafa, S.; Kumam, P.; Arif, M. Analytical Solutions of Fractional-Order Diffusion Equations by Natural Transform Decomposition Method. Entropy 2019, 21, 557. [Google Scholar] [CrossRef]
- Khan, M.A.; Ullah, S.; Okosun, K.O.; Shah, K. A fractional order pine wilt disease model with Caputo–Fabrizio derivative. Adv. Differ. Equ. 2018, 2018, 410. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D. On the analysis of fractional diabetes model with exponential law. Adv. Differ. Equ. 2018, 2018, 231. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Mathematical modeling for the impacts of deforestation on wildlife species using Caputo differential operator. Chaos Solitons Fractals 2019, 126, 32–40. [Google Scholar] [CrossRef]
- Jumarie, G. Laplace’s transform of fractional order via the Mittag–Leffler function and modified Riemann–Liouville derivative. Appl. Math. Lett. 2009, 22, 1659–1664. [Google Scholar] [CrossRef]
- Kumar, S. A new analytical modelling for fractional telegraph equation via Laplace transform. Appl. Math. Model. 2014, 38, 3154–3163. [Google Scholar] [CrossRef]
- Kazem, S. Exact solution of some linear fractional differential equations by Laplace transform. Int. J. Nonlinear Sci. 2013, 16, 3–11. [Google Scholar]
- Namias, V. The fractional order Fourier transform and its application to quantum mechanics. IMA J. Appl. Math. 1980, 25, 241–265. [Google Scholar] [CrossRef]
- Chen, C.M.; Liu, F.; Turner, I.; Anh, V. A Fourier method for the fractional diffusion equation describing sub-diffusion. J. Comput. Phys. 2007, 227, 886–897. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, M. The fractional finite Hankel transform and its applications in fractal space. J. Phys. A Math. Theor. 2009, 42, 385201. [Google Scholar] [CrossRef]
- Gorenflo, R.; Iskenderov, A.; Luchko, Y. Mapping between solutions of fractional diffusion-wave equations. Fract. Calculus Appl. Anal. 2000, 3, 75–86. [Google Scholar]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2014. [Google Scholar]
- Yang, X.J. Local Fractional Functional Analysis and Its Applications; Asian Academic Publisher Limited: Hong Kong, China, 2011. [Google Scholar]
- Neamaty, A.; Agheli, B.; Darzi, R. Applications of homotopy perturbation method and Elzaki transform for solving nonlinear partial differential equations of fractional order. Theory Approx. Appl. 2016, 6, 91–104. [Google Scholar]
- Jena, R.M.; Chakraverty, S. Solving time-fractional Navier–Stokes equations using homotopy perturbation Elzaki transform. SN Appl. Sci. 2019, 1, 16. [Google Scholar] [CrossRef]
- Taha, N.E.H.; Nuruddeen, R.I.; Abdelilah, K.; Hassan, S. Dualities between “Kamal and Mahgoub integral transforms” and “Some famous integral transforms”. Br. J. Appl. Sci. Technol. 2017, 20, 1–8. [Google Scholar] [CrossRef]
- Aboodh, K.S. The new integral transform “Aboodh Transform”. Glob. J. Pure Appl. Math. 2013, 9, 35–43. [Google Scholar]
- Aggarwal, S.; Chauhan, R. A comparative study of Mohand and Aboodh transforms. Int. J. Res. Adv. Technol. 2019, 7, 520–529. [Google Scholar] [CrossRef]
- Kılıçman, A.; Gadain, H.E. On the applications of Laplace and Sumudu transforms. J. Frankl. Inst. 2010, 347, 848–862. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S. Analytical solution of Bagley-Torvik equations using Sumudu transformation method. SN Appl. Sci. 2019, 1, 246. [Google Scholar] [CrossRef]
- Mao, Z.; Shen, J. Hermite spectral methods for fractional PDEs in unbounded domains. SIAM J. Sci. Comput. 2017, 39, A1928–A1950. [Google Scholar] [CrossRef]
- Maitama, S.; Zhao, W. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. arXiv 2019, arXiv:1904.11370. [Google Scholar]
- Rudolf, H. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Wazwaz, A.M.; Gorguis, A. Exact solutions for heat-like and wave-like equations with variable coefficients. Appl. Math. Comput. 2004, 149, 15–29. [Google Scholar] [CrossRef]

| Functional Form | Shehu Transform Form |
|---|---|
| 1 | |
| t | |
| for | |
| for |
| SDM (m = 5) | SDM (m = 3) | SDM ( m= 5) | ADM (m = 5) | AE of SDM | ||
|---|---|---|---|---|---|---|
| ℑ | ℜ | |||||
| 1 | 1 | 1.111568974 | 1.105195833 | 1.10519608 | 1.10519609 | 2.51 × 10 |
| 2 | 2 | 17.78510358 | 17.68313333 | 17.6831373 | 17.6831374 | 4.02 × 10 |
| 3 | 3 | 90.03708688 | 89.52086250 | 89.5208829 | 89.5208828 | 2.03 × 10 |
| 4 | 4 | 284.5616573 | 282.9301334 | 282.930198 | 282.930199 | 6.44 × 10 |
| 5 | 5 | 694.7306086 | 690.7473959 | 690.747553 | 690.747552 | 1.57 × 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, H.; Farooq, U.; Shah, R.; Baleanu, D.; Kumam, P.; Arif, M. Analytical Solutions of (2+Time Fractional Order) Dimensional Physical Models, Using Modified Decomposition Method. Appl. Sci. 2020, 10, 122. https://doi.org/10.3390/app10010122
Khan H, Farooq U, Shah R, Baleanu D, Kumam P, Arif M. Analytical Solutions of (2+Time Fractional Order) Dimensional Physical Models, Using Modified Decomposition Method. Applied Sciences. 2020; 10(1):122. https://doi.org/10.3390/app10010122
Chicago/Turabian StyleKhan, Hassan, Umar Farooq, Rasool Shah, Dumitru Baleanu, Poom Kumam, and Muhammad Arif. 2020. "Analytical Solutions of (2+Time Fractional Order) Dimensional Physical Models, Using Modified Decomposition Method" Applied Sciences 10, no. 1: 122. https://doi.org/10.3390/app10010122
APA StyleKhan, H., Farooq, U., Shah, R., Baleanu, D., Kumam, P., & Arif, M. (2020). Analytical Solutions of (2+Time Fractional Order) Dimensional Physical Models, Using Modified Decomposition Method. Applied Sciences, 10(1), 122. https://doi.org/10.3390/app10010122








