Simulation of the Progression of the COVID-19 Outbreak in Northwest Syria Using a Basic and Adjusted SIR Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Differential Equation and Basic SIR Model
2.2. The Basic Reproduction R0 and Effective Reproduction Re Numbers
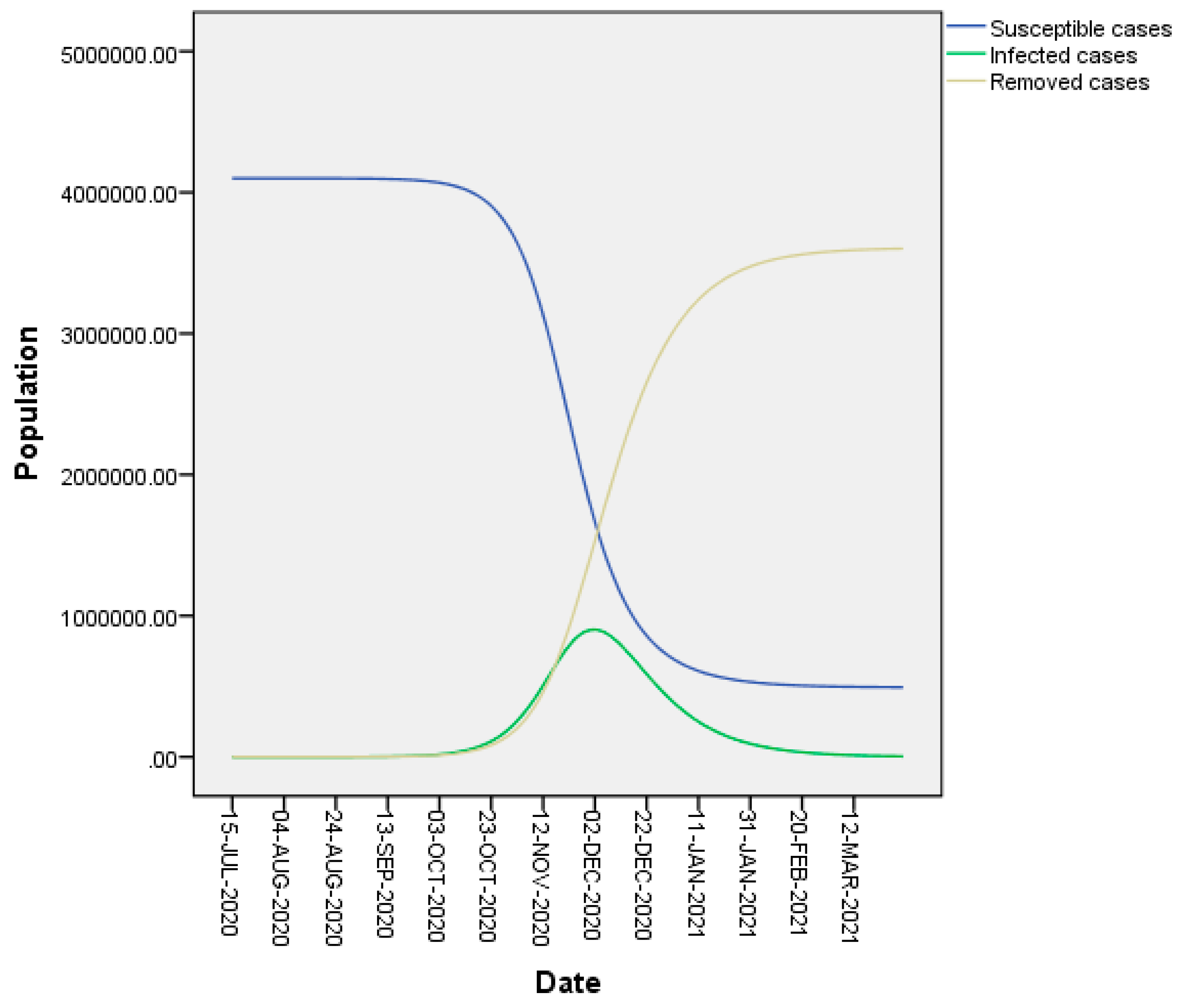
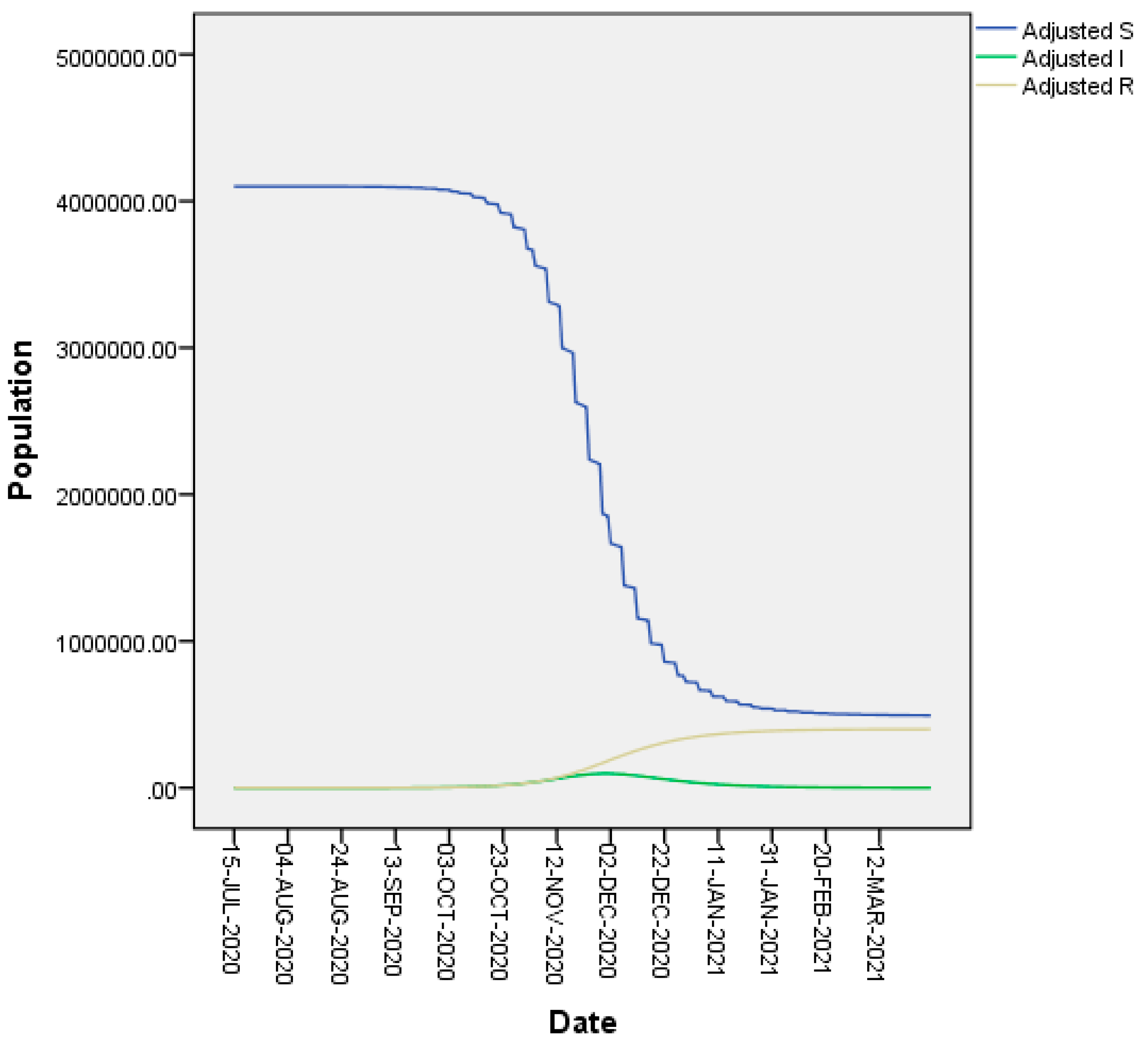
3. Results
3.1. Estimating the Basic Reproductive Numbers without Control Measures
3.2. The Impact of Using Face Masks on the Basic Reproduction Number
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
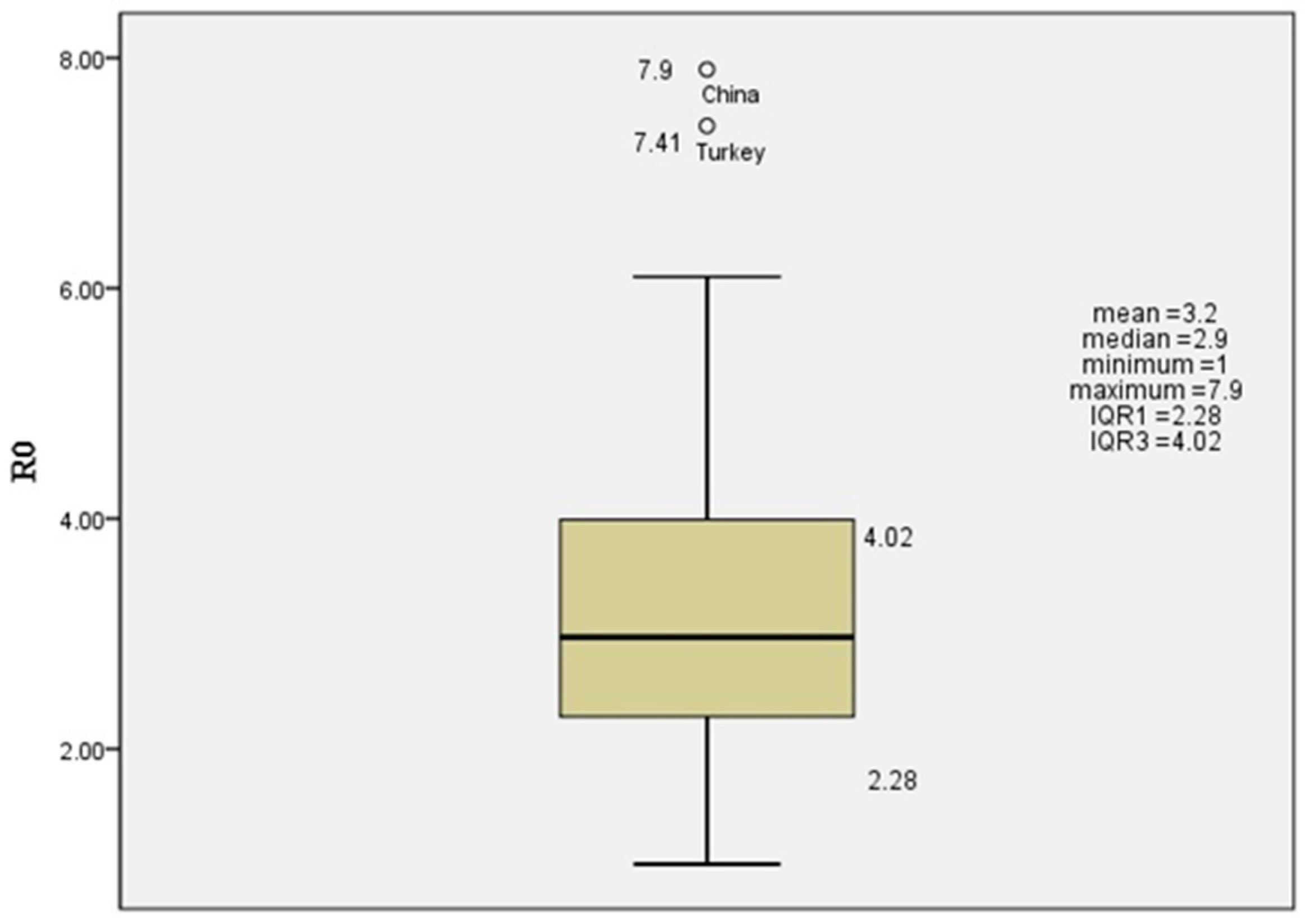
| No | R0 | Place | Reference |
|---|---|---|---|
| 1 | 2.2 | Wuhan, China | [56] |
| 2 | 2.6 | China | [57] |
| 3 | 4.6 | Hubei, China | [58] |
| 4 | 4.7 | Wuhan | [59] |
| 1.52 | China | ||
| 5.93 | Hubei | ||
| 5 | 2.79 | China | [60] |
| 6 | 5.2 | Wuhan, China | [61] |
| 7 | 7.9 | Wuhan, China | [62] |
| 8 | 5.06 | Heilongjiang, China | [63] |
| 9 | 3.2 | Wuhan, China | [64] |
| 10 | 2.7 | Wuhan, China | [65] |
| 11 | 2.55 | China | [66] |
| 1.78 | S. Korea | ||
| 3.47 | Qom, Iran | ||
| 1.82 | Iran | ||
| 3.37 | Italy | ||
| 12 | 2.1, 3.2 | Wuhan, China | [67] |
| China | |||
| 13 | 2.24, 3.58 | China | [68] |
| 14 | 3.11 | Wuhan, China | [69] |
| 15 | 2.68 | Wuhan, China | [70] |
| 16 | 3.15 | China | [71] |
| 17 | 2.2 | Wuhan, China | [72] |
| 18 | 2.97 | Anhui, China | [73] |
| 19 | 2.6 | S. Korea | [74] |
| 3.2 | S. Korea | ||
| 3.3 | Italy | ||
| 2.3 | Italy | ||
| 20 | 1.59 | S. Korea | [75] |
| 21 | 2.6 | Japan | [76] |
| 22 | 2.79 | Syria | [53] |
| 2.72 | France | ||
| 1.72 | China | ||
| 1.00 | Nigeria | ||
| 1.61 | The United States | ||
| 1.29 | Russia | ||
| 1.4 | Yemen | ||
| 1.25 | India | ||
| 23 | 3.99 | Syria | [54] |
| 3.5 | Iraq | ||
| 4.13 | Iran | ||
| 4.08 | Israel | ||
| 4.05 | Cyprus | ||
| 7.41 | Turkey | ||
| 2.7 | Kuwait | ||
| 3.39 | Bahrain | ||
| 4.18 | Qatar | ||
| 4.45 | Saudi Arabia | ||
| 2.73 | The United Emirates | ||
| 2.6 | Oman | ||
| 3.52 | Jordan | ||
| 3.35 | Egypt | ||
| 3.16 | Lebanon | ||
| 2.89 | Palestine | ||
| 24 | 2.37 | Africa | [77] |
| 25 | 1.56 | Cameroon | [78] |
| 26 | 1.06 | Iraq | [79] |
| 1.03 | Egypt | ||
| 27 | 4.86 | Iran | [80] |
| 28 | 2.7 | Shahroud, Iran | [81] |
| 29 | 2.38 | Italy | [82] |
| 30 | 4.9 | Italy | [83] |
| 3.8 | Belgium | ||
| 4.4 | France | ||
| 4.7 | Germany | ||
| 3.7 | Netherlands | ||
| 6.1 | Spain | ||
| 3.6 | Switzerland | ||
| 3.9 | The United Kingdom | ||
| 5.8 | The United States | ||
| 31 | 2.28 | Pakistan | [84] |
| 32 | 2.28 | Malaysia | [85] |
| 33 | 5.25 | Brazil | [86] |
| 34 | 2.3 | Ontario, Canada | [87] |
| 37 | 1.66 | Sri Lanka | [88] |
References
- Polack, F.P.; Thomas, S.J.; Kitchin, N.; Absalon, J.; Gurtman, A.; Lockhart, S.; Perez, J.L.; Pérez Marc, G.; Moreira, E.D.; Zerbini, C.; et al. Safety and Efficacy of the BNT162b2 mRNA COVID-19 Vaccine. N. Engl. J. Med. 2020, 383, 2603–2615. [Google Scholar] [CrossRef] [PubMed]
- Abeya, S.G.; Barkesa, S.B.; Sadi, C.G.; Gemeda, D.D.; Muleta, F.Y.; Tolera, A.F.; Ayana, D.N.; Mohammed, S.A.; Wako, E.B.; Hurisa, M.B.; et al. Adherence to COVID-19 preventive measures and associated factors in Oromia regional state of Ethiopia. PLoS ONE 2021, 16, e0257373. [Google Scholar] [CrossRef] [PubMed]
- Chu, J. A statistical analysis of the novel coronavirus (COVID-19) in Italy and Spain. PLoS ONE 2021, 16, e0249037. [Google Scholar] [CrossRef] [PubMed]
- Güner, R.; Hasanoğlu, I.; Aktaş, F. COVID-19: Prevention and control measures in community. Turk. J. Med. Sci. 2020, 50, 571–577. [Google Scholar] [CrossRef]
- Fathollahi-Fard, A.M.; Ahmadi, A.; Karimi, B. Multi-Objective Optimization of Home Healthcare with Working-Time Balancing and Care Continuity. Sustainability 2021, 13, 12431. [Google Scholar] [CrossRef]
- Pedersen, M.J.; Favero, N. Social Distancing during the COVID-19 Pandemic: Who Are the Present and Future Noncompliers? Public Adm. Rev. 2020, 80, 805–814. [Google Scholar] [CrossRef]
- Carcione, J.M.; Santos, J.E.; Bagaini, C.; Ba, J. A Simulation of a COVID-19 Epidemic Based on a Deterministic SEIR Model. Front. Public Health 2020, 8, 230. [Google Scholar] [CrossRef]
- Larsen, J.R.; Martin, M.R.; Martin, J.D.; Kuhn, P.; Hicks, J.B. Modeling the Onset of Symptoms of COVID-19. Front. Public Health 2020, 8, 473. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef] [Green Version]
- Altun, K.; Altuntas, S.; Dereli, T. An interaction-oriented multi-agent sir model to assess the spread of SARS-CoV-2. Hacet. J. Math. Stat. 2021, 50, 1548–1559. [Google Scholar] [CrossRef]
- Kaplan, E.H.; Craft, D.L.; Wein, L.M. Emergency response to a smallpox attack: The case for mass vaccination. Proc. Natl. Acad. Sci. USA 2002, 99, 10935–10940. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alrasheed, H.; Althnian, A.; Kurdi, H.; Al-Mgren, H.; Alharbi, S. COVID-19 Spread in Saudi Arabia: Modeling, Simulation and Analysis. Int. J. Environ. Res. Public Health 2020, 17, 7744. [Google Scholar] [CrossRef] [PubMed]
- Zaplotnik, Ž.; Gavrić, A.; Medic, L. Simulation of the COVID-19 epidemic on the social network of Slovenia: Estimating the intrinsic forecast uncertainty. PLoS ONE 2020, 15, e0238090. [Google Scholar] [CrossRef] [PubMed]
- Shereen, M.A.; Khan, S.; Kazmi, A.; Bashir, N.; Siddique, R. COVID-19 infection: Origin, transmission, and characteristics of human coronaviruses. J. Adv. Res. 2020, 24, 91–98. [Google Scholar] [CrossRef]
- Douedari, Y.; Alhaffar, M.; Al-Twaish, M.; Mkhallalati, H.; Alwany, R.; Ibrahim, N.B.M.; Zaseela, A.; Horanieh, N.; Abbara, A.; Howard, N. “Ten years of war! You expect people to fear a ‘germ’?”: A qualitative study of initial perceptions and responses to the COVID-19 pandemic among displaced communities in opposition-controlled northwest Syria. J. Migr. Health 2020, 1–2, 100021. [Google Scholar] [CrossRef]
- Blanchard, C.M.; Humud, C.E.; Nikitin, M.B.D. Armed conflict in Syria: Overview and U.S. response. In Internal Conflict Regions in the Middle East: Iraq and Syria; Congressional Research Services CRS, Library of Congress: Washington, DC, USA, 2014; pp. 65–98. ISBN 9781633212602. [Google Scholar]
- Bank, A. COVID-19 and the Syrian Conflict Implications for International Actors and Their Strategies Peace and Security; Friedrich-Ebert-Stiftung: Bonn/Berlin, Germany, 2020. [Google Scholar]
- Bdaiwi, Y.; Rayes, D.; Sabouni, A.; Murad, L.; Fouad, F.; Zakaria, W.; Hariri, M.; Ekzayez, A.; Tarakji, A.; Abbara, A. Challenges of providing healthcare worker education and training in protracted conflict: A focus on non-government controlled areas in north west Syria. Confl. Health 2020, 14, 1–13. [Google Scholar] [CrossRef]
- Fouad, F.M.; Sparrow, A.; Tarakji, A.; Alameddine, M.; El-Jardali, F.; Coutts, A.P.; El Arnaout, N.; Karroum, L.B.; Jawad, M.; Roborgh, S.; et al. Health workers and the weaponisation of health care in Syria: A preliminary inquiry for The Lancet–American University of Beirut Commission on Syria. Lancet 2017, 390, 2516–2526. [Google Scholar] [CrossRef] [Green Version]
- Ekzayez, A.; al-Khalil, M.; Jasiem, M.; Al Saleh, R.; Alzoubi, Z.; Meagher, K.; Patel, P. COVID-19 response in northwest Syria: Innovation and community engagement in a complex conflict. J. Public Health 2020, 42, 504–509. [Google Scholar] [CrossRef]
- Douedari, Y.; Howard, N. Perspectives on Rebuilding Health System Governance in Opposition-Controlled Syria: A Qualitative Study. Int. J. Health Policy Manag. 2019, 8, 233–244. [Google Scholar] [CrossRef] [Green Version]
- Gharibah, M.; Zaki, M. COVID-19 Pandemic: Syria’s Response and Healthcare Capacity; Conflict Research Program crp: London, UK, 2020. [Google Scholar]
- McGibney, N.; Haddad, N. Stolen Future: War and Child Marriage in Northwest Syria; OCHA: Gaziantep, Turkey, 2020. [Google Scholar]
- OCHA. Syrian Arab Republic Recent Developments in Northwest Syria; OCHA: Gaziantep, Turkey, 2021. [Google Scholar]
- Marzouk, M.; Alhiraki, O.A.; Aguas, R.; Gao, B.; Clapham, H.; Obaid, W.; Altaleb, H.; Almhawish, N.; Rihawi, H.; Abbara, A.; et al. SARS-CoV-2 transmission in opposition-controlled Northwest Syria: Modeling pandemic responses during political conflict. Int. J. Infect. Dis. 2022, 117, 103–115. [Google Scholar] [CrossRef]
- Kumar, K.V.A.; Sahana, M.N. Exponential Growth Impact of COVID-19 Pandemic-World Scenario, Preventive Measures and Drug Preferences. Health Sci. J. 2020, 1–7. [Google Scholar] [CrossRef]
- WHO. COVID-19 Response Tracking Dashboard Northwest Syria. Available online: https://app.powerbi.com/view?r=eyJrIjoiMmRiMGMxODMtNThkMi00NzA2LTk0MWUtYzc5YTgyNThlYWEyIiwidCI6ImY2MTBjMGI3LWJkMjQtNGIzOS04MTBiLTNkYzI4MGFmYjU5MCIsImMiOjh9&pageName=ReportSectionb57388c4c756b1036a93 (accessed on 16 January 2021).
- Adamu, H.A.; Muhammad, M.; Jingi, A.M.; Usman, M.A. Mathematical modelling using improved SIR model with more realistic assumptions. Int. J. Eng. Appl. Sci. 2019, 6, 64–69. [Google Scholar] [CrossRef]
- Kolifarhood, G.; Aghaali, M.; Mozafar Saadati, H.; Taherpour, N.; Rahimi, S.; Izadi, N.; Hashemi Nazari, S.S. Epidemiological and Clinical Aspects of COVID-19; a Narrative Review. Arch. Acad. Emerg. Med. 2020, 8, e41. [Google Scholar] [CrossRef]
- O’Driscoll, M.; Harry, C.; Donnelly, C.A.; Cori, A.; Dorigatti, I. A Comparative Analysis of Statistical Methods to Estimate the Reproduction Number in Emerging Epidemics, with Implications for the Current Coronavirus Disease 2019 (COVID-19) Pandemic. Clin. Infect. Dis. 2021, 73, E215–E223. [Google Scholar] [CrossRef]
- Gao, S.; Tu, Y.; Wang, J. Basic reproductive number for a general hybrid epidemic model. Adv. Differ. Equ. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmough, J. Further Notes on the Basic Reproduction Number. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 1945, pp. 159–178. ISBN 9783540789109. [Google Scholar]
- Nishiura, H.; Chowell, G. The effective reproduction number as a prelude to statistical estimation of time-dependent epidemic trends. In Mathematical and Statistical Estimation Approaches in Epidemiology; Gerardo, C., Hyman, J.M., Bettencourt, L.M.A., Castillo-Chavez, C., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 103–121. ISBN 9789048123124. [Google Scholar]
- Imai, N.; Cori, A.; Dorigatti, I.; Baguelin, M.; Donnelly, C.A.; Riley, S.; Ferguson, N.M. Transmissibility of 2019-nCoV; World Health Organization: Geneva, Switzerland, 2019; pp. 2–6. [Google Scholar]
- Cintrôn-Arias, A.; Castillo-Chavez, C.; Bettencourt, L.M.A.; Lloyd, A.L.; Banks, H.T. The estimation of the effective repro-ductive number from disease outbreak data. Math. Biosci. Eng. 2009, 6, 261–282. [Google Scholar] [CrossRef]
- Katul, G.G.; Mrad, A.; Bonetti, S.; Manoli, G.; Parolari, A.J. Global convergence of COVID-19 basic reproduction number and estimation from early-time SIR dynamics. PLoS ONE 2020, 15, e0239800. [Google Scholar] [CrossRef]
- Jayaweera, M.; Perera, H.; Gunawardana, B.; Manatunge, J. Transmission of COVID-19 virus by droplets and aerosols: A critical review on the unresolved dichotomy. Environ. Res. 2020, 188, 109819. [Google Scholar] [CrossRef]
- Manikandan, N. Are social distancing, hand washing and wearing masks appropriate measures to mitigate transmission of COVID-19? Vacunas 2020, 21, 136–137. [Google Scholar] [CrossRef]
- World Health Organization. WHO Advice for the Public: Coronavirus Disease (COVID-19). Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/advice-for-public (accessed on 28 February 2022).
- Howard, J.; Huang, A.; Li, Z.; Tufekci, Z.; Zdimal, V.; van der Westhuizen, H.-M.; von Delft, A.; Price, A.; Fridman, L.; Tang, L.-H.; et al. An evidence review of face masks against COVID-19. Proc. Natl. Acad. Sci. USA 2021, 118, e2014564118. [Google Scholar] [CrossRef]
- Karia, R.; Gupta, I.; Khandait, H.; Yadav, A.; Yadav, A. COVID-19 and its Modes of Transmission. SN Compr. Clin. Med. 2020, 2, 1798–1801. [Google Scholar] [CrossRef] [PubMed]
- Rizki, S.A.; Kurniawan, A. Efficacy of Cloth Mask in Reducing COVID-19 Transmission: A Literature Review. Kesmas Natl. Public Health J. 2020, 15, 43–48. [Google Scholar] [CrossRef]
- Lee, B.U. Minimum Sizes of Respiratory Particles Carrying SARS-CoV-2 and the Possibility of Aerosol Generation. Int. J. Environ. Res. Public Health 2020, 17, 6960. [Google Scholar] [CrossRef]
- Health Cluster Turkey Hub. Health Cluster Bulletin: August 2020; Health Cluster Turkey Hub: Gaziantep, Turkey, 2020. [Google Scholar]
- Relief Experts Association—UDER. Almost There! Fabric Facemasks to Cover 35% of Northwest Syria. Available online: https://reliefexperts.org/almost-there-fabric-facemasks-to-cover-35-of-northwest-syria/ (accessed on 25 February 2022).
- Neupane, B.B.; Mainali, S.; Sharma, A.; Giri, B. Optical microscopic study of surface morphology and filtering efficiency of face masks. PeerJ 2019, 2019, e7142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shakya, K.M.; Noyes, A.; Kallin, R.; Peltier, R.E. Evaluating the efficacy of cloth facemasks in reducing particulate matter exposure. J. Expo. Sci. Environ. Epidemiol. 2017, 27, 352–357. [Google Scholar] [CrossRef] [PubMed]
- Davies, A.; Thompson, K.A.; Giri, K.; Kafatos, G.; Walker, J.; Bennett, A. Testing the efficacy of homemade masks: Would they protect in an influenza pandemic? Disaster Med. Public Health Prep. 2013, 7, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Bae, S.; Kim, M.C.; Kim, J.Y.; Cha, H.H.; Lim, J.S.; Jung, J.; Kim, M.J.; Oh, D.K.; Lee, M.K.; Choi, S.H.; et al. Effectiveness of Surgical and Cotton Masks in Blocking SARS-CoV-2: A Controlled Comparison in 4 Patients. Ann. Intern. Med. 2020, 173, W22–W23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, Q.X.; Shan, H.; Zhang, H.L.; Li, G.M.; Yang, R.M.; Chen, J.M. Potential utilities of mask-wearing and instant hand hygiene for fighting SARS-CoV-2. J. Med. Virol. 2020, 92, 1567–1571. [Google Scholar] [CrossRef]
- REACH Initiative. COVID-19 Knowledge, Attitudes and Practices (KAP) Survey, August—September 2020 (Round 4). Reliefweb. Int. 2020, 2020, 10–20. [Google Scholar]
- Turan, C.; Hacımustafaoğlu, M. What is the R0 number and clinical significance in infectious diseases? Cocuk Enfeksiyon Derg. 2020, 14, e47–e48. [Google Scholar] [CrossRef]
- Al-Raeei, M. The basic reproduction number of the new coronavirus pandemic with mortality for India, the Syrian Arab Republic, the United States, Yemen, China, France, Nigeria and Russia with different rate of cases. Clin. Epidemiol. Glob. Health 2021, 9, 147–149. [Google Scholar] [CrossRef] [PubMed]
- Rahman, B.; Aziz, I.A.; Khdhr, F.W.; Mahmood, D.F.D. Preliminary estimation of the basic reproduction number of SARS-CoV-2 in the Middle East. Bull. World Health Organ. 2020, 20, 7. [Google Scholar] [CrossRef]
- Spiegel, P.; Musani, A.; Shaun, T.; Harlass, S.; Van Kerkhove, M. Why Is COVID-19 NOT Transmitting in Humanitarian Settings as Expected…or Is It?—READY Initiative; READY: Global Readiness for Major Disease Outbreak Response: Baltimore, Maryland, 2020. [Google Scholar]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.M.; Lau, E.H.Y.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus–Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Musa, S.S.; Lin, Q.; Ran, J.; Yang, G.; Wang, W.; Lou, Y.; Yang, L.; Gao, D.; He, D.; et al. Estimating the unreported number of novel coronavirus (2019-ncov) cases in China in the first half of january 2020: A data-driven modelling analysis of the early outbreak. J. Clin. Med. 2020, 9, 388. [Google Scholar] [CrossRef] [Green Version]
- Anastassopoulou, C.; Russo, L.; Tsakris, A.; Siettos, C. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PLoS ONE 2020, 15, e0230405. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Chen, H. Modeling the epidemic dynamics and control of COVID-19 outbreak in China. Quant. Biol. 2020, 8, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Dur-e-Ahmad, M.; Imran, M. Transmission Dynamics Model of Coronavirus COVID-19 for the Outbreak in Most Affected Countries of the World. Int. J. Interact. Multimed. Artif. Intell. 2020, 6, 4. [Google Scholar] [CrossRef]
- Mizumoto, K.; Kagaya, K.; Chowell, G. Early epidemiological assessment of the transmission potential and virulence of coronavirus disease 2019 (COVID-19) in Wuhan City, China, January–February, 2020. BMC Med. 2020, 18, 1–9. [Google Scholar] [CrossRef]
- Zhu, H.; Li, Y.; Jin, X.; Huang, J.; Liu, X.; Qian, Y.; Tan, J. Transmission dynamics and control methodology of COVID-19: A modeling study. Appl. Math. Model. 2021, 89, 1983–1998. [Google Scholar] [CrossRef]
- Sun, T.; Wang, Y. Modeling COVID-19 epidemic in Heilongjiang province, China. Chaos Solitons Fractals 2020, 138, 109949. [Google Scholar] [CrossRef]
- Davies, N.G.; Klepac, P.; Liu, Y.; Prem, K.; Jit, M.; Pearson, C.A.B.; Quilty, B.J.; Kucharski, A.J.; Gibbs, H.; Clifford, S.; et al. Age-dependent effects in the transmission and control of COVID-19 epidemics. Nat. Med. 2020, 26, 1205–1211. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, J.; Zhao, H.; Shi, Y.; Wang, K.; Wu, P.; Shi, L. Modelling and assessing the effects of medical resources on transmission of novel coronavirus (COVID-19) in Wuhan, China. Math. Biosci. Eng. 2020, 17, 2936–2949. [Google Scholar] [CrossRef]
- Aghaali, M.; Kolifarhood, G.; Nikbakht, R.; Saadati, H.M.; Hashemi Nazari, S.S. Estimation of the serial interval and basic reproduction number of COVID-19 in Qom, Iran, and three other countries: A data-driven analysis in the early phase of the outbreak. Transbound. Emerg. Dis. 2020, 67, 2860–2868. [Google Scholar] [CrossRef]
- Jung, S.M.; Akhmetzhanov, A.R.; Hayashi, K.; Linton, N.M.; Yang, Y.; Yuan, B.; Kobayashi, T.; Kinoshita, R.; Nishiura, H. Real-time estimation of the risk of death from novel coronavirus (COVID-19) infection: Inference using exported cases. J. Clin. Med. 2020, 9, 523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, S.; Lin, Q.; Ran, J.; Musa, S.S.; Yang, G.; Wang, W.; Lou, Y.; Gao, D.; Yang, L.; He, D.; et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: A data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020, 92, 214–217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Read, J.M.; Bridgen, J.R.E.; Cummings, D.A.T.; Ho, A.; Jewell, C.P. Novel coronavirus 2019-nCoV (COVID-19): Early estimation of epidemiological parameters and epidemic size estimates. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 2021, 376, 20200265. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef] [Green Version]
- Tian, H.; Liu, Y.; Li, Y.; Wu, C.H.; Chen, B.; Kraemer, M.U.G.; Li, B.; Cai, J.; Xu, B.; Yang, Q.; et al. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science 2020, 368, 638–642. [Google Scholar] [CrossRef] [Green Version]
- Riou, J.; Althaus, C.L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance 2020, 25, 2000058. [Google Scholar] [CrossRef]
- Tian, J.; Wu, J.; Bao, Y.; Weng, X.; Shi, L.; Liu, B.; Yu, X.; Qi, L.; Liu, Z.; Tian, J.; et al. Modeling analysis of COVID-19 based on morbidity data in Anhui, China. Math. Biosci. Eng. 2020, 17, 2842–2852. [Google Scholar] [CrossRef]
- Zhuang, Z.; Zhao, S.; Lin, Q.; Cao, P.; Lou, Y.; Yang, L.; Yang, S.; He, D.; Xiao, L. Preliminary estimates of the reproduction number of the coronavirus disease (COVID-19) outbreak in Republic of Korea and Italy by 5 March 2020. Int. J. Infect. Dis. 2020, 95, 308–310. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Dong, Y.; Yu, X.; Wang, H.; Tsamlag, L.; Zhang, S.; Chang, R.; Wang, Z.; Yu, Y.; Long, R.; et al. Estimation of reproduction numbers of COVID-19 in typical countries and epidemic trends under different prevention and control scenarios. Front. Med. 2020, 14, 613–622. [Google Scholar] [CrossRef] [PubMed]
- Kuniya, T. Prediction of the epidemic peak of coronavirus disease in Japan, 2020. J. Clin. Med. 2020, 9, 789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Musa, S.S.; Zhao, S.; Wang, M.H.; Habib, A.G.; Mustapha, U.T.; He, D. Estimation of exponential growth rate and basic reproduction number of the coronavirus disease 2019 (COVID-19) in Africa. Infect. Dis. Poverty 2020, 9, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Nguemdjo, U.; Meno, F.; Dongfack, A.; Ventelou, B. Simulating the progression of the COVID-19 disease in Cameroon using SIR models. PLoS ONE 2020, 15, e0237832. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.A.; Al-Najafi, A. Modeling, Control, and Prediction of the Spread of COVID-19 Using Compartmental, Logistic, and Gauss Models: A Case Study in Iraq and Egypt. Processes 2020, 8, 1400. [Google Scholar] [CrossRef]
- Sahafizadeh, E.; Sartoli, S. Epidemic curve and reproduction number of COVID-19 in Iran. J. Travel Med. 2020, 27, 1–2. [Google Scholar] [CrossRef]
- Khosravi, A.; Chaman, R.; Rohani-Rasaf, M.; Zare, F.; Mehravaran, S.; Emamian, M.H. The basic reproduction number and prediction of the epidemic size of the novel coronavirus (COVID-19) in Shahroud, Iran. Epidemiol. Infect. 2020, 148, e115. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Ke, R.; Romero-Severson, E.; Sanche, S.; Hengartner, N. Estimating the reproductive number R0 of SARS-CoV-2 in the United States and eight European countries and implications for vaccination. J. Theor. Biol. 2021, 517, 110621. [Google Scholar] [CrossRef]
- Noreen, N.; Naveed, I.; Dil, S.; Ullah Khan Niazi, S.; Saleem, S.; Mohiuddin, N.; Ullah Khan, N.; Noor, B.; Ali Khan, M.; Khudaid Khan, F. Trend analysis of exponential increase of COVID-19 cases in Pakistan: An interpretation. Glob. Biosecurity 2020, 2. [Google Scholar] [CrossRef]
- Alsayed, A.; Sadir, H.; Kamil, R.; Sari, H. Prediction of epidemic peak and infected cases for COVID-19 disease in Malaysia, 2020. Int. J. Environ. Res. Public Health 2020, 17, 4076. [Google Scholar] [CrossRef] [PubMed]
- Crokidakis, N. Modeling the early evolution of the COVID-19 in Brazil: Results from a susceptible-infectious-quarantined-recovered (SIQR) model. Int. J. Mod. Phys. C 2020, 31, 2050135. [Google Scholar] [CrossRef]
- Tuite, A.R.; Fisman, D.N.; Greer, A.L. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ 2020, 192, E497–E505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dharmaratne, S.; Sudaraka, S.; Abeyagunawardena, I.; Manchanayake, K.; Kothalawala, M.; Gunathunga, W. Estimation of the basic reproduction number (R0) for the novel coronavirus disease in Sri Lanka. Virol. J. 2020, 17, 1–7. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Abdulla, O.; Kallström, A.; Valderrama, C.; Kauhanen, J. Simulation of the Progression of the COVID-19 Outbreak in Northwest Syria Using a Basic and Adjusted SIR Model. Zoonotic Dis. 2022, 2, 44-58. https://doi.org/10.3390/zoonoticdis2020006
Al-Abdulla O, Kallström A, Valderrama C, Kauhanen J. Simulation of the Progression of the COVID-19 Outbreak in Northwest Syria Using a Basic and Adjusted SIR Model. Zoonotic Diseases. 2022; 2(2):44-58. https://doi.org/10.3390/zoonoticdis2020006
Chicago/Turabian StyleAl-Abdulla, Orwa, Agneta Kallström, Camilo Valderrama, and Jussi Kauhanen. 2022. "Simulation of the Progression of the COVID-19 Outbreak in Northwest Syria Using a Basic and Adjusted SIR Model" Zoonotic Diseases 2, no. 2: 44-58. https://doi.org/10.3390/zoonoticdis2020006
APA StyleAl-Abdulla, O., Kallström, A., Valderrama, C., & Kauhanen, J. (2022). Simulation of the Progression of the COVID-19 Outbreak in Northwest Syria Using a Basic and Adjusted SIR Model. Zoonotic Diseases, 2(2), 44-58. https://doi.org/10.3390/zoonoticdis2020006







