Abstract
Residual feed intake (RFI) is the preferred measurement for feed efficiency in beef cattle, but it is laborious to determine. Data from two experiments of growing bulls (test period durations of 56 and 63 days) were used to examine how a reduction in the number of times the animals were weighed and the shortening of the length of the observation period affect the reliability of the RFI determination. We introduce two easily understandable probability measures for assessing reliability. ‘The consistency of the pair-wise ranks’ gives the probability that the rank of any two animals compared remains the same when the amount of data is reduced. ‘The consistency of the thirds’ gives the probabilities that an individual animal will remain in the same, i.e., the lowest, middle, or highest, third of animals. The reliability of the results was not greatly affected when the weighing interval was reduced from one week to four weeks. However, shortening the test period resulted in a marked reduction in the reliability of RFI. If individual feed intake is automatically measured, the workload required for RFI measurements can most effectively be reduced by reducing the number of weighing times but keeping the duration of the test period long enough.
1. Introduction
Feed costs represent a significant part of the variable costs in beef production. Thus, animals that have high feed efficiency can improve production profitability. In addition, due to increasing environmental requirements, considerable interest exists in improving feed efficiency to reduce the environmental footprint of beef production. Residual feed intake (RFI) has become the preferred measurement of feed efficiency in beef cattle in recent years [1]. Since feed efficiency is an inheritable trait, RFI can be used to enhance productivity through selective breeding. The definition of RFI is the difference between the observed and expected feed intake needed to support both the maintenance of body weight (BW) and growth. Because RFI does not depend on the level of animal production, it is a useful concept to examine the biological mechanisms associated with inter-animal variation in feed efficiency [2].
The RFI is defined for individual animals in a given population as the residuals of a multiple regression model where dry matter (DM) intake (DMI) is regressed according to variables describing the energy expenditure [1]. The size of the animals (described typically by mid-test metabolic body weight, (MMBW)) and growth (described by average daily gain, (ADG)) are the two basic independent variables. The model can be adjusted for the fat content (described by sub-cutaneous back fat thickness, (BF) [3,4,5] and cross-sectional area of the longissimus dorsi muscle (LM) [6], as well as the breed and specific group of animals being tested [7] to improve the explanatory power of the models.
Determining the RFI requires laborious and costly test periods. Attempts have been made to determine the optimum duration of the test period and the optimum number of times the animals need to be weighed to improve the efficiency of the RFI measurements, or the effects of missing data on the reliability of RFI values [4,8,9,10]. This optimization approach necessitates methods to compare the RFIs obtained from the alternative models based on fewer data to the RFIs obtained from the models with full data (i.e., ‘gold standard’ models). The list of measures utilized in the scientific literature for these comparisons is impressive: Spearman’s correlation, Pearson’s correlation (phenotypic correlation), the concordance correlation coefficient, genetic correlation, the coefficient of determination, comparison of regression coefficients, (phenotypic) variance, and relative (phenotypic) variance [4,6,7,8,9,10,11,12]. Undoubtedly, these papers enhance the understanding of determining RFI efficiently but still reliably. However, few of them justify, in detail, the use of indices or present a priori thresholds for acceptable reliability of the RFIs based on the regression models utilizing fewer data.
The RFI of an individual animal is always in relation to the other animals used to fit the regression model from which the RFI is determined. Therefore, the rank of the individual animal has significant importance when breeding for high feed efficiency (low RFI; [4,8]. Accordingly, Spearman’s rank-order correlation coefficient ρ (and its estimate rs) is a logical index for comparing alternative RFIs (yi) to the gold-standard RFI (xi). On the other hand, the interpretation of rs is not easy, with the crucial question being what is the lowest acceptable value below 1 for rs? Scatterplots of ranks (yi on xi) may help to illustrate the situation, but do not quantify the transitions in rank in a straightforward way. An alternative to Spearman’s rank-order correlation coefficient is Kendall’s rank-order correlation coefficient τ (or more precisely, its estimate t), which is based on the number of concordant (or ‘agreement’) and discordant (or ‘disagreement’) pairs, i.e., ‘the difference between the probability that, in the observed data, X and Y are in the same order and the probability that the X and Y data are in different order’ [13]. For example, t = 0.90 means that 95% of the pair-wise orders of the animals remain the same (and 5% do not). This is also our a priori threshold for an acceptable t.
The main aim of our paper was to investigate and propose the use of Kendall’s correlation, and ‘the consistency of pair-wise ranks’ deduced from it, as an easy means to describe and concretize what rs between the alternative RFIs and gold-standard RFIs mean in practice, as we reduce the data used for calculating RFI step-by-step. In many RFI studies, experimental animals have been classified into low-, medium-, and high-RFI groups according to their RFI values, with equal numbers of animals in each of these groups. This ‘thirds approach’ is particularly common in studies on associations between RFI, physiology, and behavior of the animals [14,15,16]. Thus, our aim was also to demonstrate how the reduction of data affects this classification. We introduce ‘the consistency of the thirds’ to assess the consequences of this reduction. Here, we were particularly interested in the probability of the animals remaining in the lowest third (with the best feed efficiency), and our a priori threshold for an acceptable situation was 90%.
2. Materials and Methods
2.1. Animals, Management, Feeding and Measurements
Three experiments were conducted in the experimental cattle unit at the Natural Resources Institute Finland (Luke) in Ruukki (64°44′ N, 25°15′ E). In the experimental barn at Luke, the bulls were housed in an uninsulated barn in pens (10.0 m × 5.0 m; 5 bulls in each pen), providing 10.0 m2 per bull. The rear half of the pen area was a peat-bedded lying area, and the fore half was a feeding area with a solid concrete floor. The bulls had free access to water throughout the experiments. The animals were managed according to Finnish legislation regarding the use of animals in scientific experimentation.
The first experiment started in December 2017, the second in September 2018, and the third in November 2019. The experiments lasted 56, 56, and 63 days, respectively. The first experiment was conducted using 55 purebred Hereford (HF) and 55 purebred Charolais (CH) beef bulls. All animals were purchased from commercial herds. The bulls were born in spring, 2017, spent their first summer with their dams on pasture, and were moved to the experimental cattle unit at Luke on average at the age of seven months. The second experiment was conducted using 55 Holstein (HO) and 55 Nordic Red (NR) dairy bulls. All animals were purchased from local dairy farms at an average age of 21 d. From three weeks to six months of age, the animals were housed in an insulated barn and received milk replacer (until the age of 75 d), grass silage, and a commercial pelleted calf starter. The bulls were moved to the experimental cattle unit at Luke at the age of six months. The third experiment was conducted using 52 Aberdeen Angus (AA) and 52 Simmental (SI) beef bulls. All animals were purchased from commercial herds. The bulls were born in spring, 2019, spent their first summer with their dams on pasture, and moved to the experimental cattle unit at Luke at the age of approximately seven months.
During the experimental period, the bulls were fed total mixed rations (TMR) ad libitum (proportionate refusals of 5%). The rations were carried out using a mixer wagon (Trioliet BW, Oldenzaal, The Netherlands), produced every day and offered two times a day. In experiments 1 and 3, the diet of beef bulls included grass silage (GS) (600 g/kg DM), rolled barley grain (385 g/kg DM), and a mineral–vitamin mixture (15 g/kg DM). In experiment 2, the diet of dairy bulls included GS (500 g/kg DM), rolled barley grain (485 g/kg DM), and a mineral–vitamin mixture (15 g/kg DM). During the experiments, feed sub-samples were taken twice a week, pooled over periods of four weeks, and stored at −20 °C prior to analyses. Thawed samples were analyzed for DM, crude protein, and neutral detergent fiber as described by Huuskonen et al. [17]. The metabolizable energy and metabolizable protein concentrations were calculated according to Finnish Feed Tables [18]. The chemical compositions and feeding values of the TMR used in the experiments are presented in Table 1.

Table 1.
Chemical compositions and feeding values of the total mixed rations used in experiments 1, 2, and 3.
A GrowSafe feed intake system (model 4000E; GrowSafe Systems Ltd., Airdrie, AB, Canada; see validation studies, e.g., [19,20]) was used to record the individual daily feed intake so that each pen contained two GrowSafe feeder nodes. Before the start of the experiments, each feeder node was calibrated with standard weights. In addition, it was monitored daily during the experiments that the measuring equipment showed zero when the feeder node was empty. The animals were weighed using a TruTest scale (model EziWeigh7i, Allied Farmers, Auckland, New Zealand) in experiments 2 and 3 at the beginning of the experiment and, thereafter, approximately every 7 days until the end of the experiment and, in experiment 1, at the beginning, middle, and end of the experiment. Before the start of each weighing session, the weighing equipment was calibrated with standard weights.
The average DMI, MMBW, and ADG were calculated for the entire experimental period (all experiments; ‘gold standard’, S1, in experiments 2 and 3) and for the data subsets with fewer data (shorter period and/or fewer weighing times) in experiments 2 and 3 (standards 2–15, S2–15, Table 2 and Table 3). The daily feed intake of each animal was converted to the daily DMI based on the dietary DM content. The average DMI for each standard was calculated based on the daily DMI and the number of days in each period. The average ADG was calculated as the slope of the linear regression of weight for time (days) (i.e., the growth curve). The mid-test BW was determined from the growth curve and increased to the power of 0.75 to obtain the MMBW. For experiment 3, 10 out of the 104 DMI measurements for the first week were missing. This was accounted for by imputing values using a linear model with the animals in the second and third week feeding as covariates.

Table 2.
Timeline and comparisons of the standards (or data subsets) (S1–15) of experiment 2 with dairy breed bulls (55 Holstein and 55 Nordic Red dairy bulls). Standards S1–15 varied in terms of the duration of test periods (d) and the number of times the animals were weighed (W). Note that in the description of the standards, D refers to the total duration of the test period for standards S1–15 and d refers to the order of the days in S1. Start day of the experiment (d 1) was the day when feed intake measurements were initiated. The grey shading indicates the periods from which the daily dry matter intake data were used. The numbers in the cells of each data subset indicate the weighing days for that test period.

Table 3.
Timeline and comparisons of the standards (or data subsets) (S1–15) of experiment 3 with beef breed bulls (52 Aberdeen Angus and 52 Simmental). Standards S1–15 varied in terms of the duration of test periods (d) and the number of times the animals were weighed (W). Note that in the description of the standards, D refers to the total duration of the test period for standards S1–15 and d refers to the order of the days in S1. Start day of the experiment (d 1) was the day when feed intake measurements were initiated. The grey shading indicates the periods from which the daily dry matter intake data were used. The numbers in the cells of each data subset indicate the weighing days for that test period.
Ultrasound measurements were taken at the beginning and end of the test period in experiments 2 and 3 and only at the end of the test period in experiment 1. BF (mm) and LM (cm2) were measured at the 1st lumbar vertebrae as described by Huuskonen and Pesonen [21] with a Pie 200 SLC scanner (FPS 8; DFR 2–4 inches) equipped with the QUIP (Quality Ultrasound Indexing Program) software (Version 2.6) and an ASP-18 transducer (3.5 MHz) without a stand-off pad. The average age and live weight at the beginning of the experiment, ADG, average DMI, and MMBW of the experiments, live weight at the end of the experiment, and ultrasound measurements at the beginning (experiments 2 and 3) and end (all experiments) of the experiments are given in Table 4.

Table 4.
Age, live weight, ultrasound traits, growth, dry matter intake, and metabolic body weight of the bulls in three experiments.
2.2. Modelling and Comparing RFI Values
RFI modelling was performed in three steps: (i) Models with the full test period and all times weighed included (all experiments), (ii) models with the full test period and all times weighed included and adjusted for the BF and LM (all experiments), (iii) and models with a shortened test period and/or reduced number of times weighed.
In the first step, RFI for the animal i was modeled using a linear model
where DMI is the dry matter intake (kg/d), ADG is the average daily growth (kg/d), MMBW is the mid-test metabolic body weight (kg), and εi is the error term, which is for the fitting assumed to be independent and normally distributed. For experiment 1, all 110 animals were included in the fit. For experiment 2, two of the 110 animals were removed as significant outliers. For experiment 3, 4 of the 104 animals were removed. Removing the outliers improved the R2 values of the fits from 0.26 to 0.42 for experiment 2 and from 0.46 to 0.63 for experiment 3. In experiment 2, the two outliers were NR bulls with one having an exceptionally high average DMI of 13.3 kg/d over the experiment, while the other outlier had one of the lowest DMI values at 5.4 kg/d while simultaneously being in the highest quartile of MMBW. The ADG values for the two outliers did not significantly deviate from the average. For experiment 3, the four outliers were AA bulls with one outlier having the lowest average DMI by far at 5.3 kg/d (the second lowest had 6.5 kg/d) while the three other outliers had DMI intake values in the lower quartile, varying between 6.6 and 7.0 kg/d, while having MMBW values in the upper quartile between 91 kg and 97 kg. As in experiment 2, the outliers had rather average ADG values. As a safety measure, the analysis was also run with complete data and the conclusions did not change.
In the second step, the benefit of including BF and LM in the model was assessed by comparing models with one of these or both as additional predictors. For all three experiments, models with BF and LM measured at the end of the experiment were fitted. For experiments 2 and 3, corresponding measurements were also taken at the beginning of the experiment. For these two datasets, the models were also fitted with the average of the start and end values. The quality of the fit was compared using the Akaike Information Criterion (AIC) and an adjusted R2 value calculated using the formula
where n is the number of observations and p is the number of parameters in the model. After these predetermined comparisons, we also explored models with BF and/or LM measured at the beginning of the experiment as well as using the change in these quantities as predictors. These models turned out not to improve the fit (see Results and Discussion). The need to control for cattle breed was explored by performing permutation tests (a non-parametric test was chosen due to the non-normality of the RFI values of experiment 1) on the RFI distributions of the two breeds in each experiment. For all three experiments, p-values exceeding 0.8 were obtained, which was strong evidence that there was no need to treat the breeds separately.
Since the BF and LM did not result in improving the model fit in a remarkable way (see Results and Discussion), in the third step, comparisons between standards using the different number of times the animals were weighed and/or different durations of the test periods were carried out using the model in Equation (1). The comparisons were carried out with the data of experiments 2 and 3 using 15 different standards (i.e., data subsets) denoted by S1, S2, …, and S15 (Table 2 and Table 3). The S1 was the ‘gold standard’ with all available measurements. The S2 and S3 had the same duration for the feed intake measurements as S1 but some of the weighing measurements were left out. In S4–S11, the test period was shortened from the beginning or the end of the test period in approximately one-week steps. Standards S12–S15 were shortened by three weeks as compared to S1. In order to ensure a logical numbering system S1–S15, S6 corresponded to S12, and S10 corresponded to S13. The total length of the test period differed between the two experiments, 56 and 63 days in experiments 2 and 3, respectively. Consequently, the number of days between weighing was not exactly the same in the two experiments.
When comparing measurement standards, the quantity of interest was the ranking of the animals by RFI εi with respect to the gold-standard S1, i.e., using the full dataset. Comparisons were carried out in three ways: By calculating two rank-order correlations, Spearman’s correlations, and Kendall’s correlations between the S1 residuals and S2–S15 residuals, and by comparing the transition probabilities between the upper, middle, and lower thirds. The transition probabilities between the thirds were calculated by taking 105 re-samplings (also known as bootstrap samples [22]) of the animals with a replacement and making fits for S1–S15 for each sample. A small random term was used, so that the resampling would not result in equal ranks, which would make the determination of the thirds problematic. The transition probabilities were then calculated as the average fraction of animals that were in the third X in S1 and third Y in the comparative standard.
All models and comparisons were performed using the statistical software R [23].
3. Results
3.1. Additional Covariates
The AIC and adjusted R2 values are presented in Figure 1 for the three experiments. The estimates, standard errors, and p-values for the model with BF and LM at the end of the experiment are given in Table 5. For experiments 1 and 3, the best-fitting model based on adjusted R2 and AIC values is the simplest model without the BF and LM. The adjusted R2 values for these two datasets varied between 0.61 and 0.63. For experiment 2, the models with the LM (either at the end or the average of the beginning and end values) fitted slightly better, with adjusted R2 values of 0.44, compared to 0.42 of the model with only the MMBW and ADG as covariates. However, the p-value of the LM term was 0.02–0.04 in the two alternative models without the BF term, which is not strong evidence given that the models were fitted to three distinct datasets. A simple Bonferroni correction, without even considering the multiple parameters in the model, [24] to the p-values would result in an adjusted p-value of 0.06–0.12, i.e., the result is not statistically significant after adjusting for the three separate fits.
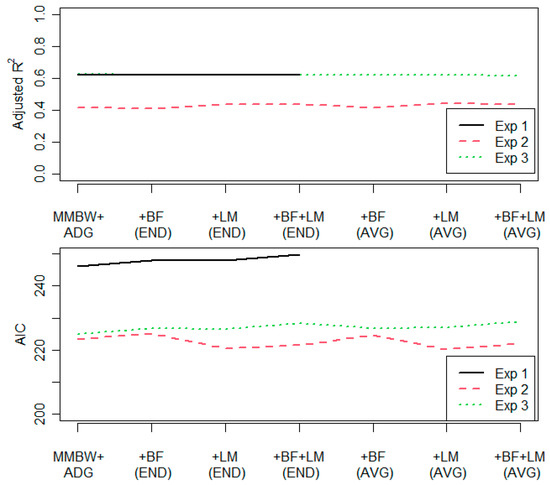
Figure 1.
The adjusted R2 values and the Akaike Information Criterion (AIC) for the fitted models with mid-test metabolic body weight (MMBW, kg) and average daily gain (ADG, kg/d), and models where various combinations of the sub-cutaneous back fat thickness (BF, mm) and the cross-sectional area of longissimus dorsi muscle (LM, cm2) are included. END refers to measurement at the end of the experimental period and AVG to an average of measurements at the end and beginning of the experimental period.

Table 5.
Estimates, standard errors (SE), and p-values for the regression coefficients with a full model including all measured variables. The sub-cutaneous back fat thickness (BF, mm) and cross-sectional area of longissimus dorsi muscle (LM, cm2) measurements are those measured at the end of the experiment since those values were available for all three experiments. For experiments 2 and 3, the model was also fitted using the average BF and LM values. The results were largely the same, except that the p-value of BF in experiment 2 was 0.04.
3.2. Reducing the Number of Times Weighed or the Duration of the Test Period
The regression coefficients, standard errors, p-values, and R2 values are given for experiment 2 in Table 6 and experiment 3 in Table 7. For experiment 2, the estimates and R2 values are not meaningfully different (R2: 0.41–0.42) for S1, S2, and S3, which have the same observation period but differ in the number of times the animals were weighed. Standards S4–S15 show some notable deviations in the estimates, with S6/12, S7, and S11 standing out with their low R2 values (R2: 0.30–0.34) as compared to S1. Experiment 3 tells a similar story, with the results for S1, S2, and S3 being consistent (R2 = 0.62–0.63) but S4–S15 deviating more either with respect to the estimates or the R2 value. In particular, S7, S8, S11, and S15 stand out with their relatively low R2 values (0.40–0.50).

Table 6.
Regression coefficients, their standard errors (SE), and the R2 value for different measurement standards (S1–15, see Table 2 for the details of the standards) based on the data from experiment 2.

Table 7.
Regression coefficients, their standard errors (SE), and the R2 value for different measurement standards (S1–15, see Table 3 for the details of the standards) based on the data from experiment 3.
The results comparing the RFI values (i.e., the residuals of these models) using Spearman’s and Kendall’s correlations are given in Table 8. The standards S1, S2, and S3 are closest to each other in terms of Spearman’s correlation estimate rs and Kendall’s correlation estimate t, with values pf rs = 0.98–0.99 and t = 0.89–0.91 for S1 vs. S2, and rs = 0.97–0.98 and t = 0.86–0.88 for S1 vs. S3. For other standards, Spearman’s correlation is below 0.9 and Kendall’s correlation is below 0.8, which can be chosen as (somewhat arbitrary) numerical limits, in at least one of the experiments. While choosing a numerical limit for Spearman’s correlation is difficult because the values are not intuitive, the choice of 0.8 as a limit for Kendall’s correlation is easier to argue. For example, Kendall’s t of 0.8 would correspond to a situation where our ranking of two cows works 90% of the time and 10% of the time it fails. For experiment 2, the worst performers as measured by t were S7, S9, and S11 with t < 0.65, and for experiment 3, were S4 and S7 with t < 0.5. For experiment 2, which was the slightly shorter experiment, even the worst standards had correlations of rs = 0.78 or t = 0.60 with the golden-standard RFIs, while for experiment 3, the values were as low as rs = 0.60 or t = 0.43.

The probabilities of transitions between the thirds are presented in Supplementary Materials (Tables S1 and S2). The probability that an individual animal remained in the same third as in S1, i.e., ‘the consistency of the thirds’, was 89–95% (the lowest third), 81–87% (the middle third), and 89–92% (the highest third) for S2 and S3, whereas the corresponding probabilities for S4–15 were 53–91%, 26–83%, and 57–93%, respectively. It is worth noting that if S9 of experiment 3 is ignored, these ranges are 53–84%, 26–72%, and 57–88%. Note that these probabilities are constantly lower for the middle third than for the lower and upper thirds, since only the middle third can ‘leak’ in both directions.
4. Discussion
4.1. Additional Covariates
Based on the used model comparisons, the ultrasound measurements of the BF and LM did not improve the prediction of DMI for young bulls when the body weight and average daily growth were controlled for. It is also possible that genetic factors related to RFI could manifest themselves through muscle size and fat composition, in which case controlling for these factors would be fundamentally problematic.
However, in this case, we would have expected the MMBW and ADG to drastically decrease in statistical significance if mediating the BF and LM were controlled for, which we did not observe. Thus, including such factors does not seem counterproductive, yet the benefits are marginal. This is in contrast to numerous other studies that have concluded that including either the BF or LM, or both, improves the prediction of the DMI [3,25,26,27,28,29,30,31]. It is beyond the scope of the present paper to discuss the possible reasons for this discordance. Instead, the main meaning of our finding is that we can neglect the BF or LM while evaluating the effects of reducing the number of times the animals are weighed or shortening the duration of the test period on the reliability of RFI results.
4.2. Reducing the Number of Times Weighed or the Duration of the Test Period
The results of all three methods, the regression equation approach, the rank correlation co-efficient approach, and the ‘consistency of the thirds’ approach, show that shortening the duration of the test period led to unreliable results, whereas reducing the number of times the animals were weighed within the full period had only minor effects on reliability. In fact, we stretch our a priori acceptability thresholds slightly here, since none of our results, not for S2 nor S3, met our original thresholds fully for Kendall’s correlation (t = 0.90) and the probability of an individual remaining in the lowest third (90%) in all experiments. In experiment 2, these values were 0.89 and 92%, and 0.91 and 89% for S2 and S3, respectively. The corresponding values in experiment 3 were 0.91 and 95% (the only case fully meeting our a priori criterion), and 0.88 and 94% for S2 and S3, respectively. However, for all the cases, at least one of the two criteria was fulfilled.
When the duration of the test periods used in this study was shortened, it reduced the reliability of the RFI. The results support earlier studies aiming at optimizing the RFI test period duration in the sense that shortening the test period too much below 8–9 weeks seems to reduce the reliability of the RFI results [7,9]. Typically, longer periods are recommended, e.g., [32] 10–12 w, [11] 12 w, and [10] 10 w. Additionally, different durations for DMI and BW (or ADG) measurements have been suggested as a way to optimize RFI measurements, e.g., [4]. We kept the test period duration the same for both DMI and ADG but optimized the workload by reducing the number of times the animals were weighed within the test period. We observed that weekly weighing was not required, but even weighing the animals only every fourth week in the test period can suffice. Less frequent weighing means less stress to the animals and less work.
To the best of our knowledge, there are no earlier beef cattle studies where t would have been utilized to assess the reliability of RFI measurements with reduced data. Instead, rs has been used widely. Either rs = 0.90 [9] or 0.95 [4,7,10,11] has been regarded as the threshold for acceptable reliability. Gilpin [33] presents a tau-to-rho conversion formula (and tables) for meta-analytic purposes, i.e., for obtaining approximate rs values if one knows the t values only. The accuracy of the approximation is best for large samples from bivariate normal populations. According to the conversion table presented by Gilpin [33], the acceptance limits of 0.90 and 0.95 for rs correspond to t-values 0.73 and 0.81, respectively. Thus, our threshold for sufficient reliability (t = 0.90) was more stringent than in the earlier studies.
Kendall’s tau is calculated as (C-D)/(C-D), where C is the number of concordant pairs (the order of two animals in the rank is the same in the alternative dataset as in the gold standard dataset) and D is the number of discordant pairs (the order of two animals is reversed compared to the gold standard) when all animal pairs are compared [13]. If the number of animals is N, the total number of comparisons is N × (N − 1)/2. With little arithmetic, one can see that tau can be converted to a percentage of C (C%) with simple formulae C% = tau × 50 + 50. C%, in turn, can be interpreted as the probability of obtaining the same rank between any two animals with the alternative method as compared to the gold standard, or ‘the consistency of rank’. We argue that this probability presentation is easier to comprehend than the commonly used rs, and, for example, rs = 0.90 corresponds to C% = 87% and rs = 0.95 to C% = 91%.
It is worth noting that earlier RFI papers [4,7,9,10,11] did not use rs as the only criteria for assessing acceptable reliability. In addition, the thresholds can be also situation specific and benefit from an inspection of the data in more detail in a way that better considers the specific aims of measuring RFI in a certain situation. This is illustrated nicely by Castilhos et al. [11] who showed that shortening the test period from 122 d to 84 d (rs = 0.954) led to only one out of eleven animals losing their ‘Elite classification’ status, whereas shortening the period to 54 d (rs = 0.879) resulted in four animals losing this status. In fact, the approach presented by Castilhos et al. [11] resembles our ‘consistency of the thirds’ approach, since our approach could be extended to use any quantiles suited best to a specific situation. Finally, the ‘consistency of the thirds’ approach also gives a simple probability that is easy to interpret while assessing the reliability of the alternative methods as compared to the gold standard.
5. Conclusions
We studied the optimization of RFI measurements in beef cattle, and the ways to assess the effects of optimization on the reliability of the results. The results showed that if an automatic system for measuring individual feed consumption is used, the workload required for RFI measurements can be most effectively reduced by reducing the number of times the animals are weighed but keeping the duration of the test period long enough. The reliability of the results is not greatly affected, although the weighing interval is reduced from one week to four weeks. Our results confirmed the earlier findings that shortening the duration of the test period much below 8–9 weeks reduces the reliability of the RFI measurements markedly.
We introduce two easily understandable probability measures for assessing the reliability of RFI. ‘The consistency of the pair-wise ranks’ is based on first calculating Kendall’s tau and converting it to the probability that the rank of any two animals compared remains the same when the amount of data for determining RFI is reduced (or optimized). ‘The consistency of the thirds’, in turn, gives the probabilities that an individual animal will remain in the same, i.e., the lowest, middle, or highest, third of animals when reduced data are used compared to the situation when the full dataset is used. A similar consistency can be calculated using any other quantiles than terciles.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ruminants2040028/s1. Table S1: The transition matrix between lowest, middle, and highest thirds in residual eating derived from experiment 2. The percentage of transitions between the thirds has been calculated using a non-parametric bootstrap approach to obtain realistic estimates for the transitions between the lowest and highest thirds, which were not observed for most measurement standards in the experiment. Table S2: The transition matrix between lowest, middle, and highest thirds in residual eating derived from experiment 3. The percentage of transitions between the thirds has been calculated using non-parametric bootstrap approach to obtain realistic estimates for the transitions between the lowest and highest thirds, which were not observed for most measurement standards in the experiment.
Author Contributions
Conceptualization, J.M., J.K., M.P., A.H. and K.M.; methodology, J.M. and J.K; validation, J.M., J.K., M.P., A.H. and K.M.; formal analysis, J.M. and J.K.; investigation, J.M., J.K., M.P., A.H. and K.M.; data curation, J.M., J.K., A.H. and K.M.; writing—original draft preparation, J.M., J.K., M.P., A.H. and K.M; writing—review and editing, J.M., J.K., M.P., A.H. and K.M.; supervision, J.M. and A.H.; project administration, K.M.; funding acquisition, J.M., A.H. and K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partly funded by the Oiva Kuusisto Foundation (grant number 20190004).
Institutional Review Board Statement
Ethical review and approval were waived for this study due to using previously published animal data in this analysis. The experimental animals in previous experiments on which the data were based were managed according to Finnish and EU legislation regarding the use of animals in scientific experimentation.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We wish to express our gratitude to Jarkko Kekkonen and his personnel for technical assistance and care of the experimental animals in the previous experiments on which the data were based.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kenny, D.A.; Fitzsimons, C.; Waters, S.M.; McGee, M. Invited Review: Improving Feed Efficiency of Beef Cattle–the Current State of the Art and Future Challenges. Animal 2018, 12, 1815–1826. [Google Scholar] [CrossRef] [PubMed]
- Arthur, J.P.F.; Herd, R.M. Residual Feed Intake in Beef Cattle. Rev. Bras. Zootec. 2008, 37, 269–279. [Google Scholar] [CrossRef]
- Savietto, D.; Berry, D.P.; Friggens, N.C. Towards an Improved Estimation of the Biological Components of Residual Feed Intake in Growing Cattle. J. Anim. Sci. 2014, 92, 467–476. [Google Scholar] [CrossRef] [PubMed]
- Manafiazar, G.; Basarab, J.; McKeown, L.; Stewart-Smith, J.; Baron, V.S.; MacNeil, M.; Plastow, G. Optimizing Feed Intake Recording and Feed Efficiency Estimation to Increase the Rate of Genetic Gain for Feed Efficiency in Beef Cattle. Can. J. Anim. Sci. 2017, 97, 456–465. [Google Scholar] [CrossRef]
- Judge, M.M.; Conroy, S.; Hegarty, P.J.; Cromie, A.R.; Fanning, R.; Kelly, D.; Crofton, E.; Berry, D.P. Eating Quality of the Longissimus Thoracis Muscle in Beef Cattle–Contributing Factors to the Underlying Variability and Associations with Performance Traits. Meat Sci. 2021, 172, 108371. [Google Scholar] [CrossRef]
- Mao, F.; Chen, L.; Vinsky, M.; Okine, E.; Wang, Z.; Basarab, J.; Crews, D.H.; Li, C. Phenotypic and Genetic Relationships of Feed Efficiency with Growth Performance, Ultrasound, and Carcass Merit Traits in Angus and Charolais Steers. J. Anim. Sci. 2013, 91, 2067–2076. [Google Scholar] [CrossRef]
- Culbertson, M.M.; Speidel, S.E.; Peel, R.K.; Cockrum, R.R.; Thomas, M.G.; Enns, R.M. Optimum Measurement Period for Evaluating Feed Intake Traits in Beef Cattle. J. Anim. Sci. 2015, 93, 2482–2487. [Google Scholar] [CrossRef]
- Archer, J.A.; Arthur, P.F.; Herd, R.M.; Parnell, P.F.; Pitchford, W.S. Optimum Postweaning Test for Measurement of Growth Rate, Feed Intake, and Feed Efficiency in British Breed Cattle. J. Anim. Sci. 1997, 75, 2024–2032. [Google Scholar] [CrossRef]
- Wang, Z.; Nkrumah, J.D.; Li, C.; Basarab, J.A.; Goonewardene, L.A.; Okine, E.K.; Crews, D.H.; Moore, S.S. Test Duration for Growth, Feed Intake, and Feed Efficiency in Beef Cattle Using the GrowSafe System. J. Anim. Sci. 2006, 84, 2289–2298. [Google Scholar] [CrossRef]
- Marzocchi, M.Z.; Sakamoto, L.S.; Canesin, R.C.; dos Santos Gonçalves Cyrillo, J.; Mercadante, M.E.Z. Evaluation of Test Duration for Feed Efficiency in Growing Beef Cattle. Trop. Anim. Health Prod. 2020, 52, 1533–1539. [Google Scholar] [CrossRef]
- De Castilhos, A.M.; Branco, R.H.; Razook, A.G.; Bonilha, S.F.M.; Mercadante, M.E.Z.; de Figueiredo, L.A. Test Post-Weaning Duration for Performance, Feed Intake and Feed Efficiency in Nellore Cattle. Rev. Bras. Zootec. 2011, 40, 301–307. [Google Scholar] [CrossRef]
- Ahlberg, C.M.; Allwardt, K.; Broocks, A.; Bruno, K.; McPhillips, L.; Taylor, A.; Krehbiel, C.R.; Calvo-Lorenzo, M.; Richards, C.J.; Place, S.E.; et al. Test Duration for Water Intake, ADG, and DMI in Beef Cattle. J. Anim. Sci. 2018, 96, 3043–3054. [Google Scholar] [CrossRef] [PubMed]
- Siegel, S.; Castellan, N.J., Jr. Nonpareamteric Statistics for the Behavioral Sciences, 2nd ed.; McGraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Aldrighi, J.; Branco, R.H.; Cyrillo, J.N.d.S.G.; Magnani, E.; do Nascimento, C.F.; Bonilha, S.F.M.; Mercadante, M.E.Z. Ingestive Behavior and Temperament of Nellore Cattle Classified for Residual Feed Intake. Semin. Cienc. Agrar. 2019, 40, 457–468. [Google Scholar] [CrossRef]
- McKenna, C.; Keogh, K.; Porter, R.K.; Waters, S.M.; Cormican, P.; Kenny, D.A. An Examination of Skeletal Muscle and Hepatic Tissue Transcriptomes from Beef Cattle Divergent for Residual Feed Intake. Sci. Rep. 2021, 11, 8942. [Google Scholar] [CrossRef] [PubMed]
- Parsons, I.L.; Johnson, J.R.; Kayser, W.C.; Tedeschi, L.O.; Carstens, G.E. Characterization of Feeding Behavior Traits in Steers with Divergent Residual Feed Intake Consuming a High-Concentrate Diet. J. Anim. Sci. 2020, 98, skaa189. [Google Scholar] [CrossRef] [PubMed]
- Huuskonen, A.K.; Jaakkola, S.; Manni, K. Intake, Gain and Carcass Traits of Hereford and Charolais Bulls Offered Diets Based on Triticale, Barley and Grass Silages. Agric. Food Sci. 2020, 29, 318–330. [Google Scholar] [CrossRef]
- Luke Feed Tables and Nutrient Requirements. Available online: http://www.luke.fi/feedtables (accessed on 19 September 2022).
- DeVries, T.J.; von Keyserlingk, M.A.G.; Weary, D.M.; Beauchemin, K.A. Technical Note: Validation of a System for Monitoring Feeding Behavior of Dairy Cows. J. Dairy Sci. 2003, 86, 3571–3574. [Google Scholar] [CrossRef]
- Mendes, E.D.M.; Carstens, G.E.; Tedeschi, L.O.; Pinchak, W.E.; Friend, T.H. Validation of a System for Monitoring Feeding Behavior in Beef Cattle. J. Anim. Sci. 2011, 89, 2904–2910. [Google Scholar] [CrossRef]
- Huuskonen, A.K.; Pesonen, M. A Comparison of First-, Second- and Third-Cut Timothy Silages in the Diets of Finishing Beef Bulls. Agric. Food Sci. 2017, 26, 16–24. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R.J. An Introduction to the Bootstrap; Chapman and Hall/CRC: Boca Raton, FL, USA, 1994. [Google Scholar]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021.
- Bonferroni, C.E. Teoria Statistica Delle Classi e Calcolo Della Probabilità; Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze: Firenze, Italy, 1936; Volume 8. [Google Scholar]
- Basarab, J.A.; Price, M.A.; Aalhus, J.L.; Okine, E.K.; Snelling, W.M.; Lyle, K.L. Residual Feed Intake and Body Composition in Young Growing Cattle. Can. J. Anim. Sci. 2003, 83, 189–204. [Google Scholar] [CrossRef]
- Schenkel, F.S.; Miller, S.P.; Wilton, J.W. Genetic Parameters and Breed Differences for Feed Efficiency, Growth, and Body Composition Traits of Young Beef Bulls. Can. J. Anim. Sci. 2004, 84, 177–185. [Google Scholar] [CrossRef]
- Lancaster, P.A.; Carstens, G.E.; Ribeiro, F.R.B.; Tedeschi, L.O.; Crews, D.H. Characterization of Feed Efficiency Traits and Relationships with Feeding Behavior and Ultrasound Carcass Traits in Growing Bulls. J. Anim. Sci. 2009, 87, 1528–1539. [Google Scholar] [CrossRef] [PubMed]
- Lancaster, P.A.; Carstens, G.E.; Crews, D.H.; Welsh, T.H.; Forbes, T.D.A.; Forrest, D.W.; Tedeschi, L.O.; Randel, R.D.; Rouquette, F.M. Phenotypic and Genetic Relationships of Residual Feed Intake with Performance and Ultrasound Carcass Traits in Brangus Heifers. J. Anim. Sci. 2009, 87, 3887–3896. [Google Scholar] [CrossRef] [PubMed]
- Montanholi, Y.R.; Swanson, K.C.; Schenkel, F.S.; McBride, B.W.; Caldwell, T.R.; Miller, S.P. On the Determination of Residual Feed Intake and Associations of Infrared Thermography with Efficiency and Ultrasound Traits in Beef Bulls. Livest. Sci. 2009, 125, 22–30. [Google Scholar] [CrossRef]
- Kelly, A.K.; McGee, M.; Crews, D.H.; Fahey, A.G.; Wylie, A.R.; Kenny, D.A. Effect of Divergence in Residual Feed Intake on Feeding Behavior, Blood Metabolic Variables, and Body Composition Traits in Growing Beef Heifers. J. Anim. Sci. 2010, 88, 109–123. [Google Scholar] [CrossRef] [PubMed]
- Basarab, J.A.; Colazo, M.G.; Ambrose, D.J.; Novak, S.; McCartney, D.; Baron, V.S. Residual Feed Intake Adjusted for Backfat Thickness and Feeding Frequency Is Independent of Fertility in Beef Heifers. Can. J. Anim. Sci. 2011, 91, 573–584. [Google Scholar] [CrossRef]
- Archer, J.A.; Bergh, L. Duration of Performance Tests for Growth Rate, Feed Intake and Feed Efficiency in Four Biological Types of Beef Cattle. Livest. Prod. Sci. 2000, 65, 47–55. [Google Scholar] [CrossRef]
- Gilpin, A.R. Table for Conversion of Kendall’S Tau to Spearman’S Rho Within the Context of Measures of Magnitude of Effect for Meta-Analysis. Educ. Psychol. Meas. 1993, 53, 87–92. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).