Next Article in Journal
Towards the Development of an Optical Quantum Frequency Standard Feasible for a Medium-Size NMI
Next Article in Special Issue
A Flexible Wheel Alignment Measurement Method via APCS-SwinUnet and Point Cloud Registration
Previous Article in Journal
Verification of Microprobe Calibration Based on Actual Diameter Measurement of the Probe Tip Sphere
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Metrology
Volume 5
Issue 4
10.3390/metrology5040074
metrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

The Critical Role of International Comparisons in Global Metrology System: An Overview

by
Patrice Salzenstein
1,*,
Thomas Y. Wu
2,* and
Ekaterina Pavlyuchenko
3
1
Centre National de la Recherche Scientifique (CNRS), Franche-Comté Electronique Optique Sciences et Technologies (FEMTO-ST) Institute, Université Marie et Louis Pasteur (UMLP), 15B Avenue des Montboucons, F-25030 Besançon, France
2
National Metrology Centre (NMC), Agency for Science, Technology and Research (A*STAR), 8 CleanTech Loop, #01-20, Singapore 637145, Singapore
3
Centre National de la Recherche Scientifique (CNRS), Avenue de la Terrasse, F-91190 Gif-sur-Yvette, France
*
Authors to whom correspondence should be addressed.
Metrology 2025, 5(4), 74; https://doi.org/10.3390/metrology5040074
Submission received: 21 October 2025 / Revised: 26 November 2025 / Accepted: 1 December 2025 / Published: 3 December 2025
(This article belongs to the Special Issue Applied Industrial Metrology: Methods, Uncertainties, and Challenges)
Browse Figures
Versions Notes

Abstract

International comparisons play a critical role in ensuring precision, accuracy, consistency, and trust in the global metrology system. The Comité International des Poids et Mesures (CIPM) established the Mutual Recognition Arrangement (MRA) in 1999 to facilitate global trade. This paper gives an overview of the critical role of international comparisons to National Metrology Institutes (NMIs), industrial calibration laboratories, and research laboratories in fostering global measurement equivalence and the CIPM MRA. NMIs rely on Key and Supplementary Comparisons to ensure the mutual recognition of calibration and reference material certificates, vital for global trade and regulatory compliance. Industrial calibration laboratories participate in inter-laboratory or international comparisons to validate their calibration and measurement capability (CMC) and balance their risk management. Research laboratories push the frontiers of measurement science and validate their measurement result via international comparisons. Through some examples of comparisons, the paper illustrates how measurement result discrepancies uncovered in comparisons drive technical improvements, uncertainty component identification, and measurement technique refinement. International comparisons enhance scientific credibility, build public trust, support industrial innovation, and drive evolution in measurement science. As technological demands grow, fostering broader participation in international comparisons by various metrology and research laboratories remains crucial to maintain a robust and reliable global metrology system.

1. Introduction

The global metrology system can be viewed as a top-down pyramid: at the top, the Comité International des Poids et Mesures (CIPM) and the Bureau International des Poids et Mesures (BIPM) maintain the International System of Units (SI) and coordinate international comparisons [1,2,3]. Below them, the Regional Metrology Organizations (RMOs) coordinate regional comparisons and peer reviews among the National Metrology Institutes (NMIs) and Designated Institutes (DIs).
CIPM and BIPM work in close cooperation with organizations like the Organisation Internationale de Métrologie Légale (OIML) and the International Laboratory Accreditation Cooperation (ILAC), among others, to support the global metrology system. The OIML plays an important role in the global metrology system by focusing on the legal metrology and regulatory aspects of measurement. It complements the scientific metrology work coordinated by the BIPM and the CIPM. The role of ILAC in the global metrology system is to ensure that measurement, testing, and calibration results from industrial accredited laboratories are technically reliable, internationally recognized, and traceable to the SI [4]. ILAC harmonizes the practices of national accreditation bodies to promote a harmonized assessment of laboratories [5], reference material producers [6], proficiency test (PT) providers [7], etc.
The CIPM has gradually established ten Consultative Committees (CCs) in various technical areas from the 1920s to the 1990s. These CCs play an instrumental role in maintaining the integrity of the global metrology system. There are eight CCs in physical metrology areas which provide technical guidance and coordinate the work of NMIs in areas such as length, mass, force, pressure, flow, temperature, humidity, electricity, magnetism, time and frequency, photometry, radiometry, acoustics and vibration, ionizing radiation, etc. The Consultative Committee for Amount of Substance: Metrology in Chemistry and Biology (CCQM) coordinates the work of NMIs in organic analysis, inorganic analysis, gas analysis, electrochemical analysis, surface analysis, isotope ratios, nucleic acid analysis, protein analysis and cell analysis [8,9,10,11]. The Consultative Committee for Units (CCU) was set up to advise the CIPM on matters concerning units of measurement, to develop and improve the SI, and to prepare and update the SI Brochure [12]. These CCs ensure that metrology standards of each country are continually updated to reflect the latest advancements in science and technology.
Each country or economy has an NMI and/or one or more DIs that realize SI units, participates in international comparisons, and provides traceability. These NMIs and DIs provide a link to industrial calibration laboratories that serve industry under ISO/IEC 17025 accreditation [5]. Research laboratories support technology innovation by developing new measurement methods or sensors with higher accuracy and precision, while industry and society form the base of the global metrology system, benefiting from reliable, globally comparable measurements and calibrations [2,3,13,14,15].
In the global metrology system, where metrological traceability and measurement uncertainty of measurement results are fundamental, international comparisons serve as a cornerstone for validating and harmonizing measurement standards across the globe. International comparisons have a long history of development, spanning nearly 140 years. In the 1st General Conference on Weights and Measures (CGPM) held in 1889 in Paris, the International Prototype of the Kilogram (IPK) and the International Prototype of the Metre (IPM) were adopted. BIPM compared each national copy of the metre bar and kilogram (standards of many countries) against the IPK and IPM and reported their differences in the 1st CGPM [16]. This can be considered the first formal international comparison for mass and length standards.
The first international comparison of electrical resistance standards (mercury–ohm standard) and voltage standards (Weston cells) was conducted in 1910 between the NMI of the United Kingdom, Germany, France, and the United States of America [17,18,19]. The first metrological international comparison of time and frequency standards (clocks) was coordinated by the BIPM and reported at the 7th CGPM in 1927 [20]. In the 1920s–1960s, international comparisons in other areas, such as temperature, photometry, pressure, and ionizing radiation, were also organized by the BIPM [2].
By the 1950s–1960s, the BIPM had broadened international comparisons into most base and derived SI quantities, providing the foundation for the establishment of the SI in 1960. This ultimately led to the CIPM Mutual Recognition Arrangement (MRA) in 1999 [21], which formalized the structure for international key comparisons (KCs) between NMIs and created the key comparison database (KCDB) as a central record of equivalence and calibration capabilities. Since then, KCs have been organized by CIPM’s CCs, and cover all SI quantities (mass, length, time, temperature, electricity, acoustics, vibration, ionizing radiation, photometry, radiometry, chemistry, biology, etc.).
RMOs also run supplementary comparisons (SC) and regional key comparisons, which are linked back to the CIPM KCs for equivalence. Pilot studies organized by each CC and the SCs run by RMO are designed to allow research laboratories to participate, gain experience, and compare their measurement result to the respective international KC. These activities enhance global measurement capability while maintaining traceability through linking NMIs.
The CIPM established the MRA in 1999 to ensure that measurement standards maintained by different countries are comparable and equivalent [21]. The MRA relies on KCs and SCs among NMIs to support the international trust in national metrology systems [22,23,24,25,26]. International comparisons are used to verify that measurement results from different countries are traceable to equivalent national reference standards, and ultimately to the SI. This builds confidence in the accuracy and equivalence of measurements worldwide. Such comparisons help NMIs align their national metrology standards, ensuring mutual recognition of measurement capabilities across borders.
By participating in international comparisons, an individual country or economy demonstrates its measurement competence to satisfy trade partners and reduce technical barriers to trade. Demonstration of a quality management system (QMS) that has been reviewed and accepted through peer review or accreditation is an essential component of the CIPM MRA. The QMS of an NMI should comply with ISO/IEC 17025 for calibration and measurement services [5], and, where applicable, ISO 17034 for NMIs producing reference materials [6]. Based on the successful peer review of both their technical capabilities and their QMS, NMIs may submit their Calibration and Measurement Capabilities (CMCs) to the KCDB. These submitted CMCs will be reviewed first by the NMI’s own RMO (intra-RMO review), then by other RMOs (inter-RMO review). After the CMCs are approved, they are published in the KCDB.
Certified Reference Materials (CRMs) are widely regarded as the preferred means for disseminating metrological traceability in chemistry, biological, and materials measurements where direct calibration against physical standards is not feasible. CRMs from NMIs or DIs must be produced in accordance with ISO 17034. Their certified values are traceable to SI units via measurements covered by the CIPM MRA if their CMCs are published in the KCDB. Such CRMs provide well-characterized reference values with stated uncertainties and traceability to SI units, enabling reliable dissemination of traceable measurements to industry. CRMs form a robust and internationally recognized route to establishing traceability, thereby complementing the traditional calibration-based dissemination used in physical metrology.
In a broader sense, international comparisons or inter-laboratory comparisons involve a wider network of participating laboratories—NMIs, industrial calibration laboratories, and research laboratories—all of which have contributed to the global consistency of measurements. Many bilateral/multi-lateral comparisons (not registered with the BIPM), hybrid comparisons [27] and informal comparisons between these laboratories are conducted to validate their measurement results. The importance of international comparisons extends beyond scientific rigour; it has practical implications for industry, trade, regulation, and research.
An important reason for NMIs and DIs to participate in KCs is to meet the requirements of clause 7.7 in ISO/IEC 17025 (to ensure the validity of their measurement results). International comparisons serve as performance benchmarks for participating laboratories to identify gaps, support training, and drive continuous improvement in measurement technologies. High-precision measurements are essential for cutting-edge research in various research laboratories. International comparisons ensure that research conducted across countries is comparable and reproducible.
This paper begins with an introduction to the measurement uncertainty estimation and description of the methodology and process of international KC. Section 4 discusses how NMIs ensure global measurement consistency via international comparisons. We then discuss how industrial calibration laboratories validate their CMCs and balance their risk management. Section 6 addresses how research laboratories push the frontiers of measurement science and validate their measurement result via international comparisons. In Section 7, we underline the technical value of international comparisons with two case studies. A summary of the main findings is presented in Section 8, followed by the conclusions drawn from this review paper.

2. Uncertainty in Measurement

Measurement results must be assigned an estimated uncertainty when they are reported; otherwise, they have no meaning. Without measurement uncertainty, you do not know the 95% confidence interval of the measured result, or whether it can meet a specification or tolerance. The measurement uncertainties are also important to compare measurement results made by various laboratories and for assessing a product’s compliance with limits and specifications [28,29,30]. One of the central purposes of international comparisons is to validate the measurement uncertainties claimed by metrology laboratories. By demonstrating that results from different laboratories agree within their stated uncertainties, these comparisons confirm the credibility of each laboratory’s measurement capability.
Measurement uncertainties are estimated following the Guide to the Expression of Uncertainty in Measurement (GUM) [28]. The GUM was originally published in 1993 and republished with minor corrections in 1995. In GUM, measurement uncertainty is divided into Type A and Type B evaluations. Type A uncertainty comes from statistical analysis of repeated measurements. Type B uncertainty includes components evaluated using non-statistical methods, such as calibration certificate information, manufacturer specifications, reference data, instrument limits, previous measurement data, physical constants, environmental effects, uncertainty in bias correction, instrument resolution, long-term stability, drift, noise, modelling errors, etc. All Type A and Type B uncertainty components are first expressed as standard uncertainties and then combined using the law of uncertainty propagation (LUP) to derive the expanded uncertainty at a 95% confidence level.
For non-linear models or non-normal probability distributions, the classical GUM approach for propagation of uncertainty can be inadequate. In 2008, GUM Supplement 1 was published to introduce the Monte Carlo method for propagating uncertainty in non-linear models and non-normal input distributions. The GUM is under ongoing revision to accommodate modern measurement methods, complex models, and digital metrology [31,32].
Measurement uncertainty analysis in diverse metrology standards has been well described in the literature [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. Careful analysis of all possible uncertainty contributions is needed to derive reliable measurement uncertainties of a measurement system. Rigorous uncertainty analysis can also help to improve the accuracy of such systems. Uncertainty analysis can provide valuable insights into instruments’ performance and support the development of instruments with higher precision [50,51]. A detailed uncertainty analysis of Liquified Natural Gas (LNG) flow measurement [52,53] has revealed theoretically the best accuracy that can be achieved for LNG bunkering and cryogenic liquid flow measurement.
Measurement uncertainty is essential for interpreting results reported in international or inter-laboratory comparisons. Without quantifying uncertainty, it becomes difficult to assess the significance of differences in measurement results between laboratories. Reliable uncertainty assessments are needed so that a laboratory can demonstrate the equivalence of its metrology standards and maintain traceability to the SI.
For each KC, one or more key comparison reference values (KCRV) can be derived. The KCRV is a reference value representing the best estimate of the “true” measurand in the comparison, based on all valid results reported by participating laboratories. KCRV is used as a common reference point to compare all results of participating laboratories and derive each laboratory’s degree of equivalence (DoE), which is the deviation of their measured result from the KCRV. The uncertainty of the KCRV and DoE must also be estimated in the KC report. Many statistical methods for the evaluation of key comparison data to identify outliers and derive KCRV with uncertainty estimation have been proposed [54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69].
For RMO comparisons or pilot studies, measurement results from participating laboratories need to be combined using statistical methods, considering their respective measurement uncertainties to derive a comparison reference value (CRV) and to evaluate its associated uncertainty. Methods for data analysis and linking the CRV in RMO comparisons to KCRV have been proposed [58,70,71,72,73,74].

3. Methodology and Process of International Key Comparisons

In this section, we briefly describe how a typical KC is conducted. An international KC begins with planning by a CC or the BIPM, which appoints a pilot laboratory responsible for preparing the comparison protocol. This technical protocol specifies the comparison’s scope, measurands, travelling standard, participating laboratories, circulation scheme (e.g., sequential loop or star configuration), measurement procedures, principal components of the uncertainty budget, environmental conditions, results and uncertainty reporting format, schedule, data submission deadlines, etc. [75]. The comparison protocol needs to be reviewed and approved by the CC.
Before travelling standard circulation, the pilot laboratory verifies its suitability—ensuring stability, transportability, and traceability to primary standards—and performs initial characterization measurements. During the circulation phase, each participating NMI receives the travelling standard, performs measurements, and reports the results with complete measurement uncertainty budgets. The stability of the travelling standard is monitored using the pilot laboratory’s repeated measurements during the circulation phase. Data validation is performed to identify inconsistencies or drift for the travelling standard.
After measurements are completed by all participating laboratories, the pilot laboratory analyses all submitted data using statistical methods to identify outliers and determine the KCRV with its expanded uncertainty [55,56,57,62,63]. The DoE between each laboratory’s result and the KCRV are then calculated. Pairwise DoE among all participating laboratories is also derived.
The KC report prepared by the pilot laboratory will go through the Draft A and Draft B stages. In the Draft A report stage, all participating laboratories will review their own submitted results and uncertainties, outlier identification, proposed KCRV and DoE, statistical processing method, etc., in the report. When the final version of Draft A report has been agreed upon by all participants, it becomes the Draft B report. In this stage, the Draft B report will be sent to CC for technical review and formal approval. Once approved, the KC final report is published in the BIPM KCDB.

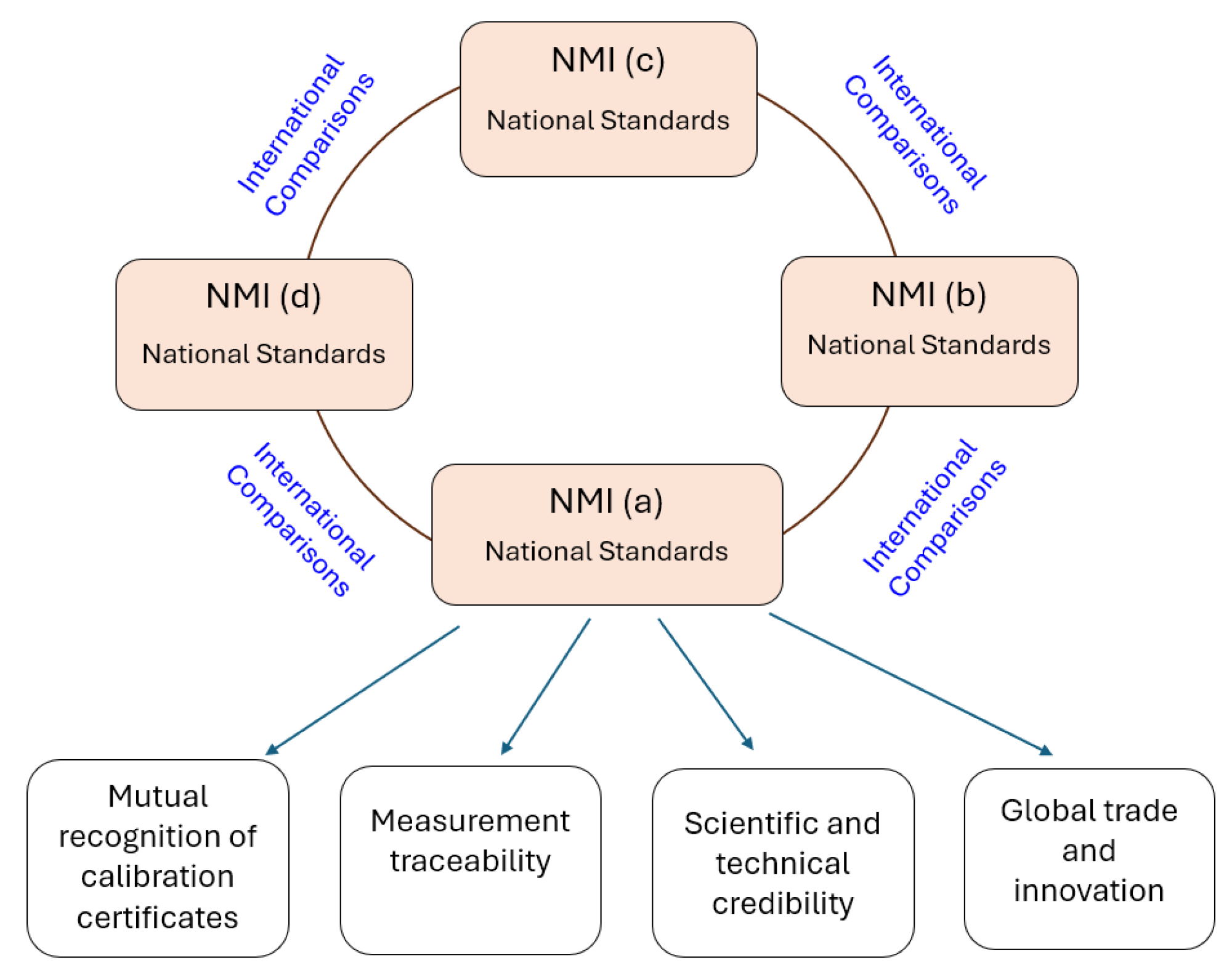
4. National Metrology Institutes: Ensuring Global Measurement Consistency and Traceability

NMIs play a crucial role in ensuring the accuracy and consistency of measurements within their respective countries, but their responsibilities extend far beyond national borders. Participation in international comparisons is essential for NMIs to uphold their status as custodians of national metrology standards. These standards and CMCs are validated against other NMIs through international comparisons, ensuring a robust traceability chain for calibration laboratories and industry. Successful comparison results can confirm that an NMI’s measurement standards are comparable to those of other countries. NMIs demonstrate the international equivalence of their measurement capabilities through KCs and SCs coordinated by the BIPM and its associated CCs.
The international comparisons support the mutual recognition of calibration certificates, which are recognized by all MRA signatory countries. This mutual recognition is vital for industries and businesses that operate internationally. The calibration of their products can meet internationally accepted standards. Many products benefit from the MRA through appropriate testing and conformity assessment. This can eliminate disputes over measurement discrepancies, facilitating smooth international trade.
Accurate measurements are crucial for safety, quality, and compliance with regulations. Nowadays, industries rely on standardized measurements to ensure that their products meet international specifications. Satisfactory results in comparisons reinforce the credibility and international standing of NMIs. For industries such as aerospace, automotive, electronics, and pharmaceuticals, the reliable standards of NMIs can ensure smooth trade globally.
NMIs participate in various comparisons to ensure their measurement standards and CMCs evolve with scientific progress [76,77,78,79,80,81,82,83,84,85,86,87,88,89]. Such standards also need to maintain their relevance in a rapidly changing world. We give some examples of international key comparisons between NMIs in this section.
-
The Consultative Committee for Length (CCL) has conducted key comparisons of optical frequency and wavelength standards, such as CCL-K11 [79,90,91]. These comparisons are used to ensure uniformity in laser wavelength measurements across different NMIs. The comparisons CCL-K1 focus on the calibration of gauge blocks by optical interferometry, to maintain length measurement equivalence and traceability [83,92]. These CCL key comparisons have supported length metrology development and the realization of the metre.
-
The Consultative Committee for Mass and Related Quantities (CCM) organized the first key comparison CCM.M-K8.2019 for realizations of the kilogram definition based on the Planck constant, with a final report published in 2020 [93]. This comparison is used to determine agreement between realizations of the kilogram using Kibble balances, joule balances, and the X-ray Crystal Density (XRCD) method. The KCRV has a deviation of −0.0188 mg (with a standard uncertainty of 0.0075 mg) from the mass unit maintained by the BIPM working standards (nominal mass is 1 kg). The second CCM key comparison CCM.M-K8.2021 for realizations of the kilogram definition was conducted in 2021–2022 [94]. Its KCRV has a standard uncertainty of 0.0074 mg and a deviation of −0.0152 mg from the 1 kg mass unit maintained by the BIPM working standards.
-
BIPM has carried out an ongoing on-site key comparison of Josephson voltage standards among NMIs under the denomination BIPM.EM-K10.a (1 V) and BIPM.EM-K10.b (10 V) under the auspices of the Consultative Committee for Electricity and Magnetism (CCEM) [95]. A recent comparison between the NMI of Finland and BIPM was reported in 2021 [96]. Their final results were in good agreement within the combined relative standard uncertainty of 2.5 parts in 1010 for the nominal voltage of 10 V.
-
CCT-K7.2021 key comparison of water-triple-point (TPW) cells was conducted between 19 NMIs, with its final report approved by the Consultative Committee for Thermometry (CCT) in 2023 [97]. The maximum difference between two transfer cells was 92 μK, with a standard deviation of 26 µK, which shows an almost factor-of-two improvement compared to CCT-K7 results. Compared to the previous comparison, CCT-K7 [98], this recent comparison has shown major improvements in the quality of TPW cells, definition of national references, and quality of uncertainty assessments.
-
The Consultative Committee for Photometry and Radiometry (CCPR) has organized a key comparison CCPR-K1.a.2017 for Spectral Irradiance in the wavelength range of 250 to 2500 nm using Tungsten quartz halogen lamps (1000 W) as artifacts [99]. The relative standard uncertainties of the KCRV were estimated to be 0.08% to 0.28%. The measurement uncertainties reported by the participants in CCPR-K1.a.2017 were, in general, less than those claimed in the previous comparison for Spectral Irradiance (CCPR-K1.a). The final report shows that ~80% of all results (at all wavelengths) agree with the KCRV within 1% at 250 to 2500 nm, which is similar to the results of the previous CCPR-K1.a comparison (published in 2006) [100].
-
The Consultative Committee for Acoustics, Ultrasound and Vibration (CCAUV) organized the first key comparison CCAUV.A-K4 for free-field microphone sensitivity derived using the reciprocity technique [101]. The travelling standards were two ½ inch laboratory-standard microphones (Brüel & Kjær 4180), which were calibrated at 1 kHz to 40 kHz under free-field conditions in an anechoic chamber. The submitted results of all seven NMIs were included in the estimation of the KCRVs. The final report shows that ~94% of all results (for all frequencies) agree with the KCRV within the uncertainties.
-
The CCQM has organized three KCs on natural gas mixtures, namely CCQM-K1, CCQM-K16 and CCQM-K23, to ensure comparability in natural gas composition reference standards among the NMIs [80,102,103,104,105]. The final report for a more recent KC for natural gas (CCQM-K118) was published in 2022 [106]. In this comparison, the KCRVs have been derived using a weighted mean computed from the largest consistent subset (LCS) of the submitted results. Some of the participants reported one or a few discrepant results, partly due to the heterogeneity and heteroscedasticity of the datasets. Overall, the results in CCQM-K118 have shown good comparability of the metrology standards for natural gas composition in the 14 participating institutes.
As illustrated in Figure 1, the role of NMIs is essential for maintaining the traceability and credibility of the global metrology system. The equivalence of measurement standards across borders, verified through international comparisons, also fosters scientific innovation. Researchers working with international partners can trust that the measurement data they exchange is consistent, which supports collaborative research work.
To publish a CMC in the BIPM KCDB, an NMI must demonstrate its technical competence and QMS by peer review or accreditation before the CMCs can be submitted to the KCDB. The QMS of an NMI should comply with ISO/IEC 17025 [5] for calibration and measurement services and ISO 17034 if the NMI produces reference materials [6]. The QMS ensures that an NMI implements systematic controls and proper documentation over measurement processes and traceability to the SI [1,107,108,109,110]. The QMS, CMCs, and MRA form an integrated framework to ensure global confidence in measurement results. The audited QMS practices build mutual confidence among NMIs, which form the basis for global equivalence in measurement standards.

5. Industrial Calibration Laboratories: CMC Validation and Risk Management

5.1. Validation of CMC

Industrial calibration laboratories need to demonstrate their competence through ISO/IEC 17025 accreditation. Their calibration standards must be traceable to SI units, usually through calibration services provided by NMIs or other accredited calibration laboratories. For these laboratories, participation in international comparisons, inter-laboratory comparisons or PT plays a crucial role in validating their claimed CMCs and meeting the requirements of accreditation assessment [111,112,113,114,115,116,117].
Accreditation bodies request accredited calibration laboratories to regularly participate in PT or inter-laboratory comparison (when PT is not available) to show their competence in calibration [7]. Such PT can be conducted by an NMI or a commercial organization which offers PT services with ISO/IEC 17043 accreditation [7]. PT provides an external, unbiased check of a laboratory’s ability to perform accurate calibrations. Successful PT results enable the calibration laboratory to be recognized internationally under the ILAC MRA [118].

5.2. Financial and Legal Binding of Measurements

These calibration laboratories often provide calibration services or develop products where precise measurements are legally or financially binding. Thus, their reported measurement uncertainties and CMCs carry significant weight. To mitigate potential legal and financial risks, industrial laboratories may need to declare uncertainties with a conservative margin. Liability and financial risk management influence the measurement uncertainty declared by industrial calibration laboratories.
In many industries, the calibration reports directly impact product quality, safety and regulatory compliance. The uncertainty affects how reliable and trustworthy their measurements are perceived to be. For example, any deviation in measurement in pharmaceutical products could lead to a batch being rejected. In the aerospace industry, even minor calibration discrepancies can result in catastrophic outcomes. As a result, industrial calibration laboratories are under pressure to provide measurements with a high level of reliability, as reflected in the reported measurement uncertainty.
Overly optimistic uncertainty in calibration certificates means the laboratory could have underestimated the true measurement uncertainty, resulting in a reported uncertainty that is too small to be realistic. This could expose the laboratory to liability in legal disputes or claims for damages. The measurement uncertainty also often has regulatory implications; in many jurisdictions, products and processes need to conform to standards and such conformance decisions are influenced by the uncertainty values. In this context, measurement uncertainty becomes part of a risk management strategy. Calibration laboratories must ensure their uncertainty values have an adequate cushion against potential errors.

5.3. Risk Management and Decision Rule

Industrial laboratories have to consider the potentially unknown uncertainty factors in the calibration process. This is to protect themselves from potential legal claims or financial repercussions. Thus, a conservative approach is often adopted in estimating the measurement uncertainty. A safety margin, or uncertainty guard-banding, is included to account for any unforeseen errors during calibration [119,120]. This decision rule can mitigate the risk of underestimating uncertainty. This conservative approach also helps to ensure that their calibration reports comply with industry standards and regulations. Measurement uncertainty with guard banding means adding a safety margin to the estimated measurement uncertainty. Their final reported uncertainty (or CMC) includes a margin factor to ensure their calibration results can comply with contractual obligations.
The priority of industrial laboratories is to ensure that their measurement results are reliable with acceptable uncertainty. They need to focus on risk and responsibility. In the automotive or pharmaceutical sectors, precise instrument calibration can affect product performance or patient safety. In these cases, a measurement result with a reliable uncertainty estimation is most important.
In industrial laboratories, uncertainty estimation and decision rules are tools for managing legal and financial risk [119,120,121]. A conservative approach in declaring uncertainty helps safeguard against disputes and legal challenges. This becomes an essential part of the laboratory’s overall risk management strategy. ISO/IEC 17025 emphasizes that calibration laboratories should identify, evaluate, and control risks that could affect the validity of calibration results or the reliability of decisions [5]. ILAC has published a guideline ILAC G8:09/2019 on the use of decision rules when issuing statements of conformity to specifications or standards [122].
Participation in inter-laboratory comparisons or PTs enables a calibration laboratory to compare its measurement results with peers or comparison reference values and to validate its claimed uncertainties (with guard banding). The deviations detected in such comparisons can reveal sources of error which are not captured in the uncertainty budget. Thus, participation in such comparisons is also a risk management tool for industrial laboratories.

6. Research Laboratories: Pushing the Frontiers of Measurement Science

Research laboratories in academia and industry operate under a distinctive paradigm compared to NMIs and industrial calibration laboratories. While the calibration laboratories typically focus on providing calibration services with legal liability, research laboratories primarily concentrate on advancing scientific understanding and technology. Their role is to explore the limits of measurement science and develop cutting-edge methodologies for high-precision measurement [123,124,125,126,127,128,129,130,131,132,133].
Many NMIs also have research laboratories or R&D groups with a role distinct from other groups that focus on routine metrology functions (e.g., performing calibration service, maintaining national standards and supporting traceability chains). Instead, their role is to advance measurement science, conduct cutting-edge research, and develop new metrology standards using novel methods.
Research laboratories focus on the pursuit of knowledge and technological innovation. In this context, their core objective is often to reduce measurement uncertainty to its lowest possible levels, exploring new ways to push the boundaries of measurement precision and accuracy. Such research works are often highly experimental, leading to innovations that could eventually revolutionize measurement techniques. Some of these research findings have been used by NMIs to develop new metrology standards (e.g., quantum time standards [134,135,136,137,138,139,140,141], graphene electrical resistance standards [142,143,144,145,146], quantum voltage standards [147,148], primary realization of the kilogram using a Kibble balance and XRCD [149,150,151,152,153,154,155,156,157,158,159,160,161], etc.).

6.1. Pushing the Frontiers of Measurement Science

Research laboratories focus on achieving the lowest possible measurement uncertainty by developing novel measurement methods that outperform traditional approaches. This drive for superiority aimed to prove the scientific robustness of their work, for instance, by achieving high measurement precision in fields like quantum technology, nanotechnology, or space science.
Research laboratories have contributed to the development of metrology and pushed the boundaries of measurement precision and accuracy. Research laboratories innovate new measurement techniques to achieve smaller uncertainties. Their research findings may ultimately lead to new instruments and methodologies with higher precision.

6.2. Benchmarking via International Comparisons

Many research laboratories have participated in international comparisons, including those pilot studies organized by the BIPM, SCs organized by RMO and inter-laboratory comparisons [77,78,81,162,163,164,165]. These comparisons allow research laboratories to benchmark their measurement performance against NMIs and other leading metrology laboratories. They validate their measurement capabilities and identify areas for improvement via the comparisons. Contributions from many research laboratories help drive new developments in metrology. A few examples are given below to show significant developments in these areas:
-
The Consultative Committee for Time and Frequency (CCTF) has initiated a roadmap for redefining the SI second to enhance precision, accuracy, and long-term stability of timekeeping. This initiative is driven by advancements in optical frequency standards, such as those based on 171Yb and 87Sr, which are intrinsically accurate at the level of parts in 1018, two orders of magnitude lower than that of traditional 133Cs microwave atomic clocks [166,167,168,169,170]. The redefinition aims to improve the accuracy and stability of International Atomic Time (TAI) and Coordinated Universal Time (UTC) [12,164,167,170,171,172,173]. An international comparison of optical frequencies via a transportable optical lattice clock and another comparison of optical clocks through very long baseline interferometry (VLBI) have been conducted to check the consistency of optical clocks at the fractional uncertainty of 10−18 level on an intercontinental scale [81,162].
-
NPL and the University of Cambridge had reported their work to develop a quantum current standard using single-electron pumps [174]. They compared the electron pump current with a reference current generated outside the pump cryostat, with an uncertainty on the order of 1 ppm. This is an important work in Quantum Metrology Triangle (QMT) experiments to check the self-consistency of the three fundamental quantum electrical standards [163,175,176].
-
A pilot study on AC voltage comparisons was conducted in 2024 by the National Institute of Standards and Technology (NIST) and BIPM [147,148]. The aim of this comparison is to harmonize quantum voltage standards globally. This pilot study focuses on quantum-based Josephson voltage standards to ensure consistency in AC voltage measurements. The BIPM’s transportable Programmable Josephson Voltage Standards (PJVSs) were compared to NIST’s Josephson Arbitrary Waveforms Synthesizer (JAWS). They have achieved a type A uncertainty of a few parts in 109 for a 10 Hz sine wave at 2 V rms in this comparison.
-
Comparison between NIST and National Institute for Advanced Industrial Science and Technology (AIST) has been conducted using Graphene and GaAs Quantized Hall resistance (QHR) Devices [82]. In this work, several graphene QHR devices from NIST were compared to GaAs QHR devices and a 100 Ω standard resistor from AIST. Comparisons between the QHR devices have been reported with uncertainties of less than 5 nΩ/Ω.
-
An inter-laboratory comparison on quantum resistance (memristor) between 3 NMIs and 3 research laboratories has been reported [165]. The results show the consensus values of this comparison have deviations of −3.8% and 0.6% from the agreed SI values for the fundamental quantum of conductance, G0 and 2G0, respectively. The consensus values’ deviations from the SI values are well covered by their expanded measurement uncertainty.
-
A comparison was conducted by four laboratories for measuring the detection efficiency of free-running InGaAs/InP single-photon avalanche detectors (SPAD) at the wavelength of 1550 nm [177]. The detection efficiency for the mean photon number per pulse was between 0.01 and 2.4. The measured efficiency values by the participants are all consistent within the claimed uncertainties. This study is a good preparation for organizing future international comparisons of the detection efficiency of single-photon detectors at telecom wavelengths.
Over time, research laboratories have been responsible for many breakthroughs that form the backbone of modern measurement systems, such as the development of new metrology standards for time (microwave atomic clocks and optical clocks) [178], the invention of laser interferometry for precision dimensional measurement [179,180], etc. Together with NMIs, research laboratories play a vital role in the advancement of precision measurement technologies. Their work ensures that measurement science continues to evolve and improve, benefiting industries and government agencies in the long run.

7. The Technical Value of International Comparisons

International comparisons also provide a unique opportunity for all participating laboratories to validate their measurement setups. When the same standard or artefact is circulated among multiple laboratories, it allows each participant to confirm the consistency of their measurements. If a laboratory obtains a result that significantly deviates from the consensus, it prompts an internal review. This discrepancy can lead to improvements in the measurement system. Thus, comparisons are a powerful method of external validation.
Discrepancies in comparison results will trigger an investigation of the source of the error. This could involve re-examining calibration procedures, identifying potential systematic errors, or revisiting the uncertainty analysis framework. Additionally, when a laboratory’s results diverge notably from others, it may prompt a re-evaluation of measurement protocols or equipment maintenance schedules to ensure alignment with established standards. Two case studies are given below to show this technical value.

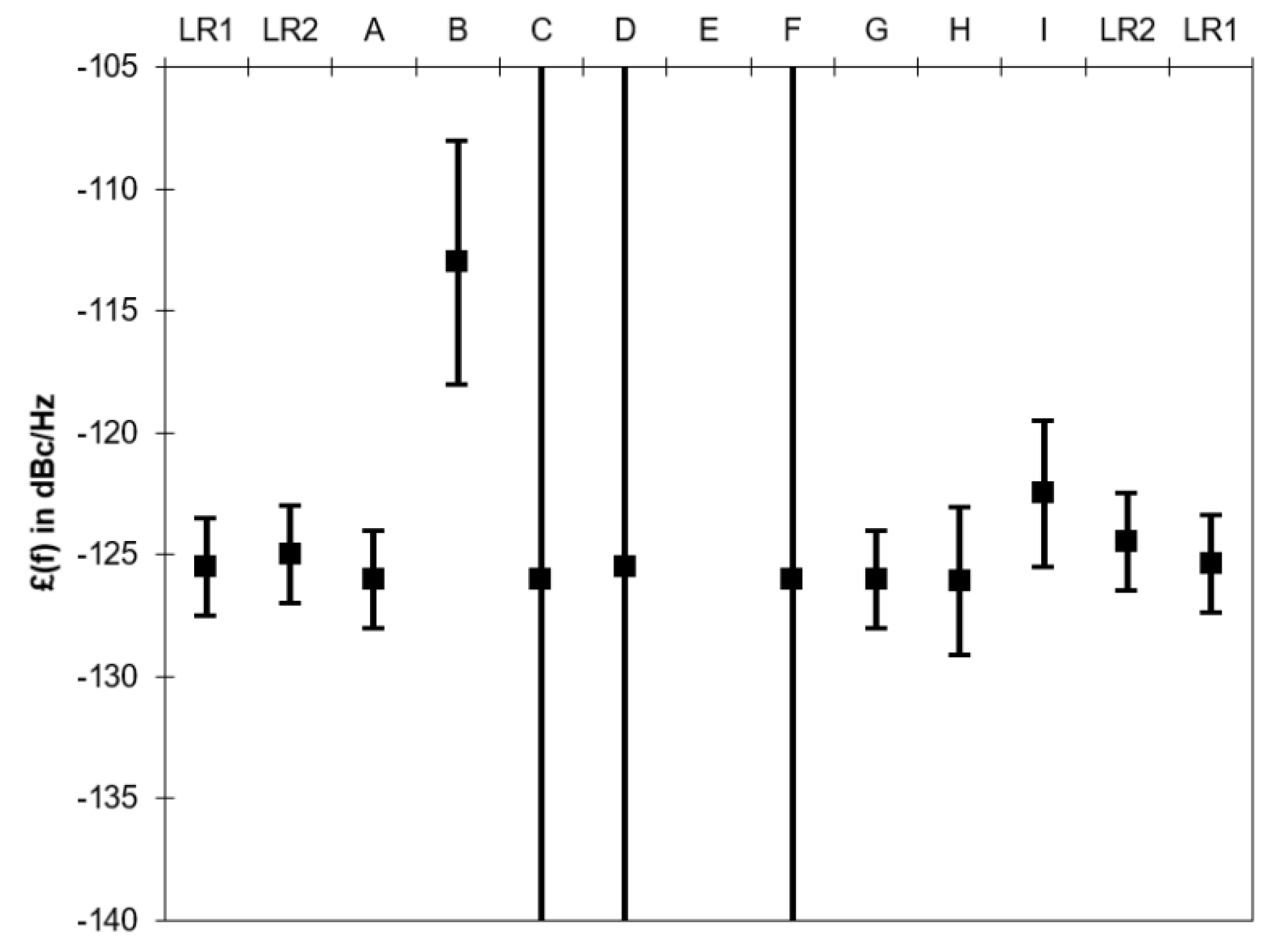
7.1. Case Study: Phase Noise Inter-Laboratory Comparison

The first international comparison in the area of phase noise was held in 1993 [181]. More than 10 years later, another important international comparison for phase noise was conducted and reported by Salzenstein et al. in 2006 [111]. This study involved various industrial calibration laboratories and research laboratories across Europe and aimed to assess the consistency and reliability of multiple phase noise measurement systems. The preliminary results, published in the proceedings of the 20th European Frequency and Time Forum, revealed disparities among participants that sparked valuable technical discussions.
As an illustration, we provide some results of this comparison in Figure 2. At 5 MHz, one of the participating laboratories (B) shows a big deviation from the other participants. After some investigation, this laboratory (B) found it was due to a technical issue. Three other laboratories did not report their measurement uncertainties. The reported phase noise levels appear to be quite similar across most participating laboratories.
Technical discussions were sparked due to these differences in the results. These differences also led to modifications in some participants’ measurement setups and a deeper understanding of the measurement process itself. The comparison facilitated not only performance benchmarking but also the identification of best practices for phase noise characterization. Such inter-laboratory comparisons are vital in niche areas like phase noise metrology, where measurement complexity and system sensitivity make standardization particularly challenging.

7.2. Case Study: Comparison of Particle Charge Concentration and Particle Number Concentration

The European Association of National Metrology Institutes (EURAMET) organized a pilot study for comparison of aerosol electrometers (EuRAMET comparison #1244) in 2013 [182]. This is the first comprehensive international comparison of particle charge concentration measured by aerosol electrometers for particle sizes from 6 nm to 200 nm. This pilot study shows that some laboratories may have underestimated their uncertainties at certain particle number concentrations, and that their relative deviations from the CRVs exceeded their claimed uncertainty. The result of this comparison has led to a review of uncertainty budgets and to the identification of other possible sources of measurement errors (noise floor of electrometer, port bias error, sample flow rate error, etc.) to derive reliable measurement uncertainty.
After this EuRAMET pilot study, the CCQM organized the first and second KC for particle number concentration and particle charge concentration in 2017 and 2024, respectively (CCQM-K150, CCQM-K185) [85,183,184]. The results of CCQM-K150 and CCQM-K185 show that many NMIs have improved their measurement accuracy, and the estimated uncertainties are more realistic, which ensures that their results agree with the KCRVs within the uncertainties.

7.3. Discussion

International comparisons have helped to support continuous improvement in the metrology laboratory. The deviation from the CRV can highlight potential bias errors in their system or insufficient measurement uncertainty. Laboratories may need to develop new calibration techniques to enhance their measurement system.
Such comparisons act as a catalyst for sustained improvement in measurement technique. This process of comparison, review, and improvement can enhance the quality of metrology standards. NMIs can identify needs for better reference materials, more accurate instruments, or improved calibration methods via such international comparisons. This ensures that metrology can keep pace with scientific innovations.

8. Summary

We have given an overview of the critical role of international comparisons in the global metrology system. Since the first international comparison of mass and length standards in 1889, we have seen the impact of such comparisons on the development of metrology standards. International comparisons ensure the precision, accuracy, consistency, and mutual trust within the global metrology system. Measurement uncertainty analysis is essential for interpreting the results of each participating laboratory in international comparisons. Reliable uncertainty assessments and analysis ensure that various laboratories can demonstrate the equivalence of their metrology standards with CRVs and validate their traceability to the SI. The data from each comparison needs to be analyzed using appropriate statistical methods to identify outliers and derive a CRV with reliable uncertainty.
This paper has discussed the challenges faced by NMIs, industrial calibration laboratories, and research laboratories. NMIs have relied on KCs, SCs and pilot studies coordinated by the BIPM and CCs to ensure the mutual recognition of metrology standards and traceability to the SI, which are vital for global trade and regulatory compliance. NMIs have been developing quantum metrology standards and have organized many international comparisons to validate the measurement uncertainties and precision.
Industrial calibration laboratories regularly participate in inter-laboratory or international comparisons to validate their CMCs and meet ISO/IEC 17025 accreditation requirements. They also need to balance the claimed uncertainties with their risk management, as their calibration reports would be subject to legal liability for compliance with regulatory standards.
The focus of research laboratories is to push the frontiers of measurement science and develop cutting-edge measurement techniques with breakthroughs in measurement precision. Research laboratories have participated in international comparisons to validate their measurement result and benchmark their capabilities with other NMIs or research laboratories.
We have given some examples of international comparisons to illustrate their technical value. Measurement result discrepancies uncovered during these comparisons have driven technical improvements, the identification of uncertainty components, and the refinement of measurement techniques. This helps NMIs to improve their metrology standards, leading to higher accuracy and more reliable uncertainty assessment.
It is known that large discrepancies have appeared in some international comparisons, which could be due to travelling standard drift, differences in measurement methods, environmental conditions, differences in traceability, etc. Sometimes these issues can lead to large uncertainty of KCRV or CRV, arguments over the identification of outliers, or a suitable statistical method for processing comparison data. In the future, it will require more mature measurement techniques, more stable artifacts, or more accurate reference standards to improve the results of international comparisons for those more challenging areas.

9. Conclusions

International comparisons are more than just technical exercises—they are foundational to the integrity, coherence, and advancement of measurement science. They have played a critical role in validating measurement capabilities, building public trust, supporting international trade, enhancing scientific credibility, and fostering continuous technology innovation. Each stakeholder—be it an NMI ensuring global measurement consistency, an industrial calibration laboratory providing calibration services, or a research laboratory striving for scientific excellence—derives distinct yet equally vital benefits from these international comparisons.
KC and SC protocols and final reports are all published to foster public trust in the global metrology system. Comparison reports with satisfactory results reassure the public that measurements are accurate and traceable. Regulatory bodies and industrial stakeholders can benefit from this transparency and trust. Ultimately, this will support more collaboration between nations to develop globally accepted metrology standards.
As science and technology continue to evolve, the role of international comparisons in ensuring measurement traceability and validating measurement uncertainties will remain central. To build a robust global metrology system, we need to encourage international comparisons with broader coverage of measurands, greater participation by more laboratories, and deeper integration into scientific and industrial practices.

Author Contributions

Conceptualization, P.S.; methodology, P.S., T.Y.W. and E.P.; figures, P.S. and T.Y.W.; validation, P.S. and T.Y.W.; formal analysis, P.S., T.Y.W. and E.P.; investigation, P.S. and T.Y.W.; resources, P.S.; writing—original draft preparation, P.S. and T.Y.W.; writing—review and editing, P.S. and T.Y.W.; supervision, P.S.; project administration, P.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data is available upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
BIPMBureau International des Poids et Mesures
CCConsultative Committees
CGPMGeneral Conference on Weights and Measures
CIPMComité International des Poids et Mesures
CMCCalibration and measurement capability
ILACInternational Laboratory Accreditation Cooperation
IPKInternational Prototype of the Kilogram
IPMInternational Prototype of the Metre
KCKey comparison
KCDBKey comparison database
MRAMutual Recognition Arrangement
NMINational Metrology Institute
OIMLInternational Organization of Legal Metrology
RMORegional Metrology Organization
SCsupplementary comparison
SIInternational System of Units
AISTAdvanced Industrial Science and Technology
CCLConsultative Committee for Length
CCQMConsultative Committee for Amount of Substance: Metrology in Chemistry and Biology
CCTFConsultative Committee for Time and Frequency
CRVComparison reference value
DoEDegree of equivalence
EURAMETEuropean Association of National Metrology Institutes
GUMGuide to the Expression of Uncertainty in Measurement
JAWSJosephson Arbitrary Waveforms Synthesizer
KCRVkey comparison reference value
LNGLiquefied Natural Gas
NISTNational Institute of Standards and Technology
PJVSProgrammable Josephson Voltage Standard
PTProficiency testing
QHRQuantized Hall resistance
QMTQuantum Metrology Triangle
SSBSingle sideband
TAIInternational Atomic Time
TFPITandem Fabry–Pérot interferometer
UTCCoordinated Universal Time
VLBIVery long baseline interferometry
ISOInternational Organisation for Standardization
QMSQuality management system
LCSLargest consistent subset
CCUConsultative Committee for Units
CCEMConsultative Committee for Electricity and Magnetism
CCTConsultative Committee for Thermometry
CCAUVConsultative Committee for Acoustics, Ultrasound and Vibration
CCPRConsultative Committee for Photometry and Radiometry
CCMConsultative Committee for Mass and Related Quantities
SPADSingle-photon avalanche detector
XRCDX-ray crystal density
CRMCertified Reference Material

References

  1. Wallard, A.J. The Organization of Metrology. In Proceedings of the International School of Physics “Enrico Fermi”; IOS Press: Amsterdam, The Netherlands, 2007; Volume 166, pp. 21–33. [Google Scholar] [CrossRef]
  2. Quinn, T. From Artefacts to Atoms: The BIPM and the Search for Ultimate Measurement Standards; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
  3. Quinn, T. The Metre Convention and World-Wide Comparability of Measurement Results. In Proceedings of the Accreditation and Quality Assurance; Springer: Berlin/Heidelberg, Germany, 2004; Volume 9, pp. 533–538. [Google Scholar]
  4. Placko, D. Metrology in Industry: The Key for Quality; Wiley: Hoboken, NJ, USA, 2010; ISBN 9781905209514. [Google Scholar]
  5. ISO/IEC 17025:2017; ISO/IEC General Requirements for the Competence of Testing and Calibration Laboratories. International Organization for Standardization: Geneva, Switzerland, 2017.
  6. ISO/IEC 17034; ISO/IEC General Requirements for the Competence of Reference Material Producers. International Organization for Standardization: Geneva, Switzerland, 2016.
  7. ISO/IEC 17043; ISO/IEC Conformity Assessment—General Requirements for Proficiency Testing. International Organization for Standardization: Geneva, Switzerland, 2010.
  8. Richter, W. Comparability and Recognition of Chemical Measurement Results—An International Goal. Fresenius J. Anal. Chem. 1999, 365, 569–573. [Google Scholar] [CrossRef]
  9. Konopelko, L.A.; Kustikov, Y.A.; Okrepilov, M.V.; Kolobova, A.V.; Migal, P.V.; Krylov, A.I.; Vonskiy, M.S.; Chubchenko, I.K.; Efremova, O.V.; Kulyabina, E.V.; et al. Development of International Key Comparisons in the Field of Chemico-Analytical Measurements. Meas. Tech. 2021, 64, 598–605. [Google Scholar] [CrossRef]
  10. Wielgosz, R.I. International Comparability of Chemical Measurement Results. Anal. Bioanal. Chem. 2002, 374, 767–771. [Google Scholar] [CrossRef]
  11. Richter, W. How to Achieve International Comparability for Chemical Measurements. Accredit. Qual. Assur. 2000, 5, 418–422. [Google Scholar] [CrossRef]
  12. BIPM. The International System of Units (SI), 9th ed.; The Bureau International Des Poids et Mesures: Sèvres, France, 2019. [Google Scholar]
  13. Semerjian, H.G.; Watters, R.L. Impact of Measurement and Standards Infrastucture on the National Economy and International Trade. Measurement 2000, 27, 179–196. [Google Scholar] [CrossRef]
  14. Seiler, E. From the International System of Units to a Global Metrology System. In Proceedings of the XVII IMEKO World Congress Metrology in the 3rd Millennium, Dubrovnik, Croatia, 22–27 June 2003. [Google Scholar]
  15. Kumar, A.; Bangal, P.R.; Panja, S.; Sharma, S.K. Metrological Innovations for Science, Technology and Global Trade. Mapan J. Metrol. Soc. India 2023, 38, 557–559. [Google Scholar] [CrossRef]
  16. BIPM. Compte Rendu Des Séances de La 1re Conférence Générale Des Poids et Mesures (CGPM); The Bureau International Des Poids et Mesures: Sèvres, France, 1889. [Google Scholar]
  17. Rosa, E.B. Report to the International Committee on Electrical Units and Standards. Available online: https://www.google.com.sg/books/edition/Report_to_the_International_Committee_on/ccRGAQAAMAAJ?hl=en&gbpv=0 (accessed on 19 September 2025).
  18. Rosa, E.B.; Wolff, F.A. Work of the International Technical Committee on Electrical Units. J. Wash. Acad. Sci. 1912, 2, 259–267. [Google Scholar]
  19. Elmquist, R.E.; Cage, M.E.; Tang, Y.H.; Jeffery, A.M.; Kinard, J.; Dziuba, R.F.; Oldham, N.M.; Williams, E.R. The Ampere and Electrical Standards. J. Res. Natl. Inst. Stand. Technol. 2001, 106, 65. [Google Scholar] [CrossRef]
  20. BIPM. Compte Rendu Des Séances de La 7th Conférence Générale Des Poids et Mesures (CGPM); The Bureau International Des Poids et Mesures: Sèvres, France, 1927. [Google Scholar]
  21. CIPM. Mutual Recognition of National Measurement Standards and of Calibration and Measurement Certificates Issued by National Metrology Institutes (CIPM MRA); The Bureau International Des Poids et Mesures: Sèvres, France, 1999. [Google Scholar]
  22. Werhahn, O.; Olson, D.A.; Kuanbayev, C.; Henson, A. The CIPM MRA—Success and Performance. Metrologia 2023, 60, 042001. [Google Scholar] [CrossRef]
  23. Henson, A. The CIPM MRA: Past, Present and Future. Rev. Esp. Metrol. 2015, 24. Available online: https://www.e-medida.es/numero-8/the-cipm-mra-past-present-and-future/ (accessed on 19 September 2025).
  24. Krietsch, A.; Werhahn, O. CIPM MRA Support for Hydrogen Metrology—A Case Study. Measurement 2024, 235, 115041. [Google Scholar] [CrossRef]
  25. Schwitz, W.; Hetherington, P. The CIPM MRA in Its 3rd Year of Implementation in Europe. In Proceedings of the CPEM Digest (Conference on Precision Electromagnetic Measurements), Ottawa, ON, Canada, 16–21 June 2002; pp. 270–271. [Google Scholar] [CrossRef]
  26. Quinn, T. World-Wide Recognition of National Measurement Standards: Ten Years of the CIPM MRA: Recalibration. IEEE Instrum. Meas. Mag. 2010, 13, 42–46. [Google Scholar] [CrossRef]
  27. APMP. APMP Guideline for Using Hybrid Comparisons as CMC Evidence. Available online: https://www.apmpweb.org/upload/portal/20231205/44023c95738e28e3f93e9a394feb8327.pdf (accessed on 19 October 2025).
  28. JCGM 100:2008; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement. The Bureau International Des Poids et Mesures: Sèvres, France, 2008.
  29. JCGM GUM-1:2023; Guide to the Expression of Uncertainty in Measurement—Part 1: Introduction. The Bureau International Des Poids et Mesures: Sèvres, France, 2023.
  30. JCGM 106:2012; Evaluation of Measurement Data-The Role of Measurement Uncertainty in Conformity Assessment. The Bureau International Des Poids et Mesures: Sèvres, France, 2012.
  31. Bich, W.; Cox, M.; Michotte, C. Towards a New GUM—An Update. Metrologia 2016, 53, S149. [Google Scholar] [CrossRef]
  32. Bich, W.; Cox, M.G.; Dybkaer, R.; Elster, C.; Estler, W.T.; Hibbert, B.; Imai, H.; Kool, W.; Michotte, C.; Nielsen, L.; et al. Revision of the ‘Guide to the Expression of Uncertainty in Measurement’. Metrologia 2012, 49, 702. [Google Scholar] [CrossRef]
  33. Hamilton, C.A.; Tang, Y.H. Evaluating the Uncertainty of Josephson Voltage Standards. Metrologia 1999, 36, 53. [Google Scholar] [CrossRef]
  34. Wu, T.Y.; Lu, Y.L. Error Analysis and Uncertainty Estimation for a Millimeter-Wave Phase-Shift Measurement System at 325 GHz. Measurement 2015, 59, 198–204. [Google Scholar] [CrossRef]
  35. Haloua, F.; Foulon, E.; Allard, A.; Hay, B.; Filtz, J.R. Traceable Measurement and Uncertainty Analysis of the Gross Calorific Value of Methane Determined by Isoperibolic Calorimetry. Metrologia 2015, 52, 741. [Google Scholar] [CrossRef]
  36. Coquelin, L.; Le Brusquet, L.; Fischer, N.; Gensdarmes, F.; Motzkus, C.; Mace, T.; Fleury, G. Uncertainty Propagation Using the Monte Carlo Method in the Measurement of Airborne Particle Size Distribution with a Scanning Mobility Particle Sizer. Meas. Sci. Technol. 2018, 29, 055801. [Google Scholar] [CrossRef]
  37. Wu, T.Y.; Horender, S.; Tancev, G.; Vasilatou, K. Evaluation of Aerosol-Spectrometer Based PM2.5 and PM10 Mass Concentration Measurement Using Ambient-like Model Aerosols in the Laboratory. Measurement 2022, 201, 111761. [Google Scholar] [CrossRef]
  38. Siegwarth, J.D. Estimated Uncertainty of Calibrations of Freestanding Prismatic Liquefied Natural Gas Cargo Tanks; NBSIR 81-1655; National Bureau of Standards: Washington, DC, USA, 1981. [Google Scholar]
  39. Siegwarth, J.D. Volume Uncertainty of a Large Tank Calibrated by Photogrammetry. Photogramm. Eng. Remote Sens. 1984, 50, 1127–1134. [Google Scholar]
  40. Scott, J.; Lewis, M. Uncertainty Analysis of the NIST Nitrogen Flow Facility. NIST Tech. Note 1994, 1364. Available online: https://www.nist.gov/system/files/documents/calibrations/tn1364.pdf (accessed on 19 October 2025).
  41. van der Beek, M.; Lucas, P.; Kerkhof, O.; Mirzaei, M.; Blom, G. Results of the Evaluation and Preliminary Validation of a Primary LNG Mass Flow Standard. Metrologia 2014, 51, 539–551. [Google Scholar] [CrossRef]
  42. Von Martens, H.J. Investigations into the Uncertainties of Interferometric Measurements of Linear and Circular Vibrations. Shock. Vib. 1997, 4, 327–340. [Google Scholar] [CrossRef]
  43. Guenther, F.R.; Possolo, A. Calibration and Uncertainty Assessment for Certified Reference Gas Mixtures. Anal. Bioanal. Chem. 2011, 399, 489–500. [Google Scholar] [CrossRef]
  44. Milton, M.J.T.; Vargha, G.M.; Brown, A.S. Gravimetric Methods for the Preparation of Standard Gas Mixtures. Metrologia 2011, 48, R1. [Google Scholar] [CrossRef]
  45. Schley, P.; Beck, M.; Uhrig, M.; Sarge, S.M.; Rauch, J.; Haloua, F.; Filtz, J.R.; Hay, B.; Yakoubi, M.; Escande, J.; et al. Measurements of the Calorific Value of Methane with the New GERG Reference Calorimeter. Int. J. Thermophys. 2010, 31, 665–679. [Google Scholar] [CrossRef]
  46. Wu, T.Y.; Chua, S.W.; Lu, Y.L. Noise Floor and Dynamic Range Analysis of a Microwave Attenuation Measurement Receiver from 50 MHz to 26.5 GHz. Measurement 2011, 44, 1516–1525. [Google Scholar] [CrossRef]
  47. Wu, T.Y. Accurate Measurement of Millimeter-Wave Attenuation from 75 GHz to 110 GHz Using a Dual-Channel Heterodyne Receiver. Measurement 2012, 45, 1105–1110. [Google Scholar] [CrossRef]
  48. Salzenstein, P.; Pavlyuchenko, E.; Hmima, A.; Cholley, N.; Zarubin, M.; Galliou, S.; Chembo, Y.K.; Larger, L. Estimation of the Uncertainty for a Phase Noise Optoelectronic Metrology System. Phys. Scr. 2012, T149, 14025. [Google Scholar] [CrossRef]
  49. Wu, T.Y.; Kenbar, A. Investigation of Measurement Uncertainties in LNG Density and Energy for Custody Transfer. Meas. Sci. Technol. 2021, 32, 45005. [Google Scholar] [CrossRef]
  50. Salzenstein, P.; Wu, T.Y. Uncertainty Analysis for a Phase-Detector Based Phase Noise Measurement System. Measurement 2016, 85, 118–123. [Google Scholar] [CrossRef]
  51. Salzenstein, P.; Pavlyuchenko, E. Uncertainty Evaluation on a 10.52 Ghz (5 Dbm) Optoelectronic Oscillator Phase Noise Performance. Micromachines 2021, 12, 474. [Google Scholar] [CrossRef]
  52. Wu, T.Y.; Kenbar, A.; Pruysen, A. LNG Mass Flowrate Measurement Using Coriolis Flowmeters: Analysis of the Measurement Uncertainties. Measurement 2021, 177, 109258. [Google Scholar] [CrossRef]
  53. Wu, T.Y.; Kenbar, A. LNG Mass Flow Measurement Uncertainty Reduction Using Calculated Young’s Modulus and Poisson’s Ratio for Coriolis Flowmeters. Measurement 2022, 188, 110413. [Google Scholar] [CrossRef]
  54. Cox, M.G.; Eiø, C.; Mana, G.; Pennecchi, F. The Generalized Weighted Mean of Correlated Quantities. Metrologia 2006, 43, S268. [Google Scholar] [CrossRef]
  55. Cox, M.G. The Evaluation of Key Comparison Data. Metrologia 2002, 39, 589. [Google Scholar] [CrossRef]
  56. Cox, M.G.; Harris, P.M. The Evaluation of Key Comparison Data Using Key Comparison Reference Curves. Metrologia 2012, 49, 437–445. [Google Scholar] [CrossRef]
  57. Cox, M.G. The Evaluation of Key Comparison Data: Determining the Largest Consistent Subset. Metrologia 2007, 44, 187–200. [Google Scholar] [CrossRef]
  58. Cox, M.; Shirono, K. Analysis of a Regional Metrology Organization Key Comparison: Model-Based Unilateral Degrees of Equivalence. Metrologia 2023, 60, 055014. [Google Scholar] [CrossRef]
  59. Milton, M.J.T.; Cox, M.G. Evaluating Degrees of Equivalence Using “exclusive” Statistics. Metrologia 2003, 40, L1. [Google Scholar] [CrossRef]
  60. Cox, M.G.; Harris, P.M. Technical Aspects of Guidelines for the Evaluation of Key Comparison Data. Meas. Tech. 2004, 47, 102–111. [Google Scholar] [CrossRef]
  61. Kacker, R.; Datla, R.; Parr, A. Combined Result and Associated Uncertainty from Interlaboratory Evaluations Based on the ISO Guide. Metrologia 2002, 39, 279–293. [Google Scholar] [CrossRef]
  62. Kacker, R.N.; Datla, R.U.; Parr, A.C. Statistical Analysis of CIPM Key Comparisons Based on the ISO Guide. Metrologia 2004, 41, 340–352. [Google Scholar] [CrossRef]
  63. Kacker, R.N.; Datla, R.U.; Parr, A.C. Statistical Interpretation of Key Comparison Reference Value and Degrees of Equivalence. J. Res. Natl. Inst. Stand. Technol. 2003, 108, 439–446. [Google Scholar] [CrossRef] [PubMed]
  64. Willink, R. Forming a Comparison Reference Value from Different Distributions of Belief. Metrologia 2005, 43, 12. [Google Scholar] [CrossRef]
  65. Koepke, A.; Lafarge, T.; Possolo, A.; Toman, B. Consensus Building for Interlaboratory Studies, Key Comparisons, and Meta-Analysis. Metrologia 2017, 54, S34. [Google Scholar] [CrossRef]
  66. van der Veen, A.M.H. Dark Uncertainty in Key Comparisons in the Gas Analysis Area. Metrologia 2023, 60, 064002. [Google Scholar] [CrossRef]
  67. Cecelski, C.E.; Toman, B.; Liu, F.H.; Meija, J.; Possolo, A. Errors-in-Variables Calibration with Dark Uncertainty. Metrologia 2022, 59, 045002. [Google Scholar] [CrossRef]
  68. Randa, J. Proposal for KCRV & Degree of Equivalence for GTRF Key Comparisons. In Document of the CCEM Working Group on Radiofrequency Quantities, GT-RF/2000-12; 2000. [Google Scholar]
  69. CCQM. CCQM Guidance Note: Estimation of a Concensus KCRV and Associated Degrees of Equivalence; The Bureau International Des Poids et Mesures: Sèvres, France, 2013. [Google Scholar]
  70. Sutton, C.M. Analysis and Linking of International Measurement Comparisons. Metrologia 2004, 41, 272. [Google Scholar] [CrossRef]
  71. Elster, C.; Chunovkina, A.G.; Wöger, W. Linking of a RMO Key Comparison to a Related CIPM Key Comparison Using the Degrees of Equivalence of the Linking Laboratories. Metrologia 2010, 47, 96–102. [Google Scholar] [CrossRef]
  72. Elster, C.; Link, A.; Wöger, W. Proposal for Linking the Results of CIPM and RMO Key Comparisons. Metrologia 2003, 40, 189. [Google Scholar] [CrossRef]
  73. Delahaye, F.; Witt, T.J. Linking the Results of 10 PF Capacitance Key Comparisons CCEM-K4 and Euromet 345. In Proceedings of the CPEM Digest (Conference on Precision Electromagnetic Measurements), Ottawa, ON, Canada, 16–21 June 2002; pp. 526–527. [Google Scholar] [CrossRef]
  74. Frahm, E.; Wright, J. Evaluation of Inter-Laboratory Comparison Results: Representative Examples. Measurement 2023, 223, 113723. [Google Scholar] [CrossRef]
  75. CIPM MRA-D-05; CIPM Measurement Comparisons in the CIPM MRA. The Bureau International Des Poids et Mesures: Sèvres, France, 2016.
  76. Shang, X.; Naftaly, M.; Skinner, J.; Ausden, L.; Gregory, A.; Ridler, N.M.; Arz, U.; Phung, G.N.; Ulm, D.; Kleine-Ostmann, T.; et al. Interlaboratory Comparison of Dielectric Measurements from Microwave to Terahertz Frequencies Using VNA-Based and Optical-Based Methods. IEEE Trans. Microw. Theory Technol. 2024, 72, 6473–6484. [Google Scholar] [CrossRef]
  77. Mubarak, F.; Phung, G.N.; Arz, U. An Interlaboratory Comparison of On-Wafer S-Parameter Measurements up to 1.1 THz. IEEE Trans. Terahertz Sci. Technol. 2025, 15, 2025. [Google Scholar] [CrossRef]
  78. Celep, M.; Stokes, D.; Danacı, E.; Ziadé, F.; Zagrajek, P.; Wojciechowski, M.; Phung, G.N.; Kuhlmann, K.; Kazemipour, A.; Durant, S.; et al. Interlaboratory Comparison of Power Measurements at Millimetre- and Sub-Millimetre-Wave Frequencies. Metrology 2024, 4, 279–294. [Google Scholar] [CrossRef]
  79. Matus, M.; Margolis, H.S.; Seppä, J.; Karlsson, H.; Hanquist, C.-H.; Lancaster, A.J.; Lewis, A.J.; Brawer, M.; Pérez, M.d.M.; Bisi, M.; et al. The CCL-K11 Ongoing Key Comparison. Final Report for 2023. Metrologia 2024, 61, 04002. [Google Scholar] [CrossRef]
  80. Alink, A. First Key Comparison of Primary Standard Gas Mixtures. Metrologia 2000, 37, 35–49. [Google Scholar] [CrossRef]
  81. Amy-Klein, A.; Benkler, E.; Blondé, P.; Bongs, K.; Cantin, E.; Chardonnet, C.; Denker, H.; Dörscher, S.; Feng, C.-H.; Gaudron, J.-O.; et al. International Comparison of Optical Frequencies with Transportable Optical Lattice Clocks. arXiv 2024, arXiv:2410.22973. [Google Scholar] [CrossRef]
  82. Oe, T.; Rigosi, A.F.; Kruskopf, M.; Wu, B.Y.; Lee, H.Y.; Yang, Y.; Elmquist, R.E.; Kaneko, N.H.; Jarrett, D.G. Comparison between NIST Graphene and AIST GaAs Quantized Hall Devices. IEEE Trans. Instrum. Meas. 2019, 69, 3103–3108. [Google Scholar] [CrossRef]
  83. Viliesid, M.; Colin, C.; Dube, P. Calibration of Gauge Blocks by Optical Interferometry Comparison—Final Report. Metrologia 2022, 59, 04005. [Google Scholar] [CrossRef]
  84. Kuramoto, N.; Chang, K.H.; Fujii, K.; Lee, Y.J. International Comparison of Volume Measurement for a 1 kg Silicon Sphere between KRISS and NMIJ. Measurement 2014, 49, 187–195. [Google Scholar] [CrossRef]
  85. Brown, A.S.; Quincey, P.; Ebert, V.; Nowak, A.; Tompkins, J.T.; Hessey, I.; Ciupek, K.; Schaefer, C.; Werhahn, O.; Vasilatou, K.; et al. International Comparison CCQM-K150: Particle Number Concentration (100 to 20,000 cm−3) and Particle Charge Concentration (0.15 to 3 fC cm−3). Metrologia 2023, 60, 08014. [Google Scholar] [CrossRef]
  86. Vasilatou, K.; Dirscherl, K.; Iida, K.; Sakurai, H.; Horender, S.; Auderset, K. Calibration of Optical Particle Counters: First Comprehensive Inter-Comparison for Particle Sizes up to 5 µm and Number Concentrations up to 2 cm−3. Metrologia 2020, 57, 25005. [Google Scholar] [CrossRef]
  87. Wu, T.Y.; Murashima, Y.; Sakurai, H.; Iida, K. A Bilateral Comparison of Particle Number Concentration Standards via Calibration of an Optical Particle Counter for Number Concentration up to ∼1000 cm−3. Measurement 2022, 189, 110446. [Google Scholar] [CrossRef]
  88. Broda, R.; Bonková, I.; Capogni, M.; Carconi, P.; Cassette, P.; Coulon, R.; Courte, S.; De Felice, P.; Dziel, T.; Fazio, A.; et al. The CCRI(II)-K2.Fe-55.2019 Key Comparison of Activity Concentration Measurements of a 55Fe Solution. Metrologia 2021, 58, 06010. [Google Scholar] [CrossRef]
  89. Vykydal, Z.; Park, H.; Kim, J.; Pereira, W.W.; da Fonseca, E.S.; Thiam, C.; Hui, Z.; Dewey, M.S.; Mumm, H.P.; Harano, H.; et al. International Comparison of Measurements of Neutron Source Emission Rate (2016–2021)—CCRI(III)-K9.Cf.2016. Metrologia 2024, 61, 06001. [Google Scholar] [CrossRef]
  90. Colín, C.; Viliesid, M.; Chaudhary, K.P.; Decker, J.; Dvorácek, F.; Franca, R.; Ilieff, S.; Rodríguez, J.; Stoup, J. Final Report on SIM Regional Key Comparison SIM.L-K1.2007: Calibration of Gauge Blocks by Optical Interferometry. Metrologia 2012, 49, 04010. [Google Scholar] [CrossRef]
  91. BIPM Comparison of Optical Frequency and Wavelength Standards, CCL-K11. Available online: https://www.bipm.org/kcdb/comparison?id=978 (accessed on 16 September 2025).
  92. Thalmann, R. CCL Key Comparison: Calibration of Gauge Blocks by Interferometry. Metrologia 2002, 39, 165. [Google Scholar] [CrossRef]
  93. Stock, M.; Conceição, P.; Fang, H.; Bielsa, F.; Kiss, A.; Nielsen, L.; Kim, D.; Kim, M.; Lee, K.C.; Lee, S.; et al. Report on the CCM Key Comparison of Kilogram Realizations CCM.M-K8.2019. Metrologia 2020, 57, 07030. [Google Scholar] [CrossRef]
  94. Stock, M.; Conceição, P.; Fang, H.; Bielsa, F.; Kiss, A.; Nielsen, L.; Beaudoux, F.; Espel, P.; Thomas, M.; Ziane, D.; et al. Final Report on the CCM Key Comparison of Kilogram Realizations CCM.M-K8.2021. Metrologia 2023, 60, 07003. [Google Scholar] [CrossRef]
  95. Solve, S.; Stock, M. BIPM Direct On-Site Josephson Voltage Standard Comparisons: 20 Years of Results. Meas. Sci. Technol. 2012, 23, 124001. [Google Scholar] [CrossRef]
  96. Solve, S.; Chayramy, R.; Stock, M.; Immonen, P.; Nissilä, J.; Manninen, A. Comparison of the Josephson Voltage Standards of the MIKES and the BIPM. Metrologia 2021, 58, 01007. [Google Scholar] [CrossRef]
  97. Peruzzi, A.; Dedyulin, S.; Levesque, M.; Del Campo, D.; Izquierdo, B.C.G.; Gomez, M.E.; Quelhas, K.N.; Neto, M.A.P.; Lozano, B.M.; Eusebio, L.; et al. CCT-K7.2021: CIPM Key Comparison of Water-Triple-Point Cells. Metrologia 2023, 60, 03002. [Google Scholar] [CrossRef]
  98. Stock, M.; Solve, S.; del Campo, D.; Chimenti, V.; Méndez-Lango, E.; Liedberg, H.; Steur, P.P.M.; Marcarino, P.; Dematteis, R.; Filipe, E.; et al. Final Report on CCT-K7: Key Comparison of Water Triple Point Cells. Metrologia 2006, 43, 03001. [Google Scholar] [CrossRef]
  99. Khlevnoy, B.B.; Solodilov, M.V.; Kolesnikova, S.S.; Otryaskin, D.A.; Pons, A.; Campos, J.; Shin, D.J.; Park, S.; Obein, G.; Valin, M.H.; et al. CIPM Key Comparison CCPR-K1.a.2017 for Spectral Irradiance 250 nm to 2500 nm. Final Report. Metrologia 2023, 60, 02002. [Google Scholar] [CrossRef]
  100. Woolliams, E.R.; Fox, N.P.; Cox, M.G.; Harris, P.M.; Harrison, N.J. Final Report on CCPR K1-a: Spectral Irradiance from 250 nm to 2500 nm. Metrologia 2006, 43, 02003. [Google Scholar] [CrossRef]
  101. Barrera-Figueroa, S.; Nielsen, L.; Rasmussen, K.; Matzumoto, A.E.P.; Razo, J.N.R. Final Report on the Key Comparison CCAUV.A-K4. Metrologia 2010, 47, 09003. [Google Scholar] [CrossRef]
  102. van der Veen, A.M.H.; Heine, H.J.; Brinkmann, F.N.C.; Ziel, P.R.; De Leer, E.W.B.; Zhen, W.L.; Kato, K.; Konopelko, L.A.; Popova, T.A.; Alexandrov, Y.I.; et al. International Comparison CCQM-K16: Composition of Natural Gas Types IV and V. Metrologia 2005, 42, 8003. [Google Scholar] [CrossRef]
  103. van der Veen, A.M.H.; Chander, H.; Ziel, P.R.; de Leer, E.W.B.; Smeulders, D.; Besley, L.; da Cunha, V.S.; Zhou, Z.; Qiao, H.; Heine, H.-J.; et al. International Comparison CCQM K23b: Natural Gas Type II. Metrologia 2010, 47, 08013. [Google Scholar] [CrossRef]
  104. van der Veen, A.M.H.; Ziel, P.R.; de Leer, E.W.B.; Smeulders, D.; Besley, L.; da Cunha, V.S.; Zhou, Z.; Qiao, H.; Heine, H.-J.; Tichy, J.; et al. Final Report on International Comparison CCQM K23ac: Natural Gas Types I and III. Metrologia 2007, 44, 08001. [Google Scholar] [CrossRef]
  105. Alink, A.; Milton, M.; Guenther, F.; de Leer, E.; Heine, H.; Marschal, A.; Suk Heo, G.; Takahashi, C.; Wang, L.; Kustikov, Y.; et al. Final Report of Key Comparison CCQM-K1; Technical report; Nederlands Meetinstituut, Van Swinden Laboratory: Delft, The Netherlands, 1999; Corrected version, September 2001; Available online: https://www.bipm.org/documents/20126/44595999/CCQM-K1.pdf/f8a8b735-2530-5bf3-1cfa-d924475e52dd?version=1.3&t=1643120279736 (accessed on 19 September 2025).
  106. van der Veen, A.M.H.; Zalewska, E.T.; Kipphardt, H.; Beelen, R.R.; Tuma, D.; Maiwald, M.; Füko, J.; Büki, T.; Szilágyi, Z.N.; Beránek, J.; et al. International Comparison CCQM-K118 Natural Gas. Metrologia 2022, 59, 08017. [Google Scholar] [CrossRef]
  107. CIPM. Quality Management Systems in the CIPM MRA: Guidelines for Monitoring and Reporting, MRA-G-12; The Bureau International Des Poids et Mesures: Sèvres, France, 2021. [Google Scholar]
  108. Mandal, G.; Ansari, M.A.; Aswal, D.K. Quality Management System at NPLI: Transition of ISO/IEC 17025 From 2005 to 2017 and Implementation of ISO 17034: 2016. Mapan J. Metrol. Soc. India 2021, 36, 657–668. [Google Scholar] [CrossRef]
  109. Kumar, V.; Al-Bashrawi, S.A. Quality Infrastructure: Metrology, Accreditation, and Standards. In Handbook of Quality System, Accreditation and Conformity Assessment; Springer: Berlin/Heidelberg, Germany, 2024; pp. 753–802. [Google Scholar] [CrossRef]
  110. Brandi, H.S.; De Souza, T.L. Metrology Infrastructure for Sustainable Development of the Americas: The Role of SIM. Accredit. Qual. Assur. 2009, 14, 567–573. [Google Scholar] [CrossRef]
  111. Salzenstein, P.; Lefebvre, F.; Barillet, R.; Čermak, J.; Schaefer, W.; Cibiel, G.; Sauvage, G.; Franquet, O.; Llopis, O.; Meyer, F.; et al. Phase Noise Inter-Laboratory Comparison Preliminary Results. In Proceedings of the 20th European Frequency and Time Forum, EFTF 2006, Braunschweig, Germany, 27–30 March 2006; pp. 147–151. [Google Scholar]
  112. Patan Alper, M. Inter-Laboratory Comparison of a Digital Multimeter Measurement in Turkey. Sci. Rep. 2023, 13, 19406. [Google Scholar] [CrossRef]
  113. Furuichi, N.; Terao, Y.; Ogawa, S.; Cordova, L.; Shimada, T. Inter-Laboratory Comparison of Small Water Flow Calibration Facilities with Extremely Low Uncertainty. Measurement 2016, 91, 548–556. [Google Scholar] [CrossRef]
  114. Mittal, M.K.; Biswas, J.C.; Yadav, A.S. Proficiency Testing in AC Power and Energy. Mapan J. Metrol. Soc. India 2009, 24, 41–66. [Google Scholar] [CrossRef]
  115. Guimarães, J.V.; Dias, M.H.C.; Dos Santos, J.C.A. Proficiency Testing of Electromagnetic Compatibility (EMC) Labs in Brazil by Measurement Comparisons. Meas. Sci. Technol. 2009, 20, 115107. [Google Scholar] [CrossRef]
  116. Yadav, S.; Prakash, O.; Gupta, V.K.; Kumaraswamy, B.V.; Bandyopadhyay, A.K. Evaluation of Interlaboratory Performance through Proficiency Testing Using Pressure Dial Gauge in the Hydraulic Pressure Measurement up to 70 MPa. Mapan J. Metrol. Soc. India 2008, 23, 79–99. [Google Scholar]
  117. Salzenstein, P. Rapport de Comparaison Internationale Interlaboratoire N° EM 03-99 (Haute Fréquence—Facteur de Réflexion). In Comité Français d’accréditation (COFRAC) Report; COFRAC: Paris, France, 1999. [Google Scholar]
  118. ILAC B7:10/2015; ILAC The ILAC Mutual Recognition Arrangement. International Laboratory Accreditation Cooperation: Newton, Australia, 2015.
  119. Salsbury, J. Uncertainty Management versus Risk Management in Calibration. NCSLI Meas. 2010, 5, 60–67. [Google Scholar] [CrossRef]
  120. Dobbert, M. A Guard-Band Strategy for Managing False-Accept Risk. NCSLI Meas. 2008, 3, 44–48. [Google Scholar] [CrossRef]
  121. NASA. Estimation and Evaluation of Measurement Decision Risk. In NASA Measurement Quality Assurance Handbook; National Aeronautics and Space Administration: Washington, DC, USA, 2010; p. 227. [Google Scholar]
  122. ILAC-G8:09; ILAC Guidelines on Decision Rules and Statements of Conformity. International Laboratory Accreditation Cooperation: Newton, Australia, 2019.
  123. Casacio, C.A.; Madsen, L.S.; Terrasson, A.; Waleed, M.; Barnscheidt, K.; Hage, B.; Taylor, M.A.; Bowen, W.P. Quantum-Enhanced Nonlinear Microscopy. Nature 2021, 594, 201–206. [Google Scholar] [CrossRef] [PubMed]
  124. Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-Enhanced Measurements: Beating the Standard Quantum Limit. Science 2004, 306, 1330–1336. [Google Scholar] [CrossRef]
  125. Ho, L.B. Squeezing-Induced Quantum-Enhanced Multiphase Estimation. Phys. Rev. Res. 2024, 6, 033292. [Google Scholar] [CrossRef]
  126. Li, T.; Li, F.; Liu, X.; Yakovlev, V.V.; Agarwal, G.S. Quantum-Enhanced Stimulated Brillouin Scattering Spectroscopy and Imaging. Optica 2022, 9, 959. [Google Scholar] [CrossRef]
  127. Tse, M.; Yu, H.; Kijbunchoo, N.; Fernandez-Galiana, A.; Dupej, P.; Barsotti, L.; Blair, C.D.; Brown, D.D.; Dwyer, S.E.; Effler, A.; et al. Quantum-Enhanced Advanced LIGO Detectors in the Era of Gravitational-Wave Astronomy. Phys. Rev. Lett. 2019, 123, 231107. [Google Scholar] [CrossRef]
  128. Tóth, G.; Apellaniz, I. Quantum Metrology from a Quantum Information Science Perspective. J. Phys. A Math. 2014, 47, 39. [Google Scholar] [CrossRef]
  129. Xiang, G.; Guo, G. Quantum Metrology. Chin. Phys. B 2013, 22, 110601. [Google Scholar] [CrossRef]
  130. Degen, C.L.; Reinhard, F.; Cappellaro, P. Quantum Sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
  131. Giovannetti, V.; Lloyd, S.; MacCone, L. Advances in Quantum Metrology. Nat. Photonics 2011, 5, 222–229. [Google Scholar] [CrossRef]
  132. Jarzyna, M.; Demkowicz-Dobrzański, R. True Precision Limits in Quantum Metrology. New J. Phys. 2015, 17, 13010. [Google Scholar] [CrossRef]
  133. Carlton, M. Caves Quantum Mechanical Radiation-Pressure Fluctuations in an Interferometer. Phys. Rev. Lett. 1980, 45, 75–79. [Google Scholar]
  134. Zheng, X.; Dolde, J.; Lochab, V.; Merriman, B.N.; Li, H.; Kolkowitz, S. Differential Clock Comparisons with a Multiplexed Optical Lattice Clock. Nature 2022, 602, 425–430. [Google Scholar] [CrossRef]
  135. Ludlow, A.D.; Zelevinsky, T.; Campbell, G.K.; Blatt, S.; Boyd, M.M.; De Miranda, M.H.G.; Martin, M.J.; Thomsen, J.W.; Foreman, S.M.; Ye, J.; et al. Sr Lattice Clock at 1 × 10–16 Fractional Uncertainty by Remote Optical Evaluation with a Ca Clock. Science 2008, 319, 1805–1808. [Google Scholar] [CrossRef]
  136. Rosenband, T.; Hume, D.B.; Schmidt, P.O.; Chou, C.W.; Brusch, A.; Lorini, L.; Oskay, W.H.; Drullinger, R.E.; Fortier, T.M.; Stalnaker, J.E.; et al. Frequency Ratio of Al+ and Hg+ Single-Ion Optical Clocks; Metrology at the 17th Decimal Place. Science 2008, 319, 1808–1812. [Google Scholar] [CrossRef]
  137. Beloy, K.; Bodine, M.I.; Bothwell, T.; Brewer, S.M.; Bromley, S.L.; Chen, J.S.; Deschênes, J.D.; Diddams, S.A.; Fasano, R.J.; Fortier, T.M.; et al. Frequency Ratio Measurements at 18-Digit Accuracy Using an Optical Clock Network. Nature 2021, 591, 564–569. [Google Scholar] [CrossRef] [PubMed]
  138. Brewer, S.M.; Chen, J.S.; Hankin, A.M.; Clements, E.R.; Chou, C.W.; Wineland, D.J.; Hume, D.B.; Leibrandt, D.R. Al+ 27 Quantum-Logic Clock with a Systematic Uncertainty below 10–18. Phys. Rev. Lett. 2019, 123, 033201. [Google Scholar] [CrossRef] [PubMed]
  139. Robinson, J.M.; Miklos, M.; Tso, Y.M.; Kennedy, C.J.; Bothwell, T.; Kedar, D.; Thompson, J.K.; Ye, J. Direct Comparison of Two Spin-Squeezed Optical Clock Ensembles at the 10–17 Level. Nat. Phys. 2024, 20, 208–213. [Google Scholar] [CrossRef]
  140. Ye, J.; Yoon, T.H.; Hall, J.L.; Madej, A.A.; Bernard, J.E.; Siemsen, K.J.; Marmet, L.; Chartier, J.M.; Chartier, A. Accuracy Comparison of Absolute Optical Frequency Measurement between Harmonic-Generation Synthesis and a Frequency-Division Femtosecond Comb. Phys. Rev. Lett. 2000, 85, 3797–3800. [Google Scholar] [CrossRef]
  141. Udem, T.; Holzwarth, R.; Hänsch, T.W. Optical Frequency Metrology. Nature 2002, 416, 233–237. [Google Scholar] [CrossRef] [PubMed]
  142. He, H.; Cedergren, K.; Shetty, N.; Lara-Avila, S.; Kubatkin, S.; Bergsten, T.; Eklund, G. Accurate Graphene Quantum Hall Arrays for the New International System of Units. Nat. Commun. 2022, 13, 6933. [Google Scholar] [CrossRef]
  143. Lafont, F.; Ribeiro-Palau, R.; Kazazis, D.; Michon, A.; Couturaud, O.; Consejo, C.; Chassagne, T.; Zielinski, M.; Portail, M.; Jouault, B.; et al. Quantum Hall Resistance Standards from Graphene Grown by Chemical Vapour Deposition on Silicon Carbide. Nat. Commun. 2015, 6, 6806. [Google Scholar] [CrossRef]
  144. Yin, Y.; Kruskopf, M.; Gournay, P.; Rolland, B.; Götz, M.; Pesel, E.; Tschirner, T.; Momeni, D.; Chatterjee, A.; Hohls, F.; et al. Graphene Quantum Hall Resistance Standard for Realizing the Unit of Electrical Resistance under Relaxed Experimental Conditions. Phys. Rev. Appl. 2025, 23, 014025. [Google Scholar] [CrossRef]
  145. Giesbers, A.J.M.; Rietveld, G.; Houtzager, E.; Zeitler, U.; Yang, R.; Novoselov, K.S.; Geim, A.K.; Maan, J.C. Quantum Resistance Metrology in Graphene. Appl. Phys. Lett. 2008, 93, 222109. [Google Scholar] [CrossRef]
  146. Schopfer, F.; Poirier, W. Graphene-Based Quantum Hall Effect Metrology. MRS Bull. 2012, 37, 1255–1264. [Google Scholar] [CrossRef]
  147. NIST. NIST Broadens Collaboration with BIPM to Enhance Voltage Standards. Available online: https://www.nist.gov/news-events/news/2024/10/nist-broadens-collaboration-bipm-enhance-voltage-standards (accessed on 16 September 2025).
  148. BIPM New Pilot Study Enhances Accuracy of AC Voltage Comparisons. Available online: https://www.bipm.org/en/-/2024-10-24-pilot-study-ac-voltage (accessed on 22 September 2025).
  149. Fujii, K.; Massa, E.; Bettin, H.; Kuramoto, N.; Mana, G. Avogadro Constant Measurements Using Enriched 28Si Monocrystals. Metrologia 2018, 55, L1–L4. [Google Scholar] [CrossRef]
  150. Bartl, G.; Becker, P.; Beckhoff, B.; Bettin, H.; Beyer, E.; Borys, M.; Busch, I.; Cibik, L.; D’Agostino, G.; Darlatt, E.; et al. A New 28Si Single Crystal: Counting the Atoms for the New Kilogram Definition. Metrologia 2017, 54, 693–715. [Google Scholar] [CrossRef]
  151. Eppers, D.; Knopf, D.; Nicolaus, A.; Kuhn, E.; Borys, M.; Müller, M.; Bettin, H. Status of the Kilogram Realisation Using the XRCD Method at PTB. Meas. Sens. 2025, 38, 101353. [Google Scholar] [CrossRef]
  152. Eppers, D.; Müller, M.; Kuhn, E.; Borys, M.; Rodiek, B.; Knopf, D.; Schrader, T. Realisation of the Kilogram with the XRCD Method—Improved XRF Evaluation and Its Impact. Metrologia 2025, 62, 065001. [Google Scholar] [CrossRef]
  153. Kuramoto, N.; Mizushima, S.; Zhang, L.; Fujita, K.; Okubo, S.; Inaba, H.; Azuma, Y.; Kurokawa, A.; Ota, Y.; Fujii, K. Reproducibility of the Realization of the Kilogram Based on the Planck Constant by the XRCD Method at NMIJ. IEEE Trans. Instrum. Meas. 2021, 70, 1005609. [Google Scholar] [CrossRef]
  154. Fujii, K.; Bettin, H.; Becker, P.; Massa, E.; Rienitz, O.; Pramann, A.; Nicolaus, A.; Kuramoto, N.; Busch, I.; Borys, M. Realization of the Kilogram by the XRCD Method. Metrologia 2016, 53, A19–A45. [Google Scholar] [CrossRef]
  155. Robinson, I.A.; Schlamminger, S. The Watt or Kibble Balance: A Technique for Implementing the New SI Definition of the Unit of Mass. Metrologia 2016, 53, A46–A74. [Google Scholar] [CrossRef]
  156. Fang, H.; Bielsa, F.; Li, S.; Kiss, A.; Stock, M. The BIPM Kibble Balance for Realizing the Kilogram Definition. Metrologia 2020, 57, 045009. [Google Scholar] [CrossRef]
  157. Stock, M. The Watt Balance: Determination of the Planck Constant and Redefinition of the Kilogram. In Proceedings of the Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences; The Royal Society Publishing: London, UK, 2011; Volume 369, pp. 3936–3953. [Google Scholar]
  158. Konrad, J.; Rothleitner, C.; Vasilyan, S.; Rogge, N.; Behr, R.; Götz, M.; Kruskopf, M.; Fröhlich, T. Small Mass Value Realization Equivalent to Accuracy Class E1 Using the Planck-Balance at PTB. Metrologia 2025, 62, 025014. [Google Scholar] [CrossRef]
  159. Chao, L.; Seifert, F.; Haddad, D.; Pratt, J.; Newell, D.; Schlamminger, S. The Performance of the KIBB-G1 Tabletop Kibble Balance at NIST. Metrologia 2020, 57, 035014. [Google Scholar] [CrossRef]
  160. Keck, L.; Seifert, F.; Newell, D.; Schlamminger, S.; Theska, R.; Haddad, D. Design of an Enhanced Mechanism for a New Kibble Balance Directly Traceable to the Quantum SI. EPJ Technol. Instrum. 2022, 9, 7. [Google Scholar] [CrossRef]
  161. Robinson, I.A. Watt and Joule Balances. Metrologia 2014, 51, S1. [Google Scholar] [CrossRef]
  162. Pizzocaro, M.; Sekido, M.; Takefuji, K.; Ujihara, H.; Hachisu, H.; Nemitz, N.; Tsutsumi, M.; Kondo, T.; Kawai, E.; Ichikawa, R.; et al. Intercontinental Comparison of Optical Atomic Clocks through Very Long Baseline Interferometry. Nat. Phys. 2021, 17, 223–227. [Google Scholar] [CrossRef]
  163. Giblin, S.P.; Yamahata, G.; Fujiwara, A.; Kataoka, M. Precision Measurement of an Electron Pump at 2 GHz; the Frontier of Small DC Current Metrology. Metrologia 2023, 60, 055001. [Google Scholar] [CrossRef]
  164. Stock, M.; Davis, R.; De Mirandés, E.; Milton, M.J.T. The Revision of the SI—The Result of Three Decades of Progress in Metrology. Metrologia 2019, 56, 022001. [Google Scholar] [CrossRef]
  165. Milano, G.; Zheng, X.; Michieletti, F.; Leonetti, G.; Caballero, G.; Oztoprak, I.; Boarino, L.; Bozat, Ö.; Callegaro, L.; De Leo, N.; et al. A Quantum Resistance Memristor for an Intrinsically Traceable International System of Units Standard. Nat. Nanotechnol. 2025, 1–7. [Google Scholar] [CrossRef]
  166. Riehle, F.; Gill, P.; Arias, F.; Robertsson, L. The CIPM List of Recommended Frequency Standard Values: Guidelines and Procedures. Metrologia 2018, 55, 188. [Google Scholar] [CrossRef]
  167. BIPM. Mise En Pratique for the Definition of the Second in the SI. In SI Brochure; The Bureau International Des Poids et Mesures: Sèvres, France, 2019. [Google Scholar]
  168. Lindvall, T.; Pizzocaro, M.; Godun, R.M.; Abgrall, M.; Akamatsu, D.; Amy-Klein, A.; Benkler, E.; Bhatt, N.M.; Calonico, D.; Cantin, E.; et al. Coordinated International Comparisons between Optical Clocks Connected via Fiber and Satellite Links. Optica 2025, 12, 843. [Google Scholar] [CrossRef]
  169. Sanner, C.; Huntemann, N.; Lange, R.; Tamm, C.; Peik, E.; Safronova, M.S.; Porsev, S.G. Optical Clock Comparison for Lorentz Symmetry Testing. Nature 2019, 567, 204–208. [Google Scholar] [CrossRef]
  170. Margolis, H.S.; Panfilo, G.; Petit, G.; Oates, C.; Ido, T.; Bize, S. The CIPM List ‘Recommended Values of Standard Frequencies’: 2021 Update. Metrologia 2024, 61, 035005. [Google Scholar] [CrossRef]
  171. BIPM Vers La Redéfinition de La Seconde. Available online: https://www.bipm.org/fr/-/2024-02-20-redefinition-second (accessed on 16 September 2025).
  172. BIPM. SI Base Unit: Second (s). Available online: https://www.bipm.org/en/si-base-units/second (accessed on 16 September 2025).
  173. Dimarcq, N.; Gertsvolf, M.; Mileti, G.; Bize, S.; Oates, C.W.; Peik, E.; Calonico, D.; Ido, T.; Tavella, P.; Meynadier, F.; et al. Roadmap towards the Redefinition of the Second. Metrologia 2024, 61, 012001. [Google Scholar] [CrossRef]
  174. Giblin, S.P.; Kataoka, M.; Fletcher, J.D.; See, P.; Janssen, T.J.B.M.; Griffiths, J.P.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A. Towards a Quantum Representation of the Ampere Using Single Electron Pumps. Nat. Commun. 2012, 3, 930. [Google Scholar] [CrossRef]
  175. Bae, M.H.; Chae, D.H.; Kim, M.S.; Kim, B.K.; Park, S.I.; Song, J.; Oe, T.; Kaneko, N.H.; Kim, N.; Kim, W.S. Precision Measurement of Single-Electron Current with Quantized Hall Array Resistance and Josephson Voltage. Metrologia 2020, 57, 065025. [Google Scholar] [CrossRef]
  176. Scherer, H.; Camarota, B. Quantum Metrology Triangle Experiments: A Status Review. Meas. Sci. Technol. 2012, 23, 124010. [Google Scholar] [CrossRef]
  177. López, M.; Meda, A.; Porrovecchio, G.; Starkwood (Kirkwood), R.A.; Genovese, M.; Brida, G.; Šmid, M.; Chunnilall, C.J.; Degiovanni, I.P.; Kück, S. A Study to Develop a Robust Method for Measuring the Detection Efficiency of Free-Running InGaAs/InP Single-Photon Detectors. EPJ Quantum Technol. 2020, 7, 14. [Google Scholar] [CrossRef]
  178. Quinn, T.J. The BIPM and the Accurate Measurement of Time. Proc. IEEE 1991, 79, 894–905. [Google Scholar] [CrossRef]
  179. McNish, A.G. Lasers for Length Measurement. Science 1964, 146, 177–182. [Google Scholar] [CrossRef] [PubMed]
  180. Beers, J.S.; Penzes, W.B. The NIST Length Scale Interferometer. J. Res. Natl. Inst. Stand. Technol. 1999, 104, 225. [Google Scholar] [CrossRef]
  181. Walls, F.L.; Barillet, R.; Besson, R.J.; Groslambert, J.; Schumacher, P.; Rufenacht, J.; Hilty, K. International Comparison of Phase Noise. In Proceedings of the 8th European Frequency and Time Forum (EFTF), Weihenstephan, Germany, 25–27 June 1994; pp. 439–456. [Google Scholar]
  182. Quincey, P.; Sarantaridis, D.; Yli-Ojanperä, J.; Keskinen, J.; Högström, R.; Heinonen, M.; Lüönd, F.; Nowak, A.; Riccobono, F.; Tuch, T.; et al. EURAMET Comparison 1244 Comparison of Aerosol Electrometers, Issue 2: EURAMET REPORT. In NPL REPORT AS 85; The National Physical Laboratory: London, UK, 2014. [Google Scholar]
  183. Brown, A.; Nowak, A.; Tompkins, J.; Tomson, M.; Waheed, A.; Godau, D.; Jung, J.; Kim, H.; Wu, T.; Auderset, K.; et al. Ensuring the Worldwide Equivalence of Measurements of Nanoparticle Number Concentration and Charge Concentration: An International Comparison. In Proceedings of the European Aerosol Conference (EAC 2025), Lecce, Italy, 31 August–5 September 2025. [Google Scholar]
  184. Brown, A.; Nowak, A.; Tipler, J.; Tompkins, J.; Tomson, M.; Waheed, A.; Godau, D.; Jung, J.; Kim, H.; Wu, T.; et al. International Comparison CCQM-K185: Particle Number Concentration 1000 to 500,000 cm−3) and Particle Charge Concentration 0.16 fC to 16 fC cm−3). Final report for International Comparison CCQM-K185, to be published in BIPM website.
Metrology 05 00074 g001
Figure 1. Roles of NMIs in ensuring the global measurement consistency and traceability.
Figure 1. Roles of NMIs in ensuring the global measurement consistency and traceability.
Metrology 05 00074 g001
Metrology 05 00074 g002
Figure 2. Single sideband (SSB) phase noise at 1 Hz offset from the 5 MHz carrier, in a phase noise inter-laboratory comparison conducted in 2006 [111]. LR1 and LR2 represent the measurements carried out on the two benches of the reference laboratory. One participant (B) identified an issue after the comparison, which can explain the observed big deviation during the comparison. Three participants (C, D, and F) did not report the uncertainty of their measurements, although their results were consistent with the overall average. Participant E was unable to provide a result.
Figure 2. Single sideband (SSB) phase noise at 1 Hz offset from the 5 MHz carrier, in a phase noise inter-laboratory comparison conducted in 2006 [111]. LR1 and LR2 represent the measurements carried out on the two benches of the reference laboratory. One participant (B) identified an issue after the comparison, which can explain the observed big deviation during the comparison. Three participants (C, D, and F) did not report the uncertainty of their measurements, although their results were consistent with the overall average. Participant E was unable to provide a result.
Metrology 05 00074 g002
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Salzenstein, P.; Wu, T.Y.; Pavlyuchenko, E. The Critical Role of International Comparisons in Global Metrology System: An Overview. Metrology 2025, 5, 74. https://doi.org/10.3390/metrology5040074

AMA Style

Salzenstein P, Wu TY, Pavlyuchenko E. The Critical Role of International Comparisons in Global Metrology System: An Overview. Metrology. 2025; 5(4):74. https://doi.org/10.3390/metrology5040074

Chicago/Turabian Style

Salzenstein, Patrice, Thomas Y. Wu, and Ekaterina Pavlyuchenko. 2025. "The Critical Role of International Comparisons in Global Metrology System: An Overview" Metrology 5, no. 4: 74. https://doi.org/10.3390/metrology5040074

APA Style

Salzenstein, P., Wu, T. Y., & Pavlyuchenko, E. (2025). The Critical Role of International Comparisons in Global Metrology System: An Overview. Metrology, 5(4), 74. https://doi.org/10.3390/metrology5040074

Article Metrics

Back to TopTop