3.1. Experimental Methods
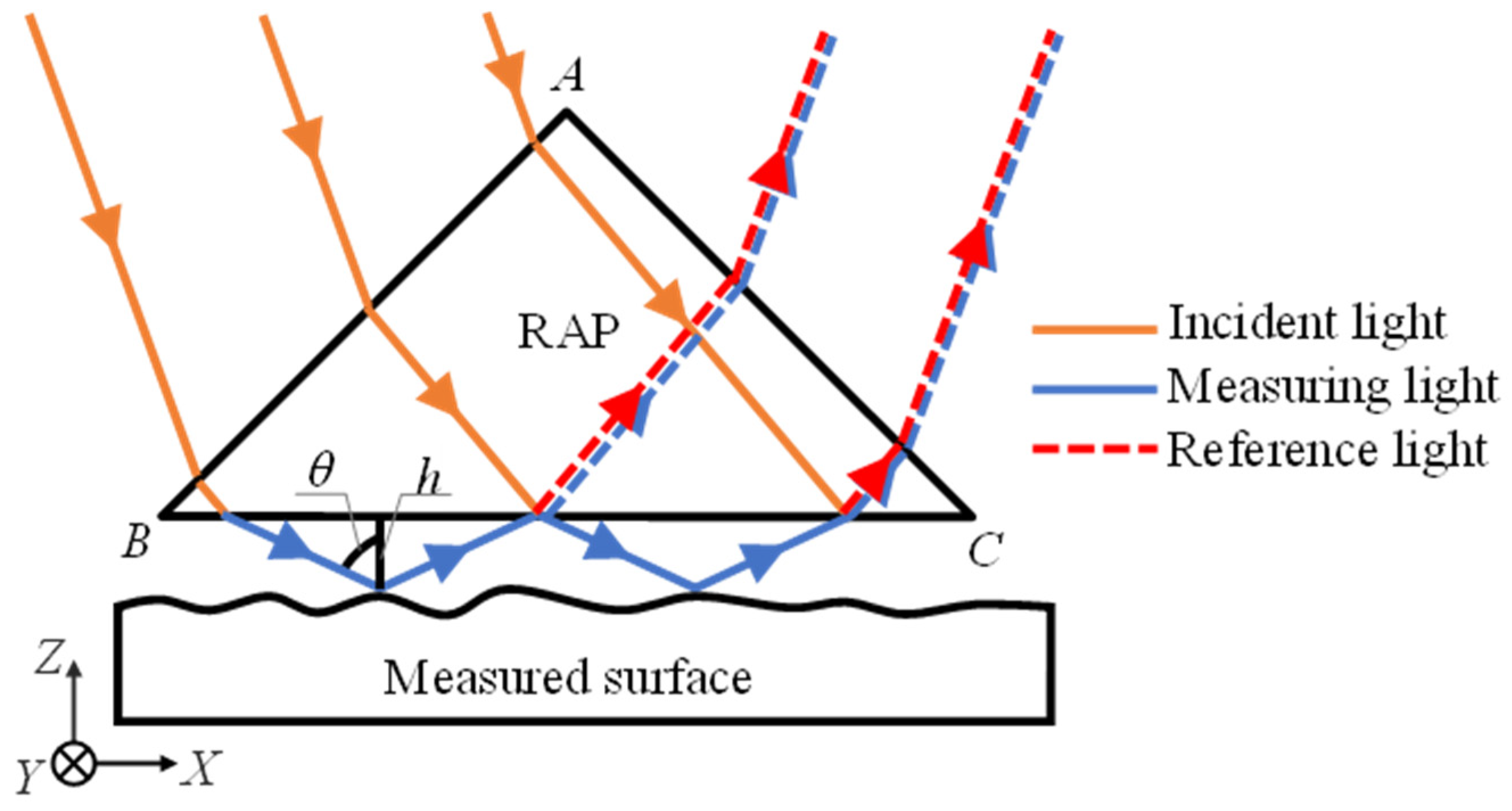
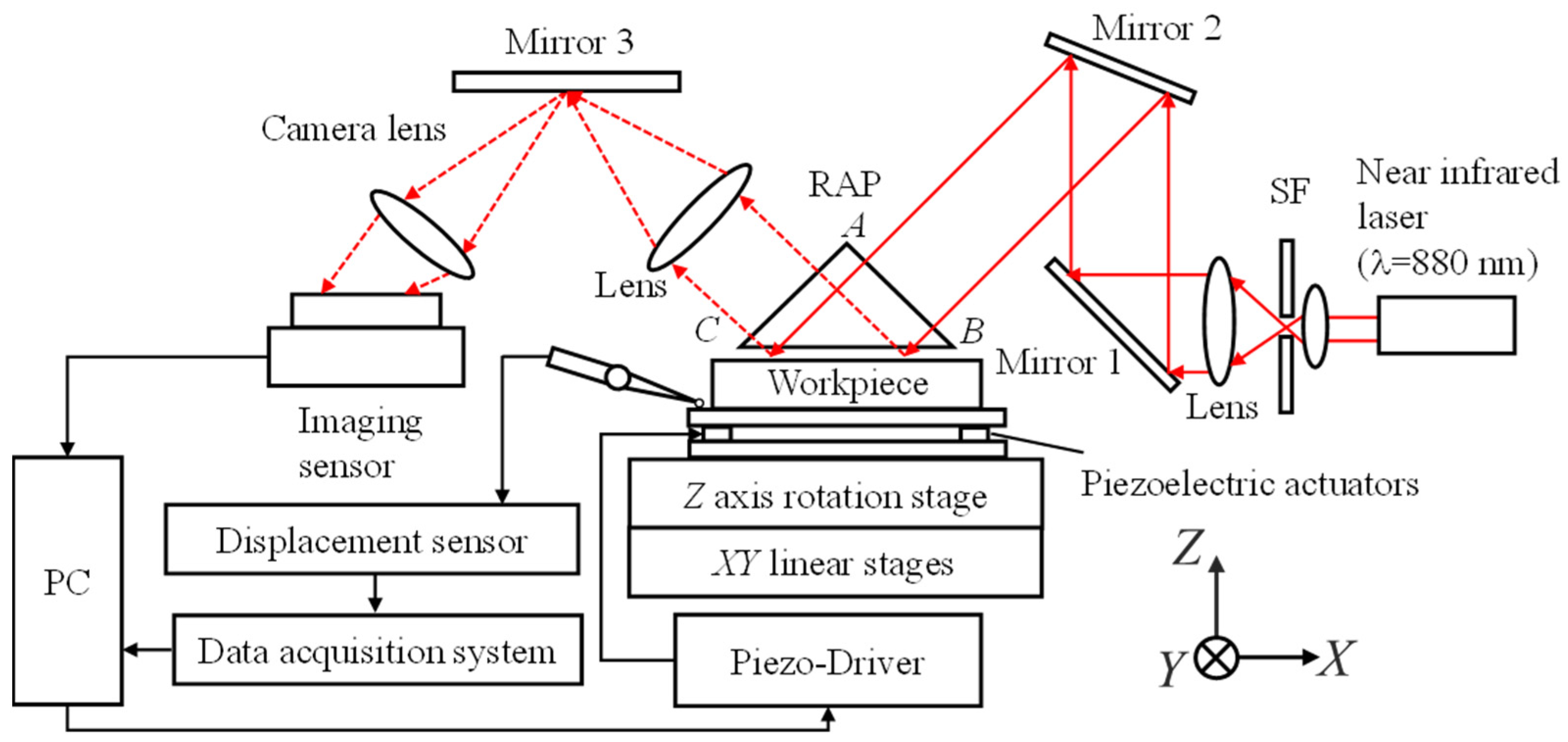
Figure 2 shows the configuration of the oblique-incident interferometer used in this study. A commercially available hand-scraped surface plate (OS-105, Ohnishi Sokutei, Higashiosaka, Japan) was used as the measurement surface. Multiple hand-scraped marks are present on the surface of the plate. The nominal flatness accuracy of the plate surface used in the study was 15 μm. A near-infrared laser with a wavelength of 880 nm (TCSQ2-08800010-4-CL, NEOARK, Hachioji, Japan) was used as the light source. The intensity of the laser light was adjusted using a neutral-density (ND) filter, and the laser beam was passed through a spatial filter (SF) consisting of a 40× objective lens and a 25 μm diameter pinhole. The laser beam was expanded into a collimated beam through the lens and incident on the
A-B plane of the RAP (RPB-20-10H, SIGMA KOKI, Hidaka, Japan). The size of the
B-C plane of the RAP was 40 mm × 56 mm, and the surface accuracy of the RAP was λ/10. The interference fringes generated on the
B-C plane of the RAP were captured using an imaging sensor (EO1312LE, Edmund Optics, NJ, USA) through a tilt-shift camera lens (TS-E 90 mm F2.8L Macro, Canon, Tokyo, Japan). The number of pixels in the imaging sensor was 1280 × 1024. The tilt-shift camera lens facilitated the focusing of the entire area of the inclined plane because the
B-C plane of the RAP and the imaging sensor satisfied the Scheimpflug principle. The size of the field of view captured by the imaging sensor was 18.1 mm × 11.7 mm; thus, the estimated lateral resolution of the interferometer was 14.1 μm × 11.4 μm. Phase-shifting of the interference fringes was achieved by moving the surface plate in the
Z-direction using piezoelectric actuators (AE0203D08DF, MESS-TEK, Wako, Japan). Four piezoelectric actuators were placed under the plate on which the surface plate was mounted, expanded, and contracted in response to the driving signal from the piezoelectric drivers, controlled using a personal computer. A homemade PZT-driven
Z axis positioning stage was mounted on a manual XY linear stage (LD-947-S1, Chuo Precision Industrial, Tokyo, Japan) and a manual Z axis rotation stage (KSPA-986M, SIGMA KOKI, Hidaka, Japan). The displacement of the piezoelectric actuator was monitored during the phase shift using a calibrated cantilever-type displacement sensor (TELEMICRO ESM-01, Ogasawara Precision Laboratory, Yamakita, Japan). The nominal resolution and accuracy of the displacement sensor are 10 nm and 75 nm, respectively. Red solid and dashed lines in
Figure 2 indicate incident measuring light and interference light, respectively.
The incident angle of the measuring light can be changed by adjusting the height along the
Z-direction and the angle around the
Y-axis of Mirror 2. Because the measured light was refracted at the
A-B and
B-C planes of the RAP, it was not easy to precisely calculate the incident angle
θ from the incident angle of the laser beam to the
A-B plane of the RAP. In addition, it was necessary to evaluate the
Z-directional displacement of the measured surface corresponding to the phase-shifting of the interference fringe of
π/2 rad for the use of the five-step phase-shifting method. In this experiment, the surface plate was displaced in the
Z-direction using piezoelectric actuators, while the interference fringes generated on the smooth surface of the surface plate were observed using the imaging sensor. The phase of the interference fringes was shifted to 6
π rad while the
Z-directional displacement of the surface plate was measured using the displacement sensor. Based on Equations (1) and (2), the interval and sensitivity of the interference fringes change with the incident angle of the measuring light. The relationship between the
Z-directional displacement of a certain point on the measured surface, Δ
h, and the incident angle of the measuring light,
θ can be expressed by Equation (4).
Consequently, the incident angle of the measuring light
θ can be calculated from the displacement Δ
h, which corresponds to the phase of the interference fringe of 2
π. The incidence angle
θ was calculated from the interference fringe phase-shifting on a smooth surface, which was the dark area shown in
Figure 3a, and the displacement of the PZT-driven
Z-stage.
3.2. Experimental Results and Discussions
The reproducibility of the surface-form measurements using the oblique-incident interferometer was investigated by measuring the same hand-scraped marks while changing the direction and angle of incidence of the measuring light.
Figure 3 shows the hand-scraped marks observed using the developed oblique-incident interferometer.
Figure 3a shows the hand-scraped marks observed under incoherent light. The hand-scraped marks appeared brighter than the smooth surface because the incident light was scattered on the rough surface created by hand-scraping.
Figure 3b shows an example of interference fringes on a hand-scraped surface irradiated by a near-infrared laser. The incident angle of the measuring light was 76.0°. The incident direction of the measuring light was changed by rotating the surface plate by 180° around the
Z-axis. Because the surface form of the hand-scraped marks was rotated around the
Z-axis after the rotation of the surface plate, the surface form data were rotated around the
Z-axis so that they were the same as before the rotation. The rotational alignment of the workpiece was adjusted to within 0.1° using the Z axis rotation stage and the images captured by the imaging sensor under incoherent light. The rotational error of the workpiece corresponded to an alignment error of ±1 pixel of at most.
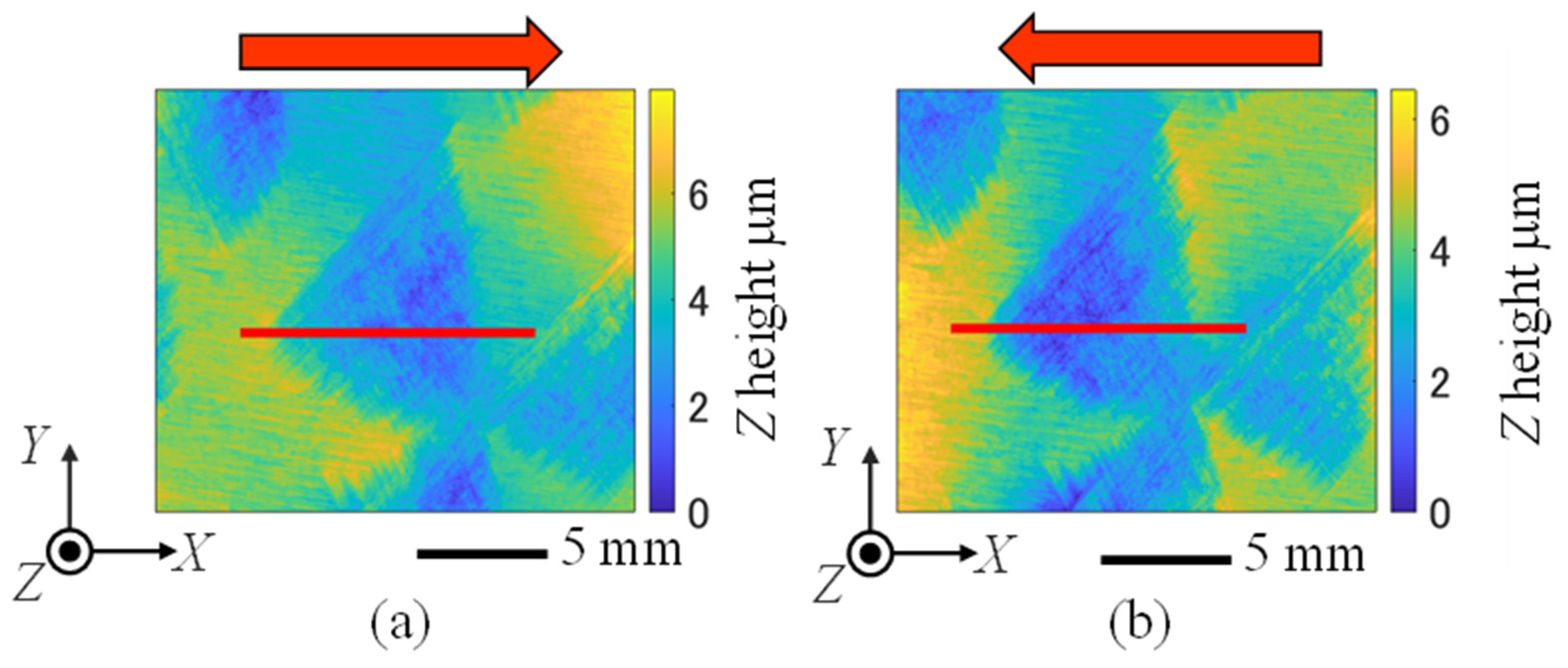
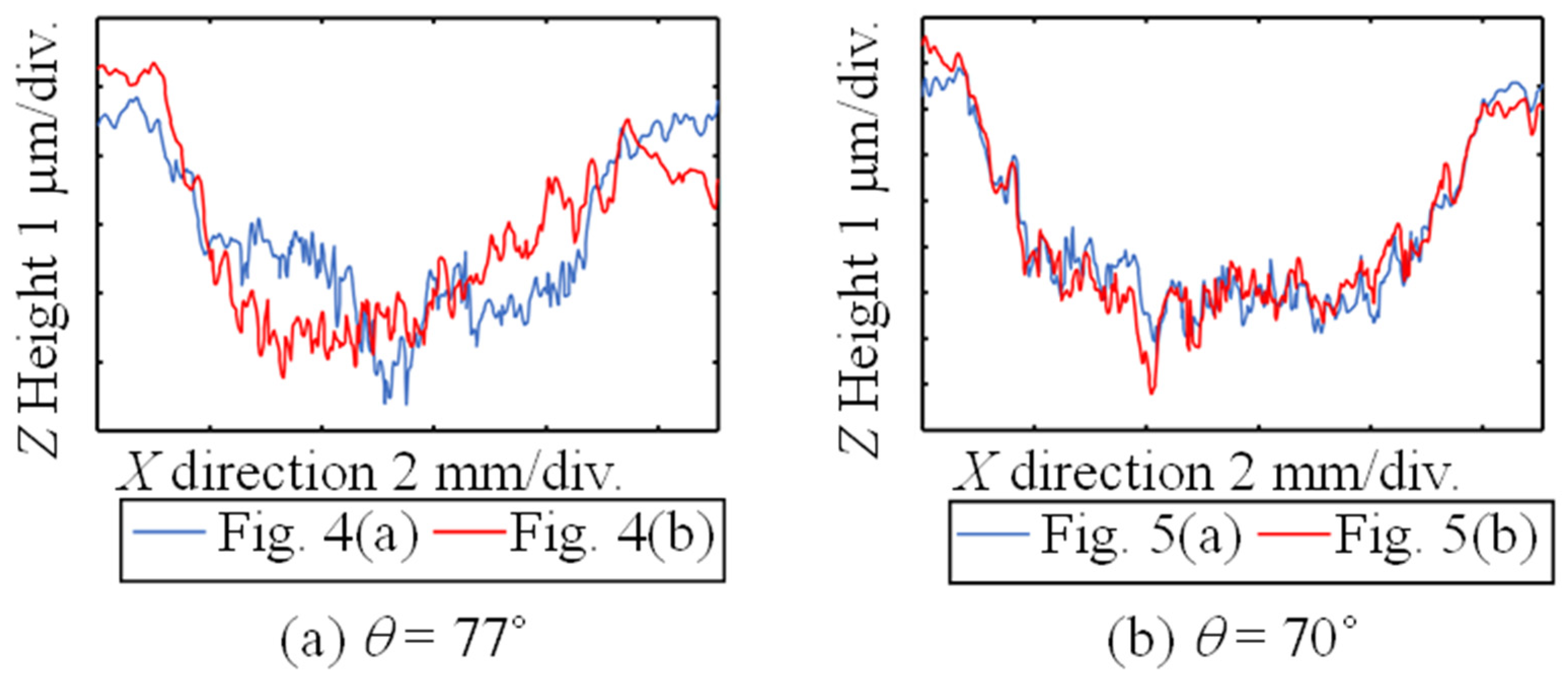
Figure 4 shows the surface forms of the hand-scraped marks calculated from the interference fringes generated when the incident angle of the measured light was set to approximately 77°. The incident angle of the measured light was the maximum angle achievable with the constructed oblique-incident interferometer. At larger incident angles, it was difficult to illuminate the entire measurement surface because of the interference between the laser beam and optical components. The arrowheads in
Figure 4 indicate the incident direction of the measured light. It can be observed that the hand-scraped marks are lower than the surrounding smooth surface. The incident angle of the measuring light and the
Z-directional displacement per step of the phase-shifting shown in
Figure 4a were set to 77.4° and 0.51 μm, respectively.
Figure 4b shows the surface form of the same hand-scraped marks measured by changing the incident direction of the measuring light. In the case of measurement results presented in
Figure 4b, the incident angle of the measuring light and the
Z-directional displacement per one step of the phase-shifting were set to be 76.0° and 0.46 μm. Although
Figure 4 shows the measurement results of the same hand-scraped marks, the right side of the hand-scraped mark in
Figure 4a is slightly deeper. However, the left side of the hand-scraping mark is somewhat deeper, as shown in
Figure 4b. Even when a near-infrared laser source was used, inconsistencies in the surface-form measurement results due to the incident direction of the measuring light were confirmed, as in a previous study [
8].
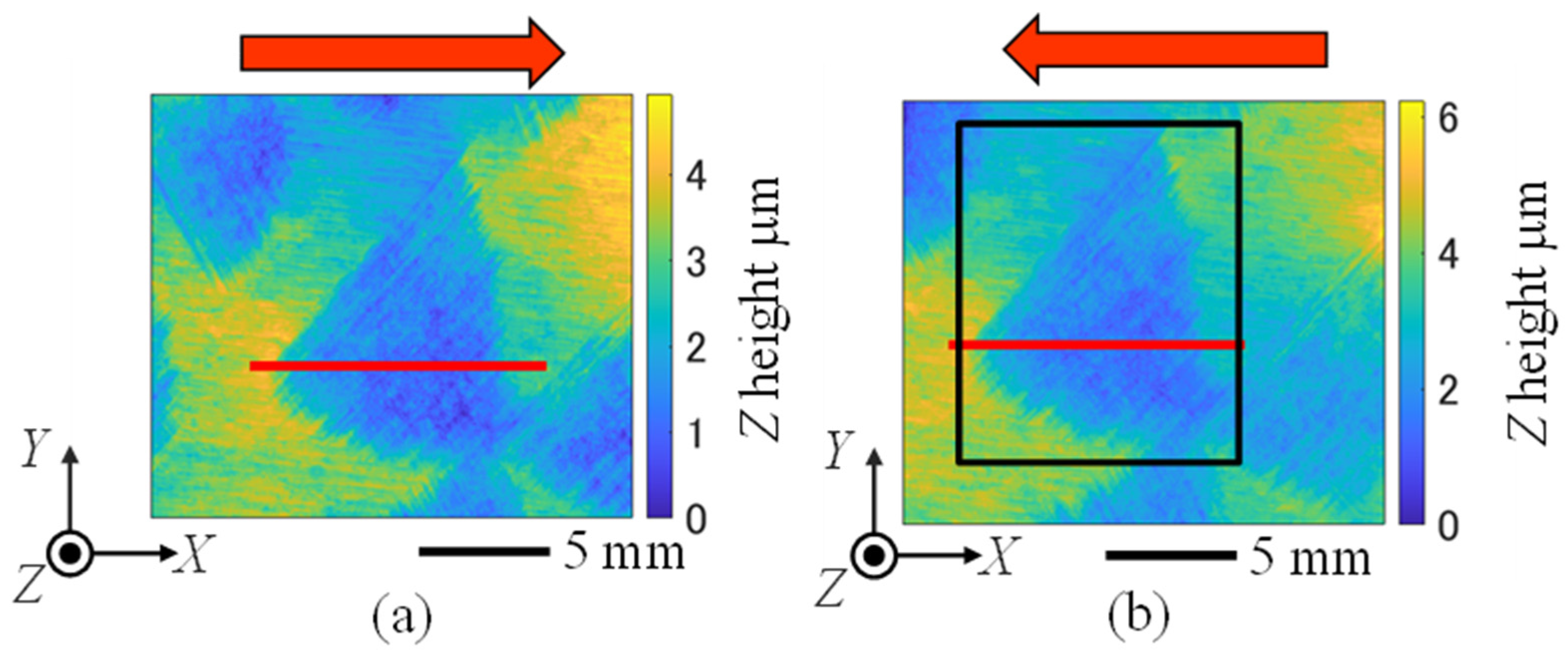
Figure 5 shows the surface forms of the hand-scraped marks measured at smaller incident angles of the measuring light. The incident angle of the measuring light was set to approximately 70°, which was the minimum incident angle in the oblique-incident interferometer used in this experiment. When the incident angle was smaller than 70°, phase-shifting of the interference fringes could not be detected because of the increase in the scattered light intensity on the rough surface of the hand-scraped marks. In addition to
Figure 4, the arrowheads in
Figure 5 indicate the direction of the incident light. In
Figure 5a, the incident angle of the measuring light and the
Z-directional displacement per step of the phase-shifting were set to 70.1° and 0.32 μm, respectively. Similarly, in
Figure 5b, the incident angle of the measuring light and the
Z-directional displacement per step of the phase-shifting were set to 70.5° and 0.33 μm, respectively.
To investigate the effects of the incident angles of the measuring light, the cross-sectional profiles of the same position on the hand-scraped marks were compared. The measurement position on each surface form was identified pixel-by-pixel by pattern matching, using the area surrounded by the black frame indicated in
Figure 5b as a template. As for the pattern matching, the method from previous research shown in Reference 13 was applied. Template matching using the normxcorr2 function in MATLAB 2023a was used. The template area was set to include the entire the hand-scraped mark near the center of
Figure 3a because it includes the lowest position of the hand-scraped mark. The red lines in
Figure 4 and
Figure 5 represent the same positions on the same hand-scraped mark identified by pattern matching.
Figure 6 shows the cross-sectional profiles represented by the red lines in
Figure 4 and
Figure 5. The number of measurement points for each profile was 786. The correlation coefficients between the template of the pattern matching and identified locations extracted from
Figure 4a,b were evaluated as 0.80 and 0.77, respectively. Similarly, the correlation coefficient between the template location and the identified location extracted from
Figure 5a was 0.94. The correlation coefficients were larger than 0.7, and each location indicated a strong correlation with the template of pattern matching. Therefore, the profiles shown in
Figure 6 are considered to be at the same position on the surface plate. As shown in
Figure 6a, when the incident angle of the measured light was approximately 77°, a significant difference in the cross-sectional profiles was observed. The correlation coefficient between the two profiles, shown in
Figure 6a, was estimated to be 0.78. However, when the incident angle of the measuring light was approximately 70°, the two profiles shown in
Figure 6b exhibited good agreement. The correlation coefficient between the two profiles, shown in
Figure 6b, was estimated to be 0.96.
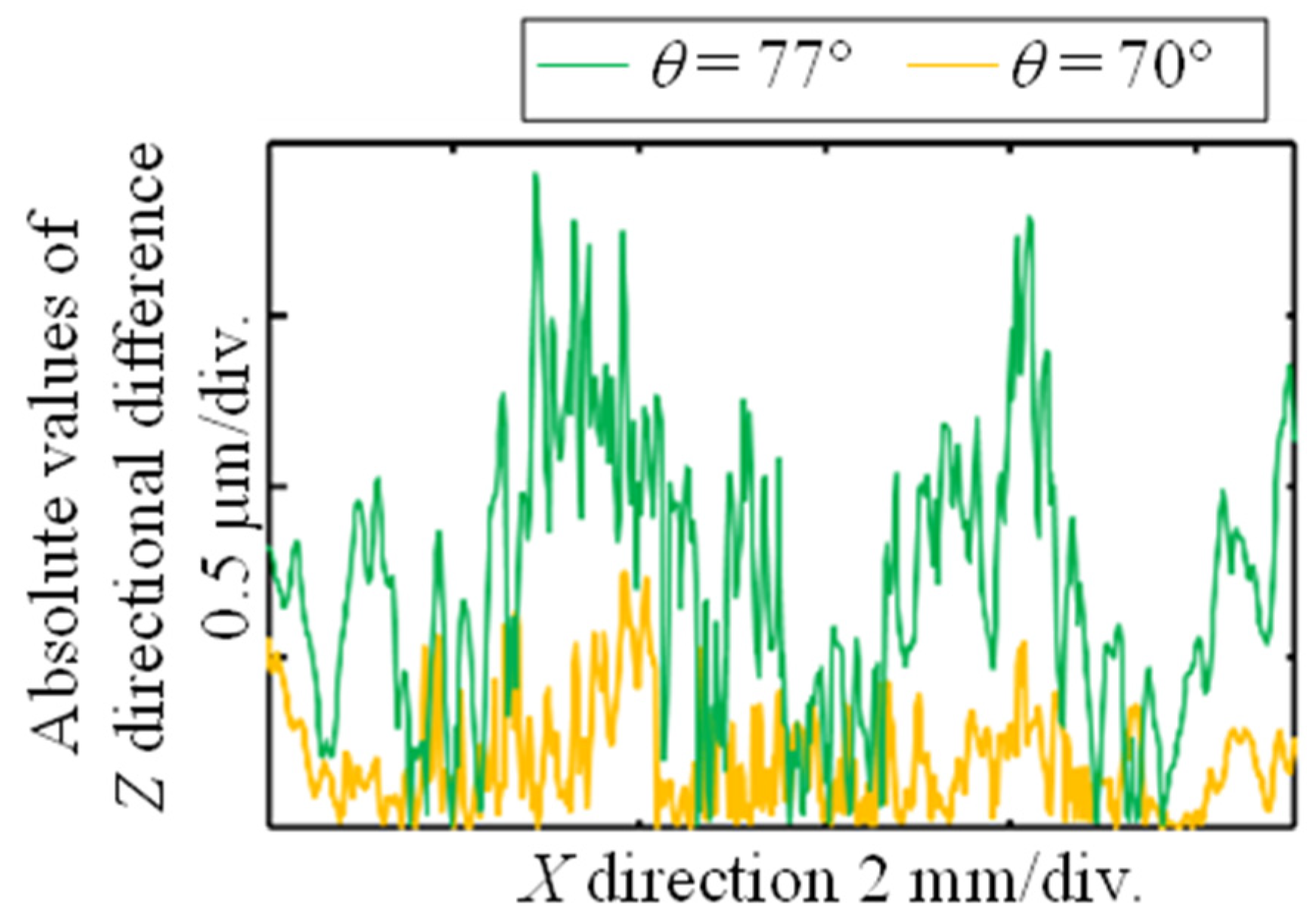
Figure 7 shows the absolute values of the differences between the two cross-sectional profiles shown in
Figure 6a,b. The green plots in
Figure 7 indicate the difference in the cross-sectional profiles when the incident angle of the measuring light is approximately 77°, and the average and the maximum difference are 0.71 μm and 1.91 μm, respectively. In contrast, the yellow plots in
Figure 7 represent the difference between the cross-sectional profiles when the incident angle of the measuring light is approximately 70°, and the average and the maximum difference are 0.20 μm and 0.75 μm, respectively. It can be observed that the discrepancy in the measurement results due to the incidence direction is significantly reduced by decreasing the incidence angle of the measurement light.
The cross-sectional profile of the same hand-scraped mark was measured using a commercially available noncontact contour-measuring instrument (Mitaka Koki, NH-3s) to confirm the validity of the surface-form measurement using the developed oblique-incident interferometer.
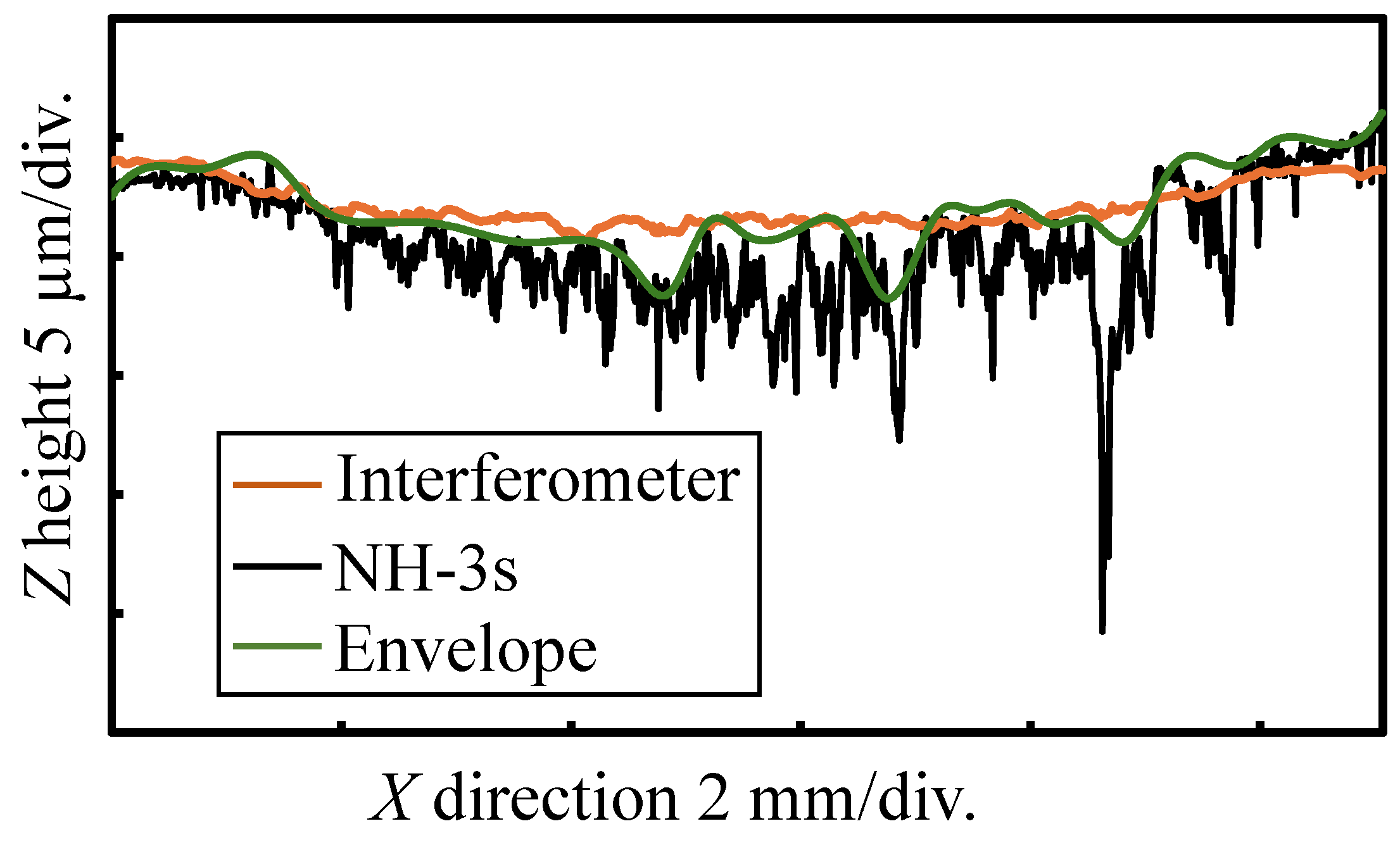
Figure 8 shows a comparison of the cross-sectional surface profiles. The orange line represents the average cross-sectional profile shown in
Figure 6b, measured using the developed oblique-incident interferometer with an incident angle of 70°. The black line represents the surface profile obtained using NH-3s. The green line represents the peak envelope of the surface profile obtained by NH-3s. The envelope was calculated using the envelope function in MATLAB 2023a. The number of samples in the envelope calculation was set to 30, which is the condition where the difference between the envelope and the oblique incidence interferometer profile was the smallest. The surface form was measured using a point autofocus probe [
18] with a 100× objective lens (numerical aperture: 0.80). The number of measurement points and measurement intervals of the NH-3s were set to 1108 and 10 μm, respectively. The measurement interval of the NH-3s was almost the same as the lateral resolution of the oblique-incident interferometer. The root-mean-square heights
Pq of the surface profiles measured using the oblique-incident interferometer and NH-3s were 0.93 μm and 2.71 μm, respectively. The maximum difference between the cross-sectional profile obtained by the oblique-incident interferometer and the envelope was evaluated to be 3.6 μm. NH-3s could measure finer and deeper groove shapes on the hand-scraped surface than the oblique-incident interferometer. These differences are attributed to the difference in the lateral resolution and incident angle of the measuring light between the oblique-incident interferometer and the NH-3s. The lateral resolution of the oblique-incident interferometer was determined from the field of view of the oblique-incident interferometer and the number of pixels of the imaging sensor, which was determined to be 14.1 μm × 11.4 μm. The laser spot diameter of the NH-3s in this experiment was 1 μm, which corresponded to the lateral resolution of the NH-3s. Since the laser spot diameter of the NH-3s was smaller than the lateral resolution of the oblique-incident interferometer, it was possible to measure finer grooves on the hand-scraped marks. Furthermore, the incident angle of the measuring light of the NH-3s is 53°, which is smaller than that of the oblique-incident interferometer. Consequently, the measured light of the NH-3s can reach deeper into the grooves than the oblique-incidence interferometer, facilitating measurements inside the deep grooves. However, the cross-sectional profile obtained using the oblique incidence interferometer was almost the same as the envelope of the surface-shaped profile measured using the NH-3s. Therefore, it is assumed that the developed oblique-incident interferometer can adequately measure the surface of hand-scraped marks to a depth of several micrometers. It was confirmed that the inconsistencies in the measurement results of the surface form of the hand-scraped marks using the oblique-incident interferometer could be improved by reducing the incident angle of the measuring light. As shown in the measurement results using NH-3s in
Figure 8, the hand-scraped marks are several μm deep, and their surfaces consist of steep undulations. In the surface-form measurement using the oblique-incident interferometer, it was assumed that the measurement results changed depending on the incident direction of the measuring light because part of the measuring light was blocked by depressions and steep undulations of the hand-scraped marks. It is believed that a reduction in the incident angle of the measuring light reduces the partial blocking of the measuring light near the surface, thereby improving the inconsistency in the measurement results.
Although the horizontal resolution of the oblique-incident interferometer was inferior to that of the NH-3s used in this study, it had an advantage in terms of measurement time. NH-3s is a line measurement, and the measurement time for one line, as shown in
Figure 8, is approximately 5 min. In contrast, the developed oblique-incidence interferometer is a surface measurement, and the measurement time for each surface form was shorter than 1 min. This is expected to achieve the rapid measurement of hand-scraped surfaces in the range of tens to hundreds of square millimeters.
The surface-form measurement using the oblique-incident interferometer consists in area scanning. In this method, discontinuities in the phase of the interference fringes make it difficult to calculate the surface form. On the other hand, since measurements are taken simultaneously in all measurement directions, errors due to drift, creep, and so on during the measurement are very small. The commercially available profiler (NH-3s) performs point scanning, which means that profiles can be obtained even if there are partially unmeasurable areas. The profile acquired in the probe scanning direction as shown in
Figure 8 shows high measurement accuracy. However, the profile in the direction perpendicular to the probe scanning direction in two-dimensional measurement is significantly affected by measurement errors due to drift, creep, and so on. Therefore, the proposed method using the oblique-incident interferometer is expected to be effective for the wide-area scan measurement of hand-scraped surfaces. Furthermore, the developed oblique-incident interferometer may be applicable to other rough surfaces as long as the intensity of the specular reflected light is sufficient to detect the interference fringes.
On the other hand, although this study qualitatively clarified the inconsistencies in the measurement results of the oblique-incident interferometer, it has not yet elucidated the cause. In particular, the quantitative relationship between the measurement accuracy and the angle of incidence of the measurement light, surface roughness, shape, and so on has not yet been clarified. In order to analyze these phenomena, the introduction of ray-tracking simulations is planned as a future direction of this study. The reflection of the measuring light on the microtopography of the workpiece surface or phase difference with the reference light will be simulated, and the relationship between the incident angle of the measuring light, the workpiece surface microtopography, and the interference fringe phase distribution will be clarified.