Simulation Uncertainty for a Virtual Ultrasonic Flow Meter
Abstract
:1. Introduction
2. Experimental Determination of Calibration Factors
2.1. Measurement Setup
2.1.1. Flow Conditions
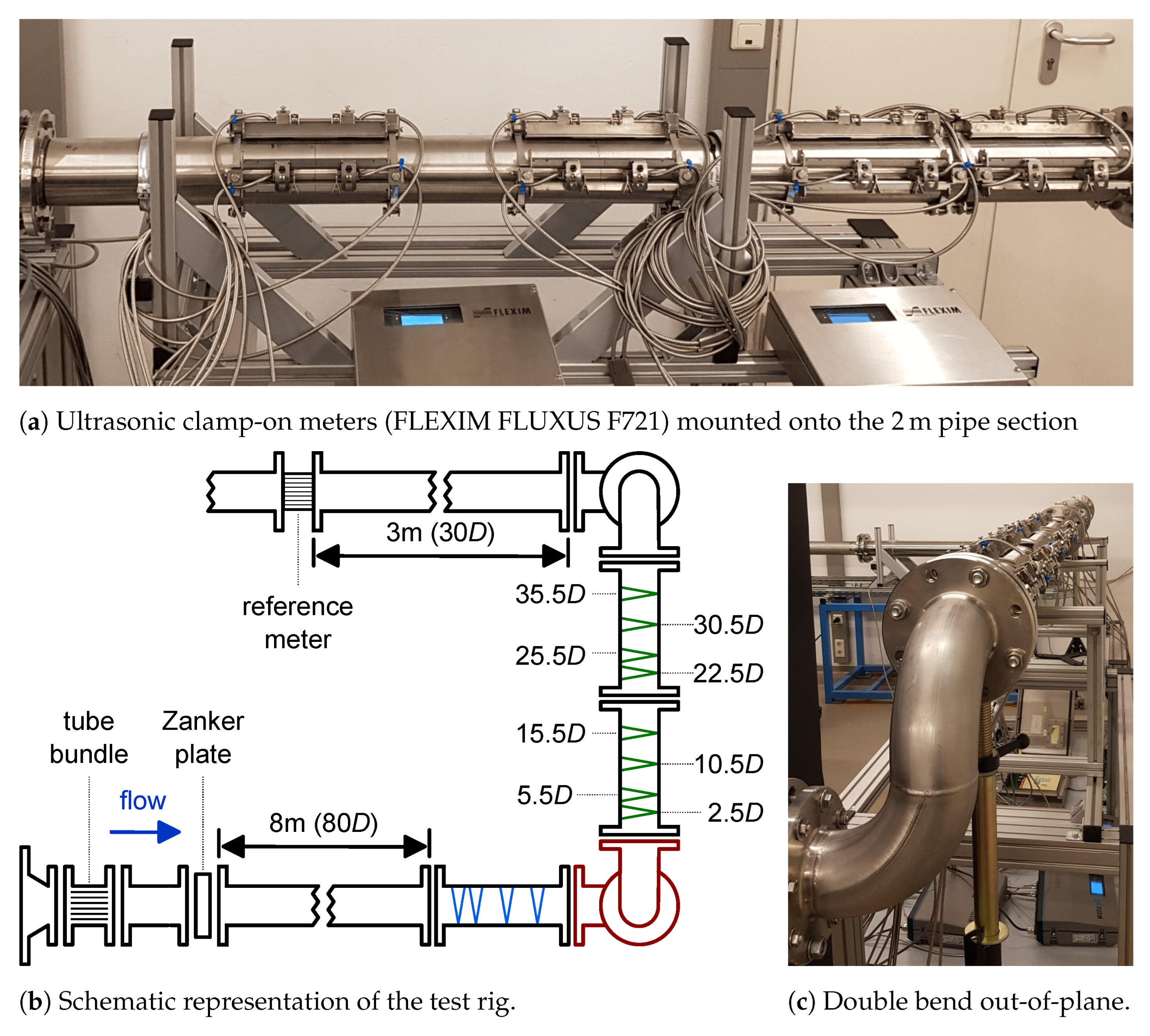
2.1.2. Test Rig
2.1.3. Clamp-On Meters
2.2. Ultrasonic Flow Rate Measurements
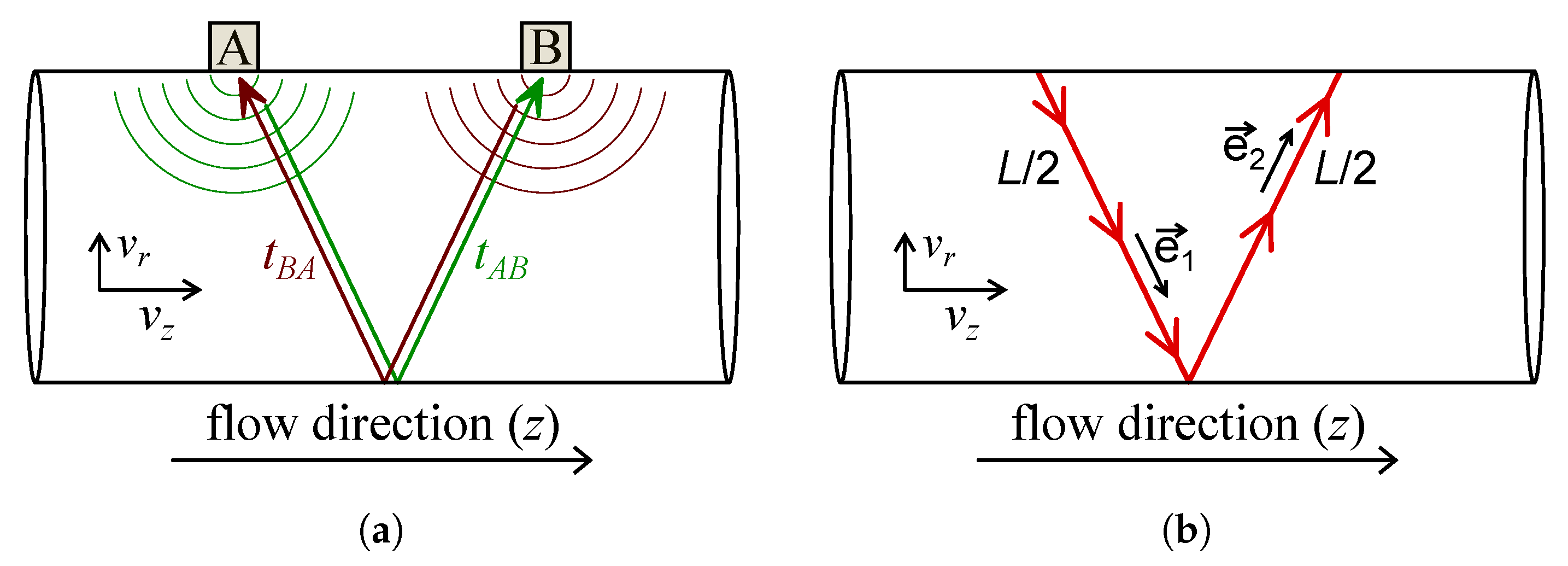
2.3. Derivation of the Calibration Factors
2.4. Measurement Uncertainty
2.4.1. Combined Uncertainty
2.4.2. Expanded Uncertainty
2.5. Experimental Results
3. Simulation-Based Determination of Calibration Factors
3.1. Simulation Setup
3.1.1. Turbulence Modeling
3.1.2. Solver Settings
3.1.3. Geometry and Meshing
3.1.4. Boundary Conditions
3.2. Implementation of the Measuring Principle
3.3. Simulation Results
3.3.1. Spatial Distribution
3.3.2. Velocity Profiles
3.4. Calculation Verification
3.4.1. Numerical Uncertainties
3.4.2. Time-Averaging Uncertainty
3.4.3. Calculation Uncertainty
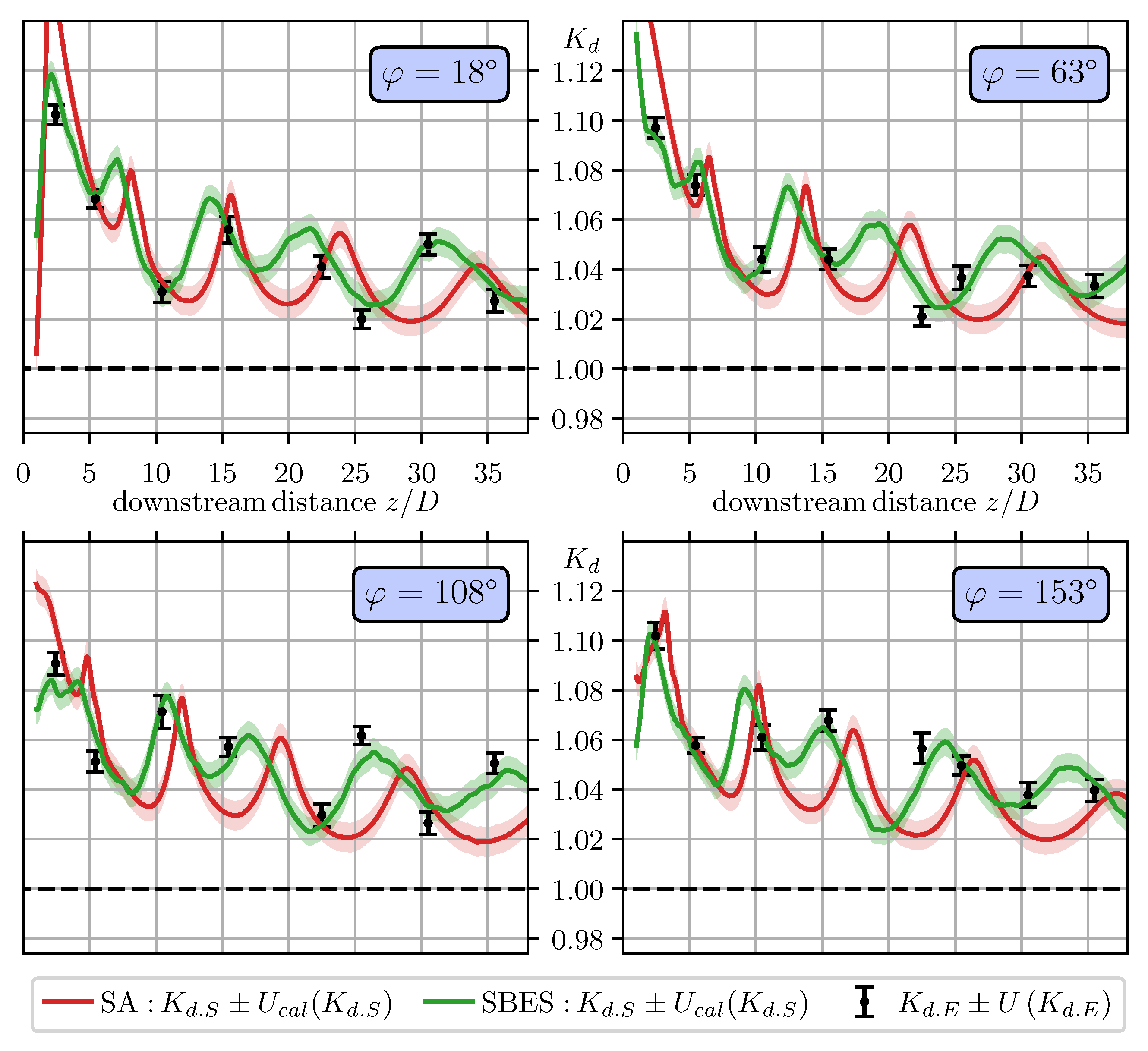
3.5. Comparison with Experimental Data
4. Simulation Uncertainty
4.1. Simulation Error
4.2. Correction of Systematic Errors
4.3. Uncertainty Quantification
4.3.1. Spatial Autocorrelation
4.3.2. Standard Uncertainty
4.3.3. Expanded Simulation Uncertainty
4.4. Comparison of Results for Different Turbulence Models
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Description of the Measurement Uncertainty
Appendix A.1. Uncertainty Estimated for the Determination of Flow Rates
Appendix A.2. Contributions to the Combined Measurement Uncertainty
| Part | Description | Symbol | Relative Standard Uncertainty | Relative Variance | Proportion of Variance in [%] | Degrees of Freedom |
|---|---|---|---|---|---|---|
| Reproducibility | 1.03 × 10−3 | 1.06 × 10−6 | 22.45 | ∞ | ||
| Reference flow rate | 7.74 × 10−4 | 5.99 × 10−7 | 12.67 | 82 | ||
| Repeatability | 4.78 × 10−4 | 2.28 × 10−7 | 4.83 | 2 | ||
| Temperature effects | 1.70 × 10−4 | 2.89 × 10−8 | 0.61 | 29 | ||
| Reproducibility | 1.03 × 10−3 | 1.06 × 10−6 | 22.45 | ∞ | ||
| Reference flow rate | 7.74 × 10−4 | 5.99 × 10−7 | 12.67 | 82 | ||
| Angular alignment | 7.22 × 10−4 | 5.21 × 10−7 | 11.03 | 9999 | ||
| Repeatability | 7.13 × 10−4 | 5.08 × 10−7 | 10.76 | 2 | ||
| Downstream distance | 3.01 × 10−4 | 9.06 × 10−8 | 1.92 | 9999 | ||
| Temperature effects | 1.70 × 10−4 | 2.89 × 10−8 | 0.61 | 29 | ||
| Combined relative variance | 4.73 × 10−6 | 100.00 | ||||
| Combined relative standard uncertainty | 2.17 × 10−3 | |||||
| Effective degrees of freedom | 136 | |||||
| Coverage factor k for the confidence level of 95.45% | 2.02 | |||||
| Expanded relative uncertainty | 4.39 × 10−3 | |||||
Appendix B. Detection of Spatial Patterns in the Simulation Errors

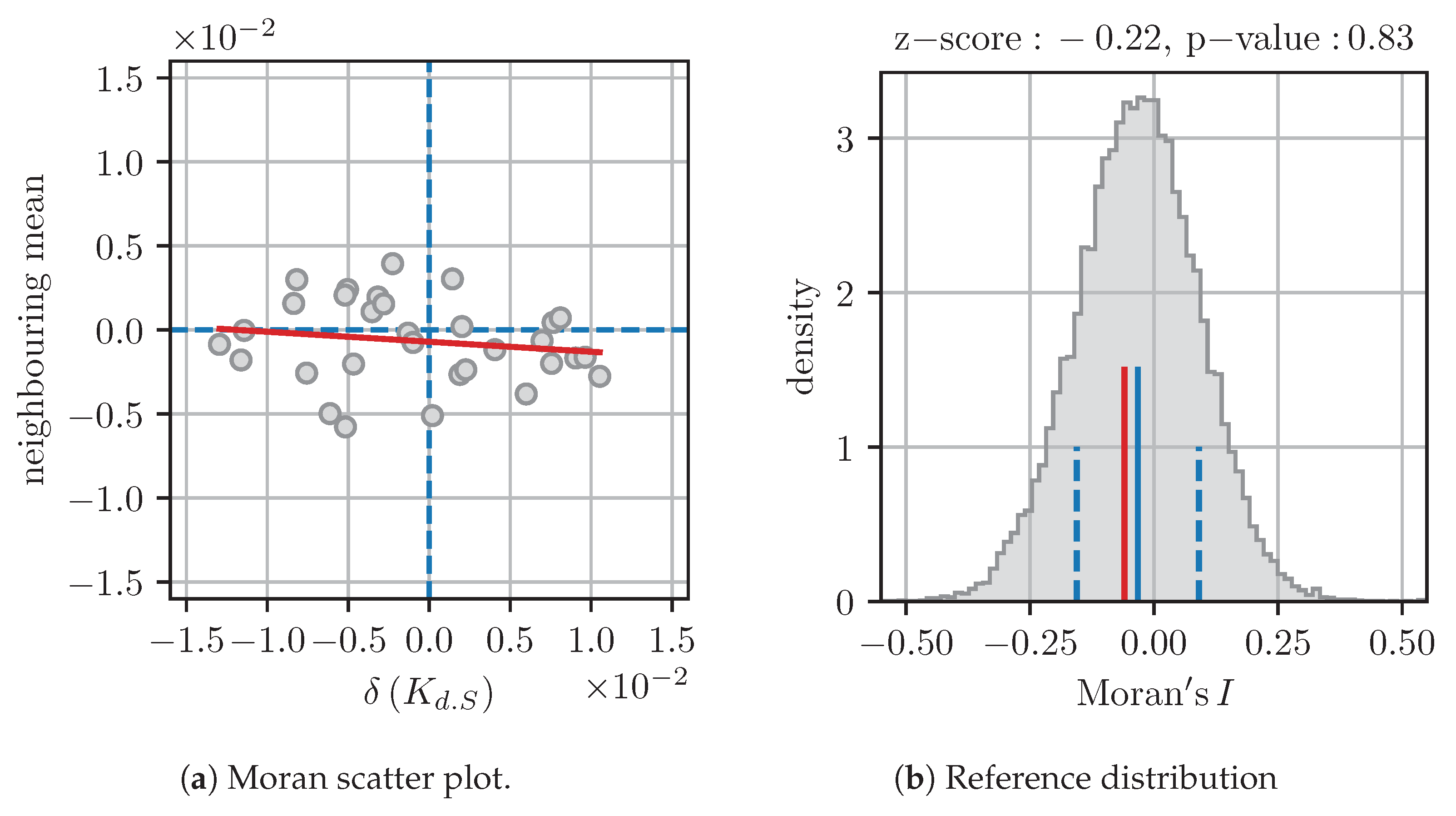
| Modeling Approach | Turbulence Model | Autocorrelation | ||
|---|---|---|---|---|
| Moran’s I | z-Score | p-Value | ||
| Hybrid LES-RANS | SBES-SST [30] | −0.06 | −0.22 | 0.83 |
| SBES-realizable k- [30] | −0.09 | −0.43 | 0.66 | |
| DES-realizable k- [31] | −0.10 | −0.53 | 0.60 | |
| DES-SST [31] | −0.13 | −0.82 | 0.41 | |
| RANS | Spalart-Allmaras [27] | 0.11 | 1.21 | 0.23 |
| SST k- [26] | −0.14 | −0.89 | 0.38 | |
| Standard k- [25] | −0.14 | −0.86 | 0.39 | |
| Linear pressure–strain [28] | −0.19 | −1.28 | 0.20 | |
| Standard k- [23] | −0.09 | −0.48 | 0.63 | |
| Realizable k- [24] | −0.18 | −1.19 | 0.24 | |
| Stress- [25] | −0.22 | −1.57 | 0.12 | |
References
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008. [Google Scholar]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Supplement 1 to the “Guide to the Expression of Uncertainty in Measurement”—Propagation of Distributions Using a Monte Carlo Method; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2008. [Google Scholar]
- Joint Committee for Guides in Metrology. Evaluation of Measurement Data—Supplement 2 to the “Guide to the Expression of Uncertainty in Measurement”—Extension to Any Number of Output Quantities; International Bureau of Weights and Measures (BIPM): Sèvres, France, 2011. [Google Scholar]
- Eichstädt, S.; Elster, C.; Härtig, F.; Heißelmann, D.; Kniel, K.; Wübbeler, G. VirtMet—Applications and Overview; International Workshop on Metrology for Virtual Measuring Instruments and Digital Twins, Physikalisch-Technische Bundesanstalt (PTB): Berlin, Germany, 2021. [Google Scholar]
- Poroskun, I.; Rothleitner, C.; Heißelmann, D. Structure of digital metrological twins as software for uncertainty estimation. J. Sens. Sens. Syst. 2022, 11, 75–82. [Google Scholar] [CrossRef]
- Grieves, M.; Vickers, J. Digital Twin: Mitigating Unpredictable, Undesirable Emergent Behavior in Complex Systems. In Transdisciplinary Perspectives on Complex Systems: New Findings and Approaches; Kahlen, F.J., Flumerfelt, S., Alves, A., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 85–113. [Google Scholar] [CrossRef]
- Fuller, A.; Fan, Z.; Day, C.; Barlow, C. Digital Twin: Enabling Technologies, Challenges and Open Research. IEEE Access 2020, 8, 108952–108971. [Google Scholar] [CrossRef]
- Wright, L.; Davidson, S. How to tell the difference between a model and a digital twin. Adv. Model. Simul. Eng. Sci. 2020, 7, 13. [Google Scholar] [CrossRef]
- Le Maître, O.P.; Knio, O.M. Spectral Methods for Uncertainty Quantification; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Schmelter, S.; Fiebach, A.; Model, R.; Bär, M. Numerical prediction of the influence of uncertain inflow conditions in pipes by polynomial chaos. Int. J. Comput. Fluid Dyn. 2015, 29, 411–422. [Google Scholar] [CrossRef]
- Schmelter, S.; Fiebach, A.; Weissenbrunner, A. Polynomial chaos for uncertainty quantification in flow simulations for metrological applications. TM Tech. Mess. 2016, 83, 71–76. [Google Scholar] [CrossRef]
- Weissenbrunner, A.; Fiebach, A.; Schmelter, S.; Bär, M.; Thamsen, P.; Lederer, T. Simulation-based determination of systematic errors of flow meters due to uncertain inflow conditions. Flow Meas. Instrum. 2016, 52, 25–39. [Google Scholar] [CrossRef] [Green Version]
- American Institute of Aeronautics and Astronautics (Ed.) AIAA Guide for the Verification and Validation of Computational Fluid Dynamics Simulations; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1998. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.; Coleman, H.; Paterson, E. Comprehensive Approach to Verification and Validation of CFD Simulations—Part 1: Methodology and Procedures. J. Fluids Eng. 2001, 123, 792. [Google Scholar] [CrossRef]
- Hosder, S.; Grossman, B.; Watson, L.; Mason, W. Observations on CFD Simulation Uncertainties. In Proceedings of the 9th AIAA/ISSMO Symposium on Multidisciplinary Analysis and Optimization, Atlanta, GA, USA, 4–6 September 2002. [Google Scholar] [CrossRef]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef] [Green Version]
- Straka, M. Vergleich Realer und Synthetisch Generierter Strömungszustände in Rohrleitungen Mittels Numerischer und Laseroptischer Verfahren. Ph.D. Thesis, Technische Universität Berlin, Berlin, Germany, 2021. [Google Scholar] [CrossRef]
- Gersten, K. Fully Developed Turbulent Pipe Flow. In Fluid Mechanics of Flow Metering; Merzkirch, W., Ed.; Springer: Berlin, Germany, 2005; pp. 1–22. [Google Scholar]
- ISO 5167-1:2003; Measurement of Fluid Flow by Means of Pressure Differential Devices Inserted in Circular Cross-Section Conduits Running Full—Part 1: General Principles and Requirements. International Organization for Standardization (ISO): Geneva, Switzerland.
- Straka, M.; Eichler, T.; Koglin, C.; Rose, J. Similarity of the asymmetric swirl generator and a double bend in the near-field range. Flow Meas. Instrum. 2019, 70, 101647. [Google Scholar] [CrossRef]
- Gersten, K.; Herwig, H. Strömungsmechanik. Grundlagen der Impuls-, Wärme- und Stoffübertragung aus Asymptotischer Sicht, 1st ed.; Springer: Braunschweig/Wiesbaden, Germany, 1992. [Google Scholar] [CrossRef]
- Straka, M.; Koglin, C.; Eichler, T. Segmental orifice plates and the emulation of the 90°- bend. TM Tech. Mess. 2019, 87, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.; Spalding, D. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD, 2nd ed.; DCW Industries, Inc.: La Canada, CA, USA, 1998. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. AIAA 1992, 439. [Google Scholar] [CrossRef]
- Launder, B.; Shima, N. Second-moment closure for the near-wall sublayer—Development and application. AIAA J. 1989, 27, 1319–1325. [Google Scholar] [CrossRef]
- Speziale, C.; Sarkar, S.; Gatski, T. Modelling the pressure-strain correlation of turbulence—An invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Menter, F. Stress-blended eddy simulation (SBES)—A new paradigm in hybrid RANS-LES modeling. In Progress in Hybrid RANS-LES Modelling; Springer: Cham, Switzerland, 2018; Volume 137, pp. 27–37. [Google Scholar] [CrossRef]
- Spalart, P.; Jou, W.H.; Strelets, M.; Allmaras, S. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Proceedings of the Advances in DNS/LES, 1st AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Straka, M.; Fiebach, A.; Koglin, C.; Eichler, T. Hybrid simulation of a segmental orifice plate. Flow Meas. Instrum. 2018, 60, 124–133. [Google Scholar] [CrossRef]
- Smagorinsky, J. General Circulation Experiments with the Primitive Equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Mathey, F.; Cokljat, D.; Bertoglio, J.P.; Sergent, E. Specifications of LES inlet boundary condition using vortex method. In Proceedings of the 4th International Symposium on Turbulence, Heat and Mass Transfer, Antalya, Turkey, 12–17 October 2003. [Google Scholar]
- Moran, P.A.P. Notes on Continuous Stochastic Phenomena. Biometrika 1950, 37, 17–23. [Google Scholar] [CrossRef] [PubMed]
- ISO 12242; Measurement of Fluid Flow in Closed Conduits—Ultrasonic Transit-Time Meters for Liquid. International Organization for Standardization (ISO): Geneva, Switzerland, 2012.
- Akima, H. A new method of interpolation and smooth curve fitting based on local procedures. J. ACM 1970, 17, 589–602. [Google Scholar] [CrossRef]


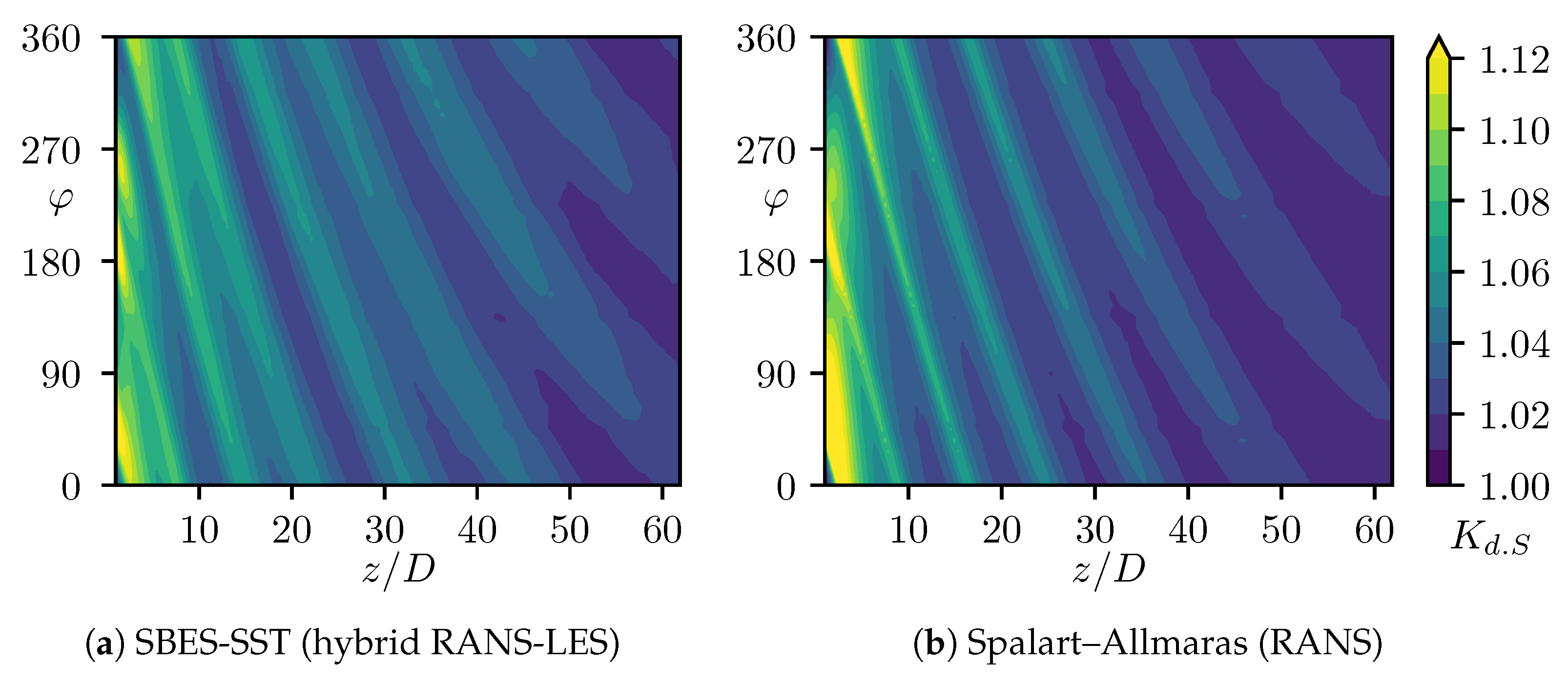
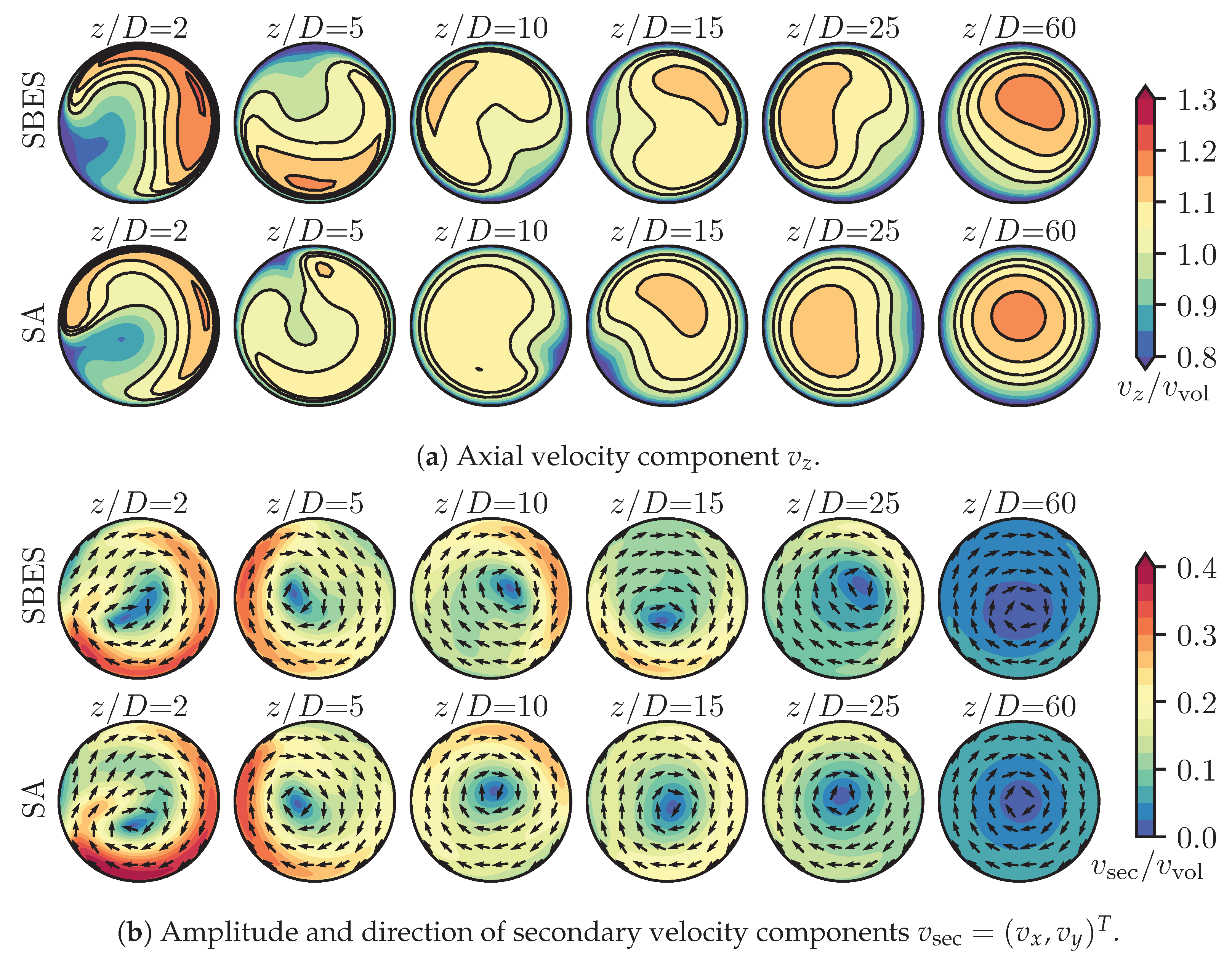

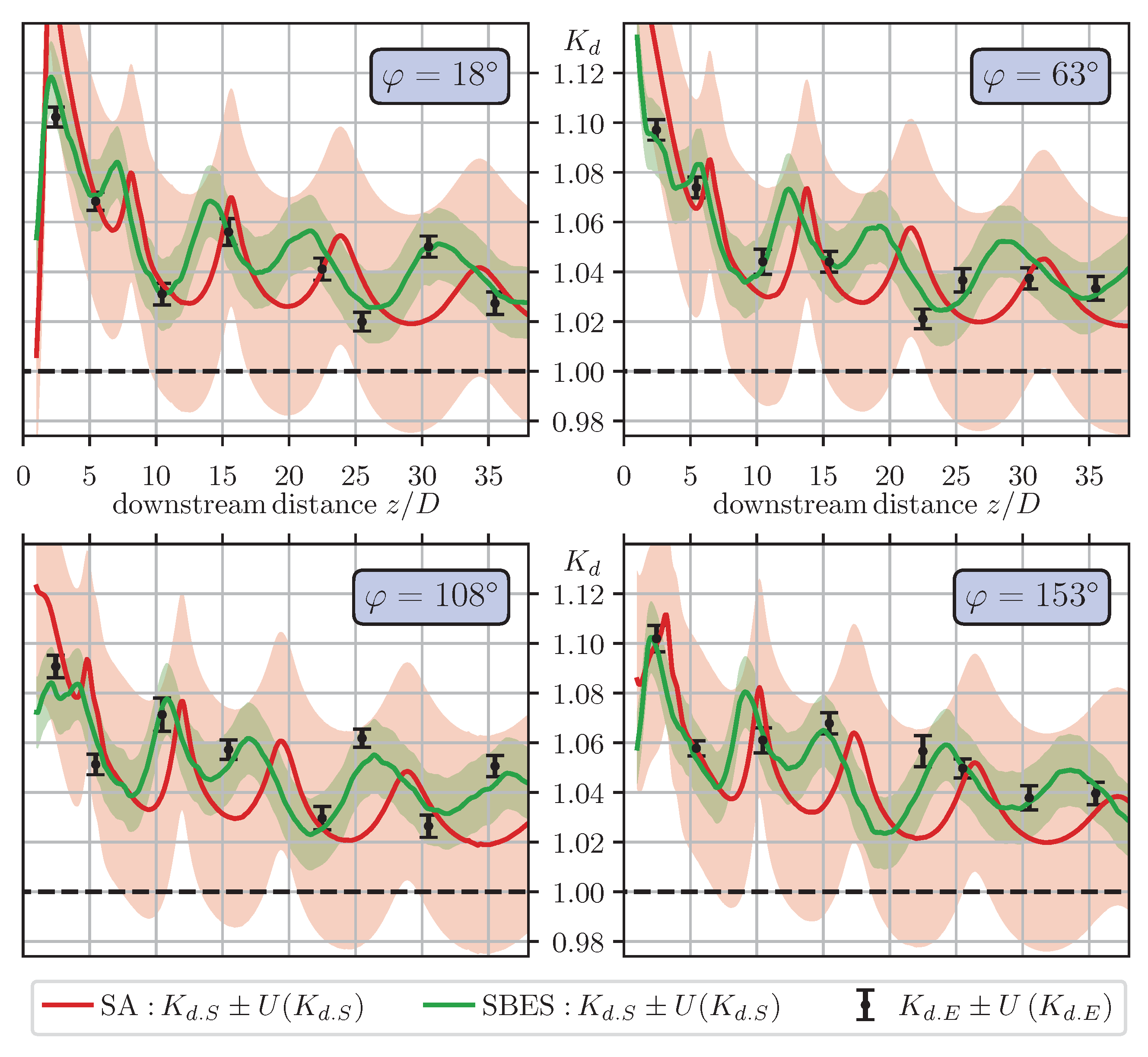
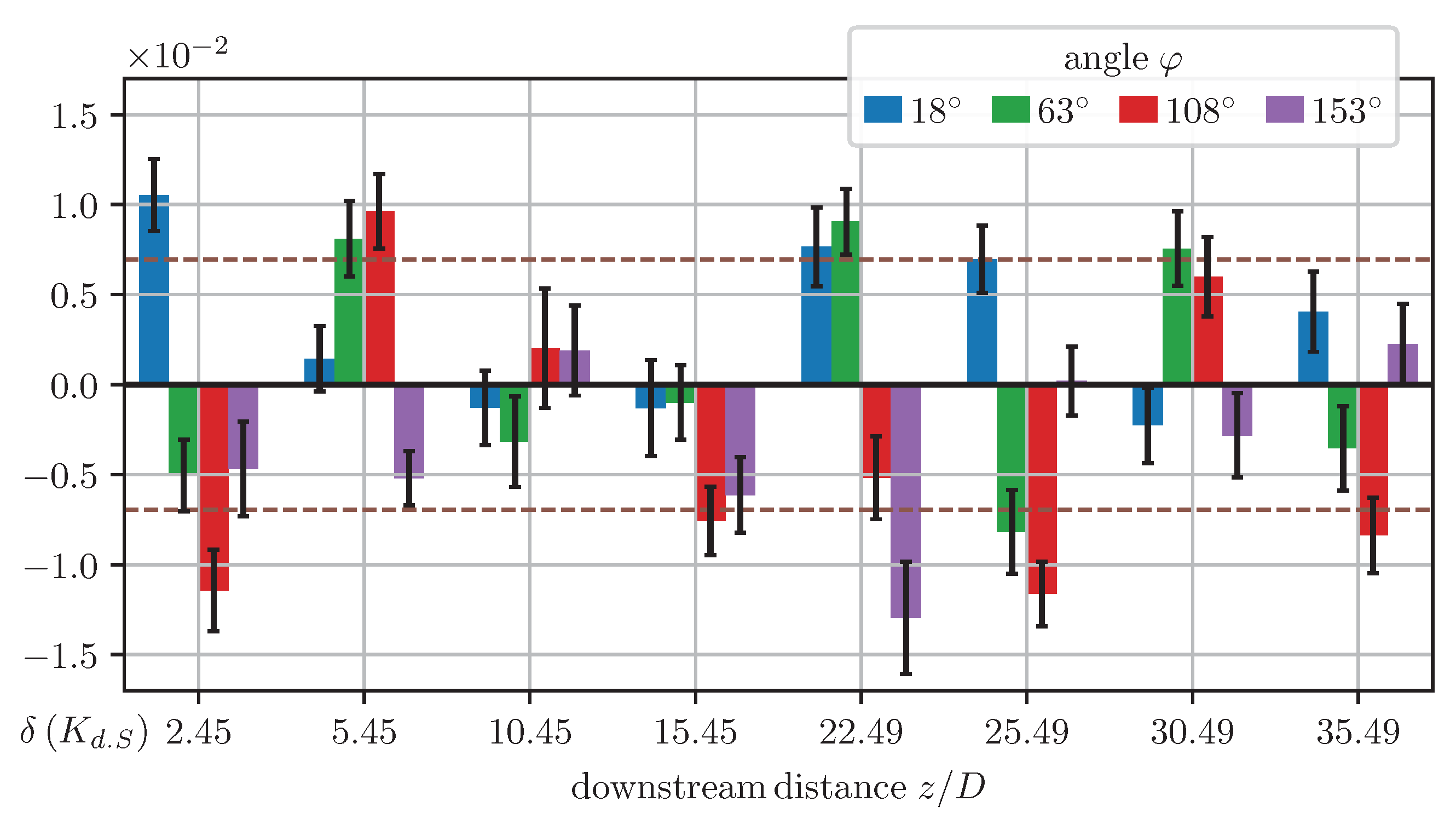
| Hybrid RANS-LES | RANS | |
|---|---|---|
| Pressure-Velocity Coupling | SIMPLE | Coupled |
| Discretization schemes | ||
| Temporal | Bounded Second-order Impl. | — |
| Spatial | ||
| Diffusion | Central differencing | Central differencing |
| Momentum | Central differencing | Second-order upwind |
| Pressure | Second-order | Second-order |
| Gradient | Green-Gauss cell-based | Least-Squares cell-based |
| Turbulent quantities | First-order upwind | Second-order upwind |
| Scaled residuals | ||
| Continuity, velocities | 1 × 10−5 | 1 × 10−15 |
| Turbulent quantities | 1 × 10−4 | 1 × 10−15 |
| Uncertainty | Variable Parameter (s) | Refinement Level | |||
|---|---|---|---|---|---|
| Error Source | Symbol | 1 | 2 | 3 | |
| spatial & temporal discretization | cells on circumference | 120 | 136 | 160 | |
| streamwise cells/diameter | 35 | 43 | 50 | ||
| cells in radial direction | 41 | 45 | 51 | ||
| time step size [ms] | 10 | 8 | 7 | ||
| spatial discretization wall-normal direction | wall-normal distance | 1.0 | 0.5 | 0.2 | |
| iterative convergence within time steps | scaled momentum residual | ||||
| Uncertainty | Turbulence Model | ||
|---|---|---|---|
| Related to | Symbol | SBES-SST (Hybrid) | Spalart–Allmaras (RANS) |
| Time-averaging | 1.32 × 10−3 | – | |
| Grid & time step size | 1.65 × 10−3 | 2.73 × 10−3 | |
| Wall-normal distance | 1.52 × 10−3 | 1.14 × 10−3 | |
| Iterative convergence | 1.13 × 10−3 | – | |
| Calculation | 2.84 × 10−3 | 2.96 × 10−3 | |
| 5.68 × 10−3 | 5.91 × 10−3 | ||
| Turbulence Model | Significant? | Coverage Factor k | ||
|---|---|---|---|---|
| SBES-SST [30] | no | 6.96 × 10−3 | 2.07 | 1.44 × 10−2 |
| SBES-realizable k- [30] | yes | 1.29 × 10−2 | 2.08 | 2.67 × 10−2 |
| DES-realizable k- [31] | no | 1.42 × 10−2 | 2.08 | 2.96 × 10−2 |
| DES-SST [31] | no | 1.63 × 10−2 | 2.08 | 3.39 × 10−2 |
| Spalart-Allmaras [27] | yes | 2.10 × 10−2 | 2.08 | 4.38 × 10−2 |
| SST k- [26] | no | 2.35 × 10−2 | 2.08 | 4.89 × 10−2 |
| Standard k- [25] | no | 2.73 × 10−2 | 2.08 | 5.69 × 10−2 |
| Linear pressure–strain [28] | yes | 2.78 × 10−2 | 2.08 | 5.80 × 10−2 |
| Standard k- [23] | no | 3.06 × 10−2 | 2.08 | 6.38 × 10−2 |
| Realizable k- [24] | no | 3.14 × 10−2 | 2.08 | 6.55 × 10−2 |
| Stress- [25] | no | 3.82 × 10−2 | 2.08 | 7.95 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straka, M.; Weissenbrunner, A.; Koglin, C.; Höhne, C.; Schmelter, S. Simulation Uncertainty for a Virtual Ultrasonic Flow Meter. Metrology 2022, 2, 335-359. https://doi.org/10.3390/metrology2030021
Straka M, Weissenbrunner A, Koglin C, Höhne C, Schmelter S. Simulation Uncertainty for a Virtual Ultrasonic Flow Meter. Metrology. 2022; 2(3):335-359. https://doi.org/10.3390/metrology2030021
Chicago/Turabian StyleStraka, Martin, Andreas Weissenbrunner, Christian Koglin, Christian Höhne, and Sonja Schmelter. 2022. "Simulation Uncertainty for a Virtual Ultrasonic Flow Meter" Metrology 2, no. 3: 335-359. https://doi.org/10.3390/metrology2030021
APA StyleStraka, M., Weissenbrunner, A., Koglin, C., Höhne, C., & Schmelter, S. (2022). Simulation Uncertainty for a Virtual Ultrasonic Flow Meter. Metrology, 2(3), 335-359. https://doi.org/10.3390/metrology2030021






