Abstract
Arterial simulators are a useful tool to simulate the cardiovascular system in many different fields of application and to carry out in vitro tests that would constitute a danger when performed in in vivo conditions. In the literature, a thriving series of in vitro experimental set-up examples can be found. Nevertheless, in the current scientific panorama on this topic, it seems that organic research from a metrological and functional perspective is still lacking. In this regard, the present review study aims to make a contribution by analyzing and classifying the main concerns for the cardiovascular simulators proposed in the literature from a metrological and functional point of view, according to their field of application, as well as for the transducers in the arterial experimental set-ups, measuring the main hemodynamic quantities in order to study their trends in specific testing conditions and to estimate some parameters or indicators of interest for the scientific community.
1. Introduction
Cardiovascular pathologies are particularly risky and life-threatening, making this group of such diseases one of the top ten causes of death worldwide [1,2]. Consequently, in recent years, a widespread interest has grown around parameters such as arterial stiffness (AS) and pulse wave velocity (PWV), as they are key importance indices for cardiovascular disease diagnosis and prevention [3,4]. Nevertheless, some studies addressed different problems regarding the approaches used for in vivo estimation of such parameters, mainly due to blood pressure variability [5,6,7]. Therefore, many researchers undertook the investigation of cardiovascular parameters with the help of in vitro circulatory simulations. In fact, these simulations have been broadly used to investigate, analyze and replicate high-complexity, hemodynamic phenomena occurring in the cardiovascular system. This kind of simulation is usually carried out through the implementation of prototypes and systems with artificial materials which are surrogates of living systems. The necessity of replicating them in vitro arises because, in a living organism, the degree of complexity in performing exhaustive hemodynamic measurements could be increased by the high probability of perturbing the physiological state and provoking damages. The possibility of replicating some circulatory phenomena is due to the fact that the fundamental hemodynamic and hydrodynamic principles stand for both biological and simulated artificial systems.
For example, the pulse wave transit time can be studied through the employment of arterial simulators able to reproduce pressure pulses in a latex rubber tube (with mechanical characteristics as similar as possible to the arterial ones [8]): the pulses cause a radial tube displacement which can be detected and measured through specific sensors, transducing the displacement quantity to be measured into an electrical signal to be stored and processed. Pulse transit time measurements can be carried out without the necessity of quantifying the radial displacement; therefore, the choice of the most proper sensor type should rely on its dynamic performance rather than on its accuracy in displacement measurements [8]. This perspective leads to the design and realization of experimental arterial phantoms whose sensitive elements are constituted by sensors able to detect the pulse wave passage at two different sites where the distance is known in order to have an estimation of the delay between the pressure waves at each site. This goal can be achieved through contact or contactless sensors and, in the literature, both typologies have been employed. On the basis of [9], the authors of this review recently developed an arterial simulator with linear variable differential transformer (LVDT) sensors, and highlighted the pros and cons of their employment in the assessment of pulse wave transit time [8]. Almeida et al., on the other hand, designed and realized a test bench able to reproduce pressure waves through an elastic tube filled with fluid: their propagation was noninvasively measured with the help of piezoelectric probes [10] which were developed and improved by Dagdeviren et al. [11] for cutaneous pressure monitoring with the aim of assessing health status in a continuous way, therefore preventing cardiovascular diseases. In 2018, Ma et al. developed an in vitro hemodynamic simulator in which two strain sensors made of carbon black-doped polydimethylsiloxane (CB-PDMS) detected the pulses at two different positions along the tube simulating the artery [12]. The idea of using strain gauge sensors has been already conceived in 2012 when Lu et al. decided to use elastomer-based strain gauges to realize high-sensitivity sensors directly mountable on the patients’ skin [13]. Other authors tried to apply micro-electro-mechanical systems (MEMS) technology to design and simulate piezoelectric sensors for arterial pulse detection in biomedical applications [14]. Some years ago, even piezoresistive elements were employed in pressure pulse wave measurements through sensor displacement analysis [15]. According to the type of applications in which they should be used, contact sensor management could be challenging, especially regarding insertion errors during measurement, the working environment (e.g., water or other chemical substances that could perturb the measurement procedure) and the characteristics of the element in which they should be mounted on (e.g., usually the flexibility of the latex tubing makes it difficult to choose the sensor placement). Therefore, despite the wide use of contact sensors in the scientific literature for cardiovascular applications, many other researchers have opted for the employment of contactless sensors. Laqua et al., for example, realized an experimental set-up with a hydraulic system for the simulation of pulsating artificial vessels to study fetal pulse oximetry. In this context, they employed capacitive sensors as sensitive elements for the tube dilatation [16]. On the other hand, Lantos et al. studied the deformation of a silicone elastomer tube by measuring the tube diameter using digital image processing after the acquisition of a set of photos through a CCD digital camera. Their goal was to build a model to take blood pressure measurements at a long distance from the heart [17]. Other authors [5] chose an optical operating principle for transit time estimation: they designed and developed an optical system for continuous and cuffless blood pressure monitoring using two signals coming from infrared optical transmitters, where the peak distance was assumed as the transit time. In the past, Berrios and Pedersen tried to use ultrasonic measurement for the detection of diameter variations in an elastic tube by applying a pressure waveform and estimating the time-shift of the ultrasound echoes from the tube walls (front and back) [18]. On the other hand, in 2019, Suhaimizan et al. investigated how an in vitro system could validate the use of plastic optical fiber (POF) sensors in measuring the pulse signal by comparing the obtained results with pressure sensor data [7].
All those studies were carried out (a) to analyze complex hemodynamic phenomena and (b) to retrieve meaningful parameters for cardiovascular performance. This goal has been achieved by using in vitro experimental set-ups designed in a common fashion among the different works, even though there have been increasing technological solutions due to technological development. Nevertheless, despite the great number of accurate studies focusing on the investigation of simulator characteristics, it seems that the scientific literature lacks organic research on how such simulators may influence the measurement quantities of interest (e.g., in terms of errors that the experimental set-up introduces, leading to a possible perturbation in the physical quantities to be measured) as well as a detailed metrological characterization of their components.
In the present review, the aim is to make a contribution to the field by analyzing and classifying the main concerns around the cardiovascular simulators currently proposed in the literature from a metrological and functional point of view. Such analysis is carried out according to the application field, as well as by investigating the types of transducers employed in the arterial experimental set-ups to measure the main hemodynamic quantities. The design issues, experimental set-up characteristics, types of sensors applied to measure the main cardiovascular quantities and, finally, the drawbacks found in set-up arrangements and the corresponding measurements are highlighted. In the following sections, all the various, state-of-the-art, experimental set-ups present are discussed and analyzed. This is carried out by focusing on the main issues found regarding the development and realization of set-ups, as well as by highlighting the variety of methodological solutions and approaches according to the subject matter in the cardiovascular field.
2. Fields of Applications for Arterial Simulators
The importance of simulating the human cardiovascular system in vitro and the complex hemodynamic phenomena occurring in such a system is related to the fact that the use of pressure and flow simulations allows us to study the system behavior, together with the replication of conditions such as stenosis and cholesterol plaques that may perturb blood flow laminarity leading to different pathologies (e.g., thrombosis, infarction, ictuses, etc.), without the intrinsic physiological problems of an in vivo system. Another important issue is the one related to hypertension, which could potentially be the cause of different cardiovascular pathologies and, in some cases, even death. In fact, with aging, the arteries generally go through a stiffening phenomenon that reduces the blood pumping efficiency, leading to possible heart hypertrophy [4,19]. It is therefore of primary importance to design and develop experimental simulators with integrated transducers and sensors, as widely discussed in the literature [20,21], taking also into account the main metrological characteristics and issues with a particular reference to (a) sensors characteristics, (b) conditioning and (c) data acquisition [20]. This would allow researchers to measure the main hemodynamic quantities necessary for the study and prediction of vascular behavior in order to provide useful knowledge and information to clinicians who have the duty of preserving population healthcare through correct diagnosis, monitoring and therapy. Among the most important parameters studied in this context, pulse wave velocity (PWV) is the most common indicator of arterial stiffness, and it is related to both mechanical and geometrical characteristics of the arterial tree. Being a velocity, it is often estimated by using a couple of sensors to detect pulse wave passage at two different sites of the artificially simulated vessel (e.g., an elastic tube), therefore allowing for the application of the well-known relationship:
where L is the distance between the transducers detecting the pulse wave and Δt is the pulse transit time, which can be conveniently defined, in an in vitro system, as the time delay due to the pressure wave propagation between two sites in the arterial surrogate [4]. From the direct estimation of PWV it is possible to indirectly retrieve a key parameter for the artery biomechanics, namely, the volumetric distensibility χ, which is defined as the ratio between the relative vessel volume variation ΔV/V and the pressure variation Δp in the expansion and contraction phases during the cardiac cycle.
The distensibility gives information about the vessel’s ability and efficiency in expanding and contracting during systole and diastole phases, respectively. The mathematical relationship used to relate the PWV to the vessel mechanical characteristics, in particular the wall distensibility χ, is given by the Bramwell–Hill formula [22] as follows:
where Δp is the vessel pressure variation, V is the vessel initial volume, ΔV is the volume variation and ρ is the inner liquid density. Since distensibility is inversely related to arterial stiffness, when the latter increases, the PWV increases as well. In [8], the authors of the present review investigated the variation in transit time according to an adjustment of vessel stiffening by using an in vitro arterial simulator designed to vary the vessel surrogate’s (e.g., an elastic tube) stiffness through the variation of the transmural pressure (i.e., the difference between the inner and outer pressures of the tube). The results obtained agreed with the expected relationship between transit time and transmural pressure, therefore encouraging novel research for the future development of an arterial simulator in which a finer transmural pressure tuning could be possible to improve both the system and measurement accuracy.
In general, the cardiovascular system can be simulated through arterial simulators that rely on the general principles for generating and measuring arterial waves, and recording and analyzing arterial waveforms as well as the pulsatile pressure-flow relationships. Given the wide range of phenomena that may occur in a hemodynamic system, there are many different clinical and biomechanical applications in which a cardiovascular set-up could be employed. In the current state-of-the-art research, the main works regarding experimental set-ups for arterial simulation investigated blood flow behavior in artery bifurcations [23,24,25,26,27,28], or in the presence of stenosis and plaques [29,30,31,32,33,34,35,36,37]. Other authors designed and developed arterial simulators with the goal of experimentally validating the mathematical models behind the relationships subsisting between flow and pressure, or between flow and geometrical and mechanical characteristics of the artery [38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. Another important and prolific field of application for arterial simulators is medical device testing, especially in the context of artificial organs, such as ventricular assist devices (mono- or biventricular) and artificial hearts (through centrifugal blood pumps). Mock circulatory systems can be also used to test stents, anastomoses, vascular grafts, prosthetic heart valves and artificial blood vessels, as well as to assess models for hemodynamic predictions after vascular access surgery (e.g., for hemodialysis patients). Some systems have been even designed as loads for real pumping hearts [55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. Finally, there are many studies in which pulse pressure has been investigated from a biomechanical point of view [73,74,75,76,77,78,79,80,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101].
In the following sections, the most common design solutions for in vitro cardiovascular systems have been reviewed according to the cardiovascular applications for which they have been employed, highlighting the systems’ characteristics, the most common realization issues and future developments, as well as the sensors used, the measured quantities, techniques for measurement protocols and parameters indirectly estimated from the measured ones.
3. Framework of the Measurement Devices Commonly Employed in Experimental Set-Ups and Their General Critical Issues
Before considering in detail the specific problems and critical issues of the most relevant cardiovascular simulator applications in the current scientific literature, it is worth providing an overall framework of the problems and critical issues that generally affect pressure, flow and velocity measurements independently of the specific application. In fact, the studies reviewed in this work employ many different devices for the measurement of the main physical quantities involved in the arterial simulators. In the current scientific literature, the most measured quantities include pressure, flow and velocity. With regard to pressure, common measurement devices are the (a) catheter manometer and (b) differential manometer. Flow is generally measured through a (a) Venturi tube, (b) orifice plate meter and (c) rotameter. Finally, flow velocities are commonly measured with (a) Doppler velocimeters, (b) particle image velocimetry (PIV) and (c) electromagnetic/ultrasonic flowmeters. Some useful metrological characteristics of such devices are summed up in Table 1.

Table 1.
Overview of devices commonly used for the measurement of physical quantities in arterial simulators.
With regard to pressure, the major problems can be encountered with manometry measurements, since these are functions of both density and gravity. The values of these two are not constant. Density is a function of temperature, whereas gravity is a function of latitude and elevation. Because of this relationship, specific ambient conditions must be selected as standard, and thus, a fixed definition for pressure can be maintained. Mercury liquid density is 13.59 g·cm−3 at 0 °C. Water density differs from the former as it is 1.00 g·cm−3 at 4 °C. Both liquids have an acceleration of gravity of 980.67 cm·s−2 at sea level and 45.54 degrees of latitude. If water fluid is used in pressure measurement applications, capillary effects occur due to surface tension between the liquid and the glass tube [104]. This can lead to difficulties in reading the pressure on the manometer scale.
With regard to flow measurements, because all three overmentioned flowmeters have similar accuracies, one strategy for selecting the most appropriate instrument is to decide if there are any good reasons for not using the cheapest flowmeter that can be used over the widest range of pipe sizes: the orifice plate. Where permanent pressure loss is important, the Venturi tube should be considered, although the high cost of this meter as well as its size can only usually be justified when large quantities of fluid are being metered. For metering dirty fluids, the Venturi tube should be preferred over the orifice plate. The choice between the two depends on cost and pressure loss requirements [21].
With regard to flow velocity measurements, the most widespread technique is particle image velocimetry. The salient characteristic of such a technique is its ability to measure flow in a two-dimensional plane, providing the two components of velocity vectors. The technique makes it also possible to capture instantaneous turbulent flow fields for the purpose of identifying fundamental mechanisms of turbulence and extracting their spatial structure. The major problems lie with (a) the limited pixel resolution of the CCD camera used to acquire PIV images, which leads to an accuracy reduction, and (b) the ambiguity of the direction of velocity vectors, which sometimes can be overcome with the acquisition of two consecutive photographic frames [106]. Flow velocities can be also measured with electromagnetic and ultrasonic flowmeters. Electromagnetic flowmeters require the fluid to have a minimum electric conductivity, whereas ultrasonic flowmeters can be used in applications with every kind of liquid. Moreover, the latter can be very expensive when inserted in pipes with a large diameter, whereas the price of ultrasonic flowmeters is almost independent of pipe size. On the other hand, transit-time ultrasonic flowmeters, which are currently the most widespread type of flowmeters, have the disadvantage of being sensitive to air bubbles or any suspended solids in the fluid, whereas Doppler ultrasonic flowmeters, despite being less expensive, suffer from a lower accuracy with respect to transit-time flowmeters. For transit-time flowmeters, when the transit time Δt is measured with a resolution of at least 100 ps, an accuracy of 1% in the flow velocity measurement can be achieved. A typical resolution value for velocity measurements is 0.8 mm·s−1 [21]. Finally, with regard to laser Doppler velocimetry (LDV), among its main advantages in measuring flows, the following ones are the most interesting when such devices are employed in the development of arterial simulators: (1) a small measuring region, (2) high measurement accuracy, (3) ability to measure any desired velocity component, (4) no probe in the flow (does not disturb the flow measurements in hostile environments) and (5) good frequency response. Nevertheless, given the nature of the signal, difficulties arise in making it continuous due to its high dependency on the scattering particle density. The fluid and the conduit walls involved in the measurement must be transparent, and such a technique needs the fluid to be seeded with the particles [21].
The abovementioned issues may occur alongside further specific critical issues depending on the single realization and application of the arterial simulators reported in the current scientific literature. These specific issues are the subject of the following sections of the present review.
4. Experimental Set-Ups in Artery Bifurcation Studies
The investigation of hemodynamics and biomechanics of the arterial system in correspondence with arterial bifurcations is considered an important issue because of the presence of important bifurcations in the arterial tree, such as the carotid bifurcation.
4.1. Suarez-Bagnasco’s Multiparameter Measurement System for Artery Bifurcation
Suarez-Bagnasco et al. [23] investigated and characterized a multiparameter measurement system in vitro with sensors able to measure different mechanical quantities such as distance, pressure, temperature, viscosity and flow, which are of key importance to understand cardiovascular system behavior and identify possible anomalies that could lead to many different pathologies such as atherosclerosis and arteriosclerosis. Their goal was the development of an experimental set-up able to model blood flow, the arterial wall and both shear and circumferential stresses of the latter in order to study biomechanics and hemodynamics of artery bifurcations, as reported in Figure 1.
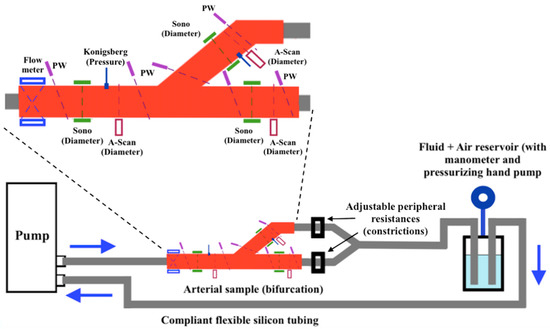
Figure 1.
Example of experimental set-up for the study of arterial bifurcation in [23].
The advantage of in vitro workbenches is that they can provide valuable information about arterial segments in a context as close as possible to in vivo studies without invasively intervening on a human subject. Therefore, they realized an experimental set-up with a simulated arterial bifurcation made of a biological specimen of an arterial segment (or artificial tubes) inserted in a closed hydraulic circuit that mimics the circulatory system.
In such a system it was possible to adjust arterial resistances through two constrictions (clamps) placed correspondingly to each output branch of the bifurcation, therefore allowing the simulation of pressure wave reflections. The flow was pumped through the circuit by using an artificial heart with adjustable frequency and ejection volume. The data retrieved at a steady regime from the sensors used were compared with numerical simulations. Wall thickness, lengths, and internal and external diameters (i.e., morphological data) were acquired with ultrasound probes using A-scan or sonomicrometer ultrasonic modules. Pressure waveforms were obtained through Königsberg sensors with a low response time located near the diameter measurement sites. Flow velocity profiles were retrieved through a Doppler system, whereas cross-sectional flows were measured through transit-time flowmeters.
The main encountered problems are due to the signal acquisition because of the interference of multiple sensor inputs. In particular, the authors studied the input signal perturbations due to noises with identical physical natures: despite the workbench’s electromagnetic isolation, all sonomicrometer measurements were perturbed by electromagnetic interference, therefore resulting in a distortion of the distance waveforms acquired. Moreover, all the ultrasound measurements were influenced by the other RF sources coming from the different subsystems. On the other hand, the flow meter measurements (i.e., cross-sectional flow) were perturbed by the vessel diameter variation due to the pulsatile flow, leading to an error up to 10%. Finally, pressure measurements were influenced by trapped air bubbles in the physiological solution injected in the circuit as well as from mechanical vibrations and uncontrolled temperature variations.
4.2. Bale-Glickman’s Carotid Bifurcation Flow Phantoms
Bale-Glickman et al. [24] carried out extensive flow studies in two carotid bifurcation flow phantoms. In this work, the authors mainly used particle image velocimetry (PIV) for flow visualization and, after the study of flow behavior in correspondence with the bifurcation, stated that the flow nature was determined by the vessel’s lumen geometry. The experimental set-up was developed to study flows inside an artificial carotid bifurcation reproduced by a rubber mold, starting from an exact replica of the carotid bifurcation made by laser stereolithography with a 260 μm resolution based on an MRI dataset taken from real, excised plaque specimens from patients that underwent endarterectomy surgery. This carotid silicone surrogate (designed to have optical characteristics as close as possible to the fluid ones) was then inserted in a flow loop for the experiments, thanks to flexible tubing with an 8 mm diameter. The fluid mixture was pumped through a gear pump capable of generating both variable amplitude pressure waves and flow rate. The optical arrangement for the flow visualization included a digital camera with a 30 Hz frame rate and a PIV laser. The main concern in the study was the flow exposure time that was set at Δt = 3 ms after several trials in order to highlight both high- and low-speed flow regions, as well as the time of separation of the two PIV images, which was set in a range between 5 and 30 μs according to the flow rate in the phantom.
4.3. Botnar’s Study on In Vitro Carotid Artery Bifurcation and MRI Techniques
Botnar et al. [25], instead, studied the hemodynamics of carotid artery bifurcation through a comparison between numerical simulations and in vitro measurements with the use of MRI techniques. The experimental set-up used in this work is reported in Figure 2.
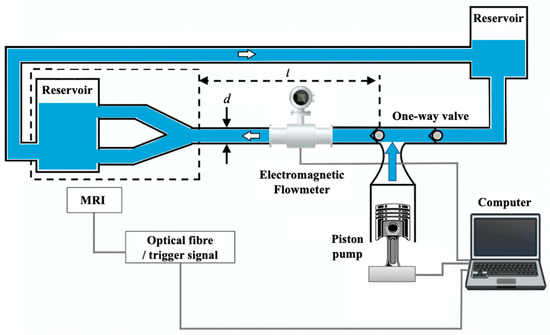
Figure 2.
Example of experimental set-up for the study of arterial bifurcation in [25]. The tubing diameter is d = 20 mm and the distance l = 4.5 m.
They developed an arterial simulator with a programmable pump driven by a step motor to simulate the physiologic flows controlled with mechanical valves. An electromagnetic flowmeter was used to monitor the pulse wave stability. Measurements of both axial flow and secondary flows (i.e., due to pathologies) were carried out through an MRI scanner. Even though the axial velocity’s numerical and in vitro results agreed, the main measurement issue found by the authors is closely related to the data achieved for the secondary flow in vitro measurements that differed from the numerical simulation data because of image artifact inaccuracies (estimated to be 5% for the 10 mm vessel diameter and 25% for the 4 mm vessel diameter) and the secondary flow sensitivity to the vessel geometry. Part of such inaccuracies could be possibly due to the insertion error of the flowmeter, which may have led to the fluid perturbation. A summary of the main sensors, relevant measurement limitations and measured quantities in the arterial simulators developed and realized according to the different artery bifurcation studies is reported in Table 2.

Table 2.
Overview of artery bifurcation studies.
5. Experimental Set-Ups in Stenosis and Plaque Studies
Arterial simulators have been widely employed to study the main physical quantities involved in the pathogenic formation of stenosis and plaques.
5.1. Bertolotti’s Experimental Test Bench for Stenosed Coronary Bypasses
Bertolotti et al. [29] developed an experimental test bench to model blood flows in stenosed coronary bypasses. The authors built an experimental set-up able to set the cardiac frequency for any flow waveform. Pressure waveforms were obtained through two pumps which forced the blood-mimicking fluid into the flexible tubing and electromagnetic flowmeters were used to record the flow rate with an accuracy of about 10%. Velocities were acquired through a Doppler velocimeter at 8 MHz. After having measured both the external diameter and flow pressure in one single location of the bench through a sonomicrometer and a microtip catheter, two parameters were estimated. Firstly, the pulsatility Pr (%) of the silicon hoses and the compliance C (mL·mmHg−1) were estimated as:
where ΔD is the external diameter variation within the cardiac cycle and Dmean is the mean diameter, ΔV is the variation in the volume of the artery, whereas Δp is the pressure difference between maximum and minimum pressures. The main problems related to the experimental set-up were due to the unavoidable imperfections that caused flow instability, contributing to an increase in the uncertainty of the results.
5.2. Brunette’s Study on a Stenosis Arterial Phantom
On the other hand, Brunette et al. [32] investigated the wall shear stress in an arterial phantom in correspondence with the stenosis location (i.e., 13.5 Pa near its throat, 3.5 Pa in its proximal portion and 2.8 Pa at its exit), because such a parameter is considered to have an active role in platelet activation and the formation of clots, possibly leading to thrombosis [107]. The shear stress had to be investigated through the flow velocity distributions in the arterial set-up, which was accomplished through PIV. In this case, the minimization of the refraction problems was the main metrological issue, as it could lead to a mismatch in PIV results. A summary of the main sensors and measured quantities of the arterial simulators developed and realized according to the different stenosis and plaque studies is reported in Table 3, together with some relevant details.

Table 3.
Overview of stenosis and plaque studies.
6. Experimental Set-Ups in Arterial Flow Studies
Another important field in which arterial simulators have been widely employed is the study of flow behavior in vessels, since this is a physical quantity playing a key role in hemodynamics and in pathogenetic processes according to its regime (i.e., laminar or turbulent). Blood flow can be perturbed by many different factors such as vessel geometry or stenosis and plaques. This is the reason why such studies are strictly linked with the ones reviewed in Section 4 and Section 5. Nevertheless, it is worth reviewing more in detail the peculiar characteristics of the arterial simulators developed for blood flow testing.
6.1. The Design of an Arterial Simulator for Backward Flows by Feng and Whir
Feng and Whir [45] designed an arterial simulator in order to investigate the behavior of backward flows in terms of wave speed and dissipation in flexible tubing. Their experimental set-up is reported in Figure 3.
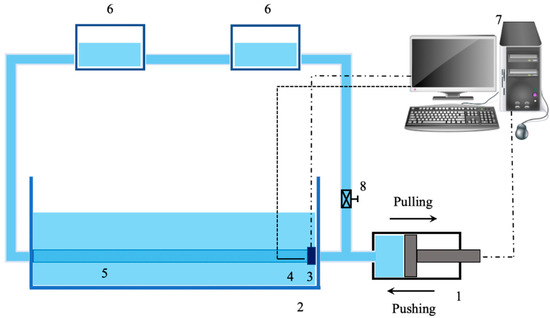
Figure 3.
Example of experimental set-up for the study of arterial bifurcation in [45]: (1) piston pump, (2) water tank, (3) flowmeter, (4) pressure catheter, (5) rubber tube, (6) reservoirs, (7) computer, (8) one-way valve.
They used a piston pump that generated a flow waveform in the hydraulic circuit and the backward and forward flows were obtained through the pulling and pushing action of the piston pump. Pressure and flows were measured by employing a pressure transducer catheter and a flowmeter, respectively, and the wave speed was estimated through the PU-loop method. The tube diameter was measured through an ultrasonic sonomicrometer to appreciate its variation during the pumping action. One of the problems encountered during the investigation was due to the variation in the local wave speed inside the tube, which was attributed to wall thickness variation along the tubing depending on its manufacturing process: this resulted in an unexpected change in wave velocity that resulted in it being higher in the middle of the latex tube and lower at the two ends.
6.2. The Investigation of Blood Flow in Experimental Set-Up of Micro-Vessels
Another interesting application was given by Stergiou et al. [46], who investigated blood flow in micro-vessels. The scientific literature contains plenty of studies reporting on blood flow behavior in large arteries. It is not so common to find a study regarding blood flow in small micro-sized arteries such as arterioles since in vivo or in vitro experiments are difficult to carry out. The authors built an experimental set-up with a reduced number of components: in fact, it was constituted by a syringe pump, the micro-sized conduit, a high-speed camera and a microscope. They employed microparticle image velocimetry (μ-PIV) in order to assess the axial blood flow velocity. The main goal of this study was the investigation of a peculiar effect which occurs inside μ-vessels, namely, the Fahraeus–Lindqvist effect, which states that during blood flow in μ-vessels, the red blood cells tend to migrate towards the center of the conduit, determining the formation of a cell-free layer along the vessel wall.
6.3. Laser Doppler Anemometer (LDA) with an Aortic Flow Phantom Designed by Liepsch
On the other hand, Liepsch et al. [51] realized a flow phantom with a silicon replica of the aortic arch in which the flow velocity was measured through a laser Doppler anemometer (LDA). Flow was measured through an ultrasonic Doppler flowmeter while the pressure between the ventricular and aortic arch was recorded through an inductive pressure transducer, which is a unique design in this review study. The main advantage of the system adopted in this study lies in the fact that flow disturbances could be easily localized and the LDA system has high temporal and spatial resolution with respect to a single ultrasound. Nevertheless, it should be pointed out that Liepsch et al. worked with a Newtonian fluid, which has very different characteristics from blood that behaves as non-Newtonian, and this choice was made because the LDA system works with transparent fluids only (e.g., a calcium chloride mixture which absorbs laser light). Moreover, the pulse wave velocity was retrieved with two assumptions: (a) a neglection of the axial strain and (b) small cross-section change.
6.4. The Employment of the PIV Method for Flow Behavior Analysis
Other studies [52,53] used the PIV method for flow behavior analysis in vessels and grafts, therefore suggesting that this is an accurate and validated method for the measurement of flow velocity and visualization of fluid flow. Despite this advantage, Giurgea et al. [53] recognized that PIV methods suffer from the mandatory matching between the phantom and the fluid refractive indices, which is hard to achieve because of the limitations in the manufacturing process, especially of curved vessel walls. A summary of the main sensors, metrological issues and measured quantities in the arterial simulators developed and realized according to above flow studies is reported in Table 4.

Table 4.
Overview of arterial flow studies.
7. Experimental Set-Ups in Clinical Practice and Device Testing
Experimental set-ups simulating arterial systems have been also employed to be both device testers and objects with the goal of helping clinicians train for surgical operations without encountering problems due to their inexperience with real patients.
7.1. Miller’s Pulsatile Blood Vessel System for Clinician Practice
Miller et al. [55] designed and developed a pulsatile blood vessel system as a simulator for young, inexperienced physicians in order to let them practice femoral arterial access, which is necessary for patients’ catheterization before cardiac interventions, reducing to a minimum the risk of causing complications due to arterial damage. Their work was born from the fact that in 2013, the number of high-fidelity simulators for femoral arterial access training was very low. The pressure pulses were obtained by a syringe piston and the exerted pressure was recorded through disposable transducers. Furthermore, a force sensor was used to quantify the relationship between the vessel pressure and the “finger force” felt by physicians during the palpation over the femoral artery. The main issues were related to the intrinsic difficulty in simulating the actual force exerted as well as to understand how it was correlated to the variation in vessel pressure. The discrepancy between experimental and software results was found to be 8.7%.
7.2. Gwak and the Improvement of Conventional Mock Circulatory Systems
In 2010, Gwak et al. [60] expressed their concern over the fact that conventional mock circulatory systems available in the literature were still lacking repeatability, flexibility and precision because of their constitutive passive components (resistance, compliance and inertance). The lack of flexibility is due to the limited response of passive elements to different pressure and flow regimes, as they are not capable of changing contour conditions in an active way according to experimental necessity. Therefore, since the impedance is fixed once the set-up is built, a continuous redevelopment of the simulator should be carried out whenever a change in physical quantities is needed. In turn, repeatability and precision problems are strictly related to the manual calibration. To overcome such drawbacks, the authors proposed an active and programmable cardiovascular impedance simulator constituted by a piston pump and a gear pump that is able to establish a given relationship between pressure and flow by making use of feedback control. In order to measure pressure and flow, they inserted differential pressure transducers and an ultrasonic flow meter, respectively: based on pressure and volume quantities, a compliance and resistance estimation was conducted in order to test the experimental set-up. This validation study, according to the authors statements, could make their simulator useful for the development of artificial hearts or artificial cardiac valves even if further improvements with the elimination of the compliance accumulator were needed.
7.3. Legendre and Vilchez-Monge’s Design of an Artificial Cardiovascular Simulator for Device Testing
Conversely, Legendre et al. [61] designed an artificial cardiovascular simulator to mimic both the physiology and pathophysiology of the human cardiovascular system. As with Gwak et al., the focus was to validate the simulator with the aim of making it suitable for cardiovascular device testing. The developers used a set of transducers to monitor pressure, temperature and flow. Despite the system showed acceptable reproducibility and repeatability, data consistency and stability still needed to be assured. Another experimental flow loop mimicking the cardiovascular system circuit was designed by Vilchez-Monge et al. [67]: the simulated circuit contained the right side of the heart, simulated arteries and veins. In order to monitor both pressure and flows, the authors inserted an absolute pressure sensor with a response time of 1 ms and accuracy of ±2.5% with respect to the FS voltage, and a flow meter with ±3% accuracy, with a measurement range from 1 to 30 L·min−1.
Both sensors were controlled through an Arduino microprocessor, which allowed for a feedback control capable of adjusting the circuit compliance. Additionally, there were issues with the calibration of pressure magnitude, mainly triggered by the compliance chamber valves; those components showed signs of wear and air leakage, which translated into inadequate pressurization ranges and a badly behaved pressure head. The authors claimed that the arterial pressure magnitude did not match with the provided values found in the literature due to calibration inaccuracies.
7.4. The Design of a Reliable Implantable Circulatory Support Device by Yoshino
Conversely, Yoshino et al. [71] aimed at testing a centrifugal blood pump in order to develop a reliable, implantable circulatory support device. In particular, they used the circulatory loop in Figure 4 with an electromagnetic flowmeter and a U-tube manometer to measure pump flow and the difference between inflow and outflow pressures.
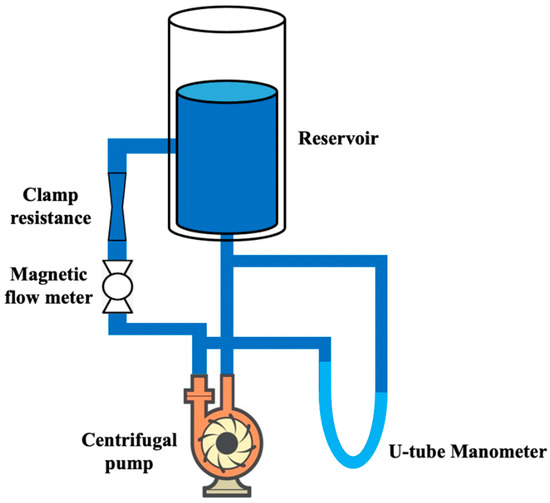
Figure 4.
Example of experimental set-up for the study of device testing in [71].
The pump efficiency ξ has been evaluated through the ratio between the pump output power and the input electrical power as follows:
where pout is the pump head pressure, Qout is the pump output flow, Vin is the input voltage and Iin is the input current. The maximum ξ found was 14% at 2.2·103 rpm. Finally, the authors used a Hall effect sensor to test the pump impeller stability, which was the greatest study concern. A summary of the main sensors and measured quantities in the above arterial simulators developed and realized according to the different clinician practice and device testing studies is reported in Table 5, with some relevant functional and metrological issues.

Table 5.
Overview of clinician practice and device testing studies.
8. Experimental Set-Ups in Pulse Pressure Studies and Biomechanics
Arterial simulators are definitely a crucial tool also used to investigate biomechanics, i.e., the study of mechanical laws that involve all the hemodynamic quantities in the cardiovascular system, and model its functioning. This application could be really difficult and critical for the study of in vivo systems. Such branch of scientific research has been carried out since the 1970s and exponentially developed in the last years. Today, the milestones of biodynamics and biomechanics studies are undoubtedly represented by Y.C. Fung’s books, which created a strong impulse to study in vitro the cardiovascular system by providing valuable information about the physical principles of circulation [108,109], as well as the mathematical models that characterize blood flow and vessel mechanics [110].
8.1. Fronek’s In Vitro Investigation on Pulse Pressure Waves
In 1976 both Lou and Fronek, working with different approaches, studied pulse pressure waves in elastic tubes in order to investigate the relationship subsisting between pressure and vessel elasticity. In particular, Fronek, with the help of Fung [73], developed an experimental set-up, reported in Figure 5, for the in vitro investigation of blood vessel deformation by measuring both longitudinal and circumferential diameter variations.
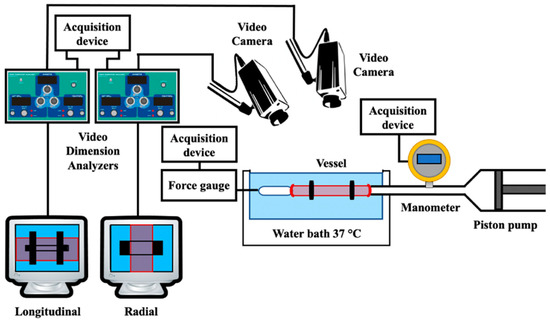
Figure 5.
Example of experimental set-up for the study of device testing in [73].
The latter measurement was possible due to using a video dimension analyzer (VDA), which used a video signal from a TV camera and provided a determined DC voltage according to the distance variation between two points chosen in the image. The experiment could be conducted both in vivo on real vessels and in vitro with an excised specimen. The wall thickness was determined through a microscope. In this way, the authors found a relationship between stress and strain (longitudinal and circumferential) with regard to changes in the vessel inner pressure. In this system, the vessel was connected to a microsyringe that was able to generate a variation in intraluminal pressure between 0 and 250 mmHg, which was measured with a low-compliance pressure transducer. The authors claimed in their study that this was a far more physiological way of retrieving vessels’ mechanical properties with respect to contact methods that were used until this study. In fact, the advantage of noncontact methods for conducting deformation measurements is due to the lack of mechanical interference (insertion error) caused by the contact measurement instrument element that touches the vessel, therefore interfering in its free movement during pulses. This issue was highlighted in a more recent study [8] as well, since the LVDT core weight interfered with the vessel movement and affected the radial displacement measurement.
8.2. Lou’s Experimental Apparatus for the Determination of Pressure Wave Velocity
On the other hand, Lou [74] developed an experimental apparatus with the goal of determining the velocity of a sinusoidal pressure wave at different frequencies, phases and amplitudes. In such a system, a screw pump provided a pulseless and adjustable flow in a hydraulic circuit it was embedded with. Moreover, the sinusoidal pressure variation was supplied by a piston pump. The tube displacement was measured in two locations with a noncontact method based on capacitive sensors that were sensitive to 5 μm-diameter variations. By knowing the distance between transducers, such a set-up allowed for measuring pulse velocity. Unfortunately, the main concern was the accuracy assessment of the experimental set-up, since the main errors were related to the different components used for the data-retrieving process and to the pulse reflections from the tube’s end that could not be eliminated by the reflection minimizer employed.
8.3. Horsten’s Investigation of Wave Propagation in Viscoelastic Tubes
Another study by Horsten et al. [75] focused its attention on the propagation of pressure pulse waves in tubes showing a viscoelastic behavior: to this aim, their experimental set-up was composed of a rigidly supported elastic tube (simulating the artery), a pressure vessel and a magnetic valve. In order to carry out the experiment without nonlinear effects, the authors had to use small velocities and pressure disturbances. The latter were measured through a catheter-tip manometer, whereas the tube diameter variations were collected through a photonic sensor. The authors managed to determine the pulse amplitude, width and velocity with uncertainties at a 95% confidence level of ±2%, ±4% and ±1%, respectively. In a similar way to [8], the transmural pressure was adjusted by means of the fluid height in the reservoir. From the relationship between the pressure and cross-sectional area, the compliance was retrieved with 4% accuracy. The main issues were related to: (a) the influence of the tube’s rigid support that prevented an axial-symmetric expansion and affected the pulse propagation in an unknown way and (b) the positioning of the photonic sensor with respect to the pressure transducer, which was really critical and affected the accuracy of the measurements.
8.4. The Introduction of Computer-Aided Simulators for the Study of Vessel Biomechanical Behavior
Some years later, Humphrey et al. [76] introduced a new system which had the great advantage of being computer aided. In a section of their work, they pointed out that none of the devices built up until then were completely under computer control. The main advantages of using a computer include the performance flexibility of many different protocols, higher reproducibility, the minimization of human error and simplification of the experimental execution. This issue was highlighted in 2009 by Zannoli et al. [77] as well, who claimed that computer systems could overcome, through software programs and mathematical functions, the problems related to the difficulty in reproducing nonlinear cardiovascular responses that led to very expensive mechanical apparatuses.
In any case, the device developed by Humphrey is very complex in its structure; in fact, it allows for the performing of different experiments on elastic tubes or excised artery specimens: it allowed tensioning and compression, as well as torsion (three ad hoc actuators were employed) in order to test and study the vessel biomechanical behavior. In a similar way to [73], they employed a VDA system in order to record vessel diameter variation according to the pressure wave propagation induced by a peristaltic pump. The latter, together with the actuators, were computer controlled throughout the experimental procedures. A summary of the main sensors and the measured quantities of the arterial simulators developed and realized according to the different biomechanics studies is reported in Table 6 with some relevant functional and metrological issues.

Table 6.
Overview of biomechanics studies.
9. Conclusions
The present work reviewed the most common arterial simulators that exist in the scientific literature from a metrological and functional perspective as to highlight the design issues, experimental set-up characteristics, types of sensors applied to measure the main cardiovascular quantities and, finally, the difficulties and drawbacks found in the set-up arrangements and the corresponding measurements. The aim is to provide an overview for researchers who are working in the cardiovascular field to help them in implementing and metrologically improving the existing cardiovascular phantoms as well as the accuracy in studying hemodynamic phenomena. Although many studies have been proposed in the literature, some general considerations can be deduced. Firstly, it can be noticed that the experimental systems often needed an elastic tube to simulate arteries with different characteristics, a pump as an actuator to produce pressure waves or desired flow rates (e.g., syringe pumps, peristaltic pump, piston pump according to the application) and a hydraulic circuit with a solution (e.g., distilled water or a mixture of water and glycerin to obtain different levels of viscosities).
Secondly, with regard to the sensors in the simulators, the main measurement methods are subdivided by contact or noncontact methods according to the presence of physical contact between the sensor and the system under test. In many studies, the arterial simulators were equipped with optical or ultrasound measurement systems to measure flow velocity or radial displacements, respectively. Most of the experimental arrangements are equipped with pressure transducers (mainly catheter-tip transducers and differential transducers), privileging intrusive techniques for pressure measurements, whereas the flow was commonly measured through ultrasonic or electromagnetic transit-time flowmeters. In the field of flow studies, particle image velocimetry (PIV) techniques are very common for flow velocity measurements, whereas for biomechanics studies, many authors adopted video dimension analyzers (VDA) to assess the specimen variations.
With regard to specific issues derived from the method employed in the measurement protocols, difficulties were found in using PIV for refractive index mismatch. Furthermore, some studies pointed out shortcomings in the agreement between simulated and experimental results because of a difficult retrieval or the monitoring of mechanical quantity variations such as inner diameters, wall thickness and Young’s modulus, as well as an improper assessment of boundary conditions. Globally, the sources of main uncertainty were due to an improper physical model used to describe the interaction between mechanical/geometrical set-up characteristics and pressure waves or flows resulting in a wrong experimental set-up design or dimensioning. Many studies highlighted that, together with the further investigation of physical models implied, future developments could be related to a wider employment of noncontact measurement methods, therefore reducing the minimum insertion errors that mainly affect flow and pressure measurements. In fact, such errors can be a burden when the study focuses on physical quantities which are highly dependent on the measurement method applied, especially when they are retrieved from an indirect measurement (e.g., PWV, transit time, etc.). Finally, other error typologies which may perturb the measured quantities, especially for noncontact measurement methods, are produced by (a) limited bandwidth, (b) resolution defects, (c) nonlinearity effects and (d) noise interference, as well as devices that have the inability to detect the lowest quantity of variation under analysis. Future developments should take all these errors into account when designing and setting up novel simulators with metrological characteristics, making them as suitable as possible to allow for an in-depth analysis of cardiovascular phenomena.
Author Contributions
Conceptualization, F.F. and A.S.; methodology, F.F. and A.S.; investigation, F.F.; writing—original draft preparation, F.F.; writing—review and editing, F.F., A.S. and S.A.S.; supervision, A.S. and S.A.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wilkins, E.; Wilson, L.; Wickramasinghe, K.; Bhatnagar, P.; Leal, J.; Luengo-Fernandez, R.; Burns, R.; Rayner, M.; Townsend, N. European Cardiovascular Disease Statistics 2017; European Heart Network: Bruselles, Belgium, 2017. [Google Scholar]
- Weaver, C.G.; Clement, F.M.; Campbell, N.R.; James, M.T.; Klarenbach, S.W.; Hemmelgarn, B.R.; Tonelli, M.; McBrien, K.A. Healthcare Costs Attributable to Hypertension: Canadian Population-Based Cohort Study. J. Hypertens. 2015, 66, 502–508. [Google Scholar] [CrossRef]
- Laurent, S.; Cockcroft, J.; Van Bortel, L.; Boutouyrie, P.; Giannattasio, C.; Hayoz, D.; Pannier, B.; Vlachopoulos, C.; Wilkinson, I.; Struijker-Boudier, H. Expert Consensus Document on Arterial Stiffness: Methodological Issues and Clinical Applications. Eur. Heart J. 2006, 27, 2588–2605. [Google Scholar] [CrossRef] [PubMed]
- Fiori, G.; Fuiano, F.; Scorza, A.; Conforto, S.; Sciuto, S.A. Non-Invasive Methods for PWV Measurement in Blood Vessel Stiffness Assessment. IEEE Rev. Biomed. Eng. 2022, 15, 169–183. [Google Scholar] [CrossRef] [PubMed]
- Younessi Heravi, M.A.; Khalilzadeh, M.A. Designing and Constructing an Optical System to Measure Continuous and Cuffless Blood Pressure Using Two Pulse Signals. Iran. J. Med. Phys. 2014, 11, 215–223. [Google Scholar] [CrossRef]
- Murakami, K.; Yoshioka, M.; Ozawa, J. Non-Contact Pulse Transit Time Measurement Using Imaging Camera, and Its Relation to Blood Pressure. In Proceedings of the 14th IAPR International Conference on Machine Vision Applications (MVA), Tokyo, Japan, 18–22 May 2015; pp. 414–417. [Google Scholar]
- Zaki, W.S.W.; Correia, R.; Korposh, S.; Hayes-Gill, B.R.; Morgan, S.P. Development of Tubular Cardiovascular Phantom System for Pulse Transit Time Simulation. Int. J. Recent. Technol. Eng. 2019, 8, 291–296. [Google Scholar] [CrossRef]
- Fuiano, F.; Fiori, G.; Vurchio, F.; Scorza, A.; Sciuto, S.A. Transit Time Measurement of a Pressure Wave through an Elastic Tube Based on LVDT Sensors. In Proceedings of the 24th IMEKO TC4 International Symposium 22nd International Workshop on ADC and DAC Modelling and Testing IMEKO TC-4 2020, Palermo, Italy, 14–16 September 2020. [Google Scholar]
- Klanchar, M.; Tarbell, J.M.; Wang, D.-M. In Vitro Study of the Influence of Radial Wall Motion on Wall Shear Stress in an Elastic Tube Model of the Aorta. Circ. Res. 1990, 66, 1624–1635. [Google Scholar] [CrossRef]
- Almeida, V.G.; Pereira, H.C.; Pereira, T.; Figueiras, E.; Borges, E.; Cardoso, J.M.R.; Correia, C. Piezoelectric Probe for Pressure Waveform Estimation in Flexible Tubes and Its Application to the Cardiovascular System. Sens. Actuator A 2011, 169, 217. [Google Scholar] [CrossRef]
- Dagdeviren, C.; Su, Y.; Joe, P.; Yona, R.; Liu, Y.; Kim, Y.-S.; Huang, Y.; Damadoran, A.R.; Xia, J.; Martin, L.W.; et al. Conformable Amplified Lead Zirconate Titanate Sensors with Enhanced Piezoelectric Response for Cutaneous Pressure Monitoring. Nat. Commun. 2014, 5, 4496. [Google Scholar] [CrossRef]
- Ma, Y.; Choi, J.; Hourlier-Fargette, A.; Xue, Y.; Chung, H.U.; Lee, J.Y.; Wang, X.; Xie, Z.; Kang, D.; Wang, H.; et al. Relation between Blood Pressure and Pulse Wave Velocity for Human Arteries. Proc. Natl. Acad. Sci. USA 2018, 115, 11144–11149. [Google Scholar] [CrossRef]
- Lu, N.; Lu, C.; Yang, S.; Rogers, J. Highly Sensitive Skin-Mountable Strain Gauges Based Entirely on Elastomers. Adv. Funct. Mater. 2012, 22, 4044–4050. [Google Scholar] [CrossRef]
- Navghare, S. Design and Simulation of MEMS Sensor for Detection of Arterial Pulse. Int. J. Comput. Appl. Technol. 2018, 17, 7247–7260. [Google Scholar] [CrossRef]
- Bae, J.-H.; Jeon, Y.J.; Kim, J.Y.; Kim, J.U. New Assessment Model of Pulse Depth Based on Sensor Displacement in Pulse Diagnostic Devices. Evid. Based Complement. Alternat. Med. 2013, 2013, 938641. [Google Scholar] [CrossRef] [PubMed]
- Laqua, D.; Pollnow, S.; Fischer, J.; Ley, S.; Husar, P. A Phantom with Pulsating Artificial Vessels for Non-Invasive Fetal Pulse Oximetry. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2014, 2014, 5631–5634. [Google Scholar] [CrossRef]
- Lantos, C.; Erd, B.; Nyers, T.; Pandula, Z.; Halász, G. The Examination of Deformation of a Silicone Elastomer Tube. In Proceedings of the 14th International Conference on Fluid Flow Technologies, Budapest, Hungary, 9–12 September 2009. [Google Scholar]
- Berrios, J.C.; Pedersen, P.C. Ultrasonic Measurement of Forced Diameter Variations in an Elastic Tube. Ultrason. Imaging 1994, 16, 124–142. [Google Scholar] [CrossRef]
- Vlachopoulos, C.; O’Rourke, M.; Nichols, W.W. McDonald’s Blood Flow in Arteries: Theoretical, Experimental and Clinical Principles, 6th ed.; CRC Press: London, UK, 2012; p. 88. [Google Scholar]
- Wilson, J.S. Sensor Technology Handbook, 1st ed.; Elsevier: London, UK, 2005; pp. 22–31. [Google Scholar]
- Webster, J.G. Measurement, Instrumentation, and Sensors Handbook: Spatial, Mechanical, Thermal, and Radiation Measurement, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 852–940. [Google Scholar]
- Bramwell, J.C.; Hill, A.V. The Velocity of Pulse Wave in Man. Proc. R. Soc. Lond. B Biol. Sci. 1922, 93, 298–306. [Google Scholar] [CrossRef]
- Suárez-Bagnasco, D.; Balay, G.; Cymberknop, L.; Armentano, R.L.; Negreira, C.A. Measurement System for an In-Vitro Characterization of the Biomechanics and Hemodynamics of Arterial Bifurcations. J. Phys. Conf. Ser. 2013, 421, 012018. [Google Scholar] [CrossRef]
- Bale-Glickman, J.; Selby, K.; Saloner, D.; Savaş, O. Experimental Flow Studies in Exact-Replica Phantoms of Atherosclerotic Carotid Bifurcations under Steady Input Conditions. J. Biomech. Eng. 2003, 125, 38–48. [Google Scholar] [CrossRef]
- Botnar, R.; Rappitsch, G.; Scheidegger, M.B.; Liepsch, D.; Perktold, K.; Boesiger, P. Hemodynamics in the Carotid Artery Bifurcation: A Comparison between Numerical Simulations and in Vitro MRI Measurements. J. Biomech. 2000, 33, 137–144. [Google Scholar] [CrossRef]
- Banks, J.; Bressloff, N.W. Turbulence Modeling in Three-Dimensional Stenosed Arterial Bifurcations. J. Biomech. Eng. 2007, 129, 40–50. [Google Scholar] [CrossRef]
- Ku, D.N.; Giddens, D.P. Laser Doppler Anemometer Measurements of Pulsatile Flow in a Model Carotid Bifurcation. J. Biomech. 1987, 20, 407–421. [Google Scholar] [CrossRef]
- Khir, A.W.; Parker, K.H. Measurements of Wave Speed and Reflected Waves in Elastic Tubes and Bifurcations. J. Biomech. 2002, 35, 775–783. [Google Scholar] [CrossRef]
- Bertolotti, C.; Deplano, V.; Fuseri, J.; Dupouy, P. Numerical and Experimental Models of Post-Operative Realistic Flows in Stenosed Coronary Bypasses. J. Biomech. 2001, 34, 1049–1064. [Google Scholar] [CrossRef]
- Deplano, V.; Siouffi, M. Experimental and Numerical Study of Pulsatile Flows through Stenosis: Wall Shear Stress Analysis. J. Biomech. 1999, 32, 1081–1090. [Google Scholar] [CrossRef]
- Tang, D.; Yang, C.; Walker, H.; Kobayashi, S.; Ku, D.N. Simulating Cyclic Artery Compression Using a 3D Unsteady Model with Fluid–Structure Interactions. Comput. Struct. 2002, 80, 1651–1665. [Google Scholar] [CrossRef]
- Brunette, J.; Mongrain, R.; Laurier, J.; Galaz, R.; Tardif, J.C. 3D Flow Study in a Mildly Stenotic Coronary Artery Phantom Using a Whole Volume PIV Method. Med. Eng. Phys. 2008, 30, 1193–1200. [Google Scholar] [CrossRef]
- Li, S.; Chin, C.; Thondapu, V.; Poon, E.K.W.; Monty, J.P.; Li, Y.; Ooi, A.S.H.; Tu, S.; Barlis, P. Numerical and Experimental Investigations of the Flow–Pressure Relation in Multiple Sequential Stenoses Coronary Artery. Int. J. Cardiovasc. Imaging 2017, 33, 1083–1088. [Google Scholar] [CrossRef]
- Filipovic, N.; Rosic, M.; Tanaskovic, I.; Parodi, O.; Fotiadis, D. Computer Simulation and Experimental Analysis of LDL Transport in the Arteries. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2011, 2011, 195–198. [Google Scholar] [CrossRef]
- Filipovic, N.; Zivic, M.; Obradovic, M.; Djukic, T.; Markovic, Z.; Rosic, M. Numerical and Experimental LDL Transport through Arterial Wall. Microfluid. Nanofluid. 2014, 16, 455–464. [Google Scholar] [CrossRef]
- Kenjereš, S. On Recent Progress in Modelling and Simulations of Multi-Scale Transfer of Mass, Momentum and Particles in Bio-Medical Applications. Flow Turbul. Combust 2016, 96, 837–860. [Google Scholar] [CrossRef]
- Brum, J.; Bia, D.; Benech, N.; Balay, G.; Armentano, R.; Negreira, C. Set up of a Cardiovascular Simulator: Application to the Evaluation of the Dynamical Behavior of Atheroma Plaques in Human Arteries. Phys. Procedia 2010, 3, 1095–1101. [Google Scholar] [CrossRef][Green Version]
- Čanić, S.; Hartley, C.J.; Rosenstrauch, D.; Tambača, J.; Guidoboni, G.; Mikelić, A. Blood Flow in Compliant Arteries: An Effective Viscoelastic Reduced Model, Numerics, and Experimental Validation. Ann. Biomed. Eng. 2006, 34, 575–592. [Google Scholar] [CrossRef] [PubMed]
- Flaud, P.; Guesdon, P.; Fullana, J.-M. Experiments of Draining and Filling Processes in a Collapsible Tube at High External Pressure. Eur. Phys. J. Appl. Phys. 2012, 57, 31101. [Google Scholar] [CrossRef][Green Version]
- Bessems, D.; Giannopapa, C.G.; Rutten, M.C.M.; van de Vosse, F.N. Experimental Validation of a Time-Domain-Based Wave Propagation Model of Blood Flow in Viscoelastic Vessels. J. Biomech. 2008, 41, 284–291. [Google Scholar] [CrossRef] [PubMed]
- Wang, X. 1D Modeling of Blood Flow in Networks: Numerical Computing and Applications; Université Pierre et Marie Curie: Paris, France, 2014. [Google Scholar]
- Pontiga, F.; Gaytán, S.P. An Experimental Approach to the Fundamental Principles of Hemodynamics. Adv. Physiol. Educ. 2005, 29, 165–171. [Google Scholar] [CrossRef]
- Farsirotou, E.; Kasiteropoulou, D.; Stamatopoulou, D. Experimental Investigation of Fluid Flow in Horizontal Pipes System of Various Cross-Section Geometries. EPJ Web Conf. 2014, 67, 02026. [Google Scholar] [CrossRef]
- Kung, E.O. In-Vitro Experimental Validation of Finite Element Analysis of Blood Flow and Vessel Wall Dynamics. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2010. [Google Scholar]
- Feng, J.; Khir, A.W. The Compression and Expansion Waves of the Forward and Backward Flows: An in-Vitro Arterial Model. Proc. Inst. Mech. Eng. Part H 2008, 222, 531–542. [Google Scholar] [CrossRef]
- Stergiou, Y.G.; Keramydas, A.T.; Anastasiou, A.D.; Mouza, A.A.; Paras, S.V. Experimental and Numerical Study of Blood Flow in μ-Vessels: Influence of the Fahraeus–Lindqvist Effect. Fluids 2019, 4, 143. [Google Scholar] [CrossRef]
- Holdsworth, D.W.; Rickey, D.W.; Drangova, M.; Miller, D.J.; Fenster, A. Computer-Controlled Positive Displacement Pump for Physiological Flow Simulation. Med. Biol. Eng. Comput. 1991, 29, 565–570. [Google Scholar] [CrossRef]
- Mouza, A.A.; Skordia, O.D.; Tzouganatos, I.D.; Paras, S.V. A Simplified Model for Predicting Friction Factors of Laminar Blood Flow in Small-Caliber Vessels. Fluids 2018, 3, 75. [Google Scholar] [CrossRef]
- Kung, E.O.; Les, A.S.; Figueroa, C.A.; Medina, F.; Arcaute, K.; Wicker, R.B.; McConnell, M.V.; Taylor, C.A. In Vitro Validation of Finite Element Analysis of Blood Flow in Deformable Models. Ann. Biomed. Eng. 2011, 39, 1947–1960. [Google Scholar] [CrossRef]
- Segers, P.; Verdonck, P. Role of Tapering in Aortic Wave Reflection: Hydraulic and Mathematical Model Study. J. Biomech. 2000, 33, 299–306. [Google Scholar] [CrossRef]
- Liepsch, D.; Moravec, S.; Baumgart, R. Some Flow Visualization and Laser-Doppler-Velocity Measurements in a True-to-Scale Elastic Model of a Human Aortic Arch—A New Model Technique. Biorheology 1992, 29, 563–580. [Google Scholar] [CrossRef] [PubMed]
- Shakeri, M.; Khodarahmi, I.; Sharp, M.K.; Amini, A.A. Optical Imaging of Steady Flow in a Phantom Model of Iliac Artery Stenosis: Comparison of CFD Simulations with PIV Measurements. In Proceedings of the Medical Imaging 2010: Biomedical Applications in Molecular, Structural, and Functional Imaging, San Diego, CA, USA, 14–16 February 2010; Volume 7626, p. 76260L. [Google Scholar] [CrossRef]
- Giurgea, C.; Bode, F.; Ioan Budiu, O.; Nascutiu, L.; Banyai, D.; Damian, M. Experimental Investigations of the Steady Flow through an Idealized Model of a Femoral Artery Bypass. EPJ Web Conf. 2014, 67, 02031. [Google Scholar] [CrossRef]
- Van’t Veer, M.; Geven, M.C.F.; Rutten, M.C.M.; van der Horst, A.; Aarnoudse, W.H.; Pijls, N.H.J.; van de Vosse, F.N. Continuous Infusion Thermodilution for Assessment of Coronary Flow: Theoretical Background and in Vitro Validation. Med. Eng. Phys. 2009, 31, 688–694. [Google Scholar] [CrossRef]
- Miller, S.F.; Sanz-Guerrero, J.; Dodde, R.E.; Johnson, D.D.; Bhawuk, A.; Gurm, H.S.; Shih, A.J. A Pulsatile Blood Vessel System for a Femoral Arterial Access Clinical Simulation Model. Med. Eng. Phys. 2013, 35, 1518–1524. [Google Scholar] [CrossRef] [PubMed]
- Huberts, W.; Van Canneyt, K.; Segers, P.; Eloot, S.; Tordoir, J.H.M.; Verdonck, P.; van de Vosse, F.N.; Bosboom, E.M.H. Experimental Validation of a Pulse Wave Propagation Model for Predicting Hemodynamics after Vascular Access Surgery. J. Biomech. 2012, 45, 1684–1691. [Google Scholar] [CrossRef]
- Westerhof, N.; Elzinga, G.; Sipkema, P. An Artificial Arterial System for Pumping Hearts. J. Appl. Physiol. 1971, 31, 776–781. [Google Scholar] [CrossRef]
- Timms, D.; Hayne, M.; McNeil, K.; Galbraith, A. A Complete Mock Circulation Loop for the Evaluation of Left, Right, and Biventricular Assist Devices. Artif. Organs 2005, 29, 564–572. [Google Scholar] [CrossRef]
- Bazan, O.; Ortiz, J.P. Experimental Validation of a Cardiac Simulator for in Vitro Evaluation of Prosthetic Heart Valves. Braz. J. Cardiovasc. Surg. 2016, 31, 151–157. [Google Scholar] [CrossRef][Green Version]
- Gwak, K.-W.; Paden, B.E.; Antaki, J.F.; Ahn, I.-S. Experimental Verification of the Feasibility of the Cardiovascular Impedance Simulator. IEEE Trans. Biomed. Eng. 2010, 57, 1176–1183. [Google Scholar] [CrossRef] [PubMed]
- Legendre, D.; Fonseca, J.; Andrade, A.; Biscegli, J.F.; Manrique, R.; Guerrino, D.; Prakasan, A.K.; Ortiz, J.P.; Lucchi, J.C. Mock Circulatory System for the Evaluation of Left Ventricular Assist Devices, Endoluminal Prostheses, and Vascular Diseases. Artif. Organs 2008, 32, 461–467. [Google Scholar] [CrossRef] [PubMed]
- Knierbein, B.; Reul, H.; Eilers, R.; Lange, M.; Kaufmann, R.; Rau, G. Compact Mock Loops of the Systemic and Pulmonary Circulation for Blood Pump Testing. Int. J. Artif. Organs 1992, 15, 40–48. [Google Scholar] [CrossRef]
- Van Canneyt, K.; Planken, R.N.; Eloot, S.; Segers, P.; Verdonck, P. Experimental Study of a New Method for Early Detection of Vascular Access Stenoses: Pulse Pressure Analysis at Hemodialysis Needle. Artif. Organs 2010, 34, 113–117. [Google Scholar] [CrossRef]
- Milo, S.; Rambod, E.; Gutfinger, C.; Gharib, M. Mitral Mechanical Heart Valves: In Vitro Studies of Their Closure, Vortex and Microbubble Formation with Possible Medical Implications. Eur. J. Cardiothorac. Surg. 2003, 24, 364–370. [Google Scholar] [CrossRef][Green Version]
- Pantalos, G.M.; Koenig, S.C.; Gillars, K.J.; Giridharan, G.A.; Ewert, D.L. Characterization of an Adult Mock Circulation for Testing Cardiac Support Devices. ASAIO J. 2004, 50, 37–46. [Google Scholar] [CrossRef]
- Patel, S.; Allaire, P.; Wood, G.; Adams, J. Design and Construction of a Mock Human Circulatory System. In Proceedings of the Summer Bioengineering Conference, Sonesta Beach Resort, Key Biscayne, FL, USA, 25–29 June 2003. [Google Scholar]
- Vilchez-Monge, M.; Truque-Barrantes, A.; Ortiz-Leon, G. Design and Construction of a Hydro-Pneumatic Mock Circulation Loop That Emulates the Systemic Circuit of the Circulatory System. In Proceedings of the IEEE 36th Central American and Panama Convention (CONCAPAN XXXVI), San Jose, Costa Rica, 9–11 November 2011. [Google Scholar] [CrossRef]
- Wu, Y.; Allaire, P.E.; Tao, G.; Adams, M.; Liu, Y.; Wood, H.; Olsen, D.B. A Bridge from Short-Term to Long-Term Left Ventricular Assist Device--Experimental Verification of a Physiological Controller. Artif. Organs 2004, 28, 927–932. [Google Scholar] [CrossRef]
- Yoshizawa, M.; Sato, T.; Tanaka, A.; Abe, K.; Takeda, H.; Yambe, T.; Nitta, S.; Nosé, Y. Sensorless Estimation of Pressure Head and Flow of a Continuous Flow Artificial Heart Based on Input Power and Rotational Speed. ASAIO J. 2002, 48, 443–448. [Google Scholar] [CrossRef]
- Timms, D.; Hayne, M.; Tan, A.; Pearcy, M. Evaluation of Left Ventricular Assist Device Performance and Hydraulic Force in a Complete Mock Circulation Loop. Artif. Organs 2005, 29, 573–580. [Google Scholar] [CrossRef]
- Yoshino, M.; Uemura, M.; Takahashi, K.; Watanabe, N.; Hoshi, H.; Ohuchi, K.; Nakamura, M.; Fujita, H.; Sakamoto, T.; Takatani, S. Design and Evaluation of a Single-Pivot Supported Centrifugal Blood Pump. Artif. Organs 2001, 25, 683–687. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Jang, M.; Shin, S.-H. Mock Circulatory System with a Silicon Tube for the Study of Pulse Waves in an Arterial System. J. Korean Phys. Soc. 2014, 65, 1134–1141. [Google Scholar] [CrossRef]
- Fronek, K.; Schmid-Schoenbein, G.; Fung, Y.C. A Noncontact Method for Three-Dimensional Analysis of Vascular Elasticity in Vivo and in Vitro. J. Appl. Physiol. 1976, 40, 634–637. [Google Scholar] [CrossRef]
- Lou, Y.S. Experimental Study of Finite Amplitude Pulsatile Pressure Waves in Elastic Tubes. J. Biomech. 1976, 9, 747–753. [Google Scholar] [CrossRef]
- Horsten, J.B.A.M.; Van Steenhoven, A.A.; Van Dongen, M.E.H. Linear Propagation of Pulsatile Waves in Viscoelastic Tubes. J. Biomech. 1989, 22, 477–484. [Google Scholar] [CrossRef]
- Humphrey, J.D.; Kang, T.; Sakarda, P.; Anjanappa, M. Computer-Aided Vascular Experimentation: A New Electromechanical Test System. Ann. Biomed. Eng. 1993, 21, 33–43. [Google Scholar] [CrossRef]
- Zannoli, R.; Corazza, I.; Branzi, A. Mechanical Simulator of the Cardiovascular System. Phys. Med. 2009, 25, 94–100. [Google Scholar] [CrossRef]
- Feng, J.; Long, Q.; Khir, A.W. Wave Dissipation in Flexible Tubes in the Time Domain: In Vitro Model of Arterial Waves. J. Biomech. 2007, 40, 2130–2138. [Google Scholar] [CrossRef]
- Péry, E.; Blondel, W.C.P.M.; Didelon, J.; Leroux, A.; Guillemin, F. Simultaneous Characterization of Optical and Rheological Properties of Carotid Arteries via Bimodal Spectroscopy: Experimental and Simulation Results. IEEE Trans. Biomed. Eng. 2009, 56, 1267–1276. [Google Scholar] [CrossRef]
- Jang, M.; Lee, M.-W.; Kim, J.U.; Seo, S.-Y.; Shin, S.-H. Development of a Cardiovascular Simulator for Studying Pulse Diagnosis Mechanisms. J. Evid. Based Complement. Altern. Med. 2017, 2017, e6790292. [Google Scholar] [CrossRef]
- Yang, T.-H.; Kim, J.U.; Kim, Y.-M.; Koo, J.-H.; Woo, S.-Y. A New Blood Pulsation Simulator Platform Incorporating Cardiovascular Physiology for Evaluating Radial Pulse Waveform. J. Healthc. Eng. 2019, 2019, 4938063. [Google Scholar] [CrossRef]
- Alastruey, J.; Khir, A.W.; Matthys, K.S.; Segers, P.; Sherwin, S.J.; Verdonck, P.R.; Parker, K.H.; Peiró, J. Pulse Wave Propagation in a Model Human Arterial Network: Assessment of 1-D Visco-Elastic Simulations against in vitro Measurements. J. Biomech. 2011, 44, 2250–2258. [Google Scholar] [CrossRef]
- Anssari-Benam, A.; Korakianitis, T. An Experimental Model to Simulate Arterial Pulsatile Flow: In Vitro Pressure and Pressure Gradient Wave Study. Exp. Mech. 2013, 53, 649–660. [Google Scholar] [CrossRef]
- Balay, G.; Brum, J.; Bia, D.; Armentano, R.L.; Negreira, C.A. Improvement of Artery Radii Determination with Single Ultra Sound Channel Hardware & in Vitro Artificial Heart System. Annu. Int. Conf. IEEE Eng. Med. Biol. Soc. 2010, 2010, 2521–2524. [Google Scholar] [CrossRef]
- Blondel, W.C.; Didelon, J.; Maurice, G.; Carteaux, J.P.; Wang, X.; Stoltz, J.F. Investigation of 3-D Mechanical Properties of Blood Vessels Using a New in Vitro Tests System: Results on Sheep Common Carotid Arteries. IEEE Trans. Biomed. Eng. 2001, 48, 442–451. [Google Scholar] [CrossRef]
- Graf, S.; Gariepy, J.; Massonneau, M.; Armentano, R.L.; Mansour, S.; Barra, J.G.; Simon, A.; Levenson, J. Experimental and Clinical Validation of Arterial Diameter Waveform and Intimal Media Thickness Obtained from B-Mode Ultrasound Image Processing. Ultrasound Med. Biol. 1999, 25, 1353–1363. [Google Scholar] [CrossRef]
- Maryakhina, V.; Kostuganov, A. The Experimental Setup for Human Circulation Modeling. In Proceedings of the International Work-Conference on Bioinformatics and Biomedical Engineering, Granada, Spain, 1 April 2017. [Google Scholar]
- Saito, M.; Ikenaga, Y.; Matsukawa, M.; Watanabe, Y.; Asada, T.; Lagrée, P.-Y. One-Dimensional Model for Propagation of a Pressure Wave in a Model of the Human Arterial Network: Comparison of Theoretical and Experimental Results. J. Biomech. Eng. 2011, 133, 121005. [Google Scholar] [CrossRef]
- Shahmirzadi, D.; Li, R.X.; Konofagou, E.E. Pulse-Wave Propagation in Straight-Geometry Vessels for Stiffness Estimation: Theory, Simulations, Phantoms and In Vitro Findings. J. Biomech. Eng. 2012, 134, 114502–1145026. [Google Scholar] [CrossRef] [PubMed]
- Suarez-Bagnasco, D.; Cymberknop, L.J.; Ballarin, F.M.; Balay, G.; Negreira, C.A.; Abraham, G.; Armentano, R.L. An In Vitro Set Up for the Assessment of Electrospun Nanofibrous Vascular Grafts. IFMBE Proc. 2015, 49, 144–147. [Google Scholar] [CrossRef]
- Ursino, M.; Artioli, E.; Gallerani, M. An Experimental Comparison of Different Methods of Measuring Wave Propagation in Viscoelastic Tubes. J. Biomech. 1994, 27, 979–990. [Google Scholar] [CrossRef]
- Walker, R.D.; Smith, R.E.; Sherriff, S.B.; Wood, R.F. Latex Vessels with Customized Compliance for Use in Arterial Flow Models. Physiol. Meas. 1999, 20, 277–286. [Google Scholar] [CrossRef]
- Werneck, M.M.; Jones, N.B.; Morgon, J. Flexible Hydraulic Simulator for Cardiovascular Studies. Med. Biol. Eng. Comput. 1984, 22, 86–89. [Google Scholar] [CrossRef]
- Von Maltzahn, W.W.; Warriyar, R.G.; Keitzer, W.F. Experimental Measurements of Elastic Properties of Media and Adventitia of Bovine Carotid Arteries. J. Biomech. 1984, 17, 839–847. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Jang, M.; Shin, S.-H. Study on the Depth, Rate, Shape, and Strength of Pulse with Cardiovascular Simulator. J. Evid. Based Complement. Altern. Med. 2017, 2017, e2867191. [Google Scholar] [CrossRef]
- Bia, D.; Armentano, R.L.; Zócalo, Y.; Barmak, W.; Migliaro, E.; Cabrera Fischer, E.I. In Vitro Model to Study Arterial Wall Dynamics through Pressure-Diameter Relationship Analysis. Lat. Am. Appl. Res. 2005, 35, 217–224. [Google Scholar]
- Brant, A.M.; Rodgers, G.J.; Borovetz, H.S. Measurement in Vitro of Pulsatile Arterial Diameter Using a Helium-Neon Laser. J. Appl. Physiol. 1987, 62, 679–683. [Google Scholar] [CrossRef]
- Bertram, C.D.; Pythoud, F.; Stergiopulos, N.; Meister, J.J. Pulse Wave Attenuation Measurement by Linear and Nonlinear Methods in Nonlinearly Elastic Tubes. Med. Eng. Phys. 1999, 21, 155–166. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Jang, M.; Lee, S.; Kang, H.; Shin, S.-H. A Cardiovascular Simulator with Elastic Arterial Tree for Pulse Wave Studies. J. Mech. Med. Biol. 2015, 15, 1540045. [Google Scholar] [CrossRef]
- Vinall, P.E.; Simeone, F.A. Whole Mounted Pressurized In Vitro Model for the Study of Cerebral Arterial Mechanics. Blood Vessels 1987, 24, 51–62. [Google Scholar] [CrossRef]
- Jun, M.-H.; Jeon, Y.J.; Cho, J.-H.; Kim, Y.-M. Pulse Wave Response Characteristics for Thickness and Hardness of the Cover Layer in Pulse Sensors to Measure Radial Artery Pulse. BioMed Eng. OnLine 2018, 17, 118. [Google Scholar] [CrossRef]
- Gardner, R.M. Direct Arterial Pressure Monitoring. Curr. Anaesth. Crit. Care 1990, 1, 239–246. [Google Scholar] [CrossRef]
- Heimann, P.A. Assessment of Catheter-Manometer Systems Used for Invasive Blood Pressure Measurement. Master’s Thesis, University of Cape Town, Cape Town, South Africa, 1989. [Google Scholar]
- Using Manometers to Precisely Measure Pressure, Flow and Level, Meriam Instrument. 1997. Available online: Meriam.com/assets/eng/050-MHB-1.pdf (accessed on 10 June 2022).
- Liptak, B.G. Instrument Engineers’ Handbook, Volume One: Process Measurement and Analysis, 4th ed.; CRC Press: Boca Raton, FL, USA, 2003; pp. 259–374. [Google Scholar]
- Dracos, T.H. Three-Dimensional Velocity and Vorticity Measuring and Image Analysis Techniques; Springer Science & Business Media: Zürich, Switzerland, 2013; pp. 64–67. [Google Scholar]
- Pries, A.R.; Reglin, B.; Secomb, T.W. Remodeling of Blood Vessels: Responses of Diameter and Wall Thickness to Hemodynamic and Metabolic Stimuli. Hypertension 2005, 46, 725–731. [Google Scholar] [CrossRef] [PubMed]
- Fung, Y.C. Biodynamics: Circulation, 2nd ed.; Springer: New York, NY, USA, 1997; pp. 1–21. [Google Scholar]
- Fung, Y.C. Biomechanics: Motion, Flow, Stress, and Growth; Springer: New York, NY, USA, 1990; pp. 155–195. [Google Scholar]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues; Springer Nature: New York, NY, USA, 1993; pp. 66–108. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).